Lectures on Geometry of Monge–Ampère Equations with Maple

Abstract

The main goal of these lectures is to give a brief introduction to application of contact geometry to Monge–Ampère equations.

1 Introduction

The main goal of these lectures is to give a brief introduction to application of contact geometry to Monge–Ampère equations. These equations have the form

$$\begin{aligned} Av_{xx}+2Bv_{xy}+Cv_{yy}+D(v_{xx}v_{yy}-v_{xy}^{2})+E=0, \end{aligned}$$

(2.1)

where A, B, C, D and E are functions on independent variables x, y, unknown function $v=v(x,y)$ and its first derivatives $v_{x},v_{y}$.

Equations of this type arise in various fields. For example, G. Monge considered such equations in connection with the problem of the optimal transportation of sand or soil. This problem was of great importance for the construction of fortifications. A modern modification of this problem has the applications to mathematical economics, especially in taxations problem (Kantorovich–Monge problem [7]).

J.G. Darboux studied and applied such equations in his lectures on general theory of surfaces [3,4,5]. At that time, geometry was a source of various types of equations. For example, the problem of reconstructing a surface with a given Gaussian curvature K(x, y) is equivalent to solving the following equation:

$$\begin{aligned} v_{xx}v_{yy}-v_{xy}^{2}=K(x,y)\left( 1+v_x^2+v_y^2\right) ^2. \end{aligned}$$

(2.2)

Nowadays, the number of sources of Monge–Ampère equations has increased. Equations arise in physics, aerodynamics, hydrodynamics, filtration theory, in models of the development of oil and gas fields, in meteorology and so on. Some of these applications will be discussed. On the other hand, as we shall see, the Monge–Ampère equations themselves generate geometric structures. For instance, some hyperbolic equations can be considered as almost product structures, and elliptic ones as almost complex structures.

The class of equations is rather wide and contains all linear and quasi-linear equations as we can see. On the other hand, it is the minimal class that contains quasi-linear equations and that is closed with respect to contact transformations.

This fact was known to Sophus Lie, who applied contact geometry methods to this kind of equations. In this paper, S. Lie posed some classification problems for equations with respect to contact pseudogroup. In particular, he posed the problem of equivalence of equations to the quasi-linear and linear forms. This problem was solved by V.V. Lychagin and V.N. Rubtsov [20] (see also [21]) in symplectic case and by A.G. Kushner [12] in contact case. Conditions when equations can be transformed to equations with constant coefficients by contact transformations were found by D.V. Tunitskii [23]. The problem of classification for mixed type equations was solved by A.G. Kushner [9,10,11].

In 1978, V.V. Lychagin noted that the classical Monge–Ampère equations and its multi-dimensional analogues admit effective description in terms of differential forms on the space of 1-jets of smooth functions [16]. His idea was fruitful, and it generated a new approach to Monge–Ampère equations.

The lectures has the following structure.

The first lecture is an introduction to geometry of 1-jets space. We define 1-jets of scalar functions, Cartan distribution, contact transformations and contact vector fields on the 1-jets space [8, 15].

In the second lecture, we describe V.V. Lychagin approach and an introduction to geometry of the Monge–Ampère equations. We follow papers [16, 17] and books [15, 18].

The third lecture is devoted to contact transformations of the Monge–Ampère equations. We consider examples of such transformations and apply them to construct multivalued solutions. We illustrate this on the example of equation arising in filtration theory of two immiscible fluids (oil and water, for example) in porous media [1].

In the fourth lecture, we study geometrical structures associated with non-degenerated (i.e. hyperbolic and elliptic) equations. We consider also the class of so-called symplectic equations and give a criterion of their linearization by symplectic transformation [18, 19].

The last, fifth lecture is devoted to tensor invariants of the Monge–Ampère equations. We construct here differential 2-forms that generalize the well-known Laplace invariants. We follow the papers [12, 14].

All calculations in these lectures are illustrated in the program Maple. The Maple files can be found on the website d-omega.org.

2 Lecture 1. Introduction to Contact Geometry

2.1 Bundle of 1-Jets

Let M be an n-dimensional smooth manifold, $C^{\infty }(M)$ be the ring of smooth functions on M and $T^*_aM$ be the cotangent space at the point $a\in M$.

Definition 2.1

A 1-jet $[f]^1_a$ of a function $f\in C^{\infty }(M)$ at the point a is a pair

$$(f(a), df|_a) \in \mathbb {R}\times T^*M.$$

The set of 1-jets at the point $a\in M$ of all functions

$$ J^1_aM :=\left\{ [f]^1_a\, |\, f\in C^\infty (M)\right\} $$

is a vector space with respect to operations of addition and multiplication by real numbers which are pointwise is defined as

$$ [f]^1_a+[g]^1_a :=[f+g]^1_a,\qquad k[f]^1_a :=[kf]^1_a. $$

Denote by

$$ J^1M :=\mathbb {R}\times T^*M $$

the set of 1-jets of all smooth functions $f\in C^\infty (M)$ at all points $a\in M$.

This is a smooth manifold of dimension $2\dim M+1$ with local coordinates $x_1,\,\dots ,\,x_n\,u,\,p_1,\,\dots ,\, p_n$, where $x_1,\,\dots ,\,x_n$ are local coordinates on M, $p_1,\,\dots , p_n$ are the induced coordinates on the cotangent bundle and u is the standard coordinate on $\mathbb {R}$. In other words, the values of these functions at point $[f]^1_k\in J^1M$ are the following:

$$\begin{aligned} x_i([f]^1_a)=x_i(a),\quad u([f]^1_a)=f(a), \quad p_i([f]^1_a)=f_{x_i}(a), \quad i=1,\dots , n. \end{aligned}$$

(2.3)

These coordinates are called canonical.

In what follows we’ll call $J^1M$ the manifold of 1-jets, and the projection

$$ \pi _1: J^1M \longrightarrow M, \quad \text{ where }\quad \pi _1: [f]^1_a \longmapsto a $$

the 1-jet bundle .

Any function $f\in C^\infty (M)$ defines the following map:

$$\begin{aligned} j_1(f):M\longrightarrow J^1M, \end{aligned}$$

(2.4)

where

$$ j_1(f):M\ni a\longmapsto [f]_a^1\in J^1_aM\subset J^1M. $$

The image

$$ \Gamma _f^1:=j_1(f)(M)\subset J^1M, $$

which is a smooth submanifold of $J^1M$, is called the 1-graph of the function f.

Consider the following differential 1-form

$$ \varkappa :=du-p_1dx_1-\cdots -p_ndx_n $$

on the 1-jet space $J^1M$ which we’ll call Cartan form .

It is easy to check that this form does not depend on a choice of canonical coordinates in $J^1M$.

This form allows us to separate submanifolds of the form $\Gamma ^1_f\subset J^1M$ from arbitrary submanifolds of dimension n by observation that

$$ \varkappa |_{\Gamma ^1_f}=0, $$

for any $f\in C^\infty (M)$. Indeed,

$$ \varkappa |_{\Gamma ^1_f}=df-f_{x_1}dx_1-\cdots -f_{x_i}dx_i=0. $$

On the other hand, if a submanifold $N\subset J^1M$ is a graph of section $s:M\longrightarrow J^1M$, i.e. $\pi _1:N\longrightarrow M$ is a diffeomorphism, and

$$ \varkappa |_N=0, $$

then one can easily check that $N=\Gamma ^1_f$ for some smooth function $f\in C^\infty (M)$.

This observation shows that zeroes of the Cartan form (but not the form itself) is important to distinguish 1-graphs from arbitrary submanifolds in $J^1M$.

Denote by $\mathcal {C}$ the 2n-dimensional distribution (Cartan distribution) on $J^1M$ given by zeroes of the Cartan form:

$$ \mathcal {C}: J^1M\ni \theta \longmapsto \mathcal {C}(\theta ):=\ker \varkappa _\theta \subset T_\theta (J^1M). $$

In the dual way, the Cartan distribution can be defined by vector fields tangent to this distribution. Namely, vector fields

$$ \partial _{x_1}+p_1\partial _u,\,\dots ,\, \partial _{x_n}+p_n\partial _u,\, \partial _{p_1},\, \dots , \,\partial _{p_n} $$

give us a local basis in the module of vector fields tangent to $\mathcal {C}$. This module will be denoted by $D(\mathcal {C})$.

Then a submanifold $N\subset J^1M$ is a graph of a smooth function if and only if

• 1. N is an integral submanifold of the Cartan distribution and

• 2. $\pi _1:N\rightarrow M$ is a diffeomorphism.

Remind that a contact structure on an odd-dimensional manifold K, $\dim K=2k+1$, consists of 2k-dimensional distribution P on K such that

$$ \lambda \wedge \left( d \lambda \right) ^k\ne 0 $$

for any differential 1-form $\lambda$, such that locally $P=\ker \,\lambda$.

In our case, we have

$$ \varkappa \wedge \left( d \varkappa \right) ^n\ne 0 $$

and therefore the Cartan distribution defines the contact structure on the manifold of 1-jets $J^1M$.

2.2 Contact Transformations

A transformation $\Phi$ of the space $J^1M$ is called contact, if it preserves the Cartan distribution, i.e.

$$ \Phi _*(\mathcal {C})=\mathcal {C}. $$

In terms of the Cartan form, a transformation $\Phi$ is contact if

$$\begin{aligned} \Phi ^*(\varkappa )=h_\Phi \varkappa \end{aligned}$$

(2.5)

for some function $h_\Phi$, or equivalently

$$ \Phi ^*(\varkappa )\wedge \varkappa =0. $$

Examples of Contact Transformations

• 1. Translations:

  $$ (x_1,x_2,u,p_1,p_2)\longmapsto (x_1+\alpha _1,x_2+\alpha _2,u+\beta ,p_1,p_2), $$

  where $\alpha _{1}$, $\alpha _2$ and $\beta$ are constants.

• 2. The Legendre transformation:

  $$ (x_1,x_2,u,p_1,p_2)\longmapsto (p_1, p_2, u-x_1p_1-x_2p_2, -x_1,-x_2). $$

• 3. Partial Legendre’s transformation:

  $$ (x_{1},x_{2}, u, p_{1}, p_{2})\longmapsto (p_{1},x_{2},u-p_{1}x_{1},-x_{1},p_{2}). $$

Infinitesimal versions of contact transformations are contact vector fields.

A vector field X on $J^1M$ is called contact if its local translation group consists of contact transformations.

It means that

$$\begin{aligned} \Phi _t^*(\varkappa )=\lambda _t\varkappa \end{aligned}$$

(2.6)

for some function $\lambda _t$ on $J^1M$. Here, $\Phi _t$ are shifts along vector field X.

After differentiating both parts of (2.6) by t at $t=0$, we get:

$$ \left. \frac{d}{dt}\right| _{t=0}\left( \Phi _t^*(\varkappa )\right) =\left( \left. \frac{d\lambda }{dt}\right| _{t=0}\right) \varkappa . $$

The left-hand side of the equation is the Lie derivative $L_X(\varkappa )$ of the Cartan form in the direction of the vector field X and therefore, we get

$$ L_X(\varkappa )=h \varkappa , $$

where h is a function on $J^1M$.

Multiplying both parts of the last equation by $\varkappa$, we get:

$$\begin{aligned} L_X(\varkappa )\wedge \varkappa =0. \end{aligned}$$

(2.7)

In canonical coordinates, each contact vector field has the form

$$ X_{f}=-\sum _{i=1}^{n}\frac{\partial f}{\partial p_{i}}\frac{\partial }{\partial x_{i}}+\left( f-\sum _{i=1}^{n}p_{i}\frac{\partial f}{\partial p_{i}}\right) \frac{\partial }{\partial u}+\sum _{i=1}^{n}\left( \frac{\partial f}{\partial x_{i}}+p_i\frac{\partial f}{\partial u}\right) \frac{\partial }{\partial p_{i}} $$

for some function f which is called generating function of the contact vector field. Note that

$$ \varkappa (X_{f})=f. $$

Maple Code: Main Operation on $J^{1}\mathbb {R}^2$

• 1. Load libraries:

  

• 2. Set jet notation, declare coordinates on the manifold M and generate coordinates on the 1-jet space:

  

• 3. Generate the Cartan form:

  

• 4. Define partial Legendre transformation:

  

• 5. Apply this transformation to the Cartan form:

  

• 6. Prolongation of transformations from $J^0M$ to $J^1M$:

  

• 7. Define the contact vector field $X_f$ with generating function $f=p_2$:

  

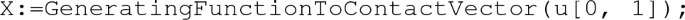
• 8. Prolongation of vector fields from the plane $M=\mathbb {R}^2$ to $J^1M$:

  

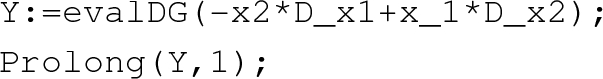
3 Lecture 2. Geometrical Approach to Monge–Ampère Equations

3.1 Non-linear Second-Order Differential Operators

Following [16], any differential n-form $\omega$ on $J^1M$ is associated with the differential operator

$$ \Delta _{\omega }:C^\infty (M)\longrightarrow \Omega ^n(M), $$

which acts in the following way:

$$\begin{aligned} \Delta _{\omega }(v):=j_1(v)^*(\omega ), \end{aligned}$$

(2.8)

where (see formula (2.4))

$$ j_1(v)^*: \Omega ^n(J^1M)\longrightarrow \Omega ^n(M). $$

This construction does not cover all non-linear second-order differential operators, but only a certain subclass of them.

Examples

• 1. The differential 1-form on $J^{1}\mathbb {R}$

  $$ \omega =(1-x^2)dp+\left( \lambda u-xp\right) dx, $$

  where

  $$ \lambda =\dfrac{a^2}{b^2}, $$

  generates the Lissajou differential operator

  $$\begin{aligned} \Delta _{\omega }(y)=\left( (1-x^2)y''- xy'+\dfrac{a^2}{b^2} y\right) dx. \end{aligned}$$

  (2.9)

  Indeed,

  $$\begin{aligned} \Delta _{\omega }(v)&=(1-x^2)d\left( y'\right) +\left( -xy' +\frac{a^2}{b^2}y \right) dx \\&=\left( (1-x^2)y''- xy'+\dfrac{a^2}{b^2} y\right) dx. \end{aligned}$$

• 2. The differential 2-form on $J^{1}\mathbb {R}^2$

  $$ \omega =dp_{1}\wedge dp_{2}$$

  generates the Hesse operator

  $$\begin{aligned} \Delta _{\omega }(v)=\left( \det {\text {*}}{Hess}v\right) dx_{1}\wedge dx_{2}. \end{aligned}$$

  (2.10)

  Indeed,

  $$\begin{aligned} \Delta _{\omega }(v)&=d\left( v_{x_{1}}\right) \wedge d\left( v_{x_{2}}\right) \\&=\left( v_{x_{1}x_{1}}dx_{1}+v_{x_{1}x_{2}}dx_{2}\right) \wedge \left( v_{x_{2}x_{1}}dx_{1}+v_{x_{2}x_{2}}dx_{2}\right) \\&=\left( v_{x_{1}x_{1}}v_{x_{2}x_{2}}-v_{x_{1}x_{2}}^{2}\right) dx_{1}\wedge dx_{2}\\&=\left( \det {\text {*}}{Hess}v\right) dx_{1}\wedge dx_{2}, \end{aligned}$$

  where ${\text {*}}{Hess}v$ is the Hessian of the function v.

• 3. The differential 3-form

  $$\begin{aligned} \omega =p_1dp_1\wedge dx_2\wedge dx_3-dx_1\wedge dp_2\wedge dx_3 - dx_1\wedge dx_2 \wedge dp_3 \end{aligned}$$

  (2.11)

  on $J^{1}\mathbb {R}^{3}$ produces the von Karman differential operator

  $$ \left( v_{x}v_{xx}-v_{yy}-v_{zz}\right) dx\wedge dy\wedge dz, $$

  where $x=x_1,\, y=x_2,\, z=x_3$.

• 4. The differential 2-form

  $$ \omega =dp_{1}\wedge dx_{2}-dp_{2}\wedge dx_{1}$$

  on $J^{1}\mathbb {R}^{2}$ represents the two-dimensional Laplace operator

  $$ \Delta _{\omega }(v)=\left( v_{xx}+v_{yy}\right) dx\wedge dy, $$

  where $x=x_1,\, y=x_2$.

• 5. Two differential 2-forms

  $$\begin{aligned} \omega =dx_{1}\wedge du\,\qquad \text { and }\qquad \varpi =p_{2}dx_{1}\wedge dx_{2} \end{aligned}$$

  (2.12)

  on $J^{1}\mathbb {R}^{2}$ generate the same operator:

  $$\begin{array} [c]{l}\Delta _{\omega }(v)=dx_{1}\wedge \left( v_{x_{1}}dx_{1}+v_{x_{2}}dx_{2}\right) =v_{x_{2}}~dx_{1}\wedge dx_{2},\\ \Delta _{\varpi }(v)=v_{x_{2}}~dx_{1}\wedge dx_{2}. \end{array} $$

• 6. Any differential n-form

  $$\begin{aligned} \omega =\varkappa \wedge \alpha +d\varkappa \wedge \beta \end{aligned}$$

  (2.13)

  on $J^{1}M$, where $\alpha \in \Omega ^{n-1}\left( J^{1}M\right)$, $\beta \in \Omega ^{n-2}\left( J^{1}M\right)$ and $\varkappa$ is the Cartan form, gives the zero operator.

All differential operators $\Delta _{\omega }$ generate differential equations of second order:

$$\begin{aligned} \Delta _{\omega }(v)=0. \end{aligned}$$

(2.14)

For example, operator (2.9) generates Lissajou equation

$$\begin{aligned} (1-x^2)y''- xy'+\dfrac{a^2}{b^2} y=0. \end{aligned}$$

(2.15)

Note that the differential operators $\Delta _{\omega }$ and $\Delta _{h\omega }$ generate the same equation for each non-zero function h.

Equation  (2.14) are called Monge–Ampère equations [16].

The following observation justifies this definition: being written in local canonical contact coordinates on $J^{1}M$, the operators $\Delta _{\omega }$ have the same type of non-linearity as the Monge–Ampère equations.

Namely, the non-linearity involves the determinant of the Hesse matrix and its minors. For instance, in the case $n=2$, for

$$\begin{aligned} \omega =&Edx_{1}\wedge dx_{2}+B\left( dx_{1}\wedge dp_{1}-dx_{2}\wedge dp_{2}\right) +\\&Cdx_{1}\wedge dp_{2}-Adx_{2}\wedge dp_{1}+Ddp_{1}\wedge dp_{2}.\nonumber \end{aligned}$$

(2.16)

we get classical Monge–Ampère equations

$$\begin{aligned} Av_{xx}+2Bv_{xy}+Cv_{yy}+D(v_{xx}v_{yy}-v_{xy}^{2})+E=0. \end{aligned}$$

(2.17)

An advantage of this approach is the reduction of the order of the jet space: we use the simpler space $J^1M$ instead of the space $J^2M$ where Monge–Ampère equations should be ad hoc as second-order partial differential equations [8].

The differential equation which is associated with a differential n-form $\omega$ will be denote by $\mathcal {E}_\omega$:

$$ \mathcal {E}_\omega :=\{\Delta _{\omega }(v)=0\}. $$

The following Maple code generates the corresponding differential operator $\Delta _{\omega }$ for a differential 2-form $\omega$ on $J^{1}\mathbb {R}^2$.

Maple Code: $\omega \longmapsto \Delta _\omega$

Construct the differential operator $\Delta$:

Define a differential 2-form:

Apply the differential operator to this differential form $\omega =dx_1\wedge dp_1-dx_2 \wedge dp_2$:

As a result, we get the differential operator

$$ 2\frac{\partial ^2}{\partial y\partial x}dx\wedge dy. $$

3.2 Multivalued Solutions of Monge–Ampère Equations

Let v be a classical solution of the Monge–Ampère equation $\mathcal {E}_\omega$, i.e. $\Delta _\omega (v)=0$. Then

$$ j_1(v)^*(\omega )=0. $$

It means that the restriction of the differential form $\omega$ to 1-graph of the function v is zero:

$$ \omega \mid _{\Gamma _v^1}=0. $$

An n-dimensional submanifold $L\subset J^1M$ is called a multivalued solution of Monge–Ampère equation if

• 1. L is an integral manifold of the Cartan distribution, i.e. the restriction of the Cartan form to L is zero: $\varkappa \mid _L=0$;

• 2. the restriction of the differential n-form $\omega$ to L is zero, too: $\omega \mid _L=0$.

Examples: Multivalued Solutions

• 1. Parameterized curves

  $$ L=\left\{ x=\sin \,bt,\,\, y=\cos \, at,\,\, p=-\frac{a\sin \,at}{b\,\cos \,bt}\right\} $$

  in the space $J^1\mathbb {R}$ are multivalued solutions of the Lissajou equation

  $$\begin{aligned} (1-x^2)y''- xy'+\dfrac{a^2}{b^2} y=0. \end{aligned}$$

  (2.18)

  Indeed, the restriction of the differential 1-form

  $$ \omega =(1-x^2)dp+\left( \frac{a^2}{b^2}y-xp\right) dx $$

  on the curve L is zero. The projections of these curves on the plane $(x,\,y)$ are well-known Lissajou curves (see Figs. 2.1, 2.2).

• 2. Projections of multivalued solutions of the Monge equation

  $$ v_{xx}v_{yy}-v_{xy}^{2}=\left( 1+v_x^2+v_y^2\right) ^2 $$

  to the space $\mathbb {R}^3$ with coordinates x, y, v are spheres with radius 1 (see Eq. (2.2).

• 3. Projections of multivalued solutions of the equation

  $$\begin{aligned} v_{xx}v_{yy}-v_{xy}^{2}=0 \end{aligned}$$

  (2.19)

  to the space $\mathbb {R}^3$ with coordinates x, y, v are deployable surfaces.

Fig. 2.1

Multivalued solutions of the Lissajou equation for $a=3, b=2$

Fig. 2.2

Multivalued solutions of the Lissajou equation for $a=1, b=\sqrt{2}$ is a curve, everywhere dense in the square (Lissajou’s Black Square)

3.3 Effective Forms

Last two examples (2.12) and (2.13) show that the constructed map

“differential n-forms” $\rightarrow$ “differential operators”

has a huge kernel.

This kernel consists of differential forms that vanish on any integral manifold of the Cartan distribution. All such forms have form (2.13) (see [15]).

Let’s find a submodule of the module $\Omega ^2(J^1M)$ of differential 2-forms such that the map is bijective (${\text {dim}}M=2$).

Differential 2-form $\omega \in \Omega ^2(J^1M)$ is called effective if

• 1. $X_1 \rfloor \omega =0$;

• 2. $\omega \wedge d\varkappa =0$.

Here, $X_1$ is the contact vector field with generating function 1. In canonical coordinates (2.3)

$$ X_1=\partial _u. $$

The first condition means that coordinate representation of $\omega$ does not contain terms $du\wedge *$, and therefore $\omega \ne \varkappa \wedge \alpha$ for some differential 1-form $\alpha$. Second condition means that $\omega \ne \beta d\varkappa$, for a function $\beta$.

The module of effective differential 2-forms will be denoted by $\Omega ^2_\epsilon (J^1M)$.

There is the projection p which maps module $\Omega ^2(J^1M)$ to the module $\Omega ^2(\mathcal {C})$ of “differential forms” on the Cartan distribution.

Namely, define

$$ p: \Omega ^2(J^1M)\longrightarrow \Omega ^2(\mathcal {C}) $$

as follows:

$$ p(\omega ):=\omega -\varkappa \wedge (X_{1} \rfloor \omega ). $$

Here, $\Omega ^2(J^1M)$ and $\Omega ^2(\mathcal {C})$ are modules of 2-forms on the 1-jet manifold $J^1M$ and on the Cartan distribution $\mathcal {C}$ respectively. Remark that

$$ X_{1} \rfloor p(\omega )=0, $$

i.e. 2-form $p(\omega )\in \Omega ^2(\mathcal {C})$.

Theorem 2.1

Any differential 2-form $\omega \in \Omega ^2(\mathcal {C})$ has the unique representation

$$\begin{aligned} \omega =\omega _\epsilon +\beta d\varkappa , \end{aligned}$$

(2.20)

where $\omega _\epsilon \in \Omega ^2_\epsilon (J^1M)$ is an effective 2-form and $\beta$ is a function.

Proof

In our case, the Cartan distribution $\mathcal {C}$ is four-dimensional. The exterior differential of the Cartan form is non-degenerated 2-form on each Cartan subspace, i.e. $d\varkappa _\theta$ is a symplectic structure on $\mathcal {C}(\theta )$ for any $\theta \in J^1M$. Therefore, formula

$$ \omega \wedge d\varkappa =\beta d\varkappa \wedge d\varkappa $$

uniquely defines a function $\beta$. Define now differential form

$$ \omega _\epsilon =\omega -\beta d\varkappa . $$

Since $\omega _\epsilon \wedge d\varkappa =0$, the form $\omega _\epsilon$ is effective.    $\square$

The constructed differential form $\omega _\epsilon$ is called the effective part of the differential form $\omega$.

Define the operator

$$ \mathrm {Eff}: \Omega ^2(J^1M)\longrightarrow \Omega ^2_\epsilon (J^1M),\quad \mathrm {Eff}(\omega ):=(p(\omega ))_\epsilon , $$

which for any differential 2-form $\omega$ on the space $J^1M$ gives its effective part.

It is obvious that differential 2-forms $\omega$ and $\mathrm {Eff}(\omega )$ generate the same Monge–Ampère equations.

In canonical coordinates

$$ d\varkappa =dx_1\wedge dp_1+dx_2\wedge dp_2 $$

and any effective differential 2-form has the following representation:

$$\begin{aligned} \omega =&Edx_{1}\wedge dx_{2}+B\left( dx_{1}\wedge dp_{1}-dx_{2}\wedge dp_{2}\right) +\\&Cdx_{1}\wedge dp_{2}-Adx_{2}\wedge dp_{1}+Ddp_{1}\wedge dp_{2},\nonumber \end{aligned}$$

(2.21)

where A, B, C, D and E are smooth functions on $J^{1}M$. This form corresponds to Eq. (2.17).

The following Maple code contains two procedures which generate effective parts of differential 2-forms.

Maple Code: $\omega \longmapsto \omega _\epsilon$

• 1. Projection of a 2-form to the Cartan distribution:

  

• 2. Calculation of effective parts of a differential 2-forms:

  

4 Lecture 3. Contact Transformations of Monge–Ampère Equations

By the definition, contact transformations preserve the Cartan distribution and multiply the Cartan form $\varkappa$ by a function (see formula (2.5)).

Therefore, contact transformations do not preserve the contact vector field $X_1$ in general. Because of this, the image of an effective differential form can be not effective.

Let $\Phi : J^1M\rightarrow J^1M$ be a contact transformation and $\omega$ be an effective differential 2-form. Then by the image of differential 2-form $\omega$, we shall understand the effective differential form $\mathrm {Eff}(\Phi ^*(\omega ))$.

Two Monge–Ampère equations $\mathcal {E}_\omega$ and $\mathcal {E}_\varpi$ are contact equivalent if there exist a contact transformation $\Phi$ such that $\varpi =h\mathrm {Eff}(\Phi ^*(\omega ))$ for some function h.

Theorem 2.2

If two equations $\mathcal {E}_\omega$ and $\mathcal {E}_\varpi$ are contact equivalent, then their contact transformation maps multivalued solutions of one to multivalued solutions of the other.

Note that, in general, contact transformations do not preserve the class of classical solutions: classical solutions can transform to multivalued solutions and vice versa.

Examples of Linearization of Equations by Contact Transformations

• 1. The von Karman equation

  $$\begin{aligned} v_{x_{1}}v_{x_{1}x_{1}}-v_{x_{2}x_{2}}=0 \end{aligned}$$

  (2.22)

  becomes the linear equation

  $$\begin{aligned} x_{1}v_{x_{2}x_{2}}+v_{x_{1}x_{1}}=0 \end{aligned}$$

  (2.23)

  after Legendre transformation (2.24). The last equation is known as the Triccomi equation.

• 2. Equation

  $$ \det {\text {Hess}}\,v=1 $$

  is generated by the effective differential 2-form

  $$ \omega =dp_{1}\wedge dp_{2}-dx_{1}\wedge dx_{2}. $$

  After the partial Legendre transformation

  $$ \Phi : (x_{1},\;x_{2},\;u,\;p_{1},\;p_{2})\mapsto (p_{1},\;x_{2},\;u-p_{1}x_{1},\;-x_{1},\;p_{2}) $$

  this form becomes

  $$ \omega =dx_{2}\wedge dp_{1}-dx_{1}\wedge dp_{2}, $$

  and corresponds to the Laplace equation

  $$\begin{aligned} v_{x_{1}x_{1}}+v_{x_{2}x_{2}}=0. \end{aligned}$$

• 3. Quasi-linear equation:

  $$ A\left( v_{x},v_{y}\right) v_{xx}+2B\left( v_{x},v_{y}\right) v_{xy}+C\left( v_{x},v_{y}\right) v_{yy}=0. $$

  This equation is represented by the following effective form:

  $$\begin{aligned} \omega =&B\left( p_{1},p_{2}\right) \left( dx_{1}\wedge dp_{1}-dx_{2}\wedge dp_{2}\right) +\,C\left( p_{1},p_{2}\right) dx_{1}\wedge dp_{2}-A\left( p_{1},p_{2}\right) dx_{2}\wedge dp_{1}. \end{aligned}$$

  After the Legendre transformation

  $$\begin{aligned} \Phi :(x_{1},\;x_{2},\;u,\;p_{1},\;p_{2})\mapsto (p_{1},\;p_{2},\;u-p_{1}x_{1}-p_{2}x_{2},\;-x_{1},\;-x_{2},) \end{aligned}$$

  (2.24)

  we get the following effective form

  $$\begin{aligned} \varphi ^{*}(\omega )&=B\left( -x_{1},-x_{2}\right) \left( dx_{1}\wedge dp_{1}-dx_{2}\wedge dp_{2}\right) +\\&-A\left( -x_{1},-x_{2}\right) dx_{1}\wedge dp_{2}+\,C\left( -x_{1},-x_{2}\right) dx_{2}\wedge dp_{1}, \end{aligned}$$

  which corresponds to the linear equation:

  $$ -A\left( -x_{1},-x_{2}\right) v_{x_{2}x_{2}}+2B\left( -x_{1},-x_{2}\right) v_{x_{1}x_{2}}-\,C\left( -x_{1},-x_{2}\right) v_{x_{1}x_{1}}=0. $$

Example

The following equation arises in filtration theory of two immiscible fluids in porous media [1]:

$$\begin{aligned} u_{xy}-u_xu_{yy}=0. \end{aligned}$$

(2.25)

It is used for finding a strategy to control wavefronts in the development of oil fields.

The corresponding differential 2-form is

$$ \omega =2p_1dp_2\wedge dx_1+dx_1\wedge dp_1-dx_2\wedge dp_2, $$

where $x_1=x$, $x_2=y$. Applying the Legendre transformation

$$ \Phi : (x_1, x_2, u, p_1, p_2)\longmapsto (p_1, p_2, u-x_1p_1-x_2p_2, -x_1, -x_2) $$

we get the following differential 2-form:

$$ \Phi ^*(\omega )=2x_1dx_2\wedge dp_1+dx_1\wedge dp_1-dx_2\wedge dp_2. $$

This form corresponds to the linear equation

$$\begin{aligned} u_{x_1x_2}-x_1u_{x_1x_1}=0. \end{aligned}$$

(2.26)

The general solution of the last equation is

$$\begin{aligned} u(x_1, x_2)=e^{-x_2}F_1(x_1e^{x2})+F_2(x_2), \end{aligned}$$

(2.27)

where $F_1$ and $F_2$ are arbitrary functions. Differentiating both sides of (2.27), we get

$$\begin{aligned}&u_{x_1}=F'_1(x_1e^{x2}),\\&u_{x_2}=-e^{-x_2}F_1(x_1e^{x2})-F'_1(x_1e^{x2})x_1 +F'_2(x_2). \end{aligned}$$

Thus, solution (2.27) generate a surface $L \subset J^1M$:

$$\begin{aligned} L: \left\{ \begin{aligned}&u-e^{-x_2}F_1(x_1e^{x2})+F_2(x_2)=0,\\&p_1-F'_1(x_1e^{x2})=0,\\&p_2+e^{-x_2}F_1(x_1e^{x2})+F'_1(x_1e^{x2})x_1-F'_2(x_2)=0. \end{aligned}\right. \end{aligned}$$

Applying the inverse Legendre transformation

$$ \Phi ^{-1}:(x_1, x_2, u, p_1, p_2)\longmapsto (-p_1, -p_2, u-x_1p_1-x_2p_2, x_1, x_2) $$

to L, we get multivalued solutions of equation (2.25) in parametric form (Fig. 2.3):

$$\begin{aligned} \Phi ^{-1}(L): \left\{ \begin{aligned}&u-x_1p_1-x_2p_2-e^{p_2}F_1(-p_1e^{-p_2})+F_2(-p_2)=0,\\&x_1-F_1'(-p_1e^{-p_2})=0,\\&x_2+e^{p_2}F_1(-p_1e^{-p_2})+p_1F'_1(-p_1e^{-p_2})+F'_2(-p_2)=0. \end{aligned}\right. \end{aligned}$$

(2.28)

Fig. 2.3

Projection of the multivalued solution $\mathcal {L}$ to the space x, y, u for $k(a)=a^9-20a^5$ and $r(b)=b^{0.01}$

In order to simplify the last formula, we introduce new parameters

$$ a=-p_1e^{-p_2}, \qquad b=-p_2, $$

and new functions

$$ k(a)=F_1(a), \qquad r(b)=F_2(b). $$

In these notation, multivalued solutions of equation (2.25) takes the form:

$$\begin{aligned} \mathcal {L}: \left\{ \begin{aligned}&x=k'(a),\\&y=e^{-b}(ak'(a)-k(a))-r'(b),\\&u =(b+1)e^{-b}(k(a)-ak'(a))+br'(b)-r(b),\\&p_1 =-ae^{-b},\\&p_2 =-b, \end{aligned}\right. \end{aligned}$$

where k(a) and r(b) are arbitrary functions.

Maple Code: Equation $u_{xy}-u_xu_{yy}=0$

Define coordinates on M:

Construct the differential operator $\Delta$:

Define the differential 2-form $\omega$:

$$ \omega =2p_1dp_2\wedge dx_1+dx_1\wedge dp_1-dx_2\wedge dp_2, $$

The Legendre transformation:

Apply the Legendre transformation to $\omega$:

Construct the differential operator $\Delta _{\omega _1}$:

$$ \left( 2\left( \frac{\partial ^2}{\partial y \partial x}u(x,y)\right) -2x\left( \frac{\partial ^2}{\partial x^2}u(x,y)\right) \right) dx \wedge dy $$

Check solution:

$$ 0 $$

Inverse Legendre transformation:

Apply this transformation to the surface L:

As a result, we get formula (2.28).

Check that $\mathcal {L}$ is a multivalued solution of equation (2.25), i.e. $\omega \mid \mathcal {L}=0$:

$$ 0 $$

Visualization of the multivalued solution $\mathcal {L}$:

5 Lecture 4. Geometrical Structures

5.1 Pfaffians

First of all, we remark that the restriction of the differential 2-form $d\varkappa$ on the Cartan distribution

$$ \Omega =d\varkappa \mid _\mathcal {C} $$

defines a symplectic structure on Cartan space $\mathcal {C}(\theta )\subset T_\theta (J^1M)$.

Using this structure and an effective 2-form $\omega \in \Omega ^2_\epsilon (J^1M)$ we define function ${\text {*}}{Pf}(\omega )$, called Pfaffian, in the following way [20]:

$$\begin{aligned} {\text {*}}{Pf}(\omega )\,\Omega \wedge \Omega =\omega \wedge \omega . \end{aligned}$$

(2.29)

This is a correct construction because $\omega \wedge \omega$ and $\Omega \wedge \Omega$ are 4-forms on the four-dimensional Cartan distribution.

In the case when

$$\begin{aligned} \omega =&Edx_{1}\wedge dx_{2}+B\left( dx_{1}\wedge dp_{1}-dx_{2}\wedge dp_{2}\right) +\\&Cdx_{1}\wedge dp_{2}-Adx_{2}\wedge dp_{1}+Ddp_{1}\wedge dp_{2},\nonumber \end{aligned}$$

(2.30)

we get

$$ {\text {Pf}}(\omega ) =B^{2}+DE-AC. $$

We say that the Monge–Ampère equation $\mathcal {E}_\omega$ is hyperbolic, elliptic or parabolic at a domain $\mathcal {D}\subset J^1M$ if the function ${\text {*}}{Pf}(\omega )$ is negative, positive or zero at each point of $\mathcal {D}$, respectively.

If the Pfaffian changes the sign in some points of $\mathcal {D}$, then the equation $\mathcal {E}_\omega$ is called a mixed type equation (see [10]).

The hyperbolic and elliptic equations are called non-degenerate.

Maple Code: Pfaffian

For example, the Pfaffian of the differential 2-form

$$ \omega =dx_1 \wedge dp_1 - dx_2 \wedge dp_2 $$

which corresponds to wave equation $u_{xy}=0$ is equal to $-1$, and as we know this equation is hyperbolic.

The Pfaffian of the differential 2-form

$$ \omega =dx_1 \wedge dp_2 - dx_2 \wedge dp_1 $$

which corresponds to Laplace equation $u_{xx}+u_{yy}=0$ is equal to 1. Indeed,

$$ -1 $$

$$ 1 $$

5.2 Fields of Endomorphisms

The standard linear algebra allows us to construct a field of endomorphisms

$$ A_\omega :D(\mathcal {C})\longrightarrow D(\mathcal {C}) $$

which is associated with an effective 2-form $\omega$. Here $D(\mathcal {C})$ is the module of vector fields tangent to $\mathcal {C}$.

Namely, the 2-form $\Omega$ is non-degenerated on $\mathcal {C}$ and the operator $A_{\omega }$ is uniquely determined by the following formula [19]:

$$\begin{aligned} A_{\omega }X\rfloor \,~\Omega =X~\rfloor \,\omega \end{aligned}$$

(2.31)

for all vector fields X tangent to $\mathcal {C}$.

Proposition 2.1

Operators $A_{\omega }$ satisfy the following properties:

• 1. $\Omega (A_{\omega }X,X)=0$.

• 2. $\Omega (A_{\omega }X,Y)=\Omega (X,A_{\omega }Y)$.

Proof

• 1. $\Omega (A_{\omega }X,X)=\omega (X,X)=0$.

• 2. $\Omega (A_{\omega }X,Y)=\omega (X,Y)=-\omega (Y,X)=-\Omega (A_{\omega }Y,X)=\Omega (X,A_{\omega }Y)$.

   $\square$

Proposition 2.2

The squares of operators $A_{\omega }$ are scalar and

$$\begin{aligned} A_\omega ^{2}+{\text {*}}{Pf}(\omega )=0. \end{aligned}$$

(2.32)

Proof

First of all

$$A_{\omega }X\rfloor (\omega \wedge \Omega )=(A_{\omega }X\rfloor \omega )\wedge \Omega +\omega \wedge (A_{\omega }X\rfloor \Omega ).$$

Using Proposition 2.1,

$$\begin{aligned} X\rfloor (A_{\omega }X\rfloor (\omega \wedge \Omega ))=&\omega (A_{\omega }X,X)\Omega -(A_{\omega }X\rfloor \omega )\wedge (X\rfloor \Omega )\\&+(X\rfloor \omega )\wedge (A_{\omega }X\rfloor \Omega )+\Omega (A_{\omega }X,X)\omega \\&=\Omega (A_{\omega }^2X,X)\Omega -(A_{\omega }^2X\rfloor \Omega )\wedge (X\rfloor \Omega )\\&+(A_{\omega }X\rfloor \Omega )\wedge (A_{\omega }X\rfloor \Omega )+\Omega (A_{\omega }X,X)\omega \\&=-(A_{\omega }^2X\rfloor \Omega )\wedge (X\rfloor \Omega ). \end{aligned}$$

Since $\omega$ is effective, $\omega \wedge \Omega =0$. Then

$$ (A_{\omega }^2X\rfloor \Omega )\wedge (X\rfloor \Omega )=0, $$

i.e. differential 1-forms $A_{\omega }^2X\rfloor \Omega$ and $X\rfloor \Omega$ are linearly dependent. Therefore the square of the operator $A_{\omega }$ is a scalar: $A_{\omega }^2=\alpha$.

Let $X\in D(\mathcal {C})$ be an arbitrary vector field. Applying the operators $A_{\omega }X\rfloor$ and $X\rfloor$ to both parts of formula (2.29) we get

$$ {\text {*}}{Pf}(\omega )(A_{\omega }X\rfloor \Omega )\wedge (X\rfloor \Omega )=(A_{\omega }X \rfloor \omega )\wedge (X\rfloor \omega )=(\alpha X \rfloor \Omega )\wedge (A_{\omega }X \rfloor \Omega ). $$

Then

$$\begin{aligned} ({\text {*}}{Pf}(\omega )+\alpha )(A_{\omega }X\rfloor \Omega )\wedge (X\rfloor \Omega )=0. \end{aligned}$$

(2.33)

Suppose that $(A_{\omega }X\rfloor \Omega )\wedge (X\rfloor \Omega )=0$. Then the vector fields X and $A_{\omega }X$ are linearly dependent. Since X is an arbitrary vector field we see that the operator $A_{\omega }$ is scalar, i.e. $A_{\omega }X=\lambda X$ for any X. Then

$$ X\rfloor \omega =A_{\omega }X\rfloor \Omega =\lambda X \rfloor \Omega . $$

Therefore $\omega =\lambda \Omega$, which is impossible. So from (2.33), it follows that ${\text {*}}{Pf}(\omega )+\alpha =0$, i.e. $A_\omega ^{2}+{\text {*}}{Pf}(\omega )=0$.    $\square$

Let’s find a coordinate representation of the operator $A_\omega$. Let

$$\begin{aligned} \dfrac{\partial }{\partial x_{1}}+p_{1}\dfrac{\partial }{\partial u},\quad \dfrac{\partial }{\partial x_{2}}+p_{2}\dfrac{\partial }{\partial u},\quad \dfrac{\partial }{\partial p_{1}},\quad \dfrac{\partial }{\partial p_{2}} \end{aligned}$$

(2.34)

be a local basis of the module $D(\mathcal {C})$. Then formula (2.31) gives:

$$\begin{aligned} A_{\omega }=\left\| \begin{array} [c]{rrrr}B &{} -A &{} 0 &{} -D\\ C &{} -B &{} D &{} 0\\ 0 &{} E &{} B &{} C\\ -E &{} 0 &{} -A &{} -B \end{array} \right\| \end{aligned}$$

(2.35)

in this basis.

Maple Code: Operator $A_\omega$

Coordinates on the 1-jet space:

Cartan’s form and its exterior differential:

Define 2-form $\omega$:

Vector fields and 1-forms on Cartan’s distribution:

Checking duality:

Construct an arbitrary vector field on Cartan’s distribution:

$$ V=a\frac{\partial }{\partial x_1}+b\frac{\partial }{\partial x_2}+(bp_2+ap_1)\frac{\partial }{\partial u}+c\frac{\partial }{\partial p_1}+d \frac{\partial }{\partial p_2} $$

General form of $A=A_\omega$. Here $a_{i,j}$ are arbitrary functions:

Action of $A_\omega$ on vector fields:

Equations with respect to $a_{i,j}$:

$$\begin{aligned}&-a_{3, 1},\quad -a_{4, 1}, \quad -1+a_{1, 1}, \quad 2p_1+a_{2, 1},\\&-a_{3, 2},\quad -a_{4, 2}, \quad a_{1, 2}, \quad 1+a_{2, 2},\\&1-a_{3, 3},\quad -a_{4, 3}, \quad a_{1, 3}, \quad a_{2, 3},\\&-2p_1-a_{3, 4},\quad -1-a_{4, 4}, \quad a_{1, 4}, \quad a_{2, 4} \end{aligned}$$

$$\begin{aligned} A_{\omega }=\left\| \begin{array} [c]{cccc}1 &{} 0\, &{} 0 &{} 0\\ -2p_1 &{} -1\, &{} 0 &{} 0\\ 0 &{} 0\, &{} 1 &{} -2p_1\\ 0 &{} 0\, &{} 0 &{} -1 \end{array} \right\| \end{aligned}$$

(2.36)

$$ 1 $$

$$ \left\| \begin{array} [c]{cccc}1 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right\| $$

5.3 Characteristic Distributions

Effective forms $\omega$ and $h\omega$, where h is any non-vanishing function, define the same Monge–Ampère equation. Therefore, for a non-degenerated equation $\mathcal {E}_\omega$ the form $\omega$ can be normed in such a way that $|{\text {*}}{Pf}(\omega )|=1$. It is sufficient to replace $\omega$ by

$$\begin{aligned} \frac{\omega }{\sqrt{|{\text {*}}{Pf}(\omega )|}}. \end{aligned}$$

(2.37)

By (2.32), the hyperbolic equations generate a product structure

$$ A_{\omega ,a}^2=1 $$

and elliptic equations generate a complex structure

$$ A_{\omega ,a}^2=-1 $$

on the Cartan space $\mathcal {C}(a)$ [18].

Therefore, a non-degenerated Monge–Ampère equation generates two two-dimensional (complex—for elliptic case) distributions on $J^1M$, which are eigenspaces of the operator $A_{\omega }$.

These distributions $\mathcal {C}_{+}(a)$ and $\mathcal {C}_{-}(a)$ correspond to the eigenvalues 1 and $-1$ for the hyperbolic equations or to $\iota$ and $-\iota$ for the elliptic ones, respectively. Here $\iota =\sqrt{-1}$.

The distributions $\mathcal {C}_{+}$ and $\mathcal {C}_{-}$ are called characteristic.

The characteristic distributions are real for the hyperbolic equations and complex for the elliptic ones. They are complex conjugate for the elliptic equations.

Proposition 2.3

([18]) 1. The characteristic distributions $\mathcal {C}_{+}$ and $\mathcal {C}_{-}$ are skew orthogonal with respect to the symplectic structure $\Omega$, i.e. $\Omega (X_+, X_-)=0$ for $X_\pm \in D(\mathcal {C}_\pm )$.

2. On each of them, the 2-form $\Omega$ is non-degenerate.

On the other hand, any pair of arbitrary real distributions $\mathcal {C}_{1,0}$ and $\mathcal {C}_{0,1}$ on $J^{1}M$ such that

• 1. $\dim \mathcal {C}_{1,0}=\dim \mathcal {C}_{0,1}=2$;

• 2. $\mathcal {C}=\mathcal {C}_{1,0}\oplus \mathcal {C}_{0,1}$;

• 3. $\mathcal {C}_{1,0}$ and $\mathcal {C}_{0,1}$ are skew-orthogonal with respect to the symplectic structure $\Omega$

determines the operator A. Therefore, a hyperbolic Monge–Ampère equation can be regarded as such pair $\left\{ \mathcal {C}_{1,0}, \mathcal {C}_{0,1}\right\}$ of distributions.

Maple Code: Characteristic Distributions

Calculation of eigenvalues and eigenvectors of the operator $A_\omega$:

Find the vector fields from the Cartan distribution

For example, the characteristic distribution $\mathcal {C}_+$ and $\mathcal {C}_-$ of operator (2.36) are generated by the following vector fields:

$$ \mathcal {C}_+=\left\langle p_1\frac{\partial }{\partial p_1}+\frac{\partial }{\partial p_2},\quad \frac{\partial }{\partial x_2}+p_2\frac{\partial }{\partial u}\right\rangle $$

and

$$ \mathcal {C}_-=\left\langle \frac{\partial }{\partial p_1},\quad p_1\frac{\partial }{\partial x_2}+p_1(p_2-1)\frac{\partial }{\partial u}-\frac{\partial }{\partial x_1}\right\rangle . $$

5.4 Symplectic Monge–Ampère Equations

Monge–Ampère equation (2.17) is called symplectic if its coefficients A, B, C, D, E do not depend on v.

In this case, the structures described above (effective differential forms, the differential operator $\Delta _\omega$, field of endomorphisms $A_\omega$) can be considered on the four-dimensional cotangent bundle $T^*M$ instead of the five-dimensional jet bundle $J^1M$.

Below, we repeat main constructions for the symplectic case.

A smooth function $f\in C^\infty (M)$ defines a section $s_f: M\longrightarrow T^*M$ of the cotangent bundle

$$ \pi : T^*M\longrightarrow M $$

by the following formula:

$$ s_f: a\longmapsto df_a. $$

Let $\omega$ be a differential 2-form on $T^*M$. Define a differential operator

$$ \Delta _\omega : C^\infty (M) \longrightarrow \Omega ^2(M),\quad \Delta _\omega (v):=(s_v)^*(\omega ). $$

Then equation $\Delta _\omega (v)=0$ is a symplectic Monge–Ampère equation.

Let $\Omega$ be the symplectic structure on $T^*M$. In canonical coordinates $x_1, x_2, p_1, p_2$ on $T^*M$

$$ \Omega =dx_1\wedge dp_1 +dx_2 \wedge dp_2. $$

The differential form $\omega$ is said to be effective if

$$ \omega \wedge \Omega =0. $$

Pfaffian ${\text {*}}{Pf}(\omega )$ of the differential 2-form $\omega$ is defined by the following equality:

$$ {\text {*}}{Pf}(\omega )\,\Omega \wedge \Omega =\omega \wedge \omega , $$

and formula

$$ A_{\omega }X\rfloor \,~\Omega =X~\rfloor \,\omega $$

defines the field of endomorphisms $A_{\omega }$ on $T^*M$.

The square of operator $A_{\omega }$ is scalar:

$$ A_\omega ^{2}+{\text {*}}{Pf}(\omega )=0. $$

Consider now the case when equation is non-degenerated, i.e. ${\text {*}}{Pf}(\omega )\ne 0$ on $T^*M$. Then, the operator $A_\omega$ can be normed (see formula (2.37).

For hyperbolic equations we get almost product structure: $A_\omega ^2=1$, and for elliptic ones we get almost complex structure: $A_\omega ^2=-1$.

We say that two symplectic equation $\mathcal {E}_\omega$ and $\mathcal {E}_\varpi$ are symplectically equivalent if there exist a symplectic transformation $\Phi$ such that

$$ \Phi ^*(\omega )=h\varpi $$

for some function h.

The following theorem gives a criterion of symplectic equivalence of non-degenerated Monge–Ampère equation to linear equations with constant coefficients.

Theorem 2.3

([19]) Non-degenerated symplectic Monge–Ampère equation $\mathcal {E}_\omega$ is symplectically equivalent to wave equation

$$\begin{aligned} v_{xx}-v_{yy}=0 \end{aligned}$$

(2.38)

(in hyperbolic case), or to Laplace equation

$$ v_{xx}+v_{yy}=0 $$

(in elliptic case) if and only if the Nijenhuis tensor

$$\begin{aligned} N_{A_\omega }=0, \end{aligned}$$

(2.39)

where $A_\omega$ is the normed operator.

Recall that the Nijenhuis tensor $N_A$ of an operator A is a tensor field of rank (1, 2) given by

$$ N_A(X,Y):=-A^2[X,Y]+A[AX,Y]+A[X,AY]-[AX,AY] $$

for vector fields X and Y.

Condition (2.39) can be written in the following equivalent form [20]:

$$ d\omega =\frac{1}{2}d\left( \ln |{\text {*}}{Pf}(\omega )|\right) \wedge \omega . $$

Maple Code: Symplectic Equation and Nijenhuis Tensor

Below we construct the operator $A_{\omega }$ for non-linear wave equation

$$\begin{aligned} v_{xy}=f(x, y, v_x, v_y). \end{aligned}$$

(2.40)

Then we calculate the Nijenhuis tensor $N_{A_\omega }$ and find conditions under which is this equation symplectically equivalent to the linear wave equation with constant coefficients.

As a result we get

$$ f=F1(x1,x2), $$

where F is an arbitrary function.

So, Eq. (2.40) is symplectically equivalent to wave equation (2.38) if and only if f is a function in $x_1$ and $x_2$ only.

5.5 Splitting of Tangent Spaces

Let us return to the space $J^1M$.

A non-degenerate equation is called regular if the derivatives $\mathcal {C}_\pm ^{(k)}$ $(k=1,2,3)$ of the characteristic distributions are constant rank distributions, too.

Below we consider regular equations only. Then, the first derivatives of the characteristic distributions

$$ \mathcal {C}_{\pm }^{(1)}:=\mathcal {C}_{\pm }+[\mathcal {C}_{\pm },\mathcal {C}_{\pm }] $$

are three-dimensional. Their intersection

$$ l:=\mathcal {C}_{+}^{(1)}\cap \mathcal {C}_{-}^{(1)} $$

is a one-dimensional distribution, which is transversal to Cartan distribution.

Therefore, for hyperbolic equations, the tangent space $T_a(J^1M)$ splits into the direct sum (see Fig. 2.4)

$$\begin{aligned} T_a(J^1M)=\mathcal {C}_+(a)\oplus l(a)\oplus \mathcal {C}_-(a) \end{aligned}$$

(2.41)

at each point $a\in J^1M$ [18].

For elliptic equations, we get a similar decomposition of the complexification of $T_a(J^1M)$. In this case, the distribution l is real, too.

Fig. 2.4

Splitting of the tangent space $T_a(J^1M)$

6 Lecture 5. Tensor Invariants of Monge–Ampère Equations

6.1 Decomposition of de Rham Complex

Let us construct the decomposition of the de Rham complex, which is generated by the splitting of tangent spaces.

Decomposition (2.41) generates a decomposition of the module of exterior s-forms (or its complexification for elliptic equations). Denote the distributions $\mathcal {C}_{+},l$, and $\mathcal {C}_{-}$ by $P_{1},P_{2}$, and $P_{3}$, respectively.

Let $D(J^{1}M)$ be the module of vector fields on $J^{1}M$, and let $D_j$ be the module of vector fields tangent to distribution $P_j$.

Define the following submodules of modules of differential s-forms $\Omega ^s(J^1M)$:

$$\begin{aligned} \Omega _i^s:=\{\alpha \in \Omega ^s(J^1M)|X\rfloor \alpha =0\; \forall \; X\in D_j,\; j\ne i\} \quad (i=1,2,3). \end{aligned}$$

Then we get the following decomposition of the module of differential s-forms on $J^1M$:

$$\begin{aligned} \Omega ^s(J^1M)=\underset{\left| \mathbf {k}\right| =s}{{\displaystyle \bigoplus } }\Omega ^{\mathbf {k}}, \end{aligned}$$

(2.42)

where $\mathbf {k=}(k_{1},k_2,k_{3})$ is a multi-index, $k_{i}\in \left\{ 0,1,\ldots ,\dim P_{i}\right\}$,

$$\vert \mathbf {k}\vert =k_1+k_2+k_3,$$

and

$$\begin{aligned} \Omega ^{\mathbf {k}}:=\left\{ \sum _{j_{1}+j_{2}+j_{3}=|\mathbf {k}|}\alpha _{j_{1}}\wedge \alpha _{j_{2}}\wedge \alpha _{j_{3}}\text{, } \text{ where } \alpha _{j_{i}} \in \Omega ^{k_{i}}_i\right\} \subset \bigotimes _{i=1}^{3}\Omega ^{k_i}_i. \end{aligned}$$

Three first terms of the decomposition are presented in the diagram (see Fig. 2.5).

The exterior differential also splits into the direct sum

$$\begin{aligned} d=\underset{\left| \mathbf {t}\right| =1}{{\displaystyle \bigoplus }}d_{\mathbf {t}}, \end{aligned}$$

where

$$d_\mathbf {t}:\Omega ^{\mathbf {k}}\rightarrow \Omega ^\mathbf {k+t}.$$

Fig. 2.5

Decomposition of de Rham complex

Theorem 2.4

([12])   If the multi-index $\mathbf {t}$ contains one negative component and this component is $-1$, then the operator $d_{\mathbf {t}}$ is a $C^\infty (J^1M)$-homomorphism, i.e.,

$$\begin{aligned} d_{\mathbf {t}}(f\alpha ) =fd_{\mathbf {t}}\alpha \end{aligned}$$

(2.43)

for any function f and any differential form $\alpha \in \Omega ^\mathbf {k}$.

Due to this theorem, we have the seven homomorphisms, and three of them are zeroes. The non-trivial homomorphisms are the following:

$$ d_{2,-1,0},\quad d_{0,-1,2},\quad d_{-1,1,1}\quad \text{ and }\quad d_{1,1,-1}. $$

6.2 Tensor Invariants

Consider a case

$$ \mathbf {t}=\mathbf {1}_{j}+\mathbf {1}_{k}-\mathbf {1}_{s}. $$

Then the differential $d_{\mathbf {t}}$ is a $C^\infty (J^1M)$-homomorphism. Note that

$$ d_{\mathbf {1}_{j}+\mathbf {1}_{k}-\mathbf {1}_{s}}:\Omega ^{\mathbf {1}_{q}}\rightarrow 0, $$

if $q\ne s$. Then, the only non-trivial of $d_{\mathbf {1}_{j}+\mathbf {1}_{k}-\mathbf {1}_{s}}$ is the restriction to the module $\Omega ^{\mathbf {1}_{s}}$:

$$ d_{\mathbf {1}_{j}+\mathbf {1}_{k}-\mathbf {1}_{s}}:\Omega ^{\mathbf {1}_{s}}\rightarrow \Omega ^{\mathbf {1}_{j}}\wedge \Omega ^{\mathbf {1}_{k}}. $$

Therefore, the homomorphism $d_{\mathbf {1}_{j}+\mathbf {1}_{k}-\mathbf {1}_{s}}$ defines a tensor field of the type (2,1). This tensor field we denote by $\tau _{\mathbf {1}_{j}+\mathbf {1}_{k}-\mathbf {1}_{s}}$:

$$ \tau _{\mathbf {1}_{j}+\mathbf {1}_{k}-\mathbf {1}_{s}}\in \Omega ^{\mathbf {1}_{j}}\wedge \Omega ^{\mathbf {1}_{k}}\otimes D_s. $$

A unique non-trivial component of this tensor field is its restriction to $\Omega ^{\mathbf {1}_{s}}$. Note that

$$ \tau _{\mathbf {1}_{j}+\mathbf {1}_{k}-\mathbf {1}_{s}}:\Omega ^{\mathbf {1}_{s}}\rightarrow \Omega ^{\mathbf {1}_{j}}\wedge \Omega ^{\mathbf {1}_{k}} $$

coincides with $d_{\mathbf {1}_{j}+\mathbf {1}_{k}-\mathbf {1}_{s}}$.

Tensor fields $\tau _{\mathbf {1}_{j}+\mathbf {1}_{k}-\mathbf {1}_{s}}$ are differential invariants of Monge–Ampère equations. So, we get four tensors of (2,1)-type [12]:

$$\begin{aligned} \tau _{2,-1,0},\quad \tau _{0,-1,2},\quad \tau _{-1,1,1}\quad \text{ and }\quad \tau _{1,1,-1}. \end{aligned}$$

(2.44)

Maple Code: Tensor Invariants

Below, we present a program for calculating the tensor $\tau _{-1, 1, 1}$. The remaining tensors can be found similarly after a small adjustment of the program. In this program, we omit the calculation of the characteristic distributions. They must be calculated in advance (see “Maple Code: Operator $A_\omega$” and “Maple Code: Characteristic distributions”).

Construct the distribution l (transversal to the Cartan distribution). We are looking for l as an intersection of derivatives of the characteristic distributions $C_-^{(1)}$ and $C_+^{(1)}$. This intersection is one-dimensional and it is generated by the vector field Z which we are looking for.

Basis of the module of vector fields on $J^1M$ and dual basis:

Decomposition of de Rham complex. Bases of $\Omega ^1(J^1M)$ and $\Omega ^2(J^1M)$:

List of elements of the basis of $\Omega ^2$:

Construct the tensor $\tau _{-1, 1, 1}$:

Arbitrary differential 2-form:

Arbitrary 2-form from $\Omega ^{1, 0, 0}$:

Projection of a differential 2-form to $\Omega ^{0, 1, 1}$:

Example: Hunter–Saxton Equation

Consider the Hunter–Saxton equation

$$\begin{aligned} v_{tx}=vv_{xx}+\kappa v_{x}^{2}, \end{aligned}$$

(2.45)

where $\kappa$ is a constant. This equation is hyperbolic, and it has applications in the theory of liquid crystals [6].

The corresponding effective differential 2-form and the operator $A_\omega$ are the following:

$$ \omega =2udq_2\wedge dp_1+dq_1\wedge dp_1-dq_2\wedge dp_2-2\kappa p_1^2dq_1\wedge dq_2 $$

and

$$ A_{\omega }=\left\| \begin{array} [c]{cccc}1 &{} 2u &{} 0 &{} 0\\ 0 &{} -1 &{} 0 &{} 0\\ 0 &{} -2\kappa p_{1}^{2} &{} 1 &{} 0\\ 2\kappa p_{1}^{2} &{} 0 &{} 2u &{} -1 \end{array} \right\| . $$

Let’s take the following base in the module of vector fields on $J^1M$:

$$\begin{aligned} X_{1}&=\dfrac{\partial }{\partial q_{1}}{\,+\,p_{1}\dfrac{\partial }{\partial u}+\,{\kappa p_{1}^{2}\dfrac{\partial }{\partial p_{2}},}}\\ X_{2}&=\dfrac{\partial }{\partial p_{1}}{\,+\,u}\dfrac{\partial }{\partial p_{2}},\\ Z&=\dfrac{\partial }{\partial u}{\,+\,}\left( {2\text { }{\kappa -1}}\right) p_{1}{\dfrac{\partial }{\partial p_{2}},}\\ Y_{1}&=\dfrac{\partial }{\partial q_{2}}{\,+\,{\kappa }p_{1}^{2}\dfrac{\partial }{\partial p_{1}}\,-\,u\dfrac{\partial }{\partial q_{1}}+\left( p_{2}-up_{1}\right) \dfrac{\partial }{\partial u}},\\ Y_{2}&=\dfrac{\partial }{\partial p_{2}}. \end{aligned}$$

The dual basis of the module of differential 1-forms is

$$\begin{aligned} \alpha _{1}&=dq_{1}+udq_{2},\\ \alpha _{2}&=dp_{1}-\kappa p_{1}^{2}dq_{2},\\ \theta&=du-p_{1}dq_{1}-p_{2}dq_{2},\\ \beta _{1}&=dq_{2},\\ \beta _{2}&={dp_{2}+}\left( 1-{2\kappa }\right) {p}_{1}{du+\,}\left( {\kappa -}1\right) {p_{1}^{2}{dq{_{1}}+\,}}\left( {2\kappa -1}\right) {p_{1}p_{2}{dq{_{2}}}-udp_{1}}. \end{aligned}$$

The vector fields $X_1,X_2$ and $Y_1,Y_2$ form bases in the modules $D(\mathcal {C}_+)$ and $D(\mathcal {C}_-)$ respectively. Tensor invariants of Eq. (2.45) have the form

$$\begin{aligned} \tau _{-1,1,1}&=-\left( p_{1}dq_{1}\wedge dq_{2}+dq_{2}\wedge du\right) \otimes \left( \dfrac{\partial }{\partial q_{1}}{\,+\,p_{1}\dfrac{\partial }{\partial u}+\,{\kappa p_{1}^{2}\dfrac{\partial }{\partial p_{2}}}}\right) ,\\ \tau _{1,1,-1}&=2(\,\kappa -1)\,\left( \kappa p_{1}^{3}dq_{1}\wedge dq_{2}+\kappa p_{1}^{2}dq_{2}\wedge du\right. -\\&\left. \,dp_{1}\wedge \ du\,-\,p_{1}dq_{1}\wedge dp_{1}-\,p_{2}dq_{2}\wedge dp_{1}\right) \otimes \dfrac{\partial }{\partial p_{2}},\\ \tau _{2,-1,0}&=\left( dq_{1}\wedge dp_{1}-\kappa p_{1}^{2}dq_{1}\wedge dq_{2}+udq_{2}\wedge dp_{1}\right) \otimes \\&\left( \dfrac{\partial }{\partial u}{\,+\,}\left( {2\text { }{\kappa -1}}\right) p_{1}{\dfrac{\partial }{\partial p_{2}}}\right) , \\ \tau _{0,-1,2}&=\left( dq_{2}\wedge dp_{2}+\left( 1-2\kappa \right) p_{1}dq_{2}\wedge du+\left( 1-\kappa \right) p_{1}^{2}dq_{1}\wedge dq_{2}-udq_{2}\wedge dp_{1}\right) \otimes \\&\left( \dfrac{\partial }{\partial u}{\,+\,}\left( {2\text { }{\kappa -1}}\right) p_{1}{\dfrac{\partial }{\partial p_{2}}}\right) . \end{aligned}$$

6.3 The Laplace Forms

Define bracket $\left\langle \alpha \otimes X,\beta \otimes Y\right\rangle$ for decomposable tensors $\alpha \otimes X$ and $\beta \otimes Y$ of types (2,1) as follows [12]:

$$ \left\langle \alpha \otimes X,\,\beta \otimes Y\right\rangle =\left( Y\rfloor \alpha \right) \wedge \left( X\rfloor \beta \right) . $$

For non-decomposable tensors the bracket is defined by linearity.

Define two differential 2-forms $\lambda _{-}$ and $\lambda _{+}$ from the module $\Omega ^{1,0,1}$ as “wedge contractions” of the tensor fields:

$$\begin{aligned} \lambda _+:=\left\langle \tau _{0,-1,2},\, \tau _{1,1,-1}\right\rangle ,\qquad \lambda _-:=\left\langle \tau _{2,-1,0},\,\tau _{-1,1,1}\right\rangle . \end{aligned}$$

(2.46)

Then tensors (2.46) are called Laplace forms of Monge–Ampère equations $\mathcal {E}_\omega$.

Example: Laplace Form for Linear Equations

For linear hyperbolic equation

$$\begin{aligned} v_{xy}=a(x,y)v_x+b(x,y)v_y +c(x,y)v+g(x,y), \end{aligned}$$

(2.47)

the Laplace forms are

$$\begin{aligned} \lambda _-=kdx\wedge dy \quad \text{ and } \quad \lambda _+=-hdx\wedge dy, \end{aligned}$$

(2.48)

where

$$\begin{aligned} k=ab+c-b_y \qquad \qquad h=ab+c-a_x \end{aligned}$$

(2.49)

are the classical Laplace invariants. This observation justifies our definition.

For linear elliptic equations

$$\begin{aligned} v_{xx}+v_{yy}=a(x,y)v_x+b(x,y)v_y +c(x,y)v+g(x,y), \end{aligned}$$

(2.50)

Laplace forms generalize Cotton invariants [2].

We emphasize that the classical Laplace invariants (2.49) of Eq. (2.50) are not absolute invariants even with respect to transformations

$$\begin{aligned} \phi :(x,\,y,\,v)\mapsto (X(x),\, Y(y),\, A(x,y)v), \qquad A(x,y)\ne 0 \end{aligned}$$

(2.51)

in contrast to forms $\lambda _\pm$, which are contact invariants.

Example: Laplace Forms for Hunter–Saxton Equation

The Laplace forms for the Hunter–Saxton equation (2.45) are

$$ \lambda _-=-dq_{2}\wedge dp_{1},\quad \lambda _+=2\left( 1-\kappa \right) dq_{2}\wedge dp_{1}. $$

6.4 Contact Linearization of the Monge–Ampère Equations

It is well known that if the classical Lagrange invariants h and k of a linear hyperbolic equation is zero, then the equation can be reduced to the wave equation (see [22], for example).

Similar statement is true for the Monge–Ampère equations [14]:

Theorem 2.5

A hyperbolic Monge–Ampère equation is locally contact equivalent to the wave equation

$$v_{xy}=0$$

if and only if its Laplace invariants are zero: $\lambda _+=\lambda _-=0$.

Corollary 2.1

The equation

$$ v_{xy}=f\left( x,y,v,v_{x},v_{y}\right) $$

is locally contact equivalent to the wave equation $v_{xy}=0$ if and only if the function f has the following form:

$$ f=\varphi _y v_x+\varphi _x v_y +(\varphi _v+\Phi _v)v_xv_y+R, $$

where the function $R=R(x,y,v)$ satisfies to the following ordinary linear differential equation:

$$ R_v=(\varphi _v+\Phi _v)R+\varphi _{xy}-\varphi _x \varphi _y. $$

Solving this equation we get

$$ R=e^{\varphi +\Phi }\left( \int (\varphi _{xy}-\varphi _x \varphi _y)e^{-\varphi -\Phi }dv +g \right) , $$

where $\varphi =\varphi (x,y,v)$, $\Phi =\Phi (v)$, and $g=g(x,y)$ are arbitrary functions.

The general problem of linearization of non-degenerated Monge–Ampère equations with respect to the contact transformations was solved in [13].