CP and Hybrid Models for Two-Stage Batching and Scheduling

Abstract

Batch scheduling is a common problem faced in industrial scheduling when groups of related jobs must be processed consecutively or simultaneously on the same resource. Motivated by the composites manufacturing industry, we present a complex batch scheduling problem combining two-stage bin packing with hybrid flowshop scheduling. We propose five solution approaches: a constraint programming model, a three-phase logic-based Benders decomposition model, an earliest due date heuristic, and two hybrid heuristic/constraint programming approaches. We then computationally test these approaches on generated problem instances modelled on real-world instances. Numeric results show that the heuristic approaches perform as well as or better than the exact models, especially on large instances. The relative success of a simple heuristic suggests that such problems pose an interesting challenge for further research in mathematical and constraint programming.

1 Introduction

Batch scheduling arises when it is desirable that a set of jobs that share common characteristics are processed together either consecutively or simultaneously on the same resource. Many motivating examples for batch scheduling come from semiconductor manufacturing, where batching can be modelled as a one-stage bin packing problem [12]. In contrast, we study a two-stage batching and scheduling problem motivated by composites manufacturing.

In the first stage, called layup, multiple parts are created by layering alternating sheets of raw materials and epoxy resin in a mould tool. The mould tool with its sheets of materials is then cured in the second stage by a high-temperature and pressure autoclave oven. The extreme conditions of the autoclave compress and heat the material sheets to create parts made of a new composite material. The parts are then delivered to downstream machines for further processing. Because of the high expense incurred by the autoclave stage, it is desirable to group multiple tools and cure them together as an autoclave batch. This hierarchical two-stage process requires parts, hereby referred to as jobs, to be batched onto mould tools and then the tools themselves to be batched in the autoclave.

The one-stage bin packing and scheduling problem, as appears in semiconductor production, is well-studied for both exact [3, 10] and heuristic [11, 14] methods. Existing literature on scheduling for composites manufacturing [1, 7] does not consider batching jobs onto tools, and hence is also one-stage. The presence of tool batches changes the batching aspect into a Two-Stage Bin Packing Problem [5]. In addition, the two-stage scheduling aspect of this problem is a Two-Stage Hybrid Flow Shop Scheduling Problem [6]. The actual composites manufacturing process is complex and multi-layered; in this paper, we study an abstraction that captures its core complexities. We denote this abstracted problem as the Two-Stage Bin Packing and Hybrid Flow Shop Scheduling Problem (2BPHFSP), and formally define it in the next section.

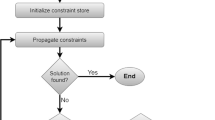
While our motivation comes from an industrial problem, and we will use the terms of composite manufacturing in our problem description, the problem we study abstracts away the application-specific details. Our goal is to investigate the core complexities of the hybridization of hierarchical bin packing with scheduling. Figure 1 provides an overview of the 2BPHFSP.

Fig. 1.

Overview of the flow through the 2BPHFSP.

2 Problem Definition

In the layup stage, jobs are grouped onto mould tools. Each tool has a one-dimensional capacity that cannot be exceeded. We will refer to these groups of jobs on tools as tool batches. Each job has a layup processing time; as the jobs are laid up sequentially, the processing time to assemble a tool batch is the sum of its job processing times. The layup stage is thus an example of the Family Batch Scheduling model [13]. There are multiple unary capacity machines at stage 1; the process to form a tool batch requires one such machine.

After a tool batch is created in stage 1, it is cured in an autoclave in stage 2. Autoclaves are capable of curing more than one tool at a time, so multiple tool batches can be aggregated into an autoclave batch. Autoclaves are constant-capacity and identical, therefore, all autoclave batches have the same capacity and the sum of tool volumes within each autoclave batch cannot exceed that capacity. Similar to stage 1, there are multiple parallel identical autoclave machines; each machine is capable of processing one autoclave batch at a time. However, each autoclave batch is processed for the same length of time regardless of the contained tool batches. Therefore, autoclave batches fall under the Batching Machines model [13]. Lastly, there is an upper limit on the time a laid-up tool batch can wait before entering an autoclave due to the epoxy that is layered between the material sheets. We will refer to this time limit as the restricted waiting time.

Now, let us formally present the parameters that define the 2BPHFSP. We are given a set of jobs $\mathcal {J}^{}$, a set of empty tool batches $\mathcal {B}^{1}$, and a set of empty autoclave batches $\mathcal {B}^{2}$. There exists three sets of resources: an unlimited set of tools $\mathcal {T}$, a set of unary-capacity stage 1 machines $\mathcal {M}^1$, and a set of single-batch-capacity stage 2 machines $\mathcal {M}^2$. Each job $j \in {\mathcal {J}^{}}$ is associated with a one-dimensional volume parameter $s_j$, a due date $d_j$, and a layup processing time $p_j$, and each tool $t \in \mathcal {T}$ is associated with a one-dimensional volume parameter $v_t$. The volume of a tool batch $k \in {\mathcal {B}^{1}}$ is therefore the volume of its assigned tool. Each job $j \in \mathcal {J}^{}$ needs to be assigned to a tool batch $k \in {\mathcal {B}^{1}}$, and each tool batch $k \in {\mathcal {B}^{1}}$ needs to be assigned to an autoclave batch $i \in {\mathcal {B}^{2}}$. Each tool batch $k \in {\mathcal {B}^{1}}$ is scheduled on one machine from $\mathcal {M}^1$ for a length of time equal to $\sum _{j \in k} p_j$, and each autoclave batch is scheduled on one machine from $\mathcal {M}^2$ for a length of time equal to $P^2$. There are precedence constraints and a restricted waiting time between the end of tool batches and the start of their assigned autoclave batches.

The upper bound on the number of tool batches and autoclave batches is the number of jobs (i.e. each job assigned to its own tool batch and each tool batch assigned to its own autoclave batch). Thus, we create $|{\mathcal {J}^{}}|$ empty batches in $\mathcal {B}^{1}$ and $\mathcal {B}^{2}$. However, we almost always find solutions that use fewer batches, so we denote any non-empty batch as open.

The objective of the 2BPHFSP is to minimize a weighted sum of the number of open autoclave batches and job tardiness. We minimize the number of open autoclave batches to decrease autoclave operational costs and we minimize job tardiness to ensure parts are delivered to downstream machines on time.

3 Mathematical Programming Approaches

We developed two mathematical programming approaches to solve the 2BPHFSP, a monolithic constraint programming (CP) and a hybrid CP/mixed integer programming (MIP) logic-based Benders decomposition (LBBD).¹

3.1 Constraint Programming

This formulation uses two sets of interval decision variables for bin packing and two sets of interval decision variables for scheduling. The variables and parameters are shown in Table 1.

Table 1. CP model variables and parameters.

The first set of bin packing variables are optional two-indexed interval variables, $x_{j, k}$. We assign job j to a tool batch k by enforcing one variable from $\{x_{j, k}; k \in {\mathcal {B}^{1}}\}$ to be present for each job j. The same concept is applied to the second set of bin packing variables, $y_{k, i}$, where each present variable indicates tool batch k is assigned to autoclave batch i. We use two sets of single-index interval variables for scheduling batches on the horizon $\mathcal {H}$, $\gamma _k$ for tool batches and $\sigma _i$ for autoclave batches. We also defined a set of variables $t_k$ that assigns tool batch k to a specific tool so we can calculate the volume of k, $\tau _k$.

We present this model in two sections, focusing on bin packing and scheduling, respectively.

$$\begin{aligned} \text {min} \quad&\beta \sum _{i \in {\mathcal {B}^{2}}} \texttt {presenceOf}(\sigma _i) + \sum _{j \in {\mathcal {J}^{}}} \alpha _j l_j&\end{aligned}$$

(1)

$$\begin{aligned} \text {s.t.} \quad&\sum _{k \in {\mathcal {B}^{1}}} \texttt {presenceOf}(x_{j, k}) = 1&\forall j \in {\mathcal {J}^{}}\end{aligned}$$

(2)

$$\begin{aligned}&\sum _{i \in {\mathcal {B}^{2}}} \texttt {presenceOf}(y_{k, i}) = \texttt {presenceOf}(\gamma _k)&\forall k \in {\mathcal {B}^{1}}\end{aligned}$$

(3)

$$\begin{aligned}&\texttt {presenceOf}(\gamma _k) \ge \texttt {presenceOf}(\gamma _{k + 1})&\forall k \in \{0, ..., |{\mathcal {B}^{1}}| - 1\}\end{aligned}$$

(4)

$$\begin{aligned}&\texttt {presenceOf}(\sigma _i) \ge \texttt {presenceOf}(\sigma _{i + 1})&\forall i \in \{0, ..., |{\mathcal {B}^{2}}| - 1\}\end{aligned}$$

(5)

$$\begin{aligned}&\tau _k = \texttt {element}(\{v_t; t \in \mathcal {T}\}, t_k)&\forall k \in {\mathcal {B}^{1}}\end{aligned}$$

(6)

$$\begin{aligned}&\sum _{j \in {\mathcal {J}^{}}} s_j \times \texttt {presenceOf}(x_{j, k}) \le \tau _k&\forall k \in {\mathcal {B}^{1}}\end{aligned}$$

(7)

$$\begin{aligned}&\sum _{k \in {\mathcal {B}^{1}}} \tau _k \times \texttt {presenceOf}(y_{k, i}) \le V^2&\forall i \in {\mathcal {B}^{2}} \\&{t_k \in \{0, ...\mathcal {T}\} \text {; } \tau _k \in \{0, ...V^1\}}\nonumber \end{aligned}$$

(8)

Constraint (2) assigns each job to one tool batch. Constraint (3) assigns each open tool batch to one autoclave batch. Constraints (4) and (5) enforce that batches are opened in order of index, to reduce symmetry. Constraint (6) is an element constraint that assigns the tool capacity associated with tool $t_k \in \mathcal {T}$ to $\tau _k$.² Constraint (7) makes sure the sum of job volumes in each tool batch is less than its tool volume and constraint (8) makes sure the sum of tool volumes in each autoclave batch is less than the autoclave capacity.

The standard global pack constraint does not allow the size of an item to be variable, and therefore cannot be used for two-stage bin packing. Thus, we choose to use interval variables for the packing stage to easily connect them with the corresponding scheduling variables via existing global constraints.

Next, we present the scheduling constraints.

$$\begin{aligned}&\texttt {sizeOf}(x_{j, k}) = p_j&\forall j \in {\mathcal {J}^{}} \quad \forall k \in {\mathcal {B}^{1}}\end{aligned}$$

(9)

$$\begin{aligned}&\texttt {span}\left( \gamma _k, \{x_{j, k}; j \in {\mathcal {J}^{}}\}\right\rangle )&\forall k \in {\mathcal {B}^{1}}\end{aligned}$$

(10)

$$\begin{aligned}&\texttt {sizeOf}(\gamma _k) = \sum _{j \in {\mathcal {J}^{}}} p_j \times \texttt {presenceOf}(x_{j, k})&\forall k \in {\mathcal {B}^{1}}\end{aligned}$$

(11)

$$\begin{aligned}&\texttt {sizeOf}(y_{k, i}) = P^2&\forall k \in {\mathcal {B}^{1}} \quad \forall i \in {\mathcal {B}^{2}}\end{aligned}$$

(12)

$$\begin{aligned}&\texttt {synchronize}(\sigma _i, \{y_{k, i}; i \in {\mathcal {B}^{2}}\})&\forall i \in {\mathcal {B}^{2}}\end{aligned}$$

(13)

$$\begin{aligned}&\texttt {alwaysIn}\left( \sum _{k \in {\mathcal {B}^{1}}} \texttt {pulse}(\gamma _k, 1), 0, |\mathcal {H}|, 0, C^1\right)&\end{aligned}$$

(14)

$$\begin{aligned}&\texttt {alwaysIn}\left( \sum _{i \in {\mathcal {B}^{2}}} \texttt {pulse}(\sigma _i, 1), 0, |\mathcal {H}|, 0, C^2\right)&\end{aligned}$$

(15)

$$\begin{aligned}&\texttt {endBeforeStart}(\gamma _k, y_{k, i})&\forall k \in {\mathcal {B}^{1}} \quad \forall i \in {\mathcal {B}^{2}}\end{aligned}$$

(16)

$$\begin{aligned}&\texttt {startBeforeEnd}(y_{k, i}, \gamma _k, -W)&\forall k \in {\mathcal {B}^{1}} \quad \forall i \in {\mathcal {B}^{2}}\end{aligned}$$

(17)

$$\begin{aligned}&l_j \ge \text {endOf}(\sigma _i) - d_j&\forall j \in {\mathcal {J}^{} } | \text { } j \text { assigned to } i\\&l_j \in \{0, ...|\mathcal {H}|\}&\nonumber \end{aligned}$$

(18)

Constraint (9) sets the processing time of each job. Constraints (10) and (11) make sure jobs in a tool batch are processed sequentially without overlapping. The actual sequence of jobs in a tool batch does not matter because their processing times are not sequence-dependent and jobs cannot leave the first stage until the entire tool batch is processed. Thus, a span constraint is sufficient. Constraint (12) sets the processing time of each tool batch. Constraint (13) makes sure all tool batches in the same autoclave batch are processed simultaneously. Constraints (14) and (15) enforce that the total number of tool batches or autoclave batches processed at one time is at most the respective stage’s capacity. Constraint (16) says that each tool batch must finish processing before its associated autoclave batch can begin processing. Constraint (17) restricts the waiting time between tool batches and their associated autoclave batches. Constraint (18) defines job tardiness.

3.2 Logic-Based Benders Decomposition

As the 2BPHFSP is clearly composed of packing and scheduling problems, we are motivated to investigate a decomposition approach. Thus, in this section, we present a three-stage decomposition, shown in Fig. 2, that separates the 2BPHFSP into a one-stage bin packing problem, a pattern bin packing problem, and a two-stage hybrid flow shop scheduling problem, denoted as the m-master problem, the m-subproblem, and the subproblem, respectively. Each of these problems is much smaller and simpler to solve than the 2BPHFSP in its entirety, so a decomposition approach may scale better than a monolithic approach.

Fig. 2.

Decomposition flow between problems, each iteration of loop 2 finds a feasible solution to the entire problem.

The two loops shown in Fig. 2 show the order in which the problems are solved. The m-master problem is a one-stage bin packing problem which packs jobs into capacity-constrained autoclave batches, while minimizing the number of open autoclave batches. Autoclave batches have a constant capacity, so the sum of job volumes in each batch must be less than the capacity. We chose to assign jobs to autoclave batches directly because part of the objective is to minimize the number of open autoclave batches and the job-to-autoclave batching is a relaxation of the two-stage batching requirement.

A feasible packing of jobs in an autoclave batch may not be feasibly partitionable into tool batches as jobs may not fit perfectly on tools. The m-subproblem attempts to find such a feasible partitioning for each autoclave batch. We denote this constrained partitioning problem as the Pattern Bin Packing Problem. If we find a feasible packing for all autoclave batches, we schedule the tool and autoclave batches in the subproblem. If no feasible packing exists for an autoclave batch, a cut is added to the m-master problem.

Table 2. M-Master problem variables.

Table 3. M-subproblem variables.

M-Master Problem. The m-master problem was modelled using CP. The objective is to minimize the number of open autoclave batches. The variables in the m-master problem are shown in Table 2; see Table 1 for parameter descriptions.

$$\begin{aligned} \text {min} \quad&q&\end{aligned}$$

(19)

$$\begin{aligned} \text {s.t.} \quad&\texttt {pack}\left( \{\theta _{i}; i \in {\mathcal {B}^{2}}\}, \{x_j; j \in {\mathcal {J}^{}}\}, \{s_j; j \in {\mathcal {J}^{}}\}\right)&\end{aligned}$$

(20)

$$\begin{aligned}&q = \texttt {max}\left( \{x_j; j \in {\mathcal {J}^{}}\}\right)&\\&x_j \in \{0, ...|{\mathcal {B}^{2}}|\} \text {; } \theta _{i} \in \{0, ...V^2\} \text {; } q \in \{0, ...|{\mathcal {B}^{2}}|\}&\nonumber \end{aligned}$$

(21)

Constraint (20) is a global constraint which packs jobs in set $\mathcal {J}^{}$ into autoclave batches in set $\mathcal {B}^{2}$ while keeping the sum of job volumes in each autoclave batch below the autoclave capacity. Constraint (21) defines the number of open bins.

M-Subproblem. Inspired by approaches to related problems [4, 9], we modelled the m-subproblem using MIP with two sets of binary decision variables. The first set creates tool batches from jobs and the second set assigns each tool batch to a tool. The objective function minimizes the total sum of tool volumes.

Consider a tool batch k that contains the set of jobs $\mathcal {J}^{*}$, let $j^{'}$ be the job with the lowest index in $\mathcal {J}^{*}$. We denote job $j^{'}$ as the representative job of tool batch k and create decision variables $y_{j, j^{'}}$ that assign jobs to representative jobs instead of directly to tool batches. If job j is assigned to the tool batch with representative job $j^{'}$, then $y_{j, j^{'}} = 1$, otherwise, $y_{j, j^{'}} = 0$. Therefore, each $y_{j^{'}, j^{'}} = 1$ indicates an open tool batch. Only jobs in the same autoclave batch can be assigned to the same tool batch, so we define a $|{\mathcal {J}^{}}| \times |{\mathcal {J}^{}}|$ matrix, where entry $A_{j, j^{'}}$ is equal to 1 if job j and job $j^{'}$ are in the same autoclave batch in the m-master problem solution, and equal to 0 otherwise. The variables in the m-master problem are presented in Table 3; see Table 1 for parameter descriptions.

$$\begin{aligned} \text {min} \quad&\sum _{j^{'} \in {\mathcal {J}^{}}} \tau _{j^{'}}&\end{aligned}$$

(22)

$$\begin{aligned} \text {s.t.} \quad&\sum _{j^{'} \in {\mathcal {J}^{}}} y_{j, j^{'}} = 1&\forall j \in {\mathcal {J}^{}}\end{aligned}$$

(23)

$$\begin{aligned}&y_{j, j^{'}} \le A_{j, j^{'}}&\forall j, j^{'} \in {\mathcal {J}^{}}\end{aligned}$$

(24)

$$\begin{aligned}&y_{j, j^{'}} = 0&\forall j, j^{'} \in {\mathcal {J}^{}} : j < j^{'}\end{aligned}$$

(25)

$$\begin{aligned}&y_{j, j^{'}} \le y_{j^{'}, j^{'}}&\forall j, j^{'} \in {\mathcal {J}^{}}\end{aligned}$$

(26)

$$\begin{aligned}&\sum _{t \in \mathcal {T}} z_{j^{'}, t} = y_{j^{'}, j^{'}}&\forall j^{'} \in {\mathcal {J}^{}}\end{aligned}$$

(27)

$$\begin{aligned}&\tau _{j^{'}} = \sum _{t \in \mathcal {T}} v_t z_{j^{'}, t}&\forall j^{'} \in {\mathcal {J}^{}}\end{aligned}$$

(28)

$$\begin{aligned}&\tau _{j^{'}} \ge \sum _{j \in {\mathcal {J}^{}}} s_j y_{j, j^{'}} - \sum _{j \in {\mathcal {J}^{}}} s_j (1 - y_{j^{'}, j^{'}})&\forall j^{'} \in {\mathcal {J}^{}}\end{aligned}$$

(29)

$$\begin{aligned}&\rho _{j^{'}} = \sum _{j \in {\mathcal {J}^{}}} p_j y_{j, j^{'}}&\forall j^{'} \in {\mathcal {J}^{}}\\&{y_{j, j^{'}} \in \{0, 1\} \text {; } z_{j^{'}, t} \in \{0, 1\} \text {; } \tau _{j^{'}} \in \{0, ...V^1\} \text {; } \rho _{j^{'}} \in \{0, ..., \sum _{j \in {\mathcal {J}^{}}} p_j\}}&\nonumber \end{aligned}$$

(30)

Constraint (23) makes sure each job is assigned to one tool batch. Constraints (24) and (25) enforce assignment restrictions. If job $j^{'}$ defines a tool batch, it is forced by constraint (25) to be the lowest indexed job in that tool batch, so constraint (26) tightens the linear relaxation. Each open tool batch is associated with a job $j^{'}$, and only jobs with a higher index than $j^{'}$ can be assigned to the tool batch associated with $j^{'}$. Constraint (27) makes sure each open tool batch is assigned to a specific tool. Constraints (28) and (29) define and enforce the tool volume for each tool batch to be larger than the sum of job volumes. Constraint (30) defines the processing time for each tool batch.

Feasibility Cuts. Once the m-subproblem is solved to optimality, if the sum of tool volumes for autoclave batch $i^*$ is larger than the autoclave capacity then $i^*$ is an infeasible batch. Cuts are added to prevent the subset of jobs in each infeasible autoclave batch from being packed together again. Let $\hat{{\mathcal {B}^{2}}}$ be the set of infeasible autoclave batches from the incumbent m-master problem solution, and let ${\mathcal {J}^{i^*}}$ be the set of jobs assigned to batch $i^* \in \hat{{\mathcal {B}^{2}}}$.

These cuts are written as a global cardinality constraint (GCC) for each infeasible autoclave batch. The standard GCC format is $\texttt {gcc}\left( \{cards\}, \{vals\}, \{vars\}\right)$, where sets $\{cards\}$ and $\{vals\}$ are the same size. Over the set of variables in $\{vars\}$, each value val[i] should only be taken cards[i] times; cards[i] can be a single value or a range of values. Using GCC cuts also removes symmetrical solutions arising from batch indexing. Constraint (31) forms the feasibility cut.

$$\begin{aligned}&\texttt {gcc}\left( \{[0, ..., |{\mathcal {J}^{i^*}}| - 1], ...\}, \{1, ..., |{\mathcal {B}^{2}}|\}, \{x_j; j \in {\mathcal {J}^{i^*}}\}\right)&\forall i^* \in \hat{{\mathcal {B}^{2}}} \end{aligned}$$

(31)

Subproblem. The subproblem is modelled using CP and has two sets of interval decision variables, one to schedule tool batches and one to schedule autoclave batches. The objective is to minimize the sum of job tardiness. The subproblem variables and model-specific parameters are presented in Table 4; see Table 1 for other parameter descriptions.

Table 4. Subproblem variables and parameters.

$$\begin{aligned} \text {min} \quad&\sum _{j \in {\mathcal {J}^{}}} \alpha _j l_j&\end{aligned}$$

(32)

$$\begin{aligned} \text {s.t.} \quad&\texttt {sizeOf}(\gamma _{k}) = \rho _{k}^*&\forall k \in {\mathcal {B}^{1}}^*\end{aligned}$$

(33)

$$\begin{aligned}&\texttt {sizeOf}(\sigma _{i}) = P^2&\forall i \in {\mathcal {B}^{2}}^*\end{aligned}$$

(34)

$$\begin{aligned}&\texttt {endBeforeStart}\left( \gamma _{k}, \sigma _{i}\right)&\forall (k, i) \in \mathcal {E}^*\end{aligned}$$

(35)

$$\begin{aligned}&\texttt {startBeforeEnd}\left( \sigma _{i}, \gamma _{k}, -W\right)&\forall (k, i) \in \mathcal {E}^*\end{aligned}$$

(36)

$$\begin{aligned}&\texttt {alwaysIn}\left( \sum _{k \in {\mathcal {B}^{1}}} \texttt {pulse}(\gamma _{k}, 1), 0, |\mathcal {H}|, 0, C^1\right)&\end{aligned}$$

(37)

$$\begin{aligned}&\texttt {alwaysIn}\left( \sum _{i \in {\mathcal {B}^{2}}} \texttt {pulse}(\sigma _{i}, 1), 0, |\mathcal {H}|, 0, C^2\right)&\end{aligned}$$

(38)

$$\begin{aligned}&l_j = \texttt {endOf}(\sigma _{i}) - d_j&\forall (j, i) \in \mathcal {F}^*\\&l_j \in \{0, ...|\mathcal {H}|\}&\nonumber \end{aligned}$$

(39)

Constraints (33) and (34) define the interval variable lengths for tool and autoclave batches, respectively. Constraint (35) makes sure any autoclave batch starts after all its associated tool batches have finished processing. Constraint (36) restricts the waiting time between stages. Constraints (37) and (38) enforce resource capacities for each stage. Constraint (39) defines job tardiness.

Optimality Cuts. Once the subproblem is solved after a loop 2 cycle, a feasible solution to the entire problem has been found. Thus, to start the cycle again, the incumbent solution must be removed from the search space. Due to the fact that only one autoclave batch needs to be changed to cut off the incumbent solution, we need to add a disjunction to require at least one autoclave batch to be different. GCC constraints cannot be disjoined in the solver we are using [8]. Thus, we introduce a new set of binary variables, $\omega _{i^*} \in \{0, 1\}$, where $i^* \in {\mathcal {B}^{2}}^*$ is the set of open autoclave batches.

The binary variable $\omega _{i^*}$ is set to be equal to 1 if autoclave batch $i^*$ is required to be different in subsequent solutions, and equal to 0 otherwise. If autoclave batch $i^*$ is forced to be different, then constraints must be added such that only a strict subset of jobs in that batch can be assigned to the same autoclave batch. We add a set of counting constraints that limit how many times each autoclave batch index can be assigned in the set of decision variables belonging to jobs in that batch. Then, a final constraint needs to be added to enforce that at least one binary variable out of the set $\{\omega _{i^*}; i^* \in {\mathcal {B}^{2}}^*\}$ is equal to 1, forcing the incumbent solution to change. Constraints (40) and (41) form the optimality cuts.

$$\begin{aligned}&(\omega _{i^*} == 1) \rightarrow \left( \texttt {count}(\{x_j; j \in {\mathcal {J}^{i^*}}\}, i) \le |{\mathcal {J}^{i^*}}| - 1\right)&i \in {\mathcal {B}^{2}} \quad i^* \in {\mathcal {B}^{2}}^*\end{aligned}$$

(40)

$$\begin{aligned}&\sum _{i^* \in {\mathcal {B}^{2}}^*} \omega _{i^*} \ge 1&\end{aligned}$$

(41)

Theoretical Results. The proof of the validity of the m-subproblem cut is straightforward and, following Chu and Xia [2], can be sketched as follows. Given a solution with an infeasible autoclave batch $i^*$:

• 1. Cut (31) removes $i^*$ from the search space. Suppose we have an infeasible autoclave batch $i^*$ containing the set of jobs ${\mathcal {J}^{i^*}}$. The decision variables associated with jobs in $i^*$, $\{x_j; j \in {\mathcal {J}^{i^*}}\}$ take on values ranging from $\{1, ..., |{\mathcal {B}^{2}}|\}$, where $|{\mathcal {B}^{2}}|$ is the total number of autoclave batches available. If $\{x_j; j \in {\mathcal {J}^{i^*}}\}$ are assigned to the same autoclave batch, then in any solution where these jobs are grouped into an autoclave batch one of the values from $\{1, ..., |{\mathcal {B}^{2}}|\}$ appears $|{\mathcal {J}^{i^*}}|$ times. Cut (31) explicitly removes all such solutions.

• 2. Cut (31) does not remove any globally optimally solutions from the search space. Suppose we have a globally optimal solution $\mathcal {S}$ to the 2BPHFSP containing autoclave batch $i^{'}$, which contains the same jobs as infeasible autoclave batch $i^*$. As $i^*$ is infeasible, the minimum sum of tool volumes that can contain all the jobs in $i^*$ is larger than the autoclave machine capacity. The m-subproblem finds the set of tools with minimal volume that can hold all jobs within each autoclave batch. Since $i^{'}$ contains the same jobs as $i^*$, it holds that $i^{'}$ is also infeasible. Therefore, $\mathcal {S}$ is infeasible and cannot be a globally optimal solutions.

Similarly, the proof of the validity of the subproblem cut is sketched as follows. Given a feasible solution, cuts (40) to (41) are sufficient to remove the incumbent solution and all symmetrical solutions from the search space. Suppose the incumbent solution has $|{\mathcal {B}^{2^*}}|$ open autoclave batches, where each autoclave batch $i \in \{1, ..., |{\mathcal {B}^{2^*}}|\}$ is associated with binary variable $\omega _{i}$. If $\omega _{i^*} = 1$, autoclave batch $i^*$ cannot appear in any subsequent solutions. Let the sum of $\omega _{i}$ over all $i \in {\mathcal {B}^{2^*}}$ be equal to $\pi$. If $\pi = 0$, then all $\omega _{i} = 0$ and no autoclave batch is enforced to be different, which would lead to the algorithm finding the same solution as the incumbent. Note that it is possible that exactly one autoclave batch from the incumbent solution can be changed to form a new distinct solution. Therefore, we forbid at least one autoclave batch from appearing again to remove the incumbent solution from the search space.

4 Heuristic Approaches

In addition to the CP and MIP models, we developed a greedy heuristic based on earliest due date (EDD) and hybridizations of the heuristic with CP.

4.1 Earliest Due Date Heuristic

The pseudocode for the heuristic is shown in Algorithm 1. See Table 1 for parameter descriptions.

This heuristic algorithm flows through three distinct sections. The first section orders jobs by due date then greedily assigns them one by one to the first available tool batch. If no tool batch is available, then a new tool batch is opened and randomly assigned to a tool. Next, all open tool batches are sorted by due date and the algorithm greedily assigns them one by one to the first available autoclave batch. If no autoclave batch is available, a new batch is opened. Lastly, the autoclave batches are sorted by due date. For each autoclave batch, the algorithm assigns each of its associated tool batches to start as soon as possible on the first available stage 1 machine. Then, the autoclave batch itself is assigned to start, after all its associated tool batches have ended, on the first available stage 2 machine.³

We also incorporated a simple randomization technique where each time an item is picked from a sorted list, i.e. picking the next job or tool batch to be batched or picking the next autoclave batch to schedule, a random item from the first L items in the list is selected. This method allows us to apply the algorithm on an instance multiple times and use the best solution found.

4.2 Hybrid Heuristic Approaches

Once EDD finds a feasible solution to the 2BPHFSP, we can try to improve the solution using CP. Thus, we formulated two hybrid heuristic-CP approaches. First, the heuristic solution can be used to warm-start the monolithic CP model, and second, packing decisions from the heuristic solution can be fixed and scheduling decisions can be improved using the subproblem from LBBD. These two approaches will be referred to as WCP and EDD-CP, respectively.

5 Numerical Results

Our five approaches were tested on 11 sets of 30 randomly generated problem instances, ranging from 5 jobs to 100 jobs per instance. All CP and MIP models were implemented in Java using CPLEX Optimization Studio 12.9. Each approach was given a sixty minute total time limit to solve each instance. For the LBBD model, each component was given a ten minute time limit to prevent the model from timing out globally within a single component.

Overall Performance. Figure 3 shows the number of instances for which each approach was able to find feasible solution(s) and the average time to find the best solution within one hour. The monolithic CP model is clearly the worst performing model: it was not able to solve any instances with more than 25 jobs. The LBBD model starts to show signs of degraded performance at 50 jobs per instance, and can only solve around 50% of instances with 100 jobs. These two results imply that we will not be able to use these non-heuristic methods to solve real-world instances, which contain at least 1000 jobs. EDD, EDD-CP, and WCP were able to find feasible solutions for all instances. Both CP and WCP are very unlikely to scale, but LBBD’s mediocre performance still warrants some exploration with the full problem. EDD and EDD-CP show strong potential, but Fig. 3b indicates that EDD-CP does not use much more time than EDD, meaning we can solely pursue EDD-CP.

Fig. 3.

Performance of all solution techniques.

Solution Quality. We compared solution qualities of each approach by calculating optimality gaps using equation (42), where z(n) is the objective value found for instance n and $z(\text {RSP}(n))$ is a lower bound for instance n. The CP and LBBD models did not find feasible solutions for some instances; the optimality gap for any unsolved instance n is not included in the associated averages in Fig. 4.

$$\begin{aligned} \text {Optimality Gap of Approach }n = \frac{z(n) - z(\text {RSP}(n))}{z(\text {RSP}(n))} \end{aligned}$$

(42)

The lower bound is obtained by solving the Relaxed Scheduling Problem (RSP). The RSP is a version of the LBBD subproblem with all batching removed: each job is processed once in the first stage and once in the second stage. We model the first stage as a multi-capacity machine and each job occupies one unit of capacity during processing. The second stage is also a multi-capacity machine, but each job occupies $s_j$ units of space during processing and the second stage machine has a constant capacity of $C^2 \times V^2$. There are precedence constraints between the stages of each job. The RSP is a relaxation of the 2BPHFSP, so the optimal objective of the RSP is a lower bound on the 2BPHFSP. There is a small subset of instances where the RSP is unable to prove optimality within one hour. These instances are not included in the averages shown in Fig. 4. This lower bound is very weak and does not serve any purpose beside providing a comparison basis for solution qualities across the different approaches.

Figure 4 shows that, other than CP, the techniques do not show a large range of solution qualities when they are all able to find feasible solutions. From 15 to 60 jobs per instance, EDD and EDD-CP find consistently worse solutions than LBBD and WCP, both of which can change packing decisions to find better schedules. However, the four techniques start to converge at 80 jobs per instance. Given the censoring of the data for instances which LBBD could not find a feasible solution, the true performance of the heuristic techniques is likely better than LBBD for the 100-job instances. We can conclude that heuristic techniques have comparable or better performance than the sophisticated mathematical models for large problem instances.

Fig. 4.

Comparing the optimality gaps of all solution techniques tested.

Hybrid Heuristic Approaches. We can calculate how much improvement CP was able to give to a heuristic solution in the two hybrid heuristic approaches by using equation (43), where $z(\text {EDD})$ is the heuristically found solution objective value and $z(\text {CP})$ is the improved objective value.

$$\begin{aligned} \text {Relative Decrease} = \frac{z(\text {EDD}) - z(\text {CP})}{z(\text {EDD})} \end{aligned}$$

(43)

Figure 5 allows us to see the convergence trend shown by Fig. 4 more clearly. WCP can make large improvements to the EDD solution up to 60 jobs per instance, where its performance starts to degrade, whereas EDD-CP shows gradually improving performance from 5 to 100 jobs per instance. We generated larger problem instances of size 110, 120, and 130 to further test WCP and EDD-CP. Figure 5b shows that EDD-CP’s performance plateaus after 100 jobs per instance. WCP was not able to solve any problems larger than 100 jobs per instance due to high memory usage. We can see that EDD-CP is clearly the most robust and promising approach to solving the full problem.

Fig. 5.

Relative decrease in objective value after using CP to improve the heuristic solution; average decrease is shown by the dotted line. The blue data points show results from larger instances that WCP was not able to solve. (Color figure online)

6 Conclusions and Next Steps

We introduced the 2BPHFSP and developed three primary solution approaches, constraint programming (CP), logic-based Benders decomposition (LBBD), and an earliest due date heuristic (EDD). Each approach was tested on 11 sets of 30 instances, with each set containing 5 to 100 jobs per instance. CP was able to solve small instances, but scaled poorly. LBBD scaled better than CP but did not find feasible solutions for some instances with 50 or more jobs. EDD was able to find a feasible solution within seconds for every instance and had comparable quality to LBBD solutions for larger instances.

Two hybrid heuristic-CP approaches were tested on the same sets of problem instances. First, the EDD solution was used to warm-start the CP model (WCP), and second, the packing from the EDD solution was fixed and the scheduling subproblem from LBBD was used to improve the EDD solution schedule (EDD-CP). Both methods were able to find feasible solutions for every instance. WCP performed better within the range of problem instances tested, but showed signs of decreasing performance at around 50 to 60 jobs per instance. EDD-CP has consistent performance up to 100 jobs per instance, implying scalability.

Overall, the most interesting conclusion is the strong performance of heuristic techniques compared to the mathematical formulations. The complexity of the problem lends itself to CP, but scaling is an issue for complete approaches. Future work includes considering some complexities of the original problem that were abstracted away, and increasing instance sizes to match the real world. The positive heuristic results point us towards focusing future work on developing metaheuristic, constraint-based local search, and hybrid heuristic-CP approaches. Ultimately, the success shown by EDD and the hybrid heuristic-CP approaches suggests that complex problems, such as two-stage hierarchical batching and scheduling, pose a challenge for the development of robust and efficient exact methods.