Abstract
The objective of this chapter is to discuss purely mechanical constitutive equations. After identifying unphysical arbitrariness of the classical Lagrangian formulation of constitutive equations, an Eulerian formulation for nonlinear elastic materials is developed using evolution equations for microstructural vectors \({\mathbf {m}}_i\). The influence of kinematic constraints on constitutive equations is discussed and specific nonlinear constitutive equations are presented for a number of materials including: elastic solids, viscous fluids and elastic–inelastic materials.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
5.1 The Classical Lagrangian Formulation for Nonlinear Elastic Solids
In general, a constitutive equation is an equation that characterizes the response of a given material to deformations, deformation rates, thermal, electrical, magnetic or mechanobiological loads. An elastic material is a very special material because it exhibits ideal behavior in the sense that it has no material dissipation. One of the most important features of an elastic material is that it is characterized by a total strain energy \({\mathcal {U}}\) and a strain energy function \(\Sigma \) per unit mass defined in (4.5.2)
Generalizing the notions of a simple nonlinear elastic spring, an elastic material is characterized by the following four assumptions:
Assumption 5.1
The material response is ideal in the sense that the rate of material dissipation \({\mathcal {D}}\) in (4.5.7) vanishes
for all motions. This generalizes the notion that the elastic spring is non-dissipative.
Assumption 5.2
Within the context of the Lagrangian formulation, the strain energy \(\Sigma \) is a function of the total deformation gradient \({\mathbf {F}}\) and the reference position \({\mathbf {X}}\) only
where dependence on the reference position \({\mathbf {X}}\) has been included to allow for the possibility that the material can be inhomogeneous in the reference configuration. This generalizes the notion that the elastic energy in an elastic spring depends only on extension of the spring from its zero-stress length.
Assumption 5.3
The strain energy \(\Sigma \) is form-invariant under SRBM
With regard to a spring, this follows directly from the fact that every member of the group of SRBM has the same length of the spring at each time.
Assumption 5.4
The Cauchy stress \({\mathbf {T}}\) is independent of the rate of deformation \({\mathbf {L}}\). This is consistent with the fact that the force in an elastic spring does not depend on the rate of extension of the spring.
To explore the physical consequences of Assumption 5.1 (5.1.2), use is made of global form (4.5.1) of the rate of material dissipation to obtain
which states that for an elastic material the rate of work done on the body due to body forces and contact forces equals the rate of change of kinetic and strain energies. In particular, the total work \(W_{2/1}\) done on the body during the time interval \(t_1 \le t \le t_2\) is given by
In view of Assumption 5.2 (5.1.3), the strain energy \(\Sigma \) depends on the current configuration through the current value of \({\mathbf {F}}\) only. Similarly, the value of the kinetic energy \({\mathcal {K}}\) depends only on the values of the density \(\rho \) and the velocity \({\mathbf {v}}\) at the beginning and ends of the time interval. Moreover, the values of \(\rho \) at the beginning and end of the time interval are connected by the conservation of mass (4.1.13) which requires \(\rho \det {\mathbf {F}}= \text {constant}\). Consequently, \(\Delta {\mathcal {K}}, \Delta {\mathcal {U}}\) and the work done \(W_{2/1}\) during the time interval depend only on the values of \({\mathbf {v}}\) and \({\mathbf {F}}\) at the beginning and end of the time interval. In particular, this means that the work \(W_{2/1}\) done on the body between any two states defined by \({\mathbf {v}}(t_1)\) and \( {\mathbf {F}}(t_1)\) and \({\mathbf {v}}(t_2)\) and \({\mathbf {F}}(t_2)\) is independent of the path of the deformation between these two states. This is consistent with the notion that the work done on an elastic spring between any two states is path independent. Also, it follows that the work \(W_{2/1}\) done on the body vanishes for an arbitrary closed cycle for which the values of \({\mathbf {v}}\cdot {\mathbf {v}}\) and the deformation gradient \({\mathbf {F}}\) are the same at the beginning and end of the cycle
In this regard, it is noted that \({\mathbf {v}}\) and \({\mathbf {F}}\) are functions of position and time so the notion of a closed cycle implies that each point starts and ends with the same values of \({\mathbf {v}}\cdot {\mathbf {v}}\) and the same values of \({\mathbf {F}}\).
Assumption 5.3 (5.1.4) places restrictions on the functional form (5.1.3) of the strain energy. Using the fact that \({\mathbf {F}}^+ = {\mathbf {Q}}{\mathbf {F}}\) under SRBM, it follows that
must hold for arbitrary proper orthogonal tensors \({\mathbf {Q}}\) and all times. Since the deformation can be inhomogeneous, the rotation tensor \({\mathbf {R}}\) can be a function of position \({\mathbf {X}}\). However, for an arbitrary but specified value \({\mathbf {X}}_1\) of \({\mathbf {X}}\), choose \({\mathbf {Q}}(t)={\mathbf {R}}^T({\mathbf {X}}_1,t)\) so that this equation requires
where the dependence of \({\mathbf {R}}({\mathbf {X}}_1,t)\) on time has been suppressed for notational simplicity. Now, evaluating this expression at \({\mathbf {X}}={\mathbf {X}}_1\), it follows that locally
Thus, a necessary condition for the strain energy \(\Sigma \) to be locally invariant under SRBM is that the strain energy function \(\Sigma \) be dependent on the deformation gradient \({\mathbf {F}}\) only through its dependence on the deformation tensor \({\mathbf {C}}\). It is easy to see that this condition is also a sufficient condition for the strain energy function to be form-invariant under SRBM since \({\mathbf {C}}^+={\mathbf {C}}\). Moreover, since \({\mathbf {X}}_1\) is an arbitrary material point, this restriction on \(\Sigma \) must hold for each point \({\mathbf {X}}\) so the strain energy \(\Sigma \) can depend on \({\mathbf {F}}\) only through its dependence on \({\mathbf {C}}\) for all material points \({\mathbf {X}}\)
Next, with the help of (5.1.11) Assumption 5.1 (5.1.2) requires
However, since the coefficient of \({\mathbf {D}}\) in (5.1.12b) is independent of the rate \({\mathbf {D}}\) and is symmetric, it follows that for any fixed values of \({\mathbf {F}}\) and \({\mathbf {X}}\) the coefficient of \({\mathbf {D}}\) is fixed and yet \({\mathbf {D}}\) can be an arbitrary symmetric tensor. Therefore, the necessary condition that (5.1.12b) be valid for arbitrary motions is that the Cauchy stress be determined by a derivative of the strain energy
Using the conservation of mass (4.1.4) and the relationship (4.6.16), the symmetric Piola-Kirchhoff stress \({\mathbf {S}}\) is also determined by a derivative of the strain energy
Notice that the results (5.1.13) and (5.1.14) are automatically properly invariant under SRBM. Also, it can be seen that the result (5.1.14) is similar to the result for an elastic spring that the force is equal to the derivative of the potential (strain) energy.
Green Elasticity (Hyperelasticity)
The elastic response of the material described by (5.1.13) is called Green elasticity or hyperelasticity with all four assumptions satisfied. In particular, the stress \({\mathbf {T}}\) is independent of velocity gradient \({\mathbf {L}}\). Also, the stress is an explicit function of the deformation gradient \({\mathbf {F}}\) which is related to the derivative of a strain energy function \(\Sigma \) that depends only on \({\mathbf {F}}\) through the right Cauchy–Green deformation tensor \({\mathbf {C}}={\mathbf {F}}^T{\mathbf {F}}\). This means that the stress is determined by the deformation state \({\mathbf {F}}\) and is independent of the path of deformation. Moreover, the work done between two states of deformation \({\mathbf {F}}_1\) and \({\mathbf {F}}_2\) is independent of the path.
Cauchy Elasticity
For Cauchy elasticity, only Assumption 5.4 is satisfied with the stress \({\mathbf {T}}\) being a function of \({\mathbf {F}}\) only
This material has the property that the stress is determined by the deformation state \({\mathbf {F}}\) and is independent of the velocity gradient \({\mathbf {L}}\) and of the path of deformation. However, in general, the function in (5.1.15) does not satisfy integrability conditions necessary for a strain energy function to exist. This means that (5.1.13) is not valid and the work done between two states of deformation \({\mathbf {F}}_1\) and \({\mathbf {F}}_2\) can be path dependent. Moreover, since under SRBM the stress \({\mathbf {T}}\) must satisfy the transformation relations (4.7.17), it follows that the functional form for \({\mathbf {T}}({\mathbf {F}})\) must satisfy the restriction that
is satisfied for all proper orthogonal \({\mathbf {Q}}\). This restriction requires \({\mathbf {T}}\) to be an isotropic tensor function of the left Cauchy–Green deformation tensor \({\mathbf {B}}= {\mathbf {F}}{\mathbf {F}}^T\)
which can only characterize elastically isotropic response.
Hypoelasticity
For hypoelasticity, only Assumption 5.4 is satisfied and the stress is determined by integrating an evolution equation of the form
where \({\mathbf {K}}\) is a fourth-order tensor function of \({\mathbf {T}}\) having the symmetry properties that
Also, the rate of stress \(\overset{\nabla }{{\mathbf {T}}}\) and the stiffness tensor \({\mathbf {K}}\) transform under SRBM such that
so that the evolution equation (5.1.18) remains form-invariant under SRBM
Since this equation is homogeneous of order one in time, the predicted material response is rate independent. Stress rates which satisfy the restriction (5.1.20)\(_1\) for all SRBM are called objective.
Truesdell Stress Rate
Recalling that
it is possible to differentiate the hyperelastic constitutive equation (5.1.13) to deduce that
This equation can be rewritten in the form
where the Truesdell stress rate is defined by
Next, recalling that under SRBM
it can be shown by differentiating the expression for \({\mathbf {T}}^+\) that the Truesdell is objective
Thus, the evolution equation (5.1.24) based on the Truesdell stress rate satisfies the restriction (5.1.20)\(_1\) so it is form-invariant under SRBM and can be used to formulate hypoelastic constitutive equations of the type (5.1.18).
Jaumann Stress Rate
The Jaumann stress rate defined by
is also objective
Consequently, it can be used for form-invariant hypoelastic constitutive equations of the type (5.1.18). Moreover, it follows from (5.1.25) and (5.1.28) that the Truesdell and Jaumann stress rates are related by
for all SRBM.
In this regard, it is noted that there are an infinite number of stress rates that transform like (5.1.20)\(_1\) under SRBM. For example, consider a generalized hypoelastic material specified by the evolution equation
where \({\mathbf {K}}({\mathbf {T}},{\mathbf {D}})\) is a homogeneous function of order one in \({\mathbf {D}}\) which satisfies the restrictions
for all scalars \(\alpha \) and all proper orthogonal tensor functions \({\mathbf {Q}}\). Next, let n be an arbitrary positive integer and consider the stress rate \(\overset{\nabla }{{\mathbf {T}}}\) in (5.1.18) to be specified by the form
where \(\beta \) is a constant scaling constant having the units \([(\text {stress})^{1-n}]\) so that (5.1.33) has the units of stress. It can be shown that
for all SRBM. Consequently, since the Jaumann rate is objective, it follows that \(\overset{\nabla }{{\mathbf {T}}}\) in (5.1.33) is objective
Next, define the new function \(\hat{{\mathbf {K}}}({\mathbf {T}},{\mathbf {D}})\) by
which satisfies restrictions similar to the forms (5.1.32)
It then follows that the stress \({\mathbf {T}}\), which satisfies the form-invariant evolution equation
with \(\overset{\nabla }{{\mathbf {T}}}\) defined by (5.1.33), predicts the same hypoelastic material response as that predicted by (5.1.31). This means that for this general form of a hypoelastic material there is no fundamental physical significance of any of the infinite stress rates in (5.1.33) that satisfy under SRBM.
Summary
Equation (5.1.24) shows that any hyperelastic equation can be formulated in terms of an evolution equation for stress if the right-hand side of (5.1.18) is appropriately modified. However, in general, rate equations of the type (5.1.18) produce hypoelastic response since they do not satisfy integrability conditions necessary for a strain energy function to exist [3]. Due to the physical deficiencies of both Cauchy elasticity and hypoelasticity, the term elastic material is used here only for a material that exhibits Green elasticity (hyperelasticity) .
5.2 Unphysical Arbitrariness of the Lagrangian Formulation of Constitutive Equations
The classical Lagrangian formulation of constitutive equations for hyperelastic materials specifies the strain energy function \(\Sigma \) to be a function of the deformation gradient \({\mathbf {F}}\) through the right Cauchy–Green deformation tensor \({\mathbf {C}}\), such that
where \({\mathbf {F}}\) characterizes deformations from an arbitrary, but fixed, reference configuration. The only restriction on this reference configuration is that the mapping
be invertible, which requires
for all material points in the material region under consideration and for all time.
The strain energy function \(\Sigma \) characterizes the response of a specific material, which should be independent of arbitrariness of the choice of the reference configuration. This means that \(\Sigma \) should be a function of internal state variables that can be measured by experiments on identical samples of the material in its current state. In this regard, it is recalled from Sect. 3.11 that \({\mathbf {F}}\) is not an internal state variable in the sense of Onat [31].
To be more specific, consider a homogeneous deformation of a homogeneous hyperelastic material from a uniform zero-stress material state in its reference configuration with \({\mathbf {C}}= {\mathbf {I}}\). It is always possible to unload this material to a zero-stress material state with \({\mathbf {C}}= {\mathbf {I}}\), which is satisfied whenever \({\mathbf {F}}\) is a proper orthogonal tensor. However, anisotropic response requires characterization of the deformation and orientation of material fibers relative to observable material orientations. This arbitrariness of \({\mathbf {F}}\) makes it impossible to use experiments on the material in its current configuration to determine the orientations of specific material fibers associated with the arbitrary choice of the reference configuration used to specify \(\Sigma \) in (5.2.1).
5.3 An Eulerian Formulation for Nonlinear Elastic Solids
The Eulerian formulation of constitutive equations for nonlinear elastic solids in this section removes the unphysical arbitrariness of the choice of a reference configuration and a total strain measure. For this formulation, use is made of the microstructural vectors \({\mathbf {m}}_i\) and the elastic metric \(m_{ij}\) introduced in Sect. 3.11, determined by the equations
with the strain energy function \(\Sigma \) and the stress proposed in the forms
Using these expressions together with assumption (5.1.2) requires
for arbitrary motions and all times. Since \(m_{ij}\) is symmetric, it follows that \({\partial }\tilde{\Sigma }/ {\partial }m_{ij} ({\mathbf {m}}_i \otimes {\mathbf {m}}_j)\) is a symmetric tensor. Consequently the coefficient of \({\mathbf {D}}\) in (5.3.3) is symmetric and is independent of \({\mathbf {D}}\) so the necessary condition that (5.3.3) be valid for arbitrary motions is that the Cauchy stress be determined by a derivative of the strain energy
In this formulation, the vectors \({\mathbf {m}}_i\) are defined so that they form an orthonormal triad in any zero-stress material state (1.2.13) with
which requires the strain energy function to satisfy the restrictions
Moreover, using the conservation of mass (4.1.7), the material derivative of (5.3.4) yields the evolution equation
The microstructural vectors \({\mathbf {m}}_i\) are internal state variables in the sense of Onat [31] with their values in the current configuration being determined by experiments on identical samples of the material. Specifically, use is made of measurements of the current state of stress \({\mathbf {T}}\) and the value of \(\dot{{\mathbf {T}}}\) for different values of the loading rate \({\mathbf {L}}\). Any differences between the \({\mathbf {m}}_1, {\mathbf {m}}_2\) and \({\mathbf {m}}_3\) directions which cannot be determined by these experiments should be consistent with material symmetries of the strain energy function \(\Sigma \) which ensure that these differences do not influence the prediction of the material response to an arbitrary loading rate \({\mathbf {L}}\).
A Separation of Elastic Dilatation and Distortional Deformations
To introduce separate control over the response of the material to dilatation and distortional rates of deformation it is convenient to use the elastic dilatation \(J_e\) defined in (3.11.7), the distortional deformation vectors \({\mathbf {m}}_i^{\prime }\) defined in (3.11.14) and the elastic distortional deformation metric \(m_{ij}^{\prime }\) defined in (3.11.16), which satisfy the Eqs. (3.11.17) and (3.11.28)
Then, the strain energy function and the stress are proposed in the forms
and the condition (5.1.2) requires
Since \(m_{ij}^{\prime }\) is symmetric, it follows that \({\partial }\tilde{\Sigma }/ {\partial }m_{ij}^{\prime }({\mathbf {m}}_i \otimes {\mathbf {m}}_j)\) is a symmetric tensor. Consequently the coefficient of \({\mathbf {D}}\) in (5.3.10) is symmetric and is independent of \({\mathbf {D}}\) so the necessary condition that (5.3.10) be valid for arbitrary motions is that the Cauchy stress be determined by a derivative of the strain energy
where p is the pressure and \({\mathbf {T}^{\prime \prime }}\) is the deviatoric part of \({\mathbf {T}}\).
Also, the constitutive equation for stress is assumed to be restricted so that a zero-stress material state is characterized by
This means that the triad \({\mathbf {m}}_i^{\prime }\) has been defined so that \({\mathbf {m}}_i^{\prime }\) are orthonormal vectors in a zero-stress material state.
This form for the strain energy function makes it easy to separate the effects of dilatation and distortion. For example, a class of materials can be considered for which the strain energy function separates into two additive parts
where \(\rho _z\) is the constant zero-stress mass density, f controls the response to dilatation and \(\tilde{\Sigma }_d\) controls the response to distortional deformations. It then follows that the Cauchy stress \({\mathbf {T}}\) for this strain energy function is given by
with the restrictions that
Furthermore, using the conservation of mass in the form (4.1.16)
it follows that the pressure
for this class of materials depends on the elastic dilatation \(J_e\) only.
5.4 Difference Between the Microstructural Vectors \({\mathbf {m}}_i\) and the Deformation Gradient \({\mathbf {F}}\)
Recall that the deformation gradient \({\mathbf {F}}\) satisfies the evolution equation (3.5.4)
It has been stated in Sect. 3.11 that \({\mathbf {F}}\) is not an internal state variable in the sense of Onat [31] since its initial value depends explicitly on an arbitrary choice of the reference configuration which cannot be measured in the current configuration.
In contrast, the microstructural vectors \({\mathbf {m}}_i\) for elastic response satisfy theEqs. (3.11.6)
and Sect. 5.3 explained how their initial conditions can be determined by experiments on identical samples of material in the current state so they are internal state variables in the sense of Onat [31].
To further explore the arbitrariness of \({\mathbf {F}}\), consider an initial zero-stress material state (3.11.9) for which the measured values \({\mathbf {m}}_i(0)\) of \({\mathbf {m}}_i\) form a right-handed orthonormal triad
Furthermore, define the elastic deformation tensor \({\mathbf {F}}_e\) by
By definition, this tensor satisfies the evolution equation and initial condition
Although \({\mathbf {m}}_i(0)\) are measurable in the initial state and \({\mathbf {m}}_i(t)\) are measurable in the current state, the tensor \({\mathbf {F}}_e\) is not a state variable since it is impossible to know the orientation of \({\mathbf {m}}_i(0)\) in the reference state from experiments on the material in its current state. In this regard, it is emphasized that there is no need for the second-order tensor \({\mathbf {F}}_e\) because the microstructural vectors \({\mathbf {m}}_i\) with their elastic deformation metric \(m_{ij}\) are sufficient to characterize constitutive equations for general anisotropic elastic response (5.3.4).
To be more specific, let \({\mathbf {M}}_i\) be an arbitrary right-handed orthonormal triad of constant vectors \({\mathbf {M}}_i\) and define \({\mathbf {F}}\) by
It follows that \({\mathbf {F}}\) satisfies the evolution equation and initial condition
However, since \({\mathbf {M}}_i\) are arbitrary orthonormal vectors and \({\mathbf {m}}_i(0)\) are orthonormal vectors, it also follows that the initial value of \({\mathbf {F}}\) is an arbitrary proper orthogonal rotation tensor
with arbitrariness of the specification of \({\mathbf {M}}_i\), which represents an arbitrary orientation of the body in a reference configuration that cannot be determined by experiments on the material in its current state.
5.5 Homogeneity and Uniformity
This section presents a brief discussion of notions of homogeneous deformation, a body that is materially uniform, a homogeneous body and a uniform material state. More detailed discussion of these notions can be found in ([47], Sect. 27.3).
Homogeneous Deformation
A body is said to experience a homogenous deformation during the time period \(t_1 \le t \le t_2\) if the velocity gradient \({\mathbf {L}}\) is independent of \({\mathbf {x}}\) during this time period
With the help of (3.13.3), it follows that the relative deformation gradient \({\mathbf {F}}_r\) from the time \(t_1\) depends on time only and satisfies equations
Moreover, with the help of (3.11.1), it follows that the total deformation gradient \({\mathbf {F}}\) satisfies the evolution equation and initial condition
where the value \(\bar{{\mathbf {F}}}({\mathbf {X}},t_1)\) of \({\mathbf {F}}\) at time \(t_1\) can be a function of position \({\mathbf {X}}\). Using the relative deformation gradient \({\mathbf {F}}_r(t)\), the exact solution of \({\mathbf {F}}\) during this time period is given by
In particular, it is noted that although the deformation is homogeneous during the time period \(t_1 \le t \le t_2\) the total deformation gradient \({\mathbf {F}}\) is not necessarily independent of space \({\mathbf {X}}\).
A Materially Uniform Body
A body is said to be materially uniform if the material functions that characterize the response of the material are explicitly independent of space. For example, a body made of an elastic material characterized by the strain energy function (5.2.1) associated with the Lagrangian formulation
is materially uniform if \(\Sigma \) depends on \({\mathbf {X}}\) only through the dependence of \({\mathbf {C}}= {\mathbf {F}}^T {\mathbf {F}}\) on \({\mathbf {X}}\)
To be precise, a superposed \(\hat{(\,\,\,)}\) has been used to indicate a specific functional dependence of \(\hat{\Sigma }({\mathbf {C}})\) on \({\mathbf {C}}\) only so the dependence of \(\Sigma \) on \({\mathbf {X}}\) must be evaluated using the chain rule of differentiation
Similarly, a body made of an elastic material characterized by the strain energy function (5.3.2) associated with the Eulerian formulation
is materially uniform if \(\Sigma \) depends on \({\mathbf {x}}\) only through the dependence of elastic deformation metric \(m_{ij}\) on \({\mathbf {x}}\)
so that
For more general material response, like that of elastic–inelastic materials discussed in Sect. 5.11 or thermoelastic materials and thermoelastic–inelastic materials discussed in Chap. 6, all constitutive functions, including those in evolution equations, must be explicitly independent of \({\mathbf {x}}\) for a body to be materially uniform.
A Uniform Material State
A body is said to be in a uniform material state if the body is materially uniform and each response function characterizing the material has a value that is independent of \({\mathbf {x}}\) for all points in the body. With regard to the Eulerian formulation, it is emphasized that the notion of a uniform material state need not be connected with any specification of a configuration of the body which places the body in space at a specified time.
Homogeneous Body
A body is said to be a homogeneous body if it is materially uniform and a configuration exits for which it is also in a uniform material state.
Examples
To better understand the difference between a body that is materially uniform and a homogeneous body, consider a cylindrical region that is materially uniform. Its solid cylindrical inner core is a homogeneous body that has a zero-stress uniform material state and its outer cylindrical shell is also a homogeneous body that has a zero-stress uniform material state. Moreover, consider the case when the outer radius of the zero-stress inner core is larger than the inner radius of the zero-stress outer cylindrical shell. By cooling the inner core or heating the outer cylindrical shell, it is possible to assemble the inner core inside of the outer cylindrical shell. Then, when the temperature in returned to a uniform value, the resulting body will have residual stresses in both of its inner and outer regions even if the outer surface of the cylindrical shell is traction free. The resulting body remains materially uniform but is not in a uniform material state. Moreover, it is no longer a homogeneous body since no configuration exists in which it can be in a uniform material state.
To better understand the notion of a uniform material state, consider a homogeneous elastic body which is in a uniform zero-stress material state. Then, load the body with a body force and traction vectors that cause inhomogeneous deformation. The body remains homogeneous but the deformed material state is not in a uniform material state.
Arbitrariness of the Reference Configuration
To examine the influence of arbitrariness of the choice of the reference configuration in the Lagrangian formulation, consider a homogeneous body made from an elastic material with the strain energy function
In these expressions, the deformation gradient \({\mathbf {F}}\) is measured from a reference configuration where the body is in a zero-stress uniform material state with \({\mathbf {F}}= {\mathbf {I}}\). Next, consider an arbitrary change in the reference configuration with \(\bar{{\mathbf {F}}}\) measured relative to the new reference configuration, such that
where \({\mathbf {A}}({\mathbf {X}})\) is an arbitrary second-order tensor function of \({\mathbf {X}}\) only with positive determinant. It then follows that the strain energy function can be expressed in terms of \(\bar{{\mathbf {C}}}\) and \({\mathbf {A}}\) in the form
Since \(\bar{{\mathbf {C}}}\) is the deformation relative to the new reference configuration and since \({\mathbf {A}}\) can be an arbitrary function of \({\mathbf {X}}\), it follows that the strain energy function \(\bar{\Sigma }(\bar{{\mathbf {C}}}, {\mathbf {A}})\) depends on \({\mathbf {X}}\) explicitly through the tensor \({\mathbf {A}}\). This means that the notions of the body being materially uniform or homogeneous depend on the variables being used to describe the response and on arbitrariness of the choice of the reference configuration.
In contrast, the Eulerian formulation for a homogeneous body with the strain energy function
which is deformed from a zero-stress uniform material state is insensitive to changes in the reference configuration with associated changes in the total deformation from the reference configuration.
Influence of Inelasticity
Elastic–inelastic response will be discussed in detail in Sect. 5.11 and in Chap. 6. To discuss the influence of inelasticity on the motions of a body that is materially uniform, a homogeneous body and a uniform material state it is sufficient to consider a homogeneous body with the strain energy function (5.5.14) which is initially in a zero-stress uniform material state with \(m_{ij} = \delta _{ij}\). Loading the body with a body force and surface tractions can cause inhomogeneous total deformation with nonzero inhomogeneous inelastic deformation rate. When all external loads are removed, this inhomogeneous inelastic deformation rate causes the body to attain a nonuniform material state with nonzero residual stresses. This unloaded body remains materially uniform but is no longer homogeneous since a configuration no longer exists for which it is also in a uniform material state.
5.6 Material Symmetry
Consider a general nonlinear homogeneous elastic material which is initially in a uniform zero-stress material state with initial orthonormal values \({\mathbf {M}}_i\) of the vectors \({\mathbf {m}}_i\)
Also, consider a set of experiments where tension specimens are machined from the material with different orientations relative to \({\mathbf {M}}_i\). The dependence of the measured nonlinear response for specimens with different orientations characterizes the material symmetry of the material. If the measured nonlinear response for different specimens is different, then the material is denoted as anisotropic. Whereas, if the measured nonlinear response for specimens with all possible orientations is the same relative to the orientation of the specimen for all deformations, then the material is denoted as isotropic.
To analyze this notion of material symmetry, consider a tension specimen that has a fixed orientation relative to another orthonormal triad of vectors \(\tilde{{\mathbf {M}}}_i\) defined by the orthonormal matrix \(H_{ij}\), such that
The deformation tensor
applies the elastic deformation metric \(m_{ij}\) to a specimen which has a specific alignment relative to the vectors \({\mathbf {M}}_i\) and the deformation tensor
applies the same elastic deformation metric \(m_{ij}\) to a specimen which has the same specific alignment relative to the vectors \(\tilde{{\mathbf {M}}}_i\). These two deformation tensors (5.6.3) and (5.6.4) are different and the components \(\bar{m}_{ij}\) of (5.6.4) relative to \({\mathbf {M}}_i\) are given by
Consequently, the elastic deformation applied to a specimen taken in, say the \({\mathbf {M}}_1\) direction, will be the same as that applied to a specimen taken in the \(\tilde{{\mathbf {M}}}_1\) direction for all values of \(m_{ij}\) and all orthogonal matrices \(H_{ij}\).
Now, the response of a nonlinear elastic material to arbitrary identical nonlinear deformations \(m_{ij}\) with different material orientations will be the same provided that
or
hold for all possible deformations \(m_{ij}, J_e\) and \(m_{ij}^{\prime }\). In other words, the functional forms of the strain energies \(\hat{\Sigma }\) and \(\tilde{\Sigma }\) remain form-invariant to a group of orthogonal transformations \(H_{ij}\) which characterize the material symmetries exhibited by a given material. For the case of crystalline materials these symmetry groups can be related to the different crystal structures.
For the most general anisotropic elastic response, the material has no symmetry, so the group of \(H_{ij}\) contains only the identity \(\delta _{ij}\). Whereas an isotropic elastic material has complete symmetry, so the group of \(H_{ij}\) is the full orthogonal group. Furthermore, it is important to emphasize that the notion of material symmetry is necessarily referred to identifiable material directions which are naturally represented by the vectors \({\mathbf {m}}_i\).
Moreover, the dependence of the functional forms \(\hat{\Sigma }(m_{ij})\) and \( \tilde{\Sigma }(J_e,m_{ij}^{\prime })\) on the material directions \({\mathbf {m}}_i\) is explicit and is used to determine the initial values of \({\mathbf {m}}_i\). In particular, any anisotropic response of the material is measured relative to the microstructural vectors \({\mathbf {m}}_i\), which causes the characterization of anisotropy to be independent of arbitrariness of a specification of a reference configuration. Furthermore, any indeterminacy of \({\mathbf {m}}_i\) in the current state must be compensated by the material symmetry of the strain energy function rendering this indeterminacy irrelevant for the response of the material.
5.7 Kinematic Constraints
Some materials have special properties that can be exploited to obtain approximate constitutive equations that simplify analytical solutions to problems. For example, rubber is a material with its resistance to volumetric deformation being much larger than its resistance to distortional deformations. This means that large changes in pressure occur for small changes in volume. From a mathematical point of view, it is convenient to consider a kinematic condition which constrains the material to be incompressible.
Using (3.11.5), it follows that an elastically incompressible material can only experience deformations which satisfy the kinematic constraint
Another example is a fiber reinforced composite with stiff fibers relative to the response of its matrix. For such a material it is possible to approximate the fibers as being inextensible. Using the microstructural vectors \({\mathbf {m}}_i\) in (3.11.6), it follows that a material fiber in the \({\mathbf {m}}_1\) direction will remain inextensible (in tension and compression) if the material satisfies the kinematic constraint
In general, consider a kinematic constraint of the form
which can be rewritten in the form
In particular, it is noted that \({\varvec{\Gamma }}\) is a symmetric second-order tensor that is independent of the rate \({\mathbf {D}}\)
and under SRBM it satisfies the transformation relation
Moreover, consider a general unconstrained material that is characterized by a constitutive equation \(\hat{{\mathbf {T}}}\) for the Cauchy stress \({\mathbf {T}}\). Next, consider a model of a constrained material for which \({\mathbf {T}}\) is additively separated into the constitutive part \(\hat{{\mathbf {T}}}\) and a part \(\bar{{\mathbf {T}}}\), called the constraint response, which enforces the kinematic constraint (5.7.3)
Although \(\hat{{\mathbf {T}}}\) characterizes the response to general deformations, its value in (5.7.7) is determined by evaluating \(\hat{{\mathbf {T}}}\) only for deformations that satisfy the imposed kinematic constraint. Moreover, \(\hat{{\mathbf {T}}}\) automatically satisfies the restriction
due to the balance of angular momentum and it transforms under SRBM, such that
Now, since the reduced form (4.4.10) of the balance of angular momentum requires \({\mathbf {T}}\) to be a symmetric tensor, the constraint response \(\bar{{\mathbf {T}}}\) must also be a symmetric tensor
In addition, \(\bar{{\mathbf {T}}}\) is assumed to be workless
and independent of the rate \({\mathbf {D}}\).
Next, multiplying (5.7.3) by an arbitrary scalar \(\Gamma \) and subtracting the result from (5.7.11) yields
Now, it is noted that the coefficient of \({\mathbf {D}}\) in this equation is a symmetric tensor that is independent of \({\mathbf {D}}\) and that this equation must hold for arbitrary rates \({\mathbf {D}}\) that satisfy the constraint (5.7.4). Moreover, since the constraint (5.7.4) is nontrivial, at least one component of \({\varvec{\Gamma }}\) is nonzero. For example, let \({\partial }G / {\partial }m_{33}\) be nonzero. This means that the component \(D_{33}\) can be used to satisfy the constraint (5.7.4) for arbitrary values of the other components \(D_{ij}\). By choosing the value of \(\Gamma \) in (5.7.12) so that the coefficient of \(D_{33}\) vanishes, and choosing the other components of \(D_{ij}\) arbitrarily, it follows that the constraint response \(\bar{{\mathbf {T}}}\) must be given by
with \(\Gamma \) being an arbitrary function of \({\mathbf {x}}\) and t that is determined by the equations of motion and boundary conditions. Due to (5.7.5) it can be seen that this form for \(\bar{{\mathbf {T}}}\) automatically satisfies the restriction (5.7.10) due to the balance of angular momentum. Moreover, since \({\mathbf {T}}\) in (5.7.7) appears in the balance of linear momentum and characterizes the response of the constrained material, the restriction (R-2) in (4.7.3b), which defines how the constitutive response of the material relative to its orientation is the same for all SRBM, requires the constraint response \(\bar{{\mathbf {T}}}\) to satisfy the transformation relation
which with the help of (5.7.6) requires the arbitrary function \(\Gamma \) to be unaffected by SRBM
In addition, since the constraint response \(\bar{{\mathbf {T}}}\) is workless (5.7.11), it follows that
so the constraint response does not influence the restriction (4.5.7) characterizing the rate of material dissipation.
For the special case of an incompressible material, the constraint response is given by
where \(\bar{p}\) is an arbitrary function of \({\mathbf {x}}\) and t that is determined by the equations of motion and boundary conditions.
Furthermore, it is noted that up to five independent kinematic constraints of the type (5.7.3) can be imposed simultaneously without causing \({\mathbf {T}}\) to be totally indeterminate.
5.8 Isotropic Nonlinear Elastic Materials
For an isotropic nonlinear elastic material the strain energy function (5.6.7) remains form-invariant for the full orthogonal group of \(H_{ij}\). This means that \(\Sigma \) can depend on \(m_{ij}^{\prime }\) only through its invariants. This also means that experiments on identical samples of the material in its current state cannot distinguish between the microstructural vectors \({\mathbf {m}}_1^{\prime }, {\mathbf {m}}_2^{\prime }\) and \( {\mathbf {m}}_3^{\prime }\) so the material response functions must be insensitive to this arbitrariness of \({\mathbf {m}}_i^{\prime }\). Consequently, the symmetric, positive-definite, unimodular tensor \({\mathbf {B}_e^\prime }\) defined in (3.11.19)
can be used to characterize the response of an elastically isotropic material to elastic distortional deformations.
To discuss the invariants of \(m_{ij}^{\prime }\) it is recalled from (3.3.17) and (3.11.24) that the unimodular elastic distortional deformation tensor \({\mathbf {B}_e^\prime }\) satisfies the equations
where use has been made of (3.11.14) to conclude that
Thus, the metric \(m_{ij}^{\prime }\) of elastic distortional deformations has only two nontrivial independent invariants which can be specified by
Consequently, for an isotropic elastic material the strain energy function takes the form
Next, using the evolution equation (3.11.5) for the elastic dilatation \(J_e\)
the evolution equations for the scalar measures \(\alpha _1\) and \( \alpha _2\) of elastic distortional deformation are given by
where \({\mathbf {B}_e^{\prime \prime }}\) is the deviatoric part of \({\mathbf {B}_e^\prime }\). Consequently, the material derivative of the strain energy function (5.8.5) is given by
Then, the condition that the material response of an elastic material is non-dissipative for all motions
requires the stress to be given in the form
In particular, notice that the deviatoric stress \({\mathbf {T}^{\prime \prime }}\) vanishes whenever \({\mathbf {B}_e^\prime }= {\mathbf {I}}\) so the condition (5.3.5) characterizing a zero-stress material state requires
A Compressible Neo-Hookean Material
Significant advances in the theory of finite elasticity were made by Rivlin and co-workers [2] studying the response of natural rubber, which is a material that can experience large distortional deformations and is relatively stiff to volumetric deformations. For such a material it is convenient to additively separate the strain energy function into a part that controls the response to elastic dilatation and depends only on \(J_e\) and another part that depends only on elastic distortional deformations through the invariants \(\alpha _1, \alpha _2\). For the simplest compressible Neo-Hookean the strain energy function is specified by
where \(\mu \) is the zero-stress shear modulus and \(f(J_e)\) is a function that satisfies the conditions
It then follows from (4.1.16)
and (5.8.10) that the pressure p and deviatoric stress \({\mathbf {T}^{\prime \prime }}\) for this material are given by
A Compressible Mooney–Rivlin Material
For a compressible Mooney–Rivlin material the strain energy function is specified by
where \(f(J_e)\) satisfies the conditions (5.8.13), \(\mu \) is the positive zero-stress shear modulus and C is a material constant. Then, using (5.8.14) the associated constitutive equations for p and \({\mathbf {T}^{\prime \prime }}\) are given by
A Specific Function for Dilatation
As a special case, consider a polyconvex function \(f(J_e)\) for the strain energy of dilatation given by (e.g., [45])
with the positive constant k being the zero-stress bulk modulus. It then follows from (5.8.15) that the pressure is given by
This function has the property that the pressure becomes infinite as \(J_e\) approaches zero and it approaches negative infinity as \(J_e\) approaches infinity.
Incompressible Neo-Hookean and Mooney–Rivlin Materials
Most often, Neo-Hookean and Mooney–Rivlin materials are considered to be incompressible. Specifically, using the constraint (5.7.1), the separation (5.7.7), the constraint response (5.7.17) and the constitutive equations (5.8.15), (5.8.17) and (5.8.19), it follows that the stress for an incompressible Neo-Hookean material is given by
and the stress for an incompressible Mooney–Rivlin material is given by
where \(\bar{p}\) is an arbitrary function of \({\mathbf {x}}\) and t determined by the equations of motion and boundary conditions.
An Elastic Material with a Quadratic Strain Energy Function
For an elastic material with a quadratic strain energy function, use is made of the elastic strains \(e_{ij}\) defined in (3.11.33)
relative to zero-stress material states defined in (3.11.9)
to express \(\Sigma \) in the form
where \(K_{ijkl}\) are constant components of a fourth-order stiffness tensor having the symmetries
It then follows from (5.3.4) that the Cauchy stress for this material is given by
To analyze the material symmetry of the strain energy function (5.8.24), use is made of the condition (5.6.6) to deduce that
for all strains \(e_{ij}\) which requires \(K_{ijkl}\) to satisfy the condition that
where \(H_{ij}\) is an orthogonal tensor which characterizes the symmetry of the material defined in its zero-stress material state with microstructural vectors \({\mathbf {m}}_i\) forming a right-handed orthonormal triad.
The following considers four cases of materials:
Case I: General Anisotropic
If the material posseses no symmetry then the symmetry group of \(H_{ij}\) consists only of \(H_{ij} = \delta _{ij}\) and the \(3^4=81\) constants \(K_{ijkl}\) are restricted only by the symmetries (5.8.25) which reduce the number of independent constants to the 21 constants given by
Case II: Symmetry About One Plane
If the material possesses symmetry about the plane normal to \({\mathbf {m}}_3\) in a zero-stress material state then the restrictions (5.8.28) must hold for the group \(H_{ij}\) that includes
so that from (5.8.29) and (5.8.30), it follows that any component in which the index 3 appears an odd number of times must vanish
Thus, the remaining 13 independent constants are given by
Case III: Symmetry About Two Orthogonal Planes
If the material possesses symmetry about both planes with normals the \({\mathbf {m}}_3\) and \({\mathbf {m}}_2\) in a zero-stress material state, then the restrictions (5.8.28) must hold for the group \(H_{ij}\) that includes (5.8.30) and
so that from (5.8.32) and (5.8.33), it follows that any component in which the index 2 appears an odd number of times must vanish
Thus, the remaining 9 independent constants are given by
Notice from (5.8.35) that the index 1 only appears an even number of times so that the material also possesses symmetry about the plane normal to \({\mathbf {m}}_1\) in a zero-stress material state. This stiffness characterizes an orthotropic elastic material.
Case IV: Isotropic Elastic Material
If the material possesses symmetry with respect to the full orthogonal group then the material is called isotropic with a center of symmetry. Using the results in Appendix E, it follows that the material is characterized by only two independent constants \(\lambda \) and \(\mu \), called Lame’s constants, such that
and the fourth-order tensor \(K_{ijkl}\) can be expressed in the form
It also follows that the strain energy (5.8.24) and the stress (5.8.26) can be written in the forms
Notice that this strain energy is a function of the invariants of \(e_{ij}\), as it should be for an isotropic material.
Linearized Constitutive Equations
To obtain the fully linearized constitutive equation, it is convenient to consider the initial state of the material to be at zero stress with the vectors \({\mathbf {m}}_i\) specified by the orthonormal triad \({\mathbf {M}}_i\), such that
Recalling that the displacement \({\mathbf {u}}\) relative to this initial state is given by
and taking \(t_n= 0\) in (3.13.3), the relative deformation gradient \({\mathbf {F}}_r\) is given by
Then, neglecting quadratic terms in the displacement \({\mathbf {u}}\) and its derivatives, it follows from (3.13.9) that \({\mathbf {m}}_i\) can be approximated by
Next, separating the displacement gradient into its symmetric and skew-symmetric parts like in (4.10.7) yields
so the vectors \({\mathbf {m}}_i\) can be approximated by
It then follows that the metric \(m_{ij}\) and the strains \(e_{ij}\) are approximated by
and the stress is approximated by
Restrictions on the Material Constants
From physical considerations it is expected that any strain from a zero-stress material state should cause an increase in strain energy. Mathematically this means that the strain energy function is positive-definite
Recalling that the strain \(e_{ij}\) can be separated into its spherical and deviatoric parts
the isotropic strain energy function (5.8.38) can be rewritten in the form
Since the terms \(e_{ii}\) and \(e_{ij}^{{\prime }{\prime }} e_{ij}^{{\prime }{\prime }}\) are independent quantities, this strain energy will be positive-definite whenever
For the linearized theory, \(e_{ii}\) characterizes dilatational deformations and \(e_{ij}^{{\prime }{\prime }}\) characterizes distortional deformations.
Moreover, it is noted that this isotropic elastic material with a quadratic strain energy function can be characterized by any two of the following material constants: \(\lambda \) (Lame’s constant); \(\mu \) (shear modulus); E (Young’s modulus); \(\nu \) (Poisson’s ratio); or k (bulk modulus), which are interrelated by the expressions in Table 5.1. Using these expressions it can be shown that the restrictions (5.8.50) also require
Limitations of a Quadratic Strain Energy Function
The anisotropic elastic material characterized by (5.8.24) and (5.8.26), and the isotropic elastic material characterized by (5.8.38) both have a strain energy function that is quadratic in the strains \(e_{ij}\), with the Cauchy stress \({\mathbf {T}}\) depending nonlinearly on \(J_e\) and \(e_{ij}\) since the vectors \({\mathbf {m}}_i\) also depend on the strains \(e_{ij}\). These constitutive equations are valid for large rotations and moderate strains \(e_{ij}\).
To see that these quadratic strain energy functions are limited to moderate strains consider the simple case of an isotropic elastic material (5.8.38) experiencing uniaxial stress in the \({\mathbf {m}}_1\) direction for which
where \({\mathbf {e}}_i\) are fixed rectangular Cartesian base vectors. In these expressions, a is the axial stretch and b is the lateral stretch, both measured from a zero-stress material state. For uniaxial stress
and the constitutive equations yield the restrictions
where use has been made of Table 5.1 to write \(\lambda \) in terms of the zero-stress shear modulus \(\mu \) and Poisson’s ratio \(\nu \). Then, the solution of these equations is given by
and the restrictions on the strains can be solved to obtain
For Poisson’s ratio in the range
it can be seen that the maximum axial stretch \(a_{max}\) occurs when b vanishes and that the maximum lateral stretch \(b_{max}\) occurs when a vanishes, for which
These results are unphysical because they indicate that infinite tension causes a finite axial stress with zero volume and that the material can be compressed to zero length with a finite cross section, zero volume and zero stress.
In contrast, the stress \({\mathbf {T}}\) for the compressible Neo-Hookean material characterized by (5.8.1), (5.8.12), (5.8.15), (5.8.18) and (5.8.19) is given by
which for uniaxial stress (5.8.53) yields the restrictions
The solution of these equations can be parameterized by the axial stress \(T_{11}\). Specifically, (5.8.60b) can be solved for \(J_e\) to obtain
Then, using the expression (5.8.52) for \(J_e\), the lateral stretch b is determined by
so Eq. (5.8.60a) can be rewritten as a cubic equation for the axial stretch a of the form
which can be solved analytically choosing the root for which \(a=1\) when \(T_{11}=0\).
Figure 5.1 shows the responses predicted for uniaxial tension by the quadratic strain energy function (Q) and the Neo-Hookean strain energy function (NH) for \(\nu =1/3\). Figure 5.1a, b plot the normalized axial stress \(T_{11}\) for different axial stretch regions, Fig. 5.1c plots the lateral stretch b, Fig. 5.1d plots the dilatation \(J_e\) and Fig. 5.1e plots the nominal Poisson ratio \(\bar{\nu }\) defined by
From these figures it can be seen that the two models predict nearly identical response only for a small axial stretch range about zero stress. Most importantly it can be seen that the Neo-Hookean model predicts physically reasonable results for the full range of stretch. Orthotropic invariants for thermoelastic–inelastic soft materials which can experience large thermoelastic deformations are discussed in Sect. 6.6.
5.9 Viscous and Inviscid Fluids
This section discusses purely mechanical constitutive equations for compressible viscous and inviscid fluids. From a physical point of view it is clear that the stress \({\mathbf {T}}\) in a compressible fluid must depend on the elastic dilatation \(J_e\), which is a measure of the fluid’s density. Moreover, experience with stirring honey indicates that it is harder to stir the honey faster. This suggests that \({\mathbf {T}}\) will also depend on the velocity gradient \({\mathbf {L}}\). In addition, the pressure required to pump a viscous fluid through a pipe depends on the flow rate. Therefore, \({\mathbf {T}}\) might also depend on the velocity \({\mathbf {v}}\). Based on these observations, as a first attempt to propose a constitutive equation for fluids, it is assumed that the stress can be expressed in the form
where for convenience \({\mathbf {L}}\) has been separated into its symmetric part \({\mathbf {D}}\) and its skew-symmetric part \({\mathbf {W}}\).
In the following, use will be made of invariance under SRBM to develop restrictions on the functional form (5.9.1). Since (5.9.1) must hold for all motions it must also hold for SRBM so that
However, under SRBM the Cauchy stress \({\mathbf {T}}\) transforms by
where \({\mathbf {Q}}\) is a proper orthogonal tensor function of time only. Thus, the functional form (5.9.1) must satisfy the restrictions
Recalling that under SRBM
equation (5.9.4) requires
Since (5.9.6) must hold for all motions and all SRMB, necessary restrictions on the functional form \(\tilde{{\mathbf {T}}}\) can be obtained by considering special SRBMs.
Superposed Translational Velocity
This case considers superposed translational velocity with
Substituting (5.9.7) into (5.9.6) yields
Since this equation must hold for arbitrary values of \(\dot{{\mathbf {c}}}\) and the right-hand side is independent of \(\dot{{\mathbf {c}}}\), it follows that the Cauchy stress cannot depend on the velocity \({\mathbf {v}}\). Thus, \({\mathbf {T}}\) must be expressed as another function \(\bar{{\mathbf {T}}}\) of \(J_e, {\mathbf {D}}\) and \({\mathbf {W}}\) only
and the restriction (5.9.6) requires
Superposed Rate of Rotation
This case considers superposed rate of rotation. Since (5.9.10) must hold for all skew-symmetric tensors \({\varvec{\Omega }}\) and the right-hand side of this equation is independent of \({\varvec{\Omega }}\), it follows that the Cauchy stress \({\mathbf {T}}\) cannot depend on the spin tensor \({\mathbf {W}}\). Thus, the most general viscous fluid is characterized by the constitutive equation
where \(\hat{{\mathbf {T}}}(J_e)\) characterizes the elastic response due to dilatation and \(\overset{v}{{\mathbf {T}}}(J_e,{\mathbf {D}})\) characterizes the viscous response. Also, these constitutive equations must satisfy the restrictions that under SRBM
which require \(\hat{{\mathbf {T}}}\) to be an isotropic tensor and \(\overset{v}{{\mathbf {T}}}\) to be an isotropic tensor function of \({\mathbf {D}}\).
Reiner-Rivlin Fluid
Since the restrictions (5.9.12) must hold for all proper orthogonal \({\mathbf {Q}}\) the function \(\overset{v}{{\mathbf {T}}}\) is called an isotropic tensor function of its argument \({\mathbf {D}}\). This notion of an isotropic tensor function should not be confused with the notion of an isotropic tensor as discussed in Appendix E. Furthermore, since the restriction (5.9.12) is unaltered by the interchange of \({\mathbf {Q}}\) with \(-{\mathbf {Q}}\), it follows that \(\overset{v}{{\mathbf {T}}}\) is a hemotropic function of \({\mathbf {D}}\) (isotropic with a center of symmetry). Now, using a result from the theory of invariants, it follows that the most general form of \(\hat{{\mathbf {T}}}\) and \(\overset{v}{{\mathbf {T}}}\) can be expressed as
where \(\hat{p}(J_e)\) is a function of \(J_e\) only, \(d_0, d_1\) and \(d_2\) are scalar functions of \(J_e\) and the three independent invariants of \({\mathbf {D}}\). Alternatively, using the separation of deformation rate into dilatational and distortional deformation rates, \(\overset{v}{{\mathbf {T}}}\) can be written in the form
where \({\mathbf {D}^{\prime \prime }}\) is the deviatoric part of \({\mathbf {D}}\), \(\bar{d}_0, \bar{d}_1\) and \(\bar{d}_2\) are scalar functions of \(J_e, {\mathbf {D}}\cdot {\mathbf {I}}\), the two independent invariants of \({\mathbf {D}^{\prime \prime }}\) and the function \(\text {Sign}(x)\) is defined by
The constitutive equation characterized by (5.9.11) with the expressions (5.9.13) for the stress \({\mathbf {T}}\) described a Reiner-Rivlin fluid. An alternative form of this Reiner-Rivlin fluid is characterized by (5.9.11) for the total stress \({\mathbf {T}}\), (5.9.13) for the elastic stress \(\hat{{\mathbf {T}}}\) and (5.9.14) for the viscous stress \(\overset{v}{{\mathbf {T}}}\). Moreover, the strain energy is taken to be a function of the dilatation
so the rate material dissipation (4.5.7) requires
where use has been made of the expression (5.8.14) for the elastic dilatation \(J_e\).
Inviscid Fluid
For an inviscid fluid the Cauchy stress is independent of the rate of deformation \({\mathbf {D}}\) so that \(\overset{v}{{\mathbf {T}}}\) vanishes in (5.9.13) and (5.9.14) and (5.9.17) requires
Since the coefficient of \({\mathbf {D}}\cdot {\mathbf {I}}\) is independent of rate, it can be shown that for an inviscid fluid
This means for an inviscid fluid the traction vector \({\mathbf {t}}\) always acts normal to the surface on which it is applied
and the pressure \(\hat{p}\) is a function of the elastic dilatation \(J_e\) only.
Restrictions on a Reiner-Rivlin Fluid
Without specifying the functional form of \(\overset{v}{{\mathbf {T}}}\) it is not possible to obtain further restrictions using the dissipation equation (5.9.17). However, it is reasonable to assume that the elastic part of the stress is the same as that for an inviscid fluid which is given by (5.9.19) so the stress and the rate of material dissipation (5.9.17) associated with the viscous stress (5.9.14) become
with the rate of material dissipation restricting the functional form for the viscous stress \(\overset{v}{{\mathbf {T}}}\). Sufficient but not necessary conditions for \({\mathcal {D}}\ge 0\) are given by
Newtonian Viscous Fluid
A Newtonian viscous fluid is a special case of a Reiner-Rivlin fluid in which the viscous stress \(\overset{v}{{\mathbf {T}}}\) is a linear function of the rate of deformation \({\mathbf {D}}\). For this case, \(\overset{v}{{\mathbf {T}}}\) reduces to
where \(\lambda \) and \(\mu \) are scalar functions of \(J_e\) only. Moreover, it follows that \(\overset{v}{{\mathbf {T}}}\) can be rewritten in the alternative form
which shows that the total pressure p has an elastic part \(\hat{p}\) and a viscous part \(\overset{v}{p}\) that depends on the rate of volume expansion \({\mathbf {D}}\cdot {\mathbf {I}}\) with \(\lambda \) being the dilatational viscosity coefficient. Also, the rate of material dissipation (4.5.7) is satisfied provided that
5.10 Viscous Dissipation
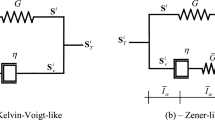
A simple generalized nonlinear Kelvin–Voigt model (see Fig. 5.2) for viscous dissipation can be proposed by adding the response of the viscous part of a Newtonian viscous fluid to that of a general elastic material. Specifically, for this model the Cauchy stress \({\mathbf {T}}\) is proposed in the form
where \(\hat{{\mathbf {T}}}\) is the response of a general nonlinear elastic material with strain energy \(\Sigma \) that satisfies equation
for all motions and \(\lambda , \mu \) are non-negative functions of \(J_e\) that control the viscosity to dilatational deformation rate and to distortional deformation rate, respectively. Also, for this material the rate of material dissipation (4.5.7) requires
which is automatically satisfied. Moreover, it follows that when \(\lambda \) and \(\mu \) are both positive, dissipation continues until the rate of deformation vanishes \({\mathbf {D}}= 0\) with \({\mathbf {T}}= \hat{{\mathbf {T}}}\).
If the elastic part of the response is isotropic then the strain energy is given by (5.8.5) and the stress \(\hat{{\mathbf {T}}}\) is given by (5.8.10). Alternatively, if the elastic part of the response is anisotropic then the strain energy is given by (5.3.9) and the stress \(\hat{{\mathbf {T}}}\) is given by (5.3.11). For either case, this model proposes isotropic viscous dissipation.
5.11 Elastic–Inelastic Materials
Figure 5.3a shows a sketch of the stress–strain response of a typical metal to uniaxial stress loading. The quantity \(T_{11}\) is the total axial component of the Cauchy stress \({\mathbf {T}}\) and the quantity \(E_1\) is the total axial extension. The material is loaded in tension along the path OABCD, unloaded along DE, reloaded along EFGH, unloaded along HI and reloaded in compression along IJKL. Inspection of the points C, E and L in Fig. 5.3a reveals that the stress in an elastic–plastic material can have significantly different values for the same value of axial extension \(E_1\). This means that the response of an elastic–plastic material depends on the past history of deformation (i.e., the responses to the deformation histories OABC, \(OAB-E\) and \(OAB-L\) are different).
The points A, F, J in Fig. 5.3a represent points on the loading paths beyond which the stress–strain relationship becomes nonlinear. Although the curve OABCD is nonlinear it is not possible to determine whether the response is elastic or elastic–inelastic until unloading is considered. Since the response shown in Fig. 5.3a does not unload along the same loading path, it is clear that the response is not elastic, but rather is elastic–inelastic. Moreover, B, G and K represent the points on the loading paths beyond which some detectable value of strain relative to the peak strain (normally taken to be \(0.2\%\)) remains when the material is unloaded to zero stress. These points are called the yield points and deformation beyond them causes permanent changes in the response of the material. It is also important to mention that the paths BCD, GH and KL represent strain hardening paths where the magnitude of the stress increases with increasing effective inelastic deformation.
To model the material response shown in Fig. 5.3a it is common to separate the response into two parts: elastic response which is reversible and inelastic response which is irreversible. Also, the material response is idealized as shown in Fig. 5.3b by making the following assumptions:
- (a):
-
There are distinct yield points (A, B), (D, F, G) and (J, K) that form the boundary between elastic and inelastic responses.
- (b):
-
Unloading along DE and reloading along EF follow the same path.
Lagrangian Formulations
Lagrangian formulations of plasticity (inelasticity) enrich the theory of hyperelastic solids with a plastic deformation measure that captures observed effects of history and rate dependence of material response. A summary of the small deformation theory within the context of thermodynamics can be found in the classical paper by Naghdi [28]. Unfortunately, the large deformation theory of plasticity still is plagued with controversies, some of which have been discussed in the critical review [29]. This section discusses three prominent formulations of large deformation theory: one by Green and Naghdi [16], another attributed to Bilby et al. [6], Kröner [21] and Lee [23], and another attributed to Besseling [4].
Green–Naghdi Formulation
Green and Naghdi [16] developed a large deformation thermomechanical theory of plasticity. Confining attention to the purely mechanical response and using the notation in this book, this theory introduces the total deformation gradient \(\mathbf{F}\) and the right Cauchy–Green deformation tensor \({\mathbf {C}}\), which satisfy equations
The theory of hyperelasticity is enriched by introducing a symmetric plastic deformation tensor \({\mathbf {C}}_p\) (similar to \({\mathbf {C}}\)) and a scalar measure of isotropic hardening \(\kappa \) by the evolution equations
where \(\bar{{\mathbf {A}}}_p\) controls the direction of plastic deformation rate, \(\Gamma \) is a non-negative function that controls the magnitude of plastic deformation rate \({\mathbf {A}}_p\) and H controls the rate of hardening. For metals, plastic deformation rate is isochoric so \(\mathbf{C}_p\) remains unimodular, which requires
Under SRBM the total deformation tensor \({\mathbf {F}}\), the right Cauchy–Green tensor \({\mathbf {C}}\), the plastic deformation \({\mathbf {C}}_p\) and the hardening variable \(\kappa \) transform to \({\mathbf {F}}^+, {\mathbf {C}}^+, {\mathbf {C}}_p^+\) and \(\kappa ^+\), such that
which place restrictions on the functional forms of \(\Gamma , \bar{{\mathbf {A}}}_p, H\).
In this theory, the strain energy \(\Sigma \) is assumed to be a function of \(\mathbf{F}, {\mathbf {C}}_p\) and \( \kappa \) but since \(\Sigma \) is uninfluenced by SRBM, it must depend on \(\mathbf{F}\) only through the deformation tensor \(\mathbf{C}\) so that
For both rate-independent and rate-dependent material response, the constitutive equation for stress is taken in the form
Moreover, the rate of material dissipation (4.5.7) requires
which places restrictions on the functional forms of \(\Sigma , \bar{{\mathbf {A}}}_p\) and H.
In addition to solving the balance of linear momentum (4.4.5), this theory requires solution of the evolution equations (5.11.1) and (5.11.2) with initial conditions
Bilby, Kröner, Lee Formulation
Bilby et al. [6], Kröner [21] and Lee [23] introduced a formulation that depends on a second-order non-symmetric plastic deformation tensor \({\mathbf {F}}_p\) (similar to \({\mathbf {F}}\)) determined by an evolution equation of the form
where \(\bar{{\varvec{\Lambda }}}_p\) controls the direction of plastic deformation rate and \(\Gamma \) is a non-negative function that controls the magnitude of plastic deformation rate \(\dot{{\mathbf {F}}}_p\). Again, for metal plasticity the plastic deformation rate is isochoric so \({\mathbf {F}}_p\) is unimodular and \(\bar{\varvec{\Lambda }}_p\) is restricted, such that
Moreover, an elastic deformation tensor \({\mathbf {F}}_e\) is defined by the multiplicative form
and a hardening variable \(\kappa \) is introduced which satisfies the evolution equation in (5.11.2). Usually this equation is written in the form \({\mathbf {F}}= {\mathbf {F}}_e {\mathbf {F}}_p\), which suggests that \({\mathbf {F}}_p\) transforms the reference configuration into an intermediate zero-stress configuration and \({\mathbf {F}}_e\) transforms an intermediate configuration into the current configuration. For general inhomogeneous deformations, \({\mathbf {F}}\) describes a compatible field with the position \({\mathbf {x}}\) of a material point in the current configuration being a differentiable function of the position \({\mathbf {X}}\) of the same material point in the reference configuration. However, in general, both \({\mathbf {F}}_p\) and \({\mathbf {F}}_e\) are incompatible tensors which are not determined by differentiation of deformation fields so unloading the material yields a configuration which has residual stresses. In other words, in general, it is not possible to unload the material to a zero-stress intermediate configuration.
The constitutive equations are restricted so that under SRBM, \(\, \Gamma , \bar{\varvec{\Lambda }}_p\) and \({\mathbf {F}}_p\) transform to \(\Gamma ^+, \bar{\varvec{\Lambda }}_p^+\) and \( {\mathbf {F}}_p^+\), such that
It then follows from (5.11.4), (5.11.11) and (5.11.12) that under SRBM the elastic deformation tensors \({\mathbf {F}}_e\) and \({\mathbf {C}}_e\) transform to \({\mathbf {F}}_e^+\) and \({\mathbf {C}}_e^+\), such that
Using the fact that
it follows that \({\mathbf {F}}_e\) and \({\mathbf {C}}_e\) satisfy the evolution equations
In this theory, the strain energy \(\Sigma \) is assumed to be a function of \({\mathbf {F}}_e\) and \( \kappa \) but since \(\Sigma \) is uninfluenced by SRBM, it must depend on \({\mathbf {F}}_e\) only through the deformation tensor \({\mathbf {C}}_e\) so that
For both rate-independent and rate-dependent material response the stress is specified by
and the rate of material dissipation (4.5.7) requires
which places restrictions on the functional forms of \(\Sigma , \bar{\varvec{\Lambda }}_p\) and H.
In addition to solving the balance of linear momentum (4.4.5), this theory requires solution of the evolution equations (5.11.1) for \({\mathbf {F}}\), (5.11.2) for \(\kappa \) and (5.11.9) for \({\mathbf {F}}_p\) with initial conditions
Besseling Formulation
The formulation discussed by Besseling [4] (see also Besseling and van der Giessen [5]) was motivated by the work of Eckart [12] and Mandel [26] and can be interpreted as proposing an evolution equation for a second-order non-symmetric tensor \(\mathbf{F}_e\) with positive determinant directly by the evolution equation
where \({\mathbf {L}}_e\) is the elastic deformation rate, \(\bar{{\mathbf {L}}}_p\) controls the direction of inelastic rate \({\mathbf {L}}_p\), \(\Gamma \) is a non-negative function that controls the magnitude of inelastic rate and \({\mathbf {F}}_e\) measures elastic deformations from a zero-stress intermediate configuration.
Moreover, the evolution equation (5.11.20) will be identical to the evolution equation for \({\mathbf {F}}_e\) in (5.11.15) if \(\bar{{\mathbf {L}}}_p\) is specified by
which under SRBM satisfies the transformation relation
For this theory, the strain energy function \(\Sigma \) is specified by (5.11.16), the stress \({\mathbf {T}}\) is specified by (5.11.17) and the rate of material dissipation \({\mathcal {D}}\) requires (5.11.18). In addition to solving the balance of linear momentum (4.4.5), this theory requires solution of the evolution equations (5.11.20) for \({\mathbf {F}}_e\) and (5.11.2) for \(\kappa \) with initial conditions
Unphysical Arbitrariness of the Lagrangian Formulation
Unphysical arbitrariness of the Lagrangian formulation has been discussed in a series of papers [36,37,38]. Specifically, for a fixed value of elastic deformation \({\mathbf {F}}_e\) and an arbitrary nonsingular tensor \({\mathbf {A}}\) with \(\text {det} {\mathbf {A}}> 0\), it follows from (5.11.11) that
This means that the reference configuration associated with \({\mathbf {F}}\) and \({\mathbf {F}}_p\) is arbitrary. In particular, \({\mathbf {A}}\) can be used to set the initial value of \({\mathbf {F}}= {\mathbf {I}}\) or to set the initial value of \({\mathbf {F}}_p = {\mathbf {I}}\) so the choice of total deformation measure \({\mathbf {F}}\) or the plastic deformation measure \({\mathbf {F}}_p\) is arbitrary.
In addition, the elastic deformation tensor \({\mathbf {F}}_e\) and the plastic deformation tensor \({\mathbf {F}}_p\) in (5.11.11) are usually presented as a separation of the total deformation gradient \({\mathbf {F}}\) into elastic and plastic parts
Using the expression (3.3.1a) which shows that \({\mathbf {F}}\) transforms a material line element \(d{\mathbf {X}}\) in the reference configuration to its deformed line element \(d{\mathbf {x}}\) in the current configuration, the separation (5.11.25) is often interpreted as \({\mathbf {F}}_p\) transforming the line element \(d{\mathbf {X}}\) to \(d{\mathbf {y}}\) in an intermediate configuration and \({\mathbf {F}}_e\) transforming \(d{\mathbf {y}}\) to \(d{\mathbf {x}}\)
Letting \(\mathbf{O}\) be a proper orthogonal tensor
the separation (5.11.25) can be rewritten in the form
which shows that both the plastic deformation tensor \({\mathbf {F}}_p\) and the elastic deformation tensor \({\mathbf {F}}_e\) contain arbitrariness to rotations of the intermediate configuration.
Eulerian Formulation of Elastically Anisotropic Elastic–Inelastic Materials
The Eulerian formulation for nonlinear elastic solids in Sect. 5.3 can be generalized for elastically anisotropic elastic–inelastic materials by modifying the evolution equation for the microstructural vectors \({\mathbf {m}}_i\) to include a second-order tensor \({\mathbf {L}}_p\) that characterizes the inelastic rate. Specifically, an Eulerian formulation for elastically anisotropic inelastic material response, which was motivated by the work of Eckart [12] and Leonov [24], was developed in [35]. The main idea is to model the following physical features of inelastic flow in metals:
-
elastic deformations of the atomic lattice cause stress.
-
elastic deformations of the atomic lattice remain small after dislocations have moved through the lattice.
-
the atoms in a specific lattice change with time as dislocations move through the lattice.
-
edges of the parallelepiped formed by the atomic lattice do not rotate as material line elements.
In this model, the elastic deformations and orientation of the atomic lattice are modeled by the parallelepiped formed by the triad \({\mathbf {m}}_i \, (i=1,2,3)\) of linearly independent microstructural vectors
where the elastic dilatation \(J_e\) is an internal state variable that can be determined by the current state of stress in the material. These microstructural vectors are determined by the evolution equations
where \(\Gamma \) controls the magnitude and \(\bar{{\mathbf {L}}}_p\) controls the direction of the inelastic rate tensor \({\mathbf {L}}_p\), both of which require a constitutive equation. If \({\mathbf {L}}_p\) vanishes, then the solution of (5.11.30) causes \({\mathbf {m}}_i\) to evolve as material line elements so these equations characterize an Eulerian formulation of a general anisotropic hyperelastic solid. Otherwise, \({\mathbf {m}}_i\) characterize elastic deformations and the orientation of the atomic lattice, which is not directly connected to material line elements.
In addition, an isotropic hardening variable \(\kappa \) is determined by the evolution equation
where H is a function that controls the rate of hardening. More general directional hardening can be modeled by introducing directional hardening variables \(\beta _{ij} = \beta _{ji}\) which satisfy the evolution equations
where \(H_{ij} = H_{ji}\) are functions that control the relative magnitudes of \(\beta _{ij}\). These functions should not be confused with the components \(H_{ij}\) of the proper orthogonal matrix used to discuss material symmetry in Sect. 5.6.
Under SRBM the microstructural vectors \({\mathbf {m}}_i\), the inelastic deformation rate \(\Gamma \), its direction \(\bar{{\mathbf {L}}}_p\), the hardening variables \(\kappa \) and \(\beta _{ij}\) and the hardening functions H and \(H_{ij}\) transform to \({\mathbf {m}}_i^+, \Gamma ^+, \bar{{\mathbf {L}}}_p^+, \kappa ^+, \beta _{ij}^+, H^+\) and \(H_{ij}^+\), such that
The strain energy \(\Sigma \) is assumed to be a function of \({\mathbf {m}}_i, \kappa \) and \(\beta _{ij}\), but since \(\Sigma \) must be unaffected by SRBM it can depend on \({\mathbf {m}}_i\) only through the metric \(m_{ij}\) of elastic deformation, which satisfies equations
Moreover, using (5.11.30) and (5.11.34), it follows that the elastic metric satisfies the evolution equation
where the inelastic deformation rate \({\mathbf {D}}_p\) is defined by
For this model the strain energy function and the stress are proposed in the forms
It then follows that the rate of material dissipation (4.5.7) requires
Without specifying details of inelastic deformation rate and the hardening functions \(\Gamma , \bar{{\mathbf {D}}}_p, H\) and \(H_{ij}\) it is not possible to obtain necessary restrictions on the constitutive equation for stress. However, motivated by the constitutive equation (5.3.4) for a hyperelastic material and by the requirement that the constitutive equation for elastic–inelastic response contain that for a hyperelastic material as a special case, the constitutive equation for stress in an elastic–inelastic material is specified by
Then, the rate of material dissipation (4.5.7) requires the total dissipation due to the inelastic rate and the rate of hardening to be non-negative
Also, the constitutive equation for stress is assumed to be restricted so that a zero-stress material state is characterized by
where \(\delta _{ij}\) is the Kronecker delta. This means that the triad \({\mathbf {m}}_i\) has been defined so that \({\mathbf {m}}_i\) are orthonormal vectors in a zero-stress material state. In particular, it is noted that the vectors \({\mathbf {m}}_i\) in any zero-stress material state are usually not parallel to the lattice vectors in that state.
Since \({\mathbf {m}}_i\) are linearly independent and not necessarily orthonormal in the current configuration, it is convenient to introduce their reciprocal vectors \({\mathbf {m}}^i\) by
so that
Moreover, the evolution equations (5.11.30) for \({\mathbf {m}}_i\), (5.11.31) for \(\kappa \) and (5.11.32) for \(\beta _{ij}\) require initial conditions
Separation of Elastic Dilatation and Distortional Deformations
To introduce separate control over the response of the material to dilatation and distortional rates of deformation, it is convenient to use the elastic dilatation \(J_e\), the distortional deformation vectors \({\mathbf {m}}_i^{\prime }\) and the elastic distortional deformation metric \(m_{ij}^{\prime }\), which satisfy the Eqs. (5.11.43), (3.11.14), (5.11.30) and (3.11.16),
where \({\mathbf {L}^{\prime \prime }}\) is the deviatoric part of the velocity gradient \({\mathbf {L}}\) and \(\bar{{\mathbf {L}}}_p^{\prime \prime }\) is the deviatoric part of \(\bar{{\mathbf {L}}}_p\). Then, the strain energy function and stress are proposed in the forms
and the rate of material dissipation (4.5.7) requires
Again, without specifying details of the inelastic rate and the hardening functions \(\Gamma , \bar{{\mathbf {D}}}_p, H\) and \( H_{ij}\) it is not possible to obtain necessary restrictions on the constitutive equation for stress. However, motivated by the constitutive equation (5.3.11) for a hyperelastic material and by the requirement that the constitutive equation for elastic–inelastic response contain that for a hyperelastic material as a special case, the constitutive equation for stress in an elastic–inelastic material is specified by
Then, the rate of material dissipation requires the total dissipation due to the inelastic rate and the rate of hardening to be non-negative
Also, the constitutive equation for stress is assumed to be restricted so that a zero-stress material state is characterized by
This means that the triad \({\mathbf {m}}_i'\) has been defined so that \({\mathbf {m}}_i'\) are orthonormal vectors in a zero-stress material state.
Moreover, the evolution equations (5.11.43) for \(J_e\), (5.11.45) for \({\mathbf {m}}_i^{\prime }\), (5.11.31) for \(\kappa \) and (5.11.32) for \(\beta _{ij}\) require initial conditions
Eulerian Formulation of Elastically Isotropic Elastic–Inelastic Materials
For elastically isotropic elastic–inelastic materials experiments on identical samples of the material in its current state cannot distinguish between the microstructural vectors \({\mathbf {m}}_1^{\prime }, {\mathbf {m}}_2^{\prime }\) and \({\mathbf {m}}_3^{\prime }\) so the material response functions must be insensitive to this arbitrariness of \({\mathbf {m}}_i^{\prime }\). Consequently, \(J_e\) in (5.11.29) characterizes the elastic dilatation and satisfies the evolution equation (5.11.43). Also, the symmetric, positive-definite, unimodular tensor \({\mathbf {B}_e^\prime }\) defined in (5.8.1)
characterizes elastic distortional deformations. Using (5.11.45), it can be shown that \({\mathbf {B}_e^\prime }\) satisfies the evolution equation
where \(\bar{{\mathbf {L}}}_p^{\prime \prime }\) is the deviatoric part of \(\bar{{\mathbf {L}}}_p\). This evolution equation automatically satisfies the condition (3.11.26) that \({\mathbf {B}_e^\prime }\) remains unimodular [\(\det {\mathbf {B}_e^\prime }= 1\)] since
Following the work of Eckart [12] and Leonov [24] for elastically isotropic elastic–inelastic materials, an evolution equation for the elastic distortional deformation tensor \({\mathbf {B}_e^\prime }\) can be proposed directly and independently of the microstructural vectors \({\mathbf {m}}_i^{\prime }\). This means that instead of specifying a constitutive equation for \(\bar{{\mathbf {L}}}_p\), it is possible to propose an evolution equation for \({\mathbf {B}_e^\prime }\) directly in the form
where \({\mathbf {A}}_p\) is a symmetric tensor that controls the direction of inelastic distortional deformation rate. This tensor must satisfy the restriction
which ensures that \({\mathbf {B}_e^\prime }\) remains unimodular.
In this model, the strain energy function for elastically isotropic response is taken to be a function of the elastic dilatation \(J_e\), the elastic distortional deformation \({\mathbf {B}_e^\prime }\) and the hardening \(\kappa \). However, under SRBM \(J_e, {\mathbf {B}_e^\prime }\) and \({\mathbf {A}}_p\) transform to \(J_e^+, {\mathbf {B}}_e^{{\prime }+}\) and \({\mathbf {A}}_p^+\), such that
so the strain energy function can depend on \({\mathbf {B}_e^\prime }\) only through its two independent invariants \(\alpha _1\) and \( \alpha _2\), defined by
which satisfy the evolution equations
Thus, the strain energy function \(\Sigma \) and the stress are proposed in the forms
and for both rate-independent and rate-dependent response the stress is specified by
where \({\mathbf {T}^{\prime \prime }}\) is the deviatoric part of \({\mathbf {T}}\). Also, the rate of material dissipation \({\mathcal {D}}\) in (4.5.7) requires
In addition, the constitutive equation for stress is assumed to be restricted so that a zero-stress material state is characterized by
The evolution equations (5.11.43) for \(J_e\), (5.11.55) for \({\mathbf {B}_e^\prime }\) and (5.11.31) for \(\kappa \) require initial conditions
In this regard, it is assumed that the constitutive equation (5.11.61) for stress is invertible and that experiments can be performed to determine the values of hardening variable \(\kappa \) at any state of the material. In particular, the values of \(J_e\) and \({\mathbf {B}_e^\prime }\) in any zero-stress material state are given by (5.11.63). Also, when \(\Gamma \) vanishes, the theory represents an Eulerian formulation of a general elastically isotropic hyperelastic material.
Since the inelastic deformation rate causes a tendency for the deviatoric stress \({\mathbf {T}^{\prime \prime }}\) to approach zero, Rubin and Attia [42] proposed \({\mathbf {A}}_p\) in the form
so the evolution equation (5.11.55) is given by
As discussed in [42], since \({\mathbf {B}_e^\prime }\) is a unimodular positive-definite tensor, the spectral form of \({\mathbf {B}_e^\prime }\) can be used to show that
As a special case, the strain energy function is given by a compressible Neo-Hookean form
where \(\rho _z\) is a constant that is not necessarily the zero-stress density, \(f(J_e)\) controls the response to elastic dilatation and \(\mu \) is the positive zero-stress shear modulus. Moreover, from (5.11.61) the stress is specified by
with the function \(f(J_e)\) satisfying the restrictions
imposed by the condition (5.11.63) for a zero-stress material state and the condition that the bulk modulus is positive. Also, the rate of material dissipation (5.11.62) requires
In Sect. 6.8 the volumetric inelastic rate \(\bar{{\mathbf {D}}}_p \cdot {\mathbf {I}}\) will be related to the rate of change of porosity in a porous material. However, for nonporous metals plastic deformation rate is considered to be isochoric, which requires
and the rate of material dissipation (5.11.71) requires
which in view of (5.11.67), is automatically satisfied. In this expression, use has been made of the evolution equation (5.11.45) for \(J_e\), the expressions (4.1.16) and (5.11.69)–(5.11.73) to deduce that
where \(\rho _z\) is the mass density in any zero-stress state.
Additional Comments on Arbitrariness
From the perspective of the definition of internal state variables by Onat [31], the total deformation tensor \({\mathbf {F}}\), the plastic deformation tensors \({\mathbf {C}}_p\) and \({\mathbf {F}}_p\) and the elastic deformation tensors \({\mathbf {F}}_e\) and \({\mathbf {C}}_e\) are not internal state variables since they cannot be measured, in principle, by experiments on identical samples of the material in its current state. In particular, they are affected by arbitrariness of the choices of: the reference configuration; an intermediate configuration; a total deformation measure and a plastic deformation measure, which have been discussed in [36,37,38].
In [38] it was proved that when this arbitrariness is removed from the Lagrangian multiplicative formulation associated with (5.11.11), that formulation must reduce to the Eulerian formulation based on the microstructural vectors \({\mathbf {m}}_i\). Moreover in [38] it was shown that \({\mathbf {m}}_i\) are internal state variables in the sense of Onat [31] because their initial values can be measured, in principle, by experiments on identical samples of the material in its current state.
Elastic anisotropy of a material with the strain energy function specified by (5.11.37) is characterized by the dependence of the strain energy on the vectors \({\mathbf {m}}_i\). It is important to emphasize that the index (i) in \({\mathbf {m}}_i\) refers to distinct directions of the atomic lattice. If any of these directions cannot be distinguished by experiments, then the strain energy function must satisfy symmetry conditions which ensure that the material response is also insensitive to these indistinguishable directions.
Comparison of the evolution equation (5.11.20) for \({\mathbf {F}}_e\) and (5.11.30) for \({\mathbf {m}}_i\) suggests that these formulations may be identical. The discussion in Sect. 5.4, which describes the difference between \({\mathbf {F}}_e\) and \({\mathbf {m}}_i\) for an elastic material, is similar for an elastic–inelastic material. Specifically, consider an arbitrary right-handed orthonormal set of constant base vectors \({\mathbf {M}}_i\) and define the elastic deformation tensor \({\mathbf {F}}_e\) by
which satisfies the evolution equation and initial condition
However, in [38] it was shown that the elastic response of the material depends on \({\mathbf {m}}_i\) through the evolution equation (5.11.30) and on their initial values \({\mathbf {m}}_i(0)\). Although \({\mathbf {m}}_i(0)\) are measurable, the tensor \({\mathbf {F}}_e\) contains unphysical arbitrariness of the orientation of \({\mathbf {M}}_i\) which can be removed by considering the Eulerian formulation based on \({\mathbf {m}}_i\).
Rate-Independent Inelasticity with a Yield Function
For rate-independent inelasticity a yield function g is introduced which characterizes elastic response for \(g < 0\) and the elastic–inelastic boundary for \(g=0\). For states at the elastic–inelastic boundary, it is necessary to specify unloading, neutral loading and loading conditions which have zero inelastic rate for unloading and neutral loading, and nonzero inelastic rate for loading. Differences in the loading conditions for stress-space and strain-space formulations have been discussed in [30]. In particular, the strain-space formulation can model strain softening with decrease in stress that occurs due to damage mechanisms. Moss [27] pointed out that the numerical algorithm developed by Wilkins [48] is consistent with the loading conditions in the strain-space formulation developed by Naghdi and Trapp [30].
Here, use is made of the strain-space loading conditions and the yield function for elastically anisotropic response is specified by
With the help of the evolution equations (5.11.35) for \(m_{ij}\), (5.11.31) for \(\kappa \) and (5.11.32) for \(\beta _{ij}\), it follows that
where the functional form of g has been restricted so that \(\bar{g}\) remains positive. Then, the values of \(\Gamma \) for elastic response, unloading from the elastic–inelastic boundary, neutral loading on the elastic–inelastic boundary and inelastic loading on the elastic–inelastic boundary are specified by
where the value of \(\Gamma \) for loading has been determined by the consistency condition which ensures that g remains zero (\(\dot{g} = 0\)) during inelastic loading. From these conditions it can be seen that for elastic response with \(\Gamma = 0\), the rate of change of the yield function \(\dot{g} = \hat{g}\) so that \(\hat{g} > 0\) on the elastic–inelastic boundary requires nonzero inelastic deformation rate (\(\Gamma > 0\)) to satisfy the consistency condition.
Also, since during loading \(\Gamma \) is linear in the rate \({\mathbf {D}}\), it follows that the evolution equations (5.11.31), (5.11.32) and (5.11.35) are homogeneous of order one in time when H and \(H_{ij}\) are independent of \({\mathbf {D}}\), so the material response is rate independent.
Rate-Dependent Response
For the rate-independent theory, the rate of inelastic deformation \(\Gamma \) is a homogeneous function of order one in the total rate of deformation \({\mathbf {D}}\). In contrast, if \(\Gamma \) is not is a homogeneous function of order one in \({\mathbf {D}}\), then the material response is rate dependent. Examples of rate-dependent response can be found in [7,8,9,10,11, 25, 33, 34].
A model exhibiting a smooth elastic–inelastic transition for both rate-independent and rate-dependent response can be found in [18, 19]. In this model the function \(\Gamma \) in (5.11.30) for elastically anisotropic response or in (5.11.55) for elastically isotropic response, which controls the magnitude of inelastic deformation rate, is specified in the form
where \(\dot{{\varepsilon }}\) is the effective total distortional deformation rate, g is a yield function and the Macaulay brackets \(\langle g \rangle \) are defined by
When \(a_0 = b_0 = b_1 = 0\) this form yields a rate-dependent overstress model like that developed in [25, 33]. Also, when \(a_0 = b_0 = a_1 = 0\) the model yields a rate-independent overstress model, which approximates a standard rate-independent yield function when \(b_1\) is large enough to ensure that g remains a small positive value during inelastic loading. In addition, the constants \(a_0\) and \(b_0\) control the inelastic rate that is active for all nonzero values of \(\bar{{\mathbf {L}}}_p\) in (5.11.30) or \({\mathbf {A}}_p\) in (5.11.55), which can model the response observed in soils. It is also noted that this smooth-transition model has been generalized and numerical algorithms have been developed in [20].
Strongly Objective, Robust Numerical Integration Algorithms
Elastically Isotropic Response
Strongly objective, robust numerical algorithms for integrating the evolution equations for elastic–inelastic response have been discussed in [18, 19, 32, 40, 43, 44]. In this section, attention is limited to elastically isotropic elastic–inelastic material response of metals for which the elastic dilatation \(J_e\) and the symmetric, positive-definite, unimodular elastic distortional deformation tensor \({\mathbf {B}_e^\prime }\) satisfy the evolution equation (3.11.30) for \(J_e\) and (5.11.66) for \({\mathbf {B}_e^\prime }\)
Moreover, the deviatoric part of the evolution equation for \({\mathbf {B}_e^\prime }\) can be written in the form
where \({\mathbf {L}^{\prime \prime }}\) and \({\mathbf {D}^{\prime \prime }}\) are the deviatoric parts of \({\mathbf {L}}\) and \({\mathbf {D}}\), respectively, and \({\mathbf {B}}_e^{{\prime }{\prime }}\) is the deviatoric part of \({\mathbf {B}}_e^{\prime }\) (3.11.38).
Following the discussion in Sect. 3.13 and the work in [14, 46] and considering a typical time step which begins at \(t=t_n\), ends at \(t=t_{n+1}\), with time increment \(\Delta t= t_{n+1}-t_n\), the relative dilatation \(J_r\) and unimodular part \({\mathbf {F}}_r^{\prime }\) of the relative deformation gradient during the time step satisfy the evolution equations and initial conditions (3.13.5) and (3.13.7)
Then, the exact solution of the evolution equation for \(J_e\) is given by
Also, the elastic trial value \({\mathbf {B}}_e^{{\prime }{\prime }*}(t)\) defined by (3.13.9) and (3.13.11)
satisfies the evolution equation and initial condition
Consequently, \({\mathbf {B}}_e^{{\prime }{\prime }*}(t_{n+1})\) is the exact solution of (5.11.83) when inelastic deformation rate vanishes (i.e., \(\Gamma =0\)).
Next, the evolution equation (5.11.83) is approximated by
which with the help of a backward Euler approximation of the derivative can be solved to obtain
where \(\Gamma (t_{n+1})\) is an approximation of \(\Gamma \) at the end of the time step that is uninfluenced by SRBM. This expression is similar to the radial-return numerical algorithm developed by Wilkins [48] which scales the trial deviatoric stress to obtain the solution at the end of the time step.
For a general functional form of \(\Gamma \) it is necessary to iterate on the guess for \(\Delta \Gamma \) and integrate the other evolution equations for the values of the history-dependent variables at the end of the time step. This procedure continues until (5.11.89b) is consistent with the guess for \(\Delta \Gamma \) and the functional form for \(\Gamma \) evaluated using the predicted values of the history-dependent variables at the end of the time step. It is important to emphasize that each iteration step must start with the initial values of the history-dependent variables equal to their accepted values at the beginning of the step to not accumulate history dependence of inaccurate trial solutions.
As described in [42], once the value of \({\mathbf {B}_e^{\prime \prime }}\) has been determined at the end of the time step, the value of \({\mathbf {B}_e^\prime }\) at the end of the time step is determined by solving the cubic equation
for the associated value of the invariant \(\alpha _1\). In this regard, it was noted in [18] that the solution (49a) in [42] is more accurate than the solution (54) there.
As a simple example, the strain energy function is specified by (5.11.68) and the von Mises effective stress \(\sigma _e\) is determined by
where \({\mathbf {g}_e^{\prime \prime }}\) is the elastic distortional strain tensor defined in (3.11.37) and \(\gamma _e\) is a scalar measure of elastic distortional strain. Motivated by these expressions a simple form for the yield function g is specified by
which indicates that the onset of yield occurs when \(\gamma _e = \kappa \).
Next, the elastic trial value \(\gamma _e^*(t_{n+1})\) and the value \(\gamma _e(t_{n+1})\) at the end of the time step are defined by
It then follows from (5.11.89a) that
Moreover, the elastic trial value \(g^*(t_{n+1})\) of the yield function (5.11.92) at the end of the time step is given by
If \(g^*(t_{n+1}) \le 0\), then the response during the time step is elastic with
On the other hand, if \(g^*(t_{n+1}) > 0\), then the response during the time step is inelastic and the value of \(\Delta \Gamma \) is determined by requiring the yield function at the end of the time step to vanish
where \(\kappa (t_{n+1})\) is an estimate of the value of \(\kappa \) at the end of the time step that must satisfy the restriction
Then, for inelastic response the solution of (5.11.97) yields
Although the Eulerian formulations does not introduce a measure of inelastic strain, many evolution equations for hardening are formulated in terms of an effective inelastic strain rate \(\dot{{\varepsilon }}_p\). To help translate these evolution equations into an Eulerian formulation, with the help of (3.11.37) and (5.11.91), the evolution equation (5.11.83) suggests that the effective inelastic strain rate \(\dot{{\varepsilon }}_p\) be defined by
which can be integrated by the expression
where use has been made of (5.11.94).
Elastically Anisotropic Response
Recently Kroon and Rubin [22] developed a strongly objective, robust numerical algorithm for integrating the evolution equations (5.11.45) for the elastic dilatation \(J_e\) and for the elastic distortional deformation vectors \({\mathbf {m}}_i^{\prime }\) as well as evolution equations for isotropic \(\kappa \) in (5.11.31) and directional hardening \(\beta _{ij}\) in (5.11.32).
To present the main idea of this algorithm, consider a fully anisotropic elastic–inelastic material with a strain energy function \(\Sigma \) of the form
for which the Cauchy stress is given by (5.11.48)
Also, for definiteness the function \(\Gamma \) in the evolution equations (5.11.45) is specified by the form (5.11.80) proposed for the model with a smooth elastic–inelastic transition. Specifically, \(\Gamma \) is specified by
where the effective total distortional deformation rate \(\dot{{\varepsilon }}\) is defined in (5.11.80).
For the numerical algorithm, \(\Delta \Gamma _I\) represents the Ith estimate of \(\Delta t \Gamma (t_{n+1})\) evaluated at the end of the time step. The evolution equations (5.11.102) are solved for the values \(J_e(t_{n+1})\) and \({\mathbf {m}}_i^{\prime }(t_{n+1})\) at the end of the time step, which together with estimates of the hardening variables \(\kappa (t_{n+1})\) and \( \beta _{ij}(t_{n+1})\) are used to obtain the value \(\Gamma (t_{n+1})\) of \(\Gamma \) at the end of the time step. Convergence of the algorithm is obtained by iterating on the value \(\Delta \Gamma _I\) until the function
is sufficiently small.
Using the relative dilatation \(J_r\) in (5.11.84), the elastic trial \(J_e^*\) of the elastic dilatation \(J_e\) satisfies equations
so the evolution equation (5.11.102) for \(J_e\) can be rewritten in the form
which can be integrated approximately to obtain
In this equation, \(\bar{{\mathbf {D}}}_p(t_{n+1})\) is an estimate of the value of \(\bar{{\mathbf {D}}}_p\) at the end of the time step and \(\Delta \Gamma _I\) is the Ith estimate of \(\Delta t \Gamma (t_{n+1})\) evaluated at the end of the time step.
Next, using (5.11.84) the elastic trial values \({\mathbf {m}}_i^{{\prime }*}\) of the elastic distortional deformation vectors \({\mathbf {m}}_i^{\prime }\) satisfy equations
Then, the evolution equation (5.11.102) for \({\mathbf {m}}_i^{\prime }\) is approximated by
Using a backward Euler approximation of the derivative, this equation integrates to obtain
where \({\mathbf {A}}^*\) has been normalized to be unimodular [i.e., \(\det {\mathbf {A}}^* = 1\)] which ensures that the vectors \({\mathbf {m}}_i^{\prime }(t_{n+1},I)\) satisfy the condition
The tensor \(\bar{{\mathbf {L}}}_p^{{\prime \prime }*}\) in (5.11.112) is an estimate of \(\bar{{\mathbf {L}}}_p^{\prime \prime }\) defined by
For an arbitrary time step \(t=t_n\) with \(n >1\), \({\varvec{\Lambda }_p}\) is specified by
where \(\bar{{\mathbf {L}}}_p^{\prime \prime }(t_n)\) and \({\mathbf {m}}^{i {\prime }}(t_n)\) are the converged values of \(\bar{{\mathbf {L}}}_p^{\prime \prime }\) and \({\mathbf {m}}^{i {\prime }}\) from the previous time step with the reciprocal vectors \({\mathbf {m}}^{i {\prime }}\) defined in (3.11.18). The value of \({\varvec{\Lambda }_p}\) at the beginning of the integration process \(t=t_1\) is specified to be a fraction of its elastic trial value
where \(\bar{{\mathbf {L}}}_p^{{\prime \prime }*}(t_{n+1})\) is the value of \(\bar{{\mathbf {L}}}_p^{\prime \prime }\) evaluated using the elastic trial values \(J_e^*(t_{n+1})\) and \( {\mathbf {m}}_i^*(t_{n+1})\) and estimates of the hardening variables \(\kappa (t_{n+1})\) and \( \beta _{ij}(t_{n+1})\) at the end of the time step. Also, the strongly objective average total distortional deformation rate \(\tilde{{\mathbf {D}}}^{\prime \prime }\) developed in [41] and recorded in (3.13.20) can be used for a strongly objective approximation of \(\dot{{\varepsilon }}\) at the end of the time step
where the relative deformation \({\mathbf {B}}_r^{\prime }\) is defined by
Since under SRBM the quantities \(J_e, {\mathbf {m}}_i^{\prime }, J_r\) and \( {\mathbf {F}}_r^{\prime }\) transform to \(J_e^+, {\mathbf {m}}_i^{{\prime }+}, J_r ^+\) and \( {\mathbf {F}}_r^{{\prime }+}\) according to the transformation relations (3.11.31) and (3.13.8)
it follows that the numerical estimates \(J_e(t_{n+1})\) and \({\mathbf {m}}_i^{\prime }(t_{n+1})\) transform to \(J_e^+(t_{n+1})\) and \({\mathbf {m}}_i^{{\prime }+} (t_{n+1})\) under SRBM, such that
when the estimates \(\kappa (t_{n+1})\) and \( \beta _{ij}(t_{n+1})\) are insensitive to SRBM. This means that these numerical estimates are strongly objective since the vector and tensor estimates satisfy the same invariance transformation relations under SRBM as the exact values.
Robustness of the numerical algorithm developed in [22] was tested by taking large time steps which in one time step load the material from zero stress to a point in the inelastic range. It was found that the algorithm worked well for the constant \(\alpha \) in (5.11.116) specified by
It is emphasized that if the first time step causes elastic response, then there is no influence of the parameter \(\alpha \) since \(\Delta \Gamma _1 = 0\).
Elastically Isotropic Response to Simple Shear
With reference to fixed rectangular Cartesian base vectors \({\mathbf {e}}_i\), the velocity gradient \({\mathbf {L}}\) for simple shear can be specified by
Using the zero-stress initial conditions (5.11.63), the solution of the evolution equation (5.11.43) for \(J_e\) requires for a metal with isochoric inelasticity (5.11.72) that
and the evolution equation (5.11.66) admits a solution for the elastic distortional deformation \({\mathbf {B}_e^\prime }\) of the form
where a, b and d are functions of time determined by solving the three nontrivial scalar evolution equations associated with (5.11.66). Moreover, it was shown in [44] that for monotonic loading with
and constant \(\gamma _s\), that these evolution equations admit a steady-state solution for which
Also, the steady-state values of \(\dot{{\varepsilon }}\) in (5.11.80) and \(\gamma _e\) in (5.11.91) are given by
For simplicity, consider the case when the yield function is specified by (5.11.92)
with the hardening variable \(\kappa \) being constant. It then follows that for standard rate-independent inelasticity, the loading conditions (5.11.79) require \(g=0\) during inelastic loading, which determines the steady-state value of \(\gamma _s\) by the solution of equation
Alternatively, for the simple rate-independent smooth elastic–inelastic transition model (5.11.80) characterized by
the steady-state value of \(\gamma _s\) is determined by equation
Cyclic loading of the smooth-transition model in simple shear. Plots of the shear stress \(T_{12}^{\prime \prime }\) versus the total shear strain \(\gamma \) for different material constants: a \(b_1 = 100, \kappa =0.019670\) and b \(b_1 = 300, \kappa =0.029675\), which produce the same steady-state value of shear stress. The symbols indicate the locations of the elastic–inelastic transitions
Using the Neo-Hookean model, the pressure vanishes and deviatoric stress is given by (5.11.69). To examine the influence of the constant \(b_1\) on the solution of the smooth model, it is convenient to determine values of the pair of constants \(b_1, \kappa \) which yield the same steady-state value of the shear stress. Specifically, as a special case, the steady-state value of \(\gamma _s\) is determined by solving equation
and (5.11.131) is used to determine the values
Figure 5.4 shows the transient solution of shear stress \(T_{12}^{\prime \prime }\) versus total shear strain \(\gamma \) determined by integrating the evolution equation
subject to the initial condition \(\gamma (0) = 0\). The symbols in Fig. 5.4a, b indicate the locations of the elastic–inelastic transitions for cyclic simple shear loading. Figure 5.4a shows that for \(b_1=100\), the response exhibits significant overstress with inelasticity continuing to occur during the onset of unloading. Even though the hardening parameter \(\kappa \) is constant, the model exhibits effective hardening due to the overstress. Figure 5.4b shows that for \(b_1=300\) the effects of the overstress are significantly reduced. In this regard, it is noted that in the limit that \(b_1 \rightarrow \infty \), the smooth model yields standard rate-independent response with the yield function \(g=0\) during inelastic loading.
5.12 Viscoelastic Response
A simple generalized nonlinear Maxwell model (see Fig. 5.5) for viscoelastic response can be proposed by adding the response of a viscoplastic material to that of a general elastic material. To model dilatational dissipation of viscoplastic component, it is necessary to enhance the model described in Sect. 5.11. To this end, the viscoplastic component is modeled by the elastic dilatation \(J_v>0\) and the unimodular elastic distortional deformation tensor \({\mathbf {B}_e^\prime }\) which satisfy the evolution equations
where \(\Gamma _v\) and \(\Gamma \) are positive constants that, respectively, control the time-dependent relaxation of \(J_v\) toward unity and \({\mathbf {B}_e^\prime }\) toward the unity tensor \({\mathbf {I}}\). The functional form of the evolution equation for \(J_v\) is motivated by the work in [39] which introduced a modified evolution equation for a cardiac muscle that simplified the numerical integration algorithm. Also, the first invariant of \({\mathbf {B}_e^\prime }\) satisfies equations
where \({\mathbf {B}_e^{\prime \prime }}\) is the deviatoric part of \({\mathbf {B}_e^\prime }\).
Now, the strain energy function of the viscoelastic material is specified in the form
where \(\rho _z\) is a constant density not necessarily equal to a zero-stress density, \(\hat{\Sigma }\) characterizes the strain energy of a general nonlinear elastic material and \(\overset{v}{\Sigma }\) characterizes the strain energy of the viscoplastic component, with \(K_v\) being the positive elastic bulk modulus and \(\mu _v\) being the positive shear modulus of the viscoplastic component.
For this model the Cauchy stress \({\mathbf {T}}\) is proposed in the form
where the response \(\hat{{\mathbf {T}}}\) of a general nonlinear elastic material satisfies equation
for all motions. Then, for this material, the rate of material dissipation (4.5.7) requires
Specifying \(\overset{v}{{\mathbf {T}}}\) by
the rate of material dissipation requires
which in view of the constitutive equation (5.12.7) for the pressure \(\overset{v}{p}\) and (5.11.67) is automatically satisfied. Since \(\Gamma _v\) and \(\Gamma \) are both positive, dissipation continues until \(J_v = 1\) and \({\mathbf {B}_e^\prime }= {\mathbf {I}}\) with \({\mathbf {T}}= \hat{{\mathbf {T}}}\).
If the elastic part of the response is isotropic, then the strain energy is given by (5.8.5) and the stress \(\hat{{\mathbf {T}}}\) is given by (5.8.10). Alternatively, if the elastic part of the response is anisotropic, then the strain energy is given by (5.3.9) and the stress \(\hat{{\mathbf {T}}}\) is given by (5.3.11). For either case, this model proposes elastically isotropic viscoplastic dissipation.
A robust, strongly objective numerical integration algorithm for the evolution equation for \({\mathbf {B}_e^\prime }\) was discussed in Sect. 5.11. To develop a robust, strongly objective numerical integration algorithm for the evolution equation (5.12.1) for the elastic dilatation \(J_v\), consider the time interval \(t_n \le t \le t_{n+1}\) with time increment \(\Delta t = t_{n+1}-t_n\) and recall that the relative dilatation \(J_r\) satisfies the evolution equation (5.11.84) and initial condition
Thus, (5.12.1)\(_1\) can be rewritten in the form
Next, using a backward Euler approximation of the derivative yields equation
which can be solved to obtain
5.13 Crystal Plasticity
Crystal plasticity models (e.g., [1, 17]) identify a finite number N of slip planes in the crystal with unit normals \(_I {\mathbf {n}}\) and unit slip directions \(_I {\mathbf {s}}\) in the slip planes. In addition, a constitutive equation for the inelastic rate \({\mathbf {L}}_p\) is proposed in the form
where \({}_I \Gamma \) characterizes the inelastic rate on the Ith slip plane, which typically is a function of history-dependent variables. This form for \({\mathbf {L}}_p\) includes all slip rates on all of the slip planes and is applicable to metal plasticity with no inelastic dilatation rate
Within the context of the Eulerian formulation with evolution equations (5.11.30) for the microstructural vectors
the microstructural vectors can be used to characterize the deformation and orientation of the average crystal lattice. Moreover, the elastic distortional deformation microstructural vectors \({\mathbf {m}}_i^{\prime }\) satisfy the evolution equations (5.11.45)
where \({\mathbf {L}^{\prime \prime }}\) is the deviatoric part of the velocity gradient and \({\mathbf {L}}_p^{\prime \prime }\) is the deviatoric part of the inelastic rate \({\mathbf {L}}_p\). Since the elastic distortional microstructural vectors \({\mathbf {m}}_i^{\prime }\) can be used to model the crystal, the values of \({}_I n_i\) of the unit normals \({}_I {\mathbf {n}}\) to slip systems and \({}_I s^i\) of the unit vectors \({}_I {\mathbf {s}}\) in the slip directions in a zero-stress state (with \({\mathbf {m}}_i^{\prime }= {\mathbf {m}}^{i {\prime }}\) being orthonormal vectors) can be constants for general stress states with
where there is no sum on the repeated capital index I.
This formulation will be properly invariant under Superposed Rigid Body Motions SRBM if \({}_I \Gamma \) are uninfluenced by SRBM
If \({}_I \Gamma \) are determined by consistency conditions for standard rate-independent yield functions, then the active slip systems may not be determined uniquely. However, if \({}_I \Gamma \) are determined by functions similar to those (5.11.80) of the smooth elastic–inelastic transition model developed in [18, 19], then loading and unloading conditions are not needed and all slip systems are simultaneously active even for rate-independent response. Examples for standard small strain formulations of crystal plasticity which has been modified to use the smooth elastic–inelastic transition model can be found in [13, 15].
References
Asaro RJ (1983) Micromechanics of crystals and polycrystals. Adv Appl Mech 23:1–115
Barenblatt GI, Joseph DD (2013) Collected papers of RS Rivlin: volume I and II. Springer Science & Business Media, New York
Bernstein B (1960) Hypo-elasticity and elasticity. Arch Rational Mech Anal 6:89–104
Besseling JF (1968) A thermodynamic approach to rheology. Irreversible aspects of continuum mechanics and transfer of physical characteristics in moving fluids, pp 16–53
Besseling JF, Van Der Giessen E (1994) Mathematical modeling of inelastic deformation. CRC Press, Boca Raton
Bilby BA, Gardner LRT, Stroh AN (1957) Continuous distributions of dislocations and the theory of plasticity. In: Proceedings of the 9th international congress of applied mechanics, vol 9. University de Brussels, pp 35–44
Bodner SR (1968) Constitutive equations for dynamic material behavior. Mechanical behavior of materials under dynamic loads. Springer, Berlin, pp 176–190
Bodner SR (1987) Review of a unified elastic-viscoplastic theory. Unified constitutive equations for creep and plasticity, pp 273–301
Bodner SR (2002) Unified plasticity for engineering applications. Mathematical concepts and methods in science and engineering, vol 47. Kluwer, New York
Bodner SR, Partom Y (1972) A large deformation elastic-viscoplastic analysis of a thick-walled spherical shell. J Appl Mech 39:751–757
Bodner SR, Partom Y (1975) Constitutive equations for elastic-viscoplastic strain-hardening materials. J Appl Mech 42:385–389
Eckart C (1948) The thermodynamics of irreversible processes. IV. The theory of elasticity and anelasticity. Phys Rev 73:373–382
Farooq H, Cailletaud G, Forest S, Ryckelynck D (2020) Crystal plasticity modeling of the cyclic behavior of polycrystalline aggregates under non-symmetric uniaxial loading: global and local analyses. Int J Plast 126:102619
Flory PJ (1961) Thermodynamic relations for high elastic materials. Trans Faraday Soc 57:829–838
Forest S, Rubin MB (2016) A rate-independent crystal plasticity model with a smooth elastic-plastic transition and no slip indeterminacy. Eur J Mech-A/Solids 55:278–288
Green AE, Naghdi PM (1965) A general theory of an elastic-plastic continuum. Arch Rational Mech Anal 18:251–281
Hill R (1966) Generalized constitutive relations for incremental deformation of metal crystals by multislip. Arch Rational Mech Anal 14:95–102
Hollenstein M, Jabareen M, Rubin MB (2013) Modeling a smooth elastic-inelastic transition with a strongly objective numerical integrator needing no iteration. Comput Mech 52:649–667
Hollenstein M, Jabareen M, Rubin MB (2015) Erratum to: modeling a smooth elastic-inelastic transition with a strongly objective numerical integrator needing no iteration. Comput Mech 55:453–453
Jabareen M (2015) Strongly objective numerical implementation and generalization of a unified large inelastic deformation model with a smooth elastic-inelastic transition. Int J Eng Sci 96:46–67
Kröner E (1959) General continuum theory of dislocations and intrinsic stresses. Arch Rational Mech Anal 4:273–334
Kroon M, Rubin MB (2020) A strongly objective, robust integration algorithm for Eulerian evolution equations modeling general anisotropic elastic-inelastic material response. Finite Elem Anal Des 177:103422
Lee EH (1969) Elastic-plastic deformation at finite strains. J Appl Mech 36:1–6
Leonov AI (1976) Nonequilibrium thermodynamics and rheology of viscoelastic polymer media. Rheol Acta 15:85–98
Malvern LE (1951) The propagation of longitudinal waves of plastic deformation in a bar of material exhibiting a strain-rate effect. J Appl Mech 18:203–208
Mandel J (1973) Equations constitutives et directeurs dans les milieux plastiques et viscoplastiques. Int J Solids Struct 9:725–740
Moss WC (1984) On the computational significance of the strain space formulation of plasticity theory. Int J Numer Methods Eng 20:1703–1709
Naghdi PM (1960) Stress-strain relations in plasticity and thermoplasticity. In: Plasticity: proceedings of the second symposium on naval structural mechanics, pp 121–169
Naghdi PM (1990) A critical review of the state of finite plasticity. Zeitschrift für angewandte Mathematik und Physik ZAMP 41:315–394
Naghdi PM, Trapp JA (1975) The significance of formulating plasticity theory with reference to loading surfaces in strain space. Int J Eng Sci 13:785–797
Onat ET (1968) The notion of state and its implications in thermodynamics of inelastic solids. Irreversible aspects of continuum mechanics and transfer of physical characteristics in moving fluids, pp 292–314
Papes O (2013) Nonlinear continuum mechanics in modern engineering applications. PhD dissertation DISS ETH NO 19956
Perzyna P (1963) The constitutive equations for rate sensitive plastic materials. Q Appl Math 20:321–332
Rubin MB (1987) An elastic-viscoplastic model exhibiting continuity of solid and fluid states. Int J Eng Sci 25:1175–1191
Rubin MB (1994) Plasticity theory formulated in terms of physically based microstructural variables - Part I. Theory. Int J Solids Struct 31:2615–2634
Rubin MB (1996) On the treatment of elastic deformation in finite elastic-viscoplastic theory. Int J Plast 12:951–965
Rubin MB (2001) Physical reasons for abandoning plastic deformation measures in plasticity and viscoplasticity theory. Arch Mech 53:519–539
Rubin MB (2012) Removal of unphysical arbitrariness in constitutive equations for elastically anisotropic nonlinear elastic-viscoplastic solids. Int J Eng Sci 53:38–45
Rubin MB (2016) A viscoplastic model for the active component in cardiac muscle. Biomech Model Mechanobiol 15:965–982
Rubin MB (2019) An Eulerian formulation of inelasticity - from metal plasticity to growth of biological tissues. Trans R Soc A 377:20180071
Rubin MB (2020) A strongly objective expression for the average deformation rate with application to numerical integration algorithms. Finite Elem Anal Des 175:103409
Rubin MB, Attia AV (1996) Calculation of hyperelastic response of finitely deformed elastic-viscoplastic materials. Int J Numer Methods Eng 39:309–320
Rubin MB, Cardiff P (2017) Advantages of formulating an evolution equation directly for elastic distortional deformation in finite deformation plasticity. Comput Mech 60:703–707
Rubin MB, Papes O (2011) Advantages of formulating evolution equations for elastic-viscoplastic materials in terms of the velocity gradient instead of the spin tensor. J Mech Mater Struct 6:529–543
Schröder J, Neff P (2003) Invariant formulation of hyperelastic transverse isotropy based on polyconvex free energy functions. Int J Solids Struct 40:401–445
Simo JC (1988) A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition. Part II: computational aspects. Comput Methods Appl Mech Eng 68:1–31
Truesdell C, Noll W (2004) The non-linear field theories of mechanics. Springer, Berlin, pp 1–579
Wilkins ML (1963) Calculation of elastic-plastic flow. Technical report, UCRL7322, California University Livermore Radiation Lab
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Rubin, M.B. (2021). Purely Mechanical Constitutive Equations. In: Continuum Mechanics with Eulerian Formulations of Constitutive Equations. Solid Mechanics and Its Applications, vol 265. Springer, Cham. https://doi.org/10.1007/978-3-030-57776-6_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-57776-6_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-57775-9
Online ISBN: 978-3-030-57776-6
eBook Packages: EngineeringEngineering (R0)