1 Introduction

The significant geologic complexity involved in multi-phase flow and the treatment of strongly heterogeneous soil properties need efficient preconditioning strategies for fully implicit formulations. Multilevel techniques such as the constrained pressure residual (CPR) two-stage preconditioner allow to exploit the algebraic properties of the Jacobian matrix of the system. The two-stage CPR preconditioner was introduced by Wallis [2, 3] from the previous work of Behie and Vinsome [4] on combinative preconditioners in reservoir engineering. Lacroix et al. [5] combined a first stage preconditioner on the pressure subsystem with Algebraic Multigrid (AMG) and a second stage preconditioner on the full system with ILU-0. The CPR-AMG has proven to be efficient for the simulation of complex problems in reservoir engineering [6,7,8,9] and in basin modeling [10]. The CPR impact on h and hp adaptive DG schemes is still not well understood as most of the work with regards to the CPR has so far mainly focused on finite volume methods. To our knowledge this is the first time the CPR-AMG is applied within an adaptive DG discretization framework.

This work is organized as follows: Sect. 2 provides a description of the Jacobian matrix arising from a fully implicit discretization of a two-phase flow problem. Section 3 sets out the formulation of the CPR-AMG method. Section 4 provides numerical tests implemented within Dune [1].

2 Structure of the Jacobian Matrix

We consider a domain \(\Omega \in \mathbb {R}^d\), d ∈{2, 3}. The phases α = {w, n} are incompressible and immiscible. Unknown variables are the pressure p w and the saturation s n.

$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{aligned}{} -\nabla\cdot \biggl( (\lambda_w + \lambda_n) \mathbb{K} \nabla p_{w} + \lambda_n p^{\prime}_c \mathbb{K} \nabla s_{n} - (\rho_w\lambda_w + \rho_n \lambda_n) \mathbb{K} \mathbf{g}\biggr)& = q_w + q_n,\\ \phi \frac{\partial s_n}{\partial t} - \nabla \cdot \biggl( \lambda_n \mathbb{K} (\nabla p_{w}-\rho_n \mathbf{g})\biggr) - \nabla \cdot \biggl( \lambda_n p^{\prime}_c \mathbb{K} \nabla s_{n}\biggr) & =q_{n}.{} \end{aligned} \end{array} \end{aligned} $$
(1)

In order to have a complete system we add appropriate boundary and initial conditions. For a more thorough description of the complete system and its DG discretization see [11,12,13,14].

The development of effective and robust preconditioning techniques requires to fully understand and exploit the algebraic properties of each individual block of the Jacobian matrix J G stemming from the fully-implicit and fully-coupled DG discretization of the two-phase flow system (1). Following [11], let J G X = b be the linear system to solve and r = b − J G X the residual, where X = (X p, X s) is the unknown and \(b=(b_p,b_s)^{\intercal }\) the right-hand side. The Jacobian matrix J G is expressed as

$$\displaystyle \begin{aligned} J_G=\begin{pmatrix}{} J^{pp}& J^{ps}\\ &\\ J^{sp} & J^{ss} \end{pmatrix} =\begin{pmatrix} \frac{\partial G_{}^{p}}{\partial p_{}^{}}& \frac{\partial G_{}^{p}}{\partial s_{}^{}}\\ &\\ \frac{\partial G_{}^{s}}{\partial p_{}^{}} & \frac{\partial G_{}^{s}}{\partial s_{}^{}} \end{pmatrix}. \end{aligned} $$
(2)

Here, \(J^{pp} \in \mathbb {R}^{n_p \times n_p}\) is the pressure block, \(J^{ss} \in \mathbb {R}^{n_s \times n_s}\) is the saturation block. \(J^{ps} \in \mathbb {R}^{n_p \times n_s}\) and \(J^{sp} \in \mathbb {R}^{n_s \times n_p}\) are the coupling blocks. The term G p (resp. G s) denotes the discretization of the first (resp. second) equation of system (1).

We consider in our implementation a dof-based re-ordering of variables where J G is reformulated as

$$\displaystyle \begin{aligned} J_G= \left ( \begin{array}{ccc} \begin{array}{ll} (J^{pp})_{1,1} & (J^{ps})_{1,1} \\ (J^{ss})_{1,1} & (J^{ss})_{1,1} \\ \end{array} & \cdots & \begin{array}{ll} (J^{pp})_{1,n_s} & (J^{ps})_{1,n_s} \\ (J^{ss})_{1,n_s} & (J^{ss})_{1,n_s} \\ \end{array}\\ \vdots & \ddots & \vdots\\ \begin{array}{ll} (J^{pp})_{n_p,1} & (J^{ps})_{n_p,1} \\ (J^{ss})_{n_p,1} & (J^{ss})_{n_p,1} \\ \end{array}& \cdots & \begin{array}{ll} (J^{pp})_{n_p,n_s} & (J^{ps})_{n_p,n_s} \\ (J^{ss})_{n_p,n_s} & (J^{ss})_{n_p,n_s} \\ \end{array} \end{array} \right ). \end{aligned} $$
(3)

Above, n p is the number of dofs for the pressure and n s is the number of dofs for the saturation. (J)i,j represents the coupling between two dofs.

3 Constrained Pressure Residual Preconditioner

This section provides an extended insight into the structures and the different stages involved in the construction of the CPR preconditioner.

3.1 Method Description

The CPR belongs to the family of two-stage preconditioners, first it extracts and solves a pressure subsystem. The residual associated with this solution is subsequently corrected with an additional preconditioning step that recovers part of the global information contained in the original system. The elliptic feature exhibited by the pressure subsystem allows it to be handled well by multigrid methods. The other equation is usually degenerate parabolic and might be handled by an ILU preconditioner. Figure 1 provides a sketch of the CPR preconditioning.

Fig. 1
figure 1

Sketch of the CPR preconditioning

Full size image

Definition 1

The general formulation of a two-stage preconditioner is:

$$\displaystyle \begin{aligned} M^{-1}_{2st}= M_2^{-1}\begin{bmatrix} I -\tilde J M^{-1}_{1} \end{bmatrix} + \begin{pmatrix} M^{-1}_{1} \end{pmatrix} \end{aligned} $$
(4)

where \(M^{-1}_{1}\) (resp. \(M^{-1}_{2}\)) corresponds to the first (resp. second) stage of the preconditioner and the operator \(\tilde J\) is such that

$$\displaystyle \begin{aligned} D_{1}^{-1} J_G D_{2}^{-1}= \tilde J=\begin{pmatrix} \tilde J_{pp}& \tilde J_{ps}\\ &\\ \tilde J_{sp} & \tilde J_{ss} \end{pmatrix}.{} \end{aligned} $$
(5)

Here D 1 and D 2 are decoupling operators, different choices of D i, i ∈{1, 2} generate different first stage preconditioners [6]. We provide more details concerning the decoupling operators in the next section.

For the CPR, the first stage in (4) corresponds to

$$\displaystyle \begin{aligned} M^{-1}_{1}= C \tilde J_{pp}^{-1}C^{T}, \end{aligned} $$
(6)

where C T and C are respectively, restriction and prolongation operators. In particular, C is given by

$$\displaystyle \begin{aligned} C = \begin{pmatrix} e& & \\ & \ddots & \\ & & e \end{pmatrix} \quad \mbox{ and } \quad e = \begin{pmatrix} 1 \\ 0 \end{pmatrix}. \end{aligned} $$

The second stage in (4) is

$$\displaystyle \begin{aligned} M^{-1}_{2}= M^{-1}_{ILU}, \end{aligned} $$
(7)

where \(M^{-1}_{ILU}\) is an ILU preconditioner.

3.1.1 CPR Procedure

The CPR preconditioning step \(\delta =M^{-1}_{CPR}r\) can be outlined as follows:

  1. 1.

    Weakening of the coupling between the pressure and non pressure blocks:

    $$\displaystyle \begin{aligned} D_{1}^{-1} J_G = \tilde J=\begin{pmatrix} \tilde J_{pp}& \tilde J_{ps}\\ &\\ \tilde J_{sp} & \tilde J_{ss} \end{pmatrix};{} \end{aligned} $$
    (8)
  2. 2.

    Compute the pressure subsystem residual:

    $$\displaystyle \begin{aligned} r_p= C^{T} D_{1}^{-1} r; \end{aligned} $$
    (9)
  3. 3.

    Solve the pressure system (e.g. with an AMG preconditioner or as a solver):

    $$\displaystyle \begin{aligned} \tilde J_{pp} \delta_{p}=r_p; \end{aligned} $$
    (10)
  4. 4.

    Expand the pressure solution to the full system:

    $$\displaystyle \begin{aligned} \gamma= C \delta_{p}=\begin{pmatrix}\delta_p \\0 \end{pmatrix}; \end{aligned} $$
    (11)
  5. 5.

    Compute the new residual:

    $$\displaystyle \begin{aligned} \hat r=r - \tilde J \gamma ; \end{aligned} $$
    (12)
  6. 6.

    Prediction and correction step:

    $$\displaystyle \begin{aligned} \delta= M_2^{-1} \hat r + \gamma . {} \end{aligned} $$
    (13)

Here δ = (δ p, δ s)t denotes the correction obtained after the two stages and for the sake of simplicity, we set \(D_{2}^{-1}=I\) for the decoupling step (i.e. (8)).

Remark 1

More robust preconditioners can be formulated with the inclusion of the convective-diffusive block [6],

$$\displaystyle \begin{aligned} M^{-1}_{CPR*}= M_2^{-1}\begin{pmatrix} I - \begin{pmatrix} \tilde J - M_{2} \end{pmatrix} \begin{pmatrix} \tilde J_{pp}^{-1} & - \tilde J_{pp}^{-1} \tilde J_{ps} \tilde J{ss}^{-1}\\ 0 & \tilde J_{ss}^{-1} \end{pmatrix} \end{pmatrix}. \end{aligned} $$
(14)

3.2 Decoupling Operators

The decoupling introduced in (5) is a very important preprocessing step allowing to weaken the coupling between the pressure and non-pressure blocks while preserving the good algebraic properties for the extracted pressure subsystem [10, and references therein]. The main decoupling strategies usually considered in the literature are the Alternate-Block Factorization (ABF) procedure [15], the Quasi-IMPES procedure [5, 10] and the True-IMPES procedure [16].

Definition 2

Following Bank et al. [15], the ABF method is defined such that

$$\displaystyle \begin{aligned} D_1=\begin{pmatrix} D_{pp}& D_{ps}\\ &\\ D_{sp} &D_{ss} \end{pmatrix} =\begin{pmatrix} diag(J_{pp})&diag(J_{ps})\\ &\\ diag(J_{sp}) &diag(J_{ss}) \end{pmatrix} \quad \mbox{and} \quad D_2= \mathbb{I}. \end{aligned}$$

Remark 2

Considering a dof-wise re-ordering, the ABF method corresponds to a simple to block diagonal scaling with

$$\displaystyle \begin{aligned} D_1= \left ( \begin{array}{ccc} \begin{array}{ll} (J^{pp})_{1,1} & (J^{ps})_{1,1} \\ (J^{ss})_{1,1} & (J^{ss})_{1,1} \\ \end{array} & & \\ & \ddots & \\ & & \begin{array}{ll} (J^{pp})_{n_p,n_s} & (J^{ps})_{n_p,n_s} \\ (J^{ss})_{n_p,n_s} & (J^{ss})_{n_p,n_s} \\ \end{array} \end{array} \right ). \end{aligned} $$
(15)

In this work we only focus on the ABF method owing to its structural simplicity and ease of implementation. We might although expect some potential drawbacks because \(\tilde J_{pp}\) may be “strongly” non-symmetric compared to J pp. It is also important to emphasize the fact that computing the exact inverse of \(\tilde J_{pp} \) not feasible for large scale settings. It is therefore crucial to calibrate carefully inner and outer tolerances within the nested iterative procedure defined from (5) to (13).

4 CPR Preconditioner Performances

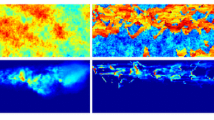
In this section, we analyze the performance of the two stage CPR preconditioner. We consider the 3d heterogeneous model in Fig. 2 introduced in [11]. We use a GMRES PetSc solver with a relative residual norm of 10−7 and a Newton tolerance of 5 × 10−7. The computations are done in serial on a standard Intel workstation. Figure 3 and Table 1 summarize the results of this test case.

Fig. 2
figure 2

3d infiltration problem

Full size image
Fig. 3
figure 3

Average number of linear iterations per Newton step

Full size image
Table 1 Comparison of different preconditioners
Full size table

The performances of the CPR and AMG are quite comparable with respect to the total CPU time. Indeed, the AMG is slightly faster up to 300,000 dofs. The relative residuals with respect to the average number of linear iterations per Newton step are depicted in Fig. 4, it illustrates the typical rate of convergence of the two preconditioners (here the Newton tolerance is 10−7). In order to converge to a residual norm of less than 10−13, AMG is slightly faster than CPR. However, the convergence rate of CPR is better than that of AMG.

Fig. 4
figure 4

Average convergence rates (60,000 dofs, T = 1500 s, Newton tol. 10−7)

Full size image

5 Conclusion

The performances of the CPR for DG discretizations of porous media multiphase flow are not yet quite satisfactory compared to classical preconditioners such as AMG or ILU. One way to improve the performances of the CPR might consist in loosening the relative residual tolerances for the solution of the pressure subsystem as suggested in [17]. Another alternative consists in implementing more efficient decoupling operators such as the True-Impes and the Quasi-Impes [5, 6, 10, 16].