hp–Adaptive Discontinuous Galerkin Methods for Porous Media Flow

Abstract

We present an adaptive Discontinuous Galerkin discretization for the solution of porous media flow problems. The considered flows are immiscible and incompressible. The adaptive approach implemented allows for refinement/coarsening in both the element size and the polynomial degree. The method is evaluated using homogeneous and heterogeneous test cases.

1 Introduction

The modeling and simulation of flow in porous media is essential in many environmental problems such as groundwater flow and petroleum engineering. The inherent geological complexity and the strong heterogeneity of the soil parameters require locally conservative methods such as Discontinuous Galerkin (DG) methods in order to be able to follow small concentrations [1].

The first h-adaptive DG framework for porous media two-phase flow was introduced by Klieber and Riviére [11]. The authors used a decoupled formulation with continuous capillary pressure functions, only 2d flow on non-conforming simplicial grids were considered and they implemented an error indicator obtained from transient linear convection diffusion problems [9]. More recently, Kane [10] implemented a higher order h-adaptive scheme for 2d and 3d two-phase flow problem with strong heterogeneity, discontinuous capillary pressure functions and gravity effects. The results in [10] show that an increase of the polynomial degree gives a considerable improvement of the solution with sharper fronts and the oscillations appearing in the vicinity of the front are reduced with the local mesh refinement. A discretization scheme independent abstract framework allowing for a more rigorous a-posteriori estimator for porous media two-phase flow problem was introduced by [13]. This paved the way for a h-adaptive strategy for a homogeneous two-phase flow problem. However it has only been applied so far to Finite Volume methods [6].

The first contribution of this work is to provide a first and second order Adam-Moulton time discretization combined with the Interior Penalty DG methods. This implicit space time discretization leads to a fully coupled nonlinear system requiring to build a Jacobian matrix at each time step for the Newton-Raphson method. The second contribution of this work is providing a hp-adaptive strategy extending the previous work of  [10], this is the first porous media two-phase flow fully adaptive scheme allowing for adaptivity for both the element size and the polynomial degree. This hp-adaptive strategy allows to refine the mesh when the solution is estimated to be rough and increase the polynomial degree when the solution is estimated to be smooth hence compensating the increased computational cost for complex models.

The rest of this document is organised as follows. In the next section, we describe the two-phase flow model. The DG discretization is introduced in Sect. 3. The adaptive strategy in space is outlined in Sect. 4. Numerical examples are provided in Sect. 5. Finally concluding remarks are provided in the last section.

2 Governing Equations

We consider an open and bounded domain $\varOmega \in \mathbb {R}^d$, $d \in \{1, 2, 3\}$ and the time interval $\mathscr {J}=(0,T)$, $T>0$. The flow of the wetting-phase and the nonwetting-phase is described by the Darcy’s law and the continuity equation for each phase, namely, with $\sum _{\alpha } s_\alpha =1$ and $p_{n} - p_{w}= p_{c}(s_{w,e})$,

$$\begin{aligned} v_{\alpha } = - \lambda _{\alpha } K (\nabla p_{\alpha } - \rho _{\alpha } g) \text{ and } \qquad \phi \frac{\partial \rho _\alpha s_{\alpha }}{\partial t} + \nabla \cdot (\rho _\alpha v_{\alpha }) =\rho _\alpha q_{\alpha } \text{. } \end{aligned}$$

(1)

Here, we search for the phase pressures $p_{\alpha }$ and the phase saturations $s_{\alpha }$, $\alpha \in \{w,n\}$. We denote with subscript w the wetting-phase and with subscript n the nonwetting-phase. K is the permeability of the porous medium, $\rho _{\alpha }$ is the phase density, $q_{\alpha }$ is a source/sink term and g is the constant gravitational vector. We assume the porosity $\phi$ is time independent and there exist $\phi _1, \phi _2 \>0$ such that $0 <\phi _1\le \phi \le \phi _2$ and with the phase mobilities $\lambda _{\alpha }=\frac{ k_{r\alpha }}{\mu _{\alpha }} \text{, } \alpha \in \{ w,n\}$, where $\mu _{\alpha }$ is the phase viscosity and $k_{r\alpha }$ is the relative permeability of phase $\alpha$. The relative permeabilities are functions that depend on the phase saturation in nonlinear fashion (i.e. $k_{r\alpha }=k_{r\alpha }(s_{\alpha })$). For example, in the Brooks-Corey model [5], $k_{rw}(s_{w,e})= s_{w,e}^{\frac{2+3\theta }{\theta }} \text{, } \,\,k_{rn}(s_{n,e})= (s_{n,e})^2 (1-(1-s_{n,e})^{\frac{2+\theta }{\theta }})$, where the effective saturation $s_{\alpha , e}$ is $s_{\alpha , e}=\frac{s_{\alpha }-s_{\alpha ,r}}{1-s_{w,r}-s_{n,r}}, \,\,\forall \alpha \in \{w,n \}.$ Here, $s_{\alpha ,r}$, $\alpha \in \{w,n\}$ are the phase residual saturations. The parameter $\theta \in [0.2, 3.0]$ is a result of the inhomogeneity of the medium. The capillary pressure $p_c= p_c(s_{w,e})$ is a function of the phase saturation $p_c(s_{w,e}) = p_d s_{w,e}^{-1/\theta }$ where $p_d \ge 0$ is the constant entry pressure.

From the constitutive relations $s_w + s_n=1$ and $p_{n} - p_{w}= p_{c}(s_{w,e})$, we can rewrite the two-phase flow problem as a system of equations with two unknowns $p_w$ and $s_n$,

$$\begin{aligned} \begin{aligned} -\nabla \cdot ( \lambda _t K \nabla p_{w} + \lambda _n K \nabla p_{c} - (\rho _w\lambda _w + \rho _n \lambda _n) K g)&= q_w + q_n,\\ \phi \frac{\partial s_n}{\partial t} - \nabla \cdot ( \lambda _n K (\nabla p_{w}-\rho _n g)) - \nabla \cdot ( \lambda _n K \nabla p_{c})&=q_{n}. \end{aligned} \end{aligned}$$

(2)

Here, $\lambda _t = \lambda _w + \lambda _n$ denotes the total mobility.

The first equation of (2) is of elliptic type with respect to the pressure $p_w$. The type of the second equation of (2) is either nonlinear hyperbolic if $\frac{\partial p_c(s_n)}{\partial s_n}\equiv 0$ or degenerate parabolic if the capillary pressure is not neglected. The diffusion term might degenerate if $\lambda _n(s_n=0)=0$. In order to have a complete system we add appropriate boundary and initial conditions. Thus, we assume that the boundary of the system is divided into disjoint open sets $\partial \varOmega = {\bar{\varGamma }}_{ D} \cup {\bar{\varGamma }}_{N}$. We define the total inflow $J_t= J_w+J_n$ as the sum of the phases inflow on the Neumann boundary ${\bar{\varGamma }}^{}_{N}$.

3 Discretization

Let $\mathscr {T}_h = \{E\}$ be a family of non-degenerate, quasi-uniform, possibly non-conforming partitions of $\varOmega$ consisting of $N_h$ elements (quadrilaterals or triangles in 2d, tetrahedrons or hexahedrons in 3d) of maximum diameter h. Let $\varGamma ^{h}$ be the union of the open sets that coincide with internal interfaces of elements of $\mathscr {T}_h$. Dirichlet and Neumann boundary interfaces are collected in the set $\varGamma ^{h}_{D}$ and $\varGamma ^{h}_{N}$. Let e denote an interface in $\varGamma ^{h}$ shared by two elements $E_{-}$ and $E_{+}$ of $\mathscr {T}_h$; we associate with e a unit normal vector $n_e$ directed from $E_{-}$ to $E_{+}$. We also denote by $\left| e\right|$ the measure of e. The discontinuous finite element space is $\mathscr {D}_r(\mathscr {T}_h)= \{ v \in \mathbb {L}^2(\varOmega ) : v_{\mid E} \in \mathscr {P}_r(E) \forall E \in \mathscr {T}_{h} \}$, where $\mathscr {P}_r(E)$ denotes $\mathbb {Q}_r$ (resp. $\mathbb {P}_r$) the space of polynomial functions of degree at most $r \ge 1$ on E (resp. the space of polynomial functions of total degree $r \ge 1$ on E). We approximate the pressure and the saturation by discontinuous polynomials of total degrees $r_p$ and $r_s$ respectively.

For any function $q\in \mathscr {D}_r(\mathscr {T}_h)$, we define the jump operator $\llbracket \cdot \rrbracket$ and the average operator $\{ \cdot \}$ over the interface e: $\forall e \in \varGamma ^{h}$,     $\llbracket q \rrbracket := q_{E_{-}} - q_{E_{+}}$,     $\{ q \} := \frac{1}{2} q_{E_{-}} + \frac{1}{2} q_{E_{+}}$, and $\forall e \in \partial \varOmega$,     $\llbracket q \rrbracket = \{ q \} := q_{E_{-}}$.

In order to treat the strong heterogeneity of the permeability tensor, we follow [8] and introduce a weighted average operator $\{ \cdot \}_\omega$:

$\forall e \in \varGamma ^{h}, \quad \{ q\}_\omega = \omega _{E_{-}} q_{E_{-}} +\omega _{E_{+}} q_{E_{+}}$ and $\forall e \in \partial \varOmega , \quad \{ q\}_\omega = q_{E_{-}}$.

The weights are $\omega _{E_{-}}= \frac{\delta _K^{E_{+}}}{\delta _K^{E_{+}}+\delta _K^{E_{-}}}$,     $\omega _{E_{+}}= \frac{\delta _K^{E_{-}}}{\delta _K^{E_{+}} + \delta _K^{E_{-}}}$ with $\delta _K^{E_{-}}= n_e^T K_{E_{-}} n_e$ and $\delta _K^{E_{+}}= n_e^T K_{E_{+}} n_e$. Here, $K_{E_{-}}$ and $K_{E_{+}}$ are the permeability tensors for the elements $E_{-}$ and $E_{+}$.

3.1 Semi Discretization in Space

The derivation of the semi-discrete DG formulation is standard (see [11]). First, we multiply each equation of (2) by a test function and integrate over each element, then we apply Green formula to obtain the semi-discrete weak DG formulation. Hence, the aforementioned formulation consists in finding the continuous in time approximations $p_{w,h}(\cdot ,t) \in \mathscr {D}_{r_{p}}(\mathscr {T}_h)$, $s_{n,h}(\cdot ,t) \in \mathscr {D}_{r_{s}}(\mathscr {T}_h)$ such that:

$$\begin{aligned} \begin{aligned} \mathscr {B}_{h}(p_{w,h},\varphi ;s_{n,h}) = l_{h}(\varphi ) \quad \forall \varphi \in \mathscr {D}_{r_{p}}(\mathscr {T}_h) \text{, } \forall t \in \mathscr {J}, \, \\ (\varPhi \partial _t s_{n,h}, \psi ) + c_{h}(p_{w,h},\psi ;s_{n,h}) + d_{h}(s_{n,h},\psi ) = r_{h}(\psi ) \quad \forall \psi \in \mathscr {D}_{r_{s}}(\mathscr {T}_h) \text{, } \forall t \in \mathscr {J}. \, \end{aligned} \end{aligned}$$

(3)

The bilinear form $\mathscr {B}_{h}$ in the total fluid conservation equation of the system (3) is:

$$\begin{aligned} \begin{aligned} \mathscr {B}_{h}(p_{w,h},\varphi ;s_{n,h})&=\mathscr {B}_{bulk,h}+ \mathscr {B}_{cons,h} + \mathscr {B}_{sym,h} + \mathscr {B}_{stab,h}. \end{aligned} \end{aligned}$$

(4)

The first term $\mathscr {B}_{bulk,h}:=\mathscr {B}_{bulk,h} (p_{w,h},\varphi ;s_{n,h})$ of (4) is the volume term:

$$\begin{aligned} \begin{aligned} \mathscr {B}_{bulk,h} =\sum \limits _{E \in \mathscr {T}_{h}} \int _E (\lambda _t K \nabla p_{w,h} + \lambda _n K \nabla p_{c,h} ) \cdot \nabla \varphi -\sum \limits _{E \in \mathscr {T}_{h}} (\rho _n \lambda _n +\rho _w \lambda _w) K g \cdot \nabla \varphi . \end{aligned} \end{aligned}$$

(5)

The second term $\mathscr {B}_{cons,h}:=\mathscr {B}_{cons,h} (p_{w,h},\varphi ;s_{n,h})$, is the consistency term:

$$\begin{aligned} \begin{aligned} \mathscr {B}_{cons,h}=&- \sum \limits _{e \in \varGamma ^h \cup \varGamma ^{h}_{D} } \int _e\{ \lambda _t K \nabla p_{w,h} \}_{\omega } \cdot n_e \llbracket \varphi \rrbracket - \sum \limits _{e \in \varGamma ^h \cup \varGamma ^{h}_{ D} } \int _e\{ \lambda _n K \nabla p_{c,h} \}_{\omega }\cdot n_e \llbracket \varphi \rrbracket \\&+ \sum \limits _{e \in \varGamma ^h \cup \varGamma ^{h}_{ D} } \int _e\{ (\rho _n \lambda _n+\rho _w \lambda _w) K g) \}_{\omega } \cdot n_e \llbracket \varphi \rrbracket . \end{aligned} \end{aligned}$$

(6)

The term $\mathscr {B}_{sym,h}:=\mathscr {B}_{sym,h} (p_{w,h},\varphi ;s_{n,h})$, is the symmetry term. Depending on the choice of $\varepsilon$ we get different DG methods ($\varepsilon =-1$ SIPG, $\varepsilon =1$ NIPG, $\varepsilon =0$ IIPG):

$$\begin{aligned} \begin{aligned} \mathscr {B}_{sym,h} =&\varepsilon \sum \limits _{e \in \varGamma ^h \cup \varGamma ^{h}_{ D} } \int _e\{ \lambda _t K \nabla \varphi \}_{\omega } \llbracket p_{w,h} \rrbracket + \varepsilon \sum \limits _{e \in \varGamma ^h \cup \varGamma ^{h}_{D} } \int _e\{ \lambda _n K \nabla \varphi \}_{\omega } \llbracket s_{n,h} \rrbracket . \end{aligned} \end{aligned}$$

(7)

is the stability term.

Following [3], the penalty formulation is: .

The right hand side of the total fluid conservation equation of the system (3) is a linear form including the boundary conditions and the source terms.

$$\begin{aligned} \begin{aligned} l_{h} (\varphi )&= \int _{\varOmega } (q_w+ q_n) \varphi - \sum \limits _{e \in \varGamma ^{}_{ N} } \int _e J_t \varphi +\varepsilon \sum \limits _{e \in \varGamma ^{h}_{ D} } \int _e \lambda _{t} K \nabla \varphi \cdot n_e p_{ D} \\ {}&+ \varepsilon \sum \limits _{e \in \varGamma ^{h}_{D} } \int _e \lambda _n K \nabla \varphi \cdot n_e s_{ D} +\sum \limits _{e \in \varGamma ^{h}_{D} } {\gamma _e^p} \int _e p_D \varphi \text{, } \quad \forall \varphi \in \mathscr {D}_{r_{p}}(\mathscr {T}_h). \end{aligned} \end{aligned}$$

(8)

The second equation of the system (3) is the discrete weak formulation of the nonwetting-phase conservation equation where the convection term $- \nabla \cdot ( \lambda _n K (\nabla p_{w}-\rho _n g))$ might be approximated by an upwind discretization technique.

$$\begin{aligned} \begin{aligned} c_{h}(p_{w,h},\psi ;s_{n,h})&= \sum \limits _{E \in \mathscr {T}_{h}} \int _E ( K \lambda _n ( \nabla p_{w,h} - \rho _n g)) \cdot \nabla \psi - \sum \limits _{e \in \varGamma ^h \cup \varGamma ^{h}_{ D} } \int _e \{ K \lambda _n^{\#} \nabla p_{w,h} \}_{\omega } \llbracket \psi \rrbracket \\&+ \sum \limits _{e \in \varGamma ^h \cup \varGamma ^{h}_{ D} } \int _e \{ \rho _n K \lambda _n^{\#} g \}_{\omega } \llbracket \psi \rrbracket +\varepsilon \sum \limits _{e \in \varGamma ^h \cup \varGamma ^{h}_{D} } \int _e \{ K \lambda _n^{\#} \nabla \psi \}_{\omega } \llbracket p_{w,h} \rrbracket , \end{aligned} \end{aligned}$$

(9)

where $\lambda _n^{\#}=(1-\rho ) \lambda _{n,E} + \rho \lambda _n^{\uparrow }$ and $\lambda _n^{\uparrow }$ is the upwind mobility:

$$ \forall e \in \partial E_{-} \cap \partial E_{+}, \quad \lambda _n^{\uparrow }={\left\{ \begin{array}{ll} \lambda _{n,E_{-}}\quad \text{ if } -K (\nabla p_w + \nabla p_c - \rho _n g) \cdot n \ge 0,\\ \lambda _{n,E_{+}}\quad \text{ else }. \end{array}\right. } $$

Hence depending on the value of $\rho \in \{ 0,1\}$, we might use central differencing or upwinding of the mobility for internal interfaces.

The diffusion term $- \nabla \cdot ( \lambda _n K \nabla p_{c})$ is discretized by a bilinear form similar to that of (4). A more detailed expression can be found in [10].

3.2 Fully Coupled/Fully Implicit DG Scheme

The time interval [0, T] is divided into N intervals $\varDelta t_{i}= t_{i+1} - t_{i}$ as $0 = t_{0} \le t_{1}\le \cdot \cdot \cdot \le t_{N-1}\le t_{N}=T$. Let $p_w^i$ and $s_n^i$ be the numerical solutions at time $t^i$. The approximation $s_{n,h}^{0}$ is chosen as the $L^2$ projection of the saturation $s_n(0)$. For the sake of simplicity and easier reading, we apply a first order Adams-Moulton time discretization and Interior Penalty DG for space discretization to the semi-discrete system (3):

$$\begin{aligned} \begin{aligned} \mathscr {B}_{h}(p_{w,h}^{i+1},\varphi ;s_{n,h}^{i+1}) = l_{h}(\varphi ), \quad \forall \varphi \in \mathscr {D}_{r_{p}}(\mathscr {T}_h), \quad \\ (\varPhi \frac{ s_{n,h}^{i+1}-s_{n,h}^{i} }{\varDelta t}, \psi )_{} + c_{h}(p_{w,h}^{i+1},\psi ;s_{n,h}^{i+1}) +d_{h}(s_{n,h}^{i+1},\psi ) = r_{h}(\psi ), \quad \forall \psi \in \mathscr {D}_{r_{s}}(\mathscr {T}_h), \quad \\ ( s_{n,h}^{0}, \zeta )_{} =( s_{n}^{0} , \zeta )_{}, \quad \forall \zeta \in \mathscr {D}_{r_{s}}(\mathscr {T}_h). \quad \end{aligned} \end{aligned}$$

(10)

4 Adaptivity

The first approach considered, GradIndicator, is based on a heuristic indicator which depends on the local gradient of the DG solution measured in the $L^2$ norm. We define on each element E of the mesh, the indicator $\eta _E^i$ at time step i, such that: $\eta _E^i= ||\nabla s_n^i ||_{L^{2}(E)}, \, \forall E \in \mathscr {T}_{h}$. Each element whose indicator $\eta ^i_E$ is greater than a threshold value $\eta _{Tol} \ge 0$ is refined.

For the second approach, the choice between h-adaptivity and p-adaptivity depends heavily on the value of a smoothness indicator $\varsigma _E$. Given an error indicator $\eta _E$, $E \in \mathscr {T}_h$, we define $\eta _E^{r-1}$ the $L^{2}$ projection into a lower order polynomial space $\mathscr {D}_{r-1}(\mathscr {T}_h)$. The derivation of this $L^2$ projection is quite straightforward due to the hierarchical aspect of the modal DG bases implemented. The indicator $\eta _E=||s_n ||_{H^{1}(E)}$ allows to refine the mesh when the solution is estimated to be rough and increase the polynomial degree when the solution is estimated to be smooth. The use of heuristic error indicators requires a maximum level of allowed h-refinement maxlevel to be specified to avoid overly aggressive refinement. Whenever an element is selected for h-refinement it is also selected for p-coarsening in order to reduce the oscillations in the vicinity of the front of the propagation. An hp-adaptive strategy of this type called PRIOR2P as in [12] is implemented. In that approach, the smoothness indicator is $\varsigma _E \sim 1- \frac{log ((\eta _E^{r-1})/(\eta _E^{r-2}))}{log ((r-1)/(r-2))}$, where r is the local polynomial degree.

5 Numerical Simulations

In this section we present some numerical tests for the adaptive DG scheme. All test cases are implemented with the Interior Penalty methods. In order to ensure second order accuracy, we employ a central differencing of the mobility for internal interfaces thus following a similar approach to that of Rivière et al. [7].

5.1 2d Flow Problem

We consider here a two dimensional test case that admits an exact solution from [2] aiming to examine the $L^2$ error of the DG methods. The problem depicts the transport of a Gaussian pulse in a rotating flow field. Considering $\varOmega =(-0.5,0.5)^2$ and $J =(0,T)$, we search for (S) such that: $\frac{\partial S}{\partial t} + \nabla \cdot (u S+ K \nabla S ) = 0 \, \text{ in } \varOmega \times J$.

The problem boundary and initials conditions derive from the exact solution $S(x,y,t)=2 \sigma ^2/(2\sigma ^2 + 4Kt) ~ e^{(-\frac{(\bar{x} -x_c)^2+(\bar{y} -y_c)^2}{2\sigma ^2 +4 K t})}$ where, $u=(-4y,4x)^{T}$, $\bar{x}= x cos(4 t) + y sin(4 t)$, $\bar{y}= -x sin(4 t) + y cos(4 t)$, $x_c=-0.25$, $y_c=0$, $K=10^{-4}$ and $2\sigma ^2=0.004$.

Fig. 1

Rotating pulse, solution at T $=$ 0.4

Table 1 $L^2$ error for solution at $T=0.4$

Fig. 2

Polynomial degrees at T $=$ 0.4 for GradIndicator

Fig. 3

Polynomial degrees at T $=$ 0.4 for PRIOR2P

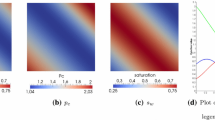
The domain is subdivided uniformly into square elements. The coarsest mesh consist of $8\times 8$ elements. The solutions are approximated by piecewise polynomials of order k, $k \in \{1,2,3,4\}$. The penalty parameter $\sigma _p=10^{-10}$. Figures 1, 2 and 3 provide contours of the solution for the IIPG scheme combined with second order Adams-Moulton method time discretization. The numerical analysis in Table 1 shows that the PRIOR2P indicator yields a smaller $L^2$ error.

5.2 3d Heterogeneous Problem

In this section, we focus on a three-dimensional case. We also consider different sand types with different permeabilities and different entry pressures (Table 2).

Table 2 3d problem parameters

The bottom of the reservoir is impermeable for both phases. Hydrostatic conditions for the pressure $p_w$ and homogeneous Dirichlet conditions for the saturation $s_n$ are prescribed at the lateral boundaries. A flux of 0.25 Kg s$^{-1}$m$^{-2}$ of the DNAPL is infiltrated from the top into a domain of depth of 1 m. The initial ALUCubeGrid mesh consist of $17\times 17\times 17$ hexahedral elements and resolves the interfaces between regions with different permeabilities. 150 time steps of length $\varDelta t =20$ s are computed (final time $T=3000$ s). This grid is locally adapted (non-conforming). We also set $r_p=r_s$ for the problem.

Table 3 $L^2$ error for solution at $T=0.4$

Fig. 4

First row from left to right, domain geometry, contour plot of saturation distribution after 3000 s of injection, mesh distribution, polynomial degree distribution along the slice y = 0.45. Second row saturation profile along the slice y = 0.45; from left to right, non-adaptive with $r_p=r_s=2$, h-adaptive with $r_p=r_s=1$, h-adaptive with $r_p=r_s=2$, hp-adaptive with max$\{r_p,r_s\}$=2

Figure 4 illustrates the evolution of the nonwetting saturation during the simulation. The effects of the hp algorithm are reflected in the mesh distribution showing an intense refinement and lower polynomial degree in the parts of the domain where the value of the indicator is above the threshold value. The second row of Fig. 4 shows the drastic improvement of the front shape and the reduction of the oscillations in the vicinity of the front when h and hp-adaptive methods are used. Table 3 provides more details concerning the computational effort.

6 Conclusion & Outlook

In this work, we have introduced an adaptive discontinuous Galerkin scheme for incompressible, immiscible two-phase flow in strongly heterogeneous porous media with gravity forces and discontinuous capillary pressures. We considered as a 3d test case a DNAPL infiltration in an initially water saturated reservoir. The oscillations appearing in the vicinity of the front of the propagation are reduced with the local mesh refinement and the decrease of the local polynomial order. Future work will be concerned with the derivation of robust anisotropic hp-adaptive methods and the extension to other DG methods such as the Compact Discontinuous Galerkin 2 (CDG2) [4].