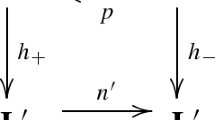Two Dualities for Weakly Pseudo-complemented quasi-Kleene Algebras

Abstract

Quasi-Nelson algebras are a non-involutive generalisation of Nelson algebras that can be characterised in several ways, e.g. as (i) the variety of bounded commutative integral (not necessarily involutive) residuated lattices that satisfy the Nelson identity; (ii) the class of (0, 1)-congruence orderable commutative integral residuated lattices; (iii) the algebraic counterpart of quasi-Nelson logic, i.e. the (algebraisable) extension of the substructural logic $\mathcal {FL}_{ew}$ by the Nelson axiom. In the present paper we focus on the subreducts of quasi-Nelson algebras obtained by eliding the implication while keeping the two term-definable negations. These form a variety that (following A. Sendlewski, who studied the corresponding fragment of Nelson algebras) we dub weakly pseudo-complemented quasi-Kleene algebras. We develop a Priestley-style duality for these algebras (in two different guises) which is essentially an application of the general approach proposed in the paper A duality for two-sorted lattices by A. Jung and U. Rivieccio.

U. Rivieccio acknowledges partial funding by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq, Brazil), under the grant 313643/2017-2 (Bolsas de Produtividade em Pesquisa - PQ). R. Jansana was financed by grant 2017 SGR 95 from the government of Catalonia and the research project MTM2016-74892-P from the government of Spain, which include feder funds from the European Union. T. Nascimento acknowledges partial support by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES, Brazil) - Finance Code 001.

1 Introduction

Nelson’s constructive logic with strong negation $\mathcal {N}$ (introduced in [10]; see also [14, 20, 25]) is a well-known non-classical logic that combines the constructive approach of (the $\{\wedge , \vee , \rightarrow \}$-fragment of) intuitionistic logic with a De Morgan involutive negation. The algebraic models of $\mathcal {N}$ form the variety of Nelson algebras (alias Nelson residuated lattices), and have been studied since the late 1950’s (first by Rasiowa; see [14] and references therein). One of the main algebraic insights on this variety is that every Nelson algebra can be represented as a special binary power (here called a twist-algebra) of a Heyting algebra. This correspondence was formulated as a categorical equivalence (first by A. Sendlewski) between Nelson algebras and a category of enriched Heyting algebras, and this made it possible to transfer a number of fundamental results from the theory of Heyting algebras to the Nelson realm.

More recent is the discovery (due to Spinks and Veroff [23, 24]) that Nelson logic can be viewed as one of the so-called substructural logics. This entails that the class of Nelson algebras is term equivalent to a variety of bounded, commutative, integral residuated lattices [4]; hence the alternative name of Nelson residuated lattices. Given the recent flourish of studies on substructural logics and residuated structures, this alternative perspective also proved fruitful. Indeed, it made it possible, in the first place, to recover or recast a number of results on Nelson algebras by specialising more general ones about residuated structures. Furthermore, and maybe more interestingly, it allows us to formulate new questions on Nelson algebras/logic that can be best appreciated within the framework of residuated lattices. Among these is the problem that led to the introduction of quasi-Nelson algebras, which can be phrased as follows.

By the results of [23, 24], Nelson algebras are term equivalent to a the class of (bounded, commutative, integral) residuated lattices that additionally satisfy the involutive law ($x \approx (x \Rightarrow 0) \Rightarrow 0$) and the Nelson identity:

$$ (x \Rightarrow (x \Rightarrow y)) \wedge (\mathop {\sim }y \Rightarrow (\mathop {\sim }y \Rightarrow \mathop {\sim }x)) \approx x \Rightarrow y. $$

Thus, all results that are specific to Nelson algebras (as opposed to general residuated lattices), including the connection with Heyting algebras given by twist-algebras, essentially depend on involutivity and on the Nelson identity.

The papers [17, 18] are aimed at establishing to which extent the structure theory of Nelson algebras can be reconstructed (within the context of residuated lattices) in the presence of the Nelson identity but without relying on the involutive law. It turns out that some of the most characteristic results indeed do not depend on the involutive law. In particular, it is shown in [17, 18] that (a suitable generalisation of) the twist-algebra construction can be performed in a not-necessarily involutive context: thus making it possible to recover the connection between Heyting algebras and ‘non-involutive Nelson algebras’, a variety we dubbed quasi-Nelson algebras (alias quasi-Nelson residuated lattices). This class can also be characterised by a purely congruence-theoretical property introduced in [22] under the name of (0, 1)-congruence orderability; the main result being that among (bounded, commutative, integral) residuated lattices, quasi-Nelson algebras are precisely the (0, 1)-congruence orderable ones. This generalises the result of [22] that, the (0, 1)-congruence orderable involutive residuated lattices are precisely the Nelson residuated lattices.

The very recent paper [15] extends the investigation of quasi-Nelson algebras initiated in [17, 18] to the implication-free fragment; in turn, [15] relies on [16], in which the $\{ \wedge , \vee , \mathop {\sim }\}$- fragment of quasi-Nelson logic was characterised. More precisely, [15] elides the implication operation $\rightarrow$ from the language while keeping the two negation operators (the primitive $\mathop {\sim }$ and a second one $\lnot$ that is defined, in the full language of quasi-Nelson algebras, by $\lnot x : = x \rightarrow 0$). It turns out that a twist-algebra construction (see Definition 5 below) can be used to characterise the class of algebras corresponding to the two-negation fragment of quasi-Nelson algebras, dubbed in [15] weakly pseudo-complemented quasi-Kleene algebras.

In fact, [15] can be viewed as a non-involutive counterpart of Sendlewski’s study on the two-negation subreducts of Nelson algebras [21]. Sendlewski shows that those subreducts form a variety (called wp-Kleene algebras) which corresponds via a twist-algebra construction to pseudo-complemented distributive lattices (i.e., the subreducts of Heyting algebras with negation but no implication). This entails that the functor between Nelson and Heyting algebras can be extended to one with similar properties relating the subreducts of both classes. Indeed, most results contained in [21] can be retrieved from [15] by restricting one’s attention to involutive algebras.

In the present paper, we take advantage of the twist representation introduced in [15] to develop a Priestley-style duality for weakly pseudo-complemented quasi-Kleene algebras (thereby obtaining a duality for Sendlewski’s wp-algebras as well). We present our duality in two guises based on the two twist representations introduced in [15]; both can be viewed as applications of the two-sorted approach to dualities proposed in [7].

2 WPQK-algebras and Their Representation

In this section we sum up the results from [15, 16] that shall be needed for our present purposes. We begin by introducing quasi-Nelson algebras, the algebras in the full language (we refer the reader to [17, 18] for further details and proofs; see also [4] for all unexplained algebraic and logical terminology). The most convenient way to do so is by taking the substructural route, starting from the notion of residuated lattice.

A commutative integral bounded residuated lattice (CIBRL) is an algebra $\mathbf {A} = \langle A; \wedge , \vee , *, \Rightarrow , 0, 1 \rangle$ of type $\langle 2, 2, 2, 2, 0, 0 \rangle$ such that:

CIBRLs form a variety that is the algebraic counterpart of the logic $\mathcal {FL}_{ew}$, i.e. the extension of the Full Lambek Calculus $\mathcal {FL}$ obtained by adding the rules of exchange (e) and weakening (w), as well as a propositional constant (usually denoted $\bot$ or by 0) to be interpreted as the least element on the algebras. The negation connective/operation is defined by the term $\mathop {\sim }x : = x \Rightarrow 0$.

Definition 1

A quasi-Nelson residuated lattice or quasi-Nelson algebra is a CIBRL that satisfies the Nelson identity:

$$\begin{aligned} (x \Rightarrow (x \Rightarrow y)) \wedge (\mathop {\sim }y \Rightarrow (\mathop {\sim }y \Rightarrow \mathop {\sim }x)) \approx x \Rightarrow y. \end{aligned}$$

(Nelson)

A Nelson residuated lattice (or Nelson algebra) is a quasi-Nelson residuated lattice that additionally satisfies the involutive identity $\mathop {\sim }\mathop {\sim }x \approx x$.

On every quasi-Nelson algebra, one can define a connective $\rightarrow$ (called weak implication, while the residuated $\Rightarrow$ is known as the strong implication) by the term $x \rightarrow y := x \Rightarrow (x \Rightarrow y)$. The weak implication is indeed a genuine implication; it is, in fact, the connective that gives (quasi-)Nelson logic a classical deduction-detachment theorem [9, Thm. 2]. As such, the weak implication can be used to introduce an alternative negation $\lnot$ (distinct from $\mathop {\sim }$) given by the term $\lnot x : = x \rightarrow 0$. This observation led Sendlewski [21] to the study of weakly pseudo-complemented Kleene algebras, alias the $\{\wedge , \vee , \mathop {\sim }, \lnot , 0, 1 \}$-subreducts of Nelson algebras. The $\{\wedge , \vee , \mathop {\sim }, \lnot , 0, 1 \}$-subreducts of quasi-Nelson algebras are characterised in [15], and the corresponding variety dubbed weakly pseudo-complemented quasi-Kleene algebras. We proceed to introduce formally these classes of algebras, starting from the $\{\wedge , \vee , \mathop {\sim }\}$-fragment of quasi-Nelson algebras, which was studied in [16].

Definition 2

([19]). An algebra $\mathbf {A} = \langle A; \wedge ,\vee , \mathop {\sim }, 0, 1 \rangle$ of type $\langle 2, 2, 1, 0, 0 \rangle$ is a semi-De Morgan algebra if the following properties and identities are satisfied:

• (SD1) $\langle A; \wedge , \vee , 0, 1 \rangle$ is a bounded distributive lattice,

• (SD2) $\mathop {\sim }0 \approx 1$ and $\mathop {\sim }1 \approx 0$,

• (SD3) $\mathop {\sim }(x \vee y) \approx \mathop {\sim }x \wedge \mathop {\sim }y$,

• (SD4) $\mathop {\sim }\mathop {\sim }(x \wedge y) \approx \mathop {\sim }\mathop {\sim }x \wedge \mathop {\sim }\mathop {\sim }y$,

• (SD5) $\mathop {\sim }x \approx \mathop {\sim }\mathop {\sim }\mathop {\sim }x$.

A lower quasi-De Morgan algebra is a semi-De Morgan algebra that satisfies:

• (QD) $x \ll \mathop {\sim }\mathop {\sim }x$,

(in the present paper, we take $\alpha \ll \beta$ as an abbreviation for the formal identity $\alpha \wedge \beta \approx \alpha$). A De Morgan algebra can be defined as a semi-De Morgan algebra that further satisfies the involutive identity $\mathop {\sim }\mathop {\sim }x \approx x$.

Besides De Morgan algebras, another well-known subvariety of semi-De Morgan algebras is the class of pseudo-complemented distributive lattices (also called distributive p-algebras or simply – as we will here – p-lattices). This class can be axiomatised, relative to semi-De Morgan algebras, by adding the lower quasi-De Morgan identity (QD) together with the following one [19, Cor. 2.8]: $\mathop {\sim }x \wedge \mathop {\sim }\mathop {\sim }x \approx 0$. The variety of p-lattices is precisely the class of $\{\wedge , \vee , \mathop {\sim }, 0, 1\}$-subreducts of Heyting algebras [1, Chapter VIII]. Alternatively, a p-lattice can be defined as a bounded distributive lattice $\langle A; \wedge , \vee , 0, 1 \rangle$, with order $\le$, bottom 0 and top 1, additionally satisfying the property that, for all $a,b \in A$,

We shall refer to (P) as to the property of the pseudo-complement. It is useful to keep in mind that, on every distributive lattice A, the pseudo-complement $\mathop {\sim }b$ of each $b \in A$ (if it exists) is uniquely determined by the lattice structure in the following way: $\mathop {\sim }b = \bigvee \{ a \in A : a \wedge b = 0 \} = \max \bigvee \{ a \in A : a \wedge b = 0 \}$. Every p-lattice is a quasi-Kleene algebra (as defined below), but not necessarily a Kleene algebra.

Definition 3

([16]). A quasi-Kleene algebra is a semi-De Morgan algebra $\mathbf {A}$ that additionally satisfies the following identities:

A Kleene algebra can be defined as a quasi-Kleene algebra that satisfies the involutive identity: $\mathop {\sim }\mathop {\sim }x \approx x$.

Every Nelson algebra has a Kleene algebra reduct; indeed, Kalman’s results [8] easily entail that Kleene algebras are precisely the $\{\wedge , \vee , \mathop {\sim }\}$-subreducts of Nelson algebras. Similarly, it is shown in [16, Cor. 6.6] that quasi-Kleene algebras are the $\{\wedge , \vee , \mathop {\sim }\}$-subreducts of quasi-Nelson algebras.

Given an algebra $\mathbf {A}$ having a quasi-Kleene algebra reduct and given $a,b \in A$, we write $\ a \preceq b\$ as a shorthand for $\ a \le \mathop {\sim }a \vee b \$ and $\ a \equiv b \$ as a shorthand for $(a \preceq b \text { and } b \preceq a)$. The binary relation associated with $\mathop {\preceq }$ is reflexive and transitive on every quasi-Kleene algebra. It is also clear that $a \le b$ implies $a \mathop {\preceq }b$, for all $a,b \in A$. Thus, in particular, we have $0 \mathop {\preceq }a \mathop {\preceq }1$ for all $a \in A$.

Definition 4

A weakly pseudo-complemented quasi-Kleene algebra (WPQK-algebra) is an algebra $\mathbf {A} = \langle A; \wedge , \vee , \mathop {\sim }, \lnot , 0, 1 \rangle$ of type $\langle 2, 2, 1, 1, 0, 0 \rangle$ such that:

Item ii.1 in Definition 4 (the property of the weak pseudo-complement) can be equivalently replaced by the following conditions: for all $a,b \in A$,

• (i) $\lnot 1 = 0$,

• (ii) $\lnot (a \wedge \mathop {\sim }a) = 1$,

• (iii) $a \wedge \lnot (a \wedge b) \equiv a \wedge \lnot b$.

Thus, the class of WPQK-algebras is a variety [15, Prop. 4.12]. The prime examples of WPQK-algebras are obviously the reducts of (quasi-)Nelson algebras [15, Prop. 4.4]. It is also easy to check that every p-lattice $\langle A; \wedge , \vee \lnot , 0, 1 \rangle$ forms a WPQK-algebra if we let $\mathop {\sim }x := \lnot x$ (cf. [19, Cor. 2.8]). Sendlewski’s wp-Kleene algebras are precisely the subvariety of WPQK-algebras satisfying the involutive identity $\mathop {\sim }\mathop {\sim }x \approx x$ [15, Prop. 4.15]. The reduct $\langle A; \wedge , \vee , \lnot , 0, 1 \rangle$ of a WPQK-algebra need not be a quasi-Kleene algebra, for the analogue of (QK2) for $\lnot$ need not be satisfied. In fact, (SD4) and (SD5) may also fail, suggesting that $\langle A; \wedge , \vee , \lnot , 0, 1 \rangle$ may not even be a semi-De Morgan algebra. For further examples and properties of WPQK-algebras, see [15].

Proposition 1

([15], Cor. 5.5). The class of $\{ \wedge , \vee , \mathop {\sim }, \lnot , 0, 1 \}$-subreducts of quasi-Nelson algebras is precisely the variety of WPQK-algebras, and the class of $\{ \wedge , \vee , \mathop {\sim }, \lnot , 0, 1 \}$-subreducts of Nelson algebras is the variety of wp-Kleene algebras.

We note that Proposition 1 is informative also because, in general, the class of subreducts of a variety of algebras (in some proper subsignature) forms a quasi-variety but not necessarily a variety. The next and most fundamental result about WPQK-algebras is the representation as twist-algebras over pairs of p-lattices. Given a p-lattice $\mathbf {L} = \langle L; \wedge , \vee , \lnot , 0, 1 \rangle$ and a lattice filter $\nabla \subseteq L$, we say that $\nabla$ is dense if $D(\mathbf {L} ) \subseteq \nabla$, where $D(\mathbf {L} ) : = \{ a \vee \lnot a : a \in L \} = \{ a \in L : \lnot a = 0 \}$. Notice that $D(\mathbf {L} )$ is itself a lattice filter.

Definition 5

A WPQK-twist-structure is a tuple $\mathbb {L} = \langle \mathbf {L} _+, \mathbf {L} _-, n, p, \nabla \rangle$ where $\mathbf {L} _+ = \langle L_+; \wedge _+, \vee _+, \lnot _+, 0_+, 1_+ \rangle$ is a p-lattice (with order $\le _+$), $\nabla \subseteq L_+$ a dense filter, $\mathbf {L} _- = \langle L_-; \wedge _-, \vee _-, 0_-, 1_- \rangle$ a bounded distributive lattice (with order $\le _-$), and $n :L_+ \rightarrow L_-$ and $p :L_- \rightarrow L_+$ are maps satisfying the following properties:

• (i) n is a bounded lattice homomorphism,

• (ii) p preserves finite meets and both lattice bounds,

• (iii) $n \circ p = Id_{L_-}$ and $Id_{L_+} \le _+ p \circ n$.

The algebra $\mathbf {L_+ \bowtie L_-} = \langle L_+ \times L_- ; \wedge , \vee , \mathop {\sim }, \lnot , 0, 1 \rangle$ is defined as follows. For all $\langle a_+,a_- \rangle , \langle b_+ , b_- \rangle \in L_+ \times L_-$,

$$\begin{aligned} 1 := \langle 1_+, 0_- \rangle ,&\quad 0 := \langle 0_+, 1_- \rangle , \\ \mathop {\sim }\langle a_+, a_- \rangle := \langle p(a_-), n(a_+) \rangle ,&\quad \lnot \langle a_+, a_- \rangle := \langle \lnot _+ a_+, n(a_+) \rangle , \\ \langle a_+ , a_- \rangle \wedge \langle b_+, b_- \rangle&:= \langle a_+ \wedge _+ b_+ , a_- \vee _- b_-\rangle , \\ \langle a_+ , a_- \rangle \vee \langle b_+, b_- \rangle&:= \langle a_+ \vee _+ b_+ , a_- \wedge _- b_-\rangle . \end{aligned}$$

The weakly pseudo-complemented quasi-Kleene twist-algebra (WPQK twist-algebra) $Tw(\mathbb {L})$ is the $\{ \wedge , \vee , \mathop {\sim }, \lnot , 0, 1 \}$-subreduct of $\mathbf {L_+ \bowtie L_-}$ with universe:

$$ \{ \langle a_+, a_- \rangle \in L_+ \times L_- : a_+ \vee _+ p(a_-) \in \nabla , \, a_+ \wedge _+ p(a_-) = 0_+ \}. $$

While the whole algebra $\mathbf {L_+ \bowtie L_-}$ does not need to be a WPQK-algebra, every WPQK twist-algebra is a WPQK-algebra [15, Prop. 4.3]. Moreover, every WPQK-algebra arises in this way [15, Thm. 6.2]. Before demonstrating this, let us comment on a few consequences of Definition 5 that will be useful in the next sections.

The maps n and p form an adjoint pair between the posets $\langle L_+, \le _+ \rangle$ and $\langle L_-, \le _- \rangle$. As is well known, this entails that n preserves arbitrary existing joins and p arbitrary existing meets. Moreover, the lattice $\mathbf {L} _-$ is also pseudo-complemented, with the pseudo-complement given by $\lnot _- a_- = n(\lnot _+ p(a_-))$ for all $a_- \in A_-$. Both maps n and p preserve the pseudo-complement operation [15, Prop. 3.4].

Let $\mathbf {A} = \langle A; \wedge , \vee , \mathop {\sim }, \lnot , 0, 1 \rangle$, be a WPQK-algebra. Then the relation $\equiv$ introduced above is a congruence of the $\{ \mathop {\sim }\}$-free reduct of $\mathbf {A}$ [15, Cor. 4.7], and the quotient algebra $\mathbf {A} _+ = \langle A / \!\! \equiv ; \wedge , \vee , \lnot , 0, 1 \rangle$ is a p-lattice [15, Prop. 4.8]. This gives us the first factor for the twist representation. The second can be obtained as follows. Endow the set $A_- : = \{ [\mathop {\sim }a ] : a \in A \} \subseteq A_+$ with operations given, for all $a,b \in A$, by:

• $[\mathop {\sim }a ] \wedge _- [\mathop {\sim }b ] := [\mathop {\sim }( a \vee b)] = [\mathop {\sim }a \wedge \mathop {\sim }b ] = [\mathop {\sim }a ] \wedge _+ [\mathop {\sim }b]$,

• $[\mathop {\sim }a ] \vee _- [\mathop {\sim }b ] := [\mathop {\sim }(a \wedge b)]$,

• $0_- := [\mathop {\sim }1] = [ 0 ] = 0_+ , \qquad \quad 1_- := [\mathop {\sim }0] = [ 1 ] = 1_+$.

The pseudo-complement operation on $A_-$ can be defined by $\lnot _- [\mathop {\sim }a ] := [\lnot \mathop {\sim }a ] = \lnot _+ [\mathop {\sim }a]$, obtaining a second p-lattice $\mathbf {A} _- = \langle A_-, \wedge _-, \vee _-, \lnot _-, 0_-, 1_- \rangle$; see [15, Prop. 4.9]. The maps $p_{\mathbf {A} } :A_- \rightarrow A_+$ and $n_{\mathbf {A} } :A_+ \rightarrow A_-$ between $\mathbf {A} _+$ and $\mathbf {A} _-$ are given as follows: $p_{\mathbf {A} }$ is the identity map on $A_-$, and $n_{\mathbf {A} }([a]) := [\mathop {\sim }\mathop {\sim }a]$ for all $a \in A$. Note that $n_{\mathbf {A} }$ is well-defined because $a \equiv b$ entails $\mathop {\sim }\mathop {\sim }a \equiv \mathop {\sim }\mathop {\sim }b$ [16, Prop. 3.15.viii]. To obtain the dense filter $\nabla _{\mathbf {A} }$, we consider the set $F(\mathbf {A} ) := \{ a \in A : \mathop {\sim }a \le a \}$ and we let $[F(\mathbf {A} )] := \{ [a] : a \equiv b \text { for some } b \in F(\mathbf {A} )\}$.

Theorem 1

([15], Thm. 6.2). Let $\mathbf {A}$ be a WPQK-algebra.

• (i) $\nabla _{\mathbf {A} } := [F(\mathbf {A} )]$ is a lattice filter of $\mathbf {A_+}$ and $D(\mathbf {A_+}) \subseteq \nabla _{\mathbf {A} }$.

• (ii) $\mathbf {A} \cong Tw (\langle \mathbf {A} _+, \mathbf {A} _-, n_{\mathbf {A} }, p_{\mathbf {A} }, \nabla _{\mathbf {A} } \rangle )$ via the map $\iota _{\mathbf {A} } :A \rightarrow A_+ \times A_-$ given by $\iota _{\mathbf {A} }(a) := \langle [a], [\mathop {\sim }a] \rangle$ for all $a \in A$.

By Theorem 1, every WPQK-algebra $\mathbf {A}$ is uniquely determined by a tuple $\langle \mathbf {A} _+, \mathbf {A} _-, n_{\mathbf {A} }, p_{\mathbf {A} }, \nabla _{\mathbf {A} } \rangle$. This correspondence at the object level can be extended to suitably defined morphisms, obtaining a (co-variant) categorical equivalence between the algebraic category $\mathsf {WPQK}$ of WPQK-algebras (with algebraic homomorphisms) and the category $\mathsf {TW}$ defined as follows.

Definition 6

Let $\mathsf {TW}$ be the category having the WPQK-twist-structure given in Definition 5 as objects and as morphisms between objects $\mathbb {L}$ and $\mathbb {L'}$ the pairs $\langle h_+, h_- \rangle$, where $h_+ :L_+ \rightarrow L'_+$ is a p-lattice homomorphism such that $h_+[\nabla ] \subseteq \nabla '$, $h_- :L_- \rightarrow L'_-$ is a bounded lattice homomorphism, $h_+ \circ p = p' \circ h_-$ and $n' \circ h_+ = h_- \circ n$. The composition of morphisms is given componentwise, that is, the composition of two composable morphisms $\langle h_+, h_- \rangle$ and $\langle k_+, k_- \rangle$ is $\langle h_+ \circ k_+, h_- \circ k_- \rangle$. The identity morphism for each $\mathbb {L} \in \mathsf {TW}$ is the morphism $\langle Id_{L_+}, Id_{L_-}\rangle$.

Checking that $\mathsf {TW}$ is indeed a category is straightforward. We define the functors $F :\mathsf {TW}\rightarrow \mathsf {WPQK}$ and $G :\mathsf {WPQK}\rightarrow \mathsf {TW}$ as follows. For every object $\mathbb {L} \in \mathsf {TW}$, we let $F(\mathbb {L}):= Tw(\mathbb {L})$. For a $\mathsf {TW}$-morphism $\langle h_+, h_-\rangle$ from $\mathbb {L}$ to $\mathbb {L'}$, we let $F(\langle h_+, h_-\rangle )$ be given, for all $\langle a_+, a_- \rangle \in L_+ \times L_-$, by $F(\langle h_+, h_-\rangle ) (\langle a_+, a_- \rangle ) := \langle h_+ (a_+), h_-(a_-)\rangle$. Conversely, for every WPQK-algebra $\mathbf {A}$, we let $G(\mathbf {A} ) : = \langle \mathbf {A} _+, \mathbf {A} _-, n_{\mathbf {A} }, p_{\mathbf {A} }, \nabla _{\mathbf {A} } \rangle$. For a $\mathsf {WPQK}$-homomorphism $k :\mathbf {A} \rightarrow \mathbf {A} '$, we let $k_+: \mathbf {A} _+ \rightarrow \mathbf {A} _+^{'}$ and $k_-: \mathbf {A} _- \rightarrow \mathbf {A} '_-$ be the homomorphisms defined, respectively, by setting $k_+([a]) := [k(a)]$ and $k_-([\mathop {\sim }a]) := [k(\mathop {\sim }a)]$ for every $a \in A$. We then let $G(k):= \langle k_+, k_- \rangle$. It is easy to check that F and G are well-defined functors (concerning the role of the filter $\nabla$, see e.g. [6]). Given $\mathbb {L} \in \mathsf {TW}$, we define the morphism $\iota _{{\mathbb {L}}}= \langle \iota _{L_+}, \iota _{L_-} \rangle$ from ${\mathbb {L}}$ to $G(F({\mathbb {L}}))$ by setting $\iota _{L_+}(a_+) := [\langle a_+, n(\lnot _+ a_+) \rangle ]$ for every $a_+ \in L_+$ and $\iota _{L_-}(a_-) := [\mathop {\sim }\langle \lnot _+ p(a_-), a_- \rangle ]$ for every $a_- \in L_-$. The morphism $\iota _{{\mathbb {L}}}$ is an isomorphism between ${\mathbb {L}}$ and $GF({\mathbb {L}})$. In this way we have a natural isomorphism from the identity functor on $\mathsf {TW}$ and the functor $G \circ F$.

Theorem 2

The functors F, G establish an equivalence between $\mathsf {TW}$ and $\mathsf {WPQK}$.

3 Two-Sorted Duality

We are now going to introduce a Priestley-style duality for the category $\mathsf {TW}$, which (in the light of Theorem 2) we view as a two-sorted alter ego of $\mathsf {WPQK}$. We assume the reader is familiar with the basic duality results on distributive lattices [11], which we now briefly recall.

Priestley duality concerns the category $\mathsf {D}$ of bounded distributive lattices and bounded lattice homomorphisms. To every bounded distributive lattice $\mathbf {L}$, one associates the set $X(\mathbf {L} )$ of its prime filters. On $X(\mathbf {L} )$ one imposes the Priestley topology $\tau$, generated by the sets $\phi (a):=\{P \in X(\mathbf {L} ):a\in P \}$ and $\phi '(a):=\{ P \in X(\mathbf {L} ):a\not \in P \}$, and the inclusion relation between prime filters as an order. The resulting ordered topological structures are called Priestley spaces¹. A homomorphism h between bounded distributive lattices $\mathbf {L}$ and $\mathbf {L} '$ gives rise to a function $X(h):X(\mathbf {L} ')\rightarrow X(\mathbf {L} )$, defined by $X(h)( P)=h^{-1}[ P]$, that is continuous and order preserving. Taking functions with these properties (called Priestley functions) as morphisms between Priestley spaces, one obtains the category $\mathsf {PrSp}$, and X is a contravariant functor from $\mathsf {D}$ to $\mathsf {PrSp}$. For a functor in the opposite direction, one associates to every Priestley space $X=\langle X,\tau ,\le \rangle$ the set $L(X)$ of clopen up-sets. This is a bounded distributive lattice with respect to the set-theoretic operations $\cap , \cup , \emptyset$, and X. To a Priestley function $f:X\rightarrow X'$ one associates the function L(f), given by $L(f)(U')=f^{-1}[U']$, which is a bounded lattice homomorphism from $L(X')$ to $L(X)$. Then L constitutes a contravariant functor from $\mathsf {PrSp}$ to $\mathsf {D}$. The two functors are adjoint to each other with the units given by:

$$\begin{array}{llll} \varPhi _{\mathbf {L} } :\mathbf {L} \rightarrow L(X(\mathbf {L} ))&{}&{} \quad \varPhi _{\mathbf {L} }(a) := \{ P \in X(\mathbf {L} ) : a \in P \}\\ \varPsi _{X}:X\rightarrow X(L(X)) &{}&{} \quad \varPsi _{X}(x) := \{ U \in L(X) : x \in U \}. \end{array}$$

These are the components of a natural transformation from the identity functor on $\mathsf {D}$ to $L \circ X$, and from the identity functor on $\mathsf {PrSp}$ to $X \circ L$, respectively. In particular, they are morphisms in their respective categories. Furthermore, they are isomorphisms and thus the central result of Priestley duality is obtained: the categories $\mathsf {D}$ and $\mathsf {PrSp}$ are dually equivalent.

A description of spaces dual to p-lattices can be found in [12, 13]; see also [1]. We recall here the basic results that shall be needed. For a subset $Y \subseteq X$ of a Priestley space X, we let $\mathop {\downarrow }Y : = \{ x \in X : x \le y \text { for some } y \in Y \}.$

Proposition 2

([12], Prop. 1). A distributive lattice $\mathbf {L}$ is a p-lattice (i.e. can be endowed with a pseudo-complement operation) if and only if, for every clopen up-set $U \in L(X(\mathbf {L} ))$, the set $\mathop {\downarrow }U$ is open in $\langle X(\mathbf {L} ), \subseteq , \tau _{\mathbf {L} } \rangle$.

Definition 7

A p-space is a Priestley space $\langle X, \le , \tau \rangle$ such that $\mathop {\downarrow }U$ is $\tau$-open for all $U \in L(X)$.

Let $\langle X, \le , \tau \rangle$ be a p-space and $U \in L(X)$. Then, defining

$$ \lnot U := X - {\mathop {\downarrow }U}= \{ x \in X : {\mathop {\uparrow }x} \cap U = \emptyset \}, $$

where $\mathop {\uparrow }x : = \{ y \in X : x \le y \}$, we have that $\lnot U \in L(X)$ is the pseudo-complement of U in L(X), turning the distributive lattice of clopen up-sets into a p-lattice. Given a Priestley space $\langle X, \le , \tau \rangle$, let $\max (X) : = \{ y \in X : y \text { is } \le \!\!\!\text {-maximal} \}$ and, for $x \in X$, $\max (x) : = \{ y \in X : x \le y \text { and } y \text { is } \le \!\text {-maximal} \}.$

Definition 8

A morphism between p-spaces $\langle X, \le , \tau \rangle$ and $\langle X', \le ', \tau ' \rangle$ is a continuous order-preserving map $f :X \rightarrow X'$ such that $f [\max (x)] = \max (f (x))$ for all $x \in X$.

Proposition 3

([13], Prop. 3). Let $\langle X, \le , \tau \rangle$ and $\langle X', \le ', \tau ' \rangle$ be p-spaces, and let $f :X \rightarrow X'$ be a continuous order-preserving map. Then f is a morphism of p-spaces if and only if $f^{-1} :L(X') \rightarrow L(X)$ preserves the pseudo-complement operation.

The above results entail that the Priestley functors L and $X$ establish a dual equivalence between the category of p-lattices (with algebraic homomorphisms) and the category of p-spaces with the morphisms given as per Definition 8. Upon this result we will build our two-sorted duality.

Let ${\mathbb {L}}= \langle \mathbf {L} _+, \mathbf {L} _-, n, p, \nabla \rangle \in \mathsf {TW}$. Then $\langle \mathbf {L} _+, \mathbf {L} _-, n, p \rangle$ is a two-sorted lattice in the sense of [7, Definition 4.1]. We thus follow [7] in defining its dual, the two-sorted Priestley space $X({\mathbb {L}}) = \langle X(\mathbf {L} _+), X(\mathbf {L} _-), X(n), X(p), X(\nabla ) \rangle ,$ as follows:

• (i) $\langle X(\mathbf {L} _+), \tau _+, \le _+ \rangle$ is the Priestley space of $\mathbf {L} _+$;

• (ii) $\langle X(\mathbf {L} _-), \tau _-, \le _- \rangle$ is the Priestley space of $\mathbf {L} _-$;

• (iii) $X(p) \subseteq X(\mathbf {L} _+) \times X(\mathbf {L} _-)$ and $X(n) \subseteq X(\mathbf {L} _-) \times X(\mathbf {L} _+)$ are relations defined as follows:

  $$ X(n) := \{ \langle P_-, P_+ \rangle \in X(\mathbf {L} _-) \times X(\mathbf {L} _+) : n^{-1}[P_-] \subseteq P_+ \} $$
  $$ X(p) := \{ \langle P_+, P_- \rangle \in X(\mathbf {L} _+) \times X(\mathbf {L} _-) : p^{-1}[P_+] \subseteq P_- \}; $$

• (iv) $X(\nabla ) : = \{ P_+ \in X(\mathbf {L} _+) : \nabla \subseteq P_+ \}$.

For item (iii), besides [7, Definition 4.1], we refer the reader to [3]. For (iv) and the subsequent treatment of $\nabla _{\mathbf {A} }$ (as well as its dual alter ego $\mathcal {C}_+$), see [6, Sec. 3.3]. Given sets X, Y, a relation $R \subseteq X \times Y$ and a subset $X' \subseteq X$, define: $R[X'] = \{ y \in Y : \text {there is } x \in X' \text { s.t. } \langle x,y \rangle \in R \}$. In particular, for $X' = \{x \}$, we write R[x] instead of $R[\{x\}]$. For $Y' \subseteq Y$, let:

$$\begin{aligned} \Box _{R} Y' = \{ x \in X : R[x] \subseteq Y' \}. \end{aligned}$$

(BoxR)

The following proposition characterises the spaces that correspond to objects in $\mathsf {TW}$.

Proposition 4

Let ${\mathbb {L}}= \langle \mathbf {L} _+, \mathbf {L} _-, n, p, \nabla \rangle \in \mathsf {TW}$, and let the corresponding two-sorted Priestley space be $X({\mathbb {L}}) = \langle X(\mathbf {L} _+), X(\mathbf {L} _-), X(n), X(p), X(\nabla ) \rangle$. Then:

• (i) $X(n)[x_-] \subseteq X(\mathbf {L} _+)$ and $X(p)[x_+] \subseteq X(\mathbf {L} _-)$ are non-empty closed up-sets;

• (ii) $\Box _{R_n} \circ \varPhi _{\mathbf {L} _+} = \varPhi _{\mathbf {L} _-} \circ n$ and $\Box _{R_p} \circ \varPhi _{\mathbf {L} _-} = \varPhi _{\mathbf {L} _+} \circ p$.

• (iii) $X(n)$ is functional, i.e., for all $x_- \in X(\mathbf {L} _-)$ there is $x_+ \in X(\mathbf {L} _+)$ such that $\mathop {\uparrow }x_+ = X(n) [x_-]$.

• (iv) $\le _{-} = X(p) \circ X(n)$.

• (v) $(X(n) \circ X(p)) \subseteq {\le _+}$.

• (vi) $X(\nabla _{\mathbf {A} })$ is a $\tau _+$-closed set such that $X(\nabla ) \subseteq \max (X(\mathbf {L} _+))$.

Proof

For items (i) and (ii), see [7, Prop. 4.2]. Item (iii) follows from [7, Prop. 5.1]. Items (iv) and (v) follow from [7, Prop. 5.3]. For (vi), see [6, Sec. 3.3].

We turn Proposition 4 into our official definition of two-sorted p-spaces.

Definition 9

(cf. [7], Def. 4.3). A two-sorted p-space is a structure $X= \langle X_+, X_-, R_n, R_p, \mathcal {C}_+\rangle$ such that:

• (i) $X_+ = \langle X, \tau _+, \le _+ \rangle$ and $X_- = \langle X, \tau _-, \le _- \rangle$ are p-spaces.

• (ii) $R_n \subseteq X_- \times X_+$, $R_p \subseteq X_+ \times X_-$ satisfy:

  • 1. $R_n[x_-]$ and $R_p[x_+]$ are non-empty closed up-sets, for all $x_-$ and $x_+$;

  • 2. for all $U_- \in L(X_-)$, $U_+ \in L(X_+)$, we have $\Box _{R_p} U_- \in L(X_+)$ and $\Box _{R_n} U_+ \in L(X_-)$.

• (iii) For all $x_- \in X_-$ there is $x_+ \in X_+$ such that $\mathop {\uparrow }x_+ = R_n [x_-]$.

• (iv) $\le _{-} = R_p \circ R_n$.

• (v) $(R_n \circ R_p) \subseteq {\le _+}$.

• (vi) $\mathcal {C}_+$ is a $\tau _+$-closed set such that $\mathcal {C}_+\subseteq \max (X_+)$.

Given a two-sorted p-space $X= \langle X_+, X_-, R_n, R_p, \mathcal {C}_+\rangle$, the dual $L(X) = \langle L(X_+), L(X_-), \Box _{R_n}, \Box _{R_p}, \nabla _{\mathcal {C}_+} \rangle$ is constructed in the expected way: $L(X_+)$ and $L(X_-)$ are as prescribed by Priestley duality (for p-lattices), $\Box _{R_n}, \Box _{R_p}$ are given as in (BoxR), and $\nabla _{\mathcal {C}_+} : = \{ U_+ \in \mathbf {L} (X_+) : C_+ \subseteq U_+ \}$.

Definition 10

Let $X= \langle X_+, X_-, R_n, R_p, \mathcal {C}_+\rangle$ and $X' = \langle X'_+, X'_-, R'_n, R'_p, \mathcal {C}_+' \rangle$ be two-sorted p-spaces and let $f_+ :X_+ \rightarrow X'_+$ and $f_- :X_- \rightarrow X'_-$ be maps. The pair $f = \langle f_+, f_- \rangle$ is a two-sorted p-space morphism if the following conditions hold:

• (i) $f_+$ and $f_-$ are p-space morphisms.

• (ii) f preserves $R_p$ and $R_n$, that is, if $\langle x_+, x_- \rangle \in R_p$, then $\langle f_+(x_+), f_-(x_-) \rangle \in R'_{p}$, etc.

• (iii) $f_+$ and $f_-$ are bounded morphisms, that is,

  • 1. if $\langle f_+(x_+), x'_- \rangle \in R'_{p}$, then there is $x_- \in X_-$ such that $f_-(x_-) \le '_- x'_-$ and $\langle x_+, x_- \rangle \in R_{p}$.

  • 2. if $\langle f_-(x_-), x'_+ \rangle \in R'_{n}$, then there is $x_+ \in X_+$ such that $f_+(x_+) \le '_+ x'_+$ and $\langle x_-, x_+ \rangle \in R_{n}$.

• (iv) $f_+[\mathcal {C}_+] \subseteq \mathcal {C}_+'$.

We denote by $\mathsf {2pSP}$ the category whose objects are two-sorted p-spaces and whose morphisms are given as in Definition 10. For every $\mathsf {TW}$-morphism $h = \langle h_+, h_-\rangle$, the dual pair of maps $\langle X(h_+), X(h_-) \rangle$ form a $\mathsf {2pSP}$-morphism (see [7, Prop. 4.8], [6, Lemma 3.5]). Conversely, for every $\mathsf {2pSP}$-morphism $f = \langle f_+, f_- \rangle$, the dual pair of maps $\langle L( f_+), L( f_-)\rangle$ forms a $\mathsf {TW}$-morphism according to Definition 6 (see [7, Prop. 4.8], [6, Lemma 3.6]). These observations, together with the above-mentioned results from Priestley duality (for $\mathsf {D}$) easily entail the following.

Theorem 3

The functors L and X establish a dual equivalence between $\mathsf {TW}$ and $\mathsf {2pSP}$. In consequence, the composite functors $F \circ L$ and $X \circ G$ establish a dual equivalence between $\mathsf {WPQK}$ and $\mathsf {2pSP}$.

4 Nuclear Duality

In this section we propose an alternative duality based on the alternative representation for WPQK-algebras introduced in [15, Sec. 8], which in turn arises from the following observations.

Let ${\mathbb {L}}= \langle \mathbf {L} _+, \mathbf {L} _-, n, p, \nabla \rangle \in \mathsf {TW}$. Define the operation $\Box :L_+ \rightarrow L_+$ by $\Box a_+ := pn(a_+)$ for all $a_+ \in L_+$. Then $\Box$ is a (dense) nucleus on $\mathbf {L} _+$ in the sense of e.g. [2]. One can further show that $\mathbf {L} _-$ is isomorphic to the algebra $\mathbf {L} _+^\Box := \langle L^{\Box }_+; \wedge _+, \vee _+^{\Box }, 0_+, 1_+ \rangle$ with universe $L^{\Box }_+ : = \{ \Box a_+ : a_+ \in A_+ \}$ and operations given by the restrictions of those of $\mathbf {L} _+$ except for the join, which is defined as $a_+ \vee _+^{\Box } b_+ : = \Box (a_+ \vee _+ b_+)$ for all $a_+,b_+ \in L^{\Box }_+$. This suggests that a tuple $\langle \mathbf {L} _+, \mathbf {L} _-, n, p, \nabla _{\mathbf {A} } \rangle$ can be represented by a pair $\langle \mathbf {L} , \nabla \rangle$, with $\mathbf {L}$ a p-lattice enriched with a nucleus (the maps n and p being replaced by, respectively, the map $\Box :L \rightarrow L^{\Box } = \{ \Box a : a \in L\}$ and the identity map on $L^{\Box }$). In this way one obtains an alternative representation for WPQK-algebras [15, Sec. 8].

Definition 11

A nuclear p-lattice (np-lattice for short) is an algebra $\mathbf {L} = \langle L; \wedge , \vee , \lnot , \Box , 0, 1 \rangle$ of type $\langle 2, 2, 1, 1, 0, 0 \rangle$ such that:

• (i) $\langle L; \wedge , \vee , \lnot , 0, 1 \rangle$ is a p-lattice (with order $\le$).

• (ii) The operator $\Box$ is a dense nucleus on L, that is, for all $a,b \in L$,

  • 1. $\Box 0 = 0$

  • 2. $\Box (a \wedge b) = \Box a \wedge \Box b$

  • 3. $a \le \Box a = \Box \Box a$.

Given an np-lattice $\mathbf {L}$ and a dense filter $\nabla \subseteq L$, we can define a bounded distributive lattice $\mathbf {L} ^{\Box }$ and maps $\Box :L \rightarrow L^{\Box }$ and $Id_{L^{\Box }} :L^{\Box } \rightarrow L$, so that $\langle \mathbf {L} , \mathbf {L} ^{\Box }, \Box , Id_{L^{\Box }}, \nabla \rangle \in \mathsf {TW}$. This gives us the following representation for WPQK-algebras.

Theorem 4

([15], Thm. 8.5). Every WPQK-algebra $\mathbf {A}$ is isomorphic to the WPQK twist-algebra $Tw \langle \mathbf {A} _+, \mathbf {A} _+^{\Box }, \Box , Id_{L_+^{\Box }}, \nabla _{\mathbf {A} } \rangle$, where $\mathbf {A} _+^{\Box }$ arises from the np-lattice $(\mathbf {A} _+, \Box )$ obtained from $\mathbf {A} _+$ with the nucleus given by $\Box [a] := [\mathop {\sim }\mathop {\sim }a]$ for all $a \in A$, and $\nabla _{\mathbf {A} } \subseteq \mathbf {A} _+$ is the dense filter of the twist representation of $\mathbf {A}$.

Relying on Theorem 4, we can proceed in parallel to Sect. 3.

Definition 12

Let $\mathsf {NP}$ be the category whose objects are tuples ${\mathbb {L}}= \langle \mathbf {L} , \nabla \rangle$, with $\mathbf {L}$ an np-lattice and $\nabla \subseteq L$ a dense filter. A morphism between objects ${\mathbb {L}}= \langle \mathbf {L} , \nabla \rangle$ and ${\mathbb {L}}' = \langle \mathbf {L'} , \nabla ' \rangle$ is an np-lattice homomorphism h such that $h[\nabla ] \subseteq \nabla '$.

Given ${\mathbb {L}}= \langle \mathbf {L} , \nabla \rangle \in \mathsf {NP}$, the WPQK twist-algebra $Tw\langle \mathbf {L} , \mathbf {L} ^{\Box }, \Box , Id_{L^{\Box }}, \nabla \rangle$ will be denoted by $Tw({\mathbb {L}})$. The equivalence between $\mathsf {NP}$ and $\mathsf {WPQK}$ is given by the functors $H :\mathsf {NP}\rightarrow \mathsf {WPQK}$ and $K :\mathsf {WPQK}\rightarrow \mathsf {NP}$ defined as follows. For every ${\mathbb {L}}= \langle \mathbf {L} , \nabla \rangle \in \mathsf {NP}$, we let $H ({\mathbb {L}}) := Tw({\mathbb {L}})$. For an $\mathsf {NP}$-morphism $h :\mathbb {L}\rightarrow \mathbb {L}'$ between ${\mathbb {L}}= \langle \mathbf {L} , \nabla \rangle$ and ${\mathbb {L}}' = \langle \mathbf {L'} , \nabla ' \rangle$, we let $H(h): H({\mathbb {L}}) \rightarrow H({\mathbb {L}}')$ be given, for all $\langle a, b \rangle \in L \times L^{\Box }$, by $H(h) (\langle a, b \rangle ) := \langle h (a), h(b)\rangle$. Conversely, for every WPQK-algebra $\mathbf {A}$, let $K(\mathbf {A} ) : = \langle \langle \mathbf {A} _+, \Box \rangle , \nabla _{\mathbf {A} } \rangle$. For a $\mathsf {WPQK}$-homomorphism $k :\mathbf {A} \rightarrow \mathbf {A} '$, let $K(k): K(\mathbf {A} ) \rightarrow K(\mathbf {A} ')$ be defined by setting $K(k)( [a]) := [k(a)]$ for every $a \in A$.

Theorem 5

The functors H and K establish a co-variant equivalence between $\mathsf {NP}$ and $\mathsf {WPQK}$.

As with Theorem 2, we can rely on Theorem 5 to introduce a duality for the category $\mathsf {NP}$ viewed as another alter ego of $\mathsf {WPQK}$. In doing so, since the nucleus is a modal-like operator, we shall rely on duality for distributive lattices with operators (see [5]).

As expected, the dual of ${\mathbb {L}}= \langle \mathbf {L} , \nabla \rangle$ is defined as a structure $X({\mathbb {L}}) = \langle X(\mathbf {L} ), X(\Box ), X(\nabla ) \rangle$, where:

• (i) $\langle X(\mathbf {L} ), \tau _+, \le _+ \rangle$ is the p-space of $\mathbf {L}$;

• (ii) $X(\Box ) \subseteq X(\mathbf {L} ) \times X(\mathbf {L} )$ is a relation given by:

  $$ X(\Box ) := \{ \langle P, Q \rangle \in X(\mathbf {L} ) \times X(\mathbf {L} ) : \Box ^{-1}[P] \subseteq Q \}; $$

• (iii) $X(\nabla ) : = \{ P \in X(\mathbf {L} ) : \nabla \subseteq P \}$.

It is well known that the relation R corresponding to an operation $\Box$ that preserves (at least) finite meets and the top element satisfies the following:

• (i) $\le \circ \, R \, \circ \le \, \subseteq R$, where $\le$ is the Priestley order on $X(\mathbf {L} )$;

• (ii) $R[P] : = \{ Q \in X(\mathbf {L} ) : \langle P, Q \rangle \in R \}$ is a closed set in the Priestley topology;

• (iii) $R^{-1}[U] : = \{ P \in X(\mathbf {L} ) : \langle P, Q \rangle \in R \text { for some } Q \in U \}$ is clopen, for all $U \in L(X(\mathbf {L} ))$.

We shall say that a relation R on a Priestley space satisfying the above properties is a $\Box$-relation, i.e., a relation corresponding to an operator $\Box$ on the distributive lattice dual to the space. We list below four further properties that the Priestley dual of every np-lattice satisfies.

Proposition 5

Let $\langle X(\mathbf {L} ), X(\Box ) \rangle$ be the dual space of an np-lattice $\mathbf {L}$ and $P, Q \in X(\mathbf {L} )$.

• (i) There is $Q' \in X(\mathbf {L} )$ such that $\langle P, Q' \rangle \in X(\Box )$.

• (ii) If $\langle P, Q\rangle \in X(\Box )$, then there is $Q' \in X(\mathbf {L} )$ s.t. $\langle P, Q' \rangle \in X(\Box )$ and $\langle Q', Q\rangle \in X(\Box )$.

• (iii) If $\langle P, Q\rangle \in X(\Box )$, then $P \subseteq Q$.

• (iv) $X(\nabla )$ is a closed set such that $X(\nabla ) \subseteq \max (X(\mathbf {L} ))$.

Items (i)–(iii) of Proposition 5 are saying that the relation $X(\Box )$ is serial, dense and included in the Priestley order (regarding item (iv) see [6, Lemma 3.1]). We include these properties in our official definition of np-spaces.

Definition 13

An np-space is a structure $X= \langle X, R, \mathcal {C}\rangle$ where X is a p-space, $\mathcal {C}$ is a closed set such that $\mathcal {C}\subseteq \max (X)$, and R is a $\Box$-relation which is serial, dense and included in the Priestley order.

We note that it is possible to show that Properties (i) to (iii) in Definition 13 can be equivalently replaced by the following one (considered e.g. in [2]): for all $x,y \in X$, $\langle x , y \rangle \in R \;\; \text { iff } \;\; \text {there is } z \in X \quad \text { s.t.} \quad \langle z, z \rangle \in R \quad \text { and } \quad x \le z \le y .$

Given an np-space $X= \langle X, R, \mathcal {C}\rangle$ and a clopen up-set $U \in L(X)$, we define $\Box _R U : = \{ x \in X : R[x] \subseteq U \}$. Defining the filter $\nabla _{\mathcal {C}} \subseteq L(X)$ as in the preceding section, it is easy to show that $\langle L(X), \Box _R, \nabla _{\mathcal {C}} \rangle \in \mathsf {NP}$. It follows from the duality for distributive lattices with a $\Box$-operator [5] that every np-lattice $\mathbf {L}$ is isomorphic to its double dual $\langle L(X(\mathbf {L})), \Box _{R_{\Box }} \rangle$. Conversely, for every np-space $X= \langle X, R, \mathcal {C}\rangle$, we have (by the duality for p-lattices) that the p-space X is homeomorphic to its double dual X(L(X)); furthermore, $\langle X, \le , R \rangle$ is isomorphic, as a relational structure, to $\langle X(L(X)), \subseteq , R_{\Box _{R}} \rangle$. It is also easy to check that the Priestley isomorphisms respect $\nabla$ and $\mathcal {C}$ [6, Lemmas 3.7 and 3.8].

Definition 14

Let $X= \langle X, R, \mathcal {C}\rangle$ and $X' = \langle X', R', \mathcal {C}' \rangle$ be np-spaces, and let $f :X \rightarrow X'$ be a p-space morphism. We say that f is an np-space morphism if the following conditions hold:

• (i) If $\langle x, y \rangle \in R$, then $\langle f(x), f (y) \rangle \in R'$, for all $x,y \in X$.

• (ii) If $\langle f (x ), x' \rangle \in R'$, then there is $y \in X$ such that $f (y ) \le ' x'$ and $\langle x , y \rangle \in R$, for every $x \in X$ and $x' \in X'$.

• (iii) $f[\mathcal {C}] \subseteq \mathcal {C}'$.

Denote by $\mathsf {npSP}$ the category having as objects np-spaces and as morphisms the maps given in Definition 14. The following propositions are immediate consequences of Priestley duality for distributive lattices with a $\Box$-operator, together with [6, Lemmas 3.5 and 3.6].

Proposition 6

Let ${\mathbb {L}}= \langle \mathbf {L} , \nabla \rangle$, ${\mathbb {L}}' = \langle \mathbf {L'} , \nabla ' \rangle \in \mathsf {NP}$, and let $h :L \rightarrow L'$ be an $\mathsf {NP}$-morphism. Then $h^{-1} :X({\mathbb {L}}') \rightarrow X({\mathbb {L}})$ is an np-space morphism.

Proposition 7

Let $X= \langle X, R, \mathcal {C}\rangle$ and $X' = \langle X', R', \mathcal {C}' \rangle$ be np-spaces, and let $f :X \rightarrow X'$ be an np-morphism. Then $f^{-1} :L(X') \rightarrow L(X)$ is an $\mathsf {NP}$-morphism.

As in the previous cases, it is straightforward to check that the above-defined categories are dually equivalent via the Priestley functors.

Theorem 6

The functors L, X establish a dual equivalence between $\mathsf {NP}$ and $\mathsf {npSP}$. In consequence, the composite functors $F \circ L$ and $X \circ G$ establish a dual equivalence between $\mathsf {WPQK}$ and $\mathsf {npSP}$.

Appendix: Proofs of Theorems 2 and 5

Theorem 2

The functors F, G establish a co-variant equivalence between $\mathsf {TW}$ and $\mathsf {WPQK}$.

Proof

First of all, we shall prove that F is a functor. Given $\mathbb {L} = \langle \mathbf {L} _+, \mathbf {L} _-, n, p, \nabla \rangle$ and $\mathbb {L}' = \langle \mathbf {L} _+^{'}, \mathbf {L} _-^{'}, n', p', \nabla ' \rangle$ two objects in $\mathsf {TW}$ and $\langle h_+, h_-\rangle$ a $\mathsf {TW}$-morphism from $\mathbb {L}$ to $\mathbb {L}'$, we will prove that $F(\langle h_+, h_-\rangle )$ is a $\mathsf {WPQK}$-morphism from $F(\mathbb {L})$ to $F(\mathbb {L}')$. Let $\langle a_+, a_- \rangle , \langle b_+, b_- \rangle$ be elements of the universe of $F(\mathbb {L})$. For $\wedge$ we have:

$$\begin{aligned} F(\langle h_+, h_-\rangle )(\langle a_+, a_- \rangle \wedge \langle b_+, b_- \rangle )&= F(\langle h_+, h_-\rangle )(\langle a_+ \wedge b_+, a_- \vee b_- \rangle ) \\&= \langle h_+ (a_+ \wedge b_+), h_-(a_- \vee b_-)\rangle \\&= \langle h_+ (a_+) \wedge h_+(b_+), h_-(a_-) \vee h_-(b_-)\rangle \\&= \langle h_+(a_+), h_-(a_-) \rangle \wedge \langle h_+(b_+), h_-(b_-) \rangle \\&= F(\langle h_+, h_-\rangle ) (\langle a_+, a_- \rangle ) \wedge F(\langle h_+, h_-\rangle ) (\langle b_+, b_- \rangle ). \end{aligned}$$

The proof for $\vee$ is analogous and will be omitted. For $\mathop {\sim }$ we have:

$$\begin{aligned} F(\langle h_+, h_-\rangle ) (\mathop {\sim }\langle a_+, a_- \rangle )&= F(\langle h_+, h_-\rangle ) \langle p(a_-), n(a_+) \rangle \end{aligned}$$

(1)

$$\begin{aligned}&= \langle (h_+ \circ p)(a_-), (h_- \circ n) (a_+) \rangle \end{aligned}$$

(2)

$$\begin{aligned}&= \langle (p' \; \circ \; h_-) (a_-), (n' \; \circ \; h_+) (a_+)\rangle \end{aligned}$$

(3)

$$\begin{aligned}&= \; \mathop {\sim }\langle h_+(a_+), h_-(a_-) \rangle \end{aligned}$$

(4)

$$\begin{aligned}&= \; \mathop {\sim }F(\langle h_+, h_-\rangle ) ( \langle a_+, a_- \rangle ) \end{aligned}$$

(5)

From (3) to (4) we used the fact that $h_+ \circ p = p' \circ h_-$ and $h_- \circ n = n' \circ h_+$. For $\lnot$ we have:

$$\begin{aligned} F(\langle h_+, h_- \rangle ) (\lnot \langle a_+, a_-\rangle )&= F(\langle h_+, h_- \rangle ) (\langle \lnot _+ a_+, n(a_+) \rangle ) \end{aligned}$$

(6)

$$\begin{aligned}&= \langle h_+(\lnot _+ a_+), h_- \; \circ \; n (a+) \rangle \end{aligned}$$

(7)

$$\begin{aligned}&= \langle \lnot _+ h_+( a_+), n' \; \circ \; h_+ (a_+) \rangle \end{aligned}$$

(8)

$$\begin{aligned}&= \lnot \langle h_+(a_+), h_-(a_-) \rangle \end{aligned}$$

(9)

$$\begin{aligned}&= \lnot F(\langle h_+, h_- \rangle ) (\langle a_+, a_-\rangle ) \end{aligned}$$

(10)

From (7) to (8) we used the identity $(h_-\circ n) = (n' \circ h_+)$. Now we move to prove that given an object $\mathbb {L} = \langle \mathbf {L} _+, \mathbf {L} _-, n, p, \nabla \rangle$ in $\mathsf {TW}$ and the identity morphism $Id_{\mathbb {L}} := \langle Id_{L_{+}}, Id_{L_{-}} \rangle$ for $\mathbb {L}$, $F(Id_{\mathbb {L}}) = Id_{F(\mathbb {L})}$, i.e. the identity homomorphism for $F(\mathbb {L})$. Notice that if $\langle a_+, a_- \rangle$ is an element of the universe of $F(\mathbb {L})$ and $F(\langle Id_{L_{+}}, Id_{L_{-}} \rangle ) (\langle a_+, a_- \rangle ) = \langle Id_{L_{+}}(a_+), Id_{L_{-}}(a_-) \rangle = \langle a_+, a_-\rangle$. Therefore, $F(Id_{\mathbb {L}}) = Id_{F(\mathbb {L})}$. Finally, given two TW-morphisms $\langle h_+, h_- \rangle : \mathbb {L} \rightarrow \mathbb {L'}$ and $\langle f_+, f_- \rangle : \mathbb {L'} \rightarrow \mathbb {L''}$, we shall prove that $F (\langle h_+, h_- \rangle \circ \langle f_+, f_- \rangle ) = F(\langle h_+, h_- \rangle ) \circ F(\langle f_+, f_- \rangle )$. Let $\langle a_+, a_- \rangle$ be an element of the universe of $F(\mathbb {L})$. Then

$$\begin{aligned} F (\langle h_+, h_- \rangle \circ \langle f_+, f_- \rangle )(\langle a_+, a_-\rangle )&= F (\langle h_+ \circ f_+, h_- \circ f_-\rangle )(\langle a_+, a_-\rangle ) \\&= \langle (h_+ \circ f_+) (a_+), (h_- \circ f_-)(a_-)\rangle \\&=\ F(\langle h_+, h_- \rangle )(\langle f_+(a), f_-(a) \rangle ) \\&=\ (F(\langle h_+, h_- \rangle ) \circ F(\langle f_+, f_- \rangle ))(\langle a_+, a_- \rangle ). \end{aligned}$$

We now prove that G is a functor. Let $\mathbf {A}$ and $\mathbf {A} '$ be two $\mathsf {WPQK}$-algebras and $k: \mathbf {A} \rightarrow \mathbf {A} '$ a homomorphism between them. In order to prove that G(k) is a $\mathsf {TW}$-morphism from $G(\mathbf {A} )$ to $G(\mathbf {A} ')$, we prove first that $k_+: \mathbf {A} _+ \rightarrow \mathbf {A} _+ '$ is a p-lattice homomorphism and $k_-: \mathbf {A} _- \rightarrow \mathbf {A} _- '$ is a bounded lattice homomorphism. Notice that for every $a \in A$, $k_+([a]) := [k(a)]$ and since k is a homomorphism of $\mathsf {WPQK}$-algebras, the morphism $k_+: A / \!\! \equiv$ $\rightarrow$ $A' / \!\! \equiv$ is a morphism of p-lattices. In order to prove that $k_-$ is a bounded lattice homomorphism, let $a, b \in A$. We have:

$$\begin{aligned} k_-([\mathop {\sim }a] \wedge [\mathop {\sim }b]) = k_-([\mathop {\sim }(a \vee b)]) = [k(\mathop {\sim }(a \vee b))] = [\mathop {\sim }k(a \vee b)]&= \\ [\mathop {\sim }(k(a) \vee k(b))] = [\mathop {\sim }k(a)] \wedge [\mathop {\sim }k(b)]&=\\ [k(\mathop {\sim }a) \wedge k(\mathop {\sim }b)] = [k(\mathop {\sim }a)] \wedge [k(\mathop {\sim }b)]&= \\ k_-([\mathop {\sim }a]) \wedge k_-([\mathop {\sim }b]). \end{aligned}$$

For $\vee$ we have:

$$\begin{aligned} k_-([\mathop {\sim }a] \vee [\mathop {\sim }b]) = k_-([\mathop {\sim }( a \wedge b)]) = [k(\mathop {\sim }( a \wedge b))] = [\mathop {\sim }k(a \wedge b)]&= \\ [\mathop {\sim }(k(a) \wedge k(b))] = [\mathop {\sim }k(a)] \vee [\mathop {\sim }k(b)]&=\\ [ k(\mathop {\sim }a)] \vee [ k(\mathop {\sim }b)]&= \\ k_-([\mathop {\sim }a]) \vee k_-([\mathop {\sim }b]). \end{aligned}$$

We now prove that $k_+ \circ p_{\mathbf {A} } = p_{\mathbf {A} '} \circ k_-$ and $n_{\mathbf {A} '} \circ k_+ = k_- \circ n_{\mathbf {A} }$. Recall that $p_\mathbf{A} : A_- \rightarrow A_+$ is the identity map on $A_-$ and that $n_\mathbf{A} : A_+ \rightarrow A_-$ is the function defined by $n_\mathbf{A} ([a]) = [\mathop {\sim }\mathop {\sim }a]$ for all $a \in A$. Given $a \in A$, we have $(k_+\circ p_{\mathbf {A} }) ([\mathop {\sim }a]) = k_+([\mathop {\sim }a])$, while $(p_{\mathbf {A} '} \circ k_-)([\mathop {\sim }a]) = p_{\mathbf {A} '}(k_-([\mathop {\sim }a])) = p_{\mathbf {A} '}([k(\mathop {\sim }a)]) = k_+([\mathop {\sim }a])$. Therefore, $(k_+\circ p_{\mathbf {A} }) ([\mathop {\sim }a]) = (p_{\mathbf {A} '} \circ k_-)([\mathop {\sim }a])$. We have that $(n_{\mathbf {A} '} \circ k_+)([a])$ = $n_{\mathbf {A} '}(k_+([a])) = [ \mathop {\sim }\mathop {\sim }k(a)] = [k(\mathop {\sim }\mathop {\sim }a)]$ = $k_-([\mathop {\sim }\mathop {\sim }a])$, while $(k_- \circ n_{\mathbf {A} })([a]) = k_- ([\mathop {\sim }\mathop {\sim }a])$. Hence, $(n_{\mathbf {A} '} \circ k_+)([a]) = (k_- \circ n_{\mathbf {A} })([a])$. We also need to prove that $k_+[\nabla _{\mathbf {A} }] \subseteq \nabla _{\mathbf {A} '}$. If $[a] \in \nabla _{\mathbf {A} }$, then $\mathop {\sim }a \le a$. Since k is a $\mathsf {WPQK}$-morphism, we have $\mathop {\sim }k(a) \le k(a)$ and therefore $k(a) \in F(A)$, which implies $k_+([a]) \in \nabla _{\mathbf {A} '}$.

Given $\mathbf {A} \in \mathsf {WPQK}$, thanks to Theorem 1 we know that the morphism $\iota _{\mathbf {A} }$ defined in its statement is an isomorphism between $\mathbf {A}$ and $F(G(\mathbf {A} ))$. Thus the morphisms $\iota _{\mathbf {A} }$ are the elements of a natural isomorphism from the identity functor on $\mathsf {WPQK}$ to the functor $F \circ G$.

We now prove that, for every ${\mathbb {L}}\in \mathsf {TW}$, one has that $\iota _{{\mathbb {L}}} = \langle \iota _{L_+}, \iota _{L_-}\rangle : {\mathbb {L}}\rightarrow G(F({\mathbb {L}}))$ is a natural isomorphism. Let ${\mathbb {L}}= \langle \mathbf {L} _+, \mathbf {L} _-, n, p, \nabla \rangle \in \mathsf {TW}$. We have $F({\mathbb {L}}) = Tw(\langle \mathbf {L} _+, \mathbf {L} _-, n, p, \nabla \rangle )$. Let us denote by $\mathbf {A}$ the WPQK-algebra $F({\mathbb {L}})$ so that then $G(F({\mathbb {L}})) = \langle \mathbf {A} _+, \mathbf {A} _-, n_{\mathbf {A} }, p_{\mathbf {A} }, \nabla _{\mathbf {A} }\rangle$. Recall that, for every $a_+ \in L_+$, we have $\iota _{L_+}(a_+) = [\langle a_+, n(\lnot _+a_+)\rangle ]$, and, for every $a_- \in L_-$, we have $\iota _{L_-}(a_-) = [\sim \langle \lnot _+p(a_-), a_-\rangle ]$. First of all, we need to prove that the maps $\iota _{L_+}$ and $\iota _{L_-}$ are respectively maps from $\mathbf {L} _+$ to $\mathbf {A} _+$ and from $\mathbf {L} _-$ to $\mathbf {A} _-$. To this end, it is enough to prove that given $\langle a_+, n(\lnot _+ a_+) \rangle$ and $\langle \lnot _+p(b_-), b_- \rangle$ in $L_+ \times L_-$, the pairs $\langle a_+, n(\lnot _+ a_+) \rangle$ and $\langle \lnot _+p(b_-), b_- \rangle$ belong to $\mathbf {A}$, that is, that we have $a_+ \vee _+ p(n(\lnot _+ a_+)) \in \nabla , \lnot _+p(b_-) \vee _+ p(b_-) \in \nabla$, $a_+ \wedge _+ p(n(\lnot _+ a_+)) = 0_+$, and $\lnot _+ p(b_-) \wedge _+ p(b_-) = 0_+$. We have that $a_+ \vee _+ \lnot _+ a_+ \le _+ a_+ \vee _+ p(n(\lnot _+ a_+))$. Since $\nabla$ is a filter and $a_+ \vee _+ \lnot _+ a_+ \in \nabla$, then $a_+ \vee _+ p(n(\lnot _+ a_+)) \in \nabla$. We have trivially that $\lnot _+p(b_-) \vee _+ p(b_-) \in \nabla$, given that $\nabla$ is a dense filter. Now, since $Id_{\mathbf {A} _+} \le _+ p \cdot n$ and p, n, preserve finite meets and the bounds, then $a_+ \wedge _+ p(n(\lnot _+ a_+)) \le _+ p(n(a_+)) \wedge _+ p(n(\lnot _+ a_+)) = p(n(a_+ \wedge _+ \lnot _+ a_+)) = p(n(0_+)) = 0_+$. Moreover, since $\lnot _+$ is a pseudo-complement, then $\lnot _+ p(b_-) \wedge _+ p(b_-) = 0_+$.

In order to prove that $\iota _{{\mathbb {L}}}$ is a morphism, we have to prove that $\iota _{L_+}$ is a p-lattice homomorphism from $\mathbf {L} _+$ to $\mathbf {A} _+$ and $\iota _{L_-}$ is a bounded lattice homomorphism from $\mathbf {L} _-$ to $\mathbf {A} _-$. Before we proceed, notice that given $a_+, b_+ \in L_+$ and $a_-, b_- \in L_-$, by [15, Lemma 3.5.iii] we have $[\langle a_+, a_- \rangle ] = [\langle b_+, b_- \rangle ]$ iff $a_+ = b_+$, and by [15, Lemma 3.5.ii] we have $[\mathop {\sim }\langle a_+, a_- \rangle ] = [\mathop {\sim }\langle b_+, b_- \rangle ]$ iff $a_- = b_-$. We will use these facts.

We first show that $\iota _{L_+}$ is a p-lattice homomorphism. Let $a_+, b_+ \in L_+$. Then:

$(\wedge _+)$:

On the one hand, $\iota _{L_+}(a_+ \wedge _+ b_+) = [\langle a_+ \wedge _+ b_+, n(\lnot _+(a_+ \wedge _+ b_+) \rangle ])$. On the other hand, $\iota _{L_+}(a_+) \wedge \iota _{L_+}(b_+) = [\langle a_+, n(\lnot _+ a_+) \rangle ] \wedge [\langle b_+, n(\lnot _+ b_+) \rangle ] = [\langle a_+ \wedge _+ b_+, n(\lnot _+ a_+) \vee _- n(\lnot _+ b_+) \rangle ]$. It follows from [15, Lemma 3.5.iii] that $\iota _{L_+}(a_+ \wedge _+ b_+) = \iota _{L_+}(a_+) \wedge \iota _{L_+}(b_+)$.

$(\vee _+)$:

On the one hand, $\iota _{L_+}(a_+ \vee _+ b_+) = [\langle a_+ \vee _+ b_+, n(\lnot _+(a_+ \vee _+ b_+) \rangle ])$. On the othert hand, $\iota _{L_+}(a_+) \vee \iota _{L_+}(b_+) = [\langle a_+, n(\lnot _+ a_+) \rangle ] \vee [\langle b_+, n(\lnot _+ b_+) \rangle ] = [\langle a_+ \vee _+ b_+, n(\lnot _+ a_+) \wedge _- n(\lnot _+ b_+) \rangle ]$. It follows from [15, Lemma 3.5.iii] that $\iota _{L_+}(a_+ \vee _+ b_+) = \iota _{L_+}(a_+) \vee \iota _{L_+}(b_+)$.

$(\lnot )$:

We have $\iota _{L_+}(\lnot _+ a) = [\langle \lnot _+ a, n(\lnot _+ \lnot _+ a) \rangle ]$. Also, $\lnot _+ \iota _{L_+}(a)$ = $\lnot [\langle a_+, n(\lnot _+ a_+) \rangle ]$ = $[\langle \lnot _+ a_+, n(n(\lnot _+ a_+)) \rangle ]$. It follows from [15, Lemma 3.5.iii] that $\iota _{L_+}(\lnot _+ a) = \lnot _+ \iota _{L_+}(a)$.

Now we prove that $\iota _{L_-}$ is a bounded lattice homomorphism. Let $a_-, b_- \in L_-$. Then:

$(\wedge _-)$:

First notice that $\iota _{L_-}(a_- \wedge _- b_-) = [\mathop {\sim }\langle \lnot _+ p(a_- \wedge _- b_-), a_- \wedge _- b_- \rangle ]$. Secondly that $\iota _{L_-}(a_-) \wedge \iota _{L_-}(b_-) = [\mathop {\sim }\langle \lnot _+ p(a_-), a_-\rangle ] \wedge [\mathop {\sim }\langle \lnot _+ p(b_-), b_- \rangle ] = [\mathop {\sim }(\langle \lnot _+ p(a_-), a_-\rangle \vee \langle \lnot _+ p(b_-), b_-\rangle )] = [\mathop {\sim }(\lnot _+ p(a_-) \vee _+ \lnot _+ p(b_-), a_- \wedge _- b_-)]$. It follows from [15, Lemma 3.5.ii] that $\iota _{L_-}(a_- \wedge _- b_-) = \iota _{L_-}(a_-) \wedge \iota _{L_-}(b_-)$.

$(\vee _-)$:

On the one hand, $\iota _{L_-}(a_- \vee _- b_-) = [\mathop {\sim }\langle \lnot _+ p(a_- \vee _- b_-), a_- \vee _- b_- \rangle ]$. On the other hand, $\iota _{L_-}(a_-) \vee \iota _{L_-}(b_-) = [\mathop {\sim }\langle _- \lnot _+ p(a_-), a_-\rangle ] \vee [\mathop {\sim }\langle \lnot _+ p(b_-), b_- \rangle ] = [\mathop {\sim }(\langle \lnot _+ p(a_-), a_-\rangle \wedge \langle \lnot _+ p(b_-), b_-\rangle )] = [\mathop {\sim }(\lnot _+ p(a_-) \wedge _+ \lnot _+ p(b_-), a_- \vee _- b_-)]$. It follows from [15, Lemma 3.5.ii] that $\iota _{L_-}(a_- \vee b_-) = \iota _{L_-}(a_-) \vee \iota _{L_-}(b_-)$.

We proceed to prove that $\iota _{L_+} \circ p = p_{\mathbf {A} } \circ \iota _{L_-}$, $n_{\mathbf {A} } \circ \iota _{L_+} = \iota _{L_-} \circ n$ and that $\iota _{L_+}[\nabla ] \subseteq \nabla _{\mathbf {A} }$. Notice that given $a_- \in L_-$, $\iota _{L_+}(p(a_-)) = [\langle p(a_-), n(\lnot _+ p(a_-)) \rangle ]$ and $(p_{\mathbf {A} } \circ \iota _{L_-})(a_-) = [\mathop {\sim }\langle \lnot _+ p(a_-), a_-\rangle ] = [\langle p(a_-), n(\lnot _+ p(a_-)) \rangle ]$. Thus we obtain that $\iota _{L_+} \circ p = p_{\mathbf {A} } \circ \iota _{L_-}$. To prove that $n_{\mathbf {A} } \circ \iota _{L_+} = \iota _{L_-} \circ n$, notice that given $a_+ \in L_+$, $n_{\mathbf {A} } \circ \iota _{L_+}(a_+) = [\mathop {\sim }\mathop {\sim }\langle a_+, n(\lnot _+ a_+) \rangle ] = [\mathop {\sim }\langle p(n(\lnot _+ a_+)), n(a_+) \rangle ]$ and $(\iota _{L_-} \circ n)(a_+) = [\mathop {\sim }\langle \lnot _+ p(n(a_+)), n(a_+)\rangle ]$. Thus, the desired equality follows. Finally, to prove that $\iota _{L_+}[\nabla ] \subseteq \nabla _{\mathbf {A} }$, notice that $\nabla _{\mathbf {A} } = [F(A)]$ and thanks to [15, Prop. 6.1], $F(A) = \{\langle a_+, 0_- \rangle : \langle a_+, 0_-\rangle \in A\}$ and therefore $[F(A)] = \{[\langle a_+, 0_- \rangle ]: \langle a_+, 0_- \rangle \in F(A)\}$. Let now $a_+ \in \nabla$. We prove that $\langle a_+, 0_- \rangle \in A$. To this end we need to show that $a_+ \vee _+ p(0_-) \in \nabla$ and $a_+ \wedge _+ p(0_-) = 0_-$. Notice that $a_+ \vee _+ p(0_-) = a_+ \vee _+ 0_+ = a_+$ and by hypothesis $a_+ \in \nabla$. Also, $a_+ \wedge _+ p(0_-) = a_+ \wedge _+ 0_+ = 0_+$. Since $\iota _{L_+}(a_+) = [\langle a_+, n(\lnot _+ a_+) \rangle ]$ using that $[\langle a_+, 0_- \rangle ] = [\langle a_+, n(\lnot _+ a_+) \rangle ]$ ([15, Lemma 3.5.iii]), we obtain $\iota _{L_+}(a_+) \in \nabla _{\mathbf {A} }$.

It remains to prove that $\iota _{L_+}$ and $\iota _{L_-}$ are injective and surjective. We prove first injectivity.

$\iota _{L_+}$:

If $\iota _{L_+}(a_+) = \iota _{L_+}(b_+)$, then $[\langle a_+, n(\lnot _+ a_+) \rangle ] = [\langle b_+, n(\lnot _+ b_+) \rangle ]$; and from [15, Lemma 3.5.iii] it follows that $a_+ = b_+$.

$\iota _{L_-}$:

If $\iota _{L_-}(a_-) = \iota _{L_-}(b_-)$, then $[\mathop {\sim }\langle \lnot _+p(a_-), a_- \rangle ] = [\mathop {\sim }\langle \lnot _+p(b_-), b_- \rangle ]$, and from [15, Lemma 3.5.ii] it follows that $a_- = b_-$.

Now we prove that $\iota _{L_+}$ and $\iota _{L_-}$ are surjective:

$\iota _{L_+}$:

Let $[\langle a_+, a_-\rangle ] \in \mathbf {A} _+$ (so that $\langle a_+, a_-\rangle$ belongs to the universe of $F({\mathbb {L}})$). By [15, Lemma 3.5.iii] $[\langle a_+, a_- \rangle ] = [\langle a_+, n(\lnot _+a_+)\rangle ]$. Therefore $\iota _{L_+}(a_+) = [\langle a_+, a_-\rangle ]$.

$\iota _{L_-}$:

Let $[\mathop {\sim }\langle a_+, a_-\rangle ] \in \mathbf {A} _-$ (so that $\langle a_+, a_-\rangle$ belongs to the universe of $F({\mathbb {L}})$). From [15, Lemma 3.5.ii], it follows that $[\mathop {\sim }\langle a_+, a_- \rangle ] = [\mathop {\sim }\langle \lnot _+p(a_-), a_-\rangle ]$. Therefore $\iota _{L_-} (a_-) = [\mathop {\sim }\langle a_+, a_- \rangle ]$.

Theorem 5

The functors H, K establish a co-variant equivalence between $\mathsf {NP}$ and $\mathsf {WPQK}$.

Proof

We prove first that H is a functor. Let ${\mathbb {L}}= \langle \mathbf {L} , \nabla \rangle$ and ${\mathbb {L}}' = \langle \mathbf {L'} , \nabla ' \rangle$ be two objects in $\mathsf {NP}$ and $h:{\mathbb {L}}' \rightarrow {\mathbb {L}}'$ a $\mathsf {NP}$-morphism. The proof that $H(h): H({\mathbb {L}}) \rightarrow H({\mathbb {L}}')$ is a $\mathsf {WPQK}$-homomorphism is similar to the proof above for morphsims in $\mathsf {TW}$ and the functor F, because $H({\mathbb {L}}) = Tw\langle \mathbf {L} , \mathbf {L} ^{\Box }, \Box , Id_{L^{\Box }}, \nabla \rangle$ and $H({\mathbb {L}}') = Tw\langle \mathbf {L} ', \mathbf {L} '^{\Box '}, \Box , Id_{L'^{\Box '}}, \nabla ' \rangle$.

Given $\mathbf {A} , \mathbf {A} '$ objects in $\mathsf {WPQK}$ and $k: \mathbf {A} \rightarrow \mathbf {A} '$ a $\mathsf {WPQK}$-homomorphism, we shall prove that $K(k): K(\mathbf {A} ) \rightarrow K(\mathbf {A} ')$ is a $\mathsf {NP}$-morphism. Since k is a morphism of $\mathsf {WPQK}$ algebras, it easily follows that K(k) is a homomorphism from $\langle \mathbf {A} _+, \Box \rangle$ to $\langle \mathbf {A} '_+, \Box '\rangle$. Let $a, b \in A$. Then:

$$\begin{aligned} K(k)([a] \wedge [b]) = K(k)([a \wedge b]) = ([k(a \wedge b)])&= \\ ([k(a) \wedge k(b)]) = [k(a)] \wedge [k(b)]&= \\ K(k)([a]) \wedge K(k)([b]), \end{aligned}$$

$$\begin{aligned} K(k)([a] \vee [b]) = K(k)([a \vee b]) = ([k(a \vee b)])&= \\ ([k(a) \vee k(b)]) = [k(a)] \vee [k(b)]&= \\ K(k)([a]) \vee K(k)([b]), \end{aligned}$$

$$\begin{aligned} K(k)(\lnot [a]) = [k (\lnot a)] = [\lnot k (a)] = \lnot K(k)([a]), \end{aligned}$$

$$\begin{aligned} K(k)( \Box [a]) = [ k(\Box a)] = [ k(\mathop {\sim }\mathop {\sim }a)] = [ \mathop {\sim }\mathop {\sim }k(a)] = [\Box k(a)] = \Box K(k)( [a]). \end{aligned}$$

It remains to prove that $K(k)[\nabla _{\mathbf {A} }] \subseteq \nabla _{\mathbf {A} '}$. Given $[a] \in \nabla _{\mathbf {A} }$, we have $a \in F(A)$ and $\sim a \le a$, since k is a morphism of $\mathsf {WPQK}$-algebras, then $k(\mathop {\sim }a) \le k(a)$ and it follows that $\mathop {\sim }k(a) \le k(a)$. Therefore $[\mathop {\sim }k(a)] \le [k(a)]$ and we conclude that $k[a] \in \nabla _{\mathbf {A} }$.

Given an object $\mathbf {A}$ in $\mathsf {WPQK}$ and the identity morphism $Id_{\mathbf {A} }: \mathbf {A} \rightarrow \mathbf {A}$, we shall prove that $K(Id_{\mathbf {A} }) = Id_{K(\mathbf {A} )}$. Let [a] be an element of the universe of $K(\mathbf {A} )$. Notice that $K(Id_{\mathbf {A} })[a] = [Id_{\mathbf {A} }(a)]= [a].$ So we are done. Given $\mathsf {WPQK}$-homomorphisms $f: \mathbf {A} \rightarrow \mathbf {A} '$ and $g: \mathbf {A} ' \rightarrow \mathbf {A} ''$, we shall prove that $K (g \circ f) = K(g) \circ K(f)$. Let [a] be an element of the universe of $K(\mathbf {A} )$.

$$\begin{aligned} K(g \circ f)([a])&= [(g \circ f)(a)] \\&= [g(f(a))] \\&= K(g)([f(a)]) \\&= K(g)(K(f)[a]) \\&= K(f) \circ K(g)([a]). \end{aligned}$$

From [15, Theorem 7.11] it is easy to obtain the natural isomorphism between the identity functor on $\mathsf {WPQK}$ and the functor $H \circ K$.

We proceed to prove that, for every ${\mathbb {L}}\in \mathsf {NP}$, the map $\iota _{\mathsf {NP}}$ defined by $\iota _{\mathsf {NP}}(a) = [\langle a, \Box \lnot a \rangle ]$ for all $a \in L$ is an isomorphism between ${\mathbb {L}}$ and $K(H({\mathbb {L}}))$. This will provide the natural isomorphism between the identity functor on $\mathsf {NP}$ and the functor $K \circ H.$

Let ${\mathbb {L}}= \langle \mathbf {L} , \nabla \rangle \in \mathsf {NP}$. We have $H({\mathbb {L}}) = Tw\langle \mathbf {L} , \mathbf {L} ^{\Box }, \Box , Id_{L^{\Box }}, \nabla \rangle$. Let us denote by $\mathbf {A}$ the $\mathsf {WPQK}$-algebra $H({\mathbb {L}})$, with A its universe, so that $K(H({\mathbb {L}})) = \langle \langle \mathbf {A} _{+}, \Box \rangle , \nabla _{\mathbf {A} } \rangle$. First of all, we need to prove that $\iota _{\mathsf {NP}}$ is a map from ${\mathbb {L}}$ to $K(H({\mathbb {L}}))$. To this end, it is enough to notice that for every $a \in L$, the element $\langle a, \Box \lnot a \rangle$ belongs to the twist-algebra, that is, that $a \vee Id_{L^{\Box }}(\Box \lnot a) \in \nabla$ and $a \wedge Id_{L^{\Box }}(\Box \lnot a) = 0$. Since $Id_{L^{\Box }}$ is the identity map, we shall prove that $a \vee \Box \lnot a \in \nabla$ and $a \wedge \Box \lnot a = 0$. We have that, $a \vee \lnot a \le a \vee \Box \lnot a$. Since $\nabla$ is a filter and $a \vee \lnot a \in \nabla$, we have $a \vee \Box \lnot a \in \nabla$. We have that $a \wedge \Box \lnot a \le \Box a \wedge \Box \lnot a = \Box (a \wedge \lnot a) = \Box (0) = 0.$ Therefore, $a \wedge \Box \lnot a = 0$.

We now prove that $\iota _{\mathsf {NP}}$ is a $\mathsf {NP}$-morphism. Before we proceed, notice that given $a, b \in L$ and $c, d \in L^{\Box }$, by [15, Lemma 3.5.iii], we have $[\langle a, c \rangle ] = [\langle b, d \rangle ]$ iff $a = b$. Also note that given $\langle a, b \rangle \in A$, according to the definition of $\Box$ in Theorem 4, we have $\Box [\langle a, b \rangle ] = [\mathop {\sim }\mathop {\sim }\langle a, b\rangle ] = [\mathop {\sim }\langle b, \Box a\rangle ] = [\langle \Box a, \Box b\rangle ]$.

$(\wedge )$:

$\iota _{\mathsf {NP}}(a \wedge b) = [\langle a \wedge b, \Box (\lnot (a \wedge b)) \rangle ]$. While, $\iota _{\mathsf {NP}}(a) \wedge \iota _{\mathsf {NP}}(b) = [\langle a, \Box (\lnot a) \rangle ] \wedge [\langle b, \Box (\lnot b) \rangle ] = [\langle a \wedge b, \Box (\lnot a) \vee \Box (\lnot b) \rangle ]$. It follows from [15, Lemma 3.5.iii] that $\iota _{\mathsf {NP}}(a \wedge b) = \iota _{\mathsf {NP}}(a) \wedge \iota _{\mathsf {NP}}(b)$.

$(\vee )$:

$\iota _{\mathsf {NP}}(a \vee b) = [\langle a \vee b, \Box (\lnot (a \vee b)) \rangle ]$. While, $\iota _{\mathsf {NP}}(a) \vee \iota _{\mathsf {NP}}(b) = [\langle a, \Box (\lnot a) \rangle ] \vee [\langle b, \Box (\lnot b) \rangle ] = [\langle a \vee b, \Box (\lnot a) \wedge \Box (\lnot b) \rangle ]$. It follows from [15, Lemma 3.5.iii] that $\iota _{\mathsf {NP}}(a \vee b) = \iota _{\mathsf {NP}}(a) \vee \iota _{\mathsf {NP}}(b)$.

$(\lnot )$:

$\iota _{\mathsf {NP}}(\lnot a) = [\langle \lnot a, \Box (\lnot (\lnot a))) \rangle ]$. While $\lnot \iota _{\mathsf {NP}}(a) =\lnot [\langle a, \Box a \rangle ] = [\langle \lnot a, n(\Box (\lnot a)) \rangle ]$. It follows from [15, Lemma 3.5.ii] that $\iota _{\mathsf {NP}}(\lnot a) = \lnot \iota _{\mathsf {NP}}(a)$.

$(\Box )$:

$\iota _{\mathsf {NP}}(\Box a) = [\langle \Box a, \Box \lnot \Box a \rangle ]$. While $\Box \iota _{\mathsf {NP}}(a) = \Box [\langle a , \Box (\lnot a) \rangle ] = [\langle \Box a, \Box \Box \lnot a\rangle ]$ It follows from [15, Lemma 3.5.iii] that $\iota _{\mathsf {NP}}(\Box a) = \Box \iota _{\mathsf {NP}}(a)$.

We shall prove now that $\iota _{\mathsf {NP}}$ is injective and surjective. Notice that if $\iota _{\mathsf {NP}} (a) = \iota _{\mathsf {NP}}(b)$, then $[\langle a, \Box (\lnot a) \rangle ] = [\langle b, \Box (\lnot b)\rangle ]$ and again from [15, Lemma 3.5.iii] it follows that $a = b$. Therefore $\iota _{\mathsf {NP}}$ is injective. Let $\langle a, b \rangle \in A$ and notice that $\iota _{\mathsf {NP}}(a) = [\langle a, \Box (\lnot a) \rangle ] = [\langle a, b \rangle ]$ by [15, Lemma 3.5.iii]; therefore $\iota _{\mathsf {NP}}$ is surjective. It remains to prove that $\iota _{\mathsf {NP}}[\nabla ] \subseteq \nabla _{\mathbf {A} }$. Notice that $\nabla _{\mathbf {A} } = [F(A)]$ and thanks to [15, Prop. 6.1], $F(A) = \{\langle a, 0 \rangle : \langle a, 0\rangle \in A\}$ and therefore $[F(A)] = \{[\langle a, 0 \rangle ]: \langle a, 0 \rangle \in F(A)\}$. Let $a \in \nabla$. In order to prove that $\iota _{\mathsf {NP}}(a) \in \nabla _{\mathbf {A} }$, we show first that $\langle a, 0 \rangle \in A$. We have that $a \vee Id_{L^{\Box }}(0) = a \vee 0 = a$. Therefore, since by assumption $a \in \nabla$, $a \vee Id_{L^{\Box }}(0) \in \nabla$. Notice also that $a \wedge Id_{L^{\Box }}(0) = a \wedge 0 = 0$. We thus obtain $\langle a, 0 \rangle \in A$. From [15, Lemma 3.5.iii] we have $[\langle a, \Box (\lnot a) \rangle ] = [\langle a, 0 \rangle ]$. Since $\iota _{\mathsf {NP}}(a) = [\langle a, \Box (\lnot a) \rangle ]$, it follows that $\iota _{\mathsf {NP}}(a) \in \nabla _{\mathbf {A} }$.