1 Introduction

Electroelastic actuators with piezoelectric or electrostriction effects are used in the nanomechatronics systems in nanotechnology, nanobiology, adaptive optics, microelectronics, and power engineering. The piezoactuators , based on the piezoelectric effect, are often used for nano- and microdisplacement in nanotechnology, microelectronics, nanobiology, energy, and astronomy. The piezoactuator is piezo mechanical device designed to actuate or control mechanisms and systems using the piezoelectric effect and to convert electrical energy into mechanical energy [1,2,3,4,5,6,7,8,9]. A cell structure combined with the piezoactuator is used in nanomechatronics systems. The nanometric accuracy of nano-mechatronic systems is provided by the piezoactuator . In nanotechnology, photonics, and adaptive optics, these piezoactuators are used for aligning the mirrors of laser ring gyroscopes, for combining and scanning in atomic-force microscopes, and in laser systems [10,11,12,13,14,15,16,17,18,19,20,21,22,23]. The structural scheme of the piezoactuator represents the system of Laplace transformation equations for the displacement of its ends due to the inverse piezoeffect, which, accounting for the electromechanical parameters of the piezoactuator , describes its structure, the conversion of electrical field energy into mechanical energy, the displacements and forces corresponding to the ends of the piezoactuator , and the appearance of the counter electromotive force due to the direct piezoelectric effect.

At this work, we obtained structural scheme of the piezoactuator obtained clearly and visually reflects the transformation of electrical energy into mechanical energy, in contrast to Cady’s and Mason’s electrical equivalent circuits of the piezotransducer [2, 3]. To construct the structural scheme of the piezoactuator , we solved the inverse piezoeffect equation and the wave equation under appropriate boundary conditions for calculating the parameters of the nanomechatronics system with the piezoactuator. Due to the reaction of the piezoactuator and considering the direct piezoeffect, the elastic compliance and rigidity of the piezoactuator are changed. The speed movement of the end the piezoactuator , considering the direct piezoeffect, affects the current through the piezoactuator and on the actual voltage on a piezoelectric actuator. The structural scheme of the piezoactuator is obtained, considering the inverse piezoelectric effect and the back electromotive force due to the direct piezoelectric effect. The elastic compliance and the stiffness of the piezoactuator are found for the transverse, longitudinal, shear, generalized piezoelectric effects and for the types of the voltage or current controls. The transfer functions of the piezoactuators for nanomechatronics with the transverse, longitudinal, shear piezoeffects and with voltage or current controls are obtained. The effects of the geometric and physical parameters of the electroelastic actuator and external load on its dynamic characteristics are determined. To calculate nanomechatronics systems with electroelastic actuator , its structural scheme and matrix transfer function are obtained.

We solve the inverse piezoeffect equation and the wave equation under appropriate boundary conditions for calculating the parameters of the nanomechatronics system with the piezoactuator. Due to the reaction of the piezoactuator and accounting for the direct piezoeffect, the elastic compliance and rigidity of the piezoactuator , which, along with the piezomodule, are the main parameters of the piezoactuator , change depending on whether the control is by voltage or by current. The high-speed movement of the end of the piezoactuator , accounting for the direct piezoeffect, affects the current through the piezoactuator and on the actual voltage on the piezoactuator .

1.1 Research Purpose

The purpose of this paper is calculation of structural scheme of the electroelastic actuator for nanomechatronics .

1.2 Research Scope

At this work, we consider the following frameworks of the problem:

  1. (i)

    Deformation of the electroelastic actuator for nanomechatronics ;

  2. (ii)

    Applied theory of the structural schemes of the electroelastic actuator for nanomechatronics ;

  3. (iii)

    Calculation of the structural-parametric model for the electroelastic actuator ;

  4. (iv)

    Determination of the transfer function for the electroelastic actuator ;

  5. (v)

    Numerical and analytical calculation of the static and dynamic characteristics of the piezoactuator .

2 Research Method

The method of mathematical physics is used to solve the wave equation with the Laplace transform to obtain the structural scheme and the structural-parametric model of the electroelastic actuator for nanomechatronics .

The problem of obtaining the structural scheme of the piezoactuator is solved using the method of mathematical physics. The solution of the wave equation is found, taking into account the boundary conditions. Using the Laplace transform, the problem of the wave equation with partial derivatives of the hyperbolic type is reduced to linear ordinary differential equation. The transfer functions of the piezoactuator are determined from its structural scheme . The structural scheme of the piezoactuator obtained in this work clearly reflects the transformation of electrical energy into mechanical energy, in contrast to the electrical equivalent circuit of the piezotransducer or the piezovibrator [2, 3]. The study accounts for the direct piezoeffect on the acting voltage on the piezoactuator . Changes in elastic compliance due to the direct piezoeffect determine the structural scheme of the piezoactuator with feedback for nanomechatronics. The paper presents the following options for constructing the structural scheme of the piezoactuator : taking into account the reverse piezoeffect and constant elastic flexibility and stiffness of the piezoactuator ; taking into account the inverse and direct piezoeffects and the variables of elastic flexibility and stiffness of the piezoactuator ; taking into account the inverse and direct piezoeffects, the variables of elastic elasticity and stiffness of the piezoactuator , and the influence of the counter electromotive force, depending on the speed of the movement of piezoactuator end.

Consider the deformation of the piezoactuator for nanomechatronics , which corresponds to its stress state. If an electric field is created in the piezoactuator , then deformation and mechanical stress will occur. Accordingly, if mechanical stress is created in the piezoactuator , electric induction and electric charge will occur on the plates of the piezoactuator . The electroelasticity equations of the piezoactuator , in general form for the inverse and direct piezoeffects [3, 5, 6, 8, 10] have the form;

$$ S_{i} = d_{mi} E_{m} + s_{ij}^{E} T_{j} , $$
(40.1)
$$ D_{m} = d_{mi} T_{i} + \varepsilon_{mk}^{E} E_{k} , $$
(40.2)

where \( i,\;j = 1,\;2, \ldots ,6 \), \( m,\;k = 1,\;2,\;3 \) are the indexes; \( l = (\delta ,h,b) \) are the working lengths of the piezoactuators with longitudinal, transverse, and shear piezoeffects along axis i; \( S_{i} \) is the relative displacement of the piezoactuator section along axis i; \( d_{mi} \) is the piezomodule; \( E_{m} (t) = u(t)/\delta \) is the electric field strength along axis m; \( u(t) \) is the voltage on the plates of the piezoactuator ; \( s_{ij}^{E} \) is the elastic compliance at E = const; \( T_{j} \) is the mechanical stress along axis j; \( \delta \) is the thickness of the piezoactuator ; \( D{}_{m}(t) \) is the electric induction along axis m; \( \varepsilon_{mk}^{T} \) is the dielectric permittivity at T = const.

From (40.1) in statics, we can obtain the steady-state movement \( \xi_{0} \) of the piezoactuator for nanomechatronics :

$$ \xi_{0} = d_{mi} (l/\delta )u_{0} , $$
(40.3)

where \( u_{0} \) is the voltage amplitude on the plates of the piezoactuator .

The equation of forces acting on the ends of the piezoactuator has the form

$$ TS_{0} = F + M\frac{{\partial^{2} \xi (x,t)}}{{\partial t^{2} }}, $$

where F is the external force applied to the piezoactuator and M is the moved mass.

Let us consider deformation of the electroelastic actuator for nanomechatronics . To compile the structural scheme of the piezoactuator for nanomechatronics with voltage control, we will jointly solve the wave equation, the equation for the inverse piezoeffect, and the force equation at its ends. Calculating the piezoactuator for nanomechatronics involves the wave equation, which describes wave propagation in the long line with attenuation and without distortion [3, 5, 7, 9, 16,17,18, 22]. Using the Laplace transform, the initial problem for the hyperbolic-type partial differential equation reduces to the simple linear ordinary differential equation [5,6,7,8,9, 17, 18].

Applying the Laplace transform to the wave equation and setting the initial conditions to zero gives the second-order linear ordinary differential equation in the form

$$ \frac{{{\text{d}}^{2} \Xi (x,p)}}{{{\text{d}}x^{2} }} - \gamma^{2} \Xi (x,p) = 0, $$
(40.4)

solution is the function

$$ \Xi (x,p) = Ce^{ - x\gamma } + Be^{x\gamma } , $$
(40.5)

where \( \Xi (x,p) \) is the Laplace transform of the bias of the piezoactuator ; x is the coordinate; p is the Laplace operator; \( \gamma = p/c^{E} + \alpha \) is the wave propagation coefficient; \( c^{E} \) is the speed of sound in the piezoactuator at \( E = {\text{const}} \); α is an attenuation coefficient, accounting for the damping of vibrations during wave propagation due to energy dissipation and heat loss.

We denote

$$ \begin{array}{*{20}l} \Xi(0,p) = \Xi_{1} (p)\quad {\text{for}}\;x = 0; \hfill \\ \Xi(l,p) = \Xi_{2} (p)\quad\; {\text{for}}\;x = l. \hfill \\ \end{array} $$

Therefore, we get the coefficients C and B for solving linear ordinary differential equation in the form

$$ C = (\Xi_{1} e^{l\gamma } - \Xi_{2} )/[2{\text{sh}}(l\gamma )],\quad B = (\Xi_{2} - \Xi_{1} e^{ - l\gamma } )/[2{\text{sh}}(l\gamma )]. $$

The solution of the linear ordinary differential equation is

$$ \Xi (x,p) = \{ \Xi_{1} (p){\text{sh}}[(l - x)\gamma ] + \Xi_{2} (p){\text{sh}}(x\gamma )/\} {\text{sh}}(l\gamma ). $$

The equations for the forces acting on the ends the piezoactuator for nanomechatronics have the form

$$ \begin{array}{*{20}l} {T_{j} (0,p)S_{0} = F_{1} (p) + M_{1} p^{2}\Xi _{1} (p)\quad \;\;\,{\text{for}}\;x = 0 ;} \hfill \\ {T_{j} (l,p)S_{0} = - F_{2} (p) - M_{2} p^{2}\Xi _{2} (p)\quad {\text{for}}\;x = l .} \hfill \\ \end{array} $$
(40.6)

We have the system of equations for mechanical stresses at the ends of the piezoactuator at x = 0 and x = l in the form

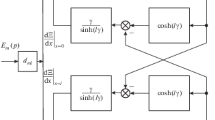
$$ \begin{array}{*{20}l} {T_{j} (0,p) = \frac{1}{{s_{ij}^{E} }}\left. {\frac{{{\text{d}}\Xi (x,p)}}{{{\text{d}}x}}} \right|_{x = 0} - \frac{{d_{mi} }}{{s_{ij}^{E} }}E_{m} (p);} \hfill \\ {T_{j} (l,p) = \frac{1}{{s_{ij}^{E} }}\left. {\frac{{{\text{d}}\Xi (x,p)}}{{{\text{d}}x}}} \right|_{x = l} - \frac{{d_{mi} }}{{s_{ij}^{E} }}E_{m} (p).} \hfill \\ \end{array} $$
(40.7)

System (40.7) gives the following system of equations for the structural-parametric model of the piezoactuator for nanomechatronics with voltage control at zero source resistance R = 0 and for the structural scheme in Fig. 40.1 of the piezoactuator for nanomechatronics

$$ \begin{array}{*{20}l} {\Xi_{1} (p) = [1/(M_{1} p^{2} )]\left\{ {\begin{array}{*{20}l} { - F_{1} (p) + (1/\chi_{ij}^{E} )} \hfill \\ { \times [d_{mi} E_{m} (p) - [\gamma /{\text{sh}}(l\gamma )][{\text{ch}}(l\gamma )\Xi_{1} (p) - \Xi_{2} (p)]]} \hfill \\ \end{array} } \right\}\begin{array}{*{20}l}{}\\{;}\end{array}} \hfill \\ {\Xi_{2} (p) = [1/(M_{2} p^{2} )]\left\{ {\begin{array}{*{20}l} { - F_{2} (p) + (1/\chi_{ij}^{E} )} \hfill \\ { \times [d_{mi} E_{m} (p) - [\gamma /{\text{sh}}(l\gamma )][{\text{ch}}(l\gamma )\Xi_{2} (p) - \Xi_{1} (p)]]} \hfill \\ \end{array} } \right\}\begin{array}{*{20}l}{}\\{,}\end{array}} \hfill \\ \end{array} $$
(40.8)

where \( \chi_{ij}^{E} = s_{ij}^{E} /S_{0} \).

Fig. 40.1
figure 1

Structural scheme of piezoactuator for nanomechatronics with voltage control at zero source resistance

Full size image

From the transformations, we obtain the system of equations of the structural-parametric model of the piezoactuator for nanomechatronics with voltage control:

$$ \begin{array}{*{20}l} \Xi_{1} \left( p \right) = \left[ {1/\left( {M_{1} p^{2} } \right)} \right]\left\{ {\begin{array}{*{20}l} { - F_{1} \left( p \right) + \left( {1/\upchi_{ij}^{E} } \right)} \hfill \\ { \times \left[ {d_{mi} E_{m} \left( p \right) - {\upgamma} {\Xi }_{1} \left( p \right)/{\text{th}}\left( {l\upgamma} \right) + {\upgamma} {\Xi }_{2} \left( p \right)/{\text{sh}}\left( {l\upgamma} \right)} \right]} \hfill \\ \end{array} } \right\}\begin{array}{*{20}l}{}\\{;}\end{array} \hfill \\ \Xi_{2} \left( p \right) = \left[ {1/\left( {M_{2} p^{2} } \right)} \right]\left\{ {\begin{array}{*{20}l} { - F_{2} \left( p \right) + \left( {1/\upchi_{ij}^{E} } \right)} \hfill \\ { \times \left[ {d_{mi} E_{m} \left( p \right) - {\upgamma} {\Xi }_{2} \left( p \right)/{\text{th}}\left( {l\upgamma} \right) + {\upgamma} {\Xi }_{1} \left( p \right)/{\text{sh}}\left( {l\upgamma} \right)} \right]} \hfill \\ \end{array} } \right\}\begin{array}{*{20}l}{}\\{.}\end{array} \hfill \\ \end{array} $$
(40.9)

Equation (40.8) for the structural-parametric model of the piezoactuator for nanomechatronics with voltage control convert to

$$ \begin{array}{*{20}l} { \Xi_{1} ( p ) = [ {1/(M_{1} p^{2} )} ]\left\{ {\begin{array}{*{20}l} { - F_{1} ( p ) + C_{ij}^{E} l} \hfill \\ { \times [ {d_{mi} E_{m} ( p ) - [ {\gamma /{\text{sh}}( {l\gamma } )} ][ {{\text{ch}}( {l\gamma } )\Xi_{1} ( p ) - \Xi_{2} ( p )} ]} ]} \hfill \\ \end{array} } \right\}\begin{array}{*{20}l}{}\\{;}\end{array}} \hfill \\ { \Xi_{2} ( p ) = [ {1/( {M_{2} p^{2} } )} ]\left\{ {\begin{array}{*{20}l} { - F_{2} ( p ) + C_{ij}^{E} l} \hfill \\ { \times [ {d_{mi} E_{m} ( p ) - [ {\gamma /{\text{sh}}( {l\gamma } )} ][ {{\text{ch}}( {l\gamma } )\Xi_{2} ( p ) - \Xi_{1} ( p )} ]} ]} \hfill \\ \end{array} } \right\}\begin{array}{*{20}l}{}\\{,}\end{array}} \hfill \\ \end{array} $$
(40.10)

where \( C_{ij}^{E} = S_{0} /(s_{ij}^{E} l) = 1/(\chi_{ij}^{E} l) \) is the stiffness of the piezoactuator with voltage control.

The structural-parametric model of the piezoactuator for nanomechatronics makes it possible to obtain its transfer functions. The joint solution of (40.10) for displacing two faces of the piezoactuator with voltage control gives the system

$$ \begin{array}{*{20}l} {\Xi_{1} ( p ) = W_{11} ( p )E_{m} ( p ) + W_{12} ( p )F_{1} ( p ) + W_{13} ( p )F_{2} ( p );} \hfill \\ {\Xi_{2} ( p ) = W_{21} ( p )E_{m} ( p ) + W_{22} ( p )F_{1} ( p ) + W_{23} ( p )F_{2} ( p ),} \hfill \\ \end{array} $$
(40.11)

and the matrix equation in the form

$$ \left( {\begin{array}{*{20}c} {\Xi_{1} (p)} \\ {\Xi_{2} (p)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {W_{11} (p)} & {W_{12} (p)} & {W_{13} (p)} \\ \end{array} } \\ {\begin{array}{*{20}c} {W_{21} (p)} & {W_{22} (p)} & {W_{23} (p)} \\ \end{array} } \\ \end{array} } \right)\;\left( {\begin{array}{*{20}c} {E_{m} (p)} \\ {F_{1} (p)} \\ {F_{2} (p)} \\ \end{array} } \right), $$
(40.12)

where the transfer functions are

$$ \begin{aligned} W_{11} (p) & = \Xi_{1} (p)/E_{m} (p) = d_{mi} \left[ {M_{2} \chi_{ij}^{E} p^{2} + \gamma th\left( {l\gamma /2} \right)} \right]/A_{ij} ;\;\chi_{ij}^{E} = s_{ij}^{E} /S_{0} ; \\ A_{ij} & = M_{1} M_{2} \left( {\upchi_{ij}^{E} } \right)^{2} p^{4} + \left\{ {\left( {M_{1} + M_{2} } \right)\upchi_{ij}^{E} /\left[ {c^{E} {\text{th}}\left( {l\upgamma} \right)} \right]} \right\}p^{3} \\ & \quad + \left[ {\left( {M_{1} + M_{2} } \right)\chi_{ij}^{E} \alpha /th\left( {l\gamma } \right) + 1/\left( {c^{E} } \right)^{2} } \right]p^{2} + 2\alpha p/c^{E} + \alpha^{2} \\ W_{21} (p) & = \Xi_{2} (p)/E_{m} (p) = d_{mi} \left[ {M_{1} \chi_{ij}^{E} p^{2} + \gamma th\left( {{{l\gamma } /2}} \right)} \right]/A_{ij} ; \\ W_{12} (p) & = {{\Xi_{1} (p)} / {F_{1} (p)}} = - \chi_{ij}^{E} \left[ {M_{2} \chi_{ij}^{E} p^{2} + \gamma /th\left( {l\gamma } \right)} \right]/A_{ij} ; \\ W_{13} (p) & = \Xi_{1} (p)/F_{2} (p); \\ W_{22} (p) & = \Xi_{2} (p)/F_{1} (p) = \left[ {\chi_{ij}^{E} \gamma /sh\left( {l\gamma } \right)} \right]/A_{ij} ; \\ W_{23} (p) & = \Xi_{2} (p)/F_{2} (p) = - \chi_{ij}^{E} \left[ {M_{1} \chi_{ij}^{E} p^{2} + \gamma /th\left( {l\gamma } \right)} \right]/A_{ij}. \\ \end{aligned} $$

Equation (40.12) for voltage control at zero source resistance R = 0 gives the transfer function of the piezoactuator for the transverse piezoelectric effect, with resonance conditions at \( M_{1} = 0 \) and \( M_{2} = 0 \), in the form

$$ {\text{tg}}(kh/2) = \infty , $$
(40.13)

where \( k = \omega /c^{E} \) is frequency coefficient; \( \omega \) is circular frequency.

This is because

$$ k_{i} h = \pi (2i - 1), $$
(40.14)

where index \( i = 1,\;2,\;3, \ldots \).

Therefore, for \( i = 1 \), the piezoactuator is the half-wave vibrator with resonance frequency

$$ f_{1} = c^{E} /(2h). $$
(40.15)

For the piezoactuator from piezoceramics PZT under the transverse piezoeffect at \( c^{E} = 3 \times 10^{3} \; {\text{m}}/{\text{s}} \) and \( h = 2.5 \times 10^{ - 2} \;{\text{m}} \), the resonance frequency is \( f_{1} = 60\, {\text{kHz}} \).

Consider the influence of the reaction of the piezoactuator for nanomechatronics due to the creation of an anti-electromotive force by the piezoactuator due to the direct piezoeffect during its static deformation.

The maximum force \( F_{ \text{max} } \) and mechanical stress \( T_{{j{ \text{max} }}} \) developed by the piezoactuator with the inverse piezoelectric effect when powered from the voltage source are

$$ F_{ \text{max} } = \frac{U}{\delta }d_{mi} \frac{{S_{0} }}{{s_{ij}^{E} }},\quad \frac{{F_{ \text{max} } }}{{S_{0} }}s_{ij}^{E} = E_{m} d_{mi} ,\quad T_{{j{ \text{max} }}} s_{ij}^{E} = E_{m} d_{mi} . $$
(40.16)

Consequently,

$$ T_{{j{ \text{max} }}} = E_{m} d_{mi} /s_{ij}^{E} ,\quad F_{ \text{max} } = E_{m} d_{mi} S_{0} /s_{ij}^{E} . $$
(40.17)

We estimate the maximum force \( F_{ \text{max} } \) and the maximum mechanical stress \( T_{{j{ \text{max} }}} \) developed by the piezoactuator for nanomechatronics when powered from the current source.

Let us consider static characteristic piezoactuator with one fixed for the longitudinal piezoeffect with the voltage control. We have in Fig. 40.2 maximum displacement \( \xi_{2m} \) for \( F_{2} = 0 \) and maximum force \( F_{2m} \) for \( \xi_{2} = 0 \) in the form

Fig. 40.2
figure 2

Static characteristic piezoactuator for longitudinal piezoeffect

Full size image
$$ \xi_{2m} = d_{33} U_{m} , $$
(40.18)
$$ F_{2m} = \frac{{d_{33} U_{m} S_{0} }}{{s_{33}^{E} \delta }}. $$
(40.19)

For the voltage-controlled piezoactuator for nanomechatronics at the longitudinal piezoeffect from piezoceramics PZT with one fixed face at zero source resistance R = 0 for \( d_{33} = 4 \times 10^{ - 10} \;{\text{m}}/{\text{V}} \), \( \delta = 6 \times 10^{ - 4} \,{\text{m}} \), \( S_{0} = 1.8 \times 10^{ - 4} \,{\text{m}}^{2} \), \( s_{33}^{E} = 3 \times 10^{ - 11} \,{\text{m}}^{2} /{\text{N}} \), \( U_{m} = 100\,{\text{V}} \) we obtain in Fig. 40.2 values of maximum displacement \( \xi_{2m} = 40\;{\text{nm}} \), maximum force \( F_{2m} = 400\;{\text{N}} \). The measurements were made on UMM-5 press. The discrepancy between the experimental data and the calculation results is 5%.

We consider the direct piezoeffect, accounting for the positive force feedback due to the direct piezoeffect, for the maximum force in the following form

$$ F_{ \text{max} } = \frac{U}{\delta }d_{mi} \frac{{S_{0} }}{{s_{ij}^{E} }} + \frac{{F_{ \text{max} } }}{{S_{0} }}d_{mi} S_{p} \frac{1}{{\varepsilon_{mk}^{T} S_{p} /\delta }}\frac{1}{\delta }d_{mi} \frac{{S_{0} }}{{s_{ij}^{E} }}, $$
(40.20)

from which

$$ \frac{{F_{ \text{max} } }}{{S_{0} }}s_{ij}^{E} \left( {1 - \frac{{d_{mi}^{2} }}{{\varepsilon_{mk}^{T} s_{ij}^{E} }}} \right) = E_{m} d_{mi} $$
(40.21)

we have

$$ T_{{j{ \text{max} }}} (1 - k_{mi}^{2} )s_{ij}^{E} = E_{m} d_{mi}, \;k_{mi} = d_{mi} /\sqrt {s_{ij}^{E} \varepsilon_{mk}^{T} } $$
(40.22)

where \( k_{mi} \) is the electromechanical coupling coefficient.

Consequently,

$$ T_{{j{ \text{max} }}} s_{ij}^{D} = E_{m} d_{mi} ; $$
(40.23)
$$ s_{ij}^{D} = (1 - k_{mi}^{2} )s_{ij}^{E} = k_{s} s_{ij}^{E} ,\quad k_{s} = 1 - k_{mi}^{2} = s_{ij}^{D} /s_{ij}^{E} ,\quad k_{s} > 0, $$

where \( k_{s} \) is the coefficient of the change of elastic compliance .

Moreover, we have

$$ F_{ \text{max} } = E_{m} d_{mi} S_{0} /(s_{ij}^{E} k_{s} ) = E_{m} d_{mi} S_{0} /s_{ij}^{D} . $$
(40.24)

Consequently,

$$ T_{{j{ \text{max} }}} = E_{m} d_{mi} /s_{ij}^{D} . $$
(40.25)

The elastic compliance \( s_{ij} \) of the piezoactuator takes the form \( s_{ij}^{E} > s_{ij} > s_{ij}^{D} \), where \( s_{ij}^{E} /s_{ij}^{D} \le 1.2 \). \( C_{ij}^{E} = S_{0} (s_{ij}^{E} l) \) is the stiffness of the piezoactuator with voltage control and \( C_{ij}^{D} = S_{0} /(s_{ij}^{D} l) \) is the stiffness of the piezoactuator with current control. Consequently, \( C_{ij}^{E} < C{}_{ij} < C_{ij}^{D} \), \( C_{ij} = S_{0} /(s_{ij} l) \) is the stiffness of the piezoactuator. When the electrodes are open, the stiffness of the piezoactuator increases when compared with closed electrodes. Increasing the resistance of the power supply and matching circuits decreases the elastic compliance and increases the rigidity of the piezoactuator. When controlling the piezoactuator from the power source with finite source resistance and accounting for positive force feedback due to the direct piezoeffect, we get the maximum force of the piezoactuator as

$$ F_{ \text{max} } = \frac{U}{\delta }d_{mi} \frac{{S_{0} }}{{s_{ij}^{E} }} + \frac{{F_{ \text{max} } }}{{S_{0} }}d_{mi} S_{p} \frac{1}{{\varepsilon_{mk}^{T} S_{p} /\delta }}k_{u} \frac{1}{\delta }d_{mi} \frac{{S_{0} }}{{s_{ij}^{E} }}, $$
(40.26)

which gives

$$ \begin{aligned} & \frac{{F_{ \text{max} } }}{{S_{0} }}s_{ij}^{E} \left( {1 - \frac{{d_{mi}^{2} k_{u} }}{{\varepsilon_{mk}^{T} s_{ij}^{E} }}} \right) = E_{m} d_{mi} ,\quad k_{mi} = d_{mi} /\sqrt {s_{ij}^{E} \varepsilon_{mk}^{T} } ; \\ & T_{{j{ \text{max} }}} \left( {1 - k_{mi}^{2} k_{u} } \right)s_{ij}^{E} = E_{m} d_{mi} ,\quad 0 \le k_{u} \le 1, \\ \end{aligned} $$
(40.27)

where \( k_{u} \) is the coefficient of control from the electric power source.

When controlling the piezoactuator from the current source, we have \( \left. {k_{u} } \right|_{R \to \infty } = 1 \); when controlling the piezoactuator from the voltage source, we have \( \left. {k_{u} } \right|_{R \to 0} = 0 \); with elastic compliance, we have

$$ \begin{aligned} & s_{ij} = (1 - k_{mi}^{2} k_{u} )s_{ij}^{E} = k_{s} s_{ij}^{E} ,\quad k_{s} = 1 - k_{mi}^{2} k_{u} ,\quad k_{s} > 0, \\ & {(1 - k_{mi}^{2} )} |_{R \to \infty } \le k_{s} \le 1 |_{R \to 0} ,\quad {k_{s} } |_{R \to \infty } = 1 - k_{mi}^{2} ,\quad {k_{s} } |_{R \to 0} = 1, \\ \end{aligned} $$
(40.28)

where \( k_{s} \) is the coefficient of change of the elastic compliance .

Controlling the piezoactuator from the power source with the finite source resistance gives expressions for positive force feedback in Fig. 40.3 in the structural-parametric model of piezoactuator for nanomechatronics

Fig. 40.3
figure 3

Structural scheme of electroelastic actuator for nanomechatronics with voltage control and finite source resistance

Full size image
$$ U_{F\alpha } (p) = \frac{{k_{u} (l/\delta )d_{mi} }}{{C_{0} }}F_{\alpha } (p),\quad \alpha = 1,\;2. $$
(40.29)

For controlling current from the source with infinitely large resistance gives \( \left. {k_{u} } \right|_{R \to \infty } = 1 \).

After transformations, we obtain the structural-parametric model of the piezoactuator for nanomechatronics with the current control and its transfer functions .

Therefore, the system of equations for the structural-parametric model and the structural scheme of the electroelastic actuator for nanomechatronics in Fig. 40.3 have the form

$$ \Xi_{1} (p) = [1/(M_{1} p^{2} )]\left\{ {\begin{array}{*{20}l} { - F_{1} (p) + (1/\chi_{ij}^{\Psi } )} \hfill \\ { \times \left[ {d_{mi} \Psi_{m} (p) - [\gamma /{\text{sh}}(l\gamma )][{\text{ch}}(l\gamma )\Xi_{1} (p) - \Xi_{2} (p)]} \right]} \hfill \\ \end{array} } \right\}\begin{array}{*{20}l}{}\\{;}\end{array} $$
(40.30)
$$ \Xi_{2} (p) = [1/(M_{2} p^{2} )]\left\{ {\begin{array}{*{20}l} { - F_{2} (p) + (1/\chi_{ij}^{\Psi } )} \hfill \\ { \times \left[ {d_{mi} \Psi_{m} (p) - [\gamma /{\text{sh}}(l\gamma )][{\text{ch}}(l\gamma )\Xi_{2} (p) - \Xi_{1} (p)]} \right]} \hfill \\ \end{array} } \right\}\begin{array}{*{20}l}{}\\{,}\end{array} $$

where \( \chi_{ij}^{\Psi } = s_{ij}^{\Psi } /S_{0} \), \( v_{mi} = \left\{ {\begin{array}{*{20}c} {d_{33} ,d_{31} ,d_{15} } \\ {g_{33} ,g_{31} ,g_{15} } \\ \end{array} } \right. \), \( \Psi _{m} = \left\{ {\begin{array}{*{20}c} {E_{3} ,E_{1} } \\ {D_{3} ,D} \\ \end{array} } \right. \), \( s_{ij}^{\Psi } = \left\{ {\begin{array}{*{20}c} {s_{33}^{E} ,s_{11}^{E} ,s_{55}^{E} } \\ {s_{33}^{D} ,s_{11}^{D} ,s_{55}^{D} } \\ \end{array} } \right. \), \( \upgamma = \left\{ {\begin{array}{*{20}c} {\upgamma^{E} } \\ {\upgamma^{D} } \\ \end{array} } \right. \), \( c^{\Psi } = \left\{ {\begin{array}{*{20}c} {c^{E} } \\ {c^{D} } \\ \end{array} } \right. \).

To account for the effect of the velocity of the ends of the piezoactuator in Fig. 40.3 due to the appearance of the counter electromotive force from the direct piezoeffect, the structural scheme of the piezoactuator is supplemented with negative feedback

$$ U_{{\dot{\Xi}}\alpha} \left( p \right) = \frac{{d_{mi} S_{0} R}}{{\delta s_{ij} }}{\dot{\Xi}}_{\alpha} \left( p \right),\;\alpha = 1,\;2. $$
(40.31)

3 Results and Discussion

The structural-parametric model and the structural scheme of the piezoactuator for nanomechatronics with feedback of the piezoactuator reflect the conversion of the electrical energy into the mechanical energy. The structural-parametric model and structural scheme change depending on whether the piezoactuator is controlled by voltage or current.

We constructed the structural scheme and the matrix transfer function of the electroelastic actuator . We obtained the matrix transfer function of the electroelastic actuator [8, 18] from the structural-parametric model (40.30) in the form

$$ \begin{aligned} & (\Xi (p)) = \left( {W(p)} \right)\;(P(p)), \\ & (\Xi (p)) = \left( {\begin{array}{*{20}c} {\Xi_{1} (p)} \\ {\Xi_{2} (p)} \\ \end{array} } \right)\begin{array}{*{20}l}{}\\{,}\end{array}\quad (W(p)) = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {W_{11} (p)} & {W_{12} (p)} & {W_{13} (p)} \\ \end{array} } \\ {\begin{array}{*{20}c} {W_{21} (p)} & {W_{22} (p)} & {W_{23} (p)} \\ \end{array} } \\ \end{array} } \right)\begin{array}{*{20}l}{}\\{,}\end{array} \\ & (P(p)) = \left( {\begin{array}{*{20}c} {\Psi_{m} (p)} \\ {F_{1} (p)} \\ {F_{2} (p)} \\ \end{array} } \right)\begin{array}{*{20}l}{}\\{,}\end{array} \\ \end{aligned} $$
(40.32)

where \( (\Xi (p)) \), \( (W(p)) \), \( (P(p)) \) are the matrices of Laplace transforms of the displacements for the faces, the transfer functions , the control parameters.

We find the displacement of both faces of the electroelastic actuator in the static regime for \( \Psi_{m} (t) = \Psi_{m0} \cdot 1(t) \), \( F_{1} (t) = F_{2} (t) = 0 \) at the inertia load. From (40.32) the static displacements of both faces of the actuator at \( m \ll M_{1} \) and \( m \ll M_{2} \) and the inertial load are respectively

$$ \xi_{1} (\infty ) = \mathop {\lim }\limits_{t \to \infty } \xi_{1} (t) = \nu_{mi} l\Psi_{m0} M_{2} /(M_{1} + M_{2} ), $$
(40.33)
$$ \xi_{2} (\infty ) = \mathop {\lim }\limits_{t \to \infty } \xi_{2} (t) = \nu_{mi} l\Psi_{m0} M_{1} /(M_{1} + M_{2} ), $$
(40.34)
$$ \xi_{1} (\infty ) + \xi_{2} (\infty ) = \mathop {\lim }\limits_{t \to \infty } (\xi_{1} (t) + \xi_{2} (t)) = \nu_{mi} l\Psi_{m0} , $$
(40.35)

where m is the mass of the piezoactuator ; \( M_{1} ,\;M_{2} \) are the load masses.

The static displacements of both faces of the piezoactuator for the longitudinal piezoeffect and the inertial load at \( m \ll M_{1} \) and \( m \ll M_{2} \) are respectively

$$ \xi_{1} (\infty ) = d_{33} U_{0} /(M_{1} + M_{2} ), $$
(40.36)
$$ \xi_{2} (\infty ) = d_{33} U_{0} M_{1} /(M_{1} + M_{2} ). $$
(40.37)

We have the static characteristics of the piezoactuator from piezoceramics PZT for the longitudinal piezoeffect at \( m \ll M_{1} \) and \( m \ll M_{2} \). At \( d_{33} = 4 \times 10^{ - 10} {\text{m}}/{\text{V}} \), \( U_{0} = 250\,{\text{V}} \), \( M_{1} = 1\,{\text{kg}} \), and \( M_{2} = 4\;{\text{kg}} \), we obtain the static displacements of both faces of the piezoactuator as \( \xi_{1} (\infty ) = 80\;{\text{nm}} \), \( \xi_{2} (\infty ) = 20\;{\text{mm}} \), and \( \xi_{1} (\infty ) + \xi_{2} (\infty ) = 100\;{\text{nm}} \).

Consider the structural schemes of the piezoactuator with distributed and lumped parameters at one fixed face with elastic-inertial load, controlled by voltage with finite source resistance. From (40.29)–(40.31) for the piezoactuator with one rigidly fixed face at elastic-inertial load for \( M_{1} \to \infty \) we obtain structural scheme in Fig. 40.4 with distributed parameters.

Fig. 40.4
figure 4

Structural scheme with distributed parameters of piezoactuator, fixed at one face and voltage control at finite source resistance for a initial scheme and b transformed scheme

Full size image

After the structural transformations of the initial structural scheme seen in Fig. 40.4a we obtain the transformed structural scheme seen in Fig. 40.4b with elastic compliance \( s_{ij} = (1 - k_{mi}^{2} k_{u} )s_{ij}^{E} \). With replacing the hyperbolic cotangent on two members of the power series and using the structural scheme in Fig. 40.4b we have coefficient \( k_{d} \) of the direct piezoeffect and coefficient \( k_{r} \) of the reverse piezoeffect of the piezoactuator in the form

$$ k_{d} = k_{r} = \frac{{d_{mi} S_{0} }}{{{\delta}s_{ij} }}. $$
(40.38)

We get the structural scheme of the piezoactuator with concentrated parameters for one rigidly fixed face under elastic-inertial load with \( M_{1} \to \infty \), as seen in Fig. 40.5.

Fig. 40.5
figure 5

Structural scheme with lumped parameters of piezoactuator, fixed at one face with elastic-inertial load and voltage control at finite source resistance

Full size image

For the structural scheme of the piezoactuator in Fig. 40.5 at \( R = 0 \), we define the following expression for its transfer function

$$ W(p) = \frac{{\Xi_{2} (p)}}{U(p)} = \frac{{k_{r} }}{{M_{2} p^{2} + k_{v} p + C_{ij}^{E} + C{}_{e}}}. $$
(40.39)

After transformations, we obtain the transfer function for the piezoactuator in the form

$$ W(p) = \frac{{\Xi_{2} (p)}}{U(p)} = \frac{{d_{mi} (l/\delta )}}{{(1 + C_{e} /C_{ij}^{E} )(T_{t}^{2} p^{2} + 2T_{t} \xi_{t} p + 1)}}; $$
(40.40)
$$ \begin{aligned} & T_{t} = \sqrt {M_{2} /(C_{ij}^{E} + C{}_{e})} ,\quad \xi_{t} = k_{v} /\left( {2(C_{ij}^{E} + C{}_{e})\sqrt {M_{2} (C_{ij}^{E} + C{}_{e})} } \right),\\ & C_{ij}^{E} = S_{0} /(s_{ij}^{E} l) = 1/(\upchi_{ij}^{E} l). \end{aligned}$$

Consequently, the transfer function of the piezoactuator with the transverse piezoelectric effect and voltage control at \( R = 0 \) has the form

$$ W(p) = \frac{{\Xi_{2} (p)}}{U(p)} = \frac{{d_{31} h/\delta }}{{(1 + C_{e} /C_{11}^{E} )(T_{t}^{2} p^{2} + 2T_{t} \xi_{t} p + 1)}}; $$
$$ \begin{aligned} & T_{t} = \sqrt {M_{2} /(C{}_{e} + C_{11}^{E} )} ,\quad \xi_{t} = {{\alpha h^{2} C_{11}^{E} } \mathord{\left/ {\vphantom {{\alpha h^{2} C_{11}^{E} } {\left( {3c^{E} \sqrt {M(C_{e} + C_{11}^{E} )} } \right)}}} \right. \kern-0pt} {\left( {3c^{E} \sqrt {M(C_{e} + C_{11}^{E} )} } \right)}};\\ & C_{11}^{E} = S_{0} /(s_{11}^{E} h) = 1/(\chi_{11}^{E} h), \end{aligned} $$

where \( \Xi_{2} (p) \) and \( U(p) \) are the Laplace transformations of the displacement of the face and the voltage on the plates of the piezoactuator ; \( \delta \) is the thickness; h is the height; \( T_{t} \) and \( \xi_{t} \) are the time constant and the attenuation coefficient of the piezoactuator .

For the piezoactuator from PZT piezoceramics with the transverse piezoeffect and voltage control with one rigidly fixed face for \( M_{1} \to \infty \), \( m \ll M_{2} \), and the step input voltage amplitude \( U_{0} = 200\;{\text{V}} \) at \( d_{31} = 2.5 \times 10^{ - 10}\; {\text{m}}/{\text{V}} \), \( h/\delta = 20 \), \( M_{2} = 1\,{\text{kg}} \), \( C_{11}^{E} = 2 \times 10^{7}\; {\text{N}}/{\text{m}} \) and \( C_{e} = 0.5 \times 10^{7}\; {\text{N}}/{\text{m}} \), we get \( \xi_{0} = 800\;{\text{nm}} \) and \( T_{t} = 0.2 \times 10^{ - 3}\; {\text{s}} \). The experimental and calculated values for the piezoactuator are in agreement up to an accuracy of 5%.

4 Conclusion

Applied theory of structural schemes of the electroelastic actuator for nanomechatronics is constructed. We determine structural-parametric model and transfer function for electroelastic actuator. We obtain numerical and analytical calculation of the static and dynamic characteristics of the piezoactuator from its transfer function. This work defines the structural-parametric model and structural scheme of the piezoactuator , taking into account the inverse piezoeffect and the back electromotive force due to the direct piezoeffect.

The structural-parametric model and structural scheme of the piezoactuator for nanomechatronics with feedback visually reflect the conversion of the piezoactuator the electrical energy into the mechanical energy. The structural-parametric model and structural scheme of the piezoactuator are shown to change depending on controlled by voltage or current. The maximum forces and mechanical stresses, which the piezoactuator develops for the transverse, longitudinal, shear piezoeffects, are determined.

The elastic compliances and the stiffness of the piezoactuators are found for the transverse, longitudinal, shear piezoeffects, depending from the type control by voltage or current. The transfer functions of the piezoactuators for nanomechatronics with the transverse, longitudinal, shear piezoeffects with voltage or current control are obtained.