Structural Scheme of an Electromagnetoelastic Actuator for Nanotechnology Research

Abstract

An electromagnetoelastic actuator is electromagnetomechanical device, intended for actuation of mechanisms, systems or management, based on the piezoelectric, piezomagnetic, electrostriction, magnetostriction effects, converts electric or magnetic signals into mechanical movement and force. The piezo actuator is used in vibration compensation and absorption systems in aircraft and rotorcraft elements, in nanotechnology research for scanning microscopy, in laser systems and ring gyroscopes. The structural scheme of an electromagnetoelastic actuator for nanotechnology research is constructed by using the equation of electromagnetoelasticity and the linear ordinary second-order differential equation of the actuator under various boundary conditions. An electromagnetoelastic actuator is using in nanotechnology, microelectronics, nanobiology, astronomy, nanophysics for the alignment, the reparation of the gravitation and temperature deformations. The nanomanipulator with the piezo actuator is applied in the matching systems in nanotechnology. In the present work, the problem of building the structural scheme of the electromagnetoelastic actuator is solving in difference from Mason’s electrical equivalent circuit. The transformation of the structural scheme under various boundary conditions of the actuator is considered. The matrix transfer function is calculated from the set of equations for the structural scheme of the electromagnetoelastic actuator in control system. This matrix transfer function for the deformation of the actuator is used in nanotechnology research. The structural schemes and the elastic compliances of the piezo actuators are obtained by voltage or current control. The structural scheme of the magnetostriction actuator is constructed for nanotechnology research. The characteristics of the piezo actuator are determined. The structural scheme of the piezo actuator with the back electromotive force is obtained. The transformation of the elastic compliances of the piezo actuators is considered for the voltage and current control.

1 Introduction

An electromagnetoelastic actuator with piezoelectric, piezomagnetic, electrostriction or magnetostriction effects is used for actuation of mechanisms and systems in nanotechnology research. The piezo actuator is applied for nanodisplacement, compensation of vibration in nanotechnology. The piezo actuator is used to actuate or control nanomechanisms and nanosystems on the piezoelectric effect and to its nanodisplacemets with convert electrical energy into mechanical energy at the nanometric accuracy [1,2,3,4,5,6,7,8,9]. The piezo actuator is used for nanodeformations the elements in atomic force microscopes and laser systems, for nanodisplacements of the mirrors of laser ring gyroscopes [6,7,8,9,10,11,12,13,14,15,16,17].

At this work, we obtained structural scheme of an electromagnetoelastic actuator, which is obtained clearly and visually reflects the transformation of electrical energy into mechanical energy in difference from Mason’s electrical equivalent circuit [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. The structural scheme of an electromagnetoelastic actuator for nanotechnology research is determined with using the equation of electromagnetoelasticity and the linear ordinary second-order differential equation. The structural scheme of the piezo actuator is obtained with using equations of the inverse piezoelectric effect and the back electromotive force due to the direct piezoelectric effect. We used the transformation of the structural scheme under various boundary conditions of an electromagnetoelastic actuator. From the set of equations for the structural scheme of an electromagnetoelastic actuator, the matrix transfer function is determined. The stiffness of the piezo actuator is found for the voltage or current controls at the longitudinal, shear and transverse piezoelectric effects. For nanosystem with an electromagnetoelastic actuator its matrix transfer function is determined.

In research scope of this work, we have the following frameworks of the problem:

• (i) deformation of an electromagnetoelastic actuator for nanotechnology research;

• (ii) applied theory of an electromagnetoelastic actuator for nanotechnology research;

• (iii) calculation of the structural scheme for an electromagnetoelastic actuator;

• (iv) determination of the matrix transfer function for an electromagnetoelastic actuator;

• (v) analytical and numerical decision of the characteristics and parameters of the piezo actuator.

For calculating the parameters of an electromagnetoelastic actuator, we solved the electromagnetoelasticity equation and the linear ordinary second-order differential equation of the actuator under appropriate boundary conditions. The characteristics of an electromagnetoelastic actuator is determined with using the matrix transfer function. The elastic compliances of the piezo actuators are obtained at the voltage and current control.

2 Research Method

2.1 Method of Mathematical Physics

The method of mathematical physics is used for the determination of the structural scheme of an electromagnetoelastic actuator for nanotechnology research from electromagnetoelasticity equation and the linear ordinary second-order differential equation of the actuator.

The electromagnetoelasticity equation of the actuator under simultaneous exposure to electric and magnetic fields [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] has the form:

$$ S_{i} = s_{ij}^{E,H} T_{j} + d_{mi}^{H} E_{m} + d_{mi}^{E} H_{m} , $$

(1)

where $S_{i}$ is the relative deformation along the axis i, indexes i = 1, 2, …, 6, j = 1, 2, …, 6, m = 1, 2, 3, $T_{j}$ is the mechanical stress along the axis j, $d_{mi}^{H}$ is the piezomodule for $H = {\text{const}}$, $E_{m}$ is the electric field strength along the axis m, $d_{mi}^{E}$ is the magnetostriction coefficient for $E = {\text{const}}$, $H_{m}$ is the magnetic field strength along the m-axis.

2.2 Structural Scheme

In general the electromagnetoelasticity equation of an electromagnetoelastic actuator under separate influence of electric and magnetic fields [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] has the form:

$$ S_{i} = s_{ij}^{\Psi } T_{j} + \nu_{mi} \Psi_{m} , $$

(2)

where $s_{ij}^{\Psi } = \left\{ {\begin{array}{*{20}c} {s_{33}^{E} ,s_{11}^{E} ,s_{55}^{E} } \\ {s_{33}^{D} ,s_{11}^{D} ,s_{55}^{D} } \\ {s_{33}^{H} ,s_{11}^{H} ,s_{55}^{H} } \\ \end{array} } \right.$, $v_{mi} = \left\{ {\begin{array}{*{20}c} {d_{33} ,d_{31} ,d_{15} } \\ {g_{33} ,g_{31} ,g_{15} } \\ {d_{33} ,d_{31} ,d_{15} } \\ \end{array} } \right.$, $\Psi_{m} = \left\{ {\begin{array}{*{20}c} {E_{3} ,E_{3} ,E_{1} } \\ {D_{3} ,D_{3} ,D_{1} } \\ {H_{3} ,H_{3} ,H_{1} } \\ \end{array} } \right.$, $\gamma = \left\{ {\begin{array}{*{20}c} {\gamma^{E} } \\ {\gamma^{D} } \\ {\gamma^{H} } \\ \end{array} } \right.$, $c^{\Psi } = \left\{ {\begin{array}{*{20}c} {c^{E} } \\ {c^{D} } \\ {c^{H} } \\ \end{array} } \right.$, $l = \left\{ {\begin{array}{*{20}c} \delta \\ h \\ b \\ \end{array} } \right.$, $E$ is the electric field strength, $D$ is the electric induction, $H$ is the magnetic field strength.

For using the Laplace transform to the wave equation, we have the second-order linear ordinary differential equation of an electromagnetoelastic actuator [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]:

$$ \frac{{d^{2} \Xi \left( {x,p} \right)}}{{dx^{2} }} - \gamma^{2} \Xi \left( {x,p} \right) = 0, $$

(3)

with its solution:

$\Xi \left( {x,p} \right) = Ce^{ - \gamma x} + Be^{\gamma x}$,

where $\Xi \left( {x,p} \right)$ is the Laplace transform of the bias of the actuator; x is the coordinate; p is the operator; $\gamma = {p \mathord{\left/ {\vphantom {p {c^{\Psi } }}} \right. \kern-0pt} {c^{\Psi } }} + \alpha$ is the wave propagation coefficient; $c^{\Psi }$ is the speed of sound in the actuator at $\Psi = {\text{const}}$; α is the attenuation coefficient.

We write:

$\begin{array}{*{20}c} {\Xi (0,p) = \Xi _{1} (p),} & {\begin{array}{*{20}c} {{\text{for}}} & {x = 0} \\ \end{array} } \\ {\Xi (l,p) = \Xi _{2} (p),} & {\begin{array}{*{20}c} {{\text{for}}} & {x = l} \\ \end{array} } \\ \end{array}$

We have the coefficients C and B in the form:

$$ C = {{\left( {\Xi_{1} e^{\gamma l} - \Xi_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {\Xi_{1} e^{\gamma l} - \Xi_{2} } \right)} {\left[ {2{\text{sh}}\left( {\gamma l} \right)} \right]}}} \right. \kern-0pt} {\left[ {2{\text{sh}}\left( {\gamma l} \right)} \right]}},\,B = {{\left( {\Xi_{2} - \Xi_{1} e^{ - \gamma l} } \right)} \mathord{\left/ {\vphantom {{\left( {\Xi_{2} - \Xi_{1} e^{ - \gamma l} } \right)} {\left[ {2{\text{sh}}\left( {\gamma l} \right)} \right]}}} \right. \kern-0pt} {\left[ {2{\text{sh}}\left( {\gamma l} \right)} \right]}}. $$

The solution of the linear ordinary differential equation has the form:

$$ \Xi \left( {x,p} \right) = {{\left\{ {\Xi_{1} \left( p \right){\text{sh}}\left[ {\gamma \left( {l - x} \right)} \right] + \Xi_{2} \left( p \right){\text{sh}}\left( {\gamma x} \right)} \right\}} \mathord{\left/ {\vphantom {{\left\{ {\Xi_{1} \left( p \right){\text{sh}}\left[ {\gamma \left( {l - x} \right)} \right] + \Xi_{2} \left( p \right){\text{sh}}\left( {\gamma x} \right)} \right\}} {{\text{sh}}\left( {\gamma l} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma l} \right)}}. $$

The equations for the forces on the ends of an electromagnetoelastic actuator are obtained as

$$ \begin{gathered} T_{j} \left( {0,p} \right)S_{0} = F_{1} \left( p \right) + M_{1} p^{2} \Xi_{1} \left( p \right),\,{\text{for}}\,x\, = \,0; \hfill \\ T_{j} \left( {l,p} \right)S_{0} = - F_{2} \left( p \right) - M_{2} p^{2} \Xi_{2} \left( p \right),\,{\text{for}}\,x\, = \,l. \hfill \\ \end{gathered} $$

(4)

The system of equations for mechanical stresses at the ends of an electromagnetoelastic actuator at x = 0 and x = l has the form:

$$ \begin{gathered} T_{j} \left( {0,p} \right) = \frac{1}{{s_{ij}^{\Psi } }}\left. {\frac{{d\Xi \left( {x,p} \right)}}{dx}} \right|_{x = 0} - \frac{{\nu_{mi} }}{{s_{ij}^{\Psi } }}E_{m} \left( p \right); \hfill \\ T_{j} \left( {l,p} \right) = \frac{1}{{s_{ij}^{\Psi } }}\left. {\frac{{d\Xi \left( {x,p} \right)}}{dx}} \right|_{x = l} - \frac{{\nu_{mi} }}{{s_{ij}^{\Psi } }}E_{m} \left( p \right). \hfill \\ \end{gathered} $$

(5)

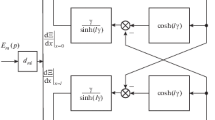
From (5), we have the structural-parametric model of an electromagnetoelastic actuator for nanotechnology research and its structural scheme in Fig. 1:

$$ \begin{gathered} \Xi_{1} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{1} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{1} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{1} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{ij}^{\Psi } }}} \right. \kern-0pt} {\chi_{ij}^{\Psi } }}} \right) \hfill \\ \times \left[ {\nu_{mi} \Psi_{m} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma l} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma l} \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma l} \right)\Xi_{1} \left( p \right) - \Xi_{2} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}; \hfill \\ \Xi_{2} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{2} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{2} p^{2} } \right)}}} \right],\left\{ \begin{gathered} - F_{2} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{ij}^{\Psi } }}} \right. \kern-0pt} {\chi_{ij}^{\Psi } }}} \right) \hfill \\ \times \left[ {\nu_{mi} \Psi_{m} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma l} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma l} \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma l} \right)\Xi_{2} \left( p \right) - \Xi_{1} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}, \hfill \\ \end{gathered} $$

(6)

where $\chi_{ij}^{\Psi } = {{s_{ij}^{\Psi } } \mathord{\left/ {\vphantom {{s_{ij}^{\Psi } } {S_{0} }}} \right. \kern-0pt} {S_{0} }}$.

Therefore, from (6) the structural-parametric model of the piezo actuator and its structural scheme are obtained for the longitudinal, transverse, shear piezo effects.

For example, for the longitudinal piezo actuator at voltage control for resistance of the power supply and matching circuit $R = 0$, its structural scheme is present in Fig. 2:

Fig. 1.

Structural scheme of electromagnetoelastic actuator for nanotechnology research.

Fig. 2.

Structural scheme of longitudinal piezo actuator at voltage control.

$$ \begin{gathered} \Xi_{1} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{1} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{1} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{1} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{33}^{E} }}} \right. \kern-0pt} {\chi_{33}^{E} }}} \right) \hfill \\ \times \left[ {d_{33} E_{3} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma \delta } \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma \delta } \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma \delta } \right)\Xi_{1} \left( p \right) - \Xi_{2} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}; \hfill \\ \Xi_{2} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{2} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{2} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{2} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{33}^{E} }}} \right. \kern-0pt} {\chi_{33}^{E} }}} \right) \hfill \\ \times \left[ {d_{33} E_{3} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma \delta } \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma \delta } \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma \delta } \right)\Xi_{2} \left( p \right) - \Xi_{1} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}, \hfill \\ \end{gathered} $$

(7)

where $\chi_{33}^{E} = {{s_{33}^{E} } \mathord{\left/ {\vphantom {{s_{33}^{E} } {S_{0} }}} \right. \kern-0pt} {S_{0} }}$.

For the longitudinal piezo actuator at current control for $R = \infty$ the structural scheme is present in Fig. 3.

$$ \begin{gathered} \Xi_{1} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{1} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{1} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{1} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{33}^{D} }}} \right. \kern-0pt} {\chi_{33}^{D} }}} \right) \hfill \\ \times \left[ {g_{33} D_{3} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma \delta } \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma \delta } \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma \delta } \right)\Xi_{1} \left( p \right) - \Xi_{2} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}; \hfill \\ \Xi_{2} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{2} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{2} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{2} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{33}^{D} }}} \right. \kern-0pt} {\chi_{33}^{D} }}} \right) \hfill \\ \times \left[ {g_{33} D_{3} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma \delta } \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma \delta } \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma \delta } \right)\Xi_{2} \left( p \right) - \Xi_{1} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}, \hfill \\ \end{gathered} $$

(8)

$$ {\text{where}}\,\chi_{33}^{D} = {{s_{33}^{D} } \mathord{\left/ {\vphantom {{s_{33}^{D} } {S_{0} }}} \right. \kern-0pt} {S_{0} }}. $$

Fig. 3.

Structural scheme of longitudinal piezo actuator at current control.

For the transverse piezo actuator at voltage control for $R = 0$ the structural scheme is present in Fig. 4:

$$ \begin{gathered} \Xi_{1} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{1} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{1} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{1} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{11}^{E} }}} \right. \kern-0pt} {\chi_{11}^{E} }}} \right) \hfill \\ \times \left[ {d_{31} E_{3} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma h} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma h} \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma h} \right)\Xi_{1} \left( p \right) - \Xi_{2} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}; \hfill \\ \Xi_{2} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{2} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{2} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{2} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{11}^{E} }}} \right. \kern-0pt} {\chi_{11}^{E} }}} \right) \hfill \\ \times \left[ {d_{31} E_{3} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma h} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma h} \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma h} \right)\Xi_{2} \left( p \right) - \Xi_{1} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}, \hfill \\ \end{gathered} $$

(9)

where $\chi_{11}^{E} = {{s_{11}^{E} } \mathord{\left/ {\vphantom {{s_{11}^{E} } {S_{0} }}} \right. \kern-0pt} {S_{0} }}$.

For the transverse piezo actuator at current control for $R = \infty$, the structural scheme is present in Fig. 5:

Fig. 4.

Structural scheme of transverse piezo actuator at voltage control.

Fig. 5.

Structural scheme of transverse piezo actuator at current control.

$$ \begin{gathered} \Xi_{1} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{1} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{1} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{1} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{11}^{D} }}} \right. \kern-0pt} {\chi_{11}^{D} }}} \right) \hfill \\ \times \left[ {g_{31} D_{3} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma h} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma h} \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma h} \right)\Xi_{1} \left( p \right) - \Xi_{2} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}; \hfill \\ \Xi_{2} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{2} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{2} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{2} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{11}^{D} }}} \right. \kern-0pt} {\chi_{11}^{D} }}} \right) \hfill \\ \times \left[ {g_{31} D_{3} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma h} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma h} \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma h} \right)\Xi_{2} \left( p \right) - \Xi_{1} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}, \hfill \\ \end{gathered} $$

(10)

where $\chi_{11}^{D} = {{s_{11}^{D} } \mathord{\left/ {\vphantom {{s_{11}^{D} } {S_{0} }}} \right. \kern-0pt} {S_{0} }}$.

For the shear piezo actuator at voltage control for $R = 0$, the structural scheme is present in Fig. 6:

Fig. 6.

Structural scheme of shear piezo actuator at voltage control

$$ \begin{gathered} \Xi_{1} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{1} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{1} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{1} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{55}^{E} }}} \right. \kern-0pt} {\chi_{55}^{E} }}} \right) \hfill \\ \times \left[ {d_{15} E_{1} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma b} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma b} \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma b} \right)\Xi_{1} \left( p \right) - \Xi_{2} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}; \hfill \\ \Xi_{2} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{2} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{2} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{2} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{55}^{E} }}} \right. \kern-0pt} {\chi_{55}^{E} }}} \right) \hfill \\ \times \left[ {d_{15} E_{1} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma b} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma b} \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma b} \right)\Xi_{2} \left( p \right) - \Xi_{1} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}, \hfill \\ \end{gathered} $$

(11)

where $\chi_{55}^{E} = {{s_{55}^{E} } \mathord{\left/ {\vphantom {{s_{55}^{E} } {S_{0} }}} \right. \kern-0pt} {S_{0} }}$.

For the shear piezo actuator at current control for $R = \infty$ the structural scheme is present in Fig. 7:

$$ \begin{gathered} \Xi_{1} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{1} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{1} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{1} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{55}^{D} }}} \right. \kern-0pt} {\chi_{55}^{D} }}} \right) \hfill \\ \times \left[ {g_{15} D_{1} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma b} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma b} \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma b} \right)\Xi_{1} \left( p \right) - \Xi_{2} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}; \hfill \\ \Xi_{2} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{2} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{2} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{2} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{55}^{D} }}} \right. \kern-0pt} {\chi_{55}^{D} }}} \right) \hfill \\ \times \left[ {g_{15} D_{1} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma b} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma b} \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma b} \right)\Xi_{2} \left( p \right) - \Xi_{1} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}, \hfill \\ \end{gathered} $$

(12)

where $\chi_{55}^{D} = {{s_{55}^{D} } \mathord{\left/ {\vphantom {{s_{55}^{D} } {S_{0} }}} \right. \kern-0pt} {S_{0} }}$.

For example, for the longitudinal magnetostriction actuator the structural scheme is present in Fig. 8:

Fig. 7.

Structural scheme of shear piezo actuator at current control.

Fig. 8.

Structural scheme of longitudinal magnetostriction actuator.

$$ \begin{gathered} \Xi_{1} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{1} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{1} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{1} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{33}^{H} }}} \right. \kern-0pt} {\chi_{33}^{H} }}} \right) \hfill \\ \times \left[ {d_{33} H_{3} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma \delta } \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma \delta } \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma \delta } \right)\Xi_{1} \left( p \right) - \Xi_{2} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}; \hfill \\ \Xi_{2} \left( p \right) = \left[ {{1 \mathord{\left/ {\vphantom {1 {\left( {M_{2} p^{2} } \right)}}} \right. \kern-0pt} {\left( {M_{2} p^{2} } \right)}}} \right]\left\{ \begin{gathered} - F_{2} \left( p \right) + \left( {{1 \mathord{\left/ {\vphantom {1 {\chi_{33}^{H} }}} \right. \kern-0pt} {\chi_{33}^{H} }}} \right) \hfill \\ \times \left[ {d_{33} H_{3} \left( p \right) - \left[ {{\gamma \mathord{\left/ {\vphantom {\gamma {{\text{sh}}\left( {\gamma \delta } \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma \delta } \right)}}} \right]\left[ {{\text{ch}}\left( {\gamma \delta } \right)\Xi_{2} \left( p \right) - \Xi_{1} \left( p \right)} \right]} \right] \hfill \\ \end{gathered} \right\}, \hfill \\ \end{gathered} $$

(13)

where $\chi_{33}^{H} = {{s_{33}^{H} } \mathord{\left/ {\vphantom {{s_{33}^{H} } {S_{0} }}} \right. \kern-0pt} {S_{0} }}$.

From (6) for displacing two faces of the actuator, we have the system:

$$ \begin{gathered} \Xi_{1} \left( p \right) = W_{11} \left( p \right)\Psi_{m} \left( p \right) + W_{12} \left( p \right)F_{1} \left( p \right) + W_{13} \left( p \right)F_{2} \left( p \right); \hfill \\ \Xi_{2} \left( p \right) = W_{21} \left( p \right)\Psi_{m} \left( p \right) + W_{22} \left( p \right)F_{1} \left( p \right) + W_{23} \left( p \right)F_{2} \left( p \right), \hfill \\ \end{gathered} $$

(14)

therefore, the matrix equation with the matrix transfer function is determined as

$$ \left( {\begin{array}{*{20}c} {\Xi_{1} \left( p \right)} \\ {\Xi_{2} \left( p \right)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {W_{11} \left( p \right)} & {W_{12} \left( p \right)} & {W_{13} \left( p \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {W_{21} \left( p \right)} & {W_{22} \left( p \right)} & {W_{23} \left( p \right)} \\ \end{array} } \\ \end{array} } \right)\;\left( {\begin{array}{*{20}c} {\Psi_{m} \left( p \right)} \\ {F_{1} \left( p \right)} \\ {F_{2} \left( p \right)} \\ \end{array} } \right), $$

where

$$ W_{11} \left( p \right) = {{\Xi_{1} \left( p \right)} \mathord{\left/ {\vphantom {{\Xi_{1} \left( p \right)} {\Psi_{m} \left( p \right)}}} \right. \kern-0pt} {\Psi_{m} \left( p \right)}} = {{\nu_{mi} \left[ {M_{2} \chi_{ij}^{\Psi } p^{2} + \gamma {\text{th}}\left( {{{\gamma l} \mathord{\left/ {\vphantom {{\gamma l} 2}} \right. \kern-0pt} 2}} \right)} \right]} \mathord{\left/ {\vphantom {{\nu_{mi} \left[ {M_{2} \chi_{ij}^{\Psi } p^{2} + \gamma {\text{th}}\left( {{{\gamma l} \mathord{\left/ {\vphantom {{\gamma l} 2}} \right. \kern-0pt} 2}} \right)} \right]} A}} \right. \kern-0pt} A}_{ij} ;\chi_{ij}^{\Psi } = {{s_{ij}^{\Psi } } \mathord{\left/ {\vphantom {{s_{ij}^{\Psi } } {S_{0} }}} \right. \kern-0pt} {S_{0} }}; $$

$$ A_{ij} = M_{1} M_{2} \left( {\chi_{ij}^{\Psi } } \right)^{2} p^{4} + \left\{ {{{\left( {M_{1} + M_{2} } \right)\chi_{ij}^{\Psi } } \mathord{\left/ {\vphantom {{\left( {M_{1} + M_{2} } \right)\chi_{ij}^{\Psi } } {\left[ {c^{\Psi } {\text{th}}\left( {\gamma l} \right)} \right]^{{}} }}} \right. \kern-0pt} {\left[ {c^{\Psi } {\text{th}}\left( {\gamma l} \right)} \right]^{{}} }}} \right\}p^{3} + \left[ {{{\left( {M_{1} + M_{2} } \right)\chi_{ij}^{\Psi } \alpha } \mathord{\left/ {\vphantom {{\left( {M_{1} + M_{2} } \right)\chi_{ij}^{\Psi } \alpha } {{\text{th}}\left( {\gamma l} \right)}}} \right. \kern-0pt} {{\text{th}}\left( {\gamma l} \right)}} + {1 \mathord{\left/ {\vphantom {1 {\left( {c^{\Psi } } \right)^{2} }}} \right. \kern-0pt} {\left( {c^{\Psi } } \right)^{2} }}} \right]p^{2} + {{2\alpha p} \mathord{\left/ {\vphantom {{2\alpha p} {c^{\Psi } }}} \right. \kern-0pt} {c^{\Psi } }} + \alpha^{2} $$

$$ W_{21} \left( p \right) = {{\Xi_{2} \left( p \right)} \mathord{\left/ {\vphantom {{\Xi_{2} \left( p \right)} {\Psi_{m} \left( p \right)}}} \right. \kern-0pt} {\Psi_{m} \left( p \right)}} = {{\nu_{mi} \left[ {M_{1} \chi_{ij}^{\Psi } p^{2} + \gamma {\text{th}}\left( {{{\gamma l} \mathord{\left/ {\vphantom {{\gamma l} 2}} \right. \kern-0pt} 2}} \right)} \right]} \mathord{\left/ {\vphantom {{\nu_{mi} \left[ {M_{1} \chi_{ij}^{\Psi } p^{2} + \gamma {\text{th}}\left( {{{\gamma l} \mathord{\left/ {\vphantom {{\gamma l} 2}} \right. \kern-0pt} 2}} \right)} \right]} A}} \right. \kern-0pt} A}_{ij} ; $$

$$ W_{12} \left( p \right) = {{\Xi_{1} \left( p \right)} \mathord{\left/ {\vphantom {{\Xi_{1} \left( p \right)} {F_{1} \left( p \right)}}} \right. \kern-0pt} {F_{1} \left( p \right)}} = - {{\chi_{ij}^{\Psi } \left[ {M_{2} \chi_{ij}^{\Psi } p^{2} + {\gamma \mathord{\left/ {\vphantom {\gamma {{\text{th}}\left( {\gamma l} \right)}}} \right. \kern-0pt} {{\text{th}}\left( {\gamma l} \right)}}} \right]} \mathord{\left/ {\vphantom {{\chi_{ij}^{\Psi } \left[ {M_{2} \chi_{ij}^{\Psi } p^{2} + {\gamma \mathord{\left/ {\vphantom {\gamma {{\text{th}}\left( {\gamma l} \right)}}} \right. \kern-0pt} {{\text{th}}\left( {\gamma l} \right)}}} \right]} A}} \right. \kern-0pt} A}_{ij} ; $$

$$ W_{13} \left( p \right) = {{\Xi_{1} \left( p \right)} \mathord{\left/ {\vphantom {{\Xi_{1} \left( p \right)} {F_{2} \left( p \right)}}} \right. \kern-0pt} {F_{2} \left( p \right)}} = W_{22} \left( p \right) = {{\Xi_{2} \left( p \right)} \mathord{\left/ {\vphantom {{\Xi_{2} \left( p \right)} {F_{1} \left( p \right)}}} \right. \kern-0pt} {F_{1} \left( p \right)}} = {{\left[ {{{\chi_{ij}^{\Psi } \gamma } \mathord{\left/ {\vphantom {{\chi_{ij}^{\Psi } \gamma } {{\text{sh}}\left( {\gamma l} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma l} \right)}}} \right]} \mathord{\left/ {\vphantom {{\left[ {{{\chi_{ij}^{\Psi } \gamma } \mathord{\left/ {\vphantom {{\chi_{ij}^{\Psi } \gamma } {{\text{sh}}\left( {\gamma l} \right)}}} \right. \kern-0pt} {{\text{sh}}\left( {\gamma l} \right)}}} \right]} A}} \right. \kern-0pt} A}_{ij} ; $$

$$ W_{23} \left( p \right) = {{\Xi_{2} \left( p \right)} \mathord{\left/ {\vphantom {{\Xi_{2} \left( p \right)} {F_{2} \left( p \right)}}} \right. \kern-0pt} {F_{2} \left( p \right)}} = - {{\chi_{ij}^{\Psi } \left[ {M_{1} \chi_{ij}^{\Psi } p^{2} + {\gamma \mathord{\left/ {\vphantom {\gamma {{\text{th}}\left( {\gamma l} \right)}}} \right. \kern-0pt} {{\text{th}}\left( {\gamma l} \right)}}} \right]} \mathord{\left/ {\vphantom {{\chi_{ij}^{\Psi } \left[ {M_{1} \chi_{ij}^{\Psi } p^{2} + {\gamma \mathord{\left/ {\vphantom {\gamma {{\text{th}}\left( {\gamma l} \right)}}} \right. \kern-0pt} {{\text{th}}\left( {\gamma l} \right)}}} \right]} A}} \right. \kern-0pt} A}_{ij} . $$

From (14), the displacements of the faces of an electromagnetoelastic actuator at inertial load are obtained in the stationary regime. The static displacements of the faces $\xi_{1} \left( \infty \right)$ and $\xi_{2} \left( \infty \right)$ of the electromagnetoelastic actuator are written in the form:

$$ \xi_{1} \left( \infty \right) = \mathop {{\text{lim}}}\limits_{t \to \infty } \xi_{1} \left( t \right) = \mathop {{\text{lim}}}\limits_{{\begin{array}{*{20}c} {p \to 0} \\ {\alpha \to 0} \\ \end{array} }} pW_{11} \left( p \right){{\Psi_{m0} } \mathord{\left/ {\vphantom {{\Psi_{m0} } p}} \right. \kern-0pt} p} = \nu_{mi} l\Psi_{m0} {{\left( {M_{2} + {m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0pt} 2}} \right)} \mathord{\left/ {\vphantom {{\left( {M_{2} + {m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0pt} 2}} \right)} {\left( {M_{1} + M_{2} + m} \right)}}} \right. \kern-0pt} {\left( {M_{1} + M_{2} + m} \right)}}, $$

(15)

$$ \xi_{2} \left( \infty \right) = \mathop {{\text{lim}}}\limits_{t \to \infty } \xi_{2} \left( t \right) = \mathop {{\text{lim}}}\limits_{{\begin{array}{*{20}c} {p \to 0} \\ {\alpha \to 0} \\ \end{array} }} pW_{21} \left( p \right){{\Psi_{m0} } \mathord{\left/ {\vphantom {{\Psi_{m0} } p}} \right. \kern-0pt} p} = \nu_{mi} l\Psi_{m0} {{\left( {M_{1} + {m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0pt} 2}} \right)} \mathord{\left/ {\vphantom {{\left( {M_{1} + {m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0pt} 2}} \right)} {\left( {M_{1} + M_{2} + m} \right)}}} \right. \kern-0pt} {\left( {M_{1} + M_{2} + m} \right)}}, $$

(16)

$$ \xi_{1} \left( \infty \right) + \xi_{2} \left( \infty \right) = \mathop {{\text{lim}}}\limits_{t \to \infty } \left( {\xi_{1} \left( t \right) + \xi_{2} \left( t \right)} \right) = \nu_{mi} l\Psi_{m0} , $$

(17)

where $m,{M}_{1},\hspace{0.33em}{M}_{2}$ are the masses of the actuator and loads.

For the piezo actuator from PZT, at $m < < M_{1}$ and $m < < M_{2}$; $d_{33} = 4 \cdot 10^{ - 10}$ m/V, $U = 100$ V, $M_{1} = 1$ kg and $M_{2} = 4$ kg, we obtain the static displacements of the faces of the piezo actuator $\xi_{1} \left( \infty \right) = 32$ nm, $\xi_{2} \left( \infty \right) = 8$ nm, $\xi_{1} \left( \infty \right) + \xi_{2} \left( \infty \right) = 40$ nm.

3 Results and Discussion

Let us consider the structural scheme of the piezo actuator at voltage control $0 < R < \infty$ [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] with negative feedback from direct piezo effect. The electromechanical coupling coefficient [8] of the piezo actuator has the form:

$$ k_{mi} = {{d_{mi} } \mathord{\left/ {\vphantom {{d_{mi} } {\sqrt {s_{ij}^{E} \varepsilon_{mk}^{T} } }}} \right. \kern-0pt} {\sqrt {s_{ij}^{E} \varepsilon_{mk}^{T} } }}. $$

(18)

The elastic compliance [8] at $D = {\text{const}}$ is determined as

$$ s_{ij}^{D} = \left( {1 - k_{mi}^{2} } \right)s_{ij}^{E} . $$

For the piezo actuator with current source $\left. {k_{u} } \right|_{R \to \infty } = 1$ at $R = \infty$ and with voltage source $\left. {k_{u} } \right|_{R \to 0} = 0$ at $R = 0$, then in general, the elastic compliance at voltage control $0 < R < \infty$ [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] in Fig. 9 has the form:

$$ \begin{gathered} s_{ij} = \left( {1 - k_{mi}^{2} k_{u} } \right)s_{ij}^{E} = k_{s} s_{ij}^{E} , \hfill \\ k_{s} = 1 - k_{mi}^{2} k_{u} ,\,\left. {\left( {1 - k_{mi}^{2} } \right)} \right|_{R \to \infty } \le k_{s} \le \left. 1 \right|_{R \to 0} , \hfill \\ \left. {k_{s} } \right|_{R \to \infty } = 1 - k_{mi}^{2} \,{\text{for}}\,\left. {k_{u} } \right|_{R \to \infty } = 1\,\left. {k_{s} } \right|_{R \to 0} = 1\,{\text{for}}\,\left. {k_{u} } \right|_{R \to 0} = 0, \hfill \\ \end{gathered} $$

(19)

where $k_{u}$ is the coefficient of control from the electric power source and $k_{s}$ is the coefficient of the change of elastic compliance.

For the counter electromotive force from the direct piezo effect in the structural scheme of the piezo actuator in Fig. 9, it is supplemented with negative feedback:

$$ U_{{\dot{\Xi }a}} \left( p \right) = \frac{{d_{mi} S_{0} R}}{{\delta s_{ij} }}\mathop \Xi \limits^{ \bullet }_{a} \left( p \right),\,a = 1,\;2. $$

(20)

For the piezo actuator at one rigidly fixed face and elastic-inertial load we have structural scheme with distributed parameters in Fig. 10.

From Fig. 11, we get the structural scheme of the piezoactuator in Fig. 10 with the coefficient $k_{d}$ for direct piezo effect and the coefficient $k_{r}$ for the reverse piezo effect in the form:

$$ k_{d} = k_{r} = \frac{{d_{mi} S_{0} }}{{\delta s_{ij} }}. $$

(21)

Fig. 9.

Structural scheme of piezo actuator at voltage control with negative feedbacks.

Fig. 10.

Structural scheme for distributed parameters of piezo actuator at fixed one face.

Fig. 11.

Structural scheme for lumped parameters of piezo actuator at fixed one face and elastic-inertial load.

At $R = 0$, the transfer function of the transverse piezo actuator has the form:

$$ \begin{gathered} W\left( p \right) = \frac{{\Xi_{2} \left( p \right)}}{U\left( p \right)} = \frac{{d_{31} {h \mathord{\left/ {\vphantom {h \delta }} \right. \kern-0pt} \delta }}}{{\left( {1 + {{C_{e} } \mathord{\left/ {\vphantom {{C_{e} } {C_{11}^{E} }}} \right. \kern-0pt} {C_{11}^{E} }}} \right)_{{}}^{{}} \left( {T_{t}^{2} p^{2} + 2T_{t} \xi_{t} p + 1} \right)}}, \hfill \\ T_{t} = \sqrt {{{M_{2} } \mathord{\left/ {\vphantom {{M_{2} } {\left( {C{}_{e} + C_{11}^{E} } \right)}}} \right. \kern-0pt} {\left( {C{}_{e} + C_{11}^{E} } \right)}}} ,\,\xi_{t} = {{\alpha h^{2} C_{11}^{E} } \mathord{\left/ {\vphantom {{\alpha h^{2} C_{11}^{E} } {\left( {3c^{E} \sqrt {M\left( {C_{e} + C_{11}^{E} } \right)} } \right)}}} \right. \kern-0pt} {\left( {3c^{E} \sqrt {M\left( {C_{e} + C_{11}^{E} } \right)} } \right)}},\,C_{11}^{E} = {{S_{0} } \mathord{\left/ {\vphantom {{S_{0} } {\left( {s_{11}^{E} h} \right)}}} \right. \kern-0pt} {\left( {s_{11}^{E} h} \right)}} \hfill \\ \end{gathered} $$

(22)

For the piezo actuator from PZT at $M_{1} \to \infty$, $m < < M_{2}$, $U_{0}$ = 100 V at $d_{31}$ = 2.5 × 10^–10 m/V, ${h \mathord{\left/ {\vphantom {h \delta }} \right. \kern-0pt} \delta }$ = 20, $M_{2}$ = 1 kg, $C_{11}^{E}$ = 1.4 × 10⁷ N/m and $C_{e}$ = 0.2 × 10⁷ N/m, we get $\xi_{0}$ = 438 nm and $T_{t}$ = 0.25 × 10^–3 s with an accuracy of 5%.

The maximum displacement $\xi_{2m}$ and the maximum force $F_{2m}$ in Fig. 12 for the piezo actuator with one fixed face are obtained in the form:

$$ \xi_{2m} = d_{33} U_{m} , $$

(23)

$$ F_{2m} = \frac{{d_{33} U_{m} S_{0} }}{{s_{33}^{E} \delta }}. $$

(24)

At $d_{33}$ = 4 × 10^–10 m/V, $\delta$ = 6 × 10^–4 m, $S_{0}$ = 1.8 × 10^–4 m², $s_{33}^{E}$ = 3 × 10^–11 m²/N, $U_{m}$ = 50 V, we have in Fig. 11 maximum displacement ${\upxi }_{2m}$ = 20 nm and maximum force $F_{2m}$ = 200 N with an accuracy of 5%.

Fig. 12.

Characteristic longitudinal piezo actuator.

The measurements of the characteristics and the parameters of the piezo actuator were made on UMM-5 press.

4 Conclusion

The structural scheme of an electromagnetoelastic actuator is constructed for nanotechnology research. We obtained structural-parametric model and matrix transfer function for an electromagnetoelastic actuator. We performed numerical and analytical calculation of the characteristics of the piezo actuator. The structural scheme of the piezo actuator with the back electromotive force is obtained. The structural schemes of the piezo actuators are constructed by voltage or current cotrol. The structural schemes are obtained for the transverse, longitudinal, shear piezo effects by voltage or current control. The elastic compliances of the piezo actuators is determined for the control by voltage or current.