Abstract
We study the impact that different ways of resolving nondeterminism within probabilistic automata have on the properties of probabilistic behavioral equivalences. Firstly, we provide a uniform definition of structure-preserving and structure-modifying resolutions of nondeterminism, respectively generated by different families of schedulers. Secondly, we exhibit a number of anomalies arising from the excessive power of the various families of schedulers, which affect the discriminating power, the compositionality, and the backward compatibility of probabilistic trace equivalence. Thirdly, we propose to remove those anomalies by enforcing coherency within resolutions of nondeterminism. This ensures that a scheduler cannot select different continuations in equivalent states of an automaton, so that also the states to which they correspond in any resolution of the automaton have equivalent continuations.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Quantitative models of computing systems describe the order in which activities are executed – possibly admitting nondeterminism in case of concurrency phenomena or to support implementation freedom – and include information about the probabilities or the timing of the activities themselves. A particularly expressive model is given by probabilistic automata [22], as they encompass fully nondeterministic models like labeled transition systems [18], fully probabilistic models like action-labeled variants of discrete-time Markov chains [19], and reactive probabilistic models like Markov decision processes [11].
Behavioral relations play a fundamental role in the analysis of quantitative models. They formalize observational mechanisms that permit relating models that, despite their different representations in the same mathematical domain, cannot be distinguished by external entities when abstracting from details deemed unimportant for specific purposes. Moreover, they support system modeling and verification by providing a means to relate system descriptions expressed at different levels of abstraction, as well as to reduce the size of a system representation while preserving specific properties to be assessed later.
In the case of fully nondeterministic models, from the first comparative work [8] to the elaboration of the full spectrum [13], a number of equivalences have emerged that range from the branching-time – i.e., (bi)simulation-based – endpoint [21] to the linear-time – i.e., trace-based – endpoint [7] passing through testing relations [9]. The spectrum becomes simpler when considering fully probabilistic models [1, 14, 17], whereas as shown in [4] it is much more variegated in the case of models with nondeterminism and probabilities like probabilistic automata. The reason is that the probability of equivalence-specific events can be calculated only after removing nondeterminism. Examples of such events are reaching via given actions certain sets of equivalent states (bisimulation semantics) or executing specific action sequences (trace semantics), with states/traces being possibly decorated with additional information.
In this paper, we study the impact on the discriminating power, the compositionality, and the backward compatibility of behavioral equivalences for nondeterministic and probabilistic models, due to the different ways of resolving nondeterminism. We restrict ourselves to simple probabilistic automata [22], i.e., state-transition graphs where each transition is labeled with an action and goes from a state to a probability distribution over states. In this model, nondeterminism is expressed by the presence of several transitions departing from the same state. A resolution of nondeterminism is obtained by applying a scheduler that decides which activity has to be performed next, where by activity we mean executing a transition or stopping the execution altogether.
The first contribution of this paper is a discussion of different families of schedulers, with the result of providing a uniform way, based on correspondence functions, of defining the resolutions induced by those schedulers.
We divide resolutions into structure preserving and structure modifying, depending on whether they respect or alter the structure of the automaton from which they are obtained. A structure-preserving resolution is produced by a deterministic scheduler, which selects at the current state one of the transitions departing from that state or no transitions at all. A structure-modifying resolution is derived via a randomized scheduler [22], which probabilistically combines the transitions departing from the current state, or an interpolating scheduler [10], which splits the current state into copies, each having at most one outgoing transition, whose probabilities sum up to the probability of the original state. We formalize any resolution as a fully probabilistic automaton, which we equip with a correspondence function from the acyclic state space of the resolution to the possibly cyclic state space of the original automaton, as done for the first time in [15] for deterministic schedulers.
The second contribution of this paper is the presentation of a number of anomalies affecting probabilistic behavioral equivalences, mostly arising under deterministic schedulers, together with a proposal for avoiding them based on limiting the excessive power of schedulers.
We focus on probabilistic trace equivalence by showing that it does not contain probabilistic bisimilarity, it is not a congruence with respect to action prefix, and it is not backward compatible with its version for fully probabilistic models. The reason is that schedulers have the freedom to make different decisions in equivalent states occurring in the target distribution of a transition, with these decisions being not necessarily replicable in equivalent distributions of distinct automata. This is especially true for deterministic schedulers, as the resolutions they induce must be structure preserving.
Such anomalies can be avoided by employing coherent resolutions in the definition of probabilistic trace equivalence. The idea is that, if several states in the target distribution of a transition are equivalent, then the states to which they correspond in a resolution must be equivalent as well. This constraint can be formalized by reasoning on trace distributions, i.e., families of sets of traces each endowed with its execution probability in a given resolution.
This paper is organized as follows. In Sect. 2, we recall simple probabilistic automata. In Sect. 3, we discuss different notions of resolution usable in probabilistic behavioral equivalences and provide a uniform way of defining all of them. In Sect. 4, we illustrate the aforementioned anomalies of probabilistic trace equivalence caused by the excessive power of schedulers. In Sect. 5, we show how to avoid those anomalies by forcing resolutions to be coherent. Finally, in Sect. 6 we present some concluding remarks.
2 Nondeterministic and Probabilistic Models
We formalize systems featuring nondeterminism and probabilities through a variant of simple probabilistic automata [22], in which we do not distinguish between external and internal actions.
Definition 1
A nondeterministic and probabilistic labeled transition system, NPLTS for short, is a triple \((S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\) where \(S \ne \emptyset \) is an at most countable set of states, \(A \ne \emptyset \) is a countable set of transition-labeling actions, and \( \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \! \subseteq S \times A \times Distr (S)\) is a transition relation with \( Distr (S)\) being the set of discrete probability distributions over S. \(\blacksquare \)
A transition \((s, a, \varDelta )\) is written \(s \, {\mathop {\longrightarrow }\limits ^{a}}_{} \, \varDelta \). We say that \(s' \in S\) is not reachable from s via that a-transition if \(\varDelta (s') = 0\), otherwise we say that it is reachable with probability \(p = \varDelta (s')\). The reachable states form the support of \(\varDelta \), i.e., \( supp (\varDelta ) = \{ s' \in S \mid \varDelta (s') > 0 \}\). An NPLTS can be depicted as a directed graph in which vertices represent states and action-labeled edges represent transitions, with states in the same support being linked by a dashed line and decorated with the respective probabilities (see the forthcoming Figs. 1, 2, 3, 4, 5, 6, 7, 8 and 9).
An NPLTS represents (i) a fully nondeterministic process when every transition has a target distribution with a singleton support, (ii) a fully probabilistic process when every state has at most one outgoing transition, or (iii) a Markov decision process when for each action any state has at most one outgoing transition labeled with that action implying the absence of internal nondeterminism.
Definition 2
Let \(\mathcal {L}= (S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\) be an NPLTS and \(s, s' \in S\). We say that the finite sequence:

is a computation of \(\mathcal {L}\) of length \(n \in \mathbb {N}\) from \(s = s_{0}\) to \(s' = s_{n}\) compatible with trace \(\alpha = a_{1} \, a_{2} \dots a_{n} \in A^{*}\), written \(c \in \mathcal {CC}(s, \alpha )\), iff for all \(i = 1, \dots , n\) there exists in \(\mathcal {L}\) a transition \(s_{i - 1} \, {\mathop {\longrightarrow }\limits ^{a_{i}}}_{} \, \varDelta _{i}\) such that \(s_{i} \in supp (\varDelta _{i})\), with:
-
\(\varDelta _{i}(s_{i})\) being the execution probability of step
 conditioned on the selection of transition \(s_{i - 1} \, {\mathop {\longrightarrow }\limits ^{a_{i}}}_{} \, \varDelta _{i}\) at state \(s_{i - 1}\), or simply the execution probability of that step if \(\mathcal {L}\) is fully probabilistic;
conditioned on the selection of transition \(s_{i - 1} \, {\mathop {\longrightarrow }\limits ^{a_{i}}}_{} \, \varDelta _{i}\) at state \(s_{i - 1}\), or simply the execution probability of that step if \(\mathcal {L}\) is fully probabilistic; -
\( prob (c) = \prod _{1 \le i \le n} \varDelta _{i}(s_{i})\) being the execution probability of c if \(\mathcal {L}\) is fully probabilistic, assuming that \( prob (c) = 1\) when \(n = 0\);
-
\( prob (C) = \sum _{c \in C} prob (c)\) if \(\mathcal {L}\) is fully probabilistic, provided that none of the computations in C is a proper prefix of one of the others. \(\blacksquare \)
3 An Overview of Resolutions of Nondeterminism
When several transitions depart from the same state s of an NPLTS \(\mathcal {L}\), they describe a nondeterministic choice among different behaviors. Eliminating these choices is necessary to perform the calculations required by probabilistic behavioral equivalences. A resolution of s is the result of a possible way of resolving nondeterministic choices starting from s, as if a scheduler were applied that decides which activity has to be performed next. A resolution of nondeterminism can thus be formalized as a fully probabilistic NPLTS \(\mathcal {Z}\) with a tree-like structure, whose branching points correspond to target distributions of transitions deriving from those of \(\mathcal {L}\).
We now present an overview of various ways of resolving nondeterminism, with the result of providing a uniform technique for defining all of them based on correspondence functions, so to facilitate their comparison. In Sects. 3.1 to 3.3 we address the notions of resolution stemming from two different approaches, respectively preserving or modifying the structure of the original NPLTS. The idea underlying the former approach is to construct a resolution by importing states and transitions from the original model. The idea at the basis of the latter approach is that (i) a transition of a resolution can be produced by probabilistically combining transitions of the original model, or (ii) a state of a resolution can be obtained by probabilistically splitting states of the original model.
3.1 Structure-Preserving Resolutions via Deterministic Schedulers
A deterministic scheduler selects one of the transitions departing from the current state or no transitions at all thus stopping the execution. As a consequence, the resulting resolution is isomorphic to a submodel of the original model (or of its unfolding, should cycles be present), thereby preserving the structure of the original model (or of its unfolding). If the model is fully nondeterministic, each of its resolutions coincides with a computation of the model; if the model is fully probabilistic, its maximal resolution coincides with the entire model.
In [26] a resolution was defined as a maximal subtree of the unfolding of the considered model – with the unfolding yielding a potentially infinite tree – in which every state has at most one outgoing transition. Resolutions were defined as fully probabilistic maximal subtrees also in [16], but the considered models were finite trees in lieu of directed graphs. Subtree maximality was required just because of the focus of those works on testing semantics.
The paper [15], instead of reasoning in terms of unfoldings and submodels, introduced for the first time a correspondence function  from the acyclic state space of the resolution \(\mathcal {Z}= (Z, A, \, {\mathop {\longrightarrow }\limits ^{}}_{\mathcal {Z}} \, \!)\) being built, to the possibly cyclic state space of the considered model \(\mathcal {L}= (S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\). This function had to satisfy the following constraint on transitions: if \(z \, {\mathop {\longrightarrow }\limits ^{a}}_{\mathcal {Z}} \, \varDelta \) then
from the acyclic state space of the resolution \(\mathcal {Z}= (Z, A, \, {\mathop {\longrightarrow }\limits ^{}}_{\mathcal {Z}} \, \!)\) being built, to the possibly cyclic state space of the considered model \(\mathcal {L}= (S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\). This function had to satisfy the following constraint on transitions: if \(z \, {\mathop {\longrightarrow }\limits ^{a}}_{\mathcal {Z}} \, \varDelta \) then  , with
, with  for all \(z' \in supp (\varDelta )\).
for all \(z' \in supp (\varDelta )\).
The correspondence function with its constraint as defined in [15] and reused in [3, 4] has the drawback of not being structure preserving in the case that the target distribution of a transition assigns the same probability to several inequivalent states. Let us see for instance the three NPLTS models in Fig. 1. The correspondence function that maps z to s, \(z'_{1}\) and \(z'_{2}\) to \(s'_{1}\), and \(z''_{1}\) and \(z''_{2}\) to \(s''_{1}\) causes the central NPLTS to be considered a legal resolution of the leftmost NPLTS, although the former is not isomorphic to any submodel of the latter. This may have no consequences on the discriminating power of testing equivalences, the subject of [15], if all transitions of testing systems are identically labeled. However, it would lead to consider the leftmost NPLTS and the rightmost NPLTS as trace equivalent, because also the leftmost one would have a resolution in which trace \(a \, b\) (resp. trace \(a \, c\)) is executable with probability 1.
The constraint was rectified in [5] by requiring the injectivity of  over \( supp (\varDelta )\), so that in Fig. 1 \(z'_{1}\) and \(z'_{2}\) can no longer be both mapped to \(s'_{1}\). We also point out that in [2] it was further observed that bijectivity between \( supp (\varDelta )\) and \( supp (\varGamma )\), rather than injectivity, is necessary to preserve the overall reachability mass in more general settings like the ULTraS metamodel where, unlike the probabilistic case, there is no predefined value like 1 for the reachability mass of the target of a transition.
over \( supp (\varDelta )\), so that in Fig. 1 \(z'_{1}\) and \(z'_{2}\) can no longer be both mapped to \(s'_{1}\). We also point out that in [2] it was further observed that bijectivity between \( supp (\varDelta )\) and \( supp (\varGamma )\), rather than injectivity, is necessary to preserve the overall reachability mass in more general settings like the ULTraS metamodel where, unlike the probabilistic case, there is no predefined value like 1 for the reachability mass of the target of a transition.
Below is the rectified definition of [5] in the style of [15], i.e., based on a correspondence function from the acyclic state space of the resolution to the possibly cyclic state space of the considered model.
Definition 3
Let \(\mathcal {L}= (S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\) be an NPLTS and \(s \in S\). An acyclic NPLTS \(\mathcal {Z}= (Z, A, \, {\mathop {\longrightarrow }\limits ^{}}_{\mathcal {Z}} \, \!)\) is a structure-preserving resolution of s, written  , iff there exists a correspondence function
, iff there exists a correspondence function  such that
such that  , for some \(z_{s} \in Z\), and for all \(z \in Z\) it holds that:
, for some \(z_{s} \in Z\), and for all \(z \in Z\) it holds that:
-
If \(z \, {\mathop {\longrightarrow }\limits ^{a}}_{\mathcal {Z}} \, \varDelta \) then
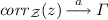 , with
, with 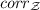 being injective over \( supp (\varDelta )\) and satisfying
being injective over \( supp (\varDelta )\) and satisfying 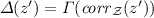 for all \(z' \in supp (\varDelta )\).
for all \(z' \in supp (\varDelta )\). -
At most one transition departs from z. \(\blacksquare \)
3.2 Structure-Modifying Resolutions via Randomization
If the current state has \(n \in \mathbb {N}_{\ge 1}\) outgoing transitions, a randomized scheduler generates \(p_{i} \in \mathbb {R}_{[0, 1]}\) for \(i = 1, \dots , n\) such that \(\sum _{i = 1}^{n} p_{i} \le 1\) and then selects transition i with probability \(p_{i}\) or stops with probability \(1 - \sum _{i = 1}^{n} p_{i}\). A deterministic scheduler is a special case in which \(p_{i} = 1\) for some i or \(p_{i} = 0\) for each i.
Randomized schedulers, proposed in [22] and applied to the definition of probabilistic trace [23] and testing [24] semantics, probabilistically combine transitions of the original model. Therefore, the resulting resolutions are not necessarily isomorphic to submodels of the original model (or of its unfolding) because a modification of the structure of the original model may have taken place. An example of this phenomenon is shown in Fig. 2, where the NPLTS in the leftmost part admits under randomized schedulers the three maximal resolutions depicted next to it in the figure. The resolution starting with \(z_{3}\) is obtained by combining the two a-transitions departing from s with probabilities p and \(1 - p\).
The formalization via a correspondence function of a resolution stemming from a randomized scheduler is not an easy task. The reason is that, according to [22], a combined transition may derive from several differently labeled transitions, as shown in the central part of the forthcoming Fig. 3. In other words, a resolution of a simple probabilistic automaton [22], in which every transition has a single label, may have a transition with several labels, thereby deviating from a simple probabilistic automaton and hence from an NPLTS.
Similar to [3], below we formalize a resolution induced by a variant of randomized scheduler consistent with the definition of probabilistic bisimilarity given in [25] for simple probabilistic automata. At the current state, the scheduler decides to stop or to perform a certain action among the available ones; in the latter case, it takes a convex combination (i.e., the sum of the values \(p_{i}\) is 1) of the outgoing transitions identically labeled with that action. To compensate for the impossibility of combining differently labeled transitions, we admit self-combinations; e.g., in Fig. 3 a combination of the a-transition departing from s with itself n times is able to reproduce the situation in the rightmost part of the same figure, which is equivalent to the one in the central part.
Definition 4
Let \(\mathcal {L}= (S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\) be an NPLTS and \(s \in S\). An acyclic NPLTS \(\mathcal {Z}= (Z, A, \, {\mathop {\longrightarrow }\limits ^{}}_{\mathcal {Z}} \, \!)\) is a structure-modifying resolution via randomization of s, written  , iff there exists a correspondence function
, iff there exists a correspondence function  such that
such that  , for some \(z_{s} \in Z\), and for all \(z \in Z\) it holds that:
, for some \(z_{s} \in Z\), and for all \(z \in Z\) it holds that:
-
If \(z \, {\mathop {\longrightarrow }\limits ^{a}}_{\mathcal {Z}} \, \varDelta \) then there exist \(n \in \mathbb {N}_{\ge 1}\), \(p_{i} \in \mathbb {R}_{]0, 1]}\) for \(1 \le i \le n\) summing up to 1, and
 for \(1 \le i \le n\), with
for \(1 \le i \le n\), with  being injective when considered from \( supp (\varDelta )\) to the disjoint union of the sets \( supp (\varGamma _{i})\) and satisfying
being injective when considered from \( supp (\varDelta )\) to the disjoint union of the sets \( supp (\varGamma _{i})\) and satisfying  for all \(z' \in supp (\varDelta )\).
for all \(z' \in supp (\varDelta )\). -
At most one transition departs from z. \(\blacksquare \)
Injectivity cannot be directly imposed as in Definition 3, otherwise in Fig. 2 the NPLTS model starting with \(z_{3}\) would not be a legal resolution induced by the self-combination of the a-transition departing from \(s'\) in the rightmost part, and hence \(s'\) would not be considered trace equivalent to s in the leftmost part.
3.3 Structure-Modifying Resolutions via Interpolation
For every state in the support of the target distribution of the current transition, an interpolating scheduler splits it into \(n \in \mathbb {N}_{\ge 1}\) copies, each having a single outgoing transition or no transitions at all, to which probabilities are assigned whose sum is the overall probability of the original state, and then selects one of the copies based on its probability. A deterministic scheduler is a special case in which \(n = 1\).
Interpolating schedulers, proposed in [10], probabilistically split states of the original model thereby inducing resolutions possibly modifying the structure of the original model. As mentioned in [10], for each resolution obtained from an interpolating (resp. randomized) scheduler, there exists a resolution obtained from a randomized (resp. interpolating) scheduler with the same trace distribution. This can be seen in Fig. 3, where in the leftmost part we have a state \(s'\) reached with probability p in the target distribution of an a-transition. The resolution in the central part, induced by a randomized scheduler that combines the transitions departing from \(s'\), is equivalent to the resolution in the rightmost part, induced by an interpolating scheduler that splits state \(s'\), where \(\sum _{i = 1}^{n + 1} q_{i} = p\).
Resolutions arising from interpolating schedulers were natively defined in [10] through a correspondence function that maps all split states to the original state from which they derive. Unlike Definitions 3 and 4, the constraint on transitions is formulated with respect to the states in the support of the corresponding transition of the original model – rather than the states in the support of the transition of the resolution – and the preservation of the overall probability associated with each such state makes injectivity requirements unnecessary.
Definition 5
Let \(\mathcal {L}= (S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\) be an NPLTS and \(s \in S\). An acyclic NPLTS \(\mathcal {Z}= (Z, A, \, {\mathop {\longrightarrow }\limits ^{}}_{\mathcal {Z}} \, \!)\) is a structure-modifying resolution via interpolation of s, written  , iff there exists a correspondence function
, iff there exists a correspondence function  such that
such that  , for some \(z_{s} \in Z\), and for all \(z \in Z\) it holds that:
, for some \(z_{s} \in Z\), and for all \(z \in Z\) it holds that:
-
If \(z \, {\mathop {\longrightarrow }\limits ^{a}}_{\mathcal {Z}} \, \varDelta \) then
 , with
, with  satisfying for all \(s \in supp (\varGamma )\)
satisfying for all \(s \in supp (\varGamma )\)  .
. -
At most one transition departs from z. \(\blacksquare \)
A variant of the structure-modifying resolution above has been proposed in [6], which combines the effect of interpolating and randomized schedulers.
4 Consequences of the Excessive Power of Schedulers
Although deterministic schedulers are very intuitive, the rigid preservation they ensure about the structure of the original model, together with their freedom of performing choices inconsistent with each other in states with equivalent continuations, causes the resulting probabilistic trace equivalence to be overdiscriminating, thereby violating certain desirable properties. This also happens, to a much lesser extent, with randomized and interpolating schedulers. In the following, after presenting in Sect. 4.1 the definition of some probabilistic behavioral equivalences, we illustrate in Sect. 4.2 a number of anomalies.
4.1 Equivalences for Nondeterministic and Probabilistic Processes
The spectrum of behavioral equivalences for nondeterministic and probabilistic processes was studied in [4]. Here we focus on the two endpoints of the spectrum by recalling the definitions of bisimulation and trace semantics.
Probabilistic bisimilarity requires that two NPLTS models are able to mimic each other behavior stepwise, in terms of the probability of reaching the same class of equivalent states when executing the same action [20, 25]. Its definition does not need to explicitly resort to resolutions, as these are implicitly built while selecting a single transition from each pair of states.
Definition 6
Let \((S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\) be an NPLTS and \(s_{1}, s_{2} \in S\). We write \(s_{1} \sim _\mathrm{PB} s_{2}\) iff there exists a probabilistic bisimulation \(\mathcal {B}\) over S such that \((s_{1}, s_{2}) \in \mathcal {B}\). An equivalence relation \(\mathcal {B}\) over S is a probabilistic bisimulation iff, whenever \((s_{1}, s_{2}) \in \mathcal {B}\), then for all \(a \in A\) it holds that for each \(s_{1} \, {\mathop {\longrightarrow }\limits ^{a}}_{} \, \varDelta _{1}\) there exists \(s_{2} \, {\mathop {\longrightarrow }\limits ^{a}}_{} \, \varDelta _{2}\) such that for all equivalence classes \(C \in S / \mathcal {B}\):
\(\blacksquare \)
In contrast, trace equivalence requires that two NPLTS models possess the same trace distributions, i.e., the same family of sets of action sequences weighted with their execution probabilities, where each set is related to a specific resolution of nondeterminism [23]. Its definition, which abstracts from branching points of process behavior, explicitly relies on  , with which we denote any of the sets of resolutions introduced in Definitions 3 to 5.
, with which we denote any of the sets of resolutions introduced in Definitions 3 to 5.
Definition 7
Let \((S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\) be an NPLTS and \(s_{1}, s_{2} \in S\). We write \(s_{1} \sim _\mathrm{PTr} s_{2}\) iff for each  there exists
there exists  such that for all traces \(\alpha \in A^{*}\):
such that for all traces \(\alpha \in A^{*}\):
and also the condition obtained by exchanging \(\mathcal {Z}_{1}\) with \(\mathcal {Z}_{2}\) is satisfied. \(\blacksquare \)
4.2 Anomalies and Counterexamples
We now present a number of counterexamples showing that:
-
\(\sim _\mathrm{PTr}\) is not coarser than \(\sim _\mathrm{PB}\) under deterministic schedulers.
-
\(\sim _\mathrm{PTr}\) is not a congruence w.r.t. action prefix under deterministic schedulers.
-
\(\sim _\mathrm{PTr}\) is not backward compatible with its version for fully prob. processes.
Consider the two NPLTS models in the leftmost part of Fig. 4. It holds that \(s_{1} \sim _\mathrm{PB} s_{2}\), but \(s_{1} \not \sim _\mathrm{PTr} s_{2}\) because of the resolution in the central part of Fig. 4, where trace \(a \, b\) is executable with probability p instead of 1. This resolution belongs to  as it does not preserve the structure of the NPLTS whose initial state is \(s_{1}\). Notice that the same resolution belongs to
as it does not preserve the structure of the NPLTS whose initial state is \(s_{1}\). Notice that the same resolution belongs to  , if the a-transition of \(s_{1}\) is combined with itself, and to
, if the a-transition of \(s_{1}\) is combined with itself, and to  , if \(z'_{2}\) and \(z''_{2}\) are both mapped to \(s'_{1}\).
, if \(z'_{2}\) and \(z''_{2}\) are both mapped to \(s'_{1}\).
One may be tempted to admit only maximal resolutions in the definition of probabilistic trace equivalences, but the problem would still be there if a c-transition departed from \(z''_{2}\). Moreover, by so doing, probabilistic trace equivalences would no longer be compatible with trace equivalence. For instance, the former would not identify the two fully nondeterministic, trace equivalent NPLTS models in Fig. 4 whose initial states are \(s_{1}\) and s, because the maximal resolution of s with an a-transition only – featuring traces \(\varepsilon \) and a – is not matched by the two maximal resolutions of \(s_{1}\) – resp. featuring also \(a \, b\) and \(a \, c\).
Let us move to examine the two NPLTS models in the leftmost part of Fig. 5. After the two a-transitions, two distributions are reached that are probabilistic trace equivalent, in the sense that for each class of equivalent states they both assign the same probability to that class. However, it holds that \(s_{3} \not \sim _\mathrm{PTr} s_{4}\) due to the resolution in the rightmost part of Fig. 5, where trace \(a \, a' \, b\) is executable with probability p instead of 1. This resolution belongs to  as it does not preserve the structure of the NPLTS whose initial state is \(s_{4}\). The same resolution belongs to
as it does not preserve the structure of the NPLTS whose initial state is \(s_{4}\). The same resolution belongs to  , if the a-transition of \(s_{4}\) is combined with itself, and to
, if the a-transition of \(s_{4}\) is combined with itself, and to  , if \(z'_{3}\) and \(z''_{3}\) are both mapped to \(s'_{4}\).
, if \(z'_{3}\) and \(z''_{3}\) are both mapped to \(s'_{4}\).
This example reveals that, under deterministic schedulers, probabilistic trace equivalence is not a congruence with respect to the action prefix operator, which concatenates the execution of an action with a process. The difference with trace equivalence for fully nondeterministic processes is that in our setting the continuation after an action is not a single process, but a probability distribution over processes. The problem arises when several equivalent states are in the support of the same distribution, as in the target distribution of the a-transition of \(s_{3}\), thereby allowing schedulers to act inconsistently.
We finally study the two NPLTS models in the leftmost part of Fig. 6. They are identified by the trace equivalence for fully probabilistic processes of [17], which does not use schedulers as in those processes there are no nondeterministic choices to be solved. However, it turns out that \(s_{5} \not \sim _\mathrm{PTr} s_{6}\) because \(\sim _\mathrm{PTr}\) does make use of schedulers, in particular their capability of stopping the execution. This is witnessed by the resolution in the rightmost part of Fig. 6, where not only trace \(a \, b \, c_{1}\) but also trace \(a \, b\) is executable with probability p. This resolution belongs only to  as it does not preserve the structure of the NPLTS whose initial state is \(s_{5}\). It does not even belong to
as it does not preserve the structure of the NPLTS whose initial state is \(s_{5}\). It does not even belong to  because in the NPLTS starting with \(s_{5}\), after performing the a-transition and the b-transition, the \(c_{1}\)-transition can be executed with probability p, while the \(c_{1}\)-transition in the resolution can be executed with probability 1 and hence its source state cannot be mapped to the source state of the former \(c_{1}\)-transition.
because in the NPLTS starting with \(s_{5}\), after performing the a-transition and the b-transition, the \(c_{1}\)-transition can be executed with probability p, while the \(c_{1}\)-transition in the resolution can be executed with probability 1 and hence its source state cannot be mapped to the source state of the former \(c_{1}\)-transition.
This further example highlights that schedulers inducing structure-modifying resolutions are not exempt from shortcomings despite their greater flexibility. The considered resolution would be ruled out by imposing maximality but, as we have seen at the beginning of this section, that may generate other anomalies.
5 Anomaly Avoidance via Coherent Resolutions
The anomalies shown in Figs. 4, 5 and 6 are due to the freedom of schedulers of making different decisions in equivalent states and cause probabilistic trace equivalence to be overdiscriminating. We thus propose to limit the excessive power of schedulers by restricting them to yield coherent resolutions. This means that, if several states in the support of the target distribution of a transition are equivalent, then the decisions made by the scheduler in those states have to be coherent with each other, so that the states to which they correspond in any resolution are equivalent as well. The coherency constraint implementing this idea will be expressed by reasoning on coherent trace distributions, i.e., families of sets of traces weighted with their execution probabilities in a given resolution, built through the following operations.
Definition 8
Let \(A \ne \emptyset \) be a countable set. For \(a \in A\), \(p \in \mathbb {R}\),  , and \(T \subseteq A^{*} \times \mathbb {R}\) we define:
, and \(T \subseteq A^{*} \times \mathbb {R}\) we define:

while for  we define:
we define:

where for \(T_{1}, T_{2} \subseteq A^{*} \times \mathbb {R}\) we define:

\(\blacksquare \)
Weighted trace set addition is commutative and associative. In the definition of \(T_{1} + T_{2}\), which is inspired by [3], probabilities of identical traces in the two summands are always added up for coherency purposes. Before Definition 3.5 of [3], the definition of \(X + Y\), i.e., \(T_{1} + T_{2}\), should have included \((\alpha , q) \in X \cup Y\) in the sum anyhow, otherwise the right-to-left implication in Lemma 3.7 of [3] cannot hold as can be seen from trace \(a \, b\) of the (incoherent) resolution in the central part of Fig. 4 of this paper; that definition of \(X + Y\) works here instead, because of the focus on coherency.
Trace distribution addition is only commutative. Intuitively, the two summands in  represent two families of sets of weighted traces executable in the resolutions of two states in the support of a target distribution. Every weighted trace set
represent two families of sets of weighted traces executable in the resolutions of two states in the support of a target distribution. Every weighted trace set  is summed with every weighted trace set
is summed with every weighted trace set  – so to characterize an overall resolution – unless
– so to characterize an overall resolution – unless  and
and  have the same family of trace sets, in which case summation is restricted to weighted trace sets featuring the same traces for the sake of coherency. In the definition below, the double summation ensures that trace distributions
have the same family of trace sets, in which case summation is restricted to weighted trace sets featuring the same traces for the sake of coherency. In the definition below, the double summation ensures that trace distributions  exhibiting the same family \(\varTheta \) of trace sets will be summed up first.
exhibiting the same family \(\varTheta \) of trace sets will be summed up first.
Definition 9
Let \(\mathcal {L}= (S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\) be an NPLTS and \(s \in S\). The coherent trace distribution of s is the subset of \(2^{A^{*} \times \mathbb {R}_{]0, 1]}}\) defined as follows:

where the coherent trace distribution of s whose traces have length at most n is defined as:

for  and
and  . \(\blacksquare \)
. \(\blacksquare \)
Let us reconsider the three counterexamples of Sect. 4 plus two more:
-
In Fig. 4 we have
 – from which
– from which  follows – but in the resolution
follows – but in the resolution  .
. -
In Fig. 5 we have
 whereas in the resolution
whereas in the resolution  .
. -
In Fig. 6 we have
 . However,
. However,  while in the resolution
while in the resolution  . This shows that we should set up separate coherency constraints relying on
. This shows that we should set up separate coherency constraints relying on  sets for every \(n \in \mathbb {N}\).
sets for every \(n \in \mathbb {N}\). -
Consider the two fully probabilistic NPLTS models in the leftmost part of Fig. 7. They are identified by the trace equivalence of [17], but \(s_{7} \not \sim _\mathrm{PTr} s_{8}\) due to the resolution in the rightmost part of the same figure. It holds that
 , with
, with  . However, we observe that
. However, we observe that 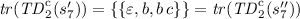 whereas
whereas  . This indicates that the coherency constraints should rely on
. This indicates that the coherency constraints should rely on  sets up to the probabilities they contain, i.e., the coherency constraints should rely on
sets up to the probabilities they contain, i.e., the coherency constraints should rely on  sets.
sets. -
The violations in Figs. 6 and 7 of backward compatibility with the trace equivalence of [17] have a twofold interpretation. The former is that incoherent selections are made by the scheduler in states having the same traces of a certain length. The latter ascribes the lack of coherency to the fact that, in both resolutions depicted in those figures, the scheduler proceeds by selecting a transition along one direction while it stops the execution along the other direction. This is even more evident with the two fully probabilistic NPLTS models in the leftmost part of Fig. 8, which are identified by [17] but told apart by the resolution on the right, where \(a \, b \, c_{1}\) is executable with probability 0.25, as
 ,
,  , and
, and  are pairwise different. In every coherent resolution of \(s_{9}\), trace \(a \, b \, c_{1}\) can be executed only with probability 0.5. This calls for a complete presence of computations of the same length in each resolution – including shorter maximal computations if any – which is different from requiring resolution maximality.
are pairwise different. In every coherent resolution of \(s_{9}\), trace \(a \, b \, c_{1}\) can be executed only with probability 0.5. This calls for a complete presence of computations of the same length in each resolution – including shorter maximal computations if any – which is different from requiring resolution maximality.
Definition 10
Let \(\mathcal {L}= (S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\) be an NPLTS, \(s \in S\), and  with correspondence function
with correspondence function  . We say that \(\mathcal {Z}\) is a coherent resolution of s, written
. We say that \(\mathcal {Z}\) is a coherent resolution of s, written  , iff for all \(z \in Z\), whenever \(z \, {\mathop {\longrightarrow }\limits ^{a}}_{\mathcal {Z}} \, \varDelta \), then for all \(n \in \mathbb {N}\):
, iff for all \(z \in Z\), whenever \(z \, {\mathop {\longrightarrow }\limits ^{a}}_{\mathcal {Z}} \, \varDelta \), then for all \(n \in \mathbb {N}\):
-
1.
 for all \(z', z'' \in supp (\varDelta )\).
for all \(z', z'' \in supp (\varDelta )\). -
2.
If there exists \(z' \in supp (\varDelta )\) such that
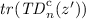 contains traces of length n, then for all \(z'' \in supp (\varDelta )\) either
contains traces of length n, then for all \(z'' \in supp (\varDelta )\) either  contains traces of length n too, or any \(\alpha \in A^{*}\) occurring in
contains traces of length n too, or any \(\alpha \in A^{*}\) occurring in  has length less than n but there exists a maximal trace in
has length less than n but there exists a maximal trace in  corresponding to \(\alpha \). \(\blacksquare \)
corresponding to \(\alpha \). \(\blacksquare \)
In the definition above,  denotes any of the sets of resolutions introduced in Definitions 3 to 5. From now on, we focus on
denotes any of the sets of resolutions introduced in Definitions 3 to 5. From now on, we focus on  . Notice that the resolutions in Figs. 4 to 8 do not respectively belong to
. Notice that the resolutions in Figs. 4 to 8 do not respectively belong to  ,
,  ,
,  ,
,  , and
, and  .
.
We conclude by proving that probabilistic trace equivalence no longer suffers from the anomalies illustrated in Sect. 4 when using coherent resolutions induced by deterministic schedulers. In the following, we lift a probabilistic behavioral equivalence \(\sim _{}\) from states to distributions over states by letting \(\varDelta _{1} \sim _{} \varDelta _{2}\) iff \(\varDelta _{1}(C) = \varDelta _{2}(C)\) for all equivalence classes C of \(\sim _{}\). Moreover, the action prefix construction \(a \, . \, \varDelta \) stands for an a-transition whose target distribution is \(\varDelta \), whereas \(\sim _\mathrm{PTr}^\mathrm{fp}\) denotes the probabilistic trace equivalence for fully probabilistic processes defined in [17] by letting \(s_{1} \sim _\mathrm{PTr}^\mathrm{fp} s_{2}\) iff \( prob (\mathcal {CC}(s_{1}, \alpha )) = prob (\mathcal {CC}(s_{2}, \alpha ))\) for all \(\alpha \in A^{*}\).
We point out that coherency was unfortunately neglected in [3, 4]. In particular, property 1 below is the rectified version of a chain of results in [4] consisting of Thms. 6.5(2), 5.9(3), 4.5(2) and property 3 below is the rectified version of Thm. 3.4(2) of [3, 4]; deterministic schedulers were considered in all those theorems. Property 3 now holds also in the case of randomized/interpolating schedulers by just imposing condition 2 of Definition 10.
Theorem 1
Let \(\mathcal {L}= (S, A, \! \, {\mathop {\longrightarrow }\limits ^{}}_{} \, \!)\) be an NPLTS, \(s_{1}, s_{2} \in S\), \(\varDelta _{1}, \varDelta _{2} \in Distr (S)\). Under coherent resolutions induced by deterministic schedulers it holds that:
-
1.
\(s_{1} \sim _\mathrm{PB} s_{2} \, \Longrightarrow \, s_{1} \sim _\mathrm{PTr} s_{2}\).
-
2.
\(\varDelta _{1} \sim _\mathrm{PTr} \varDelta _{2} \, \Longrightarrow \, a \, . \, \varDelta _{1} \sim _\mathrm{PTr} a \, . \, \varDelta _{2}\) for all \(a \in A\).
-
3.
If \(\mathcal {L}\) is fully probabilistic, then \(s_{1} \sim _\mathrm{PTr} s_{2} \, \Longleftrightarrow \, s_{1} \sim _\mathrm{PTr}^\mathrm{fp} s_{2}\). \(\blacksquare \)
We finally observe that looser coherency constraints, based on weighted trace sets rather than trace distributions as in Definition 10, would not work. Similar to  in Definition 9, one may define \(T^\mathrm{c}(s)\) by considering all weighted traces executable from s at once – i.e., without keeping track of the resolutions in which they are feasible – and use it for coherency purposes, but then probabilistic trace equivalent NPLTS models like the ones in Fig. 9 would be told apart. Indeed, we would have
in Definition 9, one may define \(T^\mathrm{c}(s)\) by considering all weighted traces executable from s at once – i.e., without keeping track of the resolutions in which they are feasible – and use it for coherency purposes, but then probabilistic trace equivalent NPLTS models like the ones in Fig. 9 would be told apart. Indeed, we would have  – whereas
– whereas  – hence in any coherent resolution of \(s'\) traces \(a \, b \, c_{1}\), \(a \, b \, c_{2}\), \(a \, b \, c\) could only be executed with probability 0.5 if present, while \(s''\) admits coherent resolutions in which those traces have execution probability 0.25.
– hence in any coherent resolution of \(s'\) traces \(a \, b \, c_{1}\), \(a \, b \, c_{2}\), \(a \, b \, c\) could only be executed with probability 0.5 if present, while \(s''\) admits coherent resolutions in which those traces have execution probability 0.25.
6 Conclusions
To guarantee a number of desirable properties for probabilistic trace equivalence over probabilistic automata, we have proposed a set of coherency constraints as a solution to the problem – addressed also in [12] for a different probabilistic model and equivalence – of limiting the excessive power of schedulers.
The highlighted anomalies mostly have to do with structure-preserving resolutions generated by deterministic schedulers, so one may wonder why not to avoid those schedulers altogether. The first reason is that, as shown in [4], the use of a specific family of schedulers has an impact on the discriminating power of behavioral equivalences, so there might be situations in which considering deterministic schedulers is more appropriate. The second reason is that, as witnessed by Fig. 6, some of the examined anomalies affect also equivalences defined on structure-modifying resolutions generated by randomized/interpolating schedulers. The third reason is that in more general frameworks, like the ULTraS metamodel [2] of which probabilistic automata are an instance, the applicability of deterministic schedulers is always possible, while this might not be the case for other families of schedulers.
References
Baier, C., Katoen, J.-P., Hermanns, H., Wolf, V.: Comparative branching-time semantics for Markov chains. Inf. Comput. 200, 149–214 (2005)
Bernardo, M.: Genesis and evolution of ULTraS: metamodel, metaequivalences, metaresults. In: Boreale, M., Corradini, F., Loreti, M., Pugliese, R. (eds.) Models, Languages, and Tools for Concurrent and Distributed Programming. LNCS, vol. 11665, pp. 92–111. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-21485-2_7
Bernardo, M., De Nicola, R., Loreti, M.: Revisiting trace and testing equivalences for nondeterministic and probabilistic processes. Logical Methods Comput. Sci. 10(1:16), 1–42 (2014)
Bernardo, M., De Nicola, R., Loreti, M.: Relating strong behavioral equivalences for processes with nondeterminism and probabilities. Theor. Comput. Sci. 546, 63–92 (2014)
Bernardo, M., Sangiorgi, D., Vignudelli, V.: On the discriminating power of testing equivalences for reactive probabilistic systems: results and open problems. In: Norman, G., Sanders, W. (eds.) QEST 2014. LNCS, vol. 8657, pp. 281–296. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10696-0_23
Bonchi, F., Sokolova, A., Vignudelli, V.: The theory of traces for systems with nondeterminism and probability. In: Proceedings of the 34th ACM/IEEE Symposium on Logic in Computer Science (LICS 2019), no. (19:62), pp. 1–14. IEEE-CS Press (2019)
Brookes, S.D., Hoare, C.A.R., Roscoe, A.W.: A theory of communicating sequential processes. J. ACM 31, 560–599 (1984)
De Nicola, R.: Extensional equivalences for transition systems. Acta Informatica 24, 211–237 (1987)
De Nicola, R., Hennessy, M.: Testing equivalences for processes. Theor. Comput. Sci. 34, 83–133 (1984)
Deng, Y., van Glabbeek, R., Morgan, C., Zhang, C.: Scalar outcomes suffice for finitary probabilistic testing. In: De Nicola, R. (ed.) ESOP 2007. LNCS, vol. 4421, pp. 363–378. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71316-6_25
Derman, C.: Finite State Markovian Decision Processes. Academic Press, Cambridge (1970)
Georgievska, S., Andova, S.: Probabilistic may/must testing: retaining probabilities by restricted schedulers. Formal Aspects Comput. 24, 727–748 (2012)
van Glabbeek, R.J.: The linear time - branching time spectrum I. In: Handbook of Process Algebra, pp. 3–99. Elsevier (2001)
Huynh, D.T., Tian, L.: On some equivalence relations for probabilistic processes. Fundamenta Informaticae 17, 211–234 (1992)
Jonsson, B., Ho-Stuart, C., Yi, W.: Testing and refinement for nondeterministic and probabilistic processes. In: Langmaack, H., de Roever, W.-P., Vytopil, J. (eds.) FTRTFT 1994. LNCS, vol. 863, pp. 418–430. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58468-4_176
Jonsson, B., Yi, W.: Compositional testing preorders for probabilistic processes. In: Proceedings of the 10th IEEE Symposium on Logic in Computer Science (LICS 1995), pp. 431–441. IEEE-CS Press (1995)
Jou, C.-C., Smolka, S.A.: Equivalences, congruences, and complete axiomatizations for probabilistic processes. In: Baeten, J.C.M., Klop, J.W. (eds.) CONCUR 1990. LNCS, vol. 458, pp. 367–383. Springer, Heidelberg (1990). https://doi.org/10.1007/BFb0039071
Keller, R.M.: Formal verification of parallel programs. Commun. ACM 19, 371–384 (1976)
Kemeny, J.G., Snell, J.L.: Finite Markov Chains. Van Nostrand, New York (1960)
Larsen, K.G., Skou, A.: Bisimulation through probabilistic testing. Inf. Comput. 94, 1–28 (1991)
Milner, R.: Communication and Concurrency. Prentice Hall, Upper Saddle River (1989)
Segala, R.: Modeling and verification of randomized distributed real-time systems. Ph.D. thesis (1995)
Segala, R.: A compositional trace-based semantics for probabilistic automata. In: Lee, I., Smolka, S.A. (eds.) CONCUR 1995. LNCS, vol. 962, pp. 234–248. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-60218-6_17
Segala, R.: Testing probabilistic automata. In: Montanari, U., Sassone, V. (eds.) CONCUR 1996. LNCS, vol. 1119, pp. 299–314. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-61604-7_62
Segala, R., Lynch, N.: Probabilistic simulations for probabilistic processes. In: Jonsson, B., Parrow, J. (eds.) CONCUR 1994. LNCS, vol. 836, pp. 481–496. Springer, Heidelberg (1994). https://doi.org/10.1007/978-3-540-48654-1_35
Yi, W., Larsen, K.G.: Testing probabilistic and nondeterministic processes. In: Proceedings of the 12th International Symposium on Protocol Specification, Testing and Verification (PSTV 1992), pp. 47–61. North-Holland (1992)
Acknowledgement
We would like to thank Valeria Vignudelli for pointing out the property violation illustrated in Fig. 4 and Rob van Glabbeek for the valuable discussions on interpolating and randomized schedulers.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Bernardo, M. (2020). Coherent Resolutions of Nondeterminism. In: Gribaudo, M., Iacono, M., Phung-Duc, T., Razumchik, R. (eds) Computer Performance Engineering. EPEW 2019. Lecture Notes in Computer Science(), vol 12039. Springer, Cham. https://doi.org/10.1007/978-3-030-44411-2_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-44411-2_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-44410-5
Online ISBN: 978-3-030-44411-2
eBook Packages: Computer ScienceComputer Science (R0)





 conditioned on the selection of transition
conditioned on the selection of transition 
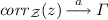 , with
, with 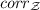 being injective over
being injective over 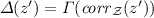 for all
for all 

 for
for  being injective when considered from
being injective when considered from  for all
for all  , with
, with  satisfying for all
satisfying for all  .
.


 – from which
– from which  follows – but in the resolution
follows – but in the resolution  .
. whereas in the resolution
whereas in the resolution  .
. . However,
. However,  while in the resolution
while in the resolution  . This shows that we should set up separate coherency constraints relying on
. This shows that we should set up separate coherency constraints relying on  sets for every
sets for every  , with
, with  . However, we observe that
. However, we observe that 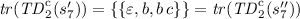 whereas
whereas  . This indicates that the coherency constraints should rely on
. This indicates that the coherency constraints should rely on  sets up to the probabilities they contain, i.e., the coherency constraints should rely on
sets up to the probabilities they contain, i.e., the coherency constraints should rely on  sets.
sets. ,
,  , and
, and  are pairwise different. In every coherent resolution of
are pairwise different. In every coherent resolution of 
 for all
for all 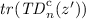 contains traces of length n, then for all
contains traces of length n, then for all  contains traces of length n too, or any
contains traces of length n too, or any  has length less than n but there exists a maximal trace in
has length less than n but there exists a maximal trace in  corresponding to
corresponding to 
