Abstract
Several formalisms for concurrent computation have been proposed in recent years that incorporate means to express stochastic continuous-time dynamics and non-determinism. In this setting, some obscure phenomena are known to exist, related to the fact that schedulers may yield too pessimistic verification results, since current non-determinism can surprisingly be resolved based on prophesying the timing of future random events. This paper provides a thorough investigation of the problem, and it presents a solution: Based on a novel semantics of stochastic automata, we identify the class of schedulers strictly unable to prophesy, and show a path towards verification algorithms with respect to that class. The latter uses an encoding into the model of stochastic timed automata under arbitrary schedulers, for which model checking tool support has recently become available.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
The modelling of concurrent systems operating in continuous time is at the heart of several branches of computing sciences. In the systems world, discrete event simulation tools like OMNeT [23], NS-2 or NS-3 [1, 2], or GlomoSim [30] are routinely used to gain insight into phenomena that are difficult to study “in the wild”. However, the validity of results obtained in this manner is often questionable, and comes with notorious suspicions about hidden assumptions that affect the simulation studies [3, 9, 19, 26]. The predominant mathematical objects that such simulators operate on are classes of stochastic processes, in particular generalised semi-Markov processes [13, 21] (GSMP). Stochasticity is used to conveniently reflect variations in behaviour due to mass effects.
Over the past decades, concurrent systems operating in stochastic continuous time have also received attention from a foundational perspective, especially in the formal methods community. Process calculi for stochastic timed systems have been proposed, starting with the work of Harrison and Strulo [15, 27]. D’Argenio proposed stochastic automata (SA) [10] as a compositional formalism akin to timed automata. Bravetti proposed the IGSMP calculus [8] for interacting GSMP. A comparative reflection of the two latter approaches can be found in [7]. The work of D’Argenio inspired the Modest language, which operates with stochastic timed automata (STA) [6] and is supported by the Modest Toolset [16]. Lately, Zeng, Nielson and Nielson proposed the stochastic quality calculus SQC [22] as an intriguing formalism to reason about distributed systems with broadcast communication.
All the approaches discussed above use semantic objects that extend the model of GSMP in a particular dimension: nondeterminism. Albeit with different flavors, the nondeterminism is essentially intertwined with the concept of an interleaving semantics, which assumes that no specific temporal ordering can be assumed for events that may happen in independent components—unless the ordering is specified in some way. In fact, it might not be far fetched to claim that in the systems community much of the above mentioned criticism which has accumulated with respect to GSMP simulation results is rooted in well-hidden assumptions determining certain event orderings, yet thereby discriminating against behaviour well possible “in the wild”. For instance, Opnet is known to use a default round-robin schedule between enabled processes if no other information is at hand, and so does GlomoSim.
The correct treatment of stochastic processes with nondeterminism can best be explained in the simplistic setting of Markov chains and their nondeterministic extension, Markov decision processes [24]. A Markov decision process turns into a Markov chain by fixing a resolution of nondeterminism. A scheduler is a mathematical object for this task, and the correct analysis of a Markov decision process is based on the principle of considering any Markov chain induced by any realistic scheduler. A verification task then gives rise to an entire range of quantitative results, such as an interval of reachability probabilities. Interestingly, if the class of schedulers at hand contains schedulers that can be considered unrealistic, then the analysis, albeit being correct, may become overly pessimistic in the sense that the interval returned is larger than realistically needed [12].
So, which family of schedulers is to be used for nondeterministic extensions of GSMP? This is the main question we aim at answering with this paper.
To shed some light on this, we discuss the problem in the context of stochastic automata. Roughly speaking, a stochastic automaton is a timed automaton where each clock, whenever reset, expires after a random amount of time. The randomness is specified by a probability measure associated to each clock. An edge is guarded by a (possibly empty) set of clocks and can be taken only when all clocks from this set are expired. When location \(\ell _{1}\) is entered in the model in Fig. 1 on the left, a clock x is reset to \(0.\) At this moment, the (random) time until its expiration, say distributed uniformly between \(0 \) and \(1\), starts. Any outgoing edge can be taken only after clock \(x\) expires. Once this happens, there are multiple concurrently enabled edges, and one of them is chosen nondeterministically. Assume we want to reach the desired state \(\checkmark \). The probabilities of this to happen now depends on the scheduler we consider. In the worst case, the probability is 0, because a scheduler can just decide to take the left edge in \(\ell _1\). Note that a random resolution of the non-determinism (or a kind of round-robin schedule) would result in a higher probability of reaching state \(\checkmark \).
The formal semantics of stochastic automata is defined by uncountable timed probabilistic transition systems (TPTS) where each state consists of the current location and the current valuation. As for timed automata, a valuation is used to store for each clock the amount of time elapsed since its last reset. In addition, it also stores the (randomly chosen) clock expiration times. Non-determinism in the TPTS is resolved by schedulers that can base their decisions on all values in the current valuation including the clock expiration times, i.e. the information when in the future each individual clock expires. Therefore, in the model in Fig. 1 on the right, a scheduler can always choose in location \(\ell _2\) the appropriate edge so that the desired state \(\checkmark \) is never reached (based on the fact whether \(y\) occurs before \(z\)). However, no realistic scheduler not knowing the timing of future random events can make the probability smaller than 1 / 2.
The semantics indicated above is known as residual lifetimes semantics [7], and is the one (at least conceptually) used in Modest, in SQC, in the works of D’Argenio, and in those of Strulo. Bravetti’s IGSMP use a different and at first sight more adequate approach, based on continuous resampling. This prevents schedulers from exploiting stored sampled values, and is called spent lifetimes semantics [7]. However we will argue that this semantics is in fact even more pessimistic and unrealistic.
We overcome this problem by introducing a new semantics based on separating the flow of time from non-deterministic choices. The set of all schedulers of the new semantics forms a strict subset of schedulers of the standard residual lifetimes semantics. As this new subclass excludes exactly those schedulers that observe the timing of future random events, we call them non-prophetic schedulers. We are then interested in worst-case and best-case guarantees with respect to non-prophetic schedulers.
We show that verification problems for non-prophetic schedulers can be translated to verification problems with respect to allschedulers on an induced model from the more expressive class of stochastic timed automata. Stochastic timed automata come from the same theoretical background and are thus also based on residual lifetimes semantics. Their higher expressiveness nevertheless allows us to emulate the behaviour of the SA while obfuscating the knowledge of the future timing. Using this translation, the verification of probabilistic reachability and expected-reward properties for stochastic automata under non-prophetic schedulers based on extensions of STA model checking techniques [14] is on the horizon.
2 Preliminaries
For a given set S, its power is \(\mathcal {P}({S}) \). We denote by \(\mathbb {R}\), \(\mathbb {R}^+ \), and \(\mathbb {R}^{+}_{0} \) the set of real numbers, positive real numbers and non-negative real numbers, respectively.
2.1 Probability Theory
A (discrete) over a countable sample space \(\varOmega \) is a function \(\mu \in \varOmega \rightarrow [0, 1]\) s.t. \(\sum _{\omega \in \varOmega }{\mu (\omega )} = 1\). The of \(\mu \) is  . We denote by \(\mathrm {Dist}({\varOmega }) \) the set of all probability distributions over \(\varOmega \). Furthermore, we write
. We denote by \(\mathrm {Dist}({\varOmega }) \) the set of all probability distributions over \(\varOmega \). Furthermore, we write  for the Dirac distribution for \(\omega \), defined by
for the Dirac distribution for \(\omega \), defined by  if \(x = \omega \) and
if \(x = \omega \) and  otherwise.
otherwise.
We say that a set \(\varOmega \) is a measurable space if it is endowed with a \(\sigma \)-algebra \(\varSigma (\varOmega )\), a collection of measurable subsets of \(\varOmega \). A (continuous) probability measure over \(\varOmega \) is a function \(\mu \in \varSigma (\varOmega ) \rightarrow [0, 1]\) such that \(\mu (\cup _{i \in I}\, B_i) = \sum _{i \in I}\, \mu (B_i)\) for any countable index set I and pairwise disjoint measurable sets \(B_i\). Each probability distribution \(\mu \) induces a probability measure and we thus also use \(\mathcal {D}(s) \) for the corresponding Dirac measure. We denote by \(\mathrm {Prob}({\varOmega })\) the set of probability measures over \(\varOmega \).
Given a a pair of probability measures \(\mu _1\), \(\mu _2\) we denote by \(\mu _1 \otimes \mu _2\) the product measure which is the unique probability measure such that
For a collection of measures \((\mu _i)_{i\in I}\), we analogously denote the product measure by \(\bigotimes _{i \in I} \mu _i\). We lift the same notation to a collection of sets of probability measures \((M_i)_{i \in I}\) by  . For a probability measure F over \(\mathbb {R}^{+}_{0} \) and any \(c \in \mathbb {R}^{+}_{0} \) such that \(F([c,\infty ))>0\), we denote by \(F_c\) the measure F
conditioned by
\(\ge c\), defined for any interval [a, b] by
. For a probability measure F over \(\mathbb {R}^{+}_{0} \) and any \(c \in \mathbb {R}^{+}_{0} \) such that \(F([c,\infty ))>0\), we denote by \(F_c\) the measure F
conditioned by
\(\ge c\), defined for any interval [a, b] by  .
.
2.2 Stochastic Automata
Definition 1
A stochastic automaton (SA) is a 6-tuple

where
-
\( Loc \) is a countable set of locations;
-
\(\mathcal {C} \) is a finite set of clock variables;
-
\(A \) is the automaton’s finite action alphabet partitioned into a set \(A _d\) of delayable and a set \(A _u\) of urgent actions;
-
\(E \in Loc \rightarrow \mathcal {P}({ \mathcal {P}({\mathcal {C}}) \times A \times \mathrm {Dist}({\mathcal {P}({\mathcal {C}}) \times Loc }) }) \) is the edge function, which maps each location to a finite set of edges, which in turn consist of a guard set, a label and a probability distribution over sets of clocks to reset and target locations;
-
\(F \in \mathcal {C} \rightarrow \mathrm {Prob}({\mathbb {R}^{+}_{0}})\) is the delay measure function that maps each clock to an absolutely continuous probability measureFootnote 1; and
-
 is the initial location.
is the initial location.
We also write  for \(\langle C, a, \mu \rangle \in E (\ell )\), and for two edge functions \(E _1\) and \(E _2\), we define
for \(\langle C, a, \mu \rangle \in E (\ell )\), and for two edge functions \(E _1\) and \(E _2\), we define
i.e. an edge function is “smaller” if it maps to “smaller” sets of edges.
Intuitively, a stochastic automaton starts its execution in the initial location with all clocks expired. Any edge  may be taken only if all clocks in its guard set C are expired. If it is taken, the action associated to the edge is a, and the distribution \(\mu \) encodes the discrete branching of this edge: when a branch \(\langle R,\ell ' \rangle \) is taken (which happens with probability \(\mu (R,\ell ')\)), all clocks from the set R get (re)started, other expired clocks remain expired, and the process moves into the successor location \(\ell '\). Here, another edge may be taken immediately or the automaton may need to wait until some further clocks expire and so on.
may be taken only if all clocks in its guard set C are expired. If it is taken, the action associated to the edge is a, and the distribution \(\mu \) encodes the discrete branching of this edge: when a branch \(\langle R,\ell ' \rangle \) is taken (which happens with probability \(\mu (R,\ell ')\)), all clocks from the set R get (re)started, other expired clocks remain expired, and the process moves into the successor location \(\ell '\). Here, another edge may be taken immediately or the automaton may need to wait until some further clocks expire and so on.
If a clock c gets started, it expires again after an amount of time chosen randomly according to the probability measure F(c). Implementing the abstract notions of clock start and clock expiration is the crucial step in defining a formal semantics. In this paper, we focus on what power such an implementation gives to schedulers—objects that choose which edge to take when several of them may be taken at the same point in time.
Defining the semantics of stochastic automata formally is the core topic of this paper. We discuss various approaches in Sects. 3 and 4. In the rest of this section, we lay the foundations for defining the semantics. First, we define probabilistic timed transition system with uncountable state and action spaces. This is needed since we need to store the current valuation of real-valued clocks and variables in each state. Second, we introduce assignments and clock expressions to simplify manipulation with these valuations.
2.3 Uncountable Transition Systems
The semantics of (non-Markovian) continuous-time stochastic models with nondeterminism can be defined using the following formalism [6, 7, 29].
Definition 2
A timed probabilistic transition system (TPTS) is a 4-tuple

where
-
\(S \) is a (usually uncountable) measurable space of states;
-
\(A = \mathbb {R}^+ \uplus A '\) is the system’s (uncountable) alphabet that can be partitioned into delays in \(\mathbb {R}^+\) and normal actions in \(A '\);
-
\(T \in S \rightarrow \mathcal {P}({A \times \mathrm {Prob}({S})}) \) is the transition function, which is explicitly allowed to map a state to an uncountable set of transitions; and
-
 is the initial state.
is the initial state.
We also write  for \(\langle a, \mu \rangle \in T (s)\), and the \(<\) relation can be defined for transition functions analogously to its definition for edge functions.
for \(\langle a, \mu \rangle \in T (s)\), and the \(<\) relation can be defined for transition functions analogously to its definition for edge functions.
A behavior of a TPTS is a run, an infinite alternating sequence \(s_0 a_0 s_1 a_1 \!\ldots \) of states and actions. The system starts in the initial state  . Assuming the current state is \(s_i\), the next transition
. Assuming the current state is \(s_i\), the next transition  is chosen non-deterministically by a scheduler based on the whole history \(s_0 a_0 \ldots a_{i-1} s_i\) up to this point. The successor state \(s_{i+1}\) is then chosen randomly according to the probability measure \(\mu \).
is chosen non-deterministically by a scheduler based on the whole history \(s_0 a_0 \ldots a_{i-1} s_i\) up to this point. The successor state \(s_{i+1}\) is then chosen randomly according to the probability measure \(\mu \).
Formally, a scheduler is a measurable function \(\sigma \) that maps every \(s_0 a_0 \ldots s_i \in (S \times A)^* \times S \) to a measure over transitions from \(T(s_i)\) (i.e. the scheduler may randomize over available transitions). Every scheduler \(\sigma \) defines a probability measure \(\mathbb {P}^\sigma \) over the set of all runs. For a full formal definition, see e.g. [29]. Following the standard approach, we restrict to non-Zeno schedulers that allow time to diverge with probability one. More precisely, we require that \(\mathbb {P}^\sigma (D) = 1\) where D is the set of runs where the sum of all actions from \(\mathbb {R}^+ \) along the run is \(\infty \).
Inspired by [25], we define the timed trace distribution \(\mathrm {Tr}(T,\sigma )\) of a TPTS T induced by a scheduler \(\sigma \) as follows. First, a timed trace is a finite or infinite sequence of actions, obtained as the natural projection (denoted \(\mathrm {ttrace}\)) mapping each run \(s_0 a_0 s_1 a_1 \cdots \) to a timed trace obtained from \(a_0 a_1 \cdots \) by merging every maximal sequence of real numbers into its sum (a potential infinite sequence at the end of a run is simply removed, resulting in a finite trace). With this, the timed trace distribution \(\mathrm {Tr}(T,\sigma )\) is a distribution over the measurable space of timed traces such that every measurable set of timed traces A has probability \(\mathbb {P}^\sigma (\mathrm {ttrace}^{-1}(A))\). We denote by \(\mathrm {Tr}(T)\) the set of timed trace distributions of T ranging over all schedulers of T. Finally, we say that two TPTS \(T_1,T_2\) are timed trace distribution equivalent if \(\mathrm {Tr}(T_1) = \mathrm {Tr}(T_2)\).
Remark 1
The example discussed in Fig. 1 works with state-based properties, in particular considering state reachability probabilities. We can encode such properties in a trace-based setting by, for example, adding a loop  to the state whose reachability probability we intend to compute, where a is a unique urgent action. We can then ask for the probability of the set of timed traces that include a instead. In this sense, timed trace distribution equivalence can be ensured to preserve timed reachability probabilities.
to the state whose reachability probability we intend to compute, where a is a unique urgent action. We can then ask for the probability of the set of timed traces that include a instead. In this sense, timed trace distribution equivalence can be ensured to preserve timed reachability probabilities.
2.4 Variables and Expressions
In this subsection, we introduce a unified way to deal with the evaluation and modification of valuations over a set of variables. For a finite set of (real-valued) variables  , we let
, we let  denote the set of valuations. By
denote the set of valuations. By  , we denote the valuation that assigns value 0 to all variables. We now first introduce an abstract notion of expressions which we use for two operations: updates to modify a valuation, and (timed automata-like) clock constraints to evaluate a valuation. Similarly to timed automata, we also define how the flow of time modifies a valuation.
, we denote the valuation that assigns value 0 to all variables. We now first introduce an abstract notion of expressions which we use for two operations: updates to modify a valuation, and (timed automata-like) clock constraints to evaluate a valuation. Similarly to timed automata, we also define how the flow of time modifies a valuation.
Expressions. By  we denote the set of over the set of variables
we denote the set of over the set of variables  . We simply write
. We simply write  for the set of expressions over the whole set
for the set of expressions over the whole set  . We treat expressions in an abstract manner: We assume a standard expression syntax (as in e.g. ML or C) with extensions for nondeterministic and randomly sampled values. We formally work only with the semantics \(\llbracket e \rrbracket \) of expressions e, which are functions that take a valuation over
. We treat expressions in an abstract manner: We assume a standard expression syntax (as in e.g. ML or C) with extensions for nondeterministic and randomly sampled values. We formally work only with the semantics \(\llbracket e \rrbracket \) of expressions e, which are functions that take a valuation over  and return the value of e depending on the expression class:
and return the value of e depending on the expression class:
-
 : Boolean expressions
e have
: Boolean expressions
e have  .
.  include e.g. $$i = 1, \quad tt , \quad x \ge 2.5. $$
include e.g. $$i = 1, \quad tt , \quad x \ge 2.5. $$ -
 : Arithmetic expressions
e have
: Arithmetic expressions
e have  .
. 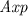 include e.g.
include e.g. 
-
 : Sampling expressions
e have
: Sampling expressions
e have  . These are conceptually arithmetic expression featuring two additional constructs: nondeterministic choice and random sampling.
. These are conceptually arithmetic expression featuring two additional constructs: nondeterministic choice and random sampling.  include, e.g.,
include, e.g., 
where
 denotes the random selection of a value according to the probability measure F and
denotes the random selection of a value according to the probability measure F and  the nondeterministic selection of a value out of the interval I. In the example, \(\textsc {Exp}(x)\) denotes the exponential distribution with rate given by the current value of variable x.
the nondeterministic selection of a value out of the interval I. In the example, \(\textsc {Exp}(x)\) denotes the exponential distribution with rate given by the current value of variable x.
The semantics of a sampling expression maps to a set (representing the nondeterministic choice) of probability measures (representing the random sampling). For example, the semantics  applied to valuation \(\mathbf {0}\) returns the set \(\{\, \mu _i \mid i \in (3,4) \,\}\) where each measure \(\mu _i\) is the exponential distribution “shifted” by i. For a sampling expression e without nondeterminism, we denote by
applied to valuation \(\mathbf {0}\) returns the set \(\{\, \mu _i \mid i \in (3,4) \,\}\) where each measure \(\mu _i\) is the exponential distribution “shifted” by i. For a sampling expression e without nondeterminism, we denote by  the function that maps a valuation v to the single probability measure in \(\llbracket e \rrbracket (v)\).
the function that maps a valuation v to the single probability measure in \(\llbracket e \rrbracket (v)\).
Updates. An , written as \(x := e\), is a pair  . Two assignments \(\langle x_1, e_1 \rangle \) and \(\langle x_2, e_2 \rangle \) are if \(x_1 \ne x_2\) or \(\llbracket e_1 \rrbracket (v) = \llbracket e_2 \rrbracket (v)\) for all valuations v. The set of all assignment is denoted by
. Two assignments \(\langle x_1, e_1 \rangle \) and \(\langle x_2, e_2 \rangle \) are if \(x_1 \ne x_2\) or \(\llbracket e_1 \rrbracket (v) = \llbracket e_2 \rrbracket (v)\) for all valuations v. The set of all assignment is denoted by  . A finite set of pairwise consistent assignments is called an (atomic) , and two updates are consistent if their union is an . The set of all updates is denoted
. A finite set of pairwise consistent assignments is called an (atomic) , and two updates are consistent if their union is an . The set of all updates is denoted  .
.
Similar to sampling expressions, the semantics of an update  is a function
is a function  . Due to consistency, we can treat every update \(U = \{\, \langle x_1, e_1 \rangle , \dots , \langle x_n, e_n \rangle \,\}\) consisting of \(n \in \mathbb {N} \) assignments as a function
. Due to consistency, we can treat every update \(U = \{\, \langle x_1, e_1 \rangle , \dots , \langle x_n, e_n \rangle \,\}\) consisting of \(n \in \mathbb {N} \) assignments as a function  (even though we may have \(x_i = x_j\) for some \(i \ne j\)). Assuming some fixed total order on the variables, we can identify valuations with tuples of values. This then allows us to define straightforwardly
(even though we may have \(x_i = x_j\) for some \(i \ne j\)). Assuming some fixed total order on the variables, we can identify valuations with tuples of values. This then allows us to define straightforwardly  .
.
Clocks and Clock Constraints. Later, (similarly to timed automata) we restrict operations that can be applied to clock variables. Let us fix a set  of clock variables. Clock constraints over \(\mathcal {C} \) are expressions constructed according to the following grammar:
of clock variables. Clock constraints over \(\mathcal {C} \) are expressions constructed according to the following grammar:
where \(\sim \ \in \{\, >, \ge , <, \le , =, \ne \,\}\), \(c, c_1, c_2 \in \mathcal {C} \), and b and e are Boolean and arithmetic expressions over  , respectively. The semantics of a clock constraint g is again a function
, respectively. The semantics of a clock constraint g is again a function  . Similarly, an update is called clock update if all its assignments to clocks \(c \in \mathcal {C} \) are of the form \(c := 0\). The set of all clock updates is denoted by
. Similarly, an update is called clock update if all its assignments to clocks \(c \in \mathcal {C} \) are of the form \(c := 0\). The set of all clock updates is denoted by  . Finally, we define for any valuation v and any delay \(t \in \mathbb {R}^+ \) a valuation \(v + t\) by
. Finally, we define for any valuation v and any delay \(t \in \mathbb {R}^+ \) a valuation \(v + t\) by

3 Prophetic and Divine Scheduling
In this section we review two existing semantics for stochastic automata. Both map SA to TPTS with uncountable state spaces. A scheduler for an SA is then defined as a scheduler in the underlying TPTS.
In the first subsection, we introduce the more common residual lifetimes semantics that however allows a scheduler to be prophetic. Then, we address the spent lifetimes semantics that at first sight appears to solve this problem. We show that (a) it still allows a scheduler to be prophetic (though in a limited way) and more importantly (b) it allows a scheduler to act divine in the sense of being able to manipulate the future in unexpected and unintuitive ways.
We fix for the rest of the paper an SA  . The presentation of the two semantics is closely inspired by their comparison in [7] which in turn slightly deviates from the respective original definitions [8, 10] without affecting core properties.
. The presentation of the two semantics is closely inspired by their comparison in [7] which in turn slightly deviates from the respective original definitions [8, 10] without affecting core properties.
3.1 Residual Lifetimes [10]
In the residual lifetimes semantics, the states of the TPTS are pairs \(\langle \ell , v \rangle \) of the current location \(\ell \) and a valuation v over the set of variables

For each clock c, the (non-clock) variable \(d_{c}\) stores the value sampled for c when c was reset most recently. For a set R of clocks, both reset and sampling can be done by the update

The value of each clock then increases with the flow of time; a clock c is called expired when its value reaches the value of the sampled variable \(d_{c}\). An edge  may be taken only if all clocks from the guard set C are expired, captured by the clock constraint
may be taken only if all clocks from the guard set C are expired, captured by the clock constraint

Let us now define the induced TPTS precisely:
Transition System. The residual lifetimes semantics of an SA M is the TPTS

where \(T _M\) is the smallest (according to relation \(<\)) transition function satisfying the following two inference rules:

where the first rule formalizes the preconditions and effects of taking an edge and the second rule states that time may flow in a location \(\ell \) only if there is no edge to be taken urgently where

Recall that when an edge  is taken, a successor location \(\ell '\) and a set R of clocks is randomly picked according to the distribution \(\mu \). For a fixed pair \(\langle R,\ell ' \rangle \), the term \(\mathcal {D}(\ell ') \otimes \llbracket \mathrm {Sample}(R) \rrbracket _1(v)\) appearing in the first rule is a distribution over states, say \(\alpha _{R,\ell '}\). The sum \(\sum _{R, \ell '} \mu (\langle R, \ell ' \rangle ) \cdot \alpha _{R,\ell '}\) then represents the overall distribution obtained by weighting the \(\alpha _{\cdots }\) by \(\mu \).
is taken, a successor location \(\ell '\) and a set R of clocks is randomly picked according to the distribution \(\mu \). For a fixed pair \(\langle R,\ell ' \rangle \), the term \(\mathcal {D}(\ell ') \otimes \llbracket \mathrm {Sample}(R) \rrbracket _1(v)\) appearing in the first rule is a distribution over states, say \(\alpha _{R,\ell '}\). The sum \(\sum _{R, \ell '} \mu (\langle R, \ell ' \rangle ) \cdot \alpha _{R,\ell '}\) then represents the overall distribution obtained by weighting the \(\alpha _{\cdots }\) by \(\mu \).
Prophetic Schedulers. In light of the TPTS as defined above, we consider the SA model on the right below, which is a notationally more formal variation of the one from Fig. 1. The TPTS starts in the initial state  . Since the outgoing edge from
. Since the outgoing edge from  has an empty guard set and we assume action a to be urgent, no delay is possible in
has an empty guard set and we assume action a to be urgent, no delay is possible in  and the only outgoing transition is with action a to a probability measure over states of the form \(\langle \ell _1,v \rangle \) where \(v(x) = v(y) = v(z) = 0\) and the values \(v(d_{x})\), \(v(d_{y})\) and \(v(d_{z})\) are sampled randomly according to the continuous uniform distributions \(\textsc {Uni}([0,1])\), \(\textsc {Uni}([2,3])\) and \(\textsc {Uni}([2,3])\), respectively.
and the only outgoing transition is with action a to a probability measure over states of the form \(\langle \ell _1,v \rangle \) where \(v(x) = v(y) = v(z) = 0\) and the values \(v(d_{x})\), \(v(d_{y})\) and \(v(d_{z})\) are sampled randomly according to the continuous uniform distributions \(\textsc {Uni}([0,1])\), \(\textsc {Uni}([2,3])\) and \(\textsc {Uni}([2,3])\), respectively.

From any such location, there are uncountably many outgoing transitions corresponding to all possible delays \(0 < t \le v(d_{x})\). If a scheduler chooses some action \(t_0 < v(d_{x})\), then the remaining time to delay decreases by \(t_0\) and in the next state, the choice options are reduced to actions \(0 < t \le v(d_{x}) - t_0\) and so on. In the end, all (non-Zeno) delay sequences \(t_0, t_1, \ldots \) end up in some state \(\langle \ell _1,v \rangle \) where \(v(x) = v(d_{x})\) where a scheduler needs to choose between b and c.
In such a state \(\langle \ell _1,v \rangle \), one possible scheduler \(\sigma \) can decide to choose action b only if \(d_{z} < d_{y}\) and action c otherwise (and to choose always maximal delay whenever delaying is possible): One can then easily argue that the probability induced by scheduler \(\sigma \) to reach a state with location \(\checkmark \) is 0, while our intuition says that less than 0.5 is not achievable. However, that scheduler can be considered prophetic, since its decisions are effectively based on the timing of events that will occur in the future.
3.2 Spent Lifetimes [8]
The spent lifetimes semantic TPTS is defined over the same state space, but in order to avoid prophetic decisions, each transition comes with a complete resampling of the variables \(d_{c}\) that represent the residual time for each clock c. Thereby, the current value of \(d_{c}\) (on which the scheduler may base its decisions) becomes irrelevant right with the execution of the decision of the scheduler, i.e. whenever taking a transition.
In order to keep the delay between resetting c and its expiration distributed according to F(c), the resampling needs to take into account the time already spent which is captured by the value of the clock c. This is achieved by conditioning the delay measure F(c) on the time spent. As an example, consider a clock c with F(c) being uniform on [1, 2]. The clock is initially sampled to, say, 1.3. After taking a delay transition of 1.1 time units, we need to resample it according to the distribution \(F(c)_{\mid 1.1}\), which is distributed uniformly on [1.1, 2]. If instead the resampling were to occur already after 0.5 time units, we actually would have \(F(c)_{\mid 0.5} = F(c)\) (as knowing that the event does not occur before 0.5 does not change the chances of when it will occur in the future). Resampling of a set \(C \subseteq \mathcal {C} \) can be expressed by the update

where F(c) should be interpreted as one literal giving a distribution that is then within the expression conditioned by the current elapsed time of c. Observe that the update resamples only values for clocks that are not expired.
Transition System. The spent lifetimes semantics of an SA M is the TPTS

where \(T _M\) is the smallest transition function satisfying the following two inference rules:

where the first rule again describes that an edge is taken and the second rule again describes the flow of time. The clock constraint \(\mathrm {Urgent}_\mathrm {s}\) is defined by

where  . It differs from \(\mathrm {Urgent}_\mathrm {r}\) used in the residual lifetimes semantics by forcing each delay not to exceed the moment when the next clock is expiring. This condition means that whenever some clock expires, all other active clocks get resampled. The rule \(\textit{delay}_\mathrm {s}\) requires \(v + t'\) to satisfy \(\lnot \mathrm {Urgent}_\mathrm {s}(\ell )\) only for positive time points \(t'\) because \(\mathrm {Expiring}(c)\) is violated by v if the clock c has just expired.
. It differs from \(\mathrm {Urgent}_\mathrm {r}\) used in the residual lifetimes semantics by forcing each delay not to exceed the moment when the next clock is expiring. This condition means that whenever some clock expires, all other active clocks get resampled. The rule \(\textit{delay}_\mathrm {s}\) requires \(v + t'\) to satisfy \(\lnot \mathrm {Urgent}_\mathrm {s}(\ell )\) only for positive time points \(t'\) because \(\mathrm {Expiring}(c)\) is violated by v if the clock c has just expired.
Prophetic Scheduling. We now discuss that the spent lifetimes semantics, despite its intention, is not free of prophetic power. In the SA in Fig. 2 on the left, after some delay \(t \in [0,1]\), clock x expires and clocks y and z get resampled both independently according to \(U[2,3]_{\mid t} = U[2,3]\). In other words, a state \(\langle \ell _1,v \rangle \) is reached where \(v(x) = v(y) = v(z) = v(d_{x}) = t\) and \(v(d_{y}), v(d_{z}) \in [2,3]\). We can distinguish two cases:
-
1.
If \(v(d_{z}) < v(d_{y})\), the scheduler \(\sigma \) may choose the maximal enabled delay \(v(d_{z}) - t\) by which z becomes expired (in one step, i.e. z does not get resampled) and the location \(\times \) is reached.
-
2.
Otherwise, the scheduler \(\sigma \) repeatedly takes the enabled self-loop edge resetting y and z until a state \(\langle \ell _1,v \rangle \) with \(v(d_{z}) < v(d_{y})\) is reached. In this state the scheduler behaves as described in point 1 above.
By this scheduler \(\sigma \), a state with location \(\checkmark \) is again reached with probability 0. In other words, the crucial property of the spent lifetimes semantics is that the scheduler observes what is the first clock to expire and when will it happen. If the scheduler prefers this observed plan, it may let it happen by one delay transition. Otherwise, it may block this from happening by taking some other (non-urgent) edge.
Divine Scheduling. Actually, the self-loop edge in the example above is not needed for a scheduler to guarantee that \(\checkmark \) is reached with probability 0. Consider the SA in Fig. 2 on the right. Remarkably, another way how a scheduler may influence the sampled timing in this SA is to take ever shorter delay transition. Each of them induces a resampling of all running clocks. Thus, such a scheduler also gets arbitrarily many chances to resample the clocks by delaying, say for 1 / 2, then for 1 / 4, 1 / 8, 1 / 16, and so on.Footnote 2 In this way, a scheduler can arguably effectuate divine power by forcing a particular ordering of events through the way in which it lets time progress.
In general, this means that a scheduler can force one of the active clocks c in some location to expire first (unless the lower bound of the support of its associated probability measure disallows that). But the power of schedulers does not stop here: A scheduler can also use the same technique to force a clock to expire in an arbitrarily small subinterval I of its support (with \(F(c)(I) > 0\)); so in the example above, it could achieve probability 1 for reaching location \(\times \) before 2.1 time units have elapsed.

Furthermore, a scheduler in the spent lifetimes semantics can prevent urgent actions from ever taking place, even when no alternative action is available, and without letting time converge. Consider the small example on the right, where we assume both actions a and d to be urgent. \(\ell _1\) must thus be reached within zero time units, and we would expect location \(\checkmark \) to be reached after a further delay according to the exponential distribution with rate 1, i.e. after on average a further 1 time unit. However, a scheduler in the spent lifetimes semantics for this model can prevent \(\checkmark \) from being reached at all: When in state \(\langle \ell _1, v_1 \rangle \) with \(v_1(d_{x}) = t_1 > 0\), it can choose to delay by \(t_1 - \epsilon \) (\(\epsilon > 0\)) time units. The value for \(d_{x}\) is then resampled, and we again end up in a state \(\langle \ell _1, v_2 \rangle \) with \(v_2(d_{x}) = t_2 > 0\). Due to the unbounded support and the memoryless property of the exponential distribution (i.e. \(\textsc {Exp}_{|t}(1) = \textsc {Exp}(1)\) for all \(t \in \mathbb {R}^{+}_{0} \)), this process can be repeated ad infinitum, and \(\sum _{i} t_i = \infty \) with probability 1.
These anomalies are clearly not intended conceptually, but overarch the existing solutions. It thus appears that the concepts currently at hand for stochastic automata and related models are not adequate. We therefore aim at settling a semantics that makes sure that the schedulers are neither prophetic nor divine. We define such a semantics, that we call non-prophetic, in the next section.
4 Non-prophetic Semantics
This section introduces a novel semantics for stochastic automata where schedulers can neither act divine nor prophetic. It is a spent lifetimes semantics in the sense that the residual times (variables \(d_{c}\) for clocks c) are resampled whenever delays are to be performed. However, the choice of the actual time to delay and this resampling are performed in one atomic step. In this way, the scheduler cannot know the residual times at the point where it has to choose the delay. After the choice and resampling, the amount of time that passes is at least the minimum of the sampled residual times and the chosen delay. Only when this amount of time has passed can a jump be performed or a new delay be chosen (including another resampling of the residual times).
4.1 Definition
Technically, to achieve this kind of behaviour, we split the evolution of the system into two alternating phases, denoted as \(\circ \) and \(\bullet \). In the \(\circ \)-phase, the scheduler may only take jump transitions, or it may decide to switch to the \(\bullet \)-phase. On this switch, it chooses the next delay, and the residual times for the clocks are resampled. Then, in the \(\bullet \)-phase, the scheduler can only let time pass via delay transitions or switch back to the \(\circ \)-phase. However, the switch back is only enabled at the exact points in time where either a clock has just expired, or the amount of time that has passed is the delay previously chosen by the scheduler. As usual, if an edge with an urgent action has become enabled, no more time can pass and the switch back to \(\circ \) must occur immediately.
Definition 3
The non-prophetic semantics of an SA M is the TPTS

where  are valuations over the set of variables
are valuations over the set of variables  where
where  are the clock variables and \(T _M\) is the smallest transition function such that the following inference rules are satisfied:
are the clock variables and \(T _M\) is the smallest transition function such that the following inference rules are satisfied:

where  and
and

The rules \(\textit{choice}_\mathrm {n}\) and \(\textit{expiring}_\mathrm {n}\) take care of switching between the phases whereas the rules \(\textit{jump}_\mathrm {n}\) and \(\textit{delay}_\mathrm {n}\) echo the rules of the residual lifetimes semantics. The precondition of \(\textit{delay}_\mathrm {n}\) uses the predicate \(\mathrm {Urgent}_\mathrm {n}\), which prevents the rule from being applied not only when the clock for an urgent action has expired (as in \(\mathrm {Urgent}_\mathrm {r}\)), but also when the new clock \(w\) or the clock of a delayable action is just expiring. The update \(d_{c} := 0\) on \(\textit{expiring}_\mathrm {n}\) makes sure that the clock can expire only once at a given moment of time.
4.2 Absence of Prophetic and Divine Behaviour
In light of the shortcomings of earlier approaches discussed in Sect. 3, the question arises in what sense this new semantics is any good. We argue in the sequel that the non-prophetic semantics meets its design goals. Formally, we consider a restricted class of schedulers on this new semantics \(\llbracket M \rrbracket _\mathrm {n}\) such that the schedulers in this class clearly only enable non-prophetic scheduling. This is because their decisions are only based on spent lifetimes. We then show that this scheduler class is no less powerful than the class of all imaginable schedulers on \(\llbracket M \rrbracket _\mathrm {n}\) w.r.t. timed trace distribution equivalence. Notably, the same does not hold for \(\llbracket M \rrbracket _\mathrm {r}\) and \(\llbracket M \rrbracket _\mathrm {s}\), as shown by our earlier examples.
Procrastination. First, we define and show one technical property that simplifies the proofs later and reveals additional structure of scheduling: we will require that after waiting for the delay previously chosen by the scheduler without being interrupted by the expiration of any clock, the scheduler cannot choose to wait further, i.e. it needs to choose some edge. We say that a scheduler \(\sigma \) in \(\llbracket M \rrbracket _\mathrm {n}\) is procrastination-free if for all histories \(h = s_0 a_0 \cdots a_{n-1} s_n\) we have the following two properties:
-
1.
if \(a_{n-1} = \tau \) and \(s_n = \langle \ell ,\circ ,v \rangle \) with \(v(w) = v(d_{w})\), then the scheduler \(\sigma \) chooses in h any \(\tau \) transition with probability zero;
-
2.
if \(s_n = \langle \ell ,\bullet ,v \rangle \), the scheduler \(\sigma \) chooses in h the delay transition with maximum possible label value (i.e. maximum delay) with probability one.
Next, we show that we can restrict to procrastination-free schedulers.
Lemma 1
For any scheduler \(\sigma \) in \(\llbracket M \rrbracket _\mathrm {n}\), there is a procrastination-free scheduler \(\sigma '\) in \(\llbracket M \rrbracket _\mathrm {n}\) such that the stochastic processes induced by \(\sigma \) and \(\sigma '\) have the same timed trace distribution.
Proof
(Sketch). We define the scheduler \(\sigma '\) for a given history h as follows. We observe the measure over sequences of several delay steps that end by choosing some non-waiting action from A. The scheduler then takes the delay according to this measure in one step. In the next step (if not interrupted by expiration of some clocks earlier), the non-waiting action is also taken according to this measure (conditioned by the chosen waiting).
Non-prophetic schedulers in \(\llbracket M \rrbracket _\mathrm {n}\) We say that a scheduler \(\sigma \) in \(\llbracket M \rrbracket _\mathrm {n}\) is non-prophetic if \(\sigma (h) = \sigma (h')\) for all histories \(h = s_0 a_0 \cdots a_{n-1} s_n\) and \(h' = s'_0 a'_0 \cdots a'_{n-1} s'_n\) such that
-
for all \(0 \le i < n\) we have \(a_i = a'_i\) and
-
for all \(0 \le i \le n\) the valuations in \(s_i\) agree on values of \(\mathcal {C} \).
Lemma 2
For any procrastination-free scheduler \(\sigma '\) in \(\llbracket M \rrbracket _\mathrm {n}\), there is a procrastination-free non-prophetic scheduler \(\sigma ''\) in \(\llbracket M \rrbracket _\mathrm {n}\) such that the stochastic processes induced by \(\sigma '\) and \(\sigma ''\) are timed trace distribution equivalent.
Proof
We define each choice of the scheduler \(\sigma ''\) by randomization over choices of \(\sigma '\) over all sampled values of variables that a non-prophetic scheduler cannot observe. This can be easily defined locally as the variables are resampled in every step and the scheduler \(\sigma \) is procrastination-free.
Non-prophetic schedulers in \(\llbracket M \rrbracket _\mathrm {r}.\) Next, we observe that every scheduler in a non-prophetic semantics can be mimicked by a scheduler in the standard residual lifetimes semantics. The following theorem bridges the two semantics.
Theorem 1
For any scheduler \(\sigma \) in \(\llbracket M \rrbracket _\mathrm {n}\), there is a scheduler \(\bar{\sigma }\) in \(\llbracket M \rrbracket _\mathrm {r}\) such that the stochastic processes induced by \(\sigma \) and \(\bar{\sigma }\) have the same timed trace distribution.
Proof
(Sketch). Owed to the preceding lemmata, we can assume \(\sigma \) to be procrastination-free and non-prophetic, since otherwise we could switch to another scheduler satisfying these assumptions with the same timed trace distribution.
We define the scheduler \(\bar{\sigma }\) in \(\llbracket M \rrbracket _\mathrm {r}\) with the same timed trace distribution as follows. It always takes the decision only based on the spent lifetimes of every clock (which are stored in the state space of \(\llbracket M \rrbracket _\mathrm {r}\)). When a decision (say to wait for t time units) is taken, it sticks to this decision: even if some clock expires earlier (say after \(t' < t\) time units), the decision is not changed up to the point where the expiration happens (so there is indeed waiting for \(t'\) time units). At this point, the observations of \(\bar{\sigma }\) do change, and it may thus take another decision according to \(\sigma \).
Finally, we say that a scheduler \(\bar{\sigma }\) in \(\llbracket M \rrbracket _\mathrm {r}\) is non-prophetic if there is a scheduler \(\sigma \) in \(\llbracket M \rrbracket _\mathrm {n}\) such that the stochastic processes induced by \(\bar{\sigma }\) and \(\sigma \) are timed trace distribution equivalent. In the next section, we address the problem of analysing SA w.r.t. the non-prophetic semantics, or equivalently w.r.t. the class of non-prophetic schedulers in the standard residual lifetimes semantics.
5 Towards Non-Prophetic Model Checking
In this section, we discuss how the non-prophetic semantics of stochastic automata can equivalently be encoded into the more expressive formalism of stochastic timed automata. This is possible despite the fact that STA use the residual lifetimes approach for expressing stochastic delays. We will finally discuss ways to perform model checking of non-prophetic SA based on this encoding.
We first define the formalism of STA and its semantics using TPTS. We then explain the translation from SA to STA, before we turn to the model checking discussion.
5.1 Stochastic Timed Automata [6]
The STA formalism is somewhat similar to SA, with the main difference being that the sampling from probability measures is now made explicit in the model: In addition to clock variables as in SA, an STA can also have real-valued non-clock variables. These do not change over time, but when an edge is taken, they can be set to values sampled according to probability measures. Edges in STA are decorated with a guard and a deadline. Both of these are clock constraints, and in particular, can contain comparisons between clocks and non-clock variables. In this way, the residual lifetimes semantics can be encoded explicitly in an STA, but at the same time, also nondeterministic timing is possible by simply not making use of the possibility of sampling and instead comparing a clock with constant values in guards and deadlines.
Definition 4
A stochastic timed automaton (STA) is a 5-tuple

where
-
\( Loc \) is a countable set of locations;
-
 is a finite set of variables with a subset \(\mathcal {C}\) of clock variables;
is a finite set of variables with a subset \(\mathcal {C}\) of clock variables; -
\(A \) is the automaton’s countable action alphabet;
-
 is the edge function, which maps each location to a set of edges, which in turn consist of a guard, a deadline, a label and a probability distribution over updates and target locations; and
is the edge function, which maps each location to a set of edges, which in turn consist of a guard, a deadline, a label and a probability distribution over updates and target locations; and -
 is the initial location.
is the initial location.
We also write  for \(\langle g, d, a, \mu \rangle \in E (\ell )\).
for \(\langle g, d, a, \mu \rangle \in E (\ell )\).
Intuitively, an STA M evolves as follows: It starts in the initial location  with all variables having value 0. When time passes, values of all clock variables synchronously increase. An outgoing edge
with all variables having value 0. When time passes, values of all clock variables synchronously increase. An outgoing edge  may be taken only when its guard g is satisfied by the current values of the variables. If the deadline d of any outgoing edge is satisfied, then some outgoing edge must be taken before time can pass again. Whenever an edge as above is taken, a clock update and a successor location is chosen randomly according to \(\mu \). The update is applied on the current values of variables and the process moves to the successor location.
may be taken only when its guard g is satisfied by the current values of the variables. If the deadline d of any outgoing edge is satisfied, then some outgoing edge must be taken before time can pass again. Whenever an edge as above is taken, a clock update and a successor location is chosen randomly according to \(\mu \). The update is applied on the current values of variables and the process moves to the successor location.

On the right, we illustrate how an STA can be used to express stochastic delays. The edges (all of which lead to Dirac distributions here, i.e. they have a single successor location each) are annotated by their guard (in green) and their deadline (in red), their action, and the updates of their single target (if non-empty). The edge from the initial location, sampling the delay for clock c, needs to be taken immediately because its deadline is \( true \). In location \(\ell _1\), we need to wait at least until “c expires”. Note that the waiting can be longer (depending on nondeterministic choice) as the deadline occurs only 1 time unit after that.
Formally, the semantics of STA [6] is defined using TPTS:
Definition 5
The semantics of an STA M is the TPTS

where \(T _M\) is the smallest function satisfying the following two inference rules:

where  .
.
Both rules above are not surprising, since they closely resemble the residual lifetimes semantics of SA.
5.2 Residual-Lifetimes Embedding of SA
Before addressing our ultimate target, the non-prophetic semantics, we start by showing that stochastic automata (with respect to the residual lifetimes semantics) are a subclass of stochastic timed automata by the following simple embedding: An SA

is mapped to an STA with the same set of locations,

For each clock c, we again have one variable \(d_{c}\) with the sampled value. For each edge in the SA, there is one edge in the STA as given by the inference rule

where \(\mathrm {Expired}(C)\) is the guard of the edge and \(\mathrm {Deadline}(a,C)\) is its deadline. The deadline coincides with the guard if the action is urgent, i.e.

5.3 Embedding of SA with Non-prophetic Semantics
We move on to the crucial translation, namely the one that embeds the non-prophetic SA semantics into STA. The embedding proceeds similar to the embedding from the previous subsection, but makes sure that nothing but spent lifetimes are considered.
Definition 6
The STA translation of an SA M as above is the STA

where  are the clock variables and \(\bar{E}\) is the smallest edge function such that the following inference rules are satisfied:
are the clock variables and \(\bar{E}\) is the smallest edge function such that the following inference rules are satisfied:

where  .
.
The update \(\mathrm {Set}_\mathrm {\bar{n}}\) resets the newly introduced clock \(w\) and allows the nondeterministic selection of a value in \(\mathbb {R}^+ \) for \(d_{w}\). It thus corresponds to the nondeterministic choice of “scheduler delay” of rule \(\textit{choice}_\mathrm {n}\) in the non-prophetic semantics of SA.
Notably, this embedding is linear in the size of the original SA. The inference rules of Definitions 5 and 6 together build the very same TPTS as the rules for the non-prophetic semantics in Definition 3, as expressed by the following theorem:
Theorem 2
We have \(\llbracket M \rrbracket = \llbracket \overline{M} \rrbracket \).
Remark 2
For decidability reasons, definitions of timed automata concepts usually avoid the possibility to read clock values in update assignments. We instead do read clock values, but, in fact, this is done only to simplify the exposition. Actually, as all delays are stored into (non-clock) variables before each waiting, we can determine the current value of any clock on expiration by accessing non-clock variables only. When adapting the STA model in such a way, the resulting TPTS would however not be identical but only bisimilar to the non-prophetic semantics of TPTS.
5.4 Analysis of STA
The above semantic translation maps on STA models, for which, in turn, two different analysis techniques are available: Simulation (also called statistical model checking), as for example implemented in the modes [5] tool, and model checking using an abstraction of the continuous measures as implemented in the mcsta tool [14]. Both are part of the Modest Toolset [16].
The simulation approach is inherently restricted to models that do not contain nondeterministic choices, neither in terms of the discrete jumps nor when it comes to delays. It is thus of limited use for the cases we consider in this paper where schedulers, and thus nondeterministic choices, play an important role. Some techniques based on partial order and confluence reduction are available to simulate restricted classes of nondeterministic models [4, 17] in a sound manner, however they focus thus far on the untimed model of Markov decision processes, and are limited to cases where the scheduler choices are guaranteed to not influence the analysis results. The confluence-based approach has been lifted to the Markov automata [28] model, which is semantically very close to stochastic automata [18]. If properly lifted to STA, it would then be applicable to SA models where scheduling power does not matter with respect to the non-prophetic semantics.
On the other hand, the model-checking technique implemented in mcsta is generally applicable across STA. It can deliver upper and lower bounds on maximum or minimum reachability probabilities and expected cumulative reward values. Technically, it proceeds by replacing the sampling from continuous probability measures by sampling from a discrete probability distribution over a number of intervals that cover the measure’s support, followed by a continuous nondeterministic choice over the concrete values from the chosen time interval. This turns an STA into an overapproximating probabilistic timed automaton (PTA), for which existing model checking techniques such as the digital clocks approach [20] can be used to compute the values in question. That PTA analysis relies on the inability to read the exact values of clock variables, as mentioned above. It therefore makes it necessary to resort to the notationally more complex workaround discussed in Remark 2. When connecting this with the mcsta approach, a technical obstacle remains in the abstraction of continuous sampling by discrete sampling plus nondeterministic choices over time intervals: The resolution of the latter is in fact delegated to the PTA analysis, but the concrete values picked inside the time intervals need to be taken into account for resampling, which so far is not supported. One viable way to overcome this lifts the digital clocks semantics to STA by restricting to integer clock valuations prior to moving to PTA. This appears not to affect the soundness of the abstraction. We consider this approach as an interesting technical challenge, for which we have presented the foundations along with this paper.
6 Discussion and Conclusion
This paper has discussed to what extent formalisms for concurrent systems operating in stochastic continuous time can be equipped with a meaningful semantics, especially in the sense that schedulers are not supposed to be prophets. The results presented do enable us to encode the SQC calculus of Zeng, Nielson and Nielson into STA, and pave the way for non-prophetic model checking provided via the Modest Toolset.
Relative to the survey paper by Bravetti and D’Argenio [7] we did, for simplicity, not consider priorities of actions. However, we see no obstacle in including this feature in our setting, since the concept is orthogonal to the other SA ingredients.
Unlike D’Argenio [10] and Bravetti [8], we only focussed on closed systems, i.e. systems which are not subject to composition with other systems. This is rooted in the observation that the semantics we propose is not compositional. Let us illustrate this on a simple example of two components that need to get synchronised by a delayable action a: component A needs to finish some task (modelled by the expiration of a clock c) before the synchronization, whereas component B is ready to synchronize from the start. In the SA \(A \Vert B\) obtained by parallel composition [11] of A and B, one naturally obtains a transition with the delayable action a that can be taken at any time after the clock c expires.
The (natural) parallel compositions of the TPTS induced by the residual lifetimes semantics or the spent lifetimes semantics, i.e. \(\llbracket A \rrbracket _\mathrm {r}\Vert \llbracket B \rrbracket _\mathrm {r}\) or \(\llbracket A \rrbracket _\mathrm {s}\Vert \llbracket B \rrbracket _\mathrm {s}\), coincide with the semantics of the composed SA, i.e. \(\llbracket A \Vert B \rrbracket _\mathrm {r}\) or \(\llbracket A \Vert B \rrbracket _\mathrm {s}\): They include the possibility of action a being scheduled at any time after clock c expires. However, as we pointed out in this paper, these semantics enable undesired prophetic or divine scheduling.
Unfortunately, the parallel composition \(\llbracket A \rrbracket _\mathrm {n}\Vert \llbracket B \rrbracket _\mathrm {n}\) of the TPTS induced by our non-prophetic semantics allows different behaviour than the semantics of the composed SA, \(\llbracket A\Vert B \rrbracket _\mathrm {n}\). The former does not allow the a-labelled transition to be freely scheduled at any time after c expires. In particular, the scheduler can take the transition at the moment when c expires only with probability 0. This is because the scheduler needs to choose a delay d first (for B); then the composed system needs to wait for d time units; and only then, action a can be taken (by A), provided clock c has expired in the meantime. If it has not expired yet, the scheduler needs to choose another delay \(d'\) and so on. This does not allow the scheduler to react immediately to the fact that c has just expired. On the other hand the latter approach, \(\llbracket A\Vert B \rrbracket _\mathrm {n}\), which applies our non-prophetic semantics to the composed SA avoids any such problems and captures exactly the desired behaviour.
We leave a compositional and non-prophetic semantics as an open problem and conjecture that it is not possible, unless striving for a different parallel composition operator that would circumvent the problem sketched above.
Notes
- 1.
In this paper we restrict all F(c) to absolutely continuous measures as it simplifies the overall notation and the technical treatment. Recall that a measure is absolutely continuous if it assigns 0 to any set with Lebesgue measure 0.
- 2.
Note that this is not Zeno behaviour: An edge will eventually be taken after a finite number of steps with probability 1.
References
ns-2 wiki. http://nsnam.isi.edu/nsnam/
ns-3. https://www.nsnam.org/
Andel, T.R., Yasinsac, A.: On the credibility of Manet simulations. IEEE Computer 39(7), 48–54 (2006)
Bogdoll, J., Ferrer Fioriti, L.M., Hartmanns, A., Hermanns, H.: Partial Order Methods for Statistical Model Checking and Simulation. In: Bruni, R., Dingel, J. (eds.) FORTE 2011 and FMOODS 2011. LNCS, vol. 6722, pp. 59–74. Springer, Heidelberg (2011)
Bogdoll, J., Hartmanns, A., Hermanns, H.: Simulation and statistical model checking for Modestly nondeterministic models. In: Schmitt, J.B. (ed.) MMB/DFT. LNCS, vol. 7201, pp. 249–252. Springer, Heidelberg (2012)
Bohnenkamp, H.C., D’Argenio, P.R., Hermanns, H., Katoen, J.-P.: MoDeST: a compositional modeling formalism for hard and softly timed systems. IEEE Trans. Software Eng. 32(10), 812–830 (2006)
Bravetti, M., D’Argenio, P.R.: Tutte le algebre insieme: concepts, discussions and relations of stochastic process algebras with general distributions. In: Baier, C., Haverkort, B.R., Hermanns, H., Katoen, J.-P., Siegle, M. (eds.) Validation of Stochastic Systems. LNCS, vol. 2925, pp. 44–88. Springer, Heidelberg (2004)
Bravetti, M., Gorrieri, R.: The theory of interactive generalized semi-Markov processes. Theor. Comput. Sci. 282(1), 5–32 (2002)
Cavin, D., Sasson, Y., Schiper, A.: On the accuracy of MANET simulators. In: POMC, pp. 38–43. ACM (2002)
D’Argenio, P.R., Katoen, J.-P.: A theory of stochastic systems, part I: stochastic automata. Inf. Comput. 203(1), 1–38 (2005)
D’Argenio, P.R., Katoen, J.-P.: A theory of stochastic systems, part II: process algebra. Inf. Comput. 203(1), 39–74 (2005)
Giro, S., D’Argenio, P.R.: Quantitative model checking revisited: neither decidable nor approximable. In: Raskin, J.-F., Thiagarajan, P.S. (eds.) FORMATS 2007. LNCS, vol. 4763, pp. 179–194. Springer, Heidelberg (2007)
Haas, P.J., Shedler, G.S.: Regenerative generalized semi-Markov processes. Commun. Stat. Stoch. Models 3(3), 409–438 (1987)
Hahn, E.M., Hartmanns, A., Hermanns, H.: Reachability and reward checking for stochastic timed automata. In: ECEASST, 70 (2014)
Harrison, P.G., Strulo, B.: SPADES - a process algebra for discrete event simulation. J. Log. Comput. 10(1), 3–42 (2000)
Hartmanns, A., Hermanns, H.: The Modest Toolset: an integrated environment for quantitative modelling and verification. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014 (ETAPS). LNCS, vol. 8413, pp. 593–598. Springer, Heidelberg (2014)
Hartmanns, A., Timmer, M.: Sound statistical model checking for MDP using partial order and confluence reduction. STTT 17(4), 429–456 (2015)
Hermanns, H., Krčál, J., Křetínský, J.: Probabilistic bisimulation: naturally on distributions. In: Baldan, P., Gorla, D. (eds.) CONCUR 2014. LNCS, vol. 8704, pp. 249–265. Springer, Heidelberg (2014)
Kurkowski, S., Camp, T., Colagrosso, M.: MANET simulation studies: the incredibles. Mob. Comput. Commun. Rev. 9(4), 50–61 (2005)
Kwiatkowska, M.Z., Norman, G., Parker, D., Sproston, J.: Performance analysis of probabilistic timed automata using digital clocks. Formal Methods Syst. Design 29(1), 33–78 (2006)
Matthes, K.: Zur Theorie der Bedienungsprozesse. In: Transactions of the 3rd Prague Conference on Information Theory, Statistics Decision Functions and Random Processes, pp. 513–528 (1962)
Nielson, F., Nielson, H.R., Zeng, K.: Stochastic model checking of the stochastic quality calculus. In: De Nicola, R., Hennicker, R. (eds.) Wirsing Festschrift. LNCS, vol. 8950, pp. 522–537. Springer, Heidelberg (2015)
Pongor, G.: OMNeT: objective modular network testbed. In: MASCOTS, pp. 323–326. The Society for Computer Simulation (1993)
Puterman, M.L.: Markov Decision Processes: Discrete Stochastic Dynamic Programming, 1st edn. John Wiley & Sons Inc, New York (1994)
Segala, R.: Modeling and Verification of Randomized Distributed Real-Time Systems. Ph.D thesis, Laboratory for Computer Science, Massachusetts Institute of Technology (1995)
Stojmenovic, I.: Simulations in wireless sensor and ad hoc networks: matching and advancing models, metrics, and solutions. IEEE Commun. Mag. 46(12), 102–107 (2008)
Strulo, B.: Process algebra for discrete event simulation. Ph.D thesis, Imperial College of Science, Technology and Medicine. University of London, October 1993
Timmer, M., van de Pol, J., Stoelinga, M.I.A.: Confluence reduction for Markov automata. In: Braberman, V., Fribourg, L. (eds.) FORMATS 2013. LNCS, vol. 8053, pp. 243–257. Springer, Heidelberg (2013)
Wolovick, N.: Continuous probability and nondeterminism in labeled transaction systems. PhD thesis, Universidad Nacional de Córdoba, Córdoba (2012)
Zeng, X., Bagrodia, R., Gerla, M.: GloMoSim: a library for parallel simulation of large-scale wireless networks. In: PADS, pp. 154–161. IEEE Computer Society (1998)
Acknowledgements
This work is partly supported by the German Research Council (DFG) as part of the Transregional Collaborative Research Center AVACS (SFB/TR 14), by the Czech Science Foundation under grant agreement P202/12/G061, by the EU 7th Framework Programme under grant agreement no. 295261 (MEALS) and 318490 (SENSATION), by the CDZ project 1023 (CAP), and by the CAS/SAFEA International Partnership Program for Creative Research Teams.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hartmanns, A., Hermanns, H., Krčál, J. (2016). Schedulers are no Prophets. In: Probst, C., Hankin, C., Hansen, R. (eds) Semantics, Logics, and Calculi. Lecture Notes in Computer Science(), vol 9560. Springer, Cham. https://doi.org/10.1007/978-3-319-27810-0_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-27810-0_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-27809-4
Online ISBN: 978-3-319-27810-0
eBook Packages: Computer ScienceComputer Science (R0)






 is the initial location.
is the initial location. is the initial state.
is the initial state. : Boolean expressions
e have
: Boolean expressions
e have  .
.  include e.g.
include e.g.  : Arithmetic expressions
e have
: Arithmetic expressions
e have  .
. 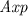 include e.g.
include e.g. 
 : Sampling expressions
e have
: Sampling expressions
e have  . These are conceptually arithmetic expression featuring two additional constructs: nondeterministic choice and random sampling.
. These are conceptually arithmetic expression featuring two additional constructs: nondeterministic choice and random sampling.  include, e.g.,
include, e.g., 
 denotes the random selection of a value according to the probability measure F and
denotes the random selection of a value according to the probability measure F and  the nondeterministic selection of a value out of the interval I. In the example,
the nondeterministic selection of a value out of the interval I. In the example, 
 is a finite set of variables with a subset
is a finite set of variables with a subset  is the edge function, which maps each location to a set of edges, which in turn consist of a guard, a deadline, a label and a probability distribution over updates and target locations; and
is the edge function, which maps each location to a set of edges, which in turn consist of a guard, a deadline, a label and a probability distribution over updates and target locations; and is the initial location.
is the initial location.