Stochastic Methods for Solving High-Dimensional Partial Differential Equations

Abstract

We propose algorithms for solving high-dimensional Partial Differential Equations (PDEs) that combine a probabilistic interpretation of PDEs, through Feynman–Kac representation, with sparse interpolation. Monte-Carlo methods and time-integration schemes are used to estimate pointwise evaluations of the solution of a PDE. We use a sequential control variates algorithm, where control variates are constructed based on successive approximations of the solution of the PDE. Two different algorithms are proposed, combining in different ways the sequential control variates algorithm and adaptive sparse interpolation. Numerical examples will illustrate the behavior of these algorithms.

1 Introduction

We consider the solution of an elliptic partial differential equation

$$\begin{aligned} \begin{aligned} {\mathscr {A}}(u)&= g \quad \text {in} \quad {\mathscr {D}}, \\ u&= f \quad \text {on} \quad \partial {\mathscr {D}}, \end{aligned} \end{aligned}$$

(1)

where $u : \overline{{\mathscr {D}}} \rightarrow {\mathbb {R}}$ is a real-valued function, and ${\mathscr {D}}$ is an open bounded domain in ${\mathbb {R}}^d$. ${\mathscr {A}}$ is an elliptic linear differential operator and $f : \partial {{\mathscr {D}}} \rightarrow {\mathbb {R}}$, $g: \overline{{\mathscr {D}}} \rightarrow {\mathbb {R}}$ are respectively the boundary condition and the source term of the PDE.

We are interested in approximating the solution of (1) up to a given precision. For high dimensional PDEs ($d \gg 1$), this requires suitable approximation formats such as sparse tensors [4, 21] or low-rank tensors [1, 15, 16, 19, 20]. Also, this requires algorithms that provide approximations in a given approximation format. Approximations are typically provided by Galerkin projections using variational formulations of PDEs. Another path consists in using a probabilistic representation of the solution u through Feynman–Kac formula, and Monte-Carlo methods to provide estimations of pointwise evaluations of u (see e.g., [14]). This allows to compute approximations in a given approximation format through classical interpolation or regression [2, 3, 22]. In [11, 12], the authors consider interpolations on fixed polynomial spaces and propose a sequential control variates method for improving the performance of Monte-Carlo estimation. In this paper, we propose algorithms that combine this variance reduction method with adaptive sparse interpolation [5, 6].

The outline is as follows. In Sect. 2, we recall the theoretical and numerical aspects associated to probabilistic tools for estimating the solution of (1). We also present the sequential control variates algorithm introduced in [11, 12]. In Sect. 3 we introduce sparse polynomial interpolation methods and present a classical adaptive algorithm. In Sect. 4, we present two algorithms combining the sequential control variates algorithm from Sect. 2 and adaptive sparse polynomial interpolation. Finally, numerical results are presented in Sect. 4.

2 Probabilistic Tools for Solving PDEs

We consider the problem (1) with a linear partial differential operator defined by ${\mathscr {A}}(u) = -{\mathscr {L}}(u) + k u$, where k is a real valued function defined on $\overline{{\mathscr {D}}}$, and where

$$\begin{aligned} {\mathscr {L}}(u)({x}) = \dfrac{1}{2} \sum _{i,j=1}^d (\sigma ({x}) \sigma ({x})^T)_{ij} \partial ^2_{{x}_i {x}_j}u({x}) + \sum _{i=1}^d b_i({x}) \partial _{{x}_i}u({x}) \end{aligned}$$

(2)

is the infinitesimal generator associated to the d-dimensional diffusion process ${X}^{{x}}$ solution of the stochastic differential equation

$$\begin{aligned} d {X}^{{x}}_t = b({X}^{{x}}_t) dt + \sigma ({X}^{{x}}_t) d W_t, \quad {X}^{{x}}_0 = {x}\in \overline{{\mathscr {D}}}, \end{aligned}$$

(3)

where W is a d-dimensional Brownian motion and $b := (b_1, \ldots , b_d)^T : {\mathbb {R}}^d \rightarrow {\mathbb {R}}^d$ and $\sigma : {\mathbb {R}}^d \rightarrow {\mathbb {R}}^{d\times d}$ stand for the drift and the diffusion respectively.

2.1 Pointwise Evaluations of the Solution

The following theorem recalls the Feynman–Kac formula (see [8, Theorem 2.4] or [9, Theorem 2.4] and the references therein) that provides a probabilistic representation of $u({x})$, the solution of (1) evaluated at ${x}\in {\overline{{\mathscr {D}}}}$.

Theorem 1

(Feynman–Kac formula) Assume that  

(H1):

${\mathscr {D}}$ is an open connected bounded domain of ${\mathbb {R}}^d$, regular in the sense that, if $\tau ^{{x}} = \inf \left\{ s > 0 ~ : ~ {X}^{{x}}_s \notin {\mathscr {D}}\right\}$ is the first exit time of ${\mathscr {D}}$ for the process ${X}^{{x}}$, we have

$$ {\mathbb {P}}(\tau ^{x}= 0) = 1, \quad {x}\in \partial {\mathscr {D}}, $$

(H2):

$b,\sigma$ are Lipschitz functions,

(H3):

f is continuous on $\partial {\mathscr {D}}$, g and $k \ge 0$ are Hölder-continuous functions on $\overline{{\mathscr {D}}}$,

(H4):

(uniform ellipticity assumption) there exists $c > 0$ such that

$$ \sum _{i,j=1}^d \left( \sigma ({x}) \sigma ({x})^T \right) _{ij} \xi _i \xi _j \ge c \sum _{i=1}^d \xi _i^2, \quad \xi \in {\mathbb {R}}^d, \; {x}\in \overline{{\mathscr {D}}}. $$

 

Then, there exists a unique solution of (1) in ${\mathscr {C}}( \overline{{\mathscr {D}}} ) \cap {\mathscr {C}}^2 \left( {\mathscr {D}}\right)$, which satisfies for all ${x}\in \overline{{\mathscr {D}}}$

$$\begin{aligned} \begin{aligned} u({x})&= \mathbb {E} \left[ F(u,{X}^{{x}}) \right] \\ \end{aligned} \end{aligned}$$

(4)

where

$$\begin{aligned} F(u,{X}^{x}) = u({X}^{{x}}_{\tau ^{{x}}}) \exp \left( - \int _0^{\tau ^{{x}}} k({X}^{{x}}_t) dt \right) + \int _0^{\tau ^{{x}}} {\mathscr {A}}(u)({X}^{{x}}_t) \exp \left( - \int _0^t k({X}^{{x}}_s) ds \right) dt, \end{aligned}$$

with $u({X}^{{x}}_{\tau ^{{x}}}) = f({X}^{{x}}_{\tau ^{{x}}})$ and ${\mathscr {A}}(u)({X}^{{x}}_t) = g({X}^{{x}}_t)$.

Note that $F(u,X^x)$ in (4) only depends on the values of u on $\partial D$ and ${\mathscr {A}}(u)$ on D, which are the given data f and g respectively. A Monte-Carlo method can then be used to estimate u(x) using (4), which relies on the simulation of independent samples of an approximation of the stochastic process ${X}^{x}$. This process is here approximated by an Euler–Maruyama scheme. More precisely, letting $t_n = n\varDelta t$, $n\in \mathbb {N}$, ${X}^{{x}}$ is approximated by a piecewise constant process ${X}^{{x}, \varDelta t}$, where ${X}^{{x}, \varDelta t}_t = {X}^{{x}, \varDelta t}_n$ for $t \in [t_n,t_{n+1}[$ and

$$\begin{aligned} \begin{aligned} {X}^{{x}, \varDelta t}_{n+1}&= {X}^{{x}, \varDelta t}_n + \varDelta t ~ b({X}^{{x}, \varDelta t}_n) + \sigma ({X}^{{x}, \varDelta t}_n) ~ \varDelta W_n, \\ {X}^{{x}, \varDelta t}_0&= {x}. \end{aligned} \end{aligned}$$

(5)

Here $\varDelta W_n = W_{n+1} - W_n$ is an increment of the standard Brownian motion. For details on time-integration schemes, the reader can refer to [17]. Letting $\{ {X}^{{x}, \varDelta t}(\omega _m) \}_{m=1}^M$ be independent samples of ${X}^{{x}, \varDelta t}$, we obtain an estimation $u_{\varDelta t,M}({x})$ of $u({x})$ defined as

$$\begin{aligned} \begin{aligned} u_{\varDelta t,M}({x})&:= \dfrac{1}{M} \sum _{m=1}^M F \left( u,{X}^{{x}, \varDelta t}(\omega _m) \right) \\&= \dfrac{1}{M} \sum _{m=1}^M \bigg [ f({X}^{{x},\varDelta t}_{\tau ^{{x},\varDelta t}}(\omega _m)) \exp \left( - \int _0^{\tau ^{{x},\varDelta t}} k({X}^{{x},\varDelta t}_t(\omega _m)) dt \right) \\&+ \int _0^{\tau ^{{x},\varDelta t}} g({X}^{{x},\varDelta t}_t(\omega _m)) \exp \left( - \int _0^t k({{X}}^{{x},\varDelta t}_s(\omega _m)) ds \right) dt \bigg ] \end{aligned} \end{aligned}$$

(6)

where $\tau ^{{x},\varDelta t}$ is the first exit time of D for the process ${X}^{{x},\varDelta t}(\omega _m)$, given by

$$ \tau ^{{x},\varDelta t} = \inf \left\{ t> 0 ~ : ~ {X}^{{x},\varDelta t}_t \notin {\mathscr {D}}\right\} = \min \left\{ t_n > 0 ~ : ~ {X}^{{x},\varDelta t}_{t_n} \notin {\mathscr {D}}\right\} . $$

Remark 1

In practice, f has to be defined over $\mathbb {R}^d$ and not only on the boundary $\partial \mathcal D$. Indeed, although $X^{{x}}_{\tau ^{{x}}} \in \partial \mathcal D$ with probability one, $X^{{x},\varDelta t}_{\tau ^{{x},\varDelta t}} \in \mathbb {R}^d \setminus \overline{{\mathscr {D}}}$ with probability one.

The error can be decomposed in two terms

$$\begin{aligned} \begin{aligned} u({x}) - u_{\varDelta t,M}({x}) =&\overbrace{u({x}) - {\mathbb {E}}\left[ F \left( u,{X}^{{x},\varDelta t} \right) \right] }^{\varepsilon _{\varDelta t}} \\&+ \underbrace{{\mathbb {E}}\left[ F \left( u,{X}^{{x},\varDelta t} \right) \right] - \dfrac{1}{M} \sum _{m=1}^M F \left( u,X^{{x}, \varDelta t}(\omega _m) \right) }_{\varepsilon _{MC}}, \end{aligned} \end{aligned}$$

(7)

where $\varepsilon _{\varDelta t}$ is the time integration error and $\varepsilon _{MC}$ is the Monte-Carlo estimation error. Before discussing the contribution of each of both terms to the error, let us introduce the following additional assumption, which ensures that ${\mathscr {D}}$ does not have singular points.¹

(H5) Each point of $\partial {\mathscr {D}}$ satisfies the exterior cone condition which means that, for all ${x}\in \partial {\mathscr {D}}$, there exists a finite right circular cone K, with vertex ${x}$, such that $\overline{K} \cap \overline{{\mathscr {D}}}= \{ {x}\}$.

Under assumptions (H1)–(H5), it can be proven [12, Sect. 4.1] that the time integration error $\varepsilon _{\varDelta t}$ converges to zero. It can be improved to $O(\varDelta t^{1/2})$ by adding differentiability assumptions on the boundary [13]. The estimation error $\varepsilon _{MC}$ is a random variable with zero mean and standard deviation converging as $O ( M^{-1/2})$. The computational complexity for computing a pointwise evaluation of $u_{\varDelta t,M}({x})$ is in $O \left( M \varDelta t^{-1} \right)$ in expectation for $\varDelta t$ sufficiently small,² so that the computational complexity for achieving a precision $\varepsilon$ (root mean squared error) behaves as $O(\varepsilon ^{-4})$. This does not allow to obtain a very high accuracy in a reasonable computational time. The convergence with $\varDelta t$ can be improved to $O(\varDelta t)$ by suitable boundary corrections [13], therefore yielding a convergence in $O(\varepsilon ^{-3}).$ To further improve the convergence, high-order integration schemes could be considered (see [17] for a survey). Also, variance reduction methods can be used to further improve the convergence, such as antithetic variables, importance sampling, control variates (see [14]). Multilevel Monte-Carlo [10] can be considered as a variance reduction method using several control variates (associated with processes $X^{{x},\varDelta t_k}$ using different time discretizations). Here, we rely on the sequential control variates algorithm proposed in [11] and analyzed in [12]. This algorithm constructs a sequence of approximations of u. At each iteration of the algorithm, the current approximation is used as a control variate for the estimation of u through Feynman–Kac formula.

2.2 A Sequential Control Variates Algorithm

Here we recall the sequential control variates algorithm introduced in [11] in a general interpolation framework. We let $V_\varLambda \subset {\mathscr {C}}^2(\overline{{\mathscr {D}}})$ be an approximation space of finite dimension $\# \varLambda$ and let ${\mathscr {I}}_\varLambda : \mathbb {R}^{\mathscr {D}}\rightarrow V_\varLambda$ be the interpolation operator associated with a unisolvent grid $\varGamma _\varLambda = \{ {x}_{\varvec{\nu }}: {\varvec{\nu }}\in \varLambda \}$. We let $(l_\nu )_{{\varvec{\nu }}\in \varLambda }$ denote the (unique) basis of $V_\varLambda$ that satisfies the interpolation property $l_\nu ({x}_{\varvec{\mu }}) = \delta _{{\varvec{\nu }}{\varvec{\mu }}}$ for all ${\varvec{\nu }},{\varvec{\mu }}\in \varLambda$. The interpolation ${\mathscr {I}}_\varLambda (w) = \sum _{\nu \in \varLambda } w(x_\nu ) l_\nu (x)$ of function w is then the unique function in $V_\varLambda$ such that

$$ {\mathscr {I}}_\varLambda (w) (x_\nu ) = w(x_\nu ), \quad \nu \in \varLambda . $$

The following algorithm provides a sequence of approximations $({\tilde{u}}^k)_{k \ge 1}$ of u in $V_\varLambda$, which are defined by ${\tilde{u}}^{k}= {\tilde{u}}^{k-1} + {\tilde{e}}^{k}$, where ${\tilde{e}}^{k}$ is an approximation of $e^k$, solution of

$$\begin{aligned} \begin{array}{rcll} &{}{\mathscr {A}}(e^k)({x}) = g({x}) - {\mathscr {A}}({\tilde{u}}^{k-1})({x}), &{} {x}\in {\mathscr {D}},\\ &{} e^k({x}) = f({x})- {\tilde{u}}^{k-1}({x}), &{}{x}\in \partial {\mathscr {D}}. \end{array} \end{aligned}$$

Note that $e^k$ admits a Feyman–Kac representation $e^k(x) = \mathbb {E}(F(e^k, X^{{x}}))$, where $F(e^k, X^{{x}})$ depends on the residuals $g - {\mathscr {A}}({\tilde{ u}}^{k-1})$ on $\mathcal D$ and $f - {\tilde{u}}^{k-1}$ on $\partial {\mathscr {D}}$. The approximation ${\tilde{e}}^k$ is then defined as the interpolation ${\mathscr {I}}_\varLambda (e^k_{\varDelta t,M})$ of the Monte-Carlo estimate $e^k_{\varDelta t,M}(x)$ of $e^k_{\varDelta t}(x) = \mathbb {E}(F(e^k, X^{{x},\varDelta t}))$ (using M samples of $X^{x,\varDelta t}$).

Algorithm 1

(Sequential control variates algorithm)

For practical reasons, Algorithm 1 is stopped using an heuristic error criterion based on stagnation. This criterion is satisfied when the desired tolerance $\varepsilon _{tol}$ is reached for $n_s$ successive iterations (in practice we chose $n_s =5$).

Now let us provide some convergence results for Algorithm 1. To that goal, we introduce the time integration error at point ${x}$ for a function h

$$\begin{aligned} e^{\varDelta t}(h,{x}) = \mathbb {E} [ F ( h, {X}^{\varDelta t, {x}} ) ] - \mathbb {E} [ F \left( h, {X}^{x}\right) ]. \end{aligned}$$

(8)

Then the following theorem [12, Theorem 3.1] gives a control of the error in expectation.

Theorem 2

Assuming (H2)–(H5), it holds

$$\begin{aligned} \sup _{{\varvec{\nu }}\in \varLambda } \left| \mathbb {E} \left[ {\tilde{u}}^{n+1}({x}_{\varvec{\nu }}) - u( {x}_{\varvec{\nu }}) \right] \right| \leqslant C(\varDelta t,\varLambda ) \sup _{{\varvec{\nu }}\in \varLambda } \left| \mathbb {E} \left[ {\tilde{u}}^{n}({x}_{\varvec{\nu }}) - u({x}_{\varvec{\nu }}) \right] \right| + C_1(\varDelta t,\varLambda ) \end{aligned}$$

with $\displaystyle C(\varDelta t,\varLambda ) = \underset{{\varvec{\nu }}\in \varLambda }{\sup } \sum _{{\varvec{\mu }}\in \varLambda } \vert e^{\varDelta t}({l}_{\varvec{\mu }},{x}_{\varvec{\nu }}) \vert$ and $C_1(\varDelta t,\varLambda ) = \sup _{{\varvec{\nu }}\in \varLambda } \left| e^{\varDelta t}(u - {\mathscr {I}}_\varLambda (u),{x}_{\varvec{\nu }}) \right|$.

Moreover if $C(\varDelta t,\varLambda ) ~ < 1$, it holds

$$\begin{aligned} \limsup _{n\rightarrow \infty } ~ \underset{{\varvec{\nu }}\in \varLambda }{\sup } \left| \mathbb {E} \left[ {\tilde{u}}^{n}({x}_{\varvec{\nu }}) - u({x}_{\varvec{\nu }}) \right] \right| \leqslant \dfrac{C_1(\varDelta t,\varLambda )}{1 - C(\varDelta t,\varLambda )}. \end{aligned}$$

(9)

The condition $C(\varDelta t,\varLambda ) < 1$ implies that in practice $\varDelta t$ should be chosen sufficiently small [12, Theorem 4.2]. Under this condition, the error at interpolation points uniformly converges geometrically up to a threshold term depending on time integration errors for interpolation functions $l_\nu$ and the interpolation error $u - {\mathscr {I}}_\varLambda (u)$.

Theorem 2 provides a convergence result at interpolation points. Below, we provide a corollary to this theorem that provides a convergence result in $L^{{\infty }}({{\mathscr {D}}})$. This result involves the Lebesgue constants in $L^{{\infty }}$-norm associated to ${\mathscr {I}}_\varLambda$, defined by

$$ {{\mathscr {L}}_{\varLambda }} = \sup _{v \in {\mathscr {C}^0(\overline{{\mathscr {D}}})}} \dfrac{\Vert {\mathscr {I}}_\varLambda (v)\Vert _{{\infty }}}{\Vert v\Vert _{{\infty }}}, $$

and such that for any $v \in {{\mathscr {C}}^0(\overline{{\mathscr {D}}})}$,

$$\begin{aligned} \Vert v - {\mathscr {I}}_\varLambda (v) \Vert _{{\infty }} \le ( 1 + {{\mathscr {L}}_\varLambda } ) \inf _{w \in V_\varLambda } \Vert v-w \Vert _{{\infty }}. \end{aligned}$$

(10)

Throughout this article, we adopt the convention that supremum exclude elements with norm 0. We recall also that the $L^\infty$ Lebesgue constant can be expressed as ${\mathscr {L}}_{\varLambda }=\sup _{x \in \overline{{\mathscr {D}}}} \sum _{\nu \in \varLambda } | l_\nu ({x})|$.

Corollary 1

(Convergence in $L^{{\infty }}$) Assuming (H2)–(H5), one has

$$\begin{aligned} \limsup _{n\rightarrow \infty } ~ \Vert \mathbb {E} \left[ {\tilde{u}}^{n} - u \right] \Vert _{{\infty }} \leqslant \dfrac{C_1(\varDelta t,\varLambda )}{1 - C(\varDelta t,\varLambda )} {{\mathscr {L}}_{\varLambda }} + \Vert u - {\mathscr {I}}_\varLambda (u)\Vert _{{\infty }}. \end{aligned}$$

(11)

Proof

By triangular inequality, we have

$$\begin{aligned} \Vert {\mathbb {E}}\left[ {\tilde{u}}^n - u \right] \Vert _{{\infty }} \leqslant \Vert {\mathbb {E}}\left[ {\tilde{u}}^n - {\mathscr {I}}_\varLambda (u) \right] \Vert _{{\infty }} + \Vert {\mathscr {I}}_\varLambda (u) - u \Vert _{{\infty }}. \end{aligned}$$

We can build a continuous function w such that $w(x_\nu ) = {\mathbb {E}}\left[ {\tilde{u}}^n(x_\nu ) - u(x_\nu ) \right]$ for all $\nu \in \varLambda$, and such that

$$\Vert w \Vert _\infty = \sup _{\nu \in \varLambda } \vert w(x_\nu ) \vert = \sup _{{\varvec{\nu }}\in \varLambda } \left| \mathbb {E} \left[ {\tilde{u}}^{n}({x}_{\varvec{\nu }}) - u({x}_{\varvec{\nu }}) \right] \right| .$$

We have then

$$\begin{aligned} \Vert {\mathbb {E}}\left[ {\tilde{u}}^n - {\mathscr {I}}_\varLambda (u) \right] \Vert _{{\infty }} = \Vert {\mathscr {I}}_\varLambda (w) \Vert _{{\infty }} \le {\mathscr {L}}_\varLambda \Vert w \Vert _{{\infty }}. \end{aligned}$$

The result follows from the definition of the function w and Theorem 2.   $\square$

Remark 2

Since for bounded domains ${\mathscr {D}}$, we have

$$\begin{aligned} \Vert v \Vert _2 \le | {\mathscr {D}}|^{1/2} \Vert v \Vert _\infty , \end{aligned}$$

for all v in ${\mathscr {C}}^0(\overline{{\mathscr {D}}})$, where $|{\mathscr {D}}|$ denotes the Lebesgue measure of ${\mathscr {D}}$, we can deduce the convergence results in $L^2$ norm from those in $L^\infty$ norm.

3 Adaptive Sparse Interpolation

We here present sparse interpolation methods following [5, 6].

3.1 Sparse Interpolation

For $1\le i \le d$, we let $\{\varphi _{k}^{(i)}\}_{k \in {{\mathbb {N}}_0}}$ be a univariate polynomial basis, where $\varphi ^{(i)}_k(x_i)$ is a polynomial of degree k. For a multi-index $\nu = (\nu _1,\dots ,\nu _d) \in {\mathbb {N}_0^d}$, we introduce the multivariate polynomial

$$\varphi _{\varvec{\nu }}({x}) = \prod _{i=1}^d \varphi _{\nu _i}^{(i)}(x_i).$$

For a subset $\varLambda \subset \mathbb {N}^d$, we let ${\mathscr {P}}_{\varLambda } = \mathrm {span} \{ \varphi _{\varvec{\nu }}: \nu \in \varLambda \}$. A subset $\varLambda$ is said to be downward closed if

$$ \forall {\varvec{\nu }}\in \varLambda , ~ {\varvec{\mu }}\le {\varvec{\nu }}\Rightarrow {\varvec{\mu }}\in \varLambda . $$

If $\varLambda$ is downward closed, then the polynomial space ${\mathscr {P}}_{\varLambda }$ does not depend on the choice of univariate polynomial bases and is such that ${\mathscr {P}}_{\varLambda } = \mathrm {span} \{ x^\nu : \nu \in \varLambda \}$, with $x^\nu = x_1^{\nu _1} \ldots x_d^{\nu _d}$.

In the case where ${\mathscr {D}}= {\mathscr {D}}_1 \times \cdots \times {\mathscr {D}}_d$, we can choose for $\{\varphi ^{(i)}_k\}_{k \in {{\mathbb {N}}_0}}$ an orthonormal basis in $L^2({\mathscr {D}}_i)$ (i.e. a rescaled and shifted Legendre basis). Then $\{\varphi _\nu \}_{\nu \in {\mathbb {N}_0^d}}$ is an orthonormal basis of $L^2(\mathcal D).$ To define a set of points $\varGamma _\varLambda$ unisolvent for ${\mathscr {P}}_{\varLambda }$, we can proceed as follows. For each dimension $1\le i\le d$, we introduce a sequence of points $\{z^{(i)}_k\}_{k \in {{\mathbb {N}}_0}}$ in $\overline{{\mathscr {D}}}_i$ such that for any $p\ge 0$, $\varGamma ^{(i)}_{p} = \{z^{(i)}_k\}_{k= 0}^{p}$ is unisolvent for ${\mathscr {P}}_p = \mathrm {span}\{\varphi ^{(i)}_k : 0\le k\le p\}$, therefore defining an interpolation operator ${\mathscr {I}}^{(i)}_{p}$. Then we let

$$\varGamma _\varLambda = \{ z_\nu = (z_{\nu _1}^{(1)}, \ldots , z_{\nu _d}^{(d)}) : \nu \in \varLambda \} \subset \overline{ {\mathscr {D}}}.$$

This construction is interesting for adaptive sparse algorithms since for an increasing sequence of subsets $\varLambda _n$, we obtain an increasing sequence of sets $\varGamma _{\varLambda _n}$, and the computation of the interpolation on ${\mathscr {P}}_{\varLambda _n}$ only requires the evaluation of the function on the new set of points $\varGamma _{\varLambda _n} \setminus \varGamma _{\varLambda _{n-1}}.$ Also, with such a construction, we have the following property of the Lebesgue constant of ${\mathscr {I}}_{\varLambda }$ in $L^{{\infty }}$-norm. This result is directly taken from [6, Sect. 3].

Proposition 1

If for each dimension $1\le i \le d$, the sequence of points $\{z_k^{(i)}\}_{k \in {{\mathbb {N}}_0}}$ is such that the interpolation operator ${\mathscr {I}}_p^{(i)}$ has a Lebesgue constant ${{\mathscr {L}}_p} \le (p+1)^s$ for some $s>0$, then for any downward closed set $\varLambda$, the Lebesgue constant ${{\mathscr {L}}_\varLambda }$ satisfies

$$\begin{aligned} {{\mathscr {L}}_\varLambda } \le \left( \# \varLambda \right) ^{s+1}. \end{aligned}$$

(12)

Leja points or magic points [18] are examples of sequences of points such that the interpolation operators ${\mathscr {I}}_p^{(i)}$ have Lebesgue constants not growing too fast with p. For a given $\varLambda$ with $\rho _i:=\max _{\nu \in \varLambda } \nu _i$, it is possible to construct univariate interpolation grids $\varGamma ^{(i)}_{\rho _i}$ with better properties (e.g., Chebychev points), therefore resulting in better properties for the associated interpolation operator ${\mathscr {I}}_\varLambda$. However for Chebychev points, e.g., $\rho _i \le \rho '_i$ does not ensure $\varGamma ^{(i)}_{\rho _i} \subset \varGamma ^{(i)}_{\rho '_i}$. Thus with such univariate grids, an increasing sequence of sets $\varLambda _n$ will not be associated with an increasing sequence of sets $\varGamma _{\varLambda _n}$, and the evaluations of the function will not be completely recycled in adaptive algorithms. However, for some of the algorithms described in Sect. 4, this is not an issue as evaluations can not be recycled anyway.

Note that for general domains ${\mathscr {D}}$ which are not the product of intervals, the above constructions of grids $\varGamma _\varLambda$ are not viable since it may yield to grids not contained in the domain ${\mathscr {D}}$. For such general domains, magic points obtained through greedy algorithms could be considered.

3.2 Adaptive Algorithm for Sparse Interpolation

An adaptive sparse interpolation algorithm consists in constructing a sequence of approximations $(u_n)_{n\ge 1}$ associated with an increasing sequence of downward closed subsets $(\varLambda _n)_{n \ge 1}$. According to (10), we have to construct a sequence such that the best approximation error and the Lebesgue constant are such that

$$ {{\mathscr {L}}_{\varLambda _n}} \inf _{w \in {\mathscr {P}}_{\varLambda _n}} \Vert u - w \Vert _{{\infty }} \longrightarrow 0 \text { as } n \rightarrow \infty $$

for obtaining a convergent algorithm. For example, if

$$\begin{aligned} \inf _{w \in {\mathscr {P}}_{\varLambda _n}}\Vert u - w \Vert _{{\infty }} = O((\#\varLambda _n)^{-r}) \end{aligned}$$

(13)

holds³ for some $r > 1$ and if ${\mathscr {L}}_{\varLambda _n} =O(( \#\varLambda _n)^k)$ for $k<r$, then the error $\Vert u - u_n \Vert _{{\infty }} = O(n^{-r'})$ tends to zero with an algebraic rate of convergence $r' = r-k>0$. Of course, the challenge is to propose a practical algorithm that constructs a good sequence of sets $\varLambda _m$.

We now present the adaptive sparse interpolation algorithm with bulk chasing procedure introduced in [5]. Let $\theta$ be a fixed bulk chasing parameter in (0, 1) and let ${\mathscr {E}}_{\varLambda }(v)= \Vert P_{\varLambda }(v)\Vert ^2_2$, where $P_\varLambda$ is the orthogonal projector over ${\mathscr {P}}_\varLambda$ for any subset $\varLambda \subset {{\mathbb {N}}_0^d}$.

Algorithm 2

(Adaptive interpolation algorithm)

At iteration n, Algorithm 2 selects a subset of multi-indices $N_n$ in the reduced margin of $\varLambda _n$ defined by

$$\begin{aligned} {\mathscr {M}}_{\varLambda _n} = \{ {\varvec{\nu }}\in {\mathbb {N}}^d \setminus \varLambda _n : \forall j \; \text {s.t.} \; \nu _j>0,\; {\varvec{\nu }}- {\varvec{e}}_j \in \varLambda _n \}, \end{aligned}$$

where $({\varvec{e}}_j)_{k} = \delta _{kj}.$ The reduced margin is such that for any subset $S\subset {\mathscr {M}}_{\varLambda _n}$, ${\varLambda _n} \cup S$ is downward closed. This ensures that the sequence $(\varLambda _n)_{n\ge 1}$ generated by the algorithm is an increasing sequence of downward closed sets. Finally, Algorithm 2 is stopped using a criterion based on

$$\begin{aligned} \varepsilon ^n = \dfrac{{\mathscr {E}}_{{\mathscr {M}}_n}({\mathscr {I}}_{\varLambda _n^\star }(u))}{{\mathscr {E}}_{\varLambda _n^\star }({\mathscr {I}}_{\varLambda _n^\star }(u))}. \end{aligned}$$

4 Combining Sparse Adaptive Interpolation with Sequential Control Variates Algorithm

We present in this section two ways of combining Algorithms 1 and 2. First we introduce a perturbed version of Algorithm 2 and then an adaptive version of Algorithm 1. At the end of the section, numerical results will illustrate the behavior of the proposed algorithms.

4.1 Perturbed Version of Algorithm 2

As we do not have access to exact evaluations of the solution u of (1), Algorithm 2 can not be used for interpolating u. So we introduce a perturbed version of this algorithm, where the computation of the exact interpolant ${\mathscr {I}}_{\varLambda }(u)$ is replaced by an approximation denoted ${\tilde{ u}}_\varLambda$, which can be computed for example with Algorithm 1 stopped for a given tolerance $\varepsilon _{tol}$ or at step k. This brings the following algorithm.

Algorithm 3

(Perturbed adaptive sparse interpolation algorithm)

4.2 Adaptive Version of Algorithm 1

As a second algorithm, we consider the sequential control variates algorithm (Algorithm 1) where at step 4, an approximation ${\tilde{e}}^k$ of $e^k$ is obtained by applying the adaptive interpolation algorithm (Algorithm 3) to the function $e^{k}_{\varDelta t,M}$, which uses Monte-Carlo estimations $e^{k}_{\varDelta t,M}(x_\nu )$ of $e^k(x_\nu )$ at interpolation points. At each iteration, ${\tilde{e}}^k$ therefore belongs to a different approximation space ${\mathscr {P}}_{\varLambda _k}.$ In the numerical section, we will call this algorithm adaptive Algorithm  1.

4.3 Numerical Results

In this section, we illustrate the behavior of algorithms previously introduced on different test cases. We consider the simple diffusion equation

$$\begin{aligned} \begin{array}{rcll} - \triangle u(x) &{}=&{} g(x), ~~~ &{} x \in {\mathscr {D}}, \\ u(x) &{}=&{} f(x), ~~~ &{} x \in \partial {\mathscr {D}}, \\ \end{array} \end{aligned}$$

(14)

were ${\mathscr {D}}= ]-1,1[^d$. The source terms and boundary conditions will be specified later for each test case.

The stochastic differential equation associated to (14) is the following

$$\begin{aligned} d X^x_t = \sqrt{2} d W_t, \quad X^x_0 = x, \end{aligned}$$

(15)

where $(W_t)_{t \ge 0}$ is a d-dimensional Brownian motion.

We use tensorized grids of magic points for the selection of interpolation points evolved in adaptive algorithms.

Small dimensional test case. We consider a first test case (TC1) in dimension $d= 5$. Here the source term and the boundary conditions in problem (14) are chosen such that the solution is given by

$$\begin{aligned} u(x) =x_1^2+sin(x_2)+exp(x_3)+sin(x_4) (x_5+1), \qquad x \in \overline{{\mathscr {D}}}. \end{aligned}$$

(TC1)

Fig. 1

(TC1) Algorithm 1 for fixed $\varLambda$: evolution of $\Vert u-{\tilde{u}}^k_{\varLambda ^6}\Vert$ with respect to k for various M (left figure), and various $\varDelta t$ (right figure)

We first test the influence of $\varDelta t$ and M on the convergence of Algorithm 1 when $\varLambda$ is fixed. In that case, $\varLambda$ is selected a priori with Algorithm 2 using samples of the exact solution u for (TC1), stopped for $\varepsilon \in \{10^{-6}, 10^{-8},10^{-10}\}$. In what follows, the notation $\varLambda ^i$ stands for the set obtained for $\varepsilon = 10^{-i}, i\in \{6,8,10\}$. We represent on Fig. 1 the evolution of the absolute error in $L^2$-norm (similar results hold for the $L^\infty$-norm) between the approximation and the true solution with respect to step k for $\varLambda =\varLambda ^6$. As claimed in Corollary 1, we recover the geometric convergence up to a threshold value that depends on $\varDelta t$. We also notice faster convergence as M increases and when $\varDelta t$ decreases. We fix $M=1000$ in the next simulations.

Fig. 2

(TC1) Algorithm 1 for fixed $\varLambda ^i$: evolution of $\Vert u- {\tilde{u}}^k_{\varLambda ^i}\Vert _2$ with respect to k for $i=8$ (left figure), and $i=10$ (right figure)

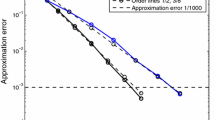
We study the impact of the choice of $\varLambda ^i$ on the convergence of Algorithm 1. Again we observe on Fig. 2 that the convergence rate gets better as $\varDelta t$ decreases. Moreover as $\# \varLambda$ increases the threshold value decreases. This is justified by the fact that interpolation error decreases as $\#\varLambda ^i$ increases (see Table 1). Nevertheless, we observe that it may also deteriorate the convergence rate if it is chosen too large together with $\varDelta t$ not sufficiently small. Indeed for the same number of iterations $k=10$ and the same time-step $\varDelta t = 2.5 \cdot 10^{-3}$, we have an approximate absolute error equal to $10^{-7}$ for $\varLambda ^{8}$ against $10^{-4}$ for $\varLambda ^{10}$.

Table 1 Algorithm 2 computed on the exact solution of (TC1): evolution of $\#\varLambda _n$, error criterion $\varepsilon ^n$ and interpolation errors in norms $L^2$ and $L^\infty$ at each step n

We present now the behavior of Algorithm 3. Simulations are performed with a bulk-chasing parameter $\theta = 0.5$. At each step n of Algorithm 3, we use Algorithm 1 with $(\varDelta t,M) = (10^{-4},1000)$, stopped when a stagnation is detected. As shown on the left plot of Fig. 3, for $\#\varLambda _n = 55$ we reach approximately a precision of $10^{-14}$ as for Algorithm 2 performed on the exact solution (see Table 1). According to the right plot of Fig. 3, we also observe that the enrichment procedure behaves similarly for both algorithms (${\tilde{\varepsilon }}^n$ and $\varepsilon ^n$ are almost the same). Here using the approximation provided by Algorithm 1 has a low impact on the behavior of Algorithm 2.

Fig. 3

(TC1) Comparison of Algorithm 2 applied to exact solution and Algorithm 3: (left) absolute error in $L^2$-norm (right) evolution of $\varepsilon ^n$ and ${\tilde{\varepsilon }}^n$ with respect to $\#\varLambda _n$

We present then results provided with the adaptive Algorithm 1. The parameters chosen for the adaptive interpolation are $\varepsilon =5 \cdot 10^{-2}$, $\theta = 0.5$. $K=30$ ensures the stopping of Algorithm 1. As illustrated by Fig. 4, we recover globally the same behavior as for Algorithm 1 without adaptive interpolation. Indeed as k increases, both absolute errors in $L^2$-norm and $L^\infty$-norm decrease and then stagnate. Again, we notice the influence of $\varDelta t$ on the stagnation level. Nevertheless, the convergence rates are deteriorated and the algorithm provides less accurate approximations than Algorithm 3. This might be due to the sparse adaptive interpolation procedure, which uses here pointwise evaluations based on Monte-Carlo estimates, unlike Algorithm 3 which relies on pointwise evaluations resulting from Algorithm 1 stopping for a given tolerance.

Fig. 4

(TC1) Adaptive Algorithm 1: evolution of $\Vert u-u^k_{\varLambda _k}\Vert _2$ (continuous line) and $\Vert u-u^k_{\varLambda _k}\Vert _\infty$ (dashed line) with respect to step k and $\varDelta t$

Finally in Table 2, we compare the algorithmic complexity of these algorithms to reach a precision of $3 \cdot 10^{-5}$ for $(\varDelta t,M)=(10^{-4},1000)$. For adaptive Algorithm 1, $\varLambda _k$ refers to the set of multi-indices considered at step k of Algorithm 1. For Algorithm 3, $N_n$ stands for the number of iteration required by Algorithm 1 to reach tolerance $\varepsilon _{tol}$ at step n. Finally, Algorithm 1 is run with full-grid $\varLambda =\varLambda _{max}$ where $\varLambda _{max} = \{ \nu \in {\mathbb {N}}^d ~:~ \nu _i \le 10 \}$ is the set of multi-indices allowing to reach the machine precision. In this case, N stands for the number of steps for this algorithm to converge.

Table 2 (TC1) Comparison of the algorithmic complexity to reach the precision $3 \cdot 10^{-5}$, with $(\varDelta t,M)=(10^{-4},1000)$

We observe that both the adaptive version of Algorithms 1 and 3 have a similar complexity, which is better than for the full-grid version of Algorithm 1. Moreover, we observed that while adaptive version of Algorithm 1 stagnates at a precision of $3 \cdot 10^{-5}$, Algorithm 3, with the same parameters $\varDelta t$ and M, converges almost up to the machine precision. This is why the high-dimensional test cases will be run only with Algorithm 3.

Higher-dimensional test cases. Now, we consider two other test cases noted respectively (TC2) and (TC3) in higher dimension.  

(TC2):

As second test case in dimension $d=10$, we define (14) such that its solution is the Henon–Heiles potential

$$u(x) = \dfrac{1}{2} \sum _{i=1}^d x_i^2 +0.2 \sum _{i=1}^{d-1} \left( x_i x_{i+1}^2 - x_i^3 \right) + 2.5~10^{-3} \sum _{i=1}^{d-1} \left( x_i^2 + x^2_{i+1} \right) ^2, \qquad x \in \overline{{\mathscr {D}}}.$$

We set $(\varDelta t, M) =(10^{-4},1000)$ and $K = 30$ for Algorithm 1.

(TC3):

We also consider the problem (14) whose exact solution is a sum of non-polynomial functions, like (TC1) but now in dimension $d=20$, given by

$$\begin{aligned} \begin{aligned} u(x) = x_1^2+sin(x_{12})+exp(x_5)+sin(x_{15})(x_8+1). \end{aligned} \end{aligned}$$

Here, the Monte-Carlo simulations are performed for $(\varDelta t, M) = (10^{-4},1000)$ and $K=30$.

  Since for both test cases the exact solution is known, we propose to compare the behavior of Algorithms 3 and 2. Again, the approximations ${\tilde{u}}_n$, at each step n of Algorithm 3, are provided by Algorithm 1 stopped when a stagnation is detected. In both cases, the parameters for Algorithm 3 are set to $\theta = 0.5$ and $\varepsilon = 10^{-15}$.

In Tables 3 and 4, we summarize the results associated to the exact and perturbed sparse adaptive algorithms for (TC2) and (TC3) respectively. We observe that Algorithm 3 performs well in comparison to Algorithm 2, for (TC2). Indeed, we get an approximation with a precision below the prescribed value $\varepsilon$ for both algorithms.

Table 3 (TC2) Comparison of Algorithm 2 (first four columns) and Algorithm 3 (last four columns)

Similar observation holds for (TC3) in Table 4 and this despite the fact that the test case involves higher dimensional problem.

Table 4 (TC3) Comparison of Algorithm 2 (first four columns) and Algorithm 3 (last four columns)

5 Conclusion

In this paper we have introduced a probabilistic approach to approximate the solution of high-dimensional elliptic PDEs. This approach relies on adaptive sparse polynomial interpolation using pointwise evaluations of the solution estimated using a Monte-Carlo method with control variates.

Especially, we have proposed and compared different algorithms. First we proposed Algorithm 1 which combines the sequential algorithm proposed in [11] and sparse interpolation. For the non-adaptive version of this algorithm we recover the convergence up to a threshold as the original sequential algorithm [12]. Nevertheless it remains limited to small-dimensional test cases, since its algorithmic complexity remains high. Hence, for practical use, the adaptive Algorithm 1 should be preferred. Adaptive Algorithm 1 converges but it does not allow to reach low precision with reasonable number of Monte-Carlo samples or time-step in the Euler–Maruyama scheme. Secondly, we proposed Algorithm 3. It is a perturbed sparse adaptive interpolation algorithm relying on inexact pointwise evaluations of the function to approximate. Numerical experiments have shown that the perturbed algorithm (Algorithm 3) performs well in comparison to the ideal one (Algorithm 2) and better than the adapted Algorithm 1 with a similar algorithmic complexity. Here, since only heuristic tools have been provided to justify the convergence of this algorithm, the proof of its convergence, under assumptions on the class of functions to be approximated, should be addressed in a future work.