Numerical Implementation of Phase-Field Models of Brittle Fracture

Abstract

These lecture notes address the main challenging computational aspects of phase-field modeling of brittle fracture. We focus, in particular, on the irreversibility constraint and the iterative solution strategy for non-convex minimization problems. In the former case, we present multiple options of incorporating the constraint and discuss the equivalence of the resulting formulations. For the latter, we also consider various available options and critically assess the efficiency and robustness of some of them. Numerical examples on well-known benchmark problems illustrate the theoretical findings.

Introduction

The phase-field framework for modeling systems with sharp interfaces consists in incorporating a continuous field variable – the so-called order parameter – which differentiates between multiple physical phases within a given system through a smooth transition. In the context of fracture, such an order parameter (termed the crack phase-field) describes the smooth transition between the fully broken and intact material phases, thus approximating the sharp crack discontinuity, as sketched in Fig. 1a. The evolution of this field as a result of the external loading conditions models the fracture process.

The phase-field approach to brittle fracture dates back to the seminal work of Francfort and Marigo (1998) on the variational formulation of quasi-static brittle fracture and to the related regularized formulation of Bourdin et al. (2000, 2008), Bourdin (2007a, b). The former is the mathematical theory of quasi-static brittle fracture mechanics, which recasts Griffith’s energy-based principle Griffith (1921) as the minimisation problem of an energy functional. The latter presents an approximation, in the sense of $\Gamma$-convergence, of the energy functional and is designed to enable the efficient numerical treatment.

Fig. 1

a Phase-field description of fracture (sketchy) with $\alpha \in C(\Omega ,[0,1])$ as the crack phase-field; b mechanical system setup used for representation purposes in Section “Formulation”

The phase-field simulation of fracture processes holds a number of advantages over classical techniques with discrete fracture description, whose numerical implementation requires explicit (in the classical finite element method, FEM) or implicit (within the extended FEM) handling of the discontinuities. The most obvious one is the ability to track automatically a cracking process by the evolution of the smooth crack field on a fixed mesh. The possibility to avoid the tedious task of tracking complicated crack surfaces in 3d significantly simplifies the finite element implementation. The second advantage is the ability to simulate complicated processes, including crack initiation (also in the absence of a singularity), propagation, coalescence, branching and bifurcation without the need for additional ad-hoc criteria. With the formulation capability to also distinguish between fracture behavior in tension and compression, no supplementary contact problem has to be posed for preventing crack faces interpenetration.

The currently available phase-field formulations of brittle fracture encompass static and dynamic models. We mention the papers by Del Piero et al. (2007), Lancioni and Royer-Carfagni (2009), Amor et al. (2009), Freddi and Royer-Carfagni (2009, 2010), Kuhn and Müller (2010), Miehe et al. (2010a, b), Pham et al. (2011), Borden (2012), Borden et al. (2014), Vignollet et al. (2014), Mesgarnejad et al. (2015), Kuhn et al. (2015), Ambati et al. (2015), Marigo et al. (2016), Strobl and Seelig (2016), Weinberg and Hesch (2017), Tanné et al. (2018), Sargado et al. (2018), Gerasimov et al. (2018), Wu and Nguyen (2018), Wu et al. (2019), where various formulations are developed and validated. Recently, the framework has been also extended to ductile (elasto-plastic) fracture Miehe et al. (2015, 2016), Duda et al. (2015), Ambati et al. (2015), Alessi et al. (2015, 2018), Borden et al. (2016), fracture in films Mesgarnejad et al. (2013), León Baldelli et al. (2014), shells Amiria et al. (2014), Ambati and De Lorenzis (2016), Kiendl et al. (2016), Reinoso et al. (2017), fracture under thermal loading Sicsic et al. (2013), Bourdin et al. (2014), Miehe et al. (2015), hydraulic fracture Bourdin et al. (2012), Wheeler et al. (2014), Mikelić et al. (2015a, b, c), Wilson and Landis (2016), fracture in porous media Miehe and Mauthe (2016), Wu and De Lorenzis (2016), Cajuhi et al. (2018), anisotropic fracture Li et al. (2015), Teichtmeister et al. (2017), Zhang et al. (2017), Nguyen et al. (2017), Bleyer and Alessi (2018), Li and Maurini (2019), fracture in laminates Alessi and Freddi (2017), to name a few.

Fig. 2

Challenging aspects of phase-field computing of brittle fracture with implications

The three important aspects of the formulation in the brittle case, which give rise to algorithmic challenges within the finite element treatment, and which have recently been a subject of intensive studies are the following:

• (A) non-convexity of the governing energy functional with respect to the displacement and the phase-field arguments,

• (B) irreversibility constraint for the crack phase-field,

• (C) smallness of the regularization parameter (i.e., the length scale inherent to the diffusive crack approximation).

Figure 2 sketches the above aspects along with the related implications.

The lack of convexity (A) poses the major difficulty within the so-called monolithic treatment of the weak formulation, which aims at solving for both unknowns simultaneously. It is manifested via convergence issues of the direct Newton-Raphson iterative procedure Gerasimov and De Lorenzis (2016), Heister et al. (2015), Wick (2017a, b). Some new results by Gerasimov and De Lorenzis (2016), Heister et al. (2015), and Wick (2017a, b) on modified Newton-Raphson schemes, and by Kopanicakova and Krause (2019) on the trust region method hold a promise for improving the robustness of the monolithic approach. Alternatively (and more commonly), the staggered (also termed partitioned, or alternate minimization) solution strategy based on decoupling of the weak formulation into a system and then iterating between the equations is used Bourdin et al. (2000, 2008), Bourdin (2007a, b), Amor et al. (2009), Miehe et al. (2010a, b), Pham et al. (2011), Borden et al. (2014), Mesgarnejad et al. (2015), Ambati et al. (2015). The staggered scheme is intrinsically robust, but typically has a very slow convergence behavior of the iterative solution process, see e.g., Ambati et al. (2015), Gerasimov and De Lorenzis (2016), Farrell and Maurini (2017). Recently, the results by Farrell and Maurini (2017) on accelerated over-relaxed partitioned schemes indicate the possibility for the staggered approach to gain better efficiency. The aforementioned approaches are outlined in Fig. 3.

Fig. 3

Iterative solution approaches for solving the weak formulation $\mathcal {E}^\prime =0$ with $\mathcal {E}$ denoting the energy functional for the mechanical system under consideration

Due to (B), the formulation is a constrained minimization problem, whose optimality condition is a variational inequality Amor et al. (2009), Pham et al. (2011), Mesgarnejad et al. (2015), Marigo et al. (2016), thus requiring special solution algorithms. Several options of enforcing the constraint that lead to a simpler equality-based formulation and which can be classified as relaxed, penalized, and implicit ones are found in the literature, see Gerasimov and De Lorenzis (2019) for an overview. Within the first class Bourdin et al. (2000, 2008), Bourdin (2007a, b), Del Piero et al. (2007), Lancioni and Royer-Carfagni (2009), Gerasimov and De Lorenzis (2016), Burke et al. (2010a, b, 2013), Artina et al. (2014, 2015), the irreversibility of the crack phase-field is enforced only on the so-called ‘crack-set’ (the points of the domain where the phase-field variable exceeds some threshold value). In this case, irreversibility of only a fully developed crack is modeled, and therefore the technique is termed relaxed. With regard to the second class, we recall the augmented-Lagrangian method in Wheeler et al. (2014), Wick (2017a, b), as well as an advancement of the Lagrange multipliers method using a primal-dual active set strategy Heister et al. (2015). Both approaches allow for both the staggered and the fully monolithic treatment, but may require solving for extra variable(s) Wheeler et al. (2014), Wick (2017a, b), and the necessity of tracing explicitly various (active and inactive) sets in which the corresponding sub-problems are to be solved Heister et al. (2015). Also, a simpler penalization procedure is advocated in Gerasimov and De Lorenzis (2019), with the advantage that the optimally defined penalty parameter guarantees a sufficiently accurate user-prescribed enforcement of the crack phase-field irreversibility. Finally, the implicit enforcement of the constraint using a so-called ‘history field’ was proposed in Miehe et al. (2010b) and has been adopted in a major amount of works on the topic. This approach, however, yields a problem of non-variational nature, whose equivalence to the original formulation cannot be proven. Also, in this case, only the staggered solution scheme can be employed. The above options of incorporating the constraint are summarized in Fig. 4.

Fig. 4

Options to incorporate the irreversibility constraint $\dot{\alpha }\ge 0$ for the crack phase-field

Finally, property (C) calls for extremely fine meshes, at least locally in the crack phase-field transition zone. Modeling a failure process whose final pattern is not known in advance precludes the construction of a suitably pre-refined mesh, thus forcing to compute on fixed uniform meshes (unless adaptivity is introduced). In this case, the computational cost is very high. Already in the seminal paper by Bourdin et al. (2000) and later in Mesgarnejad et al. (2015) parallel computing has been advocated for the staggered solution scheme combined with uniformly fine meshes. Recent findings by Burke et al. (2010a, b, 2013), Artina et al. (2014, 2015) and Wick (2016) on error-controlled adaptive mesh refinement strategies, as well as by Heister et al. (2015), Klinsmann et al. (2015) and Nagaraja et al. (2018) on physics-motivated procedures for mesh adaptivity provide a basis to efficiently tackle (C) as well.

The rest of this chapter is organized as follows. In Section “Formulation”, we outline the main concepts of phase-field modeling of brittle fracture including major ingredients of the formulation such as coupling function, tension-compression split of the elastic energy density function, local energy dissipation function etc. The incremental variational problem which models a quasi-static fracture evolution, required for the numerical treatment, is then presented. Section “Treatment of Irreversibility” presents various ideas for incorporating the irreversibility constraint and the resulting weak formulations, whereas Section “Solution Strategies” discusses the available iterative solution strategies for the formulations. Both sections are complemented by illustrative numerical examples. In the simulations, we employ the numerical package FreeFem++ Hecht et al. (2019). Both the displacement field and the crack phase-field are approximated using linear triangles on fixed (non-adaptive) finite element meshes, which are pre-adapted (refined) in the region where crack propagation is expected.

Formulation

In this section, for a mechanical system undergoing brittle fracture we recall the phase-field formulation that models this process, and outline its main ingredients.

Governing Energy Functional

Let $\Omega \subset \mathbb {R}^d$, $d=2,3$ be an open and bounded domain representing the configuration of a d-dimensional linear elastic body, and let $\Gamma _{D,0},\Gamma _{D,1}$ and $\Gamma _{N,1}$ be the (non-overlapping) portions of the boundary $\partial \Omega$ of $\Omega$ on which homogeneous Dirichlet, non-homogeneous Dirichlet and Neumann boundary conditions are prescribed, respectively. The body is assumed to be linearly elastic and isotropic, with the elastic strain energy density function given by $\Psi (\varvec{\varepsilon }):=\frac{1}{2}\varvec{\varepsilon }:\mathbb {C}:\varvec{\varepsilon }=\frac{1}{2}\lambda \mathrm {tr}^2(\varvec{\varepsilon })+\mu \mathrm {tr}(\varvec{\varepsilon }\cdot \varvec{\varepsilon })$, where, in turn, $\varvec{\varepsilon }$ is the second-order infinitesimal strain tensor, $\mathbb {C}$ is the fourth-order elasticity tensor, and $\lambda$ and $\mu$ are the Lamé constants. Also, let $G_c$ be the material fracture toughness. A quasi-static loading process with the discrete pseudo-time step parameter $n=1,2,\ldots$, such that the displacement $\bar{\varvec{u}}_n$ and traction $\bar{\varvec{t}}_n$ loading data are prescribed on the corresponding parts of the boundary is considered. Finally, let $\Gamma _c\subset \Omega$ be the crack surface that is evolving during the process, see Fig. 1b.

For the mechanical system at hand, the variational approach to brittle fracture in Francfort and Marigo (1998) relies on the energy functional

$$\begin{aligned} \mathcal {E}(\varvec{u},\Gamma _c) = \underbrace{ \int _{\Omega \setminus \Gamma _c} \Psi (\varvec{\varepsilon }(\varvec{u})) \, \mathrm {d}{\varvec{x}}}_{\displaystyle E_\mathrm {el.}(\varvec{u},\Gamma _c)} + \underbrace{ G_c\int _{\Gamma _c} \mathrm {d}s}_{\displaystyle E_S(\Gamma _c)} -\int _{\Gamma _{N,1} } \bar{\varvec{t}}_n \cdot \varvec{u} \, \mathrm {d}s, \end{aligned}$$

(1)

with $\varvec{u}:\Omega \backslash \Gamma _c\rightarrow \mathbb {R}^d$ such that $\varvec{u}=\varvec{0}$ on $\Gamma _{D,0}$ and $\varvec{u}=\bar{\varvec{u}}_n$ on $\Gamma _{D,1}$ as the displacement field, $\Gamma _c$ as the crack set, and the related minimization problem at each $n\ge 1$. In (1), the functionals termed $E_\mathrm {el.}$ and $E_S$ represent the elastic energy stored in the body and the fracture surface energy dissipated within the fracture process. The latter rigorously reads $E_S(\Gamma _c)=G_c\mathcal {S}^{d-1}(\Gamma _c)$ with $\mathcal {S}^p$ as the so-called p-dimensional Hausdorff measure of the crack set $\Gamma _c$. In simple terms, $\mathcal {S}^1(\Gamma _c)$ and $\mathcal {S}^2(\Gamma _c)$ represent the length and the surface area of $\Gamma _c$ when $d=2$ and 3, respectively.

The regularization of (1) á la Bourdin et al. (2000, 2008), Bourdin (2007a, b), which is the basis for a variety of fracture phase-field formulations, reads as follows:

$$\begin{aligned} \mathcal {E}(\varvec{u},\alpha ) = \underbrace{ \int _\Omega {g}(\alpha )\Psi (\varvec{\varepsilon }(\varvec{u})) \, \mathrm {d}{\varvec{x}}}_{\displaystyle E_\mathrm {el.}(\varvec{u},\alpha )} + \underbrace{ \frac{G_c}{c_{w}} \int _\Omega \left( \frac{w(\alpha )}{\ell }+\ell |\nabla \alpha |^2\right) \mathrm {d}{\varvec{x}}}_{\displaystyle E_S(\alpha )} -\int _{\Gamma _{N,1} } \bar{\varvec{t}}_n \cdot \varvec{u} \, \mathrm {d}s, \end{aligned}$$

(2)

with $\varvec{u}:\Omega \rightarrow \mathbb {R}^d$ and $\alpha :\Omega \rightarrow [0,1]$ standing for the smeared counterparts of the discontinuous displacement and the crack set in (1). The phase-field variable $\alpha$ takes the value 1 on $\Gamma _c$, decays smoothly to 0 in a subset of $\Omega \backslash \Gamma _c$ and then takes the 0-value in the rest of the domain. With this definition, the limits $\alpha =1$ and $\alpha =0$ represent the fully broken and the intact (undamaged) material phases, respectively, whereas the intermediate range $\alpha \in (0,1)$ mimics the transition zone between them. The function g is responsible for the material stiffness degradation. The function w defines the decaying profile of $\alpha$, whereas the parameter $0<\ell \ll \mathrm {diam}(\Omega )$ controls the size of the localization zone of $\alpha$, in other words, the thickness of the transition zone between the two material states.

Degradation and local dissipation functions

The functions g and w are the major ingredients of (2), and their specific choice establishes the rigorous link between (1) and (2) when $\ell \rightarrow 0$ via the notion of $\Gamma$-convergence, see e.g., Braides (1998), Chambolle (2004), also giving a meaning to the induced constant $c_{w}$. Thus, g is a continuous monotonic function that fulfills the properties: ${g}(0)=1$, ${g}(1)=0$, ${g}^\prime (1)=0$ and ${g}^\prime (\alpha )<0$ for $\alpha \in [0,1)$, see e.g., Pham et al. (2011) for argumentation and discussion. The quadratic polynomial

$$\begin{aligned} {g}(\alpha ):=(1-\alpha )^2, \end{aligned}$$

(3)

is the simplest choice of the kind. The function w, also called the local part of the dissipated fracture energy density function Pham et al. (2011), is continuous and monotonic such that ${w}(0)=0$, ${w}(1)=1$ and ${w}^\prime (\alpha )\ge 0$ for $\alpha \in [0,1]$. The constant $c_{w}:=4\int _0^1\sqrt{w(t)}\,\mathrm {d}t$ is a normalization constant in the sense of $\Gamma$-convergence. The two suitable candidates for w reading

$$\begin{aligned} {w}(\alpha ): =\left\{ \begin{array}{l} \alpha , \\ \alpha ^2, \end{array} \right. \quad \text {such that} \quad c_{w}=\left\{ \begin{array}{ll} \frac{8}{3}, \\ 2, \end{array} \right. \end{aligned}$$

(4)

are widely adopted. Formulation (2) combined with the aforementioned choices for g and w are typically termed the $\mathtt {AT}$-1 and $\mathtt {AT}$-2 models, see Table 1. $\mathtt {AT}$ stands for Ambrosio-Tortorelli and the corresponding type of regularization, see Ambrosio and Tortorelli (1990). The main difference between the two models is that $\mathtt {AT}$-1 leads to the existence of an elastic stage before the onset of fracture, whereas using $\mathtt {AT}$-2 the phase-field starts to evolve as soon as the material is loaded, see e.g., Amor et al. (2009), Pham et al. (2011), Marigo et al. (2016) for a more detailed explanation.

Table 1 Ingredients of formulation (2) and (5)

Other representations for g and w are available in the literature, see e.g., Borden (2012), Borden et al. (2016), Kuhn et al. (2015), Sargadoa et al. (2018), Ambati et al. (2015), Alessi et al. (2015), Wilson and Landis (2016), Burke et al. (2010b, 2013).

Tension-compression split. Regarding the elastic strain energy function $\Psi$ the following must be noted. Due to the symmetry of $\Psi$ with respect to the variable $\varvec{u}$, formulation (2) does not distinguish between fracture behavior in tension and compression. In the numerical simulations, this is manifested by the mesh interpenetration inside of the compressed fractured zones, as reported e.g., in Bourdin et al. (2000, Sect. 3.3), Del Piero et al. (2007, Sect. 7) and Lancioni and Royer-Carfagni (2009, Sects. 4.1–4.3). In the discrete crack setting, this would be equivalent to compressive interpenetration of the crack faces. One of the proposed remedies for avoiding such a non-physical behavior implies placing $\Psi$ into the context of non-linear (finite) elasticity, as first presented in Del Piero et al. (2007). To remain within the framework of linear elasticity, the alternative is to break the symmetry by introducing an additive split of $\Psi$ into the so-called ‘tensile’ and ‘compressive’ parts $\Psi ^+$ and $\Psi ^-$, respectively, and enabling the degradation of $\Psi ^+$ only. This option is advocated in Lancioni and Royer-Carfagni (2009), Amor et al. (2009), Freddi and Royer-Carfagni (2009, 2010), Miehe et al. (2010a, b) and yields the following enhanced representation of (2):

$$\begin{aligned} \mathcal {E}(\varvec{u},\alpha )&= \int _\Omega \left[ {g}(\alpha )\Psi ^+(\varvec{\varepsilon }(\varvec{u}))+\Psi ^-(\varvec{\varepsilon }(\varvec{u})) \right] \mathrm {d}{\varvec{x}} + \frac{G_c}{c_w} \int _\Omega \left( \frac{w(\alpha )}{\ell }+\ell |\nabla \alpha |^2\right) \mathrm {d}{\varvec{x}} \nonumber \\&\quad -\int _{\Gamma _{N,1} } \bar{\varvec{t}}_n \cdot \varvec{u} \, \mathrm {d}s. \end{aligned}$$

(5)

The two widely adopted options for tension-compression splits $\Psi ^\pm$ are based respectively on the so-called volumetric-deviatoric decomposition of the strain tensor $\varvec{\varepsilon }$, i.e.,

$$\begin{aligned} \varvec{\varepsilon }=\varvec{\varepsilon }^\mathrm {dev}+\varvec{\varepsilon }^\mathrm {vol}, \end{aligned}$$

where $\varvec{\varepsilon }^\mathrm {vol}:=\frac{1}{d}\mathrm {tr}(\varvec{\varepsilon })\varvec{I}$, $\varvec{\varepsilon }^\mathrm {dev}:=\varvec{\varepsilon }-\varvec{\varepsilon }^\mathrm {vol}$ and $\varvec{I}$ is the second-order identity tensor, and the spectral decomposition of $\varvec{\varepsilon }$, namely,

$$\begin{aligned} \varvec{\varepsilon }=\varvec{\varepsilon }_{+}+\varvec{\varepsilon }_{-}, \end{aligned}$$

where $\varvec{\varepsilon }_{\pm }:=\sum _{i=1}^3\langle \varepsilon _i\rangle _{\pm }\varvec{n}_i\otimes \varvec{n}_i$ with $\{\varepsilon _i\}_{i=1}^3$ and $\{\varvec{n}_i\}_{i=1}^3$ as the principal strains and principal strain directions, respectively, and $\langle a\rangle _{\pm }:=\frac{1}{2}(a\pm |a|)$. The resulting representations read

$$\begin{aligned} \left\{ \begin{array}{l} \Psi ^{+}(\varvec{\varepsilon }):= \frac{1}{2}K_d\langle \mathrm {tr}(\varvec{\varepsilon }) \rangle _{+}^2 + \mu \mathrm {tr}(\varvec{\varepsilon }^\mathrm {dev}\cdot \varvec{\varepsilon }^\mathrm {dev}) \\ \Psi ^{-}(\varvec{\varepsilon }):= \frac{1}{2}K_d\langle \mathrm {tr}(\varvec{\varepsilon }) \rangle _{-}^2 \end{array} \right. \end{aligned}$$

(6)

with $K_d:=\lambda +\frac{2\mu }{d}$, and

$$\begin{aligned} \Psi ^\pm (\varvec{\varepsilon }):= \tfrac{1}{2}\lambda \langle \mathrm {tr}(\varvec{\varepsilon }) \rangle _{\pm }^2 + \mu \mathrm {tr}(\varvec{\varepsilon }_\pm \cdot \varvec{\varepsilon }_\pm ), \end{aligned}$$

(7)

respectively. Notice that (6) is independently presented in Amor et al. (2009) and Freddi and Royer-Carfagni (2009) (based on an extension of the split in Lancioni and Royer-Carfagni 2009), and (7) is considered in Miehe et al. (2010a, b). An idea similar to the latter one is also developed in Freddi and Royer-Carfagni (2010, Sect. 3.4). We refer the interested reader to the aforementioned publications and to Li (2016), where options for constructing $\Psi ^\pm$ and the related implications are explained.

Our final note here is that formulation (5) is what is usually referred to as phase-field model of brittle fracture (at least in the engineering literature). Despite the wide employment of the formulation, the $\Gamma$-convergence result that relates (5) to the original Francfort-Marigo formulation (1) is, in general, not available. Some particular results have recently been established in Chambolle et al. (2018).

Quasi-Static Evolution (Incremental Variational Problem)

With $\mathcal {E}$ defined by (5), the state of the system at a given loading step $n\ge 1$ is represented by

$$\begin{aligned} \mathrm {arg\,min} \{ \mathcal {E}(\varvec{u},\alpha ): \; {\varvec{u}}\in {\varvec{V}}_{\bar{\varvec{u}}_n}, \alpha \in \mathcal {D}_{\alpha _{n-1}} \}, \end{aligned}$$

(8)

where

$$\begin{aligned} {\varvec{V}}_{\bar{\varvec{u}}_n}:=\{ \varvec{u}\in {\varvec{H}}^1(\Omega ): \; \varvec{u}=\varvec{0} \; \mathrm {on} \; \Gamma _{D,0}, \; \varvec{u}=\bar{\varvec{u}}_n\; \mathrm {on} \; \Gamma _{D,1} \} \end{aligned}$$

is the kinematically admissible displacement space with ${\varvec{H}}^1(\Omega ):=[H^1(\Omega )]^d$ and $H^1$ denoting the usual Sobolev space, and

$$\begin{aligned} \mathcal {D}_{\alpha _{n-1}}:=\{ \alpha \in H^1(\Omega ): \; \alpha \ge \alpha _{n-1} \; \mathrm {in} \; \Omega \} \end{aligned}$$

is the admissible space for $\alpha$ with $\alpha _{n-1}$ known from the previous step. The condition $\alpha \ge \alpha _{n-1}$ in $\Omega$ is used to enforce the irreversibility of the crack phase-field evolution. It is the backward difference quotient form of $\dot{\alpha }\ge 0$ in $\Omega$.

Thus, quasi-static evolution of fracture within the system is then given by the sequence of the solution snapshots $\{(\varvec{u}_n,\alpha _n)\}$, $n\ge 1$.

Due to the $\alpha \ge \alpha _{n-1}$ requirement, the incremental variational problem (8) is a constrained minimization problem and its necessary optimality condition for computing the solution $(\varvec{u},\alpha )\in {\varvec{V}}_{\bar{\varvec{u}}_n}\times \mathcal {D}_{\alpha _{n-1}}$ is a variational inequality. Written down in the partitioned form, it reads

$$\begin{aligned} \boxed { \left\{ \begin{array}{l} {\mathcal E}^\prime _{\varvec{u}}(\varvec{u},\alpha ;\varvec{v})=0, \quad \forall \; \varvec{v}\in {\varvec{V}}_0, \\ {\mathcal E}^\prime _\alpha (\varvec{u},\alpha ;\beta -\alpha )\ge 0, \quad \forall \; \beta \in \mathcal {D}_{\alpha _{n-1}}, \end{array} \right. } \end{aligned}$$

(9)

see e.g. Burke et al. (2010b, 2013), Pham et al. (2011), Farrell and Maurini (2017), where ${\mathcal E}^\prime _{\varvec{u}}$ and ${\mathcal E}^\prime _\alpha$ are the directional derivatives of the energy functional with respect to $\varvec{u}$ and $\alpha$, respectively,

$$\begin{aligned} {\mathcal E}^\prime _{\varvec{u}}(\varvec{u},\alpha ;\varvec{v}):=\int _\Omega \left[ {g}(\alpha )\frac{\partial \Psi ^+}{\partial \varvec{\varepsilon }}(\varvec{\varepsilon }(\varvec{u})) +\frac{\partial \Psi ^-}{\partial \varvec{\varepsilon }}(\varvec{\varepsilon }(\varvec{u})) \right] :\varvec{\varepsilon }(\varvec{v})\,\mathrm {d}{\varvec{x}} -\int _{\Gamma _{N,1} } \bar{\varvec{t}}_n \cdot \varvec{v}\,\mathrm {d}s, \end{aligned}$$

(10)

$$\begin{aligned} {\mathcal E}^\prime _\alpha (\varvec{u},\alpha ;\beta ):=\int _\Omega \left[ {g}^\prime (\alpha )\Psi ^+(\varvec{\varepsilon }(\varvec{u}))\beta +\frac{G_c}{c_w}\left( \frac{1}{\ell }w^\prime (\alpha )\beta + 2\ell \nabla {\alpha }\cdot \nabla {\beta } \right) \right] \,\mathrm {d}{\varvec{x}}. \end{aligned}$$

(11)

The displacement test space in (9) is defined as ${\varvec{V}}_0:=\{ \varvec{v}\in {\varvec{H}}^1(\Omega ): \varvec{v}=\varvec{0} \; \mathrm {on} \; \Gamma _{D,0}\cup \Gamma _{D,1} \}$.

Treatment of Irreversibility

The variational inequality ${\mathcal E}^\prime _\alpha \ge 0$ in (9) that stems from the irreversibility constraint $\alpha \ge \alpha _{n-1}$ requires special solution algorithms, see e.g., Kinderlehrer and Stampacchia (1980), Glowinski et al. (1981) and Burke et al. (2010b, Sect. 5). In the following, we provide details about the three available options of handling $\alpha \ge \alpha _{n-1}$ mentioned in the introduction, which lead to the equality-based formulations and, hence, allow for simpler algorithmic treatment. The equivalence between the corresponding formulations and the reference one in (9) is highlighted and then illustrated by the numerical examples.

Relaxed (‘Crack-Set’ Irreversibility)

This is a version of irreversibility introduced by Bourdin et al. (2000, 2008), Bourdin (2007a, b) and also adopted e.g. by Burke et al. (2010a), which relies on the notion of a crack set: if at the current loading step n the (crack) set

$$\begin{aligned} \mathtt {CR}_{n-1}:=\{{\varvec{x}}\in \overline{\Omega }:\; \alpha _{n-1}({\varvec{x}})\ge \mathtt {CRTOL}\}, \end{aligned}$$

(12)

see Fig. 5 for a sketch where $0\ll \texttt {CRTOL}<1$ is a specified threshold, is non-empty, one explicitly sets $\alpha =1$ for all ${\varvec{x}}\in \texttt {CR}_{n-1}$, and the corresponding analogue to (8) to be solved at step n is

$$\begin{aligned} \mathrm {arg\,min} \{ \mathcal {E}(\varvec{u},d): \; {\varvec{u}}\in {\varvec{V}}_{\bar{\varvec{u}}_n}, \alpha \in \{H^1(\Omega ): \alpha |_{\mathtt {CR}_{n-1}}=1\} \}. \end{aligned}$$

(13)

The weak system of equations for $(\varvec{u},\alpha )$ in this case reads

$$\begin{aligned} \boxed { \left\{ \begin{array}{l} {\mathcal E}^\prime _{\varvec{u}}(\varvec{u},\alpha ;\varvec{v})=0, \quad \forall \; \varvec{v}\in {\varvec{V}}_0 \\ {\mathcal E}^\prime _\alpha (\varvec{u},\alpha ;\beta )=0, \quad \forall \; \beta \in \{H^1(\Omega ): \beta |_{\mathtt {CR}_{n-1}}=0\}, \end{array} \right. } \end{aligned}$$

(14)

where ${\mathcal E}^\prime _{\varvec{u}}$ and ${\mathcal E}^\prime _\alpha$ are given by (10) and (11), respectively. As noted in Amor et al. (2009), the present option can be viewed as a relaxed version of the requirement $\alpha \ge \alpha _{n-1}$ in $\Omega$ since it only enforces irreversibility of a fully developed crack, whereas phase-field patterns with $\alpha ({\varvec{x}})<\mathtt {CRTOL}$ for all ${\varvec{x}}\in \Omega$, which from the mechanical standpoint may be viewed as partially damaged regions, are allowed to heal.

Fig. 5

Illustration of a fully-developed crack phase-field $\alpha _{n-1}$ (left) and the related crack set $\mathtt {CR}_{n-1}$ (right); $\Gamma _c$ indicates the crack $\alpha _{n-1}$ relates to

Remark 3.1

Various algorithmic treatments of the ‘crack-set’ irreversibility can be found in Del Piero et al. (2007), and in Lancioni and Royer-Carfagni (2009). Its more sophisticated version is considered in Burke et al. (2010b, 2013).

Remark 3.2

In Artina et al. (2014, 2015) and Gerasimov and De Lorenzis (2016), the Dirichlet condition $\alpha |_{\mathtt {CR}_{n-1}}=1$ is enforced via penalization by introducing into (5) the functional

$$\begin{aligned} P(\alpha ;\tau ):=\frac{1}{2\tau }\int _{\mathtt {CR}_{n-1}}(1-\alpha )^2 \, \mathrm {d}{\varvec{x}}, \quad 0<\tau \ll 1, \end{aligned}$$

thus yielding the penalized counterpart of (13) and (14).

The choice of the threshold value $\mathtt {CRTOL}$ in (12) is subtle and may have a strong impact on the computational results, as shown in Burke et al. (2010b, 2013). A similar concern applies to the choice of $\tau$ in the corresponding penalized realization.

Implicit (‘History-Field’ Irreversibility)

In Miehe et al. (2010b), Miehe and co-workers proposed the idea of enforcing the irreversibility constraint $\alpha \ge \alpha _{n-1}$ implicitly, via the notion of a history-field. Their major assumption is that the tensile energy $\Psi ^+$ can be viewed as the driving force of the phase-field evolution and, hence, the maximal $\Psi ^+$ accumulated within the loading history, denoted as

$$\begin{aligned} \mathcal {H}_n({\varvec{x}}):= \max _{n\ge 1} \{ \mathcal {H}_{n-1}({\varvec{x}}),\Psi ^+(\varvec{\varepsilon }(\varvec{u})) \}, \quad \mathcal {H}_0\equiv 0, \end{aligned}$$

(15)

must guarantee the fulfillment of $\alpha \ge \alpha _{n-1}$. Technically, one substitutes $\mathcal {H}_n$ to $\Psi ^+$ in the original $\mathcal {E}^\prime _\alpha$ in (11) such that

$$\begin{aligned} \widetilde{\mathcal E}^\prime _\alpha (\varvec{u},\alpha ;w):=\int _\Omega \left[ {g}^\prime (\alpha )\mathcal {H}_n \beta +\frac{G_c}{c_w}\left( \frac{1}{\ell }w(\alpha ) \beta + 2\ell \nabla {\alpha }\cdot \nabla {\beta } \right) \right] \,\mathrm {d}{\varvec{x}}, \end{aligned}$$

(16)

and forms the system for computing the solution $(\varvec{u},\alpha )\in {\varvec{V}}_{\bar{\varvec{u}}_n}\times H^1(\Omega )$:

$$\begin{aligned} \boxed { \left\{ \begin{array}{l} {\mathcal E}^\prime _{\varvec{u}}(\varvec{u},\alpha ;\varvec{v})=0, \quad \forall \; \varvec{v}\in {\varvec{V}}_0 \\ \widetilde{\mathcal E}^\prime _\alpha (\varvec{u},\alpha ;\beta )=0, \quad \forall \; \beta \in H^1(\Omega ), \end{array} \right. } \end{aligned}$$

(17)

where ${\mathcal E}^\prime _{\varvec{u}}$ is given by (10). System (17) is composed of equalities and also uses unconstrained spaces for $\alpha$ and $\beta$.

This approach is employed in a large number of publications on the topic due to its simplicity. It should be noted, however, that the constructed $\widetilde{\mathcal E}^\prime _\alpha$ is no longer of variational nature. The equivalence between (17) and the original formulation in (9) is not evident and, to the best of our knowledge, no theoretical results that can prove it are available. For numerical comparisons we refer to the recent publication Gerasimov and De Lorenzis (2019), as well as to Section “Implicit (‘History-Field’ Irreversibility)”.

Interestingly, in the seminal paper of Miehe et al. (2010a), the authors considered the penalization option similar to representation (18) below, yet already in Miehe et al. (2010b) they switched to the notion of $\mathcal {H}_n$ and have been using it in all their following publications.

Penalized

The third alternative of addressing $\alpha \ge \alpha _{n-1}$, which results in the equality to be solved instead of the inequality, is via penalization. Several available options are listed below.

Option : In the most straightforward case, one can add the penalty term

$$\begin{aligned} P(\alpha ;\gamma ):=\frac{\gamma }{2}\int _\Omega \langle \alpha -\alpha _{n-1} \rangle _{-}^2 \; \mathrm {d}{\varvec{x}}, \quad \gamma \gg 1, \end{aligned}$$

(18)

to the energy functional $\mathcal {E}$ in (5).¹ In (18), $\langle y \rangle _{-}:=\min (0,y)$. The corresponding variational problem reads

$$\begin{aligned} \mathrm {arg\,min} \{ \mathcal {E}(\varvec{u},\alpha )+P(\alpha ;\gamma ): \; {\varvec{u}}\in {\varvec{V}}_{\bar{\varvec{u}}_n}, \alpha \in H^1(\Omega ) \}. \end{aligned}$$

(19)

and the resulting weak system for $(\varvec{u},\alpha )$ is as follows

$$\begin{aligned} \boxed { \left\{ \begin{array}{l} {\mathcal E}^\prime _{\varvec{u}}(\varvec{u},\alpha ;\varvec{v})=0, \quad \forall \; \varvec{v}\in {\varvec{V}}_0, \\ \displaystyle {\mathcal E}^\prime _\alpha (\varvec{u},\alpha ;\beta )+\gamma \int _\Omega \langle \alpha -\alpha _{n-1} \rangle _{-}\beta \; \mathrm {d}{\varvec{x}} =0, \quad \forall \; \beta \in H^1(\Omega ), \end{array} \right. } \end{aligned}$$

(20)

with ${\mathcal E}^\prime _{\varvec{u}}$ and ${\mathcal E}^\prime _\alpha$ given again by (10) and (11), respectively. Note that the admissible space for $\alpha$ and the test space for $\beta$ are no longer constrained. The obtained penalized un-constrained problem (20) approximates the original constrained problem (9) and thus is equivalent to it in the limit of $\gamma \rightarrow \infty$. Thus the appropriate choice of $\gamma$ is always viewed as a critical point of the technique also within the numerical experiments. A too small penalty parameter will lead to inaccurate (i.e., insufficient) enforcement of the constraint, a too large one will result in ill-conditioning (i.e., a so-called stability issue).

In Gerasimov and De Lorenzis (2019), an analytical procedure for the ‘reasonable’ choice of a lower bound for $\gamma$ that guarantees a sufficiently accurate enforcement of the crack phase-field irreversibility constraint and, seemingly, does not manifest ill-conditioning is devised. It is shown that the optimal penalty parameter $\gamma$ is a function of two formulation parameters (the fracture toughness $G_c$ and the regularization length scale $\ell$), but is independent of the problem setup (geometry, boundary conditions etc.), the formulation ingredients (degradation function g, tension–compression split $\Psi _\pm$ etc.), as well as the discretization (mesh size). The carried out numerical studies validate the findings.

Option : The augmented Lagrangian approach is adopted by Wheeler et al. (2014) and Wick (2017a, b). It implies adding to (5) the functional

$$\begin{aligned} P(\alpha ;\Xi ,\gamma ):=\frac{1}{2\gamma }\int _\Omega \langle \Xi + \gamma \alpha \rangle _{+}^2 \; \mathrm {d}{\varvec{x}} +\frac{1}{2\gamma }\int _\Omega \langle \Xi + \gamma (\alpha -\alpha _{n-1}) \rangle _{-}^2 \; \mathrm {d}{\varvec{x}} -\frac{1}{2\gamma }\int _\Omega \Xi ^2 \; \mathrm {d}{\varvec{x}}, \end{aligned}$$

(21)

with an unknown $\Xi \in L^2(\Omega )$ and a user-prescribed penalty constant $\gamma >0$. The aforementioned P is the so-called Moreau-Yosida approximation of the indicator function $I_{\mathcal {D}_{\alpha _{n-1}}}$ in (C), see Wheeler et al. (2014) for details. It is advocated that using (21), the stability issues possibly occurring in case of (18) are avoided. We notice that simplified representations for P in (21) which contain only the first two terms and only the second term are considered in Wheeler et al. (2014) and in Wick (2017a, b), respectively. Furthermore, in either case, a ‘fixed-point iteration’-like strategy for calculating $\Xi$ using $P^\prime$ is also employed, see e.g., Wheeler et al. (2014, Algorithm 1) and Wick (2017a, Algorithm 4.1). This is done to prevent the possibly significant increase of the computational effort in the case the field $\Xi$ is to be solved for.

Option : In Heister et al. (2015), $\alpha \ge \alpha _{n-1}$ is incorporated using a Lagrange multiplier and, following Hintermüller et al. (2002), the obtained formulation is then tackled using a primal-dual active set strategy. As noticed by the authors, this approach can be viewed as a semi-smooth Newton method with the advantage that the fully-monolithic solution scheme would “allow for fast (super-linear) convergence”, and that, “in contrast to other (penalization) methods, no adjustment of parameters is required”. On the other hand, the necessity of tracing explicitly various (active and inactive) sets in which the corresponding sub-problems are to be solved makes the approach computationally more expensive than a simple penalization approach.

Examples

In this section we compare the solutions of the formulations in (17) and (20) for two benchmark problems. Recall that the former problem is the weak formulation based on the use of a history-field of Miehe and co-workers (2010b), and the latter is the penalized formulation recently proposed in Gerasimov and De Lorenzis (2019). As explained in Section “Treatment of Irreversibility”, (17) is not equivalent to the original inequality-based problem (9), whereas (20) is equivalent [more precisely, it is a good approximation of (9)]. For every benchmark problem, formulations (17) and (20) are computed using the staggered scheme, see Section “Solution Strategies” for details.

The considered benchmark problems are the so-called single edge notched (SEN) specimen under shear originally considered in Bourdin et al. (2000), and later adopted with some modifications in many related papers, see, e.g., Miehe et al. (2010b), Borden et al. (2014), Ambati et al. (2015), Gerasimov and De Lorenzis (2016, 2019), and the traction test on a fiber-reinforced matrix Bourdin et al. (2008) (also in Bourdin et al. 2000; Bourdin 2007a; Amor et al. 2009), see Fig. 6. The first example is a crack propagation problem under external displacement-controlled loading, where the pre-existing crack is modeled discretely and the propagating crack is represented by the phase-field evolution. The problem setup is simple, but the failure pattern is not symmetric, being the result of a non-trivial combination of local tension–compression within the specimen during shear. The second example describes a more complicated process, since it encompasses crack initiation in the absence of a strong crack-tip singularity, which precedes the propagation stage. For either case, the pure monotonic loading regimes are simulated.

Fig. 6

Problem setup (sketchy) and the computed failure patterns for the single edge notched (SEN) specimen subject to shear (left) and the traction experiment on a fiber-reinforced matrix (right)

The SEN shear test is computed using both formulations in (17) and (20) in which functional $\mathcal {E}$ in (5) uses both the volumetric-deviatoric and spectral splits (for the sake of compactness, we denote them as $\mathtt {VD}$- and $\mathtt {S}$-split, respectively) and the models $\mathtt {AT}$-1 and $\mathtt {AT}$-2 given in Table 1. That is, there are four available combinations of split and model type in this case. The fiber-reinforced matrix test is computed using (17) and (20) and only for the $\mathtt {S}$-split and the $\mathtt {AT}$-2 model combination.

In Figs. 7 and 8, we present and compare, respectively, the load-/energy-displacement curves and the crack phase-field profiles obtained for the SEN shear test using the two irreversibility approaches. Similarly, Figs. 9 and 10 depict and compare the corresponding results for the traction test on a fiber-reinforced matrix.

Fig. 7

Comparison of the load–displacement and energy–displacement curves obtained for the SEN specimen shear test using the formulations in (17) and (20) and various combinations of split and model type

Fig. 8

Comparison of the crack phase-field profile obtained at the last loading step for the SEN specimen shear test using the formulations in (17) and (20) and various combinations of split and model type

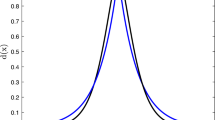
In all considered cases, both irreversibility approaches yield qualitatively and quantitatively rather similar, but not identical results. Taking the $\gamma$-penalized results as reference, it can be seen that the history field approach yields under-estimation of the elastic energy and over-estimation of the fracture surface energy. We attribute this to the observation drawn from the crack phase-field plots in Figs. 8 and 10 that the support of the phase-field profile in the latter case is visibly thicker.

Fig. 9

Comparison of the load–displacement and energy–displacement curves obtained for the fiber-reinforced matrix traction test using the formulations in (17) and (20) for the $\mathtt {S}$-split and the $\mathtt {AT}$-2 model combination

Fig. 10

Comparison of the crack phase-field profile obtained at the last loading step for the fiber-reinforced matrix traction test using the formulations in (17) and (20) for the $\mathtt {S}$-split and the $\mathtt {AT}$-2 model combination

Solution Strategies

In this section we discuss two iterative strategies for solving the equation $\mathcal {E}^\prime =\mathcal {E}_{\varvec{u}}^\prime +\mathcal {E}_\alpha ^\prime =0$: the so-call staggered and the monolithic ones.² Their advantages and disadvantages are already outlined in the introductory part and were also extensively discussed in the related references. The purpose of the following section is to provide the necessary technical details for both approaches, as well as to illustrate their performance for three benchmark problems.

Staggered

The staggered solution algorithm applied to $\mathcal {E}^\prime =0$ implies partitioning of this equation into the system $\mathcal {E}_{\varvec{u}}^\prime =0$ and $\mathcal {E}_\alpha ^\prime =0$, as has been already encountered in Section “Treatment of Irreversibility”. By alternately fixing $\varvec{u}$ and $\alpha$, the above coupled system is then solved in an iterative manner until convergence is achieved. The algorithm is sketched in Table 2 in a general form, that is, regardless of the system in (14), (17) and (20). Adaptation of step 2 to the corresponding equation in (14), (17) and (20) is straightforward.³

Table 2 Staggered iterative solution process for $\mathcal {E}^\prime =0$ at loading step $n\ge 1$

Both equations in Table 2 are non-linear: for the first one this is due to the non-linearity of ${g}(\alpha )\frac{\partial \Psi ^+}{\partial \varvec{\varepsilon }}(\varvec{\varepsilon }(\varvec{u}))$ $+\frac{\partial \Psi ^-}{\partial \varvec{\varepsilon }}(\varvec{\varepsilon }(\varvec{u}))=:\varvec{\sigma }(\varvec{u},\alpha )$, whereas for the second one it is due to the Macaulay bracket term $\langle \cdot \rangle _{-}$. Therefore, the Newton-Raphson procedure is used to iteratively compute $\varvec{u}^k$ and $\alpha ^k$ with $\varvec{u}^{k-1}$ and $\alpha ^{k-1}$ taken as the corresponding initial guesses, and $\mathtt {TOL}_\mathrm {NR}$ as the tolerance. Owing to the nested nature of the Newton-Raphson loops, we impose that $\mathtt {TOL}_\mathrm {NR}<\mathtt {TOL}_\mathrm {Stag}$.

The definition of $\mathrm {Res}_\mathrm {Stag}^k$ in Table 2 used for stopping the staggered process is not unique. As an example, the quantity $||\alpha ^k-\alpha ^{k-1}||_\infty$ is considered as the residual e.g., in Amor et al. (2009), Pham et al. (2011), Mesgarnejad et al. (2015), Farrell and Maurini (2017) when solving (9) and in Bourdin et al. (2000, 2008), Bourdin (2007a, b) while solving (14). Another option for $\mathrm {Res}_\mathrm {Stag}^k$ is a relative change in the normalized energy $\mathcal {E}$. It has been taken as a residual in Ambati et al. (2015) while solving (17), and as an auxiliary convergence-tracing quantity in Gerasimov and De Lorenzis (2016) while considering (14).

Finally, as already mentioned in the introductory part, the problem size of the system in (9), (14), (20) and (17) after finite element discretization is typically very large, since both the phase-field and the deformation localize in bands of width of order $\ell$. Solving the system in a staggered way in this case is computationally very demanding, see e.g., Mesgarnejad et al. (2015), Ambati et al. (2015), Gerasimov and De Lorenzis (2016), Farrell and Maurini (2017) for detailed studies.

Remark 4.1

In recent work of Farrell and Maurini (2017), various strategies for accelerating the partitioned solution schemes are discussed. It is shown that a better efficiency of the staggered approach presented above can be gained.

Monolithic (Newton-Raphson with Line-Search)

The lack of convexity of the governing energy functional $\mathcal {E}$ in (5) typically results in iterative convergence issues while solving $\mathcal {E}^\prime =0$ monolithically, that is, for both arguments $(\varvec{u},\alpha )$ using, e.g., the Newton-Raphson procedure. With the known guess $(\varvec{u}^{i-1},\alpha ^{i-1})$ and the computed increment $(\Delta \varvec{u},\Delta \alpha )$, the divergence of the iterative process is manifested by the increase of the energy for the solution update $(\varvec{u}^{i-1}+\Delta \varvec{u},\alpha ^{i-1}+\Delta \alpha )$. More precisely, it is $\mathcal {E}(\varvec{u}^{i-1}+\Delta \varvec{u},\alpha ^{i-1}+\Delta \alpha )>\mathcal {E}(\varvec{u}^{i-1},\alpha ^{i-1})$. A significant increase of the magnitude of the residual for the updated solution is typically detected as well. Once occurred, the trend will typically continue at the following Newton-Raphson iterations (no self-stabilization is observed), eventually producing no meaningful solution.

In Gerasimov and De Lorenzis (2016), to cope with the aforementioned convergence issues, a specific line-search procedure is devised and validated. The idea is sketched in Fig. 11: once an increase of energy is detected for the direct solution update $(\varvec{u}^i+\Delta \varvec{u},\alpha ^i+\Delta \alpha )$, one rescales the search increment $(\Delta \varvec{u},\Delta \alpha )$ by a multiplier $\tau \in (0,1)$ called line-search parameter in order to arrive at a converged energy level. With the optimal value $\tau ^\star$ computed, the updated $(\varvec{u}^i+\tau ^\star \Delta \varvec{u},\alpha ^i+\tau ^\star \Delta \alpha )$ is then taken as the guess for the next Newton-Raphson iteration.

Fig. 11

The divergence $\mathcal {E}(\varvec{u}^i+\Delta \varvec{u},\alpha ^i+\Delta \alpha )>\mathcal {E}(\varvec{u}^i,\alpha ^i)$, with $(\Delta \varvec{u},\Delta \alpha )$ as the known increment, of the Newton-Raphson solution process is detected; a properly determined line-search parameter $\tau ^\star$ provides a converging update Gerasimov and De Lorenzis (2016)

The resulting monolithic procedure for solving $\mathcal {E}^\prime =0$ based on the combined use of the Newton-Raphson method and the line-search procedure is depicted in Table 3. The items 3(a) and 3(b) in the table constitute the line-search procedure.

Table 3 Monolithic iterative solution process for $\mathcal {E}^\prime =0$ at loading step $n\ge 1$ using Newton-Raphson equipped with line-search

Remark 4.2

Recently, in Kopanicakova and Krause (2019), a monolithic solution procedure based on the trust region method has been proposed. The efficiency and robustness of the approach has been demonstrated. This represents an alternative to the monolithic approach using the Newton-Raphson method with line-search presented above. The comparison of the two approaches is the matter of forthcoming research.

Examples

We compare the performance of the two solution schemes illustrated above by considering three benchmark problems. The first problem is the SEN under shear already depicted in the left plot of Fig. 6 and explored in the context of the different irreversibility approaches. The second and the third one are the plate with hole under tension, see, e.g., Ambati et al. (2015), Gerasimov and De Lorenzis (2016), and the L-shaped panel experiment Mesgarnejad et al. (2015), Ambati et al. (2015), Wick (2017a), Gerasimov and De Lorenzis (2016), Gerasimov and De Lorenzis (2019), see Fig. 12. In all cases, the results are obtained for the combination of the $\texttt {S}$-split and the $\texttt {AT}$-2 model. They are taken from the recent publication Gerasimov and De Lorenzis (2016). In the plots we designate our monolithic solution scheme using Newton-Raphson with line-search as $\mathtt {MON}$-$\mathtt {ls}$. It is assumed that $\mathtt {TOL}_\mathrm {Stag}=\mathtt {TOL}_\mathrm {NR}=:\mathtt {Tol}$ with $\mathtt {TOL}_\mathrm {Stag}$ and $\mathtt {TOL}_\mathrm {NR}$ as in Tables 2 and 3, respectively.

Fig. 12

Problem setup (sketchy) and the computed failure patterns for the notched plate with hole under tension (left) and the L-shaped specimen experiment (right)

For the three problems, Figs. 13, 14 and 15 report and compare the load-displacement curves computed by the two approaches, as well as the cumulative computational time and the ratio in this time. It can be observed that with the same loading setup and under comparable accuracy requirements expressed through the corresponding tolerance $\mathtt {Tol}$ the monolithic scheme appears far superior to the staggered one, at least for these benchmark examples. For the detailed study of the energy and the residual convergence at each loading step, we refer the interested reader to Gerasimov and De Lorenzis (2016). There it is shown in particular that even though the monolithic process typically starts with higher residual and energy levels, it converges to the same level of residual and (approximately) the same minimum value of energy faster than the staggered one.

Fig. 13

SEN shear test: comparisons of the load–displacement curves and of the time–displacement diagrams representing the cumulative computational cost for the staggered and monolithic (Newton-Raphson with line-search) approaches

Fig. 14

Notched plate with hole: comparisons of the load–displacement curves and of the time–displacement diagrams representing the cumulative computational cost for the staggered and monolithic (Newton-Raphson with line-search) approaches

Fig. 15

L-shaped specimen experiment: comparisons of the load–displacement curves and of the time–displacement diagrams representing the cumulative computational cost for the staggered and monolithic (Newton-Raphson with line-search) approaches

Conclusions

We have addressed the main challenging computational aspects of phase-field modeling of brittle fracture, focusing on the treatment of the phase-field irreversibility constraint and on the choice of the iterative solution strategy for the non-convex minimization problem stemming from the formulation. For treatment of irreversibility, we have introduced and discussed the available options for enforcing the constraint, in terms of equivalence of the final unconstrained formulation to the original constrained one and of computational efficiency. For solution of the non-convex minimization problem, we have also considered various available options and critically assessed the efficiency and robustness of two of them. Numerical examples on well-known benchmark problems were used for illustrative purposes. At the computational level, finding an optimal compromise between robustness and efficiency seems to be a major and still open issue for phase-field computation of brittle fracture problems. Despite the progress achieved with line-search and trust region methods to improve robustness of the monolithic approach, and with accelerated staggered schemes to improve efficiency of the alternate minimization approach, there seems to be still room for substantial improvement. Another interesting aspect, where theory and numerics closely interact, is the issue of solution non-uniqueness stemming from the non-convexity of the energy functional to be minimized. The occurrence of multiple solutions has been occasionally reported in the literature, e.g., in Bourdin et al. (2000, 2008), Bourdin (2007a), Amor et al. (2009), Burke et al. (2010a), Artina et al. (2014), Artina et al. (2015). However, to the best of our knowledge no attempt has been made so far to investigate and characterize these multiple solutions. Finally, mesh adaptivity has been only briefly mentioned in this chapter but certainly deserves further attention as a key technology for reducing the computational cost.