11.1 Introduction

Since the last two or three decades, fractional calculus has become valuable tool in many branches of science and engineering. However, its history goes back to eighteenth century. Many scientists, including famous mathematicians such as Fourier (1822), Abel (1823–1826), Liouville (1822–1837), Riemann (1847), have contributed significant works for development of fractional calculus. There are many possible generalizations of \(\frac {d^{n}f(x)}{dx^{n}} \), where n is not an integer, but the most important of these are the Riemann–Liouville and Caputo derivatives. The first of these appeared earlier than the others and was developed in works of Abel, Riemann, and Liouville in the first half of the nineteenth century. The mathematical theory of this derivative has been well established so far, but it has disadvantage that leads to difficulties especially for initial and boundary values, since in real world problems, these conditions cannot be described by fractional derivatives. Thus, the latter one, the Caputo derivative was derived by Caputo to eliminate the difficulties in identifying initial and boundary conditions. Both derivatives are very well known in the theory of fractional differential equations and the definitions of these derivatives will be given in the following section.

It has been proved that many physical processes can be well defined and modelled by fractional order differential equations. Moreover, fractional analysis provides many benefits for identifying and best modelling the physical systems which are suggested by scientists. Therefore, fractional order derivatives are much more suitable than the ordinary derivatives (see references [1,2,3,4]). For instance, it is not easy to explain abnormal diffusion behaviours by integer order differential equations since these processes appear abnormally with respect to time and space variables and it requires fractional models.

There are many application areas where these mathematical models are used and some of them can be listed here as physics, chemistry, biology, economics, control theory, signal and image processing, blood flow phenomenon, aerodynamics, fitting of experimental data, etc. Usually these models have complex nature; therefore, analytical solutions can only be obtained for certain classes of equations. Many numerical and approximate methods have been developed to solve these kinds of equations so far. Some of these methods are given as follows: finite difference approximation methods [5,6,7,8,9,10], fractional linear multistep methods [11,12,13], quadrature method [14,15,16,17,18,19], adomian decomposition method [20,21,22], variational iteration method [22, 23], differential transform method [24], Laplace perturbation method [25, 26], homotopy analysis method [27], etc. On the other hand, existing pure numerical techniques have usually first order convergency. However, it is well known that raising the order of convergency is a factor that increases the power of the method [28].

Nowadays, there are further developments in the analysis of fractional order differential equations and some studies are dealt with variable order fractional derivatives [29]. Thus, the need to develop more reliable methods in parallel with the developments in this field is inevitable.

The aim of this work is to use a second order convergent method to the variable fractional order multi-term differential equations similar to the work in [30] and to obtain reliable results. In the next section, second order convergent method will be mentioned and the theory of the method will be dealt with. Sections 11.3 and 11.4 are applications of the method for adding extra y(t) and y″(t) terms to the single-term equation. The last section is the conclusion.

11.2 Problem Definition and Integration Method for Variable Order Fractional Differential Equations

In this section, we first consider the following single-term initial value problem with fractional derivative, where α(t) is a function of time. Therefore, we can write the problem as

(11.1)

where f(t) is a continuous function of t for a given interval. If y(0) = μ, then by using the transformation v(t) = y(t) − μ, we get y(0) = 0. In Eq. (11.1), α(t) denotes the order of variable fractional Caputo derivative, namely CD, and this derivative is defined as,

$$\displaystyle \begin{aligned} _{C}D_{0,t}^{\alpha(t)}y(t)=\frac{1}{\varGamma(1-\alpha(t))} \int_{0}^{t}(t-s)^{-\alpha(t)}y^{{}^{\prime }}(s)ds. \end{aligned} $$
(11.2)

We also recall the variable fractional order Riemann–Liouville derivative, RLD as

$$\displaystyle \begin{aligned} _{RL}D_{0,t}^{\alpha(t)} y(t) = \frac{1}{\varGamma(1-\alpha(t))}\frac{d}{dt} \int_{0}^{t}{(t-s)^{-\alpha(t)}} y(s) ds. \end{aligned} $$
(11.3)

Consequently, by the following lemma, we see the relation between the Riemann–Liouville and the Caputo derivatives.

Lemma 11.1

If y(t) ∈ C[0, ∞) then, similar to the constant order fractional operators, the relation between variable order Caputo and Riemann–Liouville fractional derivatives is

$$\displaystyle \begin{aligned} _{C}D_{0,t}^{\alpha(t)} y(t) =_{RL}D_{0,t}^{\alpha(t)} [y(t)-y(0)]. \end{aligned} $$
(11.4)

In Eq. (11.1), since the initial condition is y(0) = 0, this follows that

$$\displaystyle \begin{aligned}_{C}D_{0,t}^{\alpha(t)} y(t) = {}_{RL}D_{0,t}^{\alpha(t)}y(t). \end{aligned} $$
(11.5)

Consequently, for convenience, the Caputo derivative is replaced by Riemann–Liouville derivative in Eq. (11.1). To obtain a numerical approach to the Riemann–Liouville variable order fractional derivative by a second order convergent method, we first call the shifted Grünwald approximation of a function y(t)

$$\displaystyle \begin{aligned} \mathcal{A}_{\tau,p}^{\alpha(t)} y(t) = {\frac{1}{\tau^{\alpha(t)}}} \sum_{k=0}^{\infty} g_{k}^{\alpha(t)} y(t-(k-p)\tau), {} \end{aligned} $$
(11.6)

where, for k ≥ 0 ,

$$\displaystyle \begin{aligned}g_{k}^{\alpha(t)}=(-1)^{k} \left( \begin{array}{c} \alpha (t) \\ k \end{array} \right)\!. \end{aligned}$$

Now, the second order convergent method for Riemann–Liouville variable order derivative is defined as by the following theorem (see [30]).

Theorem 11.1

Let y(t) ∈ L 1(R) and its Riemann–Liouville derivative be \(_{RL}D_{-\infty ,t}^{\alpha (t) +2} y(t)\). For ∀t k ∈ R, the Fourier transform of this derivative in L 1(R) is [ 10]

$$\displaystyle \begin{aligned} \mathcal{D}_{\tau,p,q}^{\alpha(t)} y(t) = \frac{\alpha(t)-2q}{2(p-q)}\mathcal{A} _{\tau,p}^{\alpha(t)} y(t) + \frac{2p-\alpha(t)}{2(p-q)}\mathcal{A} _{\tau,q}^{\alpha(t)} y(t). {} \end{aligned} $$
(11.7)

Therefore,

$$\displaystyle \begin{aligned} \mathcal{D}_{\tau,p,q}^{\alpha(t_k)} y(t) = _{RL}D_{-\infty,t}^{\alpha(t_k)} y(t) + O(\tau^2), \end{aligned} $$
(11.8)

where p and q are integers and p≠q.

Proof

From the definition of \(\mathcal {A}_{\tau ,p}^{\alpha (t)} y(t) \) as in Eq. (11.6), we write

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{D}_{\tau,p,q}^{\alpha(t_k)} y(t) &\displaystyle =&\displaystyle \frac{\alpha(t_k)-2q}{2(p-q)} \frac{1}{ \tau^{\alpha(t_k)}} \sum_{k=0}^{\infty} g_{k}^{\alpha(t_k)} y(t-(k-p)\tau) \\ &\displaystyle +&\displaystyle \frac{2p-\alpha(t_k)}{2(p-q)} \frac{1}{\tau^{\alpha(t_k)}} \sum_{k=0}^{\infty} g_{k}^{\alpha(t_k)} y(t-(k-q)\tau). {} \end{array} \end{aligned} $$
(11.9)

If the Fourier transform is applied to both sides of Eq. (11.9), the following expression is obtained

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathcal{F} \left \{ {\mathcal{D}_{\tau,p,q}^{\alpha(t_k)}} y(t);w \right \}&\displaystyle =&\displaystyle \frac{1}{ \tau^{\alpha(t_k)}} \sum_{k=0}^{\infty} g_{k}^{\alpha(t_k)} \Bigg[ \frac{ \alpha(t_k)-2q}{2(p-q)} e^{-iw(k-p)\tau} \\ &\displaystyle &\displaystyle \quad + \frac{2p-\alpha(t_k)}{2(p-q)} e^{-iw(k-q)\tau} \Bigg] \mathcal{F}(w) \\ &\displaystyle =&\displaystyle \frac{1}{\tau^{\alpha(t_k)}}\Bigg[ \frac{\alpha(t_k)-2q}{2(p-q)} (1-e^{-iw\tau})^{\alpha(t_k)} e^{iw\tau p} \\ &\displaystyle &\displaystyle \quad +\frac{2p-\alpha(t_k)}{2(p-q)} (1-e^{-iw\tau})^{\alpha(t_k)} e^{iw\tau q} \Bigg] \mathcal{F}(w) \\ &\displaystyle =&\displaystyle (iw)^{\alpha(t_k)}\Bigg[ \frac{\alpha(t_k)-2q}{2(p-q)} W_p(iw\tau)+\frac{ 2p-\alpha(t_k)}{2(p-q)} W_q(iw\tau) \Bigg] \mathcal{F}(w), \quad \end{array} \end{aligned} $$
(11.10)

where \(\mathcal {F}(w)\) is the Fourier transform of y(t) and we writing

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} W_r(z)&\displaystyle =&\displaystyle \Bigg(\frac{1-e^{-z}}{z}\Bigg)^{\alpha(t_k)}e^{rz} \\ &\displaystyle =&\displaystyle 1+\Bigg(r-\frac{\alpha(t_k)}{2}\Bigg)z+O(z^2),\qquad {r=p,q}, \end{array} \end{aligned} $$
(11.11)

denoting,

$$\displaystyle \begin{aligned}\hat{g}\left \{w,\tau\right \}=\mathcal{F} \left \{ {\mathcal{D}_{\tau,p,q}^{ \alpha(t_k)}} y;w \right \}-\mathcal{F} \left \{ {{}_{RL}D_{-\infty,t}^{ \alpha(t_k)}} y;w \right \}\end{aligned}$$

and by using Eqs.(11.10)–(11.11) and we have

$$\displaystyle \begin{aligned} \begin{array}{rcl} \left| {\mathcal{D}_{\tau,p,q}^{\alpha(t_k)}} y(t)-{{}_{RL}D_{-\infty,t}^{\alpha(t_k)}} y(t) \right|&\displaystyle =&\displaystyle |g| \leq \frac{1}{2\pi} \int\limits_R |\hat{g}(w,\tau)|dw\leq C \| (iw)^{\alpha(t_k)+2} F(w)\|{}_{L^1} \tau^2 \\ &\displaystyle =&\displaystyle O(\tau^2). \qquad \ \end{array} \end{aligned} $$

This completes the proof [30].

11.2.1 Numerical Method

To solve Eq. (11.1) numerically, we discretize the time domain, t ∈ [0, T] by \(\tau =\frac {T}{N}\), where N is an integer and α(t k) = α k denotes the varying order fractional derivative with t k = kτ, k = 0, 1, 2, 3…, N. Moreover, choosing (p, q) = (0, −1), then by using Eq. (11.9) we have

$$\displaystyle \begin{aligned}\frac{\alpha(t)-2q}{2(p-q)} = \frac{2+\alpha(t)}{2}\end{aligned}$$

and

$$\displaystyle \begin{aligned}\frac{2p-\alpha(t)}{2(p-q)} =-\frac{\alpha(t)}{2}.\end{aligned}$$

Now, the second order convergent method can be given as follows [30]:

(11.12)

where, if k = 0, then \(w_{0}^{\alpha _k}=(\frac {2+\alpha _k}{2}) g_{0}^{\alpha _k}\),otherwise, \( w_{j}^{\alpha _k}=(\frac {2+\alpha _k}{2}) g_{j}^{\alpha _k}-(\frac {\alpha _k}{2} )g_{j-1}^{\alpha _k}\), k ≥ 1 and \(g_{j}^{\alpha _k}=(-1)^{j}\left (\begin {array}{cc}\alpha _{k} & \\ n&\end {array}\right )\!\!.\)

11.2.2 Stability Criteria of the Method

This part deals with the stability of the method and the following lemma holds.

Lemma 11.2

Being α k ∈ (0, 1), then the coefficients, \(w_{j}^{\alpha _k} \) in Eq.(11.12) satisfy the following properties:

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \left\{ \begin{array}{cc} w_{0}^{\alpha_k}=\frac{2+\alpha_k}{2}, & w_{j}^{\alpha_k}< 0, j \geq 1\\ \sum_{j=0}^{\infty} w_{j}^{\alpha_k}=0, &-\sum_{j=1}^{k} w_{j}^{\alpha_k}< w_{0}^{\alpha_k}, k \geq 1. {} \end{array}\right. \end{array} \end{aligned} $$
(11.13)

Theorem 11.2

Let y(t) ∈ C[0, ∞) denotes exact and {y k|k = 0, 1, 2, 3…N} numerical solution of Eq.(11.1) respectively, then the following inequality holds:

$$\displaystyle \begin{aligned} |y^{k}| \leq \frac{5}{(1-{\alpha_{\min})}{2^{\alpha_{\min}}}} { k^{\alpha_{\min}} } {\tau^{\alpha_{\min}}} \max_{1 \leq m \leq k} |f(t_m)|. \end{aligned} $$
(11.14)

Proof

According to the Lemma 11.2, we know that

$$\displaystyle \begin{aligned}w_{0}^{\alpha_k}=\frac{2+\alpha_k}{2}, w_{j}^{\alpha_k}< 0, j \geq 1 .\end{aligned}$$

Hence, by arranging Eq. (11.12), we have

$$\displaystyle \begin{aligned} w_{0}^{\alpha_k} y^{k} = \sum_{j=1}^{k-1} (-w_{j}^{\alpha_k}) y^{k-j}+\tau^{\alpha_k} f(t_k), \qquad 1 \leq k \leq N . \end{aligned} $$
(11.15)

For k = 1, we can write

$$\displaystyle \begin{aligned} |y^1|=|w_{0}^{\alpha_1}|{}^{-1} \tau^{\alpha_1} |f(t_1)| \leq \frac{5}{(1-{ \alpha_{\min})}{2^{\alpha_{\min}}}} {\tau^{\alpha_{\min}}} |f(t_1)|. \end{aligned} $$

Now, we have to show that Eq. (11.14) is also valid for j = 1, 2, 3, …, k − 1. Hence, taking the absolute value of Eq. (11.15) and writing Eq. (11.14) into this inequality then we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} w_{0}^{\alpha_k} |y^{k}| &\displaystyle &\displaystyle \leq \Bigg [\, \sum_{j=1}^{k-1} (-w_{j}^{\alpha_k}) |y^{k-j}|+\tau^{\alpha_k} |f(t_k)| \Bigg ]\, \\ &\displaystyle &\displaystyle \leq \sum_{j=1}^{k-1} (-w_{j}^{\alpha_k}) \frac{5}{(1-( \alpha_{\min})2^{\alpha_{\min}} (k-j)^{\alpha_{\min}} \tau^{\alpha_{\min}}} \max_{1 \leq m \leq k-j} |f(t_m)|+{\tau^{\alpha_{\min}}} |f(t_k)| \\ &\displaystyle &\displaystyle \leq \Bigg [\, {\displaystyle \sum_{j=1}^{k-1}} {(-w_{j}^{\alpha_k})} \frac{5}{(1-{\alpha_{\min})}{2^{\alpha_{\min}}}} k^{\alpha_{\min}}+1\Bigg ]\, { \tau^{\alpha_{\min}}} \max_{1 \leq m \leq k} |f(t_m)| \\ &\displaystyle &\displaystyle \leq \Bigg\{\Bigg[{w_{0}^{\alpha_k}} -\frac{1-{\alpha_{\min}}}{5} {\Bigg(\frac{2^{\alpha_{\min}}}{k^{\alpha_{\min}}}\Bigg)\Bigg]\frac{5}{(1-\alpha_{\min})} 2^{\alpha_{\min}}}+1\Bigg\}{\tau^{\alpha_{\min}}} \max_{1 \leq m \leq k}|f(t_m)| \\ &\displaystyle &\displaystyle = \frac{5w_{0}^{\alpha_{k}}}{(1-\alpha_{\min})2^{\alpha_{\min}}} k^{\alpha_{\min}} \tau^{\alpha_{\min}}\max_{1 \leq m\leq k} |f(t_m)|. \end{array} \end{aligned} $$
(11.16)

Therefore, we get

$$\displaystyle \begin{aligned} |y^{k}| \leq \frac{5}{(1-{\alpha_{\min})}{2^{\alpha_{\min}}}} k^{\alpha_{\min}} {\tau^{\alpha_{\min}}} \max_{1 \leq m \leq k} |f(t_m)| .\end{aligned} $$

As a result, by mathematical induction, Eq. (11.14) is valid for all 1 ≤ k ≤ N (See [30]).

Theorem 11.3

Let y(t) ∈ C[0, ∞) denote the exact solution and {y(t k)|k = 0, 1, 2, 3…N} define the values of y at t k. Let us also denote the numerical solution of Eq.(11.1) by {y k|k = 0, 1, 2, 3…N} at particular points t k. Therefore, absolute error in each step is denoted by e k = y(t k) − y k, k = 0, 1, …N. Hence, the following relation holds:

$$\displaystyle \begin{aligned}|e^k| \leq \frac{5c}{{(1-{\alpha_{\min})}} {2^{\alpha_{\min}}}} T^{\alpha_{\min}} \tau^2,\end{aligned}$$

where c is a positive constant independent from τ.

Proof

The proof of the theorem is given as in [30]. The error of Eq. (11.12) is

$$\displaystyle \begin{aligned} \begin{array}{rcl} \left\{ \begin{array}{cc} \tau^{-\alpha_k} \sum_{j=0}^{k}w_{j}^{\alpha_k} e^{k-j}=R^k, &1 \leq k \leq N , \\ e^0=0. & \end{array}\right. \end{array} \end{aligned} $$
(11.17)

This requires that |R k|≤ cτ 2. Then, by using Theorem 11.1 and Theorem 11.2, we write

$$\displaystyle \begin{aligned} \begin{array}{rcl} |e^{k}| &\displaystyle &\displaystyle \leq \frac{5c}{(1-{\alpha_{\min})}{2^{\alpha_{\min}}}} k^{\alpha_{\min}} {\tau^{\alpha_{\min}}} \max_{1 \leq m \leq k} |R^m| \\ &\displaystyle &\displaystyle \leq \frac{5c}{(1-{\alpha_{\min})}{2^{\alpha_{\min}}}} T^{\alpha_{\min}} { \tau^2}. \end{array} \end{aligned} $$

This completes the proof.

11.2.3 Numerical Example

So far, a second order convergent method has been considered for approximating the Riemann– Liouville derivative, where the maximum error and the order of the convergency are obtained from the following formulas:

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle E_{\infty}(\tau)=\max_{0\leq k\leq N} |y(t_k)-y^k|,\\ &\displaystyle &\displaystyle order_{\infty}(\tau)=\log_2 {\bigg( \frac{E_{\infty}(2\tau)}{ E_{\infty}(\tau)} \bigg )}\!. \end{array} \end{aligned} $$

To see the efficiency of the method the following example has been considered here. All numerical calculations have been done within MATLAB (R2015b).

Example 11.1

Assuming that 0 < α(t) < 1 and T = 1. Now, we can solve the following initial value problem [30]:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} {}_{C}D_{0,t}^{\alpha(t)} y(t)&\displaystyle =&\displaystyle \frac{3t^{1-\alpha(t)}}{\varGamma(2-\alpha(t))} + \frac{2t^{2-\alpha(t)}}{\varGamma(3-\alpha(t))},\quad 0 \leq t \leq T \end{array} \end{aligned} $$
(11.18)
$$\displaystyle \begin{aligned} \begin{array}{rcl} y(0)&\displaystyle =&\displaystyle 0. \end{array} \end{aligned} $$
(11.19)

The exact solution of the problem is known as y(t) = 3t + t 2 and two different values of α(t) will be considered here:

Case 1: :

\(\alpha (t)=\frac {1}{2}t\),

Case 2: :

α(t) = sin(t).

Consequently, by using the following numerical scheme:

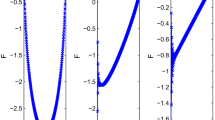
$$\displaystyle \begin{aligned} \tau^{-\alpha_k} \sum_{j=0}^{k} w_{j}^{\alpha_k} y^{k-j}=f(t_k), 1 \leq k \leq N , \end{aligned}$$

and taking y 0 = 0, numerical results are obtained. These results have been shown by tables. Tables 11.1 and 11.3 show the difference between exact and numerical solutions of the problem for \(\tau =\frac {1}{16}\) and \(\tau =\frac {1}{32}\). In Table 11.1, the first case \(\alpha (t)=\frac {1}{2}t \) has been used. Moreover, in Table 11.3, the second case, α(t) = sin(t) was applied. Tables 11.2 and 11.4 denote the maximum error and order of convergency results for \(\alpha (t)=\frac {1}{2}\) and α(t) = sin(t), respectively. Figure 11.1 shows both numerical and exact solutions in the same plot. It is clear that analytical and numerical solutions overlap.

Fig. 11.1
figure 1

Comparison of the numerical and exact solutions of y(t) of Example 11.1, where T = 1 , \( \alpha (t)= \frac {1}{2}t\)

Full size image
Table 11.1 The difference between the numerical and exact values of Example 11.1 for T = 1 and \( \alpha (t)= \frac {1}{2}t\). The calculations have been performed for both N = 16, N = 32
Full size table
Table 11.3 Comparison of the numerical and exact solutions of y(t) at particular point t k in Example 11.1, where T = 1, α(t) = sin(t). The calculations have been performed for both N = 16, N = 32
Full size table
Table 11.2 Maximum error and order of convergency results for different values of τ in Example 11.1, where T = 1 and \(\alpha (t)= \frac {1}{2}t\)
Full size table
Table 11.4 Absolute errors and order of convergency for different values of τ in Example 11.1, where T = 1 and α(t) = sin(t)
Full size table

11.3 Multi-term Variable Order Fractional Equations

In this section we will apply the second order convergent method to a new class of variable fractional order differential equations. With additional terms, we will have multi-term variable fractional order differential equation. First, we will apply y(t) term to Eq. (11.1). Hence, the following initial value problem, Eq. (11.20), will be considered here:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \left\{ \begin{array}{cc} _{C}D_{0,t}^{\alpha(t)} y(t)+ ay(t)=f(t), 0 \leq t \leq T & \\ y(0)=0.& \end{array}\right. \end{array} \end{aligned} $$
(11.20)

For convenience, taking a = 1 and each t k is in the discretized time domain, the following numerical scheme holds:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \left\{ \begin{array}{cc} \tau^{-\alpha_k} \sum_{j=0}^{k} w_{j}^{\alpha_k} y^{k-j}=f(t_k)-y(t_k), \quad 1 \leq k \leq N, &\\ y^{0}=0.& \end{array}\right. \end{array} \end{aligned} $$
(11.21)

Therefore, the following theorem is valid.

Theorem 11.4

Let y(t) ∈ C[0, ∞) denote the exact solution and {y(t k)|k = 0, 1, 2, 3…N} define the values of y at t k. Let us also denote the numerical solution of Eq.(11.1) by {y k|k = 0, 1, 2, 3…N} at particular points t k. Therefore, maximum error in each step is denoted by e k = y(t k) − y k, k = 0, 1, …N. Hence, the following relation holds:

$$\displaystyle \begin{aligned} |e^k| \leq \frac{5c}{{(1-{\alpha_{\min})}} {2^{\alpha_{\min}}}} T^{\alpha_{\min}} \tau^2, \end{aligned}$$

where c is a positive constant independent from τ.

Proof

By using Eq. (11.12), the proof of this theorem can be performed easily same as the proof of Theorem 11.3.

Following example denotes that the second order convergent method is still valid for multi-term variable fractional order differential equations.

Example 11.2

In Eq. (11.20), assuming that \(f(t)=t^2 + \frac {2}{\varGamma ( \frac {5}{2} )} t^{\frac {3}{2}}\) and T = 1, then, the exact solution of the problem is known as y(t) = t 2. But this solution is known for only \(\alpha (t)=\frac {1}{2}\). To compare numerical results with exact ones, only \(\alpha =\frac {1}{2}\) case has been considered here. Numerical calculations have been performed for different values of τ, and a code is written in MATLAB (R2015b). The following table, Table 11.5, lists maximum error and the order of convergency for different values of τ and Table 11.6 compares the numerical and exact solutions for \(\tau =\frac {1}{16}\) and \(\tau =\frac {1}{32}\).

Table 11.5 Maximum error and order of convergency results for different values of τ in Example 11.2, where T = 1 and \(\alpha (t)= \frac {1}{2}\)
Full size table
Table 11.6 The difference between numerical and exact values of Example 11.1 for T = 1 and α(t) = sin(t). The calculations have been performed for both N = 16, N = 32
Full size table

11.4 Addition of y ′′(t) Term to Variable Order Fractional Differential Equations

In this section, by using the second order convergent method which is given by Eq. (11.12), we will develop a hybrid method for wider classes of differential equations. By adding y(t) and y ′′(t) terms to Eq. (11.1), then we will have multi-term fractional differential equations. To solve the multi-term fractional equation, we approximate the second order derivative with the central differences and the fractional derivative term is evaluated as it is given in Eq. (11.12). Therefore, we will consider the following initial value problem:

(*)

Therefore, at particular values of t k, Eq. (*) is written as

$$\displaystyle \begin{aligned} \tau^{-\alpha_k} {\displaystyle\sum_{j=0}^{k}} w_{j}^{\alpha_k} y^{k-j}=f(t_k)+ay^{\prime\prime}(t_k)+by(t_{k}). \end{aligned} $$
(11.22)

Assuming that a and b are constants and for simplicity, we take their values as 1, −1 respectively. Now recalling central finite difference approximation to the second order derivative:

$$\displaystyle \begin{aligned} f^{\prime\prime}(t_k)=\frac{{f(t_{k+1})-2f(t_{k})+f(t_{k-1})}}{{h^2}},\end{aligned} $$
(11.23)

and substituting this into Eq. (11.22), then the last form of the numerical scheme is obtained easily. The method will be applied to following example (see[19]).

Example 11.3

Consider the differential equation in Eq. (*) as follows:

$$\displaystyle \begin{aligned} D^{\alpha(t)}y(t_k)=y^{\prime\prime}(t_k)-y(t_k)+f(t_k).\end{aligned} $$
(11.24)

Since the exact results are known for only \(\alpha =\frac {1}{2}\), for comparing the numerical results with exact ones, we will also use \(\alpha (t)=\frac {1}{2}\) in the calculations. Substituting the finite difference approximation to the second order ordinary derivative, then we have

$$\displaystyle \begin{aligned} \tau^{-\alpha_k} {\displaystyle\sum_{j=0}^{k}} w_{j}^{\alpha_k} y^{k-j}= \frac{{y(t_{k+1})-2y(t_{k})+y(t_{k-1})}}{{h^2}}-y(t_k)+f(t_k).\end{aligned} $$
(11.25)

The exact solution of the problem is known as y(t) = t 2, when

$$\displaystyle \begin{aligned} f(t)=t^2-2+\frac{2}{\varGamma({\frac{5}{2}})}t^{\frac{3}{2}}. \end{aligned} $$
(11.26)

Hence,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \tau^{-\alpha_k} {\displaystyle\sum_{j=0}^{k}} w_{j}^{\alpha_k} y^{k-j}&\displaystyle =&\displaystyle \frac{{y(t_{k+1})-2y(t_{k})+y(t_{k-1})}}{{h^2}}-y(t_k)+{t_k}^2-2+\frac{2}{ \varGamma({\frac{5}{2}})}{t_k}^{\frac{3}{2}},\\ {} \end{array} \end{aligned} $$
(11.27)

where h = τ. As a result, arranging Eq. (11.27) again, we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} y(t_{k+1})&\displaystyle =&\displaystyle {h^2}\tau^{-\alpha_k} {\displaystyle\sum_{j=0}^{k}} w_{j}^{\alpha_k} y^{k-j}+2y(t_{k})-y(t_{k-1})\\&\displaystyle &\displaystyle +{h^2} y(t_k)- {h^2}[{t_k}^2-2+ \frac{2}{\varGamma({\frac{5}{2}})}{t_k}^{\frac{3}{2}}]. \end{array} \end{aligned} $$
(11.28)

Table 11.7, shows the exact and numerical values of y(t) at particular points of t for different step sizes where initial conditions are taken as in Eq. (*). Figure 11.2 illustrates that both exact and numerical results are in good agreement.

Fig. 11.2
figure 2

For \( \alpha (t)= \frac {1}{2}\) and N = 100. Comparison of numerical and exact values of y(t) in Example 11.3

Full size image
Table 11.7 Results for Example 11.3, where T = 1 and \( \alpha (t)= \frac {1}{2}\). Comparison of the numerical and exact values of y(t) for two different step size, N = 10 and N = 100, respectively
Full size table

11.5 Conclusion

Here, we aimed to solve fractional-variable order differential equations and multi-term fractional order differential equations. We have used the second order convergent method as in [30]. The method is quite well when it is compared with the analytical solutions. For finer mesh, one can obtain more reliable results. As a result, the method can be applied to wider classes of fractional equations, variable order fractional differential equations.