Keywords

1 Introduction

Metamaterials are finely designed materials capable of achieving unusual behaviors thanks to the particular geometries and connection topologies in which they are arranged. Besides, thanks to the fast development, in the last decades, of micro- and nano-manufacturing technologies [1, 2], the fields of possible applications have rapidly increased. Under the name metamaterials, several kinds of materials can be classified and, among many, electromagnetic [3], acoustic [4], and elastic [5] are the ones enjoying a wider attention from the scientific community. The singular emerging phenomena involve fast light propagation [6], wave-stopping [7,8,9], unusual dissipation [10], and backward propagation [11,12,13]. The complexity of the models describing such systems, usually involving convolution terms and integral-differential equations, prevented thorough analytical dissertations on the propagation behavior, in a general panorama in which even literature provides only few examples of works dealing with nonlocal interactions [14, 15].

This work completes the investigation presented in [16], confined within the hypothesis of the linearization. Without the chance of achieving analytical solutions, this paper presents numerical simulations aimed at comparing the linear model and the nonlinear one, expanding the concept of a linear, wider connectivity [17] to a nonlinear one. The idea is not only to confirm the remarkable results obtained in [16] and in [18, 19], but also to establish them as general description of the dynamic behavior of an elastic metamaterial, since no linearization procedure is here applied.

2 Model for a Long-Range Waveguide

In a classical D’Alembert waveguide, modelled according to the principles of the local elasticity theory, each elementary particle is connected with its closest neighbors only. However, as the interaction length increases, nonlocal interactions emerge and the assumptions of the elastic theory are not effective anymore.

This work, following the guidelines presented in [16], wants to interpret the effects of nonlocal connections, beyond the linearized model, through the mean of numerical simulations.

Nonlocal connections, i.e., distance-dependent interactions, which can appear in the shape of magnetostatic, electrostatic, as well as gravitational forces, alter the intrinsic pattern of a system, with direct consequences on its dynamic response. The equation of motion for a one-dimensional, continuous, infinite waveguide, modified because of the introduction of long-range forces, already presented in [16], assumes the form:

$$\displaystyle \begin{aligned} \displaystyle \rho\frac{\partial^2 w}{\partial t^2}-E\frac{\partial^2 w}{\partial x^2}-\int_{-\infty}^{+\infty}F(r)d\xi=0, {} \end{aligned} $$
(1)

where w is the displacement, ρ and E are the mass density and the Young’s modulus, respectively, F(r) is the force exerted on the particle at x, due to the interaction with the particle at ξ, and r is the actual distance between the particles and specifically:

$$\displaystyle \begin{aligned} \displaystyle r(x,\xi,t)=\left.x\right|{}_{t=0}+w(x,t)-\left[\left.\xi\right|{}_{t=0}+w(\xi,t)\right]=x-\xi+w(x,t)-w(\xi,t). {} \end{aligned} $$
(2)

The analysis of the dynamic behavior demands the definition of a model for the interaction forces, which, even for a three-dimensional system, are chosen to be parallel to the distance vector and so that the action–reaction principle holds:

$$\displaystyle \begin{aligned} \boldsymbol{F}(\boldsymbol{r})=f(|\boldsymbol{r}|)\boldsymbol{r}. {} \end{aligned} $$
(3)

The sign of f(|r|) rules the nature of the interaction: attractive for negative f(|r|), repulsive if positive. Moreover, among many possibilities, a Gauss-like trend is selected for f(|r|), which, for a one-dimensional domain, becomes:

$$\displaystyle \begin{aligned} f(|r|)=\mu e^{-\left(\frac{r}{\beta}\right)^2}, {} \end{aligned} $$
(4)

where μ and β represent the magnitude and the characteristic length of the long-range forces, respectively. This shape, more than guaranteeing the antisymmetric configuration of F(r), implies a force vanishing with the distance, property common to many physical long-range forces, as the previously mentioned gravitational, Coulomb, etc.

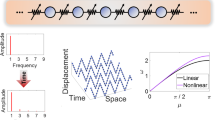
Figure 1 shows the trend of f(|r|) varying with μ and β.

Fig. 1
figure 1

Gauss-like force as function of the distance

Full size image

For this model of nonlocal interactions and assuming ε(x, ξ, t) = w(x, t) − w(ξ, t), Eq. (1) becomes:

$$\displaystyle \begin{aligned} \displaystyle \rho\frac{\partial^2 w}{\partial t^2}-E\frac{\partial^2 w}{\partial x^2}-\int_{-\infty}^{+\infty}\mu (x-\xi+\varepsilon)e^{-\left(\frac{x-\xi+\varepsilon}{\beta}\right)^2}d\xi=0. {} \end{aligned} $$
(5)

Since Eq. (1) is strongly nonlinear, it cannot be solved analytically and no closed form solutions can be provided. In fact, the investigation presented in [16], aimed at finding analytical solutions, is bounded to the linearized problem discussion.

Next sections examine the numerical approach adopted to extract the propagation characteristics of both the linearized and the nonlinear models.

3 Numerical Simulations

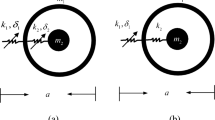
To perform numerical simulations, the finite counterpart of the waveguide is considered. The rod is assumed clamped at the ends and subjected to a repulsive Gauss-like long-range interactions, as shown in Fig. 2.

Fig. 2
figure 2

Longitudinal finite waveguide model

Full size image

Table 1 reports the physical properties of the system.

Table 1 Physical parameters
Full size table

The simulations look at the free problem under initial conditions capable of exciting several wavelength of the system.

The results of the simulations in terms of displacement w(x, t) are collected in a space-time map. A double discrete Fourier transform is applied [20] transforming the space-time variable w(x, t) into the wavenumber-frequency dependent variable W(k, ω).

The contour lines of W(k, ω) are plotted and from the exam of its crest, a curve emerges interpreted as the equivalent of a dispersion relationship.

3.1 Linearized Model

Under the hypothesis of small ε, namely for w ≪ β (see [16]), the system represented in Eq. (5) can be simplified as:

$$\displaystyle \begin{aligned} \displaystyle \rho\frac{\partial^2 w}{\partial t^2}-E\frac{\partial^2 w}{\partial x^2}+h\ast w=0, {} \end{aligned} $$
(6)

where \(h=\mu \left [1-2\left (\frac {x}{\beta }\right )^2\right ]e^{-\left (\frac {x}{\beta }\right )^2}\), and ∗ is the convolution operator (space domain), where for the simulation we use (Table 2).

Table 2 Simulations parameters
Full size table

The convolution term leads to the presence of an additional stiffness, and the system is simulated with finite differences approach for the space discretization, and with Runge–Kutta algorithms for the study of the time evolution.

Figure 3 shows a comparison between analytical and numerical solutions for the dispersion relationship in the linear case, where the numerical analysis uses also the double Fourier transform method described above.

Fig. 3
figure 3

Dispersion relationship of the simplified model: analytic result (left) and simulations (right)

Full size image

3.2 Nonlinear Simulations

The system response is simulated without any small displacement hypothesis.

Figure 4 on the right, with ripples traveling apart of the envelope, shows a highly dispersive propagation.

Fig. 4
figure 4

Displacement map of nonlinear model (left), and some frame-shots (right)

Full size image

The dispersion relationship, depicted in Fig. 5, is obtained by applying the double FFT to the equation of motion. It describes the propagation behavior and being related to the group velocity c g, it is straightforward to identify the different regimes. In fact, the dispersion curve shows the presence of three main branches, indicated with the letters A, B, and C in Fig. 5.

Fig. 5
figure 5

Dispersion relationship (surface plot) of the nonlinear model

Full size image

Since \( c_g=\frac {\partial \varOmega }{\partial K}\), where Ω = Ω(K) is the general expression of the non-dimensional dispersion relationship, the AB segment, characterized by a positive slope, is associated to a positive group velocity; in B, the curve exhibits a maximum, related to wave-stopping. From B to C, since the slope is negative, so is the group velocity. In C, corresponding to the minimum of the dispersion relationship, c g = 0 and a new wave-stopping condition emerge. Beyond C, the curve converge to the standard propagation regime, typical of the D’Alembert waveguide.

From the comparison between these two curves, it is apparent how these phenomena do not occur in a standard D’Alembert waveguide, whose propagation regime is well depicted by the straight line in Fig. 5. As the system consists of a simple longitudinal waveguide, but further equipped with nonlinear long-range forces, it is possible to conclude that the variations in the propagating behavior, with respect to the conventional one, can only be addressed to the introduction of such forces.

4 Conclusions

The paper describes the onset of unconventional propagation phenomena in long-range nonlinear elastic metamaterials, continuing the investigation presented by the authors in [16]. The physics of such media leads to strongly nonlinear and nonlocal integral-differential models. In general, these equations do not admit analytical solutions and only numerical simulations can provide insights into the dynamic response.

Numerical simulations are performed for the linearized model, corroborating the achievements analytically obtained for the simplified model in [16], and for the nonlinear problem, verifying the assumption that nonlocal interactions lead to unusual propagation regimes. Forward propagation occurs at a speed higher than the one proper of conventional D’Alembert waveguide, wave-stopping phenomenon appears for two specific combinations of \(\left (\varOmega _i,K_i\right )\), eventually backward propagation occurs when a regime of negative group velocity is established.