Abstract
In this paper we review recent progress on the analysis, experimental exploration, and application of elastic wave propagation in weakly nonlinear media and metamaterials. We provide a detailed technical discussion overviewing two broad areas of active research: (1) discrete nonlinear periodic systems and metamaterials, and (2) continuous nonlinear systems with a focus on nonlinear guided waves. The specific intent is to introduce the reader to asymptotic analysis methods currently being employed in the field of study, to highlight their results to date, and to motivate follow-on studies. Where appropriate, we include details on experimental explorations and envisioned applications, both of which have received relatively sparse attention to date.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Nonlinear elastic waves in discrete periodic structures, phononic crystals, and metamaterials
Treatment of nonlinearity in periodic structures and metamaterials may arise from practical necessity. For example, phononic devices designed to operate linearly may exhibit unusual or unexpected behavior when excited at high amplitudes. In such cases, assumptions of infinitesimal strain (or displacement) are no longer valid and the governing equations must be revisited to account for geometric and/or material nonlinearities. It is not surprising that phononic devices would be driven at high amplitudes, such as in an effort to increase the signal-to-noise ratio in bulk or surface acoustic wave filters [1,2,3,4] or offset losses due to damping in additively manufactured metamaterials [5,6,7].
Alternatively, nonlinearity can be intentionally introduced into a periodic structure to enhance functionality, exploiting behavior nonexistent in linear metamaterials. A fundamental discrete nonlinear system, the monatomic chain with cubic stiffness, exhibits complex and exploitable phenomena such as higher-harmonic generation, invariant waveform transmission, and amplitude-dependent dispersion behavior as illustrated in Fig. 1. To achieve these effects, unit cells are specifically tailored to have slender, lightweight structural members that support large displacements or rotations or possess inherently nonlinear behavior such as arising from magnetic fields. Figure 2 displays recent experiments with intentional nonlinear unit cell designs showcasing unique nonlinear behavior such as subharmonic attenuation zones [8], diode-like soliton transmission [9], and second-harmonic generation [10].
1.1 Systems
Unit cells in nonlinear periodic structures and metamaterials are typically characterized by nonlinear stiffness; i.e., restoring forces that are not linearly proportional to displacement. Nonlinear restoring forces arise in both discrete media—where momentum is concentrated at localized lattice sites [11]—as well as continuous media such as layered periodic structures [12]. In discrete media, nonlinearity stems from the force-displacement relationship of the massless springs or other restoring elements. By contrast, nonlinearity in continuous media can be traced to the material’s constitutive stress–strain law (such as the asymmetric, nonlinear Neo-Hookean relationship [13]) or higher-order terms in the strain–displacement relationship [14].
An important aspect of the description of nonlinear periodic structures and metamaterials is the strength of the nonlinearity. In general, nonlinear restoring forces have been characterized as weakly, strongly, or essentially nonlinear, in order of increasing strength of the nonlinearity. A pragmatic method of classifying the strength of the nonlinearity is to directly compare the magnitude of nonlinear restoring force to that of the linear evaluated at the given wave amplitude of interest. Weak nonlinearities are small relative to the linear terms, typically on the order of one-tenth or smaller. Strong nonlinearities are much more appreciable in size compared to the linear terms, typically on the same order or even larger than the linear forces. Essential nonlinearities arise in the absence of all linear terms, with its name suggesting that only nonlinear forces are responsible for conducting the wave propagation.
1.1.1 Monatomic chain
The nonlinear monatomic chain serves as a prototypical system for the study of nonlinear wave propagation in periodic structures. Figure 3a displays a schematic of this system with a unit cell outlined using a dashed box. Discrete masses are coupled with linear and nonlinear restoring forces. Common occurrences of nonlinearity include quadratic and/or cubic stiffness. Such stiffness may stem from a Taylor Series expansion about an equilibrium position for an arbitrary nonlinear interaction. Studies of this system date back to the seminal work of Fermi, Pasta, and Ulam in the 1950s [15]. It is well-known that wave propagation in the linear monatomic chain can be characterized completely by a band structure relating frequency and wavenumber. Due to the periodicity of the lattice, the band structure itself is periodic and has a well-known cut-off frequency above which wave propagation is forbidden. As will be discussed in Sect. 1.3.1, the presence of stiffness nonlinearity in this lattice leads to amplitude-dependent shifts of the linear band structure. This effect can be visualized with an amplitude-dependent dispersion surface as illustrated in Fig. 3b.
1.1.2 Diatomic chain
The nonlinear diatomic chain contains two masses per unit cell. Figure 3c presents a schematic of this system with the unit cell again outlined in a dashed box. Owing to the second degree of freedom, the band structure possesses two branches: a lower acoustic branch characterized in the long wavelength limit by in-phase oscillation of both masses, and an upper optical branch characterized by out-of-phase oscillation of both masses. The frequency range between each branch, termed the bandgap, contains only non-propagating evanescent waves not typically depicted in the band diagram. The bandgap’s extent depends on the impedance mismatch experienced by a wave as it propagates through the unit cell. As depicted in Fig. 3d, both the acoustic and optical branch of the nonlinear diatomic band structure shift with wave amplitude, which can be represented using an amplitude-dependent band structure. Unlike in a linear system where the band structure completely characterizes wave propagation, in a nonlinear system the amplitude-dependent band structure is non-unique, and can, for example, be presented for constant amplitude waves, constant intensity waves, or other such choices. Herein, the preferred presentation is for constant amplitude; however, the amplitude-dependent dispersion expressions derived throughout the manuscript can be used to produce band structures obeying other conventions.
Prototypical nonlinear periodic systems. a The nonlinear monatomic chain consists of discrete masses coupled with linear and nonlinear stiffness. b The dispersion behavior for a linear monatomic chain becomes amplitude-dependent in the presence of nonlinearity, giving rise to an amplitude-dependent dispersion surface. c The nonlinear diatomic lattice consists of alternating masses coupled with linear and nonlinear stiffness. d Both branches of a nonlinear diatomic chain shift with wave amplitude, which can be represented using a dispersion surface
1.1.3 Locally-resonant chain
Liu et al. [16] introduced what is widely considered the first elastic metamaterial wherein each unit cell consists of a primary mass coupled to a locally-resonant oscillator. Their study demonstrated that locally-resonant metamaterials are capable of low-frequency bandgaps since the mechanism associated with bandgap formation is no longer geometric (e.g., Bragg scattering) and instead is associated with the resonant vibration of each oscillator. Nonlinear extensions of the locally resonant chain were considered by [17,18,19] in which nonlinearity arises from quadratic or cubic stiffness in the primary chain and/or oscillator. In [20], Bukhari and Barry considered the effect of an arbitrary number of resonators in each unit cell. Other studies have considered hybridizations of the diatomic and locally-resonant chain such as can be found in [21, 22].
1.1.4 Two-dimensional lattices
Extensions of the nonlinear monatomic, diatomic, and locally-resonant chains along two orthogonal directions have also been investigated. In these systems periodicity is established by lattice vectors and the wave’s propagation constants are resolved along the associated basis vectors. The simplest case for wave propagation in these two-dimensional systems is the shear lattice wherein the displacement of each mass is perpendicular to the plane of the lattice. Such systems have been considered by [23,24,25]. The linear band structure of these lattices is represented completely by a surface relating the two propagation constants to the wave’s frequency. However, the dispersion surface can be reduced to a curve by evaluating the surface along directions of symmetry in the irreducible Brillouin zone [26]. Examination of the dispersion surface via isofrequency contours reveals that select frequencies restrict the group velocity to distinct directions, a phenomenon termed beaming. As will be discussed in Sect. 1.3.1, beaming exhibits amplitude-dependency in the presence of nonlinearity.
1.2 Analysis methods
Exact wave propagation solutions in nonlinear periodic structures and metamaterials are sparse. By contrast, a number of approximation techniques have been successfully implemented in the analysis of such systems. Herein, we review primarily the multiple scales, Lindstedt-Poincaré, and straight-forward perturbation techniques, which have been applied to weakly nonlinear systems, as well as the harmonic balance and homotopy methods, which have been applied to strongly nonlinear systems.
1.2.1 Multiple scales
This perturbation technique addresses weak nonlinearities and has been used to uncover amplitude-dependent dispersion shifting [27, 28] as well as plane wave phenomena such as waveform invariance and stability [25, 29].
The equation of motion for the \(j{\textrm{th}}\) unit cell of an arbitrary nonlinear periodic structure can be represented as,
where \({\textbf{x}}_{j}\), \(\dot{{\textbf{x}}}_j\), and \(\ddot{{\textbf{x}}}_j\) denote the position, velocity, and acceleration of the \(j{\textrm{th}}\) unit cell’s degrees of freedom. \({\textbf{M}}\) denotes the unit cell’s mass matrix and \(\mathbf {C^{(p)}}\) and \(\textbf{K}^{\mathbf {(p)}}\) denote the unit cell’s partitioned damping and stiffness matrices, respectively. Nonlinear restoring forces are collected into the \({\textbf{f}}_{\textbf{NL}}\) vector. The linear damping and nonlinear restoring force are ordered to be small using the bookkeeping device \(\varepsilon \).
Nonlinearity will be treated generally though certain aspects of quadratic and/or cubic stiffness will be highlighted. For example, in a monatomic chain with both quadratic and cubic stiffness, the nonlinear terms appear as,
where \({\textbf{x}}_{\textbf{j}}\) and \({\textbf{f}}_{{{\textbf{N}}}{{\textbf{L}}}}\) degenerate to scalar quantities \(x_j\) and \(f_{NL}\), respectively, due to the occurrence of a single degree of freedom in each unit cell. The co-existence of quadratic and cubic stiffness may arise from a Taylor expansion of an arbitrary nonlinear restoring force. Note that quadratic stiffness captures asymmetries in the stress–strain behavior such as that associated with neo-Hookean materials.
The method of multiple scales introduces slow time scales at which the system evolves,
where time derivative can be represented in operator form as,
with \(D_i() \equiv \frac{\partial }{\partial T_i}\). Additionally, the solution sought is expanded in an asymptotic series,
A set of cascading, ordered equations arises by collecting matching orders of \(\varepsilon \). The first two equations are,
The \(0{\textrm{th}}\)-order equation admits a Bloch wave. A single plane wave solution takes the form,
where \(\omega _0\) and \(\mu \) denote the wave’s frequency and propagation constant (i.e., dimensionless wavenumber), respectively; A the complex amplitude; \(\mathbf {\phi }\) the wave propagation mode shape; and c.c. denotes the complex conjugate of all preceding terms. An eigenvalue problem at zeroth-order results from substituting Eq. (8) into Eq. (6) such that the pair (\(\omega _0\), \(\mu \)) satisfies the lattice’s linear dispersion relationship. The wave propagation mode shape (or eigenvector) \(\mathbf {\phi }\) is evaluated accordingly. The number of pairs (\(\omega _0\), \(\mu \)), or equivalently the number of eigenvectors, equals the number of degrees of freedom in each unit cell.
It is beneficial to decompose the complex amplitude A into polar form,
By virtue of satisfying Eq. (6), the complex amplitude in Eq. (9) varies with respect to only the slow time scales such that,
Recognizing the slow scale variation of these parameters is critical for capturing amplitude-dependent dispersion shifts.
With the \(0{\textrm{th}}\)-order equation known, the \(1{\textrm{st}}\)-order equation can be updated. This process is aided by transformation to wave modal coordinates,
where \(\varvec{\Phi }\) denotes the modal matrix whose columns are formed by the wave propagation mode shapes. Furthermore, the damping and nonlinear terms on the right-hand side of Eq. (7) can be expanded in a Fourier series \(\sum _{l=0}^{\infty }{{\textbf{f}}_l^{\left( 1\right) }e^{il\left( \omega _0T_0-\mu j\right) }}\). Substituting the coordinate transformation and Fourier series into Eq. (7) and then pre-multiplying by the Hermetian conjugate of the \(\sigma {\textrm{th}}\) wave mode shape, \(\mathbf {\phi }_\sigma ^{H}\), yields decoupled modal wave equations,
where \(m_\sigma \) and \(k_\sigma \) denote the modal mass and wavenumber-reduced stiffness of mode \(\sigma \) and \(u_j^{\left( 1\right) }\) denotes the associated modal coordinate. Two classes of inhomogeneities exist on the right hand side of Eq. (13): secular terms with time and spatial dependence \(e^{i\left( \omega _0T_0-\mu j\right) }\), and non-secular terms with dependence \(e^{hi\left( \omega _0T_0-\mu j\right) }, h\ne 1\). Secular terms must be removed to ensure uniform convergence of the series solution in Eq. (5). For lattices with both cubic and quadratic stiffness, all secular terms contain \(e^{i\beta }\) such that their removal yields,
where \({\widetilde{{\textbf{f}}}}_1^{\left( 1\right) }={\textbf{f}}_{\textbf{1}}^{\left( {\textbf{1}}\right) }e^{-i\beta }\). Consequently, the first-order evolution equations for amplitude and phase are given by,
With secular terms now eliminated, Eq. (13) comprises solely non-secular terms at \(e^{hi\left( \omega _0T_0-\mu j\right) } (h\ne 1)\). The effect of these inhomogeneities is the production of multi-harmonic particular solutions, which can be determined after introducing the solution form
The complex amplitude of each multi-harmonic term can be solved for algebraically using the method of undetermined coefficients
Note that this particular solution can be transformed back to physical coordinates using Eq. (12).
At higher orders, a similar procedure is carried-out. The linear kernel of Eq. (7) is preserved and governs successively higher orders of the series solution. On the right-hand side, secular terms must be removed, yielding higher-order evolution equations for amplitude and phase. The remaining non-secular terms yield particular solutions resolving further the multi-harmonic magnitudes and phases revealed at lower orders.
1.2.2 Lindstedt–Poincaré
The Lindstedt–Poincaré method is another perturbation technique that has been used, as with the method of multiple scales, to predict amplitude-dependent shifts to the dispersion curves of nonlinear lattices. Its basic framework follows closely to that of the method of multiple scales and has been applied successfully to 1-D [30] and 2-D [23] lattices.
The technique begins with the equations of motion of a weakly nonlinear lattice expressed in matrix form. A dimensionless time is introduced in terms of the frequency \(\omega \),
Referencing this dimensionless time, the equations of motion of the lattice are then rewritten as,
where the effect of viscous damping is omitted. An asymptotic expansion is then introduced for both the total solution and frequency \(\omega \),
Substituting Eqs. (21) and (22) into Eq. (20), and collecting matching orders of \(\varepsilon \), again leads to a cascading set of ordered equations. The first two are,
The solution to the \(O(\varepsilon ^0)\) equations are a Bloch wave,
Updating the right-hand side of the \(O(\varepsilon ^1)\) equation, secular terms arise with dependence \(e^{i\left( \tau -\mu j\right) }\) and must be removed. This results in an algebraic equation determining the first-order frequency correction \(\omega _1\).
Similar to the higher-order procedure of the method of multiple scales, a particular solution can be determined at \(O(\varepsilon ^1)\). This multi-harmonic solution can then be used in conjunction with the \(0{\textrm{th}}\)-order solution to update higher-order equations of the asymptotic analysis. Interestingly, the authors in [30] determined this solution but neither extended the procedure beyond the first order nor commented on the significance of the particular solution at \(O(\varepsilon ^1)\). However, as will be detailed in Sect. 1.3.4, multi-harmonic solutions derived from higher-order perturbation analysis have been used to predict invariant plane wave solutions.
As discussed in [27] there are two principle drawbacks of this technique. The first is that it presumes a single-frequency solution through the introduction of \(\tau \). Thus, the Lindstedt–Poincaré technique cannot readily handle wave–wave interactions or internal resonances (which the method of multiple scales can). Furthermore, the Lindstedt–Poincaré method lacks a mechanism to uncover time-varying amplitude behavior such as that which would occur due to dissipation, amplitude modulation, or instabilities.
1.2.3 Straight-forward expansion
The straight-forward expansion method, as implied by its name, provides a relatively simple framework for analyzing weakly nonlinear wave dynamics. Similar to the method of multiple scales and Lindstedt–Poincaré, the straight-forward expansion employs an asymptotic expansion of the solution variable, but without expanding time or frequency,
Substituting Eq. (26) into Eq. (1), and matching orders of \(\varepsilon \), yields a set of cascading differential equations with the first two presented as,
The solution of the \(0{\textrm{th}}\)-order equation admits the form of a Bloch wave,
Updating the right-hand side of the \(O(\varepsilon ^1)\) equation produces inhomogeneous forcing terms, which may contain multiple harmonics, including stationary forces (zero harmonics). It is convenient to use method of undetermined coefficients and assume a particular solution \(x_j^{(1)}\) with multiple harmonics corresponding to the forcing terms. Substituting this solution back to Eq. (29) and equating terms at each harmonics yields the unknown coefficients. Noteworthy, the straight-forward expansion method is not able to remove possible secular terms based on frequency and/or amplitude correction, and hence does not derive amplitude-dependent dispersion and stability. Typically, this method only applies to systems where the expansion of the nonlinear forces does not include secular terms. This approach has been used, for example, to demonstrate spatial evolution of generated higher harmonics in a granular system [31].
1.2.4 Harmonic balance and homotopy methods
The asymptotic approaches of multiple scales and Lindstedt–Poincaré are limited in their application to weakly nonlinear lattices. By contrast, the harmonic balance and homotopy methods offer the advantage of applicability to strongly nonlinear systems. Such approaches have successfully characterized amplitude-dependent dispersion relationships for lattices with strong stiffness nonlinearity [32, 33].
The harmonic balance method begins with the matrix equations of motion for the \(j{\textrm{th}}\) unit cell of a lattice with strong nonlinearity
where \({\textbf{F}}_{{{\textbf{N}}}{{\textbf{L}}}}\) vector comprises both linear and nonlinear restoring forces. Note that similar to the Lindstedt-Poincaré approach, a dimensionless time is employed, \(\tau =\omega t\), where \(\omega \) denotes the wave’s frequency.
The essential feature of the harmonic balance method is the introduction of a truncated series composed of a fixed number of harmonics,
where A and \(\mu \) denote the wave’s amplitude and propagation constant, respectively. The unknown amplitude vectors \({\textbf{c}}_l\) and \({\textbf{s}}_l\) are normalized such that their highest component is unity
The method proceeds by substituting Eq. (31) into Eq. (30) and determining the coefficient vectors \({\textbf{c}}_l\) and \({\textbf{s}}_l\) via a Galerkin projection, reducing the set of nonlinear differential equations to nonlinear algebraic equations. Since the number of unknowns (harmonic coefficients, amplitude, frequency, and wavenumber) exceeds the number of equations, a general solution is unavailable. However, an approach for predicting amplitude-dependent dispersion curves follows by fixing the amplitude and wavenumber as known quantities and then determining the nonlinear frequency of propagation. Numerical algorithms, such as the Newton–Raphson procedure, have been implemented to solve the associated equations [32, 33].
For the special case of strongly nonlinear monatomic lattices without linear restoring forces [32], the homotopy method (also referred to as He’s method) [34, 35] exhibits comparable results to the harmonic balance method [32, 33]. Homotopy methods rely on introduction of a homotopy parameter which smoothly transitions the governing equation(s) from one(s) with a known solution (usually linear) to the desired nonlinear equation(s). Thus the desired solution can be based on a known solution and recovered by setting the homotopy parameter to one. As such, the governing equations for the strongly nonlinear lattice absent of linear restoring forces are represented as,
where \(u_j\) denotes the displacement, p denotes the homotopy parameter and \(f_{NL}\) holds nonlinear restoring forces. The homotopy parameter appears in the assumed series solutions for the plane wave frequency and displacement field,
The expanded frequency and series solution is then substituted into the governing equations and matching orders of p are collected, yielding ordered equations, the first two of which are,
Combining the solution to the linear oscillator in Eq. (36) with imposed Bloch conditions yields the completed \(0{\textrm{th}}\)-order solution for the lattice,
Substituting these expressions into Eq. (37) then results in an updated 1st-order equation,
The resulting nonlinear forcing term on the right-hand side is periodic in time and thus can be expanded in a Fourier series,
where the \(m{\textrm{th}}\) coefficient is determined using orthogonality relations,
Secular (i.e., unbounded) terms arise for \(m=1\) requiring that the corresponding right-hand side of Eq. (39) be set to zero, yielding \(\omega _1^2=\frac{c_1}{A}\). Thus, through substitution of this result into Eq. (34), a \(1{\textrm{st}}\)-order accurate nonlinear frequency can be determined after setting \(p=1\),
The dispersion behavior at a specific wave amplitude A is evaluated by varying \(\mu \) from 0 to \(\pi \) and computing the frequency \(\omega \) using Eq. (42). Such has been done for strongly nonlinear, 1-D granular chains in [32].
1.3 Phenomena and applications
Nonlinear periodic structures and metamaterials exhibit behavior absent from their linear counterparts. As such, nonlinearity may be intentionally introduced to an engineered system to enhance operation and/or provide additional functionality. In this section, we discuss phenomena and applications uniquely-enabled by nonlinearity in periodic structures and metamaterials. Specifically, we detail amplitude-dependent dispersion shifting, extra-harmonic generation, waveform invariance, and multistability. By highlighting this behavior and making note of the associated applications proposed in prior studies, we hope to inspire follow-on developments making full use of nonlinearity in periodic structures and metamaterials.
1.3.1 Amplitude-dependent dispersion
Stiffness nonlinearity appears as either softening or hardening in the lattice’s underlying linear restoring force. Thus, at higher amplitudes, the linear dispersion relationship shifts to accommodate the effective gain or loss of stiffness. Various studies have analytically characterized amplitude-dependent adjustments to the lattice’s linear dispersion relationship.
The multiple scales evolution equations provide closed-form expressions for amplitude-dependent dispersion shifting valid at all frequencies. They accurately describe the amplitude-dependent shifting in the weakly nonlinear regime [24, 25, 27, 29]. For undamped lattices, \(Im\left( \mathbf {\phi }_\sigma ^{H}{\widetilde{{\textbf{f}}}}_1^{\left( 1\right) }\right) =0\) in Eq. (15) and thus \(\alpha \) does not vary with respect to \(T_1\). It follows from Eq. (16) that \(\beta \) varies linearly with \(T_1\). For a monatomic chain with both quadratic and cubic stiffness, the expression for \(\beta \) reconstituted to the first-order is,
After substitution into the Bloch wave solution, Eq. (8), this linearly-varying phase can be interpreted as an amplitude-dependent dispersion shift,
where the total frequency can be expressed as,
Hardening stiffness (\(k_3 > 0\)) shifts the linear dispersion curve upwards whereas softening stiffness (\(k_3 < 0\)) shifts the linear dispersion curve downwards. Additionally, the magnitude of the dispersion shift grows quadratically with wave amplitude \(\alpha \). Thus, the cut-off/cut-on frequencies for lattices can be raised or lowered as a function of wave amplitude. Figure 4 plots the amplitude-dependent band structures predicted by multiple scales for 1-D monatomic and diatomic chains. Additionally, the amplitude-dependent band structure is shown for the 2-D monatomic shear lattice using the same multiple scales approach extended to two dimensions [25].
Amplitude-dependent dispersion shifting as predicted by multiple scales. Hardening nonlinearity shifts the dispersion curve upwards whereas softening nonlinearity shifts the dispersion curve downwards. a Monatomic chain with hardening cubic stiffness. b Diatomic chain with softening cubic stiffness. c Two-dimensional monatomic shear lattice with hardening cubic stiffness
It is important to note that this analysis technique still predicts amplitude-dependent dispersion shifts for damped lattices, although the expressions are less compact. For example, the evolution equations for amplitude and phase in Eqs. (15) and (16) remain coupled, and an exponentially decaying amplitude slowly weakens the magnitude of the dispersion shift over time. A time-dependent dispersion shift that slowly converges to the linear dispersion relationship effect was documented in [36] where the authors demonstrated this effect for both linear and quadratic damping using a multiple scales analysis. The same authors treated fractional damping in [36] and also reported time-dependent damping that decays to the chain’s linear dispersion curve.
Furthermore, it has been shown that quadratic stiffness does not produce secular terms at the first order and hence does not contribute to amplitude-dependent dispersion shifting until higher orders [25, 29]. Similarly, other authors have used multiple scales to compare the dynamic response of lattices with weak quadratic stiffness to purely linear lattices [37]. In particular, they commented-on the presence of higher-order amplitude-dependent shifts in frequency away from the edges of the irreducible Brillouin zone. One technology proposed by this amplitude-dependent dispersion shifting is an amplitude-dependent frequency isolator in which individual frequency components can be isolated based on an input gain applied by the device [30]. For example, at low amplitudes a two-tone signal propagates through a diatomic chain with cubic stiffness nonlinearity. However, at sufficiently high amplitudes, the optical frequency component of the signal is blocked due to shifting of the two branches of the band structure, and thus only the acoustic frequency component transmits. Isolation of an optical frequency could be achieved by lowering wave amplitude when the acoustic frequency signal is propagating near the branch’s cut-off frequency.
Gonella et al. [19, 28] modified the multiple scales approach to capture amplitude-dependent wavenumber shifts. They differentiate between the effects of either initial or boundary excitations in nonlinear lattices. In the former, an initial displacement profile prescribes the wavenumber and the frequency of propagation is corrected via the amplitude-dependent dispersion relationship. By contrast, a boundary excitation defines the frequency and the wavenumber is then determined by a separate nonlinear dispersion relationship. To allow for either case in the multiple scales analysis, a spatiotemporal variable is first introduced,
where \(\mu \) and \(\omega \) denote the plane wave’s propagation constant and frequency, respectively. The series solution is then expressed in terms of this “fast” spatiotemporal variable and slow spatial and temporal scales,
where \(J_1\equiv \varepsilon j\) is analogous to the slow temporal scale introduced in Eq. (3). Interestingly, Gonella et al. generalize the lattice equations of motion by expanding the finite differences associated with linear restoring forces to include a higher-order spatial derivative. Such addition appears in the first-order inhomogeneous terms. For example, a cubically nonlinear monatomic chain exhibits the following form at the first-order,
Elimination of the associated secular terms reveals evolution equations for amplitude and phase as coupled partial differential equations governed by space \((J_1)\) and time \((T_1)\),
where \(\lambda \) and \(\eta \) are parameterized by linear and nonlinear stiffness terms, respectively. Solutions to the coupled partial differential equations are sought in accordance with the presence of an initial or boundary excitation. The initial excitation approach yields the previous amplitude-dependent dispersion relationships expressed in Eq. (45). However, boundary excitation yields an amplitude-dependent wavenumber correction associated with a prescribed forcing frequency. While the initial and boundary excitation predictions are similar for relatively small wavenumbers, significant discrepancies arise near the band edge. Specifically, the wavenumber correction develops a jump, or kink, at frequencies near the linear cut-off frequency. Early evidence of these kinks dates to the work of Chakraborty and Mallik [38]. Gonella et al. resolved these physically unrealistic results through an iterative approach to the multiple scales procedure. They anticipated wavenumber shifts in the \(0{\textrm{th}}\)-order solution by replacing the original propagation constant \(\mu \) with one that includes an undetermined first-order shift; i.e., \(\mu \rightarrow \mu -\frac{\varepsilon \beta }{J_1}\). Substituting this ansatz into the \(0{\textrm{th}}\)-order solution, Eq. (45), and then collecting and eliminating secular terms yields a revised set of \(1{\textrm{st}}\)-order evolution equations. Continuing with the example system of the cubically nonlinear monatomic lattice, the evolution equations now appear as
where \(\lambda _0\) is parameterized by frequency and linear chain parameters. Note that these new equations recover Eqs. (49) and (50) for small wavenumber shifts; i.e., \(\mu \gg \frac{\varepsilon \beta }{J_1}\). By virtue of the boundary excitation phenomenon, conditions are imposed on amplitude and phase: \(\alpha =\alpha _0\),\(\ \beta =\beta _0\). A particular solution for phase is also sought in the form of a wavenumber shift, yet now the solution to the coupled set of equations is transcendental. For example, assuming a particular solution form of \(\beta ^*=CJ_1\) in the cubically nonlinear monatomic chain gives,
The solutions for C can be determined numerically and give updated wavenumber shifts. Interestingly, this correction is “clipped” at the linear cut-off frequency. No amplitude-dependent shifts in wavenumber occur for forcing frequencies above the lattice’s linear cut-off frequency. Such a result was confirmed in [28] with direct numerical simulation of the lattice equations of motion whereby boundary excitation above the linear cut-off frequency, yet below the nonlinear cut-off frequency, for initial excitation produced evanescent waves.
Generalizing to two-dimensional shear lattices, the direction of wave propagation is governed by dispersion surfaces, which can be reduced to curves when evaluated along the \(\Gamma \)-X-M directions in the Brillouin zone [11]. Stiffness nonlinearity shifts these surfaces, resulting in the possibility of amplitude-dependent beaming [23]. For example, in square shear lattices with weak cubic stiffness, harmonic point forcing at a low amplitude causes wave information to radiate symmetrically outward. However, when the forcing is applied at the same frequency and at higher amplitudes, the band diagram shifts such that wave information beams along \(45^\circ \) angles [23]. This amplitude-dependent redirection of energy may inspire, for example, nonlinear lattice materials that re-route large amplitude waves that would otherwise damage structural components or electronic sensors.
Inertial nonlinearities can also be treated by higher-order multiple scales analysis as presented by Settimi et al. [39]. Both quadratic and cubic nonlinear terms arise in a systems with inertial amplification. Kinematic constraints relate rigidly coupled masses within the unit cell, yet the governing equations for the degrees-of-freedom can still be expressed in matrix form. The higher-order multiple scales procedure yields both nonlinear dispersion relationships and nonlinear waveforms. Invariant manifolds can be identified associated with these nonlinear waveforms.
The Lindstedt–Poincaré method has recently been employed to predict bandgap shifting in exotic systems. Bae and Oh [40] presented near-zero frequency bandgap shift whereby the size of a quasi-static bandgap could be tuned by both unit cell geometry and wave amplitude. They considered a chain grounded with transversely-loaded linear coil springs, and their Lindstedt-Poincaré analysis was validated both numerically and experimentally. An effective parameter analysis identified tunable negative mass associated with the ultra-low frequency bandgap. He et al. [41] studied a triatomic lattice with cubic stiffness originating from pretensioned wires grounding each mass. Interestingly, the authors report a softening nonlinearity associated with the strings and were able to increase bandgap size by tensioning the string.
Dispersion relationships for continuous nonlinear elastic systems (treated in more detail in Sect. 2) have been derived in closed form as applied to homogeneous nonlinear media such as rods, beams, and plates [42,43,44,45], as well as continuous media with periodically spaced local resonators [14]. The general approach is to derive the nonlinear equations of motion, introduce frequency and wavenumber through a change of variables, integrate the transformed equations, apply amplitude-dependent initial conditions on wave phase, and then solve for a relationship between frequency and wavenumber. Notably, the assumption of a small parameter isn’t necessary. For example, the equation of motion governing a rod using a geometrically-exact Green-Lagrange strain measure can be written as [14, 46],
where u(s, t) denotes the longitudinal displacement while the operators \(\dot{( )}\) and \(( )^{'}\) denote temporal and spatial derivatives, respectively. The constant \(c_0\) can be interpreted as the rod’s non-dispersive wave speed \(c_0=\sqrt{\frac{E}{\rho }}\), where E and \(\rho \) denote the material’s elastic modulus and density, respectively.
Following the development presented in [14], a nonlinear dispersion expression is sought relating frequency \(\omega \) and wavenumber \(\kappa \). Thus, intermediate variables \({\bar{u}}=u^\prime \), \(\tau =\omega t\), and \(z=\left| \kappa \right| s+\tau \) are defined such that Eq. (54) transforms to,
Integrating Eq. (55) twice leads to,
Taking the positive root of Eq. (56) yields the strain-like quantity,
Applying the variable transformations to sinusoidal initial conditions,
introduces the wave amplitude B, which upon substitution into Eq. (57) yields the desired nonlinear dispersion relationship for the rod,
Here, \(\omega _{inf}\) denotes the frequency for non-dispersive (infinitesimal strain) waves. It is noted that in arriving at Eq. (56), non-zero integration terms (in the form of polynomials in z) are set to zero as they are secular in nature, a feature shared by the approaches described in Refs. [14, 42,43,44]. The method is thus a straight-forward perturbation approach (see Sect. 1.2.3) in which secular terms are disregarded. This can be compared and contrasted with the Lindstedt–Poincaré and multiple scales approaches described earlier where analogous terms are removed rigorously using introduced expansion quantities—see Sect. 2 for such a treatment in the case of plates. Thus, the unstated limitation of the approach presented is that the displacement field u(z) is non-physical, growing linearly in space and time. This implies further that B is not simply the wave amplitude, but instead the instantaneous wave amplitude at \(z=0\). Nonetheless, the dispersion predictions from this approach, for fundamental frequencies and extra-harmonic generation, have exhibited close agreement with numerical simulations at moderate to large amplitudes when the instantaneous amplitudes taken from the spatially- and temporally-evolving, simulated waveforms are used to inform B [44].
1.3.2 Amplitude-dependent decay of evanescent waves
Regarding evanescent waves, the authors in [47] investigated dispersion shifts and amplitude envelopes specifically when the frequency is above the nonlinear cutoff frequency. In a simple monatomic lattice, they assumed the real wavenumber remains unchanged from propagating waves at the end of the Brillouin zone, and demonstrated amplitude-dependent imaginary wavenumbers; i.e., dispersion shifts in the imaginary domain of the form,
where \(\mu _i\) denotes the imaginary component of the wavenumber, and |A| the wave amplitude. The \(0{\textrm{th}}\)-order frequency \(\omega _0\) is related to \(\mu _i\) by,
In contrast to a propagating wave, an evanescent wave has non-uniform amplitude in space, and thus the dispersion correction also changes along the propagation path. In the attenuation direction, the decreasing amplitude in space mitigates the nonlinear effects, and the far-field imaginary wavenumber converges to its linear value. For hardening nonlinear stiffness, the nonlinear cut-off frequency is above its linear counterpart, and the far-field imaginary wavenumber is nonzero, resulting in a trivial transmission. The softening nonlinear stiffness, however, induces a nonlinear cut-off frequency lower than its linear counterpart, and enables an interesting amplitude saturation effect unique to the nonlinear system.
The saturation phenomenon occurs when a signal falls in the nonlinear stopband and simultaneously the linear passband. As the wave attenuates in the stopband, the imaginary wavenumber decreases and converges to its linear value (i.e., zero), effectively slowing and eventually stalling the attenuation process. The wave amplitude thus converges to a nonzero value,
where the excitation frequency \(\omega \) is smaller than the linear cutoff frequency \(\omega _{cutoff} = 2\sqrt{\frac{k_1}{m}}\) and \(\varepsilon k_3<0\) denotes a softening nonlinearity. These results were numerically validated by direct numerical integration of the governing equations with initial condition excitation [47]. The authors also considered boundary excitation and documented time-dependent dynamics, which they related to the wavenumber clipping effect discussed earlier [28].
1.3.3 Extra-harmonic generation
A hallmark feature of wave propagation in nonlinear media is the generation of extra-harmonics from excitation at a single frequency. In the context of periodic structures, such phenomenon has been explored using analytical, computational, and experimental methods. Of particular relevance to periodic media is the situation of the fundamental and its higher (or lower) harmonics within the material’s band structure, and many studies have classified the effects of generating propagative (vis-à-vis evanescent), weakly dispersive (vis-à-vis strongly dispersive), and inter-band (vis-à-vis intra-band) harmonics.
In [48], second-harmonic generation in a statically-compressed chain of beads is analytically predicted and experimentally validated. Taylor expanding the nonlinear Hertzian contact force between beads, the equations of motion for a diatomic chain with weak quadratic nonlinearity are derived. By equating the linear kernel evaluated at the second harmonic to the nonlinear terms evaluated at the fundamental, a linear system of equations is derived that reveals the coefficients associated with fundamental and second harmonic displacement terms. The generation and propagation of the second harmonic is demonstrated to strongly depend on where the driving frequency \(\omega \) and its second harmonic \(2\omega \) are located within the linear band diagram, particularly whether they fall close to or within a bandgap. For \(\omega \) and \(2\omega \) are in the long wavelength limit, the fundamental amplitude decreases with distance while the second harmonic first grows and then diminishes due to dissipation. When \(\omega \) and \(2\omega \) are within the passband but away from the long wavelength limit, the group velocity disparity causes the second harmonic amplitude to oscillate slowly with unit cell index. If \(\omega \) is propagative but \(2\omega \) is evanescent, the second harmonic amplitude first increases slightly but ultimately decays very rapidly with distance. If \(\omega \) falls within the acoustic branch and \(2\omega \) in the optical branch there is an out-of-phase alteration between adjacent masses occurring at \(2\omega \).
Sánchez-Morcillo et al. [31] employed separate analytical treatments for fundamental and second harmonics occupying long-wavelengths (i.e., non-dispersive case) and short-wavelengths (i.e., dispersive case). Similar to [48], they analyze harmonic excitation at the boundary of a pre-compressed chain of beads featuring weak quadratic stiffness. The studied monatomic chain has dimensionless equations of motion,
For the non-dispersive case, a continuum approximation is employed and a straightforward expansion Eq. (26) yields a set of cascading wave equations. The \(0{\textrm{th}}\)-order (linear) wave equation admits a plane wave solution, \(u^{(0)} = \cos (\omega t-\mu x)\). At the next order, the forcing term emerges as a spatial derivative of the normalized nonlinear stress,
Direct substitution of Eq. (66) into Eq. (65) reveals the oscillating second harmonic forcing. However, this approach dismisses the stationary component of the nonlinear stress which generates zero-frequency (DC) offset in the chain of beads. The authors introduce artificial weak damping into the linear solution to solve this problem,
By substituting Eq. (67) into Eq. (65) and performing a time averaging operation, the DC offset can be decoupled from the oscillating terms and solved using boundary conditions and evaluated in the limit \(\alpha \rightarrow 0\),
where \(\left<\dot{~}\right>\) denotes averaging over time.
For the dispersive case, the straightforward expansion applied to the finite difference equations yields a similar set of ordinary differential equations. The linear solution is identical to the nondispersive case, and the next-order solution comprises DC, forced oscillation (twice the frequency and wavenumber), and free oscillation (satisfying the linear kernel) terms,
Substituting the solution back to the \(1{\textrm{st}}\)-order wave equation yields an algebraic equation for \(B_{2\omega }\) and a sequence equation for \(A_n\)—to be solved by time averaging. The free oscillation terms, \(B'_{2\omega }e^{i(2\omega t-\mu (2\omega ) n} +c.c\), are homogeneous solutions to the wave equation, whose amplitude coefficient derives from boundary condition. In the investigated boundary excited chain, \(B'_{2\omega } = -B_{2\omega }\), due to the absence of second harmonics at the excitation boundary (\(n=0\)). The authors carry the analysis to the second order and derive the spatial evolution of fundamental frequency and generated second harmonics. Both \(\omega \) and \(2\omega \) are propagative, and the fundamental and second harmonic amplitudes oscillate with unit cell index with a phase difference of \(\pi \), as shown in Fig. 5a. If \(2\omega \) is evanescent, the second harmonic amplitude increases slightly and saturates to a stationary level along the propagation direction, while the amplitude of the fundamental harmonic decreases slightly and sustains at that level, as depicted in Fig. 5b. Numerical simulations exhibit close agreement with analytical predictions. The authors conclude that the forced second harmonic makes a non-negligible contribution to the amplitude of the fundamental frequency at long distances.
Spatial evolution of the DC mode, fundamental, and generated second harmonic. a The spatial evolution when the second harmonic is propagative. The blue solid curves and orange dots are theoretical and numerical results, respectively. b The spatial evolution when the second harmonic is evanescent. The green solid curves and red dots are theoretical and numerical results, respectively [31]
In [49], wave propagation through a medium composed of continuous layers separated by linear and quadratic nonlinear springs is studied. A perturbation analysis establishes the equations of motion and transfer matrix approach determines the fundamental and second harmonic solutions. The effects of a single nonlinear interface and multiple consecutive nonlinear interfaces are investigated. As with [48], the propagation of the second harmonic differs qualitatively depending on its placement within the linear band structure. If both the fundamental and second harmonic lie well-below the cut-off frequency, the second harmonic amplitude grows with distance. If the second harmonic is near the cut-off frequency, the second harmonic component has a standing wave nature. If the first and second harmonic occupy two distinct branches, the second harmonic amplitude oscillates with specific wavelengths. If both the first and second harmonics are within bandgaps, there is attenuation of the fundamental and local generation of the second harmonic, and neither frequency component propagates. They also remark on the possibility of phase-matching conditions whereupon the second frequency also falls in the linear band structure and possesses the same phase velocity as the fundamental. Such a case is characterized by the spatial growth of the second harmonic amplitude.
Frandsen and Jensen [50] examine third harmonic generation in a diatomic chain with cubic nonlinearity. Using the method of multiple scales, they analytically predict the magnitude of the third harmonic generation by determining the particular solutions that other studies have proposed to describe invariant waves [25, 29]. Close agreement is documented between analytical predictions and numerical simulations of the lattice. In particular, they compare third harmonic generation for four different cases: fundamental and third harmonic in the long wavelength, fundamental and third harmonic in the acoustic band yet away from the long wavelength limit, fundamental in the acoustic band and third harmonic in the bandgap, and fundamental in the acoustic band and third harmonic in the optical band. Of particular note is that third harmonic generation is stronger in the long wavelength limit and that third harmonic generation still occurs, albeit more weakly, if the third harmonic falls in the bandgap. They remark on their model’s inability to handle internal resonances.
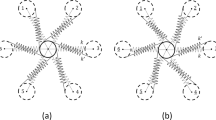
Further richness has been revealed when the generated harmonics possess a different modal character than that of the excitation. For example, Ganesh and Gonella [21] identify a so-called “modal mixing” phenomenon in which sufficiently high amplitude excitation of a lattice in a lower branch generates higher harmonics in higher branches, eliciting enriched wave propagation mode shape patterns. They demonstrate this finding in an example lattice in which low amplitude excitation in the acoustic branch produces axial-type deformation, yet when the driving amplitude exceeds a critical threshold, the optical mode is excited and shear-type deformation at twice the driving frequency mixes with the axial displacement at the fundamental. Figure 6a illustrates the spectral composition resulting from low amplitude harmonic forcing whereas Fig. 6b depicts the “modal mixing” phenomenon due to high amplitude harmonic loading. A similar mechanism was identified by Jiao and Gonella [51] in which driving a lattice at a flexural mode yielded second harmonic generation at an axial mode. Figure 6c and d displays experimental results of a lattice subjected to flexural harmonic loading. A strong flexural response at the fundamental is measured in Fig. 6c yet axial motion at the second harmonic is also recorded in Fig. 6d. Wallen and Boechler [52] reveal richness in the second harmonic generation of 2-D hexagonally closed packed lattices of microspheres. While excitation of a longitudinal mode induces second harmonic activity exclusively within the longitudinal mode, excitation of a transverse-rotational mode produces second harmonic activity at a longitudinal mode.
Higher harmonic generation exhibiting different modal character between the fundamental and harmonics. a In a nonlinear lattice system, Ganesh and Gonella [21] report “modal-mixing” via higher harmonic generation in which low amplitude excitation retains spectral energy at a single branch of a band structure. b High amplitude excitation of the same lattice system produces higher harmonics in an upper branch of the band structure culminating in enriched wave propagation mode shapes. c Jiao and Gonella [51] report harmonic flexural excitation of a lattice yielding flexural activity at the fundamental and d axial second harmonic activity
Subharmonic generation has also been studied, albeit in a more limited fashion. Tournat et al. [53] detail self-demodulation in which a high-intensity narrowband excitation produces extra harmonics and subsequent frequency mixing. A low frequency (as a result of a frequency difference) sustains wave propagation over longer distances compared to its higher frequency counterparts.
1.3.4 Waveform invariance
Higher-order multiple scales can also be employed to predict the existence of invariant plane wave solutions in weakly nonlinear lattices, which are akin to nonlinear normal modes in bounded media. The multi-harmonic particular solution coefficients found in Eq. (18) exhibit neither spatial nor temporal dependence. Furthermore, the particular solutions possess the same phase velocity as evidenced by the constant ratio of frequency to wavenumber. Consequently, these solutions suggest that nonlinear lattices admit a specific distribution of spectral energy that propagates without growth or decay of extra harmonics. Such a finding is particularly striking given the dispersive nature of lattices. These invariant plane waves share the shape-preserving character of solitons yet are spatially and temporally infinite in extent (in contrast to the soliton’s signature compact support).
To validate these solutions, direct numerical integration of the lattice equations of motion was carried-out in [29]. The solver’s initial displacement and velocity distribution corresponded to the multiple scales series solution truncated to different orders. To measure the invariance of a simulated waveform, the temporal variation of a spatial Fourier coefficient was tracked. The study documented less variation of the second and third harmonics by including higher-order multiple scales terms in the solver’s initial conditions. Figure 7a and b display the normalized reduction in the variance of the second and third harmonics, respectively, by including \(2{\textrm{nd}}\)-order multiple scales initial conditions as compared to \(1{\textrm{st}}\)-order. Note that \(\Pi _2\) and \(\Pi _3\) denote dimensionless parameters corresponding to the strength of the quadratic and cubic nonlinearity, respectively.
In two-dimensional shear lattices, the invariant plane wave solutions exhibit directional dependence. Directions with a higher magnitude of its multi-harmonic solution coefficient experience a greater reduction in its variance with the inclusion of higher-order multiple scales terms as supported by numerical simulations [25]. Figure 7c plots the magnitude of the third harmonic solution coefficient obtained from multiple scales for the diatomic lattice as a function of \(\theta \), the angle of wave propagation relative to the lattice direction. Figure 7d presents the reduction in the variance of the third harmonic obtained in numerical simulations of the acoustic branch of the diatomic lattice. Note that directions with a higher magnitude of third harmonic solution coefficient experience a larger reduction in variance in numerical simulations. In the presence of a larger “deficit” in the invariant spectral content, these directions experience comparatively more temporal variation.
Invariant plane wave solutions in nonlinear lattices. a The inclusion of higher-order multiple scales terms in a solver’s initial conditions yields a reduction in the variance of the third harmonic in numerical simulations of the monatomic chain. b A reduction in the variance of the third harmonic is also measured in simulations of the monatomic chain. c For a two-dimensional diatomic lattice, multiple scales predictions of the magnitude of the third harmonic solution coefficient vary as a function of the angle of wave propagation \(\theta \). d In numerical simulations, directions with a larger magnitude of multi-harmonic solution coefficient experience a greater reduction in the variance of a given harmonic. \(\Pi _2\) and \(\Pi _3\) denote dimensionless parameters corresponding to the strength of the quadratic and cubic nonlinearity, respectively
Interestingly, the higher-order multiple scales analysis reveals select wavenumbers at which the multi-harmonic solution is identically zero. This occurrence suggests that the \(0{\textrm{th}}\)-order solution propagates invariantly and therefore extra-harmonic generation ceases at these special frequencies [54]. Numerical simulations confirmed that extra harmonic production is drastically smaller for plane waves injected at these unique wavenumbers.
Multiple scales is also capable of resolving the invariant nature of internally-resonant plane waves; i.e. wave propagation modes with an exactly (or nearly) commensurate relationship. While not strictly invariant, internally-resonant plane waves undergo a slow-scale energy exchange across all space and time. This finding is predicated on the wave propagation modes being sufficiently near neutrally-stable centers identified by multiple scales. Such phenomenon is analytically handled by injecting two plane waves at the \(0{\textrm{th}}\)-order.
The frequency and wavenumber of the A wave and B wave satisfy or nearly satisfy the n : 1 internal resonance criteria,
where \(\sigma _\omega \) and \(\sigma _\mu \) represent small detuning parameters for the exact internally-resonant frequencies and wavenumbers, respectively. With the two wave solution introduced, secular terms arise at both \(e^{i\omega _{0,A}T_0}e^{-i\mu _Aj}\) and \(e^{i\omega _{0,B}T_0}e^{-i\mu _Bj}\) resulting-in four evolution equations after the associated removal of secular terms: \(D_1\alpha _A\),\(\ D_1\alpha _B\),\(D_1\beta _A\), and \(D_1\beta _B\). This state space can be reduced from four dimensions to three by defining a relative phase term between the A and B waves,
A further reduction in the state space from three dimensions to two can be accomplished by deriving an elliptical relationship between the A and B wave amplitudes,
where the positive real-valued r depends on lattice parameters and frequency, and the energy-like constant E is determined by initial conditions. The lattice dynamics can then be studied using a two dimensional phase portrait, such as \(\alpha _B\) versus \(\gamma \). A local fixed-point analysis identifies neutrally stable periodic orbits: specific initial combinations of amplitude and phase that undergo slow-scale energy exchange for all space and time. This invariant behavior was validated by numerical simulations in which the temporal evolution of spatial Fourier coefficients closely matched the multiple scales predictions [55].
Hussein and Khajetourian recently uncovered spatially invariant waveforms in continuous thin rods with alternating material properties [12]. Hardening nonlinearity stems from the retention of higher-order terms in the continuum’s Green-Lagrange strain. A transfer matrix approach yields closed-form nonlinear dispersion relationships whereupon a balancing between hardening nonlinearity and softening dispersion enables the propagation of fixed profile nonlinear traveling waves. Note that this balancing of disperison and nonlinearity is similar to the mechanism behind soliton formation [56].
The multiple scales analysis in [55] generally handles either 2:1 or 3:1 internal resonances, either within or between dispersion branches. It builds-upon a prior study considering solely 2:1 internal resonances within the same branch of a monatomic chain’s passband [57]. In this work, a local fixed point analysis also identifies neutrally stable fixed points corresponding to periodic wave energy exchange. They also distinguish between phase drift and phase-locking solutions by examining the slow-scale evolution of a spatio-temporal phase term. A separatrix in the multiple-scales derived phase portrait separates the two phenomena and suggests the existence of emergent waveforms.
Lepidi and Bacigalupo [58] also present a multiple scales treatment of internal resonances in nonlinear locally-resonant lattices, including interactions between waves on different dispersion branches. Nonlinear dispersion relationships are derived after introducing a similar relative phase term as Eq. (73). The authors draw similarities to these nonlinear band structures and nonlinear normal mode analysis of finite vibratory systems. Their multiple scales analysis reveals admissible nonlinear waveforms such that, as in [39], invariant manifolds can be identified. It is important to note that some of these invariant manifolds correspond to stable periodic orbits as also predicted in [55, 57]. While 3:1 superharmonic internal resonance was the principle focus of the study, there is an interesting discussion on the existence of 1:1 resonant interactions, or curve veering, of two distinct branches of a locally-resonant band structure that coalesce at certain parameter sets enabling the potential for strong energy transfer.
Amplitude and direction-dependent stability in nonlinear lattices. a In 1-D lattices, multiple scales predicts that plane waves propagate in a stable manner at sufficiently low amplitudes yet lose stability at high amplitudes, which is confirmed by numerical simulations. b Multiple scales analysis of 2-D shear lattices reveals directionality of the fixed points associated with a transition from stable to unstable plane wave propagation. c Numerical simulation of the 2-D shear lattice exhibits directionality of the stability consistent with the multiple scales predictions
1.3.5 Stability
The stability of wave propagation in nonlinear media is of fundamental importance. In the context of periodic media and metamaterials, stability is typically studied in bistable lattice systems [59,60,61,62,63] wherein a nonconvex curvature in the force displacement relationship enables “snap-through” behavior to occur. The propagation of unidirectional transition waves [64, 65] have been observed in such systems. Bistabile potentials have also been extended to 2-D lattices [66]. By contrast, studies of waveform stability have generally centered around localized solutions such as solitons [67,68,69] and discrete breathers [70,71,72,73]. The stability of plane waves in nonlinear periodic systems have received very little attention. One practical implication of such a study is the potential amplitude limit on band structure shifting due to a loss of plane wave stability.
The higher-order multiple scales analysis presented in Sect. 1.2.1 provides insight into the stability of plane wave propagation in nonlinear lattices. Using the higher-order evolution equations, wave amplitude is reconstituted to the original time scale,
Fixed-points can then be identified that satisfy,
Their stability can be assessed locally using the multiplier,
where \(\lambda <0\) signifies a stable fixed point, \(\lambda >0\) an unstable fixed point, and \(\lambda =0\) signifies a neutrally stable fixed point. For both the monatomic and diatomic lattices with quadratic and cubic stiffness, two fixed points arise,
where \(\delta \) is parameter associated with amplitude-dependent dispersion shifting and depends functionally on lattice parameters and frequency. The fixed point \(\alpha ^*=0\) is stable and has finite domain of attraction. Thus, sufficiently small amplitude plane waves propagate in a stable manner, decaying to zero amplitude over time due to the light viscous damping in the lattice. However, the nonzero fixed point \(\alpha ^*=\sqrt{\frac{\omega _0}{\varepsilon \delta }}\) is unstable and attracts larger waves under time reversal. These results, taken together, signify amplitude-dependent stability of plane waves in nonlinear lattices. It is worth noting that, due to the presence of \(\varepsilon \) in the denominator, the non-zero fixed-point is too large to be consistent with the weak nonlinearity assumption inherent to the multiple scales analysis [29]. However, it does qualitatively indicate amplitude dependent stability of plane waves that was subsequently validated in direct numerical simulations of the lattice equations of motion.
Figure 8a displays simulation results for a number of initial plane wave amplitudes. The stability of a given plane wave was numerically monitored in each simulation. Typical forms of plane wave instability revealed by these numerical simulations include the formation of incommensurate spectral content (generally associated with large cubic stiffness) and the unbounded growth of wave amplitude (generally associated with large quadratic stiffness). If either such form of instability manifested then the waveform was considered unstable. Note that plane waves propagate in a stable manner for relatively low amplitudes until a critical amplitude (\(\Pi _{2,crit}\) or \(\Pi _{3,crit}\)) whereupon the simulated waveform breaks down. This amplitude-dependent stability qualitatively confirms the behavior predicted by the local fixed point analysis from the multiple scales evolution equations.
In two-dimensional shear lattices, plane wave stability exhibits directionality. It was found in [25] that propagation along the lattice direction was inherently less stable than propagation along inclined directions. This result stems from the growth in magnitude of the non-zero fixed point when evaluated about wave propagation angles inclined away from the lattice direction as documented in Fig. 8b. Directions with larger non-zero fixed points require higher amplitudes to observe an instability and hence are considered more stable. This directional stability also applies to the radiation of wave energy from a point source. Wave information extracted from unstable directions are more prone to develop incommensurate frequency content as supported by numerical simulations. Figure 8 presents results from numerical simulations of a monatomic shear lattice whereupon the percentage of spectral energy outside the fundamental and harmonics (\(E_{s,\delta }\)) measured at the end of a simulation of a given plane wave. The values of \(E_{s,\delta }\) indicate the stability of a simulated waveform. As presented in Fig. 8c, the directionality of the plane wave stability observed in numerical simulations aligns with the multiple scales predictions. The counterintuitive finding of directional stability may inspire novel mechanical encryption or structural health monitoring strategies [25].
Higher-order perturbation analysis must be carried-out to observe both fixed points. A first-order multiple scales analysis is insufficient for capturing the amplitude-dependent stability. It is also important to note that damping plays a critical role in identifying the fixed points in Eq. (75). The evolution equations for amplitude are zero for undamped systems and thus indicate neutral stability. The presence of light damping enables the complete identification of fixed points even though the fixed points themselves do not depend on the damping coefficient.
1.4 Future work
In this section we identify open areas of investigation concerning nonlinear waves in discrete periodic media and metamaterials; namely, experimental developments, technology and devices, and multi-physics nonlinear periodic systems.
1.4.1 Experimental developments
The literature concerning experimental exploration of nonlinear metamaterials and periodic structures is sparse, and as such, has yet to confirm many of the theoretical findings in the field–particularly those pertaining to mechanical lattices with weak stiffness nonlinearity. Manktelow et al. [74] indirectly verified amplitude-dependent dispersion shifts using a periodic string in which the system’s natural frequencies were identified with points on a dispersion curve. Monitoring the changes in these natural frequencies then provided the dispersion shifts. This demonstration, while useful, was limited by modeling assumptions required to represent the system in discrete form, and by an amplitude limit upon which the periodic string whirled instead of vibrating in-plane as desired. Another experimental study of amplitude-dependent bandgap tuning incorporated transversely-loaded compression springs [40]; however, it was limited to low frequencies and a small number of unit cells. The nonlinear wave mechanics in granular media have also been experimentally analyzed, with notable demonstrations of solitary wave [75] and breather [76] propagation in addition to nonlinear resonances [77]. Other recent experimental studies investigated nonlinear electromechanical metamaterials showcasing effects such as piezoelectricity-enabled wave attenuation [78, 79] and long wavelength frequency shifting [80].
Focused research is needed to devise ready-to-deploy mechanical nonlinear elements with well-defined and tunable nonlinear properties rather than case-specific or circumstantial nonlinear elasticity. Such designs will enable more widespread testing and validation of nonlinear phenomena: e.g., the desired strength and type of nonlinearity would be readily tailored-to and implemented-in experiments and device prototypes. Since additive manufacturing techniques have rapidly transformed the fabrication of linear metamaterials [81, 82], such methods can similarly revolutionize the fabrication of nonlinear metamaterials [83].
1.4.2 Technology and devices
We envision advancements in technology and devices that showcase nonlinear periodic structures and metamaterials. For instance, amplitude-dependent metamaterials may inspire next-generation sensing, actuation, and cloaking technology used in, for example, medical and communications industries. Such settings may find it appealing to filter, re-route, attenuate, or focus waves as a function of their amplitude or energy. Scaling nonlinear periodic structures to operate in the MEMS regime may also prove to be a advantageous venue for these processes. Amplitude-dependent metamaterials may be exploited as discrete elements used to join ordinary materials and operate as logic elements, limiters, and switches in acoustic and elastic circuits. Indeed, there is growing knowledge of and interest in mechanical computation using metamaterials [84].
1.4.3 Multi-physics nonlinear periodic systems
An unexplored direction in the study of nonlinear metamaterials and periodic media is integration with multiple physics domains. Analogous nonlinear systems that have been studied in isolation include phonon heat transfer [85,86,87], optical media [88,89,90], electrical transmission lines [91,92,93], and magnonic crystals [94,95,96]. A high degree of richness—and perhaps technological development—would stem from coupling elastic and acoustic nonlinear metamaterials and phononic media to one or more of these other domains. This may require studies of reflection and transmission at linear-nonlinear and nonlinear-nonlinear metamaterial interfaces, which very few studies (particularly asymptotic studies) have considered to date. Phenomena such as amplitude-dependent dispersion shifting, higher-harmonic generation, and waveform stability may manifest in unusual and unexpected ways, and it may be possible that new and transformative phenomena might be uncovered in such coupled media. Recent advancements in computational power would enable efficient and large-scale simulations of nonlinear multi-physics problems.
2 Nonlinear elastic waves in continuous media
In continuous media, nonlinearities may be associated with finite strains, a nonlinear elastic stress–strain relationship, and/or boundary conditions (e.g., contact-related phenomena connected to cracks and interfaces). Depending on the source of nonlinearity, a variety of wavefield distortions may arise. Consequently, localized and distributed sources of nonlinearity display different wavefield signatures that can be used for later identification and characterization. In order to employ nonlinear wavefield features for the above-mentioned and other applications in practice, it is critical to develop analysis methods for elastic waves in continuous nonlinear media. In this section, we review recent theoretical developments for waves in nonlinear continuous media. We start by overviewing the analysis of a 1-D nonlinear problem, followed by a 2-D bounded system. In the latter case, we focus on waves in nonlinear plates. For the presented examples we explore quadratic and cubic material nonlinearities, for the 1-D and 2-D systems, respectively, in addition to quadratic strain inherent to nonlinear continuous systems. In all cases we demonstrate mechanisms behind higher-harmonic generation and nonlinear shifting of dispersion properties.
First, a special static component of the secondary wavefield, generated in quadratic-nonlinear systems, is thoroughly discussed to introduce the methods used and the phenomena encountered. In particular, we review the mechanism and properties of the DC (i.e., zero-frequency) wave mode.
2.1 Theory for a quadratically nonlinear 1-D medium
We start with a 1-D nonlinear wave propagation problem in a continuous medium governed by a quadratic stress–strain relationship. Noting that concepts and equations governing propagation of longitudinal waves in elastic solids and nondissipative fluids are identical, in [97] and subsequent contributions [98,99,100] analytical solutions for finite-amplitude waves propagating in nonlinear solids were developed. For an example 1-D system, equivalent to a single plane-wave mode propagation in the bulk of material, the nonlinear wave equation in Lagrangian coordinates employs the nonlinear Green-Lagrange strain [98, 99],
with u denoting the displacement and x the spatial coordinate taken in the undeformed configuration. Subsequently, the first Piola-Kirchoff stress is defined as the derivative of the strain energy density U with respect to the deformation gradient components F (\(F \equiv 1 + \partial u / \partial x\) in 1-D) as,
where \(\rho \) denotes the density in the undeformed state and \(\beta \) the acoustic nonlinearity parameter combining the contributions of the nonlinear strain–displacement relation, Eq. (79), and the material nonlinearity. For an isotropic elastic solid, \(\beta = - (3 + \zeta )\) with \(\zeta = 2 ({\mathcal {L}} + 2 {\mathcal {M}}) / (\lambda + 2 \mu )\), where \({\mathcal {L}}\) and \({\mathcal {M}}\) are Murnaghan third order elastic constants [99]. Using Eqs. (79) and (80) in the equation of motion, \(\partial \sigma / \partial x = \rho \partial ^2 u / \partial t^2\), yields,
It is characteristic of a quadratically-nonlinear system, and clear from Eqs. (79) and (80), that the nonlinear stress (and strain) term will display the same sign, regardless of the sign of the displacement gradient. Namely, for positive and negative \(\partial u / \partial x\), the nonlinear stress term of Eq. (80) will always be negative for \(\beta > 0\). Hence, during the compression phase of oscillatory motion, negative nonlinear stress will be generated. For the tensile part of the motion, however, the nonlinear part of the stress will also be negative, resulting in a continuous push and therefore building-up of the constant (nonzero net) offset. The latter is the consequence of the geometrical definition of the Green-Lagrange strain, Eq. (79), and the fact that the constitutive relation, Eq. (80), is derived as the deformation gradient-derivative of the strain energy density function. It should be noted that different assumptions (e.g., the Ludwick-type constitutive relation of quadratic type), may lead to sign-dependent terms (i.e., \(\sigma \propto \text {sign} (\epsilon ) |\epsilon |^{2} \)) and therefore do not produce (or substantially reduce) the constant displacement offset [101, 102].
As will be clear later, a solution of Eq. (81) requires an additional consistency condition in the form of a relation between the particle velocity \(\partial u / \partial t\) and the displacement gradient \(\partial u / \partial x\), which in general form can be written as,
with \(f \left( \partial u / \partial x \right) \) being a continuous differentiable function of the displacement gradient. Differentiating Eq. (82) with respect to the time yields,
while differentiating Eq. (82) with respect to the spatial coordinate yields,
where in Eqs. (83) and (84) the prime \('\) denotes a derivative with respect to \(\partial u / \partial x\). Combining Eqs. (83) and (84) results in
Comparison of Eq. (86) with the analogous relation of Eq. (81) allows for identification of \(f'\) as
Taking the positive square root of Eq. (86) (waves propagating to the right) and integration with respect to \(\partial u / \partial x\) gives the particle velocity (see Eq. (82)),
In Eq. (87) the casualty condition (i.e., zero displacement gradient and velocity when no wave is present) has been employed during the integration.
The relation embodied by Eq. (87) will be later relevant for computing time-averaged stresses and strains—key quantities in extracting the aforementioned zero-frequency wave component from the response. Also, the condition Eq. (87) is later used as the consistency condition in [99, 100, 103] for determining the static displacement amplitude and slope (see Sect. 2.2). The solution in [98] was given in terms of the radiation stress and strain, while [97, 99, 100, 103, 104] provide explicit static displacement formulas.
2.2 Solutions for the quadratically nonlinear 1-D medium
We briefly recall two solution approaches applied to the nonlinear problem defined in Sect. 2.1 [Eq. (81)]. The first one, proposed in [105], is based on a direct solution in terms of particle velocity. The second, developed in [99], was proposed within a classical straightforward expansion perturbation framework.
The solution to Eq. (81) was first obtained by Fubini [105] in terms of particle velocity. Assuming an excitation by prescribed traction at \(x = 0\) of the form
and propagation ranges smaller than the discontinuity distance, the Fubini solution [105] can be approximated as [98],
Clearly, the velocity solution of Eq. (89) indicates the existence of a wave component at the fundamental and second harmonic frequency. It is important to note that the second harmonic frequency component grows linearly with the propagation distance. This effect will be discussed in detail later.
An alternative, perturbation-based solution approach to Eq. (81) provides a different perspective on the displacement solution to the same problem and will be presented next [99]. Following the straightforward perturbation expansion, the solution to Eq. (81) is written as,
where \(|u_1| \gg |u_2|\). Using Eq. (90) in (81) yields two equations,
to be solved sequentially for \(u_1\) and \(u_2\). Assuming a general form of the solution to Eq. (91) as \(u_1 (x,t) = g (t-x/c)\) (with g being a twice-differentiable function of x and t), Eq. (92) can be written as [103],
with \(G(s) = \beta / c^3 g'(s) g''(s)\) and prime \('\) denoting differentiation with respect to the function argument s. The solution to Eq. (92) can be written as,
with \(\phi \) and \(\eta \) to be determined (by the boundary conditions and/or the consistency condition of Eq. (87) [99]). Performing integration in Eq. (94) yields,
Various conditions have been proposed in the literature to find the parameters \(\phi \) and \(\eta \), including assuming them equal to zero, assuming the static stress (involving \(\phi \)) equal to zero, or forcing the solution to satisfy the consistency condition, Eq. (87) [99]. This latter condition was employed in [98] and later in the perturbation solution of [99].
Qu et al. [99] noted that the general solution of the form of Eq. (95) predicts different harmonic components depending on whether prescribed displacement or prescribed traction boundary conditions are assumed, and considered continuous mono-frequency [99] and pulse excitations [103]. For the prescribed displacement case, the excitation was applied in the form,
while for the prescribed-traction excitation, the expansion defined in Eq. (90) is re-written as \(\sigma = \sigma _1 + \sigma _2\), \(|\sigma _1| \gg |\sigma _2|\) with,
and the boundary conditions as,
The function P(t) in (96) and (99) yields,
or,
for continuous, \(P_c\), and wavepacket, \(P_p\), signals, respectively.
Assuming prescribed displacement as the excitation, \(g (x,t) = u_1 (x,t)\), the solution to Eq. (92) takes the form,
where \(\phi = \beta [g'(0)]^2 / (4 c^2)\) and \(\eta = 0\) from consistency and boundary conditions, respectively, and subscript D denotes prescribed displacement excitation. Substituting Eq. (96) into Eq. (103) results in the \(u_2 (x,t)\) formula for the prescribed displacement case, composed of the static displacement and the second harmonic components
The first term in Eq. (104) is the linearly growing zero-frequency component, while the second is the second harmonic of linearly growing amplitude. Depending on the particular selection of P(t), Eq. (104) describes continuous wave or a pulse propagation through the nonlinear medium. Combining Eq. (96) and Eq. (104) according to Eq. (90) yields,
For the prescribed-traction case, we have,
Using Eqs. (106), (99) and (97) in Eq. (95) yields the \(u_2\)-displacement for the prescribed traction case,
where subscript T denotes prescribed traction excitation and the parameters \(\phi \) and \(\eta \) were determined from boundary conditions as,
Using Eq. (99) in Eq. (107) gives the secondary wavefield composed of the static and second-harmonic terms of the form,
Noting Eq. (90), the total solution to the nonlinear problem under traction excitation can be written as,
Clearly, all the solutions to the quadratic-nonlinear problem—with both displacement and traction excitation—exhibit the linear component at frequency \(\omega \) and nonlinear terms at 0 and \(2\omega \) (up to the first order of expansion).
It can be noted from the solution to the 1-D quadratic-nonlinear problem, Eqs. (105) or (111), that—apart from the second harmonic wave—a component of zero frequency arises. Indeed, it appears for systems with nonlinearities of even type (e.g., quadratic nonlinearities), that upon excitation by a primary wave of frequency \(\omega \),—among other—harmonic waves at double the fundamental frequency are generated. Depending on the particular type of nonlinearity, an additional \(\omega - \omega \) component, excited at zero frequency, may also arise. This component is frequently referred to as the DC (direct current), static, or the zero-frequency mode and results in static displacement, strain and stress. The static wave component was of interest for electromagnetic and acoustic waves in fluids as pointed out in works even prior to the paper of Rayleigh [106]. The topic was further investigated by Brillouin [26], Fubini [107], Westervelt [108] and Blackstock [109]. Over next years there have been many theoretical and experimental investigations reporting on the radiation stress, that were summarized in a number of reviews, e.g. [110,111,112].
In classical nonlinear systems, the static displacement mode follows as a consequence of the geometrical and (classical) material nonlinearity, both described by positive-only terms proportional to the square of the primary wave displacement. Alternative definitions of the stress–strain (or force-displacement) relations that depend on the sign of the strain (or displacement)—and therefore do not produce the offset for nonlinear problems (e.g., the Ludwick-type quadratic nonlinearity) may be also considered [101, 102].
It is known that this static displacement relates to the acoustic-radiation-inducted strain [98, 99] and to the acoustic (Boussinesq) radiation stress [113]. Despite being realized a long time ago that in nonlinear systems a static displacement component may be generated, and that a number of works were devoted to analytical, numerical and experimental studies of this effect, there is an ongoing debate on certain aspects of the solutions, including the definition of the radiation strain, the source of energy for the DC mode development and propagation, the shape in spatial and time domains, and the dependency on transducer type and size. The authors expect further research efforts will be devoted to the DC component, particularly for nonlinear periodic media, where almost no consideration has been given to date.
2.3 Theory for nonlinear guided waves in plates
In this section we extend the discussion of nonlinear elastic waves in continuous media to guided waves; i.e., wave patterns arising due complex interactions of bulk waves with material interfaces and boundaries in structures and their components. Propagation characteristics of these waves are more complex than the bulk wave cases considered so far. This section also addresses generation of higher harmonics, internal resonances, and amplitude-dependent effects using the example of guided waves in plates. It should be noted, however, that each type of guided wave displays individual properties and not all conclusions from this section generalize.
In plates, where longitudinal and shear partial wave components are coupled by two parallel traction-free surfaces, waves of certain wavevectors interfere constructively, leading to Lamb wave modes. Lamb waves are multimodal and dispersive; i.e., the modal velocity depends on frequency. Example dispersion characteristics for a 1 mm-thick aluminium plate (\(\lambda = 6.05 \times 10^4\) MPa, \(\mu = 2.59 \times 10^4\) MPa, and \(\rho = 2700\) kg/m\(^3\)) are shown as a wavenumber-frequency and, equivalently, velocity-frequency plots in Fig. 9a and b, respectively. Dispersion characteristics constitute the phase-frequency properties of a plate. The amplitude-frequency characteristics, known as excitability plots, are shown for the same plate in Fig. 9c (out-of-plane actuation and reception direction was assumed). When the plate material is nonlinear, higher-harmonic guided wave modes are generated whose properties are amplitude-dependent. Due to the complex dispersion properties, both generation and interaction of higher harmonics differs from those of non-dispersive media. We introduce and discuss these concepts in the following sections.
Dispersion a, b and excitability c characteristics for an example 1 mm aluminium plate (\(\lambda = 6.05 \times 10^4\) MPa, \(\mu = 2.59 \times 10^4\) MPa, and \(\rho = 2700\) kg/m\(^3\)), shown in (a) the wavenumber-frequency domain and (b) the velocity-frequency domain. Only the first five modes are labelled
2.3.1 Problem formulation
We review the formulation assuming a zero-curvature, thin structure with two parallel, traction-free boundaries. The material is assumed hyperelastic and its stress–strain relationship is elastically nonlinear. Despite small (but finite) deformations, we invoke the nonlinear strain formulation. It should be noted that, in general, other (e.g., out-of-plane) nonlinear interactions may arise and require a full 3-D analysis (see e.g. [114, 115]).
The elastodynamic equilibrium equation for a nonlinear bulk medium is given as [116],
where \( \rho \) denotes the density in the undeformed configuration, \( \pmb {X} = [u v]^T \) is the particle displacement vector in 2-D space and \( \pmb {\sigma } \) is the first Piola-Kirchoff stress tensor. The spatial derivatives in Eq. (112) are taken with respect to the undeformed coordinates. For a complete displacement-based description of wave motion, Eq. (112) is supplemented by constitutive and geometric relationships.
Assuming waves of small, but finite amplitudes, the Green-Lagrange strain tensor is considered,
where \(X_i\) denote \(i{\textrm{th}}\) component of the particle displacement vector and \(D_i\) represents \(i{\textrm{th}}\) spatial direction.
The nonlinear stress–strain relationship is derived from the strain energy density function given by [117, 118],
where \( I_1 \), \( I_2 \) and \( I_3 \) denote the strain tensor invariants, \( \lambda \) and \( \mu \) the Lamé constants, and \( A-H \) denote higher order elastic constants. Terms up to fourth-order in displacements are retained. Particular components of the first Piola-Kirchoff stress tensor are obtained by differentiating the strain energy density function with respect to the deformation gradient tensor components, as in Sect. 2.1, and can be found in [116, 119].
Combining Eqs. (112), (113) and the formulas for the stress tensor components, grouping the terms and introducing non-dimensional time, \( \tau = \omega t \), yields
where \( \pmb {f_{NL}} \) is the nonlinear force vector containing terms related to the nonlinear part of the stress tensor. Matrices \( \pmb {a_1} \), \( \pmb {a_2} \) and \( \pmb {a_3} \) are given by,
In Eq. (115), a book-keeping parameter, \( \varepsilon \), is introduced to facilitate an asymptotic analysis. Equation (115) governs the wave motion in an infinite, (hyperelastic) nonlinear elastic medium. Confining the wave propagation between two stress-free surfaces (i.e., the Rayleigh-Lamb problem definition) requires adequate boundary conditions.
The set of stress-free boundary conditions for the plate problem is given by,
where \( \pmb {n} = \pm [0 1]^T \) denotes the surface outward-pointing normal vector and 2h the plate thickness. Noting that the stress–strain relation contains nonlinear terms, Eq. (117) can be rewritten in the displacement form as,
where \( \pmb {b_1} \) and \( \pmb {b_2} \) are given by,
and \( \pmb {g_{NL}^{(\pm )}} \) results from the nonlinear components of the first Piola-Kirchoff stress components.
Equations (115) and (118) define the nonlinear Rayleigh-Lamb wave propagation problem for a nonlinear plate in 2-D space.
2.3.2 Solution for a nonlinear plate
The nonlinear plate problem, defined by Eqs. (115) and (118), cannot be solved exactly and instead requires an approximate solution approach. In [119], a simple perturbation technique was employed to find higher harmonics generated in a quadratic-nonlinear plate. Alternatively, in [45], an asymptotic approach based on the Lindstedt–Poincaré perturbation was used for quadratic and cubic nonlinear plates to determine amplitude-dependent dispersion similar to that reviewed for discrete periodic systems. We briefly review the solution procedure presented in [45].
Expansions are introduced for the displacement field and the frequency,
where subscripts 0 and 1 refer to the order of approximation. Using Eq. (120) in Eqs. (115) and (118), and collecting terms of same powers of \(\varepsilon \), yields a sequence of linear plate problems, for which the first two orders can be written as
Equations (121)–(124) can be solved sequentially, noting that the nonlinear forcing terms in Eqs. (123)–(124) depend only on the previous-order solutions. The zeroth-order problem, Eqs. (121) and (122), is a classical Rayleigh-Lamb problem that may be solved for dispersion characteristics—for simple material setups, e.g., isotropic, homogeneous, linear-elastic systems—using the method of potentials [120, 121]. For more complex materials, solutions can be generated using the partial wave technique [122]. Subsequent higher-order problems are linear and inhomogeneous. Their solution yields both generated higher harmonics and amplitude-dependent dispersion shifts. Both these aspects will be briefly reviewed.
The zeroth-order problem governs dispersion characteristics (i.e., wavenumber-frequency pairs) for propagating plate modes [121]. These linear Lamb wave modes, \(\pmb {X_0}\), are given by,
where c.c. stands for the complex conjugate of all preceding terms and \(\alpha \) denotes the wave amplitude. The vector \(\pmb {\phi ^{(S,A)}}\) represents the linear Lamb wave mode displacement profiles across the plate thickness, with S or A denoting symmetric or anti-symmetric through-the-thickness modes.
The zeroth order solution pairs \( (\omega _0, k) \) are obtained by using Eq. (125) in Eqs. (121) and (122) and solving the corresponding eigenproblem for \(\omega _0\) given k, or vice-versa. The eigenfunctions \(\pmb {\phi ^{(S,A)}}\) can be found in literature; e.g., in [121]. No explicit analytical formulas exist for the dispersion curves of Lamb waves, \(k(\omega _0)\), and thus the solutions must be obtained numerically. Example dispersion characteristics, presented in the form of wavenumber-frequency and velocity-frequency plots, are provided in Fig. 9a and b. The Rayleigh-Lamb problem can be also solved for its amplitude characteristics; i.e., excitability curves [123], as shown in Fig. 9c.
The nonlinearity leads to volumetric and boundary forcing terms at higher orders, Eqs. (123)–(124). Consequently, the solutions of the forced problem lead to the secondary wavefield composed of higher-harmonic Lamb wave modes. Next, particular features of higher-order problems will be briefly reviewed.
Higher-harmonic generation
Higher harmonic Lamb waves are excited due to the nonlinear forcing terms in Eqs. (123)–(124). Their particular form can be derived from the constitutive relation that follows from the polynomial-form of the strain energy density function, Eq. (114), and contains linear, quadratic, cubic and possibly other higher-order terms [117]. Expanding the nonlinear volumetric force, \( \pmb {f^{(1)}_{NL}} \), and surface traction, \( \pmb {g^{(1)}_{NL}} \) in a Fourier series yields,
where particular forms of \( \pmb {C^{(1)(f,g)}_1} \) are lengthy and will not be explicitly presented here. The same form of the expansion can be applied to higher perturbation expansion orders \(\varepsilon ^2\), \(\varepsilon ^3\), etc. We note that Eqs. (123)–(124) are linear and inhomogeneous, therefore classical solutions techniques can be applied for determining higher-order displacement fields \(\pmb {X_1}\), \(\pmb {X_2}\), etc. Depending on the particular application, the modal expansion approach [119] or direct harmonic solution [45] can be employed for this purpose.
Specific harmonics generated at higher order perturbation expansions depend on the order of nonlinearity in the constitutive relationship. Assuming that an excitation applied to the plate generates a single Lamb wave mode of frequency \(\omega _0\) and wavenumber k (i.e., a wavefield of the form of Eq. (125) exists throughout the plate), the quadratically nonlinear stress–strain relation will result, to first approximation, in the static (DC) component and the second harmonic wave (at \(2 \omega _0\)),
while the cubic nonlinearity will generate a forcing at the fundamental frequency \(\omega _0\), and the third harmonic (\(3 \omega _0\)),
It should be noted that the secondary wavefield solutions, as given by Eqs. (127) and (128), can be decomposed into individual Lamb wave modes of wavenumbers \(k_n\) at the respective frequencies, as proposed by Auld [122] and employed in [119]. Each individual Lamb wave mode of wavenumber \(k_n\), excited as a component of the secondary wavefield oscillates with the spatial periodicity \(L_n\), known as the dispersion length [119], where
with \(m = \{ 2, 3,... M \}\) depending on the polynomial form of the nonlinearity. Clearly, when \(k_n \rightarrow m k\) then \(L_n \rightarrow \infty \), and the cumulative effect of linear amplitude growth with the propagation distance may be observed. The latter is known as the internal resonance (or synchronism) and will be discussed later.
For the same order of magnitude of higher-order elastic constants, the quadratic nonlinearity generates secondary wavefields of nominally higher magnitudes than the cubic nonlinearity. We note that higher-harmonic generation for the multi-modal and dispersive plate system is complex and depends on the type of nonlinearity, symmetry of respective modes (exciting and excited), and presence of synchronism or internal resonance [119, 124]. A cubically nonlinear constitutive relationship gives rise to excitations at \(\omega _0\) and \(3 \omega _0\) at the first order of expansion \(\varepsilon ^1\). The latter forcing component excites the third harmonic wave. The forcing term at the fundamental frequency \(\omega _0\) is secular (resonant) and results in amplitude-dependent shifts in dispersion characteristics. We summarize this phenomenon after discussing internally resonant Lamb waves.
Internally resonant Lamb wave modes
When a secondary wavefield component falls onto a dispersion branch (i.e., the \(m{\textrm{th}}\) harmonic \((m \omega _0, m k)\) coincides with the solution to the Rayleigh-Lamb problem), the phase velocity matching between the two modes occurs. This results in the two waves propagating with the same speed and constructively interfering. As a consequence, linear growth of a higher harmonic wave may occur (see Eq. (129)). This situation is illustrated in Fig. 9a and b, where the dispersion curves for a 1 mm aluminium plate are presented. For the selected \(S_1\) primary mode propagating in a quadratic-nonlinear material, the generated second harmonic \(S_2\) mode has the same phase velocity as the primary wave, thus internal resonance may occur. The red circles mark the interacting primary and secondary modes. Please note that the matching phase velocity, clearly seen in Fig. 9b, is equivalent to the two modes’ operating points (frequency-wavenumber points on the dispersion branches) lying on a line with \(\omega _0 / k = C\), in Fig. 9a, where C denotes a constant.
It was observed in [122], and later analyzed in [114, 115, 119], that in order to excite a secondary guided wave mode, the power flux (forcing) from the primary to the secondary mode must be non-zero. While the power flux is defined as the inner product of the forcing and the velocity profile of the mode, the above condition refers to these two quantities being nonorthogonal. These considerations have been summarized in [115], where it was concluded that either a symmetric or antisymmetric primary mode can only excite symmetric secondary modes in a quadratic-nonlinear medium since the forcing is of quadratic (hence symmetric) form. In summary, an effective excitation of higher harmonics (i.e., linearly growing secondary waves) may occur under two conditions that must be satisfied simultaneously: (1) phase velocity matching and (2) non-zero power flux between the primary and secondary waves. Formally, these forcing terms are resonant at higher-order perturbation expansions and their detailed analysis is possible through, for example, the multiple scales perturbation approach (see Sect. 1.2.1) with detuning [124]. It may be noted that the aforementioned conditions for synchronism are sufficient for continuous guided waves. If a wavepacket is instead considered, an additional condition for the group velocity matching needs to be enforced for the linear growth of the higher harmonic wave component [115], as expected.
Nonlinear dispersion shifts
As the homogeneous plate problem (Eqs. (121) and (122)) has non-trivial solutions, and so have the higher-order problems (since they share the same linear kernel), the right-hand side forcing cannot be arbitrary and it is therefore necessary to determine restrictions that will allow the problem to be solvable. In other words, terms on the right-hand sides of Eqs. (123)–(124) can be secular [119, 124], requiring formulation of solvability conditions.
In [45], solvability conditions are constructed via a self-adjoint linear operator formalism and introduction of an inner product, subsequently requiring all resonant forcing terms to vanish. From the expansions of the forcing terms, Eq. (126), only the terms \( \pmb {C^{(1)(f,g)}_1} \) (i.e., at the primary wave frequency and wavenumber) are required for solvability at \(\varepsilon ^1\). Using expansions Eqs. (126), (123) and (124) can be transformed as,
where \( e^{+\textrm{i}(k x + \tau )} \) dependency has been assumed and dropped in the following notation. It follows from the analysis in [45] that the forcing must satisfy.
at the first order of expansion. Consequently, the nonlinear frequency correction, \( \omega _1 \), must satisfy,
The nonlinear dispersion relationship is recovered using Eqs. (120), (132) and (133); namely, \( k(\omega ) = k(\omega _0 + \varepsilon \omega _1)\). It is clear that Eq. (133) defines an amplitude-dependent frequency shift away from the otherwise linear dispersion relationship. These shifts depend on the form of \(\pmb {C_1^{(1)(f,g)}}\), and thus on the forcing terms \( \pmb {f^{(1)}_{NL}} \) and \( \pmb {g^{(1)}_{NL}} \). Hence, the nonlinear dispersion curves depend not only on the primary wave amplitude, but also on the frequency and the mode symmetry. Example nonlinear dispersion curves for the same 1 mm aluminum plate as the results shown in Fig. 9a–c, as analyzed in [45], are presented in Fig. 10.
Nonlinear amplitude-dependent disperion curves for a cubic-nonlinear 1 mm aluminium plate [45] (\(\lambda = 6.05 \times 10^4\) MPa, \(\mu = 2.59 \times 10^4\) MPa, \(E=F=G=H=30 \times 10^4\) MPa, \(\rho = 2700\) kg/m\(^3\), scaling for shifts = 10)
2.4 Future work
The reviewed literature on nonlinear, continuous systems has primarily concerned analysis methods, particularly for weakly nonlinear continuous systems. Applications of such continuous systems, unlike their discrete counterparts, has received little attention. Consequently, exploration on the application of nonlinear, and potentially periodic, continuous systems exploiting amplitude-dependent dispersion and bandgap behavior is an open research area. In terms of analysis, generalizing the analysis of Lamb modes to periodic nonlinear plates is non-trivial, and will likely require a hybrid analytical-numerical approach. Strongly nonlinear continuous systems will also require alternative solution methods and may lead to still further interesting applications, such as non-reciprocal materials, or materials with extended bandgap regions due to sub- and super-harmonic resonances [8, 13].
As wave propagation in 1-D and 2-D systems is typically investigated due to their lower problem complexity, higher-dimensional setups (e.g., 2.5-D and 3-D) offer additional inspiration for research explorations. Nonlinear periodic, anisotropic and/or inhomogeneous systems, whether in bulk, half-space or plate configurations, are of particular interest. Such dispersive and multi-modal systems may exhibit tunable dispersion characteristics with bandgaps and/or non-reciprocal bands and complex wave–wave interactions that may inspire new or enhanced devise functionality.
3 Concluding remarks
This review has provided the reader with a detailed and unified overview of asymptotic analysis methods currently being applied to the study of wave propagation in weakly nonlinear discrete and continuous elastic media, to include their important results and open questions. The review also detailed experimental studies and applications, both of which are nascent in the area of discrete and continuous periodic nonlinear media. While it is envisioned that the field will continue to develop and refine analysis methods for studying wave propagation in weakly nonlinear media, particularly as concerns periodic continuous media, there is an opportunity for researchers to transition behavior observed only in the nonlinear regime (e.g., self-tuning dispersion and bandgaps; stability transitions; and other amplitude dependency) to sensing, actuation, cloaking, physical computing, and communications technology.
Data availability
All data generated or analysed during this study are included in this published article.
References
Kaajakari, V., Mattila, T., Oja, A., Seppa, H.: Nonlinear limits for single-crystal silicon microresonators. J. Microelectromech. Syst. 13(5), 715 (2004)
Prochazka, I., Panek, P.: Nonlinear effects in the time measurement device based on surface acoustic wave filter excitation. Rev. Sci. Instrum. 80(7), 076102 (2009)
Kodaira, R., Omori, T., Hashimoto, K.Y., Kyoya, H., Nakagawa, R.: Considerations on nonlinearity measurement with high signal-to-noise ratio for RF surface and bulk acoustic wave devices. Jpn. J. Appl. Phys. 54(7S1), 07HD14 (2015)
Tocchio, A., Comi, C., Langfelder, G., Corigliano, A., Longoni, A.: Enhancing the linear range of MEMS resonators for sensing applications. IEEE Sens. J. 11(12), 3202 (2011)
McGee, O., Jiang, H., Qian, F., Jia, Z., Wang, L., Meng, H., Chronopoulos, D., Chen, Y., Zuo, L.: 3D printed architected hollow sphere foams with low-frequency phononic band gaps. Addit. Manuf. 30, 100842 (2019)
Fabro, A.T., Meng, H., Chronopoulos, D.: Uncertainties in the attenuation performance of a multi-frequency metastructure from additive manufacturing. Mech. Syst. Signal Process. 138, 106557 (2020)
Yao, Z., Zhao, R., Zega, V., Corigliano, A.: A metaplate for complete 3D vibration isolation. Eur. J. Mech. A Solids 84, 104016 (2020)
Zega, V., Silva, P.B., Geers, M.G., Kouznetsova, V.G.: Experimental proof of emergent subharmonic attenuation zones in a nonlinear locally resonant metamaterial. Sci. Rep. 10(1), 1 (2020)
Deng, B., Wang, P., He, Q., Tournat, V., Bertoldi, K.: Metamaterials with amplitude gaps for elastic solitons. Nature Commun. 9(1), 1 (2018)
Jiao, W., Gonella, S.: Nonlinear harmonic generation in two-dimensional lattices of repulsive magnets. Phys. Rev. E 103(1), 012213 (2021)
Kittel, C.: Introduction to Solid State Physics (1976)
Hussein, M., Khajehtourian, R.: Nonlinear Bloch waves and balance between hardening and softening dispersion. Proc. R. Soc. A Math. Phys. Eng. Sci. 474(2217), 20180173 (2018)
Silva, P., Leamy, M., Geers, M., Kouznetsova, V.: Emergent subharmonic band gaps in nonlinear locally resonant metamaterials induced by autoparametric resonance. Phys. Rev. E 99(6), 063003 (2019)
Khajehtourian, R., Hussein, M.I.: Dispersion characteristics of a nonlinear elastic metamaterial. Aip Adv. 4(12), 124308 (2014)
Fermi, E., Pasta, P., Ulam, S., Tsingou, M.: Studies of the Nonlinear Problems. Tech. rep., Los Alamos Scientific Lab., N. Mex. (1955)
Liu, Z., Zhang, X., Mao, Y., Zhu, Y., Yang, Z., Chan, C.T., Sheng, P.: Locally resonant sonic materials. Science 289(5485), 1734 (2000)
Lazarov, B.S., Jensen, J.S.: Low-frequency band gaps in chains with attached non-linear oscillators. Int. J. Non-Linear Mech. 42(10), 1186 (2007)
Manimala, J.M., Sun, C.: Numerical investigation of amplitude-dependent dynamic response in acoustic metamaterials with nonlinear oscillators. J. Acoust. Soc. Am. 139(6), 3365 (2016)
Jiao, W., Gonella, S.: Doubly nonlinear waveguides with self-switching functionality selection capabilities. Phys. Rev. E 99(4), 042206 (2019)
Bukhari, M., Barry, O.: Spectro-spatial analyses of a nonlinear metamaterial with multiple nonlinear local resonators. Nonlinear Dyn. 99(2), 1539 (2020)
Ganesh, R., Gonella, S.: From modal mixing to tunable functional switches in nonlinear phononic crystals. Phys. Rev. Lett. 114(5), 054302 (2015)
Dubus, B., Swinteck, N., Muralidharan, K., Vasseur, J., Deymier, P.A.: Nonlinear phonon modes in second-order anharmonic coupled monoatomic chains. J. Vib. Acoust. 138(4), 041016 (2016)
Narisetti, R., Ruzzene, M., Leamy, M.: A perturbation approach for analyzing dispersion and group velocities in two-dimensional nonlinear periodic lattices. J. Vib. Acoust. 133(6), 061020 (2011)
Manktelow, K.L., Leamy, M.J., Ruzzene, M.: Weakly nonlinear wave interactions in multi-degree of freedom periodic structures. Wave Motion 51(6), 886 (2014)
Fronk, M.D., Leamy, M.J.: Direction-dependent invariant waveforms and stability in two-dimensional, weakly nonlinear lattices. J. Sound Vib. 447, 137 (2019)
Brillouin, L.: Sur les tensions de radiation. Ann. Phys. 10(4), 528 (1925). https://doi.org/10.1051/anphys/192510040528
Manktelow, K., Leamy, M.J., Ruzzene, M.: Multiple scales analysis of wave–wave interactions in a cubically nonlinear monoatomic chain. Nonlinear Dyn. 63(1), 193 (2011)
Jiao, W., Gonella, S.: Wavenumber-space band clipping in nonlinear periodic structures. arXiv:2009.14357 (2020)
Fronk, M.D., Leamy, M.J.: Higher-order dispersion, stability, and waveform invariance in nonlinear monoatomic and diatomic systems. J. Vib. Acoust. 139(5), 051003 (2017)
Narisetti, R.K., Leamy, M.J., Ruzzene, M.: A perturbation approach for predicting wave propagation in one-dimensional nonlinear periodic structures. J. Vib. Acoust. 132(3), 031001 (2010)
Sánchez-Morcillo, V.J., Pérez-Arjona, I., Romero-García, V., Tournat, V., Gusev, V.: Second-harmonic generation for dispersive elastic waves in a discrete granular chain. Phys. Rev. E 88(4), 043203 (2013)
Narisetti, R.K.: Wave propagation in nonlinear periodic structures, Wave propagation in nonlinear periodic structures. Ph.D. thesis, Georgia Institute of Technology (2010)
Narisetti, R.K., Ruzzene, M., Leamy, M.J.: Study of wave propagation in strongly nonlinear periodic lattices using a harmonic balance approach. Wave Motion 49(2), 394 (2012)
He, J.H.: Modified Lindstedt–Poincare methods for some strongly non-linear oscillations: part I: expansion of a constant. Int. J. Non-Linear Mech. 37(2), 309 (2002)
He, J.H.: Modified Lindstedt–Poincare methods for some strongly non-linear oscillations: part II: a new transformation. Int. J. Non-Linear Mech. 37(2), 315 (2002)
Sepehri, S., Mashhadi, M.M., Fakhrabadi, M.M.S.: Wave propagation in nonlinear monoatomic chains with linear and quadratic damping. Nonlinear Dyn. 108(1), 457 (2022)
Panigrahi, S.R., Feeny, B.F., Diaz, A.R.: Second-order perturbation analysis of low-amplitude traveling waves in a periodic chain with quadratic and cubic nonlinearity. Wave Motion 69, 1 (2017)
Chakraborty, G., Mallik, A.: Dynamics of a weakly non-linear periodic chain. Int. J. Non-Linear Mech. 36(2), 375 (2001)
Settimi, V., Lepidi, M., Bacigalupo, A.: Nonlinear dispersion properties of one-dimensional mechanical metamaterials with inertia amplification. Int. J. Mech. Sci. 201, 106461 (2021)
Bae, M.H., Oh, J.H.: Nonlinear elastic metamaterial for tunable bandgap at quasi-static frequency. Mech. Syst. Signal Process. 170, 108832 (2022)
He, C., Lim, K.M., Zhang, F., Jiang, J.H.: Dual-tuning mechanism for elastic wave transmission in a triatomic lattice with string stiffening. Wave Motion 112, 102951 (2022)
Abedinnasab, M.H., Hussein, M.I.: Wave dispersion under finite deformation. Wave Motion 50(3), 374 (2013)
Abedin-Nasab, M.H., Bastawrous, M.V., Hussein, M.I.: Explicit dispersion relation for strongly nonlinear flexural waves using the homotopy analysis method. Nonlinear Dyn. 99(1), 737 (2020)
Khajehtourian, R., Hussein, M.I.: Time-independent harmonics dispersion relation for time-evolving nonlinear waves. Sci. Adv. 7(50), eabl3695 (2021)
Packo, P., Uhl, T., Staszewski, W.J., Leamy, M.J.: Amplitude-dependent Lamb wave dispersion in nonlinear plates. J. Acoust. Soc. Am. 140(2), 1319 (2016). https://doi.org/10.1121/1.4961489
Malvern, L.E.M.: Introduction to the Mechanics of a Continuous Medium. Prentice-Hall, Inc., Hoboken (1969)
Fang, L., Leamy, M.J.: Perturbation analysis of nonlinear evanescent waves in a one-dimensional monatomic chain. Phys. Rev. E 105(1), 014203 (2022)
Cabaret, J., Tournat, V., Béquin, P.: Amplitude-dependent phononic processes in a diatomic granular chain in the weakly nonlinear regime. Phys. Rev. E 86(4), 041305 (2012)
Biwa, S., Ishii, Y.: Second-harmonic generation in an infinite layered structure with nonlinear spring-type interfaces. Wave Motion 63, 55 (2016)
Frandsen, N.M., Jensen, J.S.: Modal interaction and higher harmonic generation in a weakly nonlinear, periodic mass-spring chain. Wave Motion 68, 149 (2017)
Jiao, W., Gonella, S.: Intermodal and subwavelength energy trapping in nonlinear metamaterial waveguides. Phys. Rev. Appl. 10(2), 024006 (2018)
Wallen, S.P., Boechler, N.: Shear to longitudinal mode conversion via second harmonic generation in a two-dimensional microscale granular crystal. Wave Motion 68, 22 (2017)
Tournat, V., Gusev, V.E., Castagnède, B.: Self-demodulation of elastic waves in a one-dimensional granular chain. Phys. Rev. E 70, 056603 (2004). https://doi.org/10.1103/PhysRevE.70.056603
Fronk, M.D., Leamy, M.J.: Isolated frequencies at which nonlinear materials behave linearly. Phys. Rev. E 100(5), 051002 (2019)
Fronk, M.D., Leamy, M.J.: Internally resonant wave energy exchange in weakly nonlinear lattices and metamaterials. Phys. Rev. E 100(3), 032213 (2019)
Remoissenet, M.: Waves Called Solitons: Concepts and Experiments. Springer, Berlin (2013)
Panigrahi, S.R., Feeny, B.F., Diaz, A.R.: Wave-wave interactions in a periodic chain with quadratic nonlinearity. Wave Motion 69, 65 (2017)
Lepidi, M., Bacigalupo, A.: Wave propagation properties of one-dimensional acoustic metamaterials with nonlinear diatomic microstructure. Nonlinear Dyn. 98(4), 2711 (2019)
Kochmann, D.M., Bertoldi, K.: Exploiting microstructural instabilities in solids and structures: from metamaterials to structural transitions. Appl. Mech. Rev. 69(5), 050801 (2017)
Bilal, O.R., Foehr, A., Daraio, C.: Bistable metamaterial for switching and cascading elastic vibrations. Proc. Natl. Acad. Sci. 114(18), 4603 (2017)
Kamrava, S., Mousanezhad, D., Ebrahimi, H., Ghosh, R., Vaziri, A.: Origami-based cellular metamaterial with auxetic, bistable, and self-locking properties. Sci. Rep. 7(1), 1 (2017)
Katz, S., Givli, S.: Solitary waves in a bistable lattice. Extreme Mech. Lett. 22, 106 (2018)
Xia, Y., Ruzzene, M., Erturk, A.: Dramatic bandwidth enhancement in nonlinear metastructures via bistable attachments. Appl. Phys. Lett. 114(9), 093501 (2019)
Nadkarni, N., Arrieta, A.F., Chong, C., Kochmann, D.M., Daraio, C.: Unidirectional transition waves in bistable lattices. Phys. Rev. Lett. 116(24), 244501 (2016)
Hwang, M., Arrieta, A.F.: Input-independent energy harvesting in bistable lattices from transition waves. Sci. Rep. 8(1), 1 (2018)
Meaud, J.: Nonlinear wave propagation and dynamic reconfiguration in two-dimensional lattices with bistable elements. J. Sound Vib. 473, 115239 (2020)
Huang, G., Hu, B.: Asymmetric gap soliton modes in diatomic lattices with cubic and quartic nonlinearity. Phys. Rev. B 57(10), 5746 (1998)
Kartashov, Y.V., Malomed, B.A., Vysloukh, V.A., Torner, L.: Two-dimensional solitons in nonlinear lattices. Opt. lett. 34(6), 770 (2009)
Borovkova, O.V., Kartashov, Y.V., Torner, L.: Stabilization of two-dimensional solitons in cubic-saturable nonlinear lattices. Phys. Rev. A 81(6), 063806 (2010)
Flach, S., Gorbach, A.V.: Discrete breathers-advances in theory and applications. Phys. Rep. 467(1–3), 1 (2008)
Gorbach, A.V., Johansson, M.: Discrete gap breathers in a diatomic Klein-Gordon chain: stability and mobility. Phys. Rev. E 67(6), 066608 (2003)
Kastner, M.: Dimension dependent energy thresholds for discrete breathers. Nonlinearity 17(5), 1923 (2004)
Butt, I.A., Wattis, J.A.: Discrete breathers in a two-dimensional Fermi–Pasta–Ulam lattice. J. Phys. A Math. General 39(18), 4955 (2006)
Manktelow, K.L., Leamy, M.J., Ruzzene, M.: Analysis and experimental estimation of nonlinear dispersion in a periodic string. J. Vib. Acoust. 136(3), 031016 (2014)
Porter, M.A., Daraio, C., Herbold, E.B., Szelengowicz, I., Kevrekidis, P.: Highly nonlinear solitary waves in periodic dimer granular chains. Phys. Rev. E 77(1), 015601 (2008)
Hasan, M.A., Cho, S., Remick, K., Vakakis, A.F., McFarland, D.M., Kriven, W.M.: Experimental study of nonlinear acoustic bands and propagating breathers in ordered granular media embedded in matrix. Granular Matter 17, 49 (2015)
Lydon, J., Theocharis, G., Daraio, C.: Nonlinear resonances and energy transfer in finite granular chains. Phys. Rev. E 91(2), 023208 (2015)
Bao, B., Lallart, M., Guyomar, D.: Manipulating elastic waves through piezoelectric metamaterial with nonlinear electrical switched Dual-connected topologies. Int. J. Mech. Sci. 172, 105423 (2020)
Jian, Y., Hu, G., Tang, L., Tang, W., Abdi, M., Aw, K.C.: Analytical and experimental study of a metamaterial beam with grading piezoelectric transducers for vibration attenuation band widening. Eng. Struct. 275, 115091 (2023)
Bukhari, M., Barry, O.: Substantial frequency conversion at long-wavelength limit in metamaterial with weakly nonlinear local electromechanical resonators: Analytical, computational, and experimental study. Int. J. Non-Linear Mech. 147, 104226 (2022)
Matlack, K.H., Bauhofer, A., Krödel, S., Palermo, A., Daraio, C.: Composite 3D-printed metastructures for low-frequency and broadband vibration absorption. Proc. Natl. Acad. Sci. 113(30), 8386 (2016)
Arretche, I., Matlack, K.H.: Experimental testing of vibration mitigation in 3D-printed architected metastructures. J. Appl. Mech. 86(11), 111008 (2019)
Mork, N., Fronk, M.D., Sinclair, M.B., Leamy, M.J.: Nonlinear hierarchical unit cell for passive, amplitude-dependent filtering of acoustic waves. Extreme Mech. Lett. 57, 101915 (2022)
Zangeneh-Nejad, F., Sounas, D.L., Alù, A., Fleury, R.: Analogue computing with metamaterials. Nature Rev. Mater. 6(3), 207 (2021)
Kim, S., Baesens, C., MacKay, R.: Phonon scattering by localized equilibria of nonlinear nearest-neighbor chains. Phys. Rev. E 56(5), R4955 (1997)
Swinteck, N.Z., Muralidharan, K., Deymier, P.A.: Phonon scattering in one-dimensional anharmonic crystals and superlattices: analytical and numerical study. J. Vib. Acoust. 135(4), 041016 (2013)
Chang, C., Zhao, L.D.: Anharmoncity and low thermal conductivity in thermoelectrics. Mater. Today Phys. 4, 50 (2018)
Teixeira, F.L.: Time-domain finite-difference and finite-element methods for Maxwell equations in complex media. IEEE Trans. Antennas Propag. 56(8), 2150 (2008)
Dissanayake, C.M., Premaratne, M., Rukhlenko, I.D., Agrawal, G.P.: FDTD modeling of anisotropic nonlinear optical phenomena in silicon waveguides. Opt. Express 18(20), 21427 (2010)
Manktelow, K., Leamy, M.J., Ruzzene, M.: Comparison of asymptotic and transfer matrix approaches for evaluating intensity-dependent dispersion in nonlinear photonic and phononic crystals. Wave Motion 50(3), 494 (2013)
Duan, W.S.: Nonlinear waves propagating in the electrical transmission line. EPL (Europhys. Lett.) 66(2), 192 (2004)
Yemélé, D., Kenmogné, F.: Compact envelope dark solitary wave in a discrete nonlinear electrical transmission line. Phys. Lett. A 373(42), 3801 (2009)
Motcheyo, A.T., Tchameu, J.T., Fewo, S.I., Tchawoua, C., Kofané, T.C.: Chameleon’s behavior of modulable nonlinear electrical transmission line. Commun. Nonlinear Sci. Numer. Simul. 53, 22 (2017)
Ustinov, A.B., Drozdovskii, A.V., Kalinikos, B.A.: Multifunctional nonlinear magnonic devices for microwave signal processing. Appl. Phys. Lett. 96(14), 142513 (2010)
Sadovnikov, A., Beginin, E., Morozova, M., Sharaevskii, Y.P., Grishin, S., Sheshukova, S., Nikitov, S.: Nonlinear spin wave coupling in adjacent magnonic crystals. Appl. Phys. Lett. 109(4), 042407 (2016)
Richardson, D., Kalinikos, B.A., Carr, L.D., Wu, M.: Spontaneous exact spin-wave fractals in magnonic crystals. Phys. Rev. Lett. 121(10), 107204 (2018)
Thurston, R.N., Shapiro, M.J.: Interpretation of ultrasonic experiments on finite-amplitude waves. J. Acoust. Soc. Am. 41(4B), 1112 (1967). https://doi.org/10.1121/1.1910443
Cantrell, J.H.: Acoustic-radiation stress in solids. I. Theory. Phys. Rev. B 30, 3214 (1984). https://doi.org/10.1103/PhysRevB.30.3214
Qu, J., Jacobs, L.J., Nagy, P.B.: On the acoustic-radiation-induced strain and stress in elastic solids with quadratic nonlinearity (L). J. Acoust. Soc. Am. 129(6), 3449 (2011). https://doi.org/10.1121/1.3583501
Nagy, P.B., Qu, J., Jacobs, L.J.: Finite-size effects on the quasistatic displacement pulse in a solid specimen with quadratic nonlinearity. J. Acoust. Soc. Am. 134(3), 1760 (2013). https://doi.org/10.1121/1.4817840
Cveticanin, L.: Vibrations of the nonlinear oscillator with quadratic nonlinearity. Phys. A Stat. Mech. Its Appl. 341, 123 (2004)
Brojan, F.K.M., Videnic, T.: Large deflections of nonlinearly elastic non-prismatic cantilever beams made from materials obeying the generalized Ludwick constitutive law. Meccanica 44, 733 (2009)
Qu, J., Nagy, P.B., Jacobs, L.J.: Pulse propagation in an elastic medium with quadratic nonlinearity (L). J. Acoust. Soc. Am. 131(3), 1827 (2012). https://doi.org/10.1121/1.3681922
Yost, W.T., Cantrell, J.H.: Acoustic-radiation stress in solids. II. Experiment. Phys. Rev. B 30, 3221 (1984). https://doi.org/10.1103/PhysRevB.30.3221
Ghiron, E.F.: Anomalie nella propagazione di onde acustiche di grande ampiezza. Alta frequenza 4(10), 530 (1935)
Rayleigh, L.: On the momentum and pressure of gaseous vibrations, and on the connection with the virial theorem. Philos. Mag. 10, 364 (1905)
Fubini-Ghiron, E.: La tension de radiation acoustique et les ondes de grande amplitude. Revue d’Acoustique 6, 118–127 (1937)
Westervelt, P.J.: The mean pressure and velocity in a plane acoustic wave in a gas. J. Acoust. Soc. Am. 22(3), 319 (1950). https://doi.org/10.1121/1.1906606
Blackstock, D.T.: Propagation of plane sound waves of finite amplitude in nondissipative fluids. J. Acoust. Soc. Am. 34(1), 9 (1962). https://doi.org/10.1121/1.1909033
Beyer, R.T.: Radiation pressure-the history of a mislabeled tensor. J. Acoust. Soc. Am. 63(4), 1025 (1978). https://doi.org/10.1121/1.381833
Hasegawa, T., Kido, T., Iizuka, T., Matsuoka, C.: A general theory of Rayleigh and Langevin radiation pressures. Acoust. Sci. Technol. 21(3), 145 (2000). https://doi.org/10.1250/ast.21.145
Sarvazyan, A.P., Rudenko, O.V., Nyborg, W.L.: Biomedical applications of radiation force of ultrasound: historical roots and physical basis. Ultrasound Med. Biol. 36(9), P1379 (2010)
Cantrell, J.H., Yost, W.T.: Acoustic nonlinearity in dispersive solids. In: Review of Progress in Quantitative Nondestructive Evaluation, vol. 10B, pp. 1805–1811 (1991)
Deng, M.: Analysis of second-harmonic generation of Lamb modes using a modal analysis approach. J. Appl. Phys. 94(6), 4152 (2003). https://doi.org/10.1063/1.1601312
Muller, M.F., Kim, J.Y., Qu, J., Jacobs, L.J.: Characteristics of second harmonic generation of Lamb waves in nonlinear elastic plates. J. Acoust. Soc. Am. 127(4), 2141 (2010). https://doi.org/10.1121/1.3294714
Packo, P., Radecki, R., Leamy, M.J., Uhl, T., Staszewski, W.J.: Modeling and numerical simulations in nonlinear acoustics used for damage detection, pp. 103–137. Springer, Cham (2019)
Landau, E.M.L.L.D.: Theory of Elasticity. Pergamon Press, Oxford (1970)
Destrade, R.W.O.M.: On the third- and fourth-order constants of incompressible isotropic elasticity. J. Acoust. Soc. Am. 128, 3334 (2010)
de Lima, W., Hamilton, M.: Finite-amplitude waves in isotropic elastic plates. J. Sound Vib. 265(4), 819 (2003). https://doi.org/10.1016/S0022-460X(02)01260-9
Viktorov, I.: Rayleigh and Lamb Waves: Physical Theory and Applications. Plenum Press, New York (1970)
Rose, J.: Ultrasonic Waves in Solid Media. Cambridge University Press, Cambridge (2004)
Solie, B.A.A.L.P.: Elastic waves in free anisotropic plates. J. Acoust. Soc. Am. 54, 50 (1973)
Kijanka, P., Staszewski, W.J., Packo, P.: Generalised semi-analytical method for excitability curves calculation and numerical modal amplitude analysis for Lamb waves. Struct. Control Health Monitor. 25(7), e2172 (2018)
Nayfeh, D.M.A.H.: Nonlinear Oscilations. Wiley, London (1979)
Acknowledgements
P.P. acknowledges support from the National Science Centre in Poland through Grant No. 2018/31/B/ST8/00753 and partial support through ’Excellence initiative—research university’ program for AGH University of Science and Technology. M.J.L. acknowledges support from the U.S. National Science Foundation under award numbers 1741565 and 1929849.
Funding
The authors list their funding sources in the Acknowledgements.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Fronk, M.D., Fang, L., Packo, P. et al. Elastic wave propagation in weakly nonlinear media and metamaterials: a review of recent developments. Nonlinear Dyn 111, 10709–10741 (2023). https://doi.org/10.1007/s11071-023-08399-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-023-08399-6