Abstract
Card-based cryptography provides simple and practicable protocols for performing secure multi-party computation (MPC) with just a deck of cards. For the sake of simplicity, this is often done using cards with only two symbols, e.g.,
 and
and
 . Within this paper, we target the setting where all cards carry distinct symbols, catering for use-cases with commonly available standard decks and a weaker indistinguishability assumption. As of yet, the literature provides for only three protocols and no proofs for non-trivial lower bounds on the number of cards. As such complex proofs (handling very large combinatorial state spaces) tend to be involved and error-prone, we propose using formal verification for finding protocols and proving lower bounds. In this paper, we employ the technique of software bounded model checking (SBMC), which reduces the problem to a bounded state space, which is automatically searched exhaustively using a SAT solver as a backend.
. Within this paper, we target the setting where all cards carry distinct symbols, catering for use-cases with commonly available standard decks and a weaker indistinguishability assumption. As of yet, the literature provides for only three protocols and no proofs for non-trivial lower bounds on the number of cards. As such complex proofs (handling very large combinatorial state spaces) tend to be involved and error-prone, we propose using formal verification for finding protocols and proving lower bounds. In this paper, we employ the technique of software bounded model checking (SBMC), which reduces the problem to a bounded state space, which is automatically searched exhaustively using a SAT solver as a backend.
Our contribution is twofold: (a) We identify two protocols for converting between different bit encodings with overlapping bases, and then show them to be card-minimal. This completes the picture of tight lower bounds on the number of cards with respect to runtime behavior and shuffle properties of conversion protocols. For computing
 , we show that there is no protocol with finite runtime using four cards with distinguishable symbols and fixed output encoding, and give a four-card protocol with an expected finite runtime using only random cuts. (b) We provide a general translation of proofs for lower bounds to a bounded model checking framework for automatically finding card- and length-minimal protocols and to give additional confidence in lower bounds. We apply this to validate our method and, as an example, confirm our new
, we show that there is no protocol with finite runtime using four cards with distinguishable symbols and fixed output encoding, and give a four-card protocol with an expected finite runtime using only random cuts. (b) We provide a general translation of proofs for lower bounds to a bounded model checking framework for automatically finding card- and length-minimal protocols and to give additional confidence in lower bounds. We apply this to validate our method and, as an example, confirm our new
 protocol to have a shortest run for protocols using this number of cards.
protocol to have a shortest run for protocols using this number of cards.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Secure multiparty computation
- Card-based cryptography
- Formal verification
- Bounded model checking
- Standard decks
1 Introduction
Card-based cryptographic protocols allow to perform secure multi-party computation (MPC), i.e., jointly computing a function while not revealing more information about each individual input than absolutely necessary, with just a (regular) deck of playing cards, as long as they have indistinguishable backs. Let us start with an example. Assume that Alice and Bob meet in a bar and spend the evening together. After quite some chat, they would like to find out whether to have a second date. They are faced with the following problem: In case only one of them likes to meet again, this would cause an uncomfortable embarrassment, if he or she is the first to come out.Footnote 1 Fortunately, Alice is a notable cryptographer and likes card games, so she has with her a standard deck of cards. She remembers the protocol by Niemi and Renvall [NR99] for computing the
 function of two bits, here for outputting “yes”, if both players share this mutual interest, and “no” otherwise. Doing so using an MPC protocol hides the input of the respective other player, unless it is obvious from their own input and output, hence hiding a “yes”-choice given of only one player, from the other.
function of two bits, here for outputting “yes”, if both players share this mutual interest, and “no” otherwise. Doing so using an MPC protocol hides the input of the respective other player, unless it is obvious from their own input and output, hence hiding a “yes”-choice given of only one player, from the other.
In order to get a feeling for how such card-based protocols work, let us introduce the said protocol by Niemi and Renvall. It uses five cards with distinguishable symbols, which we denote – for simplicityFootnote 2 – as



 and
and
 . It is essential that the cards’ backs are indistinguishable, such that when they are put face-down on the table, the only thing observable is
. It is essential that the cards’ backs are indistinguishable, such that when they are put face-down on the table, the only thing observable is
 . With these cards, the two players can encode a commitment to a bit (yes or no) by the order of two cards
. With these cards, the two players can encode a commitment to a bit (yes or no) by the order of two cards
 ,
,
 (with \(i \ne j\)) via the encoding
(with \(i \ne j\)) via the encoding

Alice inputs her bit by putting the cards
 face-down and in the respective order on the table (she puts
face-down and in the respective order on the table (she puts
 for input 0, and
for input 0, and
 for input 1), while Bob does the same using his cards
for input 1), while Bob does the same using his cards
 . We need an additional helper-card, here a
. We need an additional helper-card, here a
 , which is put to the left of the players’ cards.
, which is put to the left of the players’ cards.
The protocol starts by swapping Alice’s second card with Bob’s first card in the card sequence (pile) on the table. The resulting card configuration has an interesting property, namely that the order of the cards
 and
and
 in this sequence already encodes the output of the protocol, i.e., it reads
in this sequence already encodes the output of the protocol, i.e., it reads
 if the output is 1, and
if the output is 1, and
 otherwise. Hence, by securely removing the cards
otherwise. Hence, by securely removing the cards
 and
and
 (which is explained below), one directly obtains the output. We see this by inspecting all possible cases:
(which is explained below), one directly obtains the output. We see this by inspecting all possible cases:

We can remove the cards
 and
and
 , while keeping the relative order of all cards in the sequence intact, by cutting the cards, i.e., rotating the sequence by a random offset which is unknown to the players. We can then securely turn the first card and remove it in case it is
, while keeping the relative order of all cards in the sequence intact, by cutting the cards, i.e., rotating the sequence by a random offset which is unknown to the players. We can then securely turn the first card and remove it in case it is
 or
or
 . Due to the cut, the turned card is random, and hence it does not reveal anything about the inputs. When both cards are removed, we reach a configuration where
. Due to the cut, the turned card is random, and hence it does not reveal anything about the inputs. When both cards are removed, we reach a configuration where
 is the first card by the same procedure where the two remaining cards encode the
is the first card by the same procedure where the two remaining cards encode the
 result. Here, the
result. Here, the
 played the crucial role of a separator that keeps the relative order of the remaining cards, starting from the separator, intact when doing a random cut. (A formal version of this protocol is given in Protocol 2 and Fig. 7.)
played the crucial role of a separator that keeps the relative order of the remaining cards, starting from the separator, intact when doing a random cut. (A formal version of this protocol is given in Protocol 2 and Fig. 7.)
In this paper, we are interested in whether we can do away with the helping card
 , and whether there are simpler protocols. Moreover, in order to handle the increasing combinatorial state space (relative to protocols on decks of just
, and whether there are simpler protocols. Moreover, in order to handle the increasing combinatorial state space (relative to protocols on decks of just
 and
and
 ), we introduce formal verification to the field of card-based cryptography.
), we introduce formal verification to the field of card-based cryptography.
1.1 Secure Multiparty Computation with Cards
In combining different protocols, one can do much more than just computing the
 function. For example, it is possible to compute arbitrary Boolean circuits by combining the well-known fact that any circuit can be expressed using only
function. For example, it is possible to compute arbitrary Boolean circuits by combining the well-known fact that any circuit can be expressed using only
 and
and
 gates, with a method to duplicate the physically encoded bit in case of forking wires, which we make explicit by a
gates, with a method to duplicate the physically encoded bit in case of forking wires, which we make explicit by a
 gate. In the encoding above,
gate. In the encoding above,
 simply inverts the order of the two cards, and a
simply inverts the order of the two cards, and a
 -protocol is given, e.g., in [M16]. Using this setup, we can do general MPC for any function without needing to trust a possibly corrupted computer.
-protocol is given, e.g., in [M16]. Using this setup, we can do general MPC for any function without needing to trust a possibly corrupted computer.
A particular advantage of protocols using physical assumptions is that they can provide a bridge to reality. Examples of this are given in [GBG14, FFN14], where the authors give a protocol for proving in zero-knowledge that a nuclear warhead (to be disarmed due to an international treaty) conforms to a prescribed template, without giving away anything about its internal design. In our setting of cryptography with cards, this bridge is used if the cryptographic protocol is embedded in a real card game, e.g., to prevent cheatingFootnote 3. Here, using computers is not only cumbersome, but there is no guarantee that the card sequence on my hand is the one I input into the software, hence no bridge to the physical world.
Another application of such protocols is to explain MPC in an interesting and motivating way to students in cryptography lectures. Card-based cryptography tries to find protocols for the above-mentioned
 and
and
 functionalities which are card-minimal, simple and practicable. For simplicity, many protocols in card-based cryptography work with specially constructed decks, e.g., of only two symbols,
functionalities which are card-minimal, simple and practicable. For simplicity, many protocols in card-based cryptography work with specially constructed decks, e.g., of only two symbols,
 and
and
 . This is easy for explanation, and there are nice and easily describable protocols, such as the five-card trick by den Boer [dB89] and the six-card
. This is easy for explanation, and there are nice and easily describable protocols, such as the five-card trick by den Boer [dB89] and the six-card
 protocol by Mizuki and Sone [MS09].
protocol by Mizuki and Sone [MS09].
However, the setting where all cards are distinguishable, as described above, has several advantages. Firstly, we assume little about the indistinguishability of cards, which leads to stronger security guarantees. (This is more similar to the indistinguishable version of tamper-evident seals, such as scratch-off cards, by Moran and Naor [MN10].) We only need the backs (or envelopes wrapping the cards, if one wishes) to be indistinguishable. Secondly, these standard decks are more commonly available, in contrast to constructed decks. If one were to use standard decks for the protocols above, they would need multiple copies of the same card. Thirdly, considering this setting may lead to protocols using less cards than the optimal ones in the two-symbol deck setting. In fact, as our paper shows, one may use less cards than in the two-symbol deck setting. For example, our new four-card Las Vegas
 protocol presented in Sect. 5 uses only a very basic, practicable shuffling mechanism, namely random cuts, and uses one card less than the provably card-minimal Las Vegas
protocol presented in Sect. 5 uses only a very basic, practicable shuffling mechanism, namely random cuts, and uses one card less than the provably card-minimal Las Vegas
 protocol (restricted to certain types of practical shuffles) in the two-symbol deck setting. As of yet, there has only been little research in this direction, with [NR99, M16] being the only works that consider the setting where all cards have distinguishable symbols, called “standard deck” setting. Nothing is known about non-trivial lower bounds on the number of cards. This is likely due to the large state space, as there are many more distinguishable card re-orderings compared to the two-symbol case.
protocol (restricted to certain types of practical shuffles) in the two-symbol deck setting. As of yet, there has only been little research in this direction, with [NR99, M16] being the only works that consider the setting where all cards have distinguishable symbols, called “standard deck” setting. Nothing is known about non-trivial lower bounds on the number of cards. This is likely due to the large state space, as there are many more distinguishable card re-orderings compared to the two-symbol case.
Within this paper, our interest is to find an automatic way of constructing compact card-based protocols which are secure and correct, based on only the two standard operations turn and shuffle, given the desired number of cards. We exploit the observation that, to the best of our knowledge, all findings in the literature employ only protocols of comparatively small length using only a small number of cards. Based on the hypothesis that we may always find some number n which is greater than or equal to any length-minimal card-protocol, we apply the automatic off-the-shelf formal program-verification technique software bounded model checking (SBMC) [BCC+99]. This technique allows, given such a bound n, to encode a program verification task into a decidable set of logical equations, which can then be solved by a SAT or an SMT solver. In this work, we propose an automatic method based on SBMC that, given the desired numbers of cards and protocol length, either constructs such a protocol if and only if one exists, or proves the underlying SAT formula to be unsatisfiable, i.e., shows that no such protocol exists. Based thereon, we propose that the cumbersome and error-prone task of finding such protocols or proving their non-existence by hand may be supported or complemented by such an automatic approach which is flexibly adaptable to a variety of card-based protocols and desired restrictions.
Prior to our work, it was not yet clear which role the input encoding plays when devising new protocols. This is the question on whether it can make a difference regarding the possibility of a protocol if we provide, e.g.,
 to Alice and
to Alice and
 to Bob, or
to Bob, or
 to Alice and
to Alice and
 to Bob. We provide an analysis of this question, showing that with certain restrictions, there is a relatively large freedom in choosing the input (and/or output) bases. This is a useful prerequisite in proving the impossibility of a protocol with a given number of cards.
to Bob. We provide an analysis of this question, showing that with certain restrictions, there is a relatively large freedom in choosing the input (and/or output) bases. This is a useful prerequisite in proving the impossibility of a protocol with a given number of cards.
1.2 Contribution
Our contribution consists in providing interesting new protocols and impossibility results, as well as a fully automatic method based on formal verification to support such findings. The specific advances therein are the following (cf. also Table 1 for a comparison to the literature):
-
(1)
A four-card
 protocol in the standard deck setting, improving upon [NR99] by one card, and reaching the theoretical minimum on the number of cards. W.r.t. shuffling, this protocol only uses an expected number of 6 random cuts, compared to 7.5 random cuts in a (shortened) variant of [NR99]. Additionally, it has a natural interpretation and using only random cuts makes it easy to implement in an actively secure way, cf. [KW17].
protocol in the standard deck setting, improving upon [NR99] by one card, and reaching the theoretical minimum on the number of cards. W.r.t. shuffling, this protocol only uses an expected number of 6 random cuts, compared to 7.5 random cuts in a (shortened) variant of [NR99]. Additionally, it has a natural interpretation and using only random cuts makes it easy to implement in an actively secure way, cf. [KW17]. -
(2)
We show that under certain conditions the cards for encoding input or output can be chosen freely. For one-bit output protocols and if five or more cards are available, we can freely choose both input and output bases by only extending the protocol by expected three shuffle and three turn steps. For this matter, we identify two protocols for converting a bit encoding if the new encoding shares one card with the old one.
-
(3)
We show that there is no finite-runtime protocol for converting between bases with non-empty intersection using four cards. Moreover, there cannot be a finite-runtime
 protocol with four cards if we fix the basis in advance.
protocol with four cards if we fix the basis in advance. -
(4)
We introduce formal verification to card-based cryptography by providing a technique which automatically finds new protocols using as few as possible operations and searches for lowest bounds on card-minimal protocols.
 and basis conversion protocols, subject to the running time and shuffle restrictions specified in the first two columns. Note that random cuts are a subclass of uniform closed shuffles.
and basis conversion protocols, subject to the running time and shuffle restrictions specified in the first two columns. Note that random cuts are a subclass of uniform closed shuffles.1.3 Related Work
The feasibility of card-based cryptographic MPC is due to [dB89, CK93, NR98], with a formal model given by [MS14]. The only two papers looking at standard deck solutions are [NR99, M16]. Lower bounds on card-based cryptographic protocols are given by [KWH15, KKW+17, K18] for the two-symbol deck setting. The card-minimal protocol for this setting, using only practicable (i.e., uniform closed) shuffles, is given by [AHM+18] and uses five cards. The state trees used for protocols in this paper are devised by [KWH15, KKW+17].
To the best of our knowledge, this is the first work which applies formal methods to the field of card-based cryptography. However, a large range of research has been done using formal methods in the more general field of secure two-party and multiparty computations. This can be clustered into either analyzing security protocols given as high-level, abstract (and usually idealized) models, or program-based approaches targeting real(istic) protocol (software) implementations. Avalle, Pironti, and Sisto [APS14] further structure this into the two main approaches of automated model extraction and automated code generation. We refer the interested reader to overviews as given by Blanchet [B12] or Avalle, Pironti, and Sisto, and only go into a few selected works for which we identified closer links to our approach, e.g., using software bounded model checking (SBMC), SAT solvers on real(istic) protocol implementations, or relating in the analyzed security model. Standard cryptographic assumptions using lower-level computational models are – albeit more realistic – usually harder to formalize and automate. One notable line of research is CBMC-GC [FHK+14] which builds on top of the tool CBMC [CKL04]. It uses SBMC in a compiler framework translating secure computations of ANSI C programs into an optimized Boolean circuit which can subsequently be implemented securely utilizing the garbled circuit approach. Another similar setting to ours is analyzed in [RSH19], where also an “honest-but-curious” attacker model is assumed. Therein, a domain-specific language is built on top of the F\(^ \star \) language, a full-featured, verification-oriented, effectful programming language [SHK+16]. Swamy et al. then implement MPC programs with enabled formal verification provided by the semantics of the language.
1.4 Outline
We give the computational model of card-based protocols, security definitions, etc. and the necessary preliminaries as well as a basic setup for software bounded model checking in Sect. 2. Section 3 discusses which freedom one has when choosing the specific cards for encoding inputs and outputs to card-based protocols and introduces a formal relabeling operation. We give lower bounds on the number of cards for
 and basis-conversion protocols in Sect. 4. A four-card Las Vegas
and basis-conversion protocols in Sect. 4. A four-card Las Vegas
 protocol and two basis-conversion protocols are presented in Sect. 5 and Sect. 6, respectively. Section 7 gives results from applying our formal verification setup based on SBMC to our new
protocol and two basis-conversion protocols are presented in Sect. 5 and Sect. 6, respectively. Section 7 gives results from applying our formal verification setup based on SBMC to our new
 protocol.
protocol.
2 Preliminaries
In this section, we first formally introduce card-based protocols with their computational model (including some basic required notions), a convenient formal protocol representation, a suitable security notion, and the formal requirements for proving lower bounds. Secondly, we introduce our applied formal technique called software bounded model checking, on which, thirdly, we establish our general technique for automatically finding card- and length-minimal protocols.
2.1 Card-Based Protocols
Formally, a deck \(\mathcal {D}\) of cards is a multiset over a (deck) alphabet or symbol set \(\varSigma \). We denote multisets by
 , e.g.,
, e.g.,
 is a deck over
is a deck over
 . In this paper, we focus mainly on decks
. In this paper, we focus mainly on decks
 ,
,
 , where each symbol occurs exactly once. Following [M16], we call these decks standard decks, because decks of common card games are a good representation of such formal decks.
, where each symbol occurs exactly once. Following [M16], we call these decks standard decks, because decks of common card games are a good representation of such formal decks.
For encoding a bit, we additionally assume a linear order on the card symbols in \(\varSigma \), which is the usual order on
 for standard decks, and
for standard decks, and
 for simple two-element decks. Two face-down cards with distinct symbols
for simple two-element decks. Two face-down cards with distinct symbols
 then encode a bit via the following encoding rule introduced in [NR99]:
then encode a bit via the following encoding rule introduced in [NR99]:

Card-based protocols proceed by mainly two actions on the sequence or pile of cards: We can introduce uncertainty (about which card is which) by shuffling them in arbitrary or in certain controlled ways, e.g., by cutting the cards in quick succession, so that players do not know which card ended up where in the card sequence (or pile). Slightly more formal, a (uniform) shuffle is specified by a permutation set, from which one element is drawn uniformly at random and applied to the cards, without the players learning which one it was. Secondly, we may turn over cards and publicly learn their symbol, and act on the basis of this information. Moreover, we may deterministically permute the cards.
Permutations and Groups. Let \(S_n\) denote the symmetric group on
 . For elements
. For elements
 the cycle
the cycle
 is the cyclic permutation
is the cyclic permutation
 with
with
 for
for
 ,
,
 and
and
 for all x not occurring in the cycle. Every permutation can be written as a composition of pairwise disjoint cycles. For example, \((1\;3\;2)(4\;5)\) maps
for all x not occurring in the cycle. Every permutation can be written as a composition of pairwise disjoint cycles. For example, \((1\;3\;2)(4\;5)\) maps
 , and
, and
 . The identity permutation is denoted as
. The identity permutation is denoted as
 .
.
Given permutations
 ,
,
 denotes the group generated by
denotes the group generated by
 . A shuffle is a random cut if its permutation set is the group
. A shuffle is a random cut if its permutation set is the group
 generated by a single element
generated by a single element
 which is a cycle
which is a cycle
 . A shuffle is called a random bisection cut if its permutation set is generated by a
. A shuffle is called a random bisection cut if its permutation set is generated by a
 which is the composition of pairwise disjoint cycles of length 2. Finally, an \(S_k\)-shuffle is a shuffle with permutation set \(S_k\).
which is the composition of pairwise disjoint cycles of length 2. Finally, an \(S_k\)-shuffle is a shuffle with permutation set \(S_k\).
Computational Model and Protocol Tree Representation. For our formal descriptions, we make heavy use of the KWH trees introduced in [KWH15] and shown to be equivalent to the computational model of [MS14, MS17] in [KKW+17]. We start by the start node

and add eventually needed further cards (
 ,
,
 , ...) to the right of the players bits. The state (or KWH) tree is directed, with annotations at the outgoing edges of the state, specifying the action that is performed next. Let
, ...) to the right of the players bits. The state (or KWH) tree is directed, with annotations at the outgoing edges of the state, specifying the action that is performed next. Let
 be the state with the outgoing annotation, then the actions are defined as:
be the state with the outgoing annotation, then the actions are defined as:
-
1.
 leads to a
leads to a
 as in Fig. 1, where
as in Fig. 1, where
 is a permutation set.
is a permutation set. -
2.
\((\mathsf {turn}, T)\) branches the tree into states
 for each observation \(v\) possible by revealing the cards at positions from the set
for each observation \(v\) possible by revealing the cards at positions from the set
 , as in Fig. 2.
, as in Fig. 2.
 contains the sequences from
contains the sequences from
 which are compatible with the observation \(v\). For each sequence \(s\) compatible with \(v\), we have
which are compatible with the observation \(v\). For each sequence \(s\) compatible with \(v\), we have
 , where
, where
 is the probability of observing \(v\).
is the probability of observing \(v\). -
3.
 permutes the sequences of
permutes the sequences of
 according to
according to
 .
. -
4.
 stops the computation and returns the cards at
stops the computation and returns the cards at
 as output.
as output.
We start by a state that encodes the input sequences attached to their respective symbolic input probabilities, see [KKW+17] for a thorough explanation:

A protocol computes a Boolean function \(f:\{0,1\}^2 \rightarrow \{0,1\}\) if the start state (tree root) encodes each
 in the first four cards (the remaining cards being at fixed positions), and in the leaf nodes of the protocol’s state tree, it holds for the positions given by the result operation that the cards at these positions encode a value
in the first four cards (the remaining cards being at fixed positions), and in the leaf nodes of the protocol’s state tree, it holds for the positions given by the result operation that the cards at these positions encode a value
 if all \(X_i\) occurring in
if all \(X_i\) occurring in
 for sequence \(s\) satisfy \(f(i)=o\) (Correctness). We say that a protocol has finite runtime if its tree is finite. It is a Las Vegas protocol, if it is not finite runtime, but the expected length of any path in its tree is finite. Note that while we consider looping protocols, we do not consider the case where a complete restart is necessary. For self-similar infinite trees, we simplify by drawing edges to earlier states.
for sequence \(s\) satisfy \(f(i)=o\) (Correctness). We say that a protocol has finite runtime if its tree is finite. It is a Las Vegas protocol, if it is not finite runtime, but the expected length of any path in its tree is finite. Note that while we consider looping protocols, we do not consider the case where a complete restart is necessary. For self-similar infinite trees, we simplify by drawing edges to earlier states.
Security of Card-Based Protocols. We slightly adjust the security notion from the literature to standard decks. For more details, we refer to [K19]. Since different encodings for the same bit are possible, we want the encoding basis of the output bit to not give away anything about the inputs. We say that a protocol is secure if at any turn operation the probability for each observation \(v\) is a constant
 (using
(using
 = 1), and additionally if at any result operation the probability of each output basis is constant in the same sense.
= 1), and additionally if at any result operation the probability of each output basis is constant in the same sense.
As in [KKW+17], for our impossibility proofs and formalizations with bounded model checkers, it is useful to consider a weaker form of security, which is a necessary criterion for security as defined above: A protocol is possibilistically output-secure, if at any state of the protocol, every output can still be possible. This weakens the normal security guarantee, as the probability for a given input sequence could be higher in this state. One could even be able to exclude a specific input sequence, if the corresponding output can still be possible through another input sequence. Together with possibilistic input-security, this discussion leads to the following formal definition:
Definition 1
(cf. [KKW+17]). A protocol \(\mathcal {P}=(\mathcal {D}, U, Q, A)\) computing a function \(f:\{0,1\}^2 \rightarrow \{0,1\}\) has possibilistic input security (possibilistic output security) if it is correct, i.e., output \(O = f(I)\) almost surely and for uniformlyFootnote 4 random input I and any visible sequence trace v with \(\Pr [v] > 0\) as well as any input
 (any output
(any output
 ) we have
) we have
 (
(
 ).
).
Proving Lower Bounds. We call two states,
 and
and
 , similar, if
, similar, if
 is equal to
is equal to
 up to row or column permutation. This is an interesting equivalence relation for reducing the state space and we make use of it in our impossibility results.
up to row or column permutation. This is an interesting equivalence relation for reducing the state space and we make use of it in our impossibility results.
As in [KKW+17, Definition 3], we define reduced states, where states are not annotated by their symbolic probabilities, but by the result that is specified by their inputs. This simplifies impossibility proofs by reducing information and the state space. Any such reduced tree captures only a weak form of security, possibilistic security, as discussed above where each output (reachable in principle) needs to be still possible. Showing that a protocol is impossible even in this weak setting implies its general impossibility.
To obtain a reduced state tree, we project all the symbolic probabilities of the sequences in a state tree to a type (representing the possible future output associated with the sequence in a correct protocol, see below), which can be any
 . For this, let \(\mathcal {P}\) be a protocol computing a function \(f:\{0,1\}^2 \rightarrow \{0,1\}\) and
. For this, let \(\mathcal {P}\) be a protocol computing a function \(f:\{0,1\}^2 \rightarrow \{0,1\}\) and
 be a state in the state tree. For any sequence \(s\) with
be a state in the state tree. For any sequence \(s\) with
 being a polynomial with positive coefficients for the variables
being a polynomial with positive coefficients for the variables
 (
(
 ), set
), set
 if
if
 in the resulting reduced state
in the resulting reduced state
 . We call sequences in
. We call sequences in
 according to their type o-sequences.
according to their type o-sequences.
For proving impossibility results, we make use of the backwards calculus as given in [K18]. We highlight the main ideas here, but refer to it for reference. Denote by
 , for a set of states \(\mathcal {G}\), the set of states that are transformed into a state in \(\mathcal {G}\) by a shuffle. The trivial shuffle is allowed, i.e.,
, for a set of states \(\mathcal {G}\), the set of states that are transformed into a state in \(\mathcal {G}\) by a shuffle. The trivial shuffle is allowed, i.e.,
 . Moreover,
. Moreover,
 is the set of states being in \(\mathcal {G}\) or having a turnable position \(i\) such that all immediate successor states from a turn at \(i\) are in \(\mathcal {G}\). Define by
is the set of states being in \(\mathcal {G}\) or having a turnable position \(i\) such that all immediate successor states from a turn at \(i\) are in \(\mathcal {G}\). Define by
 the closure of
the closure of
 and
and
 operations on \(\mathcal {G}\). Hence, it holds that if the start state is not in
operations on \(\mathcal {G}\). Hence, it holds that if the start state is not in
 , then no finite-runtime protocol can exist.
, then no finite-runtime protocol can exist.
2.2 Automatic Formal Verification Using SBMC
In the following, we introduce an automatic technique from formal program verification, namely software bounded model checking (SBMC), to the field of card-based cryptography. We first describe the general technique of using SBMC to check for software properties, before we explain how we apply it to search for cryptographically secure card-based protocols. In a nutshell, we translate the task to a reachability problem in software programs (which will later-on be a program encoding operations on an abstract state tree as described above), which the SBMC tool encodes into an instance of the SAT problem.
We assume we are given an imperatively defined function f under the form of an imperative program (for example, written in the C language), that uses some parameter values taken among a set of possible start values I. An entry \(i \in I\) is a list of values, one value for each such parameter: it gives a value to everything that a run of f depends on, such as its input variables, or anything that is considered non-deterministic (i.e., of arbitrary, but fixed, value for any concrete evaluation of f) from the point of view of f. For this reason, those parameters are qualified as “non-deterministic”, to distinguish them from normal parameters used in a programming language to pass information around. Moreover, some values can be “derived”, thus, computed in f from the non-deterministic parameter values, or declared as constants in f, and both values of non-deterministic parameters or derived values can then be used as normal parameters in the program. We are also given a software property to be checked about f, in the form
 , where ant and cons stand for antecedent and consequence respectively. Both \(C^\text {ant}\) and \(C^\text {cons}\) are sets of Boolean statements. A Boolean statement is a statement of f that evaluates to a Boolean value, for example, a simple statement checking that some computed intermediate value is positive. An entry i is said to satisfy a set of Boolean statements if and only if all Boolean statements in the set evaluate to true during the execution of f using the non-deterministic parameter values i, and is said to fail the set of Boolean statements otherwise. The property
, where ant and cons stand for antecedent and consequence respectively. Both \(C^\text {ant}\) and \(C^\text {cons}\) are sets of Boolean statements. A Boolean statement is a statement of f that evaluates to a Boolean value, for example, a simple statement checking that some computed intermediate value is positive. An entry i is said to satisfy a set of Boolean statements if and only if all Boolean statements in the set evaluate to true during the execution of f using the non-deterministic parameter values i, and is said to fail the set of Boolean statements otherwise. The property
 requires that for all possible entries \(i \in I\), if i satisfies \(C^\text {ant}\), then i satisfies \(C^\text {cons}\). As an example, assume f computes, given i, two intermediate integer values \(v_1\) and \(v_2\), and then returns a third value \(v_3\). The property to be checked could, e.g., be: if \(v_1\) is negative, then \(v_2\) is positive and \(v_3\) is odd. A solver that is asked to check a software property
requires that for all possible entries \(i \in I\), if i satisfies \(C^\text {ant}\), then i satisfies \(C^\text {cons}\). As an example, assume f computes, given i, two intermediate integer values \(v_1\) and \(v_2\), and then returns a third value \(v_3\). The property to be checked could, e.g., be: if \(v_1\) is negative, then \(v_2\) is positive and \(v_3\) is odd. A solver that is asked to check a software property
 thus exhaustively searches for an entry i that satisfies \(C^\text {ant}\) but fails \(C^\text {cons}\). The property is valid if and only if there does not exist any such entry i, i.e., it is impossible to find.
thus exhaustively searches for an entry i that satisfies \(C^\text {ant}\) but fails \(C^\text {cons}\). The property is valid if and only if there does not exist any such entry i, i.e., it is impossible to find.
SBMC is a fully-automatic static program analysis technique used to verify whether such a software property is valid, given a function and a property to be checked. It covers all possible inputs within a specified bound. It is static in the sense that programs are analyzed without executing them on concrete values or considering any side channels. Instead, programs are symbolically executed and exhaustively checked for errors up to a certain bound, restricting the number of loop iterations to limit runs through the program to a bounded length. This is done by unrolling the control flow graph of the program and translating it into a formula in a decidable logic that is satisfiable if and only if a program run exists which satisfies \(C^\text {ant}\) and fails \(C^\text {cons}\). The variables in the formula are the non-deterministic parameters of f, and their possible values are taken from I.
This reduces the problem to a decidable satisfiability problem. Modern SAT-solving technology can then be used to verify whether such a program run exists, in which case an erroneous input has been found, and the run is presented to the user. If the solver cannot find such a program run, it may be either because the property is valid, or because it is invalid only for some run which exceeds the bound. In some cases, SBMC is also able to infer statically which bound is sufficient to bring a definitive conclusion.
2.3 Automatic Formal Verification for Card-Based Protocols
Our approach employs a standardized program representation of the KWH trees introduced in [KWH15] (and described in the beginning of this section). This allows a general programmatic encoding of both shuffle and turn operations, as well as of the fixed input state (indicated by the input card sequences from the table in the very beginning of this paper), the non-deterministic reachable states, and the logical function to be computed securely.
The input state is trivially derived from the specified numbers of cards as the size and order of the players’ commitments is fixed and the (without loss of generality) consecutively ordered card sequence of (distinguishable) helper-cards is simply prepended to the input card sequence, annotated with their respective input probabilities. Any input state thus consists of exactly four distinguishable card sequences. Based on this input state, the program performs a loop, which successively performs turn or shuffle operations based on the input state and computes the resulting states from which it continues performing turn or shuffle operations. The loop ends when the specified bound (representing the length of the protocol to be found) is reached, checks whether the final state is indeed a valid computation of the secure function, and (if and only if the check is successful) the found protocol is then presented to the user.
However, this task involves multiple computational complexities, most notably both the number of (possibly) reachable states, and the choice of the next operation, i.e., either choosing the card(s) to be turned or which shuffle to perform. We partially overcome the first computational complexity by not considering Las Vegas protocols as this relieves us from checking every reachable sequence of states to be finite. In fact, we compute all reachable states after every protocol operation, but only check each of them to be valid, and then proceed our operations on only one of them, which is non-deterministically chosen among them. The second computational complexity consists in first non-deterministically choosing whether to shuffle or to turn, and then to perform the respective operation. The turn operation is less interesting as it is mostly the obvious implementation for updating the computed state and its probabilities using mostly standard imperative program operations, except that the turn observations are again non-deterministically chosen, hence making the SBMC tool consider any of them to be possible. The more interesting operation is the shuffle operation, as it must randomly draw a set of permutations on which the thereby reachable states are computed. We implement this by non-deterministically choosing a set of permutations from a precomputed set of all generally possible permutations. Both the amountFootnote 5 and the choices of the respective permutations are chosen non-deterministically. Moreover, we restrict our experiments to only closed shuffles and proceed by restricting the computed set of permutations to be either closed or of size one (i.e., a simple permutation).
Finally, after iterating the afore-mentioned loop for the specified bound number with the described operations and restricting that final state indeed computes the secure function, we specify the software property \(C^\text {cons}\) to be checked simply as the Boolean value false. This trivially unsatisfiable property implies that the verification task always fails once there exist input and non-deterministic parameters such that the respective program run reaches the statement in the program which checks this property. The SBMC tool exhaustively searches for a run of the specified length through the program which leads from the starting state to a correct and secure state which satisfies the given security notion, i.e., reaches the above-mentioned statement. Hence, if there exists any protocol of the specified length which computes the secure function and for which the specified operations and valid intermediate states (representing KWH-trees) exist, such a protocol is presented by our method. If no such protocol can be found, we know there is no card-based protocol of the specified length satisfying all our restrictions on permitted turn and shuffle operations, as well as intermediate and final states. This means there exists no model for the SAT formula which encodes the set of all permitted program runs given our specified requirements.
Hence, assuming our translation of KWH trees and respective protocol operations into a simple imperative program are correct, this method can then be used in an iterative manner to strengthen the bounds from the literature. Note that this is largely based on the so-called “small-scope hypothesis”, i.e., a large number of bugs are already exposed for small program runs. We apply this hypothesis to the setting of card-based security protocols as all protocols in the literature only use a small number of turn and shuffle operations and the length of any found protocol is below ten operations.
This approach can be generalized to search for card-based protocols using a pre-defined number of actions and adhering to a given formal security notion. We have written a general programFootnote 6 to search for such situations parameterized in the desired restrictions on actions and security notions. Note that, in order to cope with the still considerable state space size, we use the refined security notion of output-possibilistic security.
3 On the Choice of Cards for Input and Output
We essentially show that the choice of input basis (or output basis, but not necessarily both) is irrelevant for the functioning of the protocol. In rare cases, one has to append two operations to existing protocols to make them fully basis flexible. In the Niemi–Renvall protocol shown above, the protocol description specifies Alice’s cards to be of symbols \(1, 2\), and Bob’s to be of symbols \(3, 4\) and the helping card to be a \(5\). To simplify later proofs and to demonstrate an interesting symmetry in card-based protocols, we show that this choice is irrelevant for the functioning of the protocol.
For this, we define a relabeling from deck alphabet \(\varSigma \) to a deck alphabet \(\varSigma '\), i.e., a bijective function
 .Footnote 7 A relabeling of a sequence
.Footnote 7 A relabeling of a sequence
 is a relabeling of each of its symbols, i.e.,
is a relabeling of each of its symbols, i.e.,
 . A relabeling of a state is given by the relabeling of all its sequences, a relabeling of a protocol/state (sub)tree is the relabeling of all its states as in Figs. 3 and 5.
. A relabeling of a state is given by the relabeling of all its sequences, a relabeling of a protocol/state (sub)tree is the relabeling of all its states as in Figs. 3 and 5.
Example of the relabel action, swapping the card symbols of 1 and 3, and of 2 and 4, respectively. This action is for abbreviated writing only, it does not actually relabel the physical cards, which seems impossible without learning their symbols. Hence, the tree on the left is virtually translated to the right. Note that the relabeling only affects the sequences, the observations at edges belonging to turn actions and may swap the order of the indices in result operations.
Example of making the basis deterministic, cf. Lemma 2. On the left you see a tree part with one-bit output and randomized basis, i.e., the output basis may be \(\{1,2\}\) or \(\{3,4\}\), each with a probability of
 . We can make it known to the players, i.e., deterministic, by splitting up the state via an \(S_k\)-shuffle (here: \(k=2\)) on the remaining cards (so that they no longer contain any information), turning these and then doing the result operation. By what is visible in the turn, one can derive the output basis.
. We can make it known to the players, i.e., deterministic, by splitting up the state via an \(S_k\)-shuffle (here: \(k=2\)) on the remaining cards (so that they no longer contain any information), turning these and then doing the result operation. By what is visible in the turn, one can derive the output basis.
Lemma 1
If \(\mathcal {P}\) is a protocol with deterministic output basis, one can relabel the cards without affecting the functioning.
Note that the deterministic output basis restriction is important, because if we have a randomized output encoding such as in Fig. 4 on the left, a relabeling might affect the monotonicity of the encoding of only one of the possible output bases. In this case, we make use of the following lemma, as illustrated Fig. 4.
Lemma 2
Every protocol with one-bit output and a randomized output basis can be transformed into a protocol with deterministic output basis, by inserting a shuffle and a turn before any result operation with randomized output basis.
4 Impossibility of Finite-Runtime Four-Card AND and Basis Conversion with Overlapping Bases
In this section we give our main impossibility results.
Theorem 1
There is no four-card finite-runtime basis conversion protocol for overlapping bases with deck
 .
.
Proof Sketch. We proceed by using the backwards calculus technique from [K18], as described in Sect. 2.1. That is, we show that if we start with the set of (highly-structured) final states
 of basis conversion protocols and enlarge this set iteratively by states which reach the given states by a shuffle or a turn, we obtain the closure
of basis conversion protocols and enlarge this set iteratively by states which reach the given states by a shuffle or a turn, we obtain the closure
 . If we consider only reduced states, the set of possible states is finite, so applying
. If we consider only reduced states, the set of possible states is finite, so applying
 and
and
 operations to the growing set of states, starting from
operations to the growing set of states, starting from
 , will become stationary. It remains to show that the start state is not contained in the closure. We assume w.l.o.g. the input basis \(\{1,2\}\) with helping cards 3 and 4, and the output basis
, will become stationary. It remains to show that the start state is not contained in the closure. We assume w.l.o.g. the input basis \(\{1,2\}\) with helping cards 3 and 4, and the output basis
 such that
such that
 . For simplicity, we want the output basis \(\{1,3\}\) and argue later why this choice did not affect the proof statement. Hence, the final state is any choice of at least one 1-sequence and one 0-sequence of the state on the left:
. For simplicity, we want the output basis \(\{1,3\}\) and argue later why this choice did not affect the proof statement. Hence, the final state is any choice of at least one 1-sequence and one 0-sequence of the state on the left:

The state on the right is the start state of a basis-conversion protocol. Both states are considered up to similarity.
We have
 , i.e., shuffling steps do not help in the last step of a output-possibilistically secure protocol, because any subset of a final state which contains at least one 1-sequence and one 0-sequence (required as 1-/0-sequences cannot be generated out of thin air by a shuffle), is already final. Hence, we consider
, i.e., shuffling steps do not help in the last step of a output-possibilistically secure protocol, because any subset of a final state which contains at least one 1-sequence and one 0-sequence (required as 1-/0-sequences cannot be generated out of thin air by a shuffle), is already final. Hence, we consider
 , i.e., the states turnable at a position i, where all immediate child nodes when turning at i are in
, i.e., the states turnable at a position i, where all immediate child nodes when turning at i are in
 . W.l.o.g. we assume the turn to be at position 4. By [K18, Lemma 3], we use that
. W.l.o.g. we assume the turn to be at position 4. By [K18, Lemma 3], we use that
 , where
, where
 is the subset of
is the subset of
 with states that have a constant column:
with states that have a constant column:

However, we aim to enlarge this set (which we can do since our claim is only made stronger by monotonicity of the backwards operations) by the states

because they would be reachable anyway via a disjoint basis conversion due to [M16, Sect. 3.2]. The states from
 look as follows:
look as follows:

where at least two of the blocks are present, and
 are pairwise distinct. Note that the start state cannot be of this form, as it contains only two sequences. To show that another backwards turn step does not enlarge the set by showing that
are pairwise distinct. Note that the start state cannot be of this form, as it contains only two sequences. To show that another backwards turn step does not enlarge the set by showing that
 . For this, note that the states from
. For this, note that the states from
 have two constant columns, but with the specific pairing that if one is 1, the other is 3 and vice versa, or if one is 2, the other is 4 and vice versa. Hence, having another constant column in the state from
have two constant columns, but with the specific pairing that if one is 1, the other is 3 and vice versa, or if one is 2, the other is 4 and vice versa. Hence, having another constant column in the state from
 above, say at position 3, would need the same symbol (given by the pairing) in the fourth column. Hence, it can only have two sequences, i.e., it is already in
above, say at position 3, would need the same symbol (given by the pairing) in the fourth column. Hence, it can only have two sequences, i.e., it is already in
 . This shows that
. This shows that
 .
.
Now, for the main step of the proof, set
 and
and
 . Because the shuffling is unrestricted, applying another backwards shuffle to
. Because the shuffling is unrestricted, applying another backwards shuffle to
 cannot give a larger set, as we can always combine two shuffles into one. The remaining proof will show that
cannot give a larger set, as we can always combine two shuffles into one. The remaining proof will show that
 in which case no further enlargement is possible. Afterwards, showing that the start state is not in
in which case no further enlargement is possible. Afterwards, showing that the start state is not in
 finishes the proof.
finishes the proof.
As
 ’s states are subsets of
’s states are subsets of
 ’s states,
’s states,
 ’s general form is on the left:
’s general form is on the left:

where \(\mathord {?}\) can be either 0 or 1 and x, y are either both a, or one is b and the other c. To see this, observe that it is a subset of the state on the right where we leave out at least all sequences interfering with our wish of a constant column in this position (in parentheses on the right). Our aim is to show that these states are more specifically the states of
 again, i.e., it is impossible to reach any state of form in
again, i.e., it is impossible to reach any state of form in
 via a shuffle from these states. Due to the complexity of the situation, we do a case distinction on the number of sequences of
via a shuffle from these states. Due to the complexity of the situation, we do a case distinction on the number of sequences of
 .
.
Let us consider only the first case, the other cases are analogously and are to be found in a full version of the paper. Let
 contain two sequences. If they were both from the first block, the state would trivially be in
contain two sequences. If they were both from the first block, the state would trivially be in
 . This leaves us with two choices, either include a sequence ending with da or exclude it. For concreteness, we choose w.l.o.g. \(a=2\), \(d=4\), \(b=1\) and \(c=3\), and have this:
. This leaves us with two choices, either include a sequence ending with da or exclude it. For concreteness, we choose w.l.o.g. \(a=2\), \(d=4\), \(b=1\) and \(c=3\), and have this:

Reaching this state on the left by a shuffle should contain at least
 . But if we apply \((1\;4\;2)\) to the first sequence gives a sequence 3241 which is not possible on the left side due to its trailing 1. The other cases are similar.
. But if we apply \((1\;4\;2)\) to the first sequence gives a sequence 3241 which is not possible on the left side due to its trailing 1. The other cases are similar.
Theorem 2
There is no four-card finite-runtime
 protocol with deck
protocol with deck
 with fixed-in-advance output basis.
with fixed-in-advance output basis.
Proof Sketch. If the output basis is not given using only Alice’s or only Bob’s cards, this follows from Theorem 1, because if there would be such an
 protocol, by fixing the second bit to \(1\) one could easily generate a basis-convert protocol, which is impossible. In the remaining case, e.g., of the output basis being Alice’s cards, say 1, 2, this would not be a basis-convert, as the bit remains unchanged. In this case, a close analysis of the proof of Theorem 1 above yields that the theorem also holds in this case. We omit the details, and refer to the full version.
protocol, by fixing the second bit to \(1\) one could easily generate a basis-convert protocol, which is impossible. In the remaining case, e.g., of the output basis being Alice’s cards, say 1, 2, this would not be a basis-convert, as the bit remains unchanged. In this case, a close analysis of the proof of Theorem 1 above yields that the theorem also holds in this case. We omit the details, and refer to the full version.
5 Card-Minimal Protocols for AND
Theorem 3
There is a four-card Las Vegas
 protocol with deck
protocol with deck
 using only random cuts.
using only random cuts.
Proof
See Fig. 6 and Protocol 1.
Four-card Las Vegas
 protocol using random cuts, cf. Protocol 1. Here,
protocol using random cuts, cf. Protocol 1. Here,
 and
and
 . The relabel operations are not actual actions to be performed but help abbreviate the write-up of the protocol, see Sect. 3.
. The relabel operations are not actual actions to be performed but help abbreviate the write-up of the protocol, see Sect. 3.
 was revealed in the first turn. The permutation to be applied is \((3\;4)\). The situation is similar in all other cases.
was revealed in the first turn. The permutation to be applied is \((3\;4)\). The situation is similar in all other cases.To get a better understanding of why the protocol works and how it is related to the protocol of [NR99], let us consider exemplarily the case that the first card to be revealed is a 1, the other cases are analogous. In this situation, let us look at the different cases, given in Table 2. Using the method as before, we can remove
 by performing a random cut while leaving the relative order intact (
by performing a random cut while leaving the relative order intact (
 here is assigned the role of the
here is assigned the role of the
 in Niemi and Renvall’s protocol) and waiting until it appears when turning. Later we can remove the
in Niemi and Renvall’s protocol) and waiting until it appears when turning. Later we can remove the
 from the remaining cards, to get the output encoded using the cards
from the remaining cards, to get the output encoded using the cards
 and
and
 . A closer analysis of the situation after removing
. A closer analysis of the situation after removing
 shows that one can take a shortcut when one is not bound to the output being cards
shows that one can take a shortcut when one is not bound to the output being cards
 (which is not our goal, because in the other cases besides the first turn being 1 it is different anyway, and one would have to add conversion protocols to ensure this). The situation is as follows: The remaining three cards are either a cyclic rotation (cut) of the sequence
(which is not our goal, because in the other cases besides the first turn being 1 it is different anyway, and one would have to add conversion protocols to ensure this). The situation is as follows: The remaining three cards are either a cyclic rotation (cut) of the sequence
 , if the output is 0, or a cyclic rotation of the sequence
, if the output is 0, or a cyclic rotation of the sequence
 , otherwise. A cut cannot rotate a sequence of the former type to become the other, or vice versa. After the cut we can safely turn any card and, from the resulting symbol, deduce in which order the other cards must be output to encode the protocol result.
, otherwise. A cut cannot rotate a sequence of the former type to become the other, or vice versa. After the cut we can safely turn any card and, from the resulting symbol, deduce in which order the other cards must be output to encode the protocol result.

For an analysis of the number of shuffle steps in the protocol, observe that we have performed two shuffles until we reach the loop condition, which holds with probability
 . After the loop, we have one additional shuffle step. Hence, the expected number of shuffles is \(3 + \sum _{n=1}^{\infty }{\left( 1-\frac{1}{4}\right) ^n} = 6\).
. After the loop, we have one additional shuffle step. Hence, the expected number of shuffles is \(3 + \sum _{n=1}^{\infty }{\left( 1-\frac{1}{4}\right) ^n} = 6\).
Comparison to [NR99]. The previous protocol, using five cards, was described in the introduction. For a pseudo-code description, see Protocol 2.

KWH tree of the five-card
 protocol of [NR99] with
protocol of [NR99] with
 using only random cuts, cf. Protocol 2. Note that
using only random cuts, cf. Protocol 2. Note that
 and
and
 . The output is in basis \(\{1,4\}\).
. The output is in basis \(\{1,4\}\).
As Niemi and Renvall state, their running time in the number of shuffle steps is calculated as follows: Their protocol starts with a shuffle and repeats this with probability
 . The second loop contains a shuffle and has a repeating probability of
. The second loop contains a shuffle and has a repeating probability of
 . The shuffle in the final loop is repeated with probability
. The shuffle in the final loop is repeated with probability
 . In total, the expected running time is \(3 + \sum _{n=1}^{\infty }{\left( \frac{3}{5}\right) ^n} + \sum _{n=1}^{\infty }{\left( \frac{3}{4}\right) ^n} + \sum _{n=1}^{\infty }{\left( \frac{2}{3}\right) ^n} = 3 + 1.5 + 3 + 2 = 9.5\). However, for a fair comparison to our protocol, we eliminate the last loop from their protocol, as its only function is to ensure that the output is in basis \(\{1,4\}\), which our protocol does not guarantee. In this case, the modified Niemi–Renvall protocol has an expected number of \(3+1.5+3=7.5\) shuffle steps. Hence, our four-card
. In total, the expected running time is \(3 + \sum _{n=1}^{\infty }{\left( \frac{3}{5}\right) ^n} + \sum _{n=1}^{\infty }{\left( \frac{3}{4}\right) ^n} + \sum _{n=1}^{\infty }{\left( \frac{2}{3}\right) ^n} = 3 + 1.5 + 3 + 2 = 9.5\). However, for a fair comparison to our protocol, we eliminate the last loop from their protocol, as its only function is to ensure that the output is in basis \(\{1,4\}\), which our protocol does not guarantee. In this case, the modified Niemi–Renvall protocol has an expected number of \(3+1.5+3=7.5\) shuffle steps. Hence, our four-card
 protocol needs one card less and outperforms the Niemi–Renvall protocol by an expected number of 1.5 shuffle steps.
protocol needs one card less and outperforms the Niemi–Renvall protocol by an expected number of 1.5 shuffle steps.
6 Card-Minimal Protocols for Basis Conversion with Overlapping Bases
In this section, we give two protocols for converting a basis encoding in the case where the old and the new encoding share a card. The first protocol has an expected (finite) running time of three shuffle and turn operations. While it has not been explicit in the literature, it is in a way implicit in the protocol by Niemi and Renvall [NR99], as the authors aimed to get a fixed-in-advance output basis.
Theorem 4
There is a three-card Las Vegas basis-conversion protocol for overlapping bases with deck
 and uniform closed shuffles.
and uniform closed shuffles.
Proof
See Fig. 8 and Protocol 3.


Theorem 5
There is a five-card finite-runtime basis conversion protocol for overlapping bases with deck
 . It only uses two random bisection cuts as shuffle operations.
. It only uses two random bisection cuts as shuffle operations.
Proof
This is just applying the basis conversion of [M16] twice, cf. Protocol 4.
7 An Illustration of Our Verification Methodology
In the following, we exemplify our translation of card-based cryptographic protocols using standard decks to a specific the bounded model checker CBMC which takes programs in the C language, and compute a secure
 function. For our experiments, we used CBMC 5.11 [CKL04] with the built-in solver based on the SAT-solver MiniSat 2.2.0 [ES03]. All experiments are performed on an AMD Opteron(tm) 2431 CPU at 2.40 GHz with 6 cores and 32 GB of RAM.
function. For our experiments, we used CBMC 5.11 [CKL04] with the built-in solver based on the SAT-solver MiniSat 2.2.0 [ES03]. All experiments are performed on an AMD Opteron(tm) 2431 CPU at 2.40 GHz with 6 cores and 32 GB of RAM.

We translate KWH trees in the C language using a simple encoding into a bounded C program with only static structures and no pointers, e.g., we employ C structs (see Listing 1) holding an array of card sequences for the sequence \(s\), attached with their respective values for each probability (for the probabilistic security notion) or dependency (for output-possibilistic security) \(X_i\) occurring in
 , which is simply encoded by another C struct
, which is simply encoded by another C struct
 . The sequences are constructed using non-deterministic values restricted by respective software conditions to enforce a lexicographic ordering. Moreover, we assign the starting values in
. The sequences are constructed using non-deterministic values restricted by respective software conditions to enforce a lexicographic ordering. Moreover, we assign the starting values in
 with fixed (i.e., deterministic) values based on the constructed sequences. Subsequently, an array of (consecutively) reachable states is constructed non-deterministically using simple implementations of the turn and the shuffle operation as explained in Sect. 2. We then repeatedly (after each turn/shuffle) check whether all possible resulting (non-deterministic) states correctly and securely compute the specified function, e.g., here a secure
with fixed (i.e., deterministic) values based on the constructed sequences. Subsequently, an array of (consecutively) reachable states is constructed non-deterministically using simple implementations of the turn and the shuffle operation as explained in Sect. 2. We then repeatedly (after each turn/shuffle) check whether all possible resulting (non-deterministic) states correctly and securely compute the specified function, e.g., here a secure
 .
.

An example shuffle operation is shown in Listing 2 for the case of output-possibilistic security. Therein, the keyword
 is used by the bounded model checker to restrict all program runs passing this statement to satisfy the specified (Boolean) condition. By assigning values using the special function
is used by the bounded model checker to restrict all program runs passing this statement to satisfy the specified (Boolean) condition. By assigning values using the special function
 , we assign a non-deterministic non-negative integer number, which is restricted to values greater than zero and at most of value
, we assign a non-deterministic non-negative integer number, which is restricted to values greater than zero and at most of value
 (which is a variable computed by the pre-processor and is the maximum number of sequences possible with the given deck) in the following program statement. In the shown example, the non-determinism is used to construct a set of permitted permutation sets (to be used by the shuffle operation), which makes the SBMC tool inspect the following program code for all possible assignments of this value. If necessary, this may result in a fully exhaustive search, however, the prover is often able to restrict the domain based on further program statements and dependencies seen in the rest of the program. A similar trick is used when computing the concrete permutations using the non-deterministic value of
(which is a variable computed by the pre-processor and is the maximum number of sequences possible with the given deck) in the following program statement. In the shown example, the non-determinism is used to construct a set of permitted permutation sets (to be used by the shuffle operation), which makes the SBMC tool inspect the following program code for all possible assignments of this value. If necessary, this may result in a fully exhaustive search, however, the prover is often able to restrict the domain based on further program statements and dependencies seen in the rest of the program. A similar trick is used when computing the concrete permutations using the non-deterministic value of
 in order to check all possible permutations which possibly move the values, but preserve all existing numbers in the sequence itself. This is done using the
in order to check all possible permutations which possibly move the values, but preserve all existing numbers in the sequence itself. This is done using the
 -array
-array
 , which is first initialized to zero and, when choosing a concrete permutation, assumed to be zero at position
, which is first initialized to zero and, when choosing a concrete permutation, assumed to be zero at position
 , however set to the number one right afterwards (such that it is not permitted to be chosen again). In the subsequent inner loop, the permutations are assigned choosing the according cards from the sequences in the start state using the non-deterministic value
, however set to the number one right afterwards (such that it is not permitted to be chosen again). In the subsequent inner loop, the permutations are assigned choosing the according cards from the sequences in the start state using the non-deterministic value
 . Finally, the shuffle is applied, resulting in the state variable
. Finally, the shuffle is applied, resulting in the state variable
 , which is then checked using a further method
, which is then checked using a further method
 to not contain any sequences with impermissible values for \(X_i\), which would result in incorrect computations of the
to not contain any sequences with impermissible values for \(X_i\), which would result in incorrect computations of the
 function.
function.
We applied our approach to the computation of a secure
 protocol using four cards in order to, firstly, substantiate our proof that no protocol of a length below six can be found, and, secondly, automatically find a permitted protocol using six operations. Using our approach, we were able to show that no four-card protocol exists using five operations within 57 h and constructed an output-possibilistic protocol using six operations within 31 h. The sizes of the constructed formulas consisted of between 150 and 180 million SAT clauses.
protocol using four cards in order to, firstly, substantiate our proof that no protocol of a length below six can be found, and, secondly, automatically find a permitted protocol using six operations. Using our approach, we were able to show that no four-card protocol exists using five operations within 57 h and constructed an output-possibilistic protocol using six operations within 31 h. The sizes of the constructed formulas consisted of between 150 and 180 million SAT clauses.
8 Conclusion
In this paper, we proposed a new method to search card-based protocols for any secure computation, by giving a general formal translation applicable to be used by the formal technique of software bounded model checking (SBMC). This method allows us to find new protocols automatically, and prove lower bounds on required shuffle and turn operations for any protocol, and provide an example for the computation of a minimal
 protocol. We also found a new protocol that only uses the theoretical minimum of four distinguishable cards for an
protocol. We also found a new protocol that only uses the theoretical minimum of four distinguishable cards for an
 computation. Moreover, we supported this finding by our automatic method in showing the impossibility of any protocol using less shuffle and turn operations using only practicable shuffles (random cuts). The protocol is hence optimal w.r.t. the running time restriction “restart-free Las-Vegas”. For the four-card standard deck setting, we showed that there is no finite runtime protocol, regardless of the shuffle operations used. This result completes the picture of tight lower bounds for four cards. Finally, we showed tight lower bounds on basis conversions for single bits and proposed the missing protocols, and establish the theorem that using a minimum of five cards, both input- and output-bases can be chosen freely, which fosters our impossibility result for four cards.
computation. Moreover, we supported this finding by our automatic method in showing the impossibility of any protocol using less shuffle and turn operations using only practicable shuffles (random cuts). The protocol is hence optimal w.r.t. the running time restriction “restart-free Las-Vegas”. For the four-card standard deck setting, we showed that there is no finite runtime protocol, regardless of the shuffle operations used. This result completes the picture of tight lower bounds for four cards. Finally, we showed tight lower bounds on basis conversions for single bits and proposed the missing protocols, and establish the theorem that using a minimum of five cards, both input- and output-bases can be chosen freely, which fosters our impossibility result for four cards.
Open Problems. Let us point out some open problems in the card-based security area that could be approached based on the findings in this paper: (1) For finite-runtime protocols, there exist no proven tight lower bounds on the required number of cards (five to eight cards). We recommend more research applying computer-aided formal methods at this point, as the state space for five or more cards is very large. (2) Our verification approach is fast for finding protocols and/or lower bounds on the operations needed in a protocol for given shuffle-restrictions. However, this is based on the assumption that protocols exist already for a given predefined length to find or confirm impossibility results. Investigating computer-aided formal methods for universal impossibility results might be worthwhile. (3) The two most common settings in card-based cryptography are the standard deck setting with only distinguishable cards and the two-color decks using
 and
and
 . However, it may be possible that by mixing these settings (e.g., only distinguishable cards with one pair of identical cards), we might find more efficient protocols (especially in the finite runtime setting). For such a mixed setting, [SM19] provide nice results to use in further research.
. However, it may be possible that by mixing these settings (e.g., only distinguishable cards with one pair of identical cards), we might find more efficient protocols (especially in the finite runtime setting). For such a mixed setting, [SM19] provide nice results to use in further research.
Notes
- 1.
This is known as the “dating problem”.
- 2.
Alice and Bob in the story might, e.g., use \(7\), \(8\), \(9\), \(10\) and a queen with any symbol.
- 3.
As an example, in a Duplicate Bridge tournament, one might prove that all sessions are handed the same cards, eliminating the need of a trusted dealer (no pun intended).
- 4.
Actually, the distribution does not matter, as long as \(\Pr [I = i] > 0\) for all
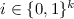 .
. - 5.
In order to keep the execution times still manageable for our experiments, we bound this amount by the (arguably quite reasonable) number 8.
- 6.
The program is available under https://github.com/mi-ki/cardCryptoVerification.
- 7.
In case of the decks being a subset of
 , we may use usual permutation notation. We require that if
, we may use usual permutation notation. We require that if
 maps \(x\) to \(y\), the cardinalities of \(x\) and \(y\) are equal in the deck.
maps \(x\) to \(y\), the cardinalities of \(x\) and \(y\) are equal in the deck.
References
Abe, Y., Hayashi, Y.-I., Mizuki, T., Sone, H.: Five-card AND protocol in committed format using only practical shuffles. In: Emura, K., et al. (ed.) APKC@AsiaCCS 2018 ACM, pp. 3–8 (2018). https://doi.org/10.1145/3197507.3197510
Avalle, M., Pironti, A., Sisto, R.: Formal verification of security protocol implementations: a survey. Formal Asp. Comput. 26(1), 99–123 (2014). https://doi.org/10.1007/s00165-012-0269-9
Blanchet, B.: Security protocol verification: symbolic and computational models. In: Degano, P., Guttman, J.D. (eds.) POST 2012. LNCS, vol. 7215, pp. 3–29. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28641-4_2
Biere, A., Cimatti, A., Clarke, E., Zhu, Y.: Symbolic model checking without BDDs. In: Cleaveland, W.R. (ed.) TACAS 1999. LNCS, vol. 1579, pp. 193–207. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-49059-0_14
Crépeau, C., Kilian, J.: Discreet solitary games. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 319–330. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_27
Clarke, E., Kroening, D., Lerda, F.: A tool for checking ANSI-C programs. In: Jensen, K., Podelski, A. (eds.) TACAS 2004. LNCS, vol. 2988, pp. 168–176. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24730-2_15
Boer, B.: More efficient match-making and satisfiability The Five Card Trick. In: Quisquater, J.-J., Vandewalle, J. (eds.) EUROCRYPT 1989. LNCS, vol. 434, pp. 208–217. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-46885-4_23
Eén, N., Sörensson, N.: An extensible SAT-solver. In: Giunchiglia, E., Tacchella, A. (eds.) SAT 2003. LNCS, vol. 2919, pp. 502–518. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24605-3_37
Fisch, B., Freund, D., Naor, M.: Physical zero-knowledge proofs of physical properties. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 313–336. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_18
Franz, M., Holzer, A., Katzenbeisser, S., Schallhart, C., Veith, H.: CBMC-GC: an ANSI C compiler for secure two-party computations. In: Cohen, A. (ed.) CC 2014. LNCS, vol. 8409, pp. 244–249. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54807-9_15
Glaser, A., Barak, B., Goldston, R.J.: A zero-knowledge protocol for nuclear warhead verification. Nature 510, 497–502 (2014). https://doi.org/10.1038/nature13457
Koch, A.: The Landscape of Optimal Card-based Protocols (2018). Cryptology ePrint Archive, Report 2018/951 https://eprint.iacr.org/2018/951
Koch, A.: Cryptographic protocols from physical assumptions. Ph.D. thesis, Karlsruhe Institute of Technology (KIT) (2019). https://doi.org/10.5445/IR/1000097756
Kastner, J., et al.: The minimum number of cards in practical card-based protocols. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10626, pp. 126–155. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_5
Koch, A., Walzer, S.: Foundations for Actively Secure Card-based Cryptography (2017). Cryptology ePrint Archive, Report 2017/423 https://eprint.iacr.org/2017/423
Koch, A., Walzer, S., Härtel, K.: Card-based cryptographic protocols using a minimal number of cards. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 783–807. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_32
Mizuki, T.: Efficient and secure multiparty computations using a standard deck of playing cards. In: Foresti, S., Persiano, G. (eds.) CANS 2016. LNCS, vol. 10052, pp. 484–499. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48965-0_29
Moran, T., Naor, M.: Basing cryptographic protocols on tamper-evident seals. Theor. Comput. Sci. 411(10), 1283–1310 (2010). https://doi.org/10.1016/j.tcs.2009.10.023
Mizuki, T., Sone, H.: Six-card secure AND and four-card secure XOR. In: Deng, X., Hopcroft, J.E., Xue, J. (eds.) FAW 2009. LNCS, vol. 5598, pp. 358–369. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02270-8_36
Mizuki, T., Shizuya, H.: A formalization of card-based cryptographic protocols via abstract machine. Int. J. Inf. Sec. 13(1), 15–23 (2014). https://doi.org/10.1007/s10207-013-0219-4
Mizuki, T., Shizuya, H.: Computational model of card-based cryptographic protocols and its applications. IEICE Trans. 100(A.1), 3–11 (2017). https://doi.org/10.1587/transfun.E100.A.3
Niemi, V., Renvall, A.: Secure multiparty computations without computers. Theor. Comput. Sci. 191(1–2), 173–183 (1998). https://doi.org/10.1016/S0304-3975(97)00107-2
Niemi, V., Renvall, A.: Solitaire zero-knowledge. Fundam. Inform. 38(1–2), 181–188 (1999). https://doi.org/10.3233/FI-1999-381214
Rastogi, A., Swamy, N., Hicks, M.: \(Wys^\star \): a DSL for verified secure multi-party computations. In: Nielson, F., Sands, D. (eds.) POST 2019. LNCS, vol. 11426, pp. 99–122. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17138-4_5
Swamy, N., et al.: Dependent types and multimonadic effects in F. In: Bodik, R., Majumdar, R. (eds.) POPL 2016, pp. 256–270. ACM (2016). https://doi.org/10.1145/2837614.2837655
Shinagawa, K., Mizuki, T.: Secure computation of any boolean function based on any deck of cards. In: Chen, Y., Deng, X., Lu, M. (eds.) FAW 2019. LNCS, vol. 11458, pp. 63–75. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-18126-0_6
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: Further Protocols
Appendix: Further Protocols
This appendix contains the 8-card
 protocol of [M16] (Fig. 9) and a second four-card protocol which uses a number of 4.5 shuffles in expectation, which are, however, non-closed and hence, more impractical to implement, cf. Fig. 10.
protocol of [M16] (Fig. 9) and a second four-card protocol which uses a number of 4.5 shuffles in expectation, which are, however, non-closed and hence, more impractical to implement, cf. Fig. 10.
The eight-card finite-runtime
 protocol of [M16], with
protocol of [M16], with
 and uniform-closed shuffles. Output is in basis \(\{5,6\}\) or \(\{7,8\}\), each with probability 1/2.
and uniform-closed shuffles. Output is in basis \(\{5,6\}\) or \(\{7,8\}\), each with probability 1/2.
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Koch, A., Schrempp, M., Kirsten, M. (2019). Card-Based Cryptography Meets Formal Verification. In: Galbraith, S., Moriai, S. (eds) Advances in Cryptology – ASIACRYPT 2019. ASIACRYPT 2019. Lecture Notes in Computer Science(), vol 11921. Springer, Cham. https://doi.org/10.1007/978-3-030-34578-5_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-34578-5_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34577-8
Online ISBN: 978-3-030-34578-5
eBook Packages: Computer ScienceComputer Science (R0)





 protocol in the standard deck setting, improving upon [
protocol in the standard deck setting, improving upon [ protocol with four cards if we fix the basis in advance.
protocol with four cards if we fix the basis in advance.
 leads to a
leads to a
 as in Fig.
as in Fig.  is a permutation set.
is a permutation set. for each observation
for each observation  , as in Fig.
, as in Fig.  contains the sequences from
contains the sequences from
 which are compatible with the observation
which are compatible with the observation  , where
, where
 is the probability of observing
is the probability of observing  permutes the sequences of
permutes the sequences of
 according to
according to
 .
. stops the computation and returns the cards at
stops the computation and returns the cards at
 as output.
as output.
 , are the possible observation by turning the cards at positions in T. For each
, are the possible observation by turning the cards at positions in T. For each
 the
the
 are the sequences from
are the sequences from
 which are compatible with
which are compatible with 


 be the output symbols (before relabeling) of some arbitrary sequence
be the output symbols (before relabeling) of some arbitrary sequence  . Then,
. Then,
 , if
, if
 implies
implies
 (
(
 is monotone on
is monotone on
 ,
,
 ) and
) and
 otherwise.
otherwise.


 with uniform closed shuffles.
with uniform closed shuffles. .
. , we may use usual permutation notation. We require that if
, we may use usual permutation notation. We require that if
 maps
maps 

 protocol with deck
protocol with deck
 and uniform shuffles. Note that
and uniform shuffles. Note that
 and
and
 . The output is in one of the bases
. The output is in one of the bases 