Towards a Call Behavior-Based Compositional Verification Framework for SysML Activity Diagrams

Abstract

SysML activity diagram is a standard modeling language for complex systems. It supports systems’ composition by providing the operator ‘call behavior’. In general, the verification of systems modeled with those diagram inherit the limitations of the developed built-in tools, especially the case of model checking. To address this shortcoming, we propose a compositional verification framework based on the call behavior operator to alleviate the state space explosion problem of model-checking. The framework decomposes a property into local sub-properties and verify them separately on the composed behavioral diagrams. Further, we propose to ignore the diagrams’ artifacts that are useless with respect to the property under verification. We prove the soundness of the proposed approach by showing that the result deduced from the verification of the local properties is always preserved. The verification results are obtained by encoding SysML activity diagrams in the probabilistic model checker ‘PRISM’. Finally, we demonstrate the effectiveness of our framework by verifying a set of properties on two use cases that require a large amount of memory and a considerable time processing.

1 Introduction

A major challenge in systems and software development process is to reduce as possible bugs by advancing the error detection at early stages of their life-cycles development. Experimentally, it has been shown that the cost of repairing a software flaw during maintenance is approximately 500 times higher than fixing it at early design phases [4]. Further, only 15% of flaws are detected in the initial design phase, whereas the cost of fixing them at this phase is extremely beneficial as compared to fixing them at the development and testing phases. Yet, a more ambitious challenge is to accelerate the verification process of a product based on its design artifacts. Here, we are interested on systems modeled by using modern and standard language like SysML [20]. The latter is a prominent object-oriented graphical language which today become defacto standard for software and systems modeling. Especially, SysML reuses a subset of UML packages [14] and extends others with specific systems’ engineering features such as probability, time, and the rate. SysML covers mainly four perspectives of systems modeling: structure, behavior, requirement, and parametric diagrams. Particularly, SysML activity diagrams are behavioral diagrams used to model system behaviors at various levels of abstraction [15].

For the verification of SysML activity diagrams, model checking is the most popular used technique [23]. Model checking [5] is a formal and automatic verification technique that checks systems specifications expressed as temporal logic formula or automata-based formalism on finite state concurrent systems. Compared to qualitative model checking, quantitative verification techniques based on probabilistic model checkers [4, 12] have recently gained popularity. Probabilistic verification offers the capability of measuring the satisfiability probability of a given property on systems that inherently exhibit probabilistic behavior. Despite its wide use, model checking in general is a resource-intensive process that requires a large amount of memory and time processing. This is due to the fact that the systems’ state space may grow exponentially with the number of variables combined with the presence of concurrent behaviors. Consequently, it is of a major importance to reduce the verification process complexity.

To overcome this issue, various techniques have been explored [4, 5] for qualitative model checking and then leveraged to the probabilistic case. Among these techniques, several solutions aim at optimizing the employed model checking algorithms by introducing symbolic data structures based on binary decision diagrams, while others target the analysis of the model itself. Besides, two classes of solutions are found in the literature: abstraction and compositional verification. The former provides a minimized representation of the global system under verification. Whereas, the latter avoids the construction of the considered global system. Abstraction techniques can be classified into four categories [5]: abstraction by state merging, on variables, by restriction, or by observer automata. Besides, the well-known compositional verification techniques [6] are: partitioned transition relation, lazy parallel composition, interface processes, and assume-guarantee.

In this paper, we are interested by the interface processes and the abstraction by restriction techniques that are consistent within the composition by call behaviors in SysML activity diagrams. The provided framework considers as input a system modeled with SysML activity diagrams and its requirements expressed in PCTL [21]. Then it decomposes a property into local sub-properties in order to verify them separately for each system’s sub-component in parallel. Further, in order to accelerate more the verification process, it ignores the diagrams’ artifacts that are useless with respect to the property and the local properties under verification. For verification, each system’s component is transformed automatically into PRISM. Finally, the framework infers safely the verification result of the target property from the obtained results of the local properties. In a nutshell, the main contributions of this paper can be summarized as follows.

• 1. Proposing a complete formalization of the existing calculus dedicated to SysML activity diagrams.

• 2. Developing an efficient verification approach that reduces the verification costs overhead of probabilistic model checking.

• 3. Proving the soundness of the proposed approach.

• 4. Showing the effectiveness of the developed framework on two real use cases.

The next section compares our approach with the existing initiatives related to the verification of SysML activity diagrams. Then, the preliminaries needed for our work are presented in Sect. 3. Section 4 describes and formalizes SysML activity diagrams. Then, our compositional verification framework is detailed in Sect. 5 and Sect. 6 presents the experimental results. Finally, Sect. 7 concludes the paper and provides future directions.

2 Related Work

In this section, we survey the research initiatives dedicated mainly to the formalization and the verification of SysML diagrams and to the compositional verification of probabilistic systems.

Yuan et al. [16] construct a set of rules to transform UML state machines to Timed Automata (TA). They apply the query view transformation approach in order to produce TA encoded in UPPAAL input language. The properties to be verified against TA are expressed in LTL. Apvrille and Saqui-Sannes [3] apply structural analysis to SysML by using the TTool open-source toolkit. They translate a subset of SysML diagrams into a Petri net and solves an equation system built upon the incidence matrix of the net. Then, a push-button approach is applied to display verification results.

Ando et al. [1] express SysML state machine diagrams in CSP# processes that could be verified by the PAT model checker. This work includes only a sub-set of rules and experimenting the transformation on a toy case study. In addition, they did not detail the temporal logic that expresses the system requirements. Carrillo et al. [8] define SysML blocks in a refinement process. The structural architecture of a SysML block is given by the internal block diagram and the behavior of each sub-block is described by an interface automaton. Their main intention in a refinement process is to ensure the consistency and the compatibility between different blocks.

Ermeson et al. [7] verify the embedded realtime systems with energy constraints that are modeled using SysML State Machine diagram, and the MARTE UML Profile (Modeling and Analysis of Real-Time and Embedded systems) is used to specify ERTS’s (Embedded Real-time Systems) constraints such as execution time and energy. They map only states and transitions into ETPN (Time Petri Net with Energy constraints). In their transformation, they don’t give the transformation of actions in a given state even the semantics of the mutual exclusive and orthogonal states by taking just the internal states into consideration. Furthermore, they propose a similar methodology [2] that maps one SysML activity diagram to time Petri Net for requirement validation of embedded real-time systems with energy constraints. The computation model formalized as an ETPN is not well presented and it misses the representation of the energy consumption values. The authors do not provide a formal transformation for SysML elements even the values represented from MARTE profile. Also, they do not clarify why they represent each constraint in an action by a separate transition.

Ouchani et al. [24] introduce the abstraction by merging states to reduce the verification cost of a SysML activity diagram. In [22], the authors transform a diagram into an equivalent hierarchical form in order to help the abstraction developed in [24].

David et al. [18] introduced an extension of UML statecharts with randomly varying duration that allows probabilistic decision in state. The Input/Output (I/O) automata is used to provide a compositional semantics for statecharts. Also, probability distribution after a continuous or discrete time is introduced as an arbitrary operator. And in [17], they introduce means to specify system randomness within statecharts, and to verify probabilistic temporal properties. The model is represented as MDP, and the properties are expressed in PCTL.

Concerning the compositional verification for probabilistic systems, Feng et al. [11] discusses assume-guarantee technique for probabilistic system by focusing more on the learning algorithm to generate the minimal deterministic automata that represents a probabilistic safety property. And in [10], they propose the assume-guarantee approach where both the assumption and the guarantee properties are probabilistic safety properties such that assumptions are generated manually. Also in [9], they apply the assume-guarantee technique on synchronous systems modeled as DTMC, where assumptions are safety properties defined as probabilistic finite automata. To our knowledge, few probabilistic model checkers support abstraction and compositional verification techniques. As example, PRISM builds the symmetry reduction and LiQuor¹ implements the bi-simulation equivalence.

3 Preliminaries

In this section, we present the probabilistic automata as a modeling formalism and PCTL temporal logic as a specification language.

Probabilistic automata (PAs) [12] are a modeling formalism for systems that exhibit probabilistic and nondeterministic features. Definition 1 illustrates a PA where Dist(S) denotes the set of convex distributions over S and $\mu =[\ldots ,s_i\mapsto p_i,\ldots ]$ is a distribution in Dist(S) that assigns a probability $\mu (s_i)=p_i$ to the state $s_i$.

Definition 1 (Probabilistic Automaton)

A probabilistic automaton is a tuple $M=\left( \overline{s},~\mathrm {S},~\mathrm {L},~\varSigma ,~\mathrm {\delta }\right)$, where:

• $\overline{s}$ is an initial state, such that $\overline{s}\in \mathrm {S}$,

• $\mathrm {S}$ is a finite set of states,

• $\mathrm {L}:S\rightarrow 2^{AP}$ is a labeling function that assigns to each state a set of atomic propositions taken from the set of atomic propositions (AP),

• $\varSigma$ is a finite set of actions,

• $\mathrm {\delta }:\mathrm {S}\times \varSigma \rightarrow \,~Dist(S)$ is a probabilistic transition function assigning for each $s\in S$ and $\alpha \in \varSigma$ a probabilistic distribution $\mu \in Dist(S)$.

For PA’s composition, this concept is modeled by the parallel composition as stipulated in Definition 2. During synchronization, each PA resolves its probabilistic choice independently. For transitions $s_1 {\mathop {\longrightarrow }\limits ^{\alpha }} \mu _1$ and $s_2{\mathop {\longrightarrow }\limits ^{\alpha }}\mu _2$ that synchronize in $\alpha$ then the composed state $(s'_1,s'_2)$ is reached from the state $(s_1,s_2)$ with probability $\mu _1(s'_1)\times \mu _2(s'_2)$. In the no synchronization case, a PA takes a transition where the other remains in its current state with probability one.

Definition 2 (Parallel Composition of PAs)

The parallel composition of two PAs: $M_1=(\overline{s}_1,~\mathrm {S}_1,~\mathrm {L}_1,~\varSigma _1,~\mathrm {\delta }_1)$ and $M_2=(\overline{s}_2,~\mathrm {S}_2,~\mathrm {L}_2,~\varSigma _2,~\mathrm {\delta }_2)$ is a PA $M=((\overline{s}_1,\overline{s}_2),~\mathrm {S}_1\times \mathrm {S}_2,~\mathrm {L}(s_1)\cup \mathrm {L}(s_2),~\varSigma _1\cup \varSigma _2,~\mathrm {\delta })$, where: $\mathrm {\delta }(\mathrm {S}_1\times \mathrm {S}_2,\varSigma _1\cup \varSigma _2)$ is the set of transitions $(s_1,s_2) {\mathop {\longrightarrow }\limits ^{\alpha }} \mu _1\times \mu _2$ such that one of the following requirements is met.

• 1. $s_1 {\mathop {\longrightarrow }\limits ^{\alpha }} \mu _1,s_2 {\mathop {\longrightarrow }\limits ^{\alpha }}\mu _2,$ and $\alpha \in \varSigma _1\cap \varSigma _2$,

• 2. $s_1 {\mathop {\longrightarrow }\limits ^{\alpha }} \mu _1,\mu _2=[s_2\mapsto 1],$ and $\alpha \in \varSigma _1\backslash \varSigma _2$,

• 3. $\mu _1=[s_1\mapsto 1], ~s_2 {\mathop {\longrightarrow }\limits ^{\alpha }} \mu _2,$ and $\alpha \in \varSigma _2\backslash \varSigma _1$.

To verify a PA, we use PCTL to express its related specifications. The following grammar represents the PCTL syntax.

$$\begin{aligned} \phi ~:\,\!:=~\top ~|~ap~|~\phi \wedge \phi ~|~\lnot \phi ~|~\mathrm {P}_{\bowtie \,p}[\psi ]\\ \psi ~:\,\!:=\mathrm {X}\phi ~|~\phi \mathrm {U}^{\le \,k}\phi ~|~\phi \mathrm {U}\phi \qquad \quad \end{aligned}$$

Where the term “$\top$” means true, “ap” is an atomic proposition, , $p\in [0,1]$, and $\bowtie \in \{<,\le ,>,\ge \}$. The operator “$\wedge$” represents the conjunction and “$\lnot$” is the negation operator, and $\mathrm {P}$ is the probabilistic operator. Also, “$\mathrm {X}$”, “$\mathrm {U}^{\le \,k}$”, and “$\mathrm {U}$” are the next, the bounded until, and the until temporal logic operators, respectively.

To specify a satisfaction relation of a PCTL formula in a state “s”, a class of adversaries has been defined to solve the nondeterminism in PAs. Hence, a PCTL formula should be satisfied under all adversaries. The satisfaction relation ($\models$) of a PCTL formula is defined as follows, where “s” is a state and “$\pi$” is a path obtained by a memoryless adversary [12].

• $s\models \top$ is always satisfied.

• $s\models ap\Leftrightarrow ~ap\in ~$L(s) and L is a labeling function.

• $s\models \phi _{1}\wedge \phi _{2}\Leftrightarrow ~s\models ~\phi _{1}\wedge ~s\models ~\phi _{2}$.

• $s\models \lnot \phi \Leftrightarrow ~s\not \models ~\phi$.

• $s\models \mathrm {P}_{\bowtie \,p}[\psi ]\Leftrightarrow ~\mathrm {P}(\{\pi ~is~a~path~starts~from~the~state~s|\pi ~\models \psi \})\bowtie \,p$.

• $\pi \models$X$\phi \Leftrightarrow \pi (1)\models \phi$ where $\pi (1)$ is the second state of $\pi$.

• $\pi \models \phi _{1}$U$^{\le k} \phi _{2}\Leftrightarrow \exists i\le k:\forall j<i,~\pi (j)\models \phi _{1}\wedge \pi (i)\models \phi _{2}$.

• $\pi \models \phi _{1}$U$\phi _{2}\Leftrightarrow \exists ~k\ge 0:~\pi \models \phi _{1}$U$^{\le k} \phi _{2}$.

4 SysML Activity Diagrams Formalization

In this section, we describe and formalize SysML activity diagrams by providing an adequate syntax and semantics.

As illustrated in Fig. 6, SysML activity diagrams are a graph-based representation where their main constructs (Fig. 1) can be decomposed into two categories: activity nodes and activity edges. The former contains three types: activity invocation, object and control nodes. Activity invocation includes receive and send signals, action, and call behavior. Activity control nodes are initial, flow final, activity final, decision, merge, fork, and join nodes. Activity edges are of two types: control flow and object flow. Control flow edges are used to show the execution path through the activity diagram and to connect activity nodes. Object flow edges are used to show the flow of data between activity nodes. Concurrency and synchronization are modeled using forks and joins, whereas, branching is modeled using decision and merge nodes. While a decision node specifies a choice between different possible paths based on the evaluation of a guard condition (and/or a probability distribution), a fork node indicates the beginning of multiple parallel control threads. Moreover, a merge node specifies a point from where different incoming control paths follow the same path, whereas a join node allows multiple parallel control threads to synchronize and rejoin. In addition, the call behavior action consumes its input tokens and invoke its specified behavior. The execution of the calling artifact is blocked until it receives a reply from the invoked behavior.

Fig. 1.

SysML activity diagram constructs.

4.1 Syntax of SysML Activity Diagrams

The UML superstructure [14] specifies basic rules for the execution of the various nodes by explaining textually how tokens are passed from one node to another. For formalization, we present in Table 1 SysML activity diagrams constructs and their representation as NuAC terms. At the beginning, a first token starts flowing from the initial node and moves downstream from one node to another with respect to the foregoing set of control routing rules defined by the control nodes until reaching either an activity final or a flow final node.

However, activity diagram semantics as specified in the standard stay informal since it is explained textually. We present in Fig. 2 the Backus-Naur-Form of the new version of Activity Calculus (NuAC) that helps to formalize SysML activity diagrams. This version of NuAC calculus optimizes the syntax presented in [24] and allows for multiplicity in join, merge, fork, and decision constructs by exploiting their commutativity and associativity properties. We denote by $\mathscr {A}[\mathscr {N}]$ to specify $\mathscr {N}$ as a sub term of $\mathscr {A}$ and by $|\mathscr {A}|$ to denote a term $\mathscr {A}$ without tokens. For the call behavior case of $a\uparrow \mathscr {A}'$, we denote $\mathscr {A}[a\uparrow \mathscr {A'}]$ by $\mathscr {A}\uparrow _a\mathscr {A}'$.

Table 1. Rewriting activity diagram constructs in NuAC.

Fig. 2.

Syntax of New Activity Calculus (NuAC).

During the execution, the structure of the activity diagram is kept unmodified and the only changes is the tokens locus. The NuAC syntax was inspired by this idea so that a NuAC term presents a static structure while tokens are the only dynamic elements. We can distinguish two main syntactic terms: marked and unmarked. A marked NuAC term corresponds to an activity diagram with tokens. An unmarked NuAC term corresponds to the static structure of the diagram. A marked term is typically used to denote a reachable state that is characterized by the set of tokens locations in a given term.

To support multiple tokens, we augment the “overbar” operator with an integer n such that ${\overline{\mathscr {N}}}^{n}$ denotes a term marked with n tokens with the convention that ${\overline{\mathscr {N}}}^{1}=\overline{\mathscr {N}}$ and ${\overline{\mathscr {N}}}^{0}=\mathscr {N}$. Multiple tokens are needed when there are loops that encompass in their body a fork node. Furthermore, we use a prefix label for each node to reference it and uniquely use it in the case of a backward flow connection (case of merge or join). Particularly, labels are useful for connecting multiple incoming flows towards merge and join nodes. Let $\mathscr {L}$ be a collection of labels ranged over by $l_{0}$, $l_{1}$, $\cdots$ and $\mathscr {N}$ be any node (except initial) in the activity diagram. We write $l:\!\mathscr {N}$ to denote an l-labeled activity node $\mathscr {N}$. It is important to note that nodes with multi-inputs (e.g. join and merge) are visited as many times as they have incoming edges. Thus, as a syntactic convention, we use either the NuAC term (i.e. $l:\!M(x,y)\!\rightarrowtail \!\mathscr {N}$ for merge and $l:\!J(x,y)\!\rightarrowtail \!\mathscr {N}$ for join) if the current node is visited for the first time or its corresponding label (i.e. $l_x$ or $l_y$) if the same node is encountered later during the traversal process. Also, we denote by $D((g,\mathscr {N}_1),(\lnot g,\mathscr {N}_2))$ or $D((p,\mathscr {N}_1),(1-p,\mathscr {N}_2))$ to express a decision without probabilities or guards, respectively.

4.2 Semantics of SysML Activity Diagrams

The execution of SysML activity diagrams is based on token’s flow. To give a meaning to this execution, we use structural operational semantics to formally describe how the computation steps of NuAC atomic terms take place. The operational semantics of NuAC is based on the informally specified tokens-passing rules defined in [14].

Fig. 3.

NuAC operational semantic rules.

We define $\varSigma$ as the set of non-empty actions labeling the transitions (i.e. the alphabet of NuAC, to be distinguished from action nodes in activity diagrams). An element $\alpha \in \varSigma$ is the label of the executing active node. Let $\varSigma ^{o}$ be $\varSigma \cup \{o\}$ where o denotes the empty action. Let p be a probability value such that $p\in ]0,1[$. The general form of a transition is $\mathscr {A}$ ${\mathop {\longrightarrow }\limits ^{\alpha }}_{p}$ $\mathscr {A}'$ and $\mathscr {A}$ ${\mathop {\longrightarrow }\limits ^{\alpha }}$ $\mathscr {A}'$ in the case of a Dirac (non probabilistic) transition. The probability value specifies the likelihood of a given transition to occur and it is denoted by $P(\mathscr {A},\alpha ,\mathscr {A}')$. Figure 3 shows the operational semantic rules of NuAC. The semantics of SysML activity diagrams expressed using $\mathscr {A}$ as a result of the defined semantic rules can be described in terms of the PA stipulated in Definition 3. In addition, we propose in Table 2 the NuAC axioms that are proved by using NuAC semantic rules.

Definition 3 (NuAC-PA)

A probabilistic automata of a NuAC term $\mathscr {A}$ is the tuple $M_{\mathscr {A}}=\left( \overline{s},~\mathrm {L},~\mathrm {S},~\varSigma ^{o},~\mathrm {\delta }\right)$, where:

• $\overline{s}$ is an initial state, such that $\mathrm {L}(\overline{s})=\{\overline{l:\!\iota }\!\rightarrowtail \!\mathscr {N}\}$,

• is a labeling function where: ,

• $\mathrm {S}$ is a finite set of states reachable from $\overline{s}$, such that, $\mathrm {S}=\{s_{i:0\le i \le n}:\mathrm {L}(s_{i})\in \{\overline{\mathscr {N}}\}\}$,

• $\varSigma ^{o}$ is a finite set of actions corresponding to labels in $\mathscr {A}$,

• $\mathrm {\delta }:\mathrm {S}\times \varSigma ^{o} \rightarrow \,~Dist(S)$ is a partial probabilistic transition function such that, for each $s\in S$ and $\alpha \in \varSigma ^{o}$ assigns a probabilistic distribution $\mu$, where:

  • For $S'\subseteq ~S$ such that $S'=\{s_{i:0\le i\le n}: s{\mathop {\longrightarrow }\limits ^{\alpha }}_{p_{i}}s_{i}\}$, each transition $s{\mathop {\longrightarrow }\limits ^{\alpha }}_{p_{i}}s_{i}$ satisfies one NuAC semantic rule and $\mu (S')=\sum _{i=0}^{n}p_{i}=\sum _{i=0}^{n}\mu (s_{i})=1$.

  • For each transition $s{\mathop {\longrightarrow }\limits ^{\alpha }}_{1}s''$ satisfying a NuAC semantic rule, $\mu$ is defined such that $\mu (s'')=1$.

Table 2. Axioms for NuAC.

5 The Approach

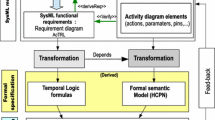
Figure 4 depicts an overview of our compositional verification framework. It takes a set of SysML activity diagrams composed by the call behavior interface and a Probabilistic Computation Tree Logic (PCTL) [12] property as input. First, we develop an abstraction approach that restricts the verification of a PCTL property only on the influenced diagrams instead of the whole composition. Then, we propose a compositional verification approach by interface processes that distributes a PCTL property into local ones which helps to verify them separately for each diagram. For verification, we encode the diagrams into the PRISM input language [19]. Finally, we deduce the result of the main property from the results of the local properties that are verified separately for each called diagram.

Fig. 4.

A compositional verification framework.

5.1 The Compositional Verification

Let $\mathscr {A}$ be a SysML activity diagram with n call behaviors denoted by $\mathscr {A}=\mathscr {A}_0\uparrow _{a_0}\mathscr {A}_1\cdots \mathscr {A}_{i-1}\uparrow _{a_{i-1}}\mathscr {A}_i\cdots \mathscr {A}_{n-1}\uparrow _{a_{n-1}}\mathscr {A}_n$. In order to reduce the diagram $\mathscr {A}$, we apply NuAC axioms and introduce the reduction rule defined in Definition 4 to remove diagrams $\mathscr {A}_{i}$ that are not influenced by the property $\phi$ to be verified. The obtained diagram after applying the reduction rule is denoted by $\widehat{\mathscr {A}}$.

Definition 4

Let $\mathscr {A}$ be a diagram that contains n call behaviors, $AP_{\phi }$ is the atomic propositions of the PCTL property $\phi$, and $AP_{\mathscr {A}_i}$ is the atomic propositions of the behavioral diagram $\mathscr {A}_i$. Reducing $\mathscr {A}$ to the diagram $\widehat{\mathscr {A}}$ with respect to $\phi$ is obtained by applying the following rule.

$$\begin{aligned} \frac{\forall 0\le i\le n,AP_{\phi }\cap AP_{\mathscr {A}_i}=\emptyset }{\mathscr {A}_{i}=\epsilon } \end{aligned}$$

Below, Proposition 1 shows the satisfiability probability after reduction.

Proposition 1

For a reduced diagram $\widehat{\mathscr {A}}$ of $\mathscr {A}$ with respect to $\phi$, we have:

$$[\widehat{\mathscr {A}}\models \phi ]\Rightarrow [\mathscr {A}\models \phi ].$$

Proof

The proof of this proposition follows an induction reasoning on the PCTL structure. First, we take the case of $\psi \,=\,\phi _1\,\mathrm {U}\,\phi _2$.

By definition, for $0\le i\le n$ where $AP_{\psi }\cap AP_{\mathscr {A}_i}=\emptyset$, then: $\mathscr {A}_{i}=\epsilon$. The result is $\widehat{\mathscr {A}}=\mathscr {A}_0\uparrow _{a_0}\mathscr {A}_1 \cdots \mathscr {A}_{k-1}\uparrow _{a_{k-1}}\mathscr {A}_k$ and $k\le n$.

From the PCTL semantics, we have $[(\mathscr {A}_0\uparrow _{a_0}\mathscr {A}_1 \cdots \mathscr {A}_{k-1}\uparrow _{a_{k-1}}\mathscr {A}_k)\models \psi ] \Leftrightarrow \exists m,~\forall j<m:\pi (j)\models \phi _{1}\wedge \pi (m)\models \phi _{2}$ where $\pi (j)$ and $\pi (m)$ are the states i and j respectively in a path $\pi$ of $\mathscr {A}$. And, by calling $\mathscr {A}_{i}$ in $a_{i}$ using BH-1, the only changes in the path $\pi$ are the propositions of $\mathscr {A}_{i}$ till executing BH-2, then: $\exists m'\ge m,~j'\ge j,~\forall j'<m':\pi (j')\models \phi _{1}\wedge \pi (m')\models \phi _{2}$ $\Leftrightarrow ~\mathscr {A}_{0}\uparrow _{a_{1}}\ldots \uparrow _{a_{k}}\mathscr {A}_{k}\ldots \uparrow _{a_{i}}\mathscr {A}_{i}\models \psi$.

By calling a new $\mathscr {A}_{i+1}$ in $a_{i+1}$ up to n, we will have: $\exists m''\ge m',~j''\ge j',~\forall j''<m'':\pi (j'')\models \phi _{1}\wedge \pi (m'')\models \phi _{2}$ $\Leftrightarrow \mathscr {A}_{0}\uparrow _{a_{1}}\ldots \uparrow _{a_{n}}\mathscr {A}_{n}\models \psi \Leftrightarrow \mathscr {A}\models \phi _1\mathrm {U}\phi _2$.

For $\phi _1\mathrm {U}^{\le \,k}\phi _2$ and $\mathrm {X}\phi$ cases, we deduce the following.

• $\forall 0\le i\le n,AP_{\phi }\cap AP_{\mathscr {A}_i}=\emptyset :[\mathscr {A}_{i}=\epsilon \wedge (\mathscr {A}_0\uparrow _{a_0}\mathscr {A}_1 \cdots \mathscr {A}_{n-1}\uparrow _{a_{n-1}}\mathscr {A}_n)\models \phi _1\mathrm {U}^{\le \,k}\phi _2]\Rightarrow [\exists k'\ge k: \mathscr {A}\models \phi _1\mathrm {U}^{\le \,k'}\phi _2]$.

• $\forall 0\le i\le n,AP_{\phi }\cap AP_{\mathscr {A}_i}=\emptyset :[\mathscr {A}_{i}=\epsilon \wedge (\mathscr {A}_0\uparrow _{a_0}\mathscr {A}_1 \cdots \mathscr {A}_{n-1}\uparrow _{a_{n-1}}\mathscr {A}_n)\models \mathrm {X}\phi ]\Rightarrow [\mathscr {A}\models \mathrm {X}\phi ]$.    $\square$

For a parallel verification, we decompose the PCTL property $\phi$ into local ones $\phi _{i:0\le i \le n}$ over $\mathscr {A}_i$ with respect to the call behavior actions $a_{i:0\le i \le n}$ (interfaces), we introduce the decomposition operator “$\natural$” proposed in Definition 5. The operator “$\natural$” is based on substituting the propositions of $\mathscr {A}_{i}$ to the propositions related to its interface $a_{i-1}$ which allows the compositional verification. We denote by $\phi [y/z]$ substituting the atomic proposition “z” in the PCTL property $\phi$ by the atomic proposition “y”.

Definition 5 (PCTL Property Decomposition)

Let $\phi$ be a PCTL property to be verified on $\mathscr {A}_1\uparrow _{a}\mathscr {A}_2$. The decomposition of $\phi$ into $\phi _1$ and $\phi _2$ is denoted by $\phi \equiv \phi _{1}\natural _{a}\phi _{2}$ where $AP_{\mathscr {A}_i}$ are the atomic propositions of $\mathscr {A}_i$, then:

• 1. $\phi _{1}=\phi ([l_a/ AP_{\mathscr {A}_2}])$, where $l_a$ is the atomic proposition related to the action a in $\mathscr {A}_1$.

• 2. $\phi _{2}=\phi ([\top / AP_{\mathscr {A}_1}])$.

The first rule is based on the fact that the only transition to reach a state in $\mathscr {A}_{2}$ from $\mathscr {A}_{1}$ is the transition of the action $l_a$ (BH-1). The second rule ignores the existence of $\mathscr {A}_{1}$ while it kept unchanged till the execution of BH-2. To handle multiplicity for the operator “$\natural$”, we have Property 1.

Property 1

The decomposition operator $\natural$ is associative for $\mathscr {A}_1\uparrow _{a_1}\mathscr {A}_2\uparrow _{a_2}\mathscr {A}_3$, i.e. :

$\phi _{1}\natural _{a_{1}}(\phi _{2}\natural _{a_{2}}\phi _{3})\equiv (\phi _{1}\natural _{a_{1}}\phi _{2})\natural _{a_{2}}\phi _{3}\equiv \phi _{1}\natural _{a_{1}}\phi _{2}\natural _{a_{2}}\phi _{3}$.

For the verification of $\phi$ on $\mathscr {A}_1\uparrow _{a_1}\mathscr {A}_{2}$, Theorem 1 deduces the satisfiability of $\phi$ from the satisfiability of local properties $\phi _1$ and $\phi _2$ obtained by the operator $\natural$.

Theorem 1 (Compositional Verification)

The decomposition of the PCTL property $\phi$ by the decomposition operator $\natural$ for $\mathscr {A}_1\uparrow _{a_1}\mathscr {A}_2$ is sound, i.e. :

$$\begin{aligned} \frac{\mathscr {A}_{1}\models \phi _{1} \quad \mathscr {A}_{2}\models \phi _{2}\quad \phi =\phi _{1}\natural _{a_1}\phi _{2}}{\mathscr {A}_1\uparrow _{a_1}\mathscr {A}_{2}\models \phi } \end{aligned}$$

Proof

The proof of Theorem 1 follows a structural induction on the PCTL structure by using Definition 5. As an example, we take the until operator “U”. Let $\phi =ap_1$ U $ap_2$ where $ap_1\in AP_{\mathscr {A}_1}$ and $ap_2\in AP_{\mathscr {A}_2}$. By applying Definition 5, we have: $\phi _1=ap_1~$U$~a_1$ and $\phi _2=\top ~$U$~ap_2$. Let $\mathscr {A}_{1}\models \phi _{1}\Leftrightarrow \exists m_1,~\forall j_1<m_1:\pi _1(j_1)\models ap_{1}\wedge \pi _1(m_1)\models ap_{1}\wedge a_{1}$ where $\pi$ is a path in the NuAC PA of $\mathscr {A}$. For $\mathscr {A}_{2}\models \phi _{2}\Leftrightarrow \exists m_2,~\forall j_2<m_2:\pi _2(j_2)\models \top \wedge \pi _2(m_2)\models ap_{2}$. To construct $\mathscr {A}_1\uparrow _{a_1}\mathscr {A}_{2}$, BH-1 is the only transition to connect $\pi _1$ and $\pi _2$ which form: $\pi =\pi _1.\pi _2'$ such that $\pi _2'(i)=\pi _2(i)\cup \pi _1(m_1)$. Then: $\exists j\le m,~ m=m_1+m_2:~\pi (j)\models ap_1\wedge \pi (m)\models ap_{2}\Leftrightarrow \mathscr {A}_1\uparrow _{a_1}\mathscr {A}_{2}\models \phi$.   $\square$

Finally, Proposition 2 generalizes Theorem 1 to support the satisfiability of $\phi$ on an activity diagram $\mathscr {A}$ with n call behaviors.

Proposition 2 (CV-Generalization)

Let $\phi$ be a PCTL property to be verified on $\mathscr {A}$, such that: $\mathscr {A}=\mathscr {A}_0\uparrow _{a_0}\cdots \uparrow _{a_{n-1}}\mathscr {A}_n$ and $\phi =\phi _{0}\natural _{a_0}\cdots \natural _{a_{n-1}}\phi _{n}$, then:

Proof

We prove Proposition 2 by induction on n.

• The base step where “$n=1$” is proved by Theorem 1.

• For the inductive step, first, we assume:

  

  Let $\mathscr {A}'=\mathscr {A}_0\uparrow _{a_0}\cdots \uparrow _{a_{n-1}}\mathscr {A}_n$ and $\phi '=\phi _{0}\natural _{a_0}\cdots \natural _{a_{n-1}}\phi _{n}$. While $\natural$ and $\uparrow$ are associative operators, then: $\mathscr {A}=\mathscr {A}'\uparrow _{a_{n}}\mathscr {A}_{n+1}$ and $\phi =\phi '\natural _{a_{n}}\phi _{n+1}$. By assuming $\mathscr {A}_{n}\models \phi _{n}$ and applying Theorem 1, then:

  

5.2 The Encoding to PRISM

To encode a SysML activity diagram $\mathscr {A}$ into its equivalent PRISM code $\mathscr {P}$, we rely to the PRISM MDP formalism that refers to the PA² which coincides with the NuAC semantics. In PRISM, we define the NuAC transition s ${\mathop {\longrightarrow }\limits ^{l}}$ $\mu$ as a probabilistic command. Mainly, the probabilistic command takes the following form: [l] $g \rightarrow p_{1}:u_{1}+...+p_{m}:u_{m}$, which means, for the action “l” if the guard “g” is true, then, an update “$u_{i}$” is enabled with a probability “$p_{i}$”. The guard “g” is a predicate of a conjunction form consisting to the evaluation of the atomic propositions related to the state s. The update $u_i$ describes the evaluation of the atomic propositions related to the next state $s_i$ of s such that s ${\mathop {\longrightarrow }\limits ^{l}}_{p_i}s_i$ ($1\le i\le m$). For the Dirac case, the command is written simply by: [l] $g \rightarrow u$.

The function $\varGamma$ presented in Listing 1.1 produces the appropriate PRISM command for each NuAC term. The action label of a command is the label of its related term “l”. The guard of this command depends on how the term is activated, therefore, a boolean proposition as a flag is assigned to define this activation. For simplicity, the flag related to a term labeled by l is denoted by a boolean proposition l that is initialized to false except for the initial node it is true which conforms to the premise of the NuAC rule “INIT-1”. Concerning the command updates, they deactivate the propositions of a term $n\in \mathscr {A}$ and activate its successors. We define three useful functions: L(n), $S(\mathscr {A}_i)$, and $E(\mathscr {A}_i)$ that return the label of a term n, the initial and the final terms of the diagram $\mathscr {A}_i$, respectively. For example, the call behavior action “$l:\!a\uparrow \mathscr {A}_i$” (line 32) produces two commands (line 34), and it calls the function $\varGamma '$ (line 34). The first command in line 34 synchronizes with the first command in line 52 produced by the function $\varGamma '$ in the action l from the diagram $\mathscr {A}$. Similarly, the second command in line 34 synchronizes with the command of line 56 in the action $L(E(\mathscr {A}_i))$ from the diagram $\mathscr {A}_i$. The first synchronization represents the NuAC rule BH-1 where the second represents the rule BH-2. The function $\varGamma '$ is similar to the function $\varGamma$ except for the initial and the final nodes as shown in lines 52 and 56, respectively. The generated PRISM fragment of each diagram $\mathscr {A}_i$ is bounded by two PRISM primitives: the module head “$Module~\mathscr {A}_i$”, and the module termination “endmodule”.

6 Implementation and Experimental Results

For the purpose of providing experimental results demonstrating the efficiency and the validity of our framework, we verify a set of PCTL properties on the online shopping system [13] and the automated teller machine [13]. To this end, we compare the verification results “$\beta$”, the verification cost in terms of the model size³ “$\gamma$”, and the verification time “$\delta$” (sec) with and without applying our approach.

6.1 Online Shopping System

The online shopping system aims at providing services for purchasing online items. Figure 5a illustrates the corresponding SysML activity diagram. It contains four call-behavior actions⁴, which are: “Browse Catalogue”, “Make Order”, “Process Order”, and “Shipment” denoted by a, b, c and d, respectively. For simplicity, we take this order to denote their called diagrams by $\mathscr {A}_{1}$ to $\mathscr {A}_{4}$, respectively, where $\mathscr {A}_{0}$ denotes the main diagram. As an example, Fig. 5b expands the diagram related to the call behavior action “Process Order” and it is denoted by $\mathscr {A}_{3}$. The whole diagram is written by: $\mathscr {A}=\mathscr {A}_{0}\uparrow _a\mathscr {A}_{1}\uparrow _b\mathscr {A}_{2}\uparrow _c\mathscr {A}_{3}\uparrow _d\mathscr {A}_{4}$. Here, we propose to verify the properties $\varPhi _{1}$ and $\varPhi _{2}$ that are expressed in PCTL.

Fig. 5.

SysML activity diagrams.

Property $\varPhi _{1}$. “For each order, what is the minimum probability value to make a delivery after browsing the catalogue?”

PCTL: $Pmin=?[(Browse~Catalogue)~\Rightarrow ~(F(Delivery))]$.

In this expression, the “Browse Catalogue” proposition is part of $\mathscr {A}_0$ and “Delivery” is a proposition of $\mathscr {A}_3$. For comparison, we verify first $\varPhi _1$ on $\mathscr {A}$. Then, by using Proposition 1, we reduce the verification of $\varPhi _1$ from $\mathscr {A}$ to $\mathscr {A}_{0}\uparrow _c\mathscr {A}_{3}$. And, by using the decomposition rules of Definition 5, $\varPhi _1$ is decomposed into two properties: $\varPhi _{11}$ and $\varPhi _{12}$ such that: $\varPhi _{11}\triangleq$ $Pmin=?[(Browse~Catalogue)~\Rightarrow ~(F(Process~Order))]$, and $\varPhi _{12}\triangleq$ $Pmin=?[(True)~\Rightarrow ~(F(Delivery))]$. After the verification of $\varPhi _{1}$ on $\mathscr {A}$, $\varPhi _{11}$ on $\mathscr {A}_0$ and $\varPhi _{12}$ on $\mathscr {A}_3$, Table 3 summarizes the verification results and costs for different values of the number of orders “n”. From the obtained results, we observe that the probability values are preserved where $\beta _1 = \beta _{11}\times \beta _{12}$. In addition, the size of the diagrams is minimized $\gamma _{11} + \gamma _{12}<\gamma _1$. Consequently, the verification time is reduced significantly $\delta _{11} + \delta _{12} \ll \delta _1$.

Table 3. The verification cost for properties $\varPhi _{1}$ $\varPhi _{11}$, and $\varPhi _{12}$.

Property $\varPhi _2$. “For each order, what is the maximum probability value to confirm a shipment?”

PCTL: $Pmax=?[G((CreateDelivery)\Rightarrow F(ConfirmShipment) ]$.

The propositions of this property “CreateDelivery” and “ConfirmShipment” belong to $\mathscr {A}_2$, and $\mathscr {A}_4$, respectively. Similarly to the verification of $\varPhi _1$, we verify $\varPhi _2$ on $\mathscr {A}$. Then, we decompose $\varPhi _2$ to $\varPhi _{21}$ and $\varPhi _{22}$ with respect to $\mathscr {A}_{0}\uparrow _b\mathscr {A}_{2}\uparrow _d\mathscr {A}_{4}$. The PCTL expressions of the decomposition are: $\varPhi _{21}\triangleq ~Pmax=?[G((CreateDelivery)\Rightarrow F(Shipment) ]$, and $\varPhi _{22}\triangleq ~Pmax=?[G((True)~\Rightarrow F(ConfirmShipment) ]$. Table 4 shows the verification results and costs of $\varPhi _{2}$ on $\mathscr {A}$, $\varPhi _{21}$ on $\mathscr {A}_{0}\uparrow _b\mathscr {A}_{2}$, and $\varPhi _{22}$ on $\mathscr {A}_{4}$ for different values of the number of orders “n”. We found: $\beta _2=\beta _{21}\times \beta _{22}$, $\gamma _{21}+\gamma _{22}<\gamma _2$ and $\delta _{21}+\delta _{22}\ll \delta _2$.

Table 4. The verification cost for properties $\varPhi _{2}$ $\varPhi _{21}$, and $\varPhi _{22}$.

6.2 Automated Teller Machine

The Automated Teller Machine (ATM) is a system that interacts with a potential customer via a specific interface and communicates with the bank over an appropriate communication protocol. Figure 6 represents the ATM SysML activity diagram ($\mathscr {A}'$) composed of the main diagram ($\mathscr {A}'_0$) “Fig. 6-(a)” and three called diagrams: ($a'$) Check Card ($\mathscr {A}'_1$)⁵, ($b'$) Authorize ($\mathscr {A}'_2$), and ($c'$) Transaction ($\mathscr {A}'_3$) that is showed in Fig. 6-(b). Our goal is to measure the satisfiability probability of the PCTL properties $\varPhi _3$ and $\varPhi _4$ on $\mathscr {A}^{'}=\mathscr {A}^{'}_{0}\uparrow _{a'}\mathscr {A}^{'}_{1}\uparrow _{b'}\mathscr {A}^{'}_{2}\uparrow _{c'}\mathscr {A}^{'}_{3}$.

Fig. 6.

ATM SysML activity diagram.

Property $\varPhi _3$. “What is the minimum probability of authorizing a transaction after inserting a card”. PCTL: $Pmin=?[G(InstertCard~\Rightarrow ~F(DebitAccount))]$.

After verifying $\varPhi _3$ on $\mathscr {A}^{'}$, we verify $\varPhi _{31}$ on $\mathscr {A}^{'}_{0}$ and $\varPhi _{32}$ on $\mathscr {A}^{'}_{3}$ such that : $\varPhi _{31}\triangleq$ $Pmin=?[G(InstertCard)~\Rightarrow ~(F(Transaction))]$ and : $\varPhi _{32}\triangleq Pmin=?[G((True)~\Rightarrow ~F(DebitAccount))]$. As a result we found the following: $\beta _3=0.8421$, $\gamma _3=606470$, $\delta _3=3.12$, $\beta _{31}=0.8421$, $\gamma _{31}=3706$, and $\delta _{31}=0.64$, $\beta _{32}=1$, $\gamma _{32}=15$, and $\delta _{32}=0.007$. From the obtained results, we found that the satisfiability probability is maintained $\beta _3=\beta _{31}\times \beta _{32}$, with a considerable verification costs $\gamma _{31}+\gamma _{32}<\gamma _3$ and $\delta _{31}+\delta _{32}\ll \delta _3$.

Property $\varPhi _4$. “What is the maximum probability of inserting a card when it is not valid.” PCTL: $Pmax=?[(CardNotValid)~\Rightarrow ~(F(InsertCard))]$.

Similarly to the verification of $\varPhi _3$, instead of verifying $\varPhi _4$ on $\mathscr {A}^{'}$ we verify $\varPhi _{41}$ on $\mathscr {A}^{'}_{1}$ and $\varPhi _{42}$ on $\mathscr {A}^{'}_{0}$ such that :

$\varPhi _{41}\triangleq$ $Pmax=?[(CardNotValid)~\Rightarrow ~(F(EndCheckCard))]$, and

$\varPhi _{42}\triangleq Pmax=?[(CheckCard)~\Rightarrow ~(F(InsertCard))]$.

After verification, we found the following: $\beta _4=0.05$, $\gamma _4=606470$, $\delta _4=11.458$, $\beta _{41}=1$, $\gamma _{41}=11$, and $\delta _{41}=0.004$, $\beta _{42}=0.05$, $\gamma _{42}=7211$, and $\delta _{42}=1.584$. From these results, we have: $\beta _4=\beta _{41}\times \beta _{42}$, $\gamma _{41}+\gamma _{42}<\gamma _4$ and $\delta _{41}+\delta _{42}\ll \delta _4$.

7 Conclusion

In this paper, we presented a compositional verification framework to improve the efficiency of probabilistic model-checking. More specifically, our target was verifying systems modeled using SysML activity diagrams composed by the call behavior interfaces. We improved their verification cost by introducing a probabilistic compositional verification approach based on decomposing a global PCTL property into local ones with respect to interfaces between diagrams. Moreover, the presented framework can ignore the called diagrams that are irrelevant to a given PCTL property. For verification, we proposed an algorithm to encode the composed diagrams into PRISM input language. Furthermore, we proposed a semantic for SysML activity diagrams that helps on proofs and to encode easily the diagrams in PRISM. We proved the soundness of the proposed framework by showing the satisfiability preservation of PCTL properties. In addition, we demonstrated the effectiveness of our framework by verifying real systems that are not symmetric, which mean, we can not benefit from the symmetry reduction built within the PRISM model checker. In future, we would like to extend our work by investigating several directions. First, we plan to extend our framework to handle more compositional verification techniques like assume-guaranty and integrate them within the PRISM implementation. Then, we explore more system features such as time and object. Finally, we intend to apply our framework on a large systems’ applications.