Keywords

1 Introduction

Dust vortices called dust devils are well-formed vortex formations with characteristic horizontal dimensions from half a meter to one hundred meters and from several meters to hundreds of meters in height in the Earth’s atmosphere. Large eddies are much less common than small ones. Such vortices are clearly visible, as they capture and carry sand and dust from the surface. The main parameters of dust vortices on the Earth, such as dimensions, vertical and horizontal velocities, electric and magnetic fields are measured in experiments on the territory of deserts, where these eddies often arise. Thus, in terrestrial vortices, electric fields of 4.35 kV/m were measured for a vortex with a diameter of 7 m [1], 20 kV/m for a vortex with a diameter of 30 m [2]. The values of electric fields for terrestrial vortices can reach 150 kV/m, without reaching breakdown values. In rarefied atmosphere of Mars breakdown values of electric fields are lower—near 25 kV/m [3] and the question of values of possible electric fields generated in dust events remains relevant. On the other side, no direct measurements of electric fields on the surface of the Red planet have been provided yet.

Dust plays a very sufficient role in a heat balance in the rarefied and arid Martian atmosphere. Dust devils, which are regularly observed on the surface of Mars along with dust storms, raise dust particles to the Martian atmosphere. Martian dust devils are large than terrestrial with horizontal dimensions reaching some kilometers and vertical dimensions up to ten kilometers. Strong electrification in these vortices suggests that in some cases breakdowns may occur [4, 5]. According to [6], upon reaching the breakdown values of the electric field, when \( pd < 200 \) (where \( p \) is the pressure in Torr, \( d \) is the distance between the electrodes in cm), a glow discharge occurs. For values \( pd > 10^{3} \) the discharge occurs according to the streamer-leader mechanism (spark discharge). For the Martian atmosphere pd ~ 105 (with a discharge length of about 1 km), so the second situation takes place.

Here we discuss similarity between the terrestrial and Martian vortices, electrification in the dust devils, dust dynamics and possible results of achieving high values of electric fields in the Martian atmosphere.

2 Similarity of Dust Vortices on the Earth and Mars

In the Earth atmosphere people have many abilities to study dust devils experimentally. Despite the fact that Martian dust devils are being observed and discussed for some tens of years there are no measurements of vertical velocities and inner structure of the vortices. Knowledge of similarity criteria can help in studying Martian vortices. The similarity theory for Martian and terrestrial dust devils has been built in [7], here we show some consequences.

The main role in the formation of dust vortices on Mars and the Earth plays thermal convection. Let us estimate the parameters (characteristic scale and velocity of gas flow) of a vortex on Mars, which is similar to a typical vortex on Earth. Let l and τ be the characteristic length and time scales, ΔT and P are the maximum temperature difference and pressure, ν, χ, and β are kinematic viscosity, thermal conductivity and thermal expansion coefficient of the atmosphere, respectively, g is gravity. Under free thermal convection conditions the Peclet number vl/χ or the Reynolds number vl/ν can be the form of the dimensionless velocity v, and the similarity criterion is the combination of Grashof Gr and Prandtl Pr criteria [8]. The Grashof criterion (number) \( {\text{Gr}} = {{gl^{3} \beta \Delta T} \mathord{\left/ {\vphantom {{gl^{3} \beta \Delta T} {\nu^{2} }}} \right. \kern-0pt} {\nu^{2} }} \) is a measure of the ratio of the Archimedean force caused by the nonuniform distribution of the gas density in a nonuniform temperature field and the viscosity forces. Prandtl criterion Pr = ν/χ characterizes the ratio between the intensities of molecular momentum transfer and heat transfer by thermal conductivity, it is almost independent of temperature for gases, about 0.72 for diatomic gases, and 0.75–1 for polyatomic gases. Since the developed dust vortex can be attributed to the situation when the inertial force has a large relative value compared to the viscosity effects, we take the dimensionless velocity in the form \( {\tilde{\mathbf{v}}} = {\mathbf{v}}{l \mathord{\left/ {\vphantom {l \chi }} \right. \kern-0pt} \chi } \), and as the similarity criterion we use the value Gr·Pr2, rather than Gr and Pr separately. In our case dimensionless velocity looks like:

$$ {\mathbf{v}} = \frac{\chi }{l}f\left( {\frac{{\mathbf{x}}}{l},\,{\text{Gr}} \cdot \Pr^{2} } \right). $$

We use the following parameter ratios (subscripts E and M denote the Earth and Mars respectively):

$$ \frac{{g_{E} }}{{g_{M} }} = 2.65,\,\,\,\,\frac{{\beta_{E} }}{{\beta_{M} }} \approx 1,\,\,\,\frac{{T_{M}^{3} }}{{T_{E}^{3} }} \approx \left( {\frac{200}{300}} \right)^{3} \approx 0.3,\,\,\,\frac{{P_{E}^{2} }}{{P_{M}^{2} }} \approx 10^{4} .\,\, $$

Let us take ΔTE/ΔTM ≈ 1, taking into account that the maximum temperature change in Martian vortices is about 5–6 °C [9], as well as in terrestrial vortices.

Assuming for similar vortices that \( \left( {{\text{Gr}} \cdot \Pr^{2} } \right)_{E} = \left( {{\text{Gr}} \cdot \Pr^{2} } \right)_{M} , \) we obtain the ratio between the characteristic scales \( l_{M} \approx 17l_{E} \). Further, from the equality of dimensionless velocities for the Earth and Mars we obtain the ratio of the characteristic speeds \( v_{M} \approx 2.6v_{E} \). The values obtained do not contradict the available data. Thus, the vertical speeds in the earth vortices have values of the order of 10 m/s, and the speeds in the Martian vortices according to estimates made on the basis of measurements of the landing gears Viking 1 and Viking 2 [10] are several times larger.

3 Charging of Dust Particles and Electric Fields in Dust Devils

Collisions and friction between dust particles in a vortex lead to charging of dust particles due to triboelectric effect. As a result small particles acquire negative charges and large particles become positively charged [3, 11]. This leads to spatial charge separation in an upward flux and electric field generation.

We study the following simplified model of the vortex. Let the upper half of the vortex be negatively charged, and the lower positive, with the absolute value of the charge \( \left| {Q^{ + } } \right| = \left| {Q^{ - } } \right| = Q \) growing in time. The absolute value of the average charge density is \( \rho_{q} = {Q \mathord{\left/ {\vphantom {Q {V_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}} \right. \kern-0pt} {V_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }} \), with \( V_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \) being the volume of the half of the vortex. The value of the rate of change of the average density \( {{\partial \rho_{q} } \mathord{\left/ {\vphantom {{\partial \rho_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}} \) may vary depending on the efficiency of tribocharging and the rate of charge separation. Assuming electroneutrality of the vortex, i.e. \( n_{L} \Delta q_{L} = n_{S} \Delta q_{S} \), where \( n_{L} \), \( n_{S} \), \( \Delta q_{L} ,\,\,\Delta q_{S} \) are densities and average charges of large and small particles, respectively, we estimate \( {{\partial \rho_{q} } \mathord{\left/ {\vphantom {{\partial \rho_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}} \) as follows:

$$ \frac{{\partial \rho_{q} }}{\partial t} = \frac{{2n_{L} \Delta q_{L} \Delta u}}{h} , $$

where \( \Delta u \) is the difference of the vertical component of the velocities of large and small particles and \( h \) is the height of the vortex column. For \( \Delta u = 1\,\, {\text{m}}/{\text{s}} \) [12], \( n_{L} = 5 \cdot 10^{6} \,\,{\text{m}}^{ - 3} \) [3], \( \Delta q_{L} = 5 \cdot 10^{ - 14} \,\,{\text{C}} \) (for particle of the radius of 50 μm) [3, 12], \( h = 10^{4} \,\,{\text{m}} \) we get \( {{\partial \rho_{q} } \mathord{\left/ {\vphantom {{\partial \rho_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}} = 5 \cdot 10^{ - 11} \,\,{\text{C}}\,\,{\text{m}}^{ - 3} \,\,{\text{s}}^{ - 1} \). Note that the obtained estimate for the value \( {{\partial \rho_{q} } \mathord{\left/ {\vphantom {{\partial \rho_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}} \) can vary significantly up or down.

Spatial charge separation in an upward flow leads to the appearance of an electric field. For building a model of electric field \( {\mathbf{E}} \) distribution taking into account atmospheric conductivity \( \sigma \) we solve Poisson’s equation for potential \( \varphi \) and the charge continuity equation for dust particles density \( \rho_{q} \):

$$ \Delta \varphi = - \frac{{\rho_{q} }}{{\varepsilon_{0} }} $$
$$ \frac{{\partial \rho_{q} }}{\partial t} + \left( {\nabla \sigma } \right) \cdot {\mathbf{E}} + \frac{{\sigma \rho_{q} }}{{\varepsilon_{0} }} = 0 $$

Here \( \varepsilon_{0} = 8.85 \cdot 10^{ - 12} \,\,{{\text{F}} \mathord{\left/ {\vphantom {{\text{F}} {\text{m}}}} \right. \kern-0pt} {\text{m}}} \). The vortex is represented in the form of a cylinder, within which the spatial separation of the charge occurs, at the initial moment of time the charge is zero. Accounting for the conductivity of the atmosphere limits the maximum charge and electric field. The charge in the vortex is given by two cylinders, in which the charge density value decreases from the center of the cylinder along a Gaussian curve with a smooth transition according to a linear law from a positive charge to a negative vertical. At each time step \( \Delta t \) the average charge density \( \bar{\rho }_{q} \) increases at the bottom of the vortex and decreases at the top by an amount \( \left( {{{\partial \bar{\rho }_{q} } \mathord{\left/ {\vphantom {{\partial \bar{\rho }_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}}} \right)\Delta t \). Then the electric field and charge relaxation are calculated.

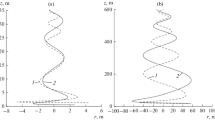
Figure 1a presents the results of the calculation of the electric field values for an intense Martian vortex with an average charge separation rate \( {{\partial \bar{\rho }_{q} } \mathord{\left/ {\vphantom {{\partial \bar{\rho }_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}} = 5.5 \cdot 10^{ - 11} \,\,{\text{C}}/({\text{m}}^{3} \,\,{\text{s}}) \), a core radius of 1.5 km and a height of 10 km in the saturation state, i.e., 10 s after the start of the charge separation process. Atmospheric conductivity is accepted \( \sigma = 5 \cdot 1 0^{ - 1 2} \,\,{\text{S/m }} \). It should be noted that the conductivity is inversely proportional to the maximum field.

Fig. 1
figure 1

a Electric field in the Martian dust devil with core radius of 1.5 km and a height of 10 km in the saturation state (average charge separation rate \( {{\partial \bar{\rho }_{q} } \mathord{\left/ {\vphantom {{\partial \bar{\rho }_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}} = 5.5 \cdot 10^{ - 11} \,\,{\text{C}}\,\,{\text{m}}^{ - 3} \,\,{\text{s}}^{ - 1} \)). b Evolution of the maximum value of the electric field in the process of charge separation. (1) \( {{\partial \bar{\rho }_{q} } \mathord{\left/ {\vphantom {{\partial \bar{\rho }_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}} = 7.4 \cdot 10^{ - 11} \,\,{\text{C}}\,\,{\text{m}}^{ - 3} \,\,{\text{s}}^{ - 1} \), (2) \( {{\partial \bar{\rho }_{q} } \mathord{\left/ {\vphantom {{\partial \bar{\rho }_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}} = 5.5 \cdot 10^{ - 11} \,\,{\text{C}}\,\,{\text{m}}^{ - 3} \,\,{\text{s}}^{ - 1} \)

Full size image

Figure 1b shows the evolution of the maximum value of the electric field in the process of charge separation. The maximum charge accumulated in the half of the vortex, corresponding to \( {{\partial \bar{\rho }_{q} } \mathord{\left/ {\vphantom {{\partial \bar{\rho }_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}} = 7.4 \cdot 10^{ - 11} \,\,{\text{C}}/({\text{m}}^{3} \,\,{\text{s}}) \), is equal to 5.37 C, and corresponding to \( {{\partial \bar{\rho }_{q} } \mathord{\left/ {\vphantom {{\partial \bar{\rho }_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}} = 5.5 \cdot 10^{ - 11} \,\,{\text{C}}/({\text{m}}^{3} \,\,{\text{s}}) \), is equal to 4.02 C. It can be seen that for large values of \( {{\partial \bar{\rho }_{q} } \mathord{\left/ {\vphantom {{\partial \bar{\rho }_{q} } {\partial t}}} \right. \kern-0pt} {\partial t}} \) breakdown values of the electric field (about 25 kV/m) can be achieved, and at lower rates of charge separation, the maximum field is set below breakdown values. In the case when the field in the vortex reaches breakdown values, one can speak about the possibility of lightning discharges in Martian dust devils.

To study dust dynamics in dust devils we use model [13, 14], where dust particle is moving under the action of the gravity force, the electrostatic force and the hydrodynamic force acting from the vortex structure. Particles are efficiently uplifted by both the terrestrial and Martian vortices. The trajectory for particle of 1 μm carrying the charge of \( - 1.6 \cdot 10^{ - 17} \,\,{\text{C}} \) in the typical terrestrial dust devil with the radius of 10 m is shown in the Fig. 2. It should be mentioned that for the conditions in the Earth’s atmosphere the process of charge stabilization takes about 10 min with maximum values of electric field being equal to about 100 kV/m.

Fig. 2
figure 2

Trajectories of the 1 μm particle carrying charge of \( - 1.6 \cdot 10^{ - 17} \,\,{\text{C}} \) in terrestrial dust devil (radius 10 m). (1) Without electric field, (2) with electric field generated by the vortex

Full size image

4 Results and Discussion

We have shown hydrodynamic similarity for terrestrial and Martian dust devils and found characteristic scales and velocities of gas flow in the Martian vortices similar to terrestrial ones. We have studied electrification in dust devils and calculated electric field pattern for different conditions. The electric field modelled has been used for dust dynamics calculations. At high rate of charge separation in big Martian vortices breakdown values of electric fields can be reached. This can result in lightning activity. Lightning can excite oscillation in Schumann cavity on Mars. There is no experimental evidence on lightning on Mars nowadays [15]. Nevertheless in 2009 [16] with the help of radiotelescope during the Martian dust storm the emission spectrum peaks in the vicinity of the predicted values of the first three modes of Schumann oscillations on Mars were observed. Aspects of the influence of dust particles in the Earth’s atmosphere on Schumann oscillations were discussed in [17]. Here we can estimate the number of suitable dust devils that must simultaneously be on the surface of Mars for the amplitude of Schumann resonances on Mars to be comparable with that on the Earth.

Let’s estimate the energy released during the discharge of lightning as

$$ W = \frac{1}{{8\pi \varepsilon_{0} }}\frac{{Q^{2} }}{l}, $$

where \( Q \) is the charge carrying by the discharge, \( l \) is the length of the discharge. For average terrestrial lightning \( W_{E} \approx 2 \cdot 10^{9} \,\,{\text{J}} \) [18]. According to the calculations given in the previous paragraph for a dust vortex on Mars \( Q \approx 5\,\,{\text{C}} \), \( l \approx 5\,\,{\text{km}} \), an estimate of the energy of a possible single discharge gives \( W_{M} \approx {{W_{E} } \mathord{\left/ {\vphantom {{W_{E} } {20}}} \right. \kern-0pt} {20}} \). According to [18], only 0.01–0.1% of the total discharge energy goes directly to the pumping of the resonator. Possible discharge frequency can be estimated on the speed of reaching the electric field breakdown values due to charge separation. Let us estimate the required number of dust vortices, in which the electric field reaches breakdown values, so that the amplitude of Schumann resonances on Mars is comparable to that on the Earth. We take into account that the square of the amplitude of the electric field in the resonator is proportional to the radiated energy and we set \( \left( {{{\nu_{M} W_{M}^{(1)} } \mathord{\left/ {\vphantom {{\nu_{M} W_{M}^{(1)} } {\nu_{E} W_{E}^{(1)} }}} \right. \kern-0pt} {\nu_{E} W_{E}^{(1)} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {{{V_{E} } \mathord{\left/ {\vphantom {{V_{E} } {V_{M} }}} \right. \kern-0pt} {V_{M} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} = 1 \), where \( \nu_{M} \)(\( \nu_{E} \)), \( W_{M}^{(1)} \), (\( W_{M}^{(1)} \)) are the frequency of discharges and the energy of single discharges on Mars (on the Earth), \( V_{E} \)(\( V_{M} \)) is the volume of the Earth (Martian) resonator. Thus \( \nu_{M} \approx 5.7\,\nu_{E} \), from where we get the estimate for the number of dust vortices \( N \approx 5.7\,\,\nu_{E} \Delta t_{M} \). For the characteristic frequency of discharges on Earth \( \nu_{E} = 100\,\,{\text{s}}^{ - 1} \) [18], and the time of charge separation in the Martian vortex \( \Delta t_{M} \approx 10\,\,{\text{s}} \), the number of suitable dust vortices that must simultaneously be on the surface of Mars is \( N \approx 5.7\,\, \cdot 10^{3} \).