Keywords

1 Model Verification

The scale of computational systems nowadays varies from simple toggle-buttons to various embedded systems and network routers up to complex multi-purpose computers. In safety critical applications, we need to provide guarantees about system behaviour in all situations/configurations that the system can encounter. Such guarantees are classically provided by first creating a formal model of the system (at an appropriate abstraction level) and then using formal methods such as model checking and equivalence checking to rigorously argue about the behaviour of the models. At the highest abstraction level, systems are usually modelled as labelled transition systems or Kripke structures (see [5] for an introduction). In labelled transition systems (LTS), a process changes its (unobservable) internal states by performing visible actions. Kripke structures on the other hand allow to observe the validity of a number of atomic predicates revealing some (partial) information about the current state of a given process, whereas the state changes are not labelled by any visible actions.

Fig. 1.
figure 1

Traffic light LTS variants

Full size image

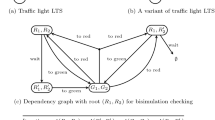
An example of LTS modelling a simple traffic light is given in Fig. 1a. Although the states have been named for convenience, they are considered opaque. Instead, this formalism uses the action-based perspective where the actions of the transitions are considered visible. For example from \(R_1\) there is a transition to \(R'_1\) labelled with a ‘wait’ action that allows to extend the duration of the red color, after which only the action ‘to green’ is available. A slight variant of the LTS is given in Fig. 1b where from \(G_2\) it is possible to enter directly the state \(R'_2\) by performing the ‘to red’ action. We can now ask the (equivalence checking) question whether the two systems are equivalent up to some given notion of equivalence (see e.g. [22]), e.g. bisimilarity [36], which is not the case in our example.

The simple traffic light can also be modelled as a Kripke structure that is depicted in Fig. 2a. Here the transitions are not labelled by any actions while the states are labelled with the propositions ‘red’ and ‘green’ that indicate the status of the light in that state. We note that the states R and \(R'\) are indistinguishable as they are labelled by the same proposition ‘red’. We can now ask the (model checking) question whether the initial state R satisfies the property that on any execution the proposition ‘green’ will eventually hold and until this happens the light is in ‘red’. This can be e.g. expressed by the CTL property ‘\(A \ \text {red}\ U\ \text {green}\)’ and it indeed holds for R in the depicted Kripke structure.

Fig. 2.
figure 2

Kripke structure of traffic light

Full size image

1.1 On-the-Fly Verification

The challenge is how to decide the equivalence and model checking problems even for systems described in high level formalism such as automata networks or Petri nets. These formalisms allow for a compact representation of the system behaviour, meaning that even though their configurations and transitions can still be given as a labelled transition system or a Kripke structure, the size of these can be exponential in the size of the input formalism. This phenomena is known as the state-space explosion problem and it makes (in many cases) the full enumeration of the state-space infeasible for practical applications. In order to deal with state-space explosion, on-the-fly verification algorithms are preferable as they construct the reachable state-space step by step and hence avoid the (expensive) a priory enumeration of all system configurations. In case a conclusive answer about the system behaviour can be drawn by exploring only a part of the state-space, this may grant a considerable speed up in the verification time.

The idea of local or on-the-fly model checking was discovered simultaneously and independently by various people in the end of the 80s all engaged in making model checking and equivalence checking tools for various process algebras, e.g. the Concurrency Workbench CWB [15]. Due to its high expressive power—as demonstrated in [16, 37]—particular focus was on truly local model-checking algorithms for the modal mu-calculus [28]. Several discussions and exchanges of ideas between Henrik Reif Andersen, Kim G. Larsen, Colin Stirling and Glynn Winskel lead to the first local model-checking methods [3, 10, 29, 30, 38, 40]. Besides the CWB these were implemented in the model checking tools TAV [9, 23] for CCS and EPSILON [12] for timed CCS.

Simultaneously, in France a tool named VESAR was developed that combined the model checking idea (from the Sifakis team in Grenoble) and the simulation world (from Roland Groz at CNET Lannion and Claude Jard in Rennes, who were checking properties on-the-fly using observers). The VESAR tool was developed by a French company named Verilog and its technology was later reused for another tool named Object-Geode from the same company, which was heavily sold in the telecom sector [1].

As an alternative to encoding into the modal mu-calculus, it was realized that an even simpler formalism—Boolean equation systems (BES)—would provide a universal framework for recasting all model checking and equivalence checking problems. Whereas [31] introduces BES and first local algorithms, the work in [2] provides the first optimal (linear-time) local algorithm. Later extensions and adaptions of BES were implemented in the tools CADP [35] and muCRL [24].

1.2 Dependency Graphs Related Work

In this paper we survey the (extensions) of dependency graphs [33] (DG) introduced in 1998 Liu and Smolka. Similar to Boolean equation systems, DG serve as a universal tool for the representation of various model checking and equivalence checking problems, providing us with a universal method for on-the-fly exploration of DG. The elegant local (on-the-fly) algorithm presented in [33] runs in linear time with respect to the size of the DG and allows for an early termination in case the chosen search strategy manages to reveal a conclusive answer without necessarily exploring the whole graph.

Recently, the ideas of DG have been extended to various domains such as timed [11], weighted [25, 26] and probabilistic [34] systems. We shall account for some of the most notable extensions and further improvements to the local algorithm from [33] such as its parallelization. We shall start by defining the notion of dependency graphs as introduced by Liu and Smolka [33].

2 Dependency Graphs

Dependency graphs are a variant of directed graphs where each edge, also called a hyperedge, may have multiple target nodes [33]. The intuition is that a property of a given node in a dependency graph depends simultaneously on all the properties of the target nodes for a given hyperedge, while different outgoing hyperedges provide alternatives for deriving the desirable properties. Formally, a dependency graph (DG) is a pair \(G = (V, E)\) where V is a set of nodes and \(E \subseteq V \times 2^V\) is the set of hyperedges.

Figure 3a graphically depicts a dependency graph. For example the root node \(v_1\) has two hyperedges: the first hyperedge has the target node \(v_2\) and the second hyperedge has two targets \(v_3\) and \(v_4\). The node \(v_2\) has no outgoing hyperedges, while the node \(v_3\) has a single outgoing hyperedge with no targets (shown by the empty set).

Fig. 3.
figure 3

Example of dependency graph

Full size image

As shown in Fig. 3b it is possible to interpret the dependencies among the nodes in dependency graph as a system of Boolean equations, using the general formula

$$\begin{aligned} v = \bigvee _{(v, T) \in E} \bigwedge _{u \in T} u \ \end{aligned}$$

where by definition the conjunction of zero terms is true, and the disjunction of zero terms is false. We denote false by \( ff \) (or 0), and true by \( tt \) (or 1).

We can now ask the question whether there is an assignment of Boolean values to all nodes in the graph such that all constructed Boolean equations simultaneously hold. Formally, an assignment is a function \(A : V \rightarrow \{0, 1\}\) and an assignment A is a solution if it satisfies the equality:

$$A(v) = \bigvee _{(v, T) \in E} \bigwedge _{u \in T} A(u).$$

In our case, there are three solutions as listed in Fig. 3c. The existence of several such possible assignments that solve the equations is caused by cyclic dependencies in the graph as e.g. \(v_5\) depends on \(v_6\) and at the same time \(v_6\) also depends of \(v_5\).

However, if we let the set of all possible assignments be \(\mathcal {A}\) and define \(A_1 \le A_2\) if and only if \(A_1(v) \le A_2(v)\) for all \(v \in V\) where \(A_1, A_2 \in \mathcal {A}\), then we can observe that \((\mathcal {A}, \le )\) is a complete lattice [4, 19] which guarantees the existence of the minimum and maximum assignment in the lattice.

There is a standard procedure how to compute such a minimum/maximum solution. For example for the minimum solution we can define a function \(F : \mathcal {A} \rightarrow \mathcal {A}\) that transforms an assignment as follows:

$$F(A)(v) = \bigvee _{(v, T) \in E} \bigwedge _{u \in T} A(u).$$

Clearly, the function F is monotonic and an assignment A is a solution to a given dependency graph if and only if A is a fixed point of A, i.e. \(F(A)=A\). From the Knaster-Tarski fixed-point theorem [39] we get that the monotonic function F on the complete lattice \((\mathcal {A}, \le )\) has a unique minimum fixed point (solution).

By repeatedly applying F to the initial assignment \(A^0\) where \(A^0(v)=0\) for all nodes v, we can iteratively find a minimum fixed point as formulated in the following theorem.

Theorem 1

Let \(A_ min \) denote the unique minimum fixed point of F. If there is an integer i such that \(F^i(A^0) = F^{i+1}(A^0)\) then \(F^i(A^0)=A_ min \).

Clearly \(F^i(A^0)\) is a fixed point as \(F(F^i(A^0))=F^i(A^0)\) by the assumption of the theorem. We notice that \(A^0 \le A_ min \) and because F is monotonic and \(A_ min \) is a fixed point, we also know that \(F^j(A^0) \le F^j(A_ min ) = A_ min \) for an arbitrary j. Then in particular \(F^i(A^0) \le A_ min \) and because \(A_ min \) is the minimum fixed point and \(F^i(A^0)\) is a fixed point, necessarily \(F^i(A^0)=A_ min \).

figure a

For any finite dependency graph, the iterative computation of \(A_ min \) as summarized in Algorithm 1, also referred to as the global algorithm, is guaranteed to terminate after finitely many iterations and return the minimum fixed-point assignment. Dually, the iterative algorithm can be used to compute maximum fixed points on finite dependency graphs.

3 Encoding of Problems into Dependency Graphs

We shall now demonstrate how equivalence and model checking problems can be encoded into the question of finding a minimum fixed-point assignment on dependency graphs. Typically, the nodes in the dependency graph encode the configurations of the problem in question and the hyperedges create logical connections between the subproblems. We provide two examples showing how to encode strong bisimulation checking and CTL model checking into dependency graphs.

3.1 Encoding of Strong Bisimulation

Recall that two states s and t in a given LTS are strongly bisimilar [36], written \(s \sim t\), if there is a binary relation R over the states such that \((s,t) \in R\) and

  • whenever \(s \xrightarrow {\alpha } s'\) then there is \(t \xrightarrow {\alpha } t'\) such that \((s', t') \in R\), and

  • whenever \(t \xrightarrow {\alpha } t'\) then there is \(s \xrightarrow {\alpha } s'\) such that \((s', t') \in R\).

We encode the question whether \(s_0 \sim t_0\) for given two states \(s_0\) and \(t_0\) into a dependency graph where the nodes (configurations) are pairs of states of the form (s, t) and the hyperedges represent all possible ‘attacks’ on the claim that s and t are bisimilar. For example, if one of the two states can perform an action that is not enabled in the other state, we will introduce a hyperedge with the empty set of target nodes, meaning that the minimum fixed-point assignment of the node (s, t) will get the value 1 standing for the fact that \(s \not \sim t\). In general the aim is to construct the DG in such a way that for any node (s, t) we have \(A_ min ((s, t)) = 0\) if and only if \(s \sim t\). The construction, as mentioned e.g. in [19], is given in Fig. 4. The rule says that if s can take an \(\alpha \)-action to \(s'\), then the configuration (s, t) should have a hyperedge containing all target configurations \((s', t')\) where \(t'\) are all possible \(\alpha \)-successors of t. Symmetrically for the outgoing transitions for t that should be matched by transitions from s.

Fig. 4.
figure 4

Encoding rule for strong bisimulation checking

Full size image

Let us consider again the transition systems from Fig. 1. The dependency graph to decide whether \(R_1\) is bisimilar with \(R_2\) is given in Fig. 1c where we can note that the configuration \((R_1, R'_2)\) has a hyperedge with no target nodes. This is because \(R_1\) can perform the ‘wait’ action that \(R'_2\) can not match. If we now compute \(A_ min \), for example using the global algorithm in Fig. 1d, we notice that \(A_ min ((R_1, R'_2)) = 1\) which means that \(R_1\) and \(R'_2\) are not bisimilar.

3.2 Encoding of CTL Model Checking

We shall now provide an example of encoding a model checking problem into dependency graphs. In particular, we demonstrate the encoding for CTL logic as described e.g. in [18]. We want to check whether a state s of a given LTS satisfies the CTL formula \(\varphi \). We let the nodes of the dependency graph be of the form \((s,\varphi )\) and these nodes will be decomposed into a number of subgoals depending of the structure of the formula \(\varphi \). The encoding will ensure that \(A_ min ((s, \varphi )) = 1\) if and only if \(s \models \varphi \) for any node \((s, \varphi )\) in the dependency graph [17]. Figure 5 shows the rules for constructing such a dependency graph.

Fig. 5.
figure 5

Encoding to determine whether \(s \models \varphi \) where \(\{s_1, \dots , s_n\} = \{s' \mid s \rightarrow s'\}\)

Full size image

Returning to our example from Fig. 2, we see in Fig. 2b the constructed dependency graph for the model checking question \(R \models A \; \text {red} \; U \; \text {green}\). The fixed-point computation using the global algorithm is given in Fig. 2c and because \(A_ min (v_1)=1\), we can conclude that the state R indeed satisfies the CTL formula \(A \; \text {red} \; U \; \text {green}\). For simplicity, the encoding as shown in Fig. 5 does not include negation, but the construction can be extended to support negation [17].

4 Local Algorithm for Dependency Graphs

The encodings of verification problems into dependency graphs, as discussed in the previous section, construct a graph with a root node \(v_0\) such that from the value of the minimum fixed-point assignment of the node \(v_0\), we can deduce the answer to the verification problem in question.

In Algorithm 1 we have already seen a method for computing iteratively the minimum fixed point \(A_ min \) for all nodes in the dependency graph. However, due to the state-space explosion problem, such a graph can be exponentially large (or even infinite) and hence it is infeasible to explore it completely. As we are often only interested in \(A_ min (v_0)\) for a given node \(v_0\), we do not necessarily have to explore the whole dependency graph. This is shown in Fig. 7a, where we can see that \(A_ min (v_1)=1\) due to the outgoing hyperedge from \(v_1\) with empty set of targets, and this value can propagate directly to the node \(v_0\) and we can also conclude that \(A_ min (v_0)=1\); all this without the need to explore the (possibly large or even infinite) subtree with the root \(v_2\). This idea is formalized in Liu and Smolka’s local algorithm [33] that computes the value of \(A_ min (v_0)\) for a given node \(v_0\) in an on-the-fly manner.

Algorithm 2 shows the pseudocode of the local algorithm. The algorithm maintains the waiting set W of hyperedges to be explored (initially all outgoing hyperedges from the root node \(v_0\)) as well as the list of dependencies D for every node v, such that D(v) contains the list of all hyperedges that should be reentered into the waiting list in case the value of the node v changes from 0 to 1. Due to a small technical omission, the original algorithm of Liu and Smolka did not guarantee termination even for finite dependency graph. This is fixed in Algorithm 2 by inserting the if-test at line 10 that makes sure that we do not reinsert the dependencies D(v) of a node v in case that the value of v is already known to be 1.

figure b
Fig. 6.
figure 6

Demonstration of local algorithm for minimum fixed-point computation

Full size image

In Fig. 6b we see the computation of the local algorithm on the dependency graph from Fig. 6a. Under the assumption that the algorithm makes optimal choices when picking among hyperedges from the waiting list (third column in the table), we can see that only a subset of nodes is ever visited and the value of \(A_ min (v_1)\) can be determined by exploring only the middle subtree of \(v_1\) because once in the 6th iteration the value \(A(v_1)\) is improved from 0 to 1, we terminate early and announce the answer.

4.1 Optimizations of the Local Algorithm

The local algorithm begins with all nodes being assigned ? such that whenever a new node is discovered during the forward search, it gets the value 0 and this value may be possibly increased to 1. Hence the assignment values grow as shown in Fig. 7b. As soon as the root receives the value 1, the local algorithm can terminate. If the root never receives the value 1, we need to explore the whole graph and wait until the waiting set is empty before we can terminate and return the value 0. Hence during the computation, the value 0 of a node is ‘uncertain’ as it can be possibly increased to 1 in the future.

Fig. 7.
figure 7

Certain-zero optimization

Full size image

Consider the dependency graph in Fig. 7c. In order to compute \(A_ min ({v_0)}\), the local algorithm computes first the minimum fixed-point assignment both for \(v_1\) and \(v_2\) before it can terminate with the answer that the final value for the root is 0. However, we can actually conclude that \(A_ min ({v_1)} = 0\) as the final value of the node \(v_1\) is clearly 0 and hence \(v_0\) can never be upgraded to 1, irrelevant of the value of \(A_ min ({v_2)}\).

This fact was noticed in [18] where the authors suggest to extend the possible values of nodes with the notation of certain-zero (see Fig. 7d for the value ordering), i.e. once the assignment of a node becomes 0, its value can never be improved anymore to 1. The certain zero value can be back-propagated and once the root receives the certain-zero value, the algorithm can terminate early and hence speed up the computation of the fixed-point value for the root. The efficiency of the certain-zero optimization was demonstrated for example on the implementation of dependency graphs for CTL model checking of Petri nets [18] and for other verification problems in the more general setting of abstract dependency graphs [21].

4.2 Distributed Implementation of the Local Algorithm

State-space explosion problem means that the size of dependency graphs may become too large to fit into the memory of a single machine and/or the verification time may become infeasible. In [19] the authors describe a distributed fixed-point algorithm for dependency graphs that distributes the workload over several machines. The algorithm is based on message passing where the nodes of the dependency graphs are partitioned among the workers and each worker is responsible for computing the fixed-point values for the nodes it owns, sometimes requiring messages to be sent once the target nodes of an hyperedge are not own by the same worker as the root of the hyperedge. The experiments confirm an average speed up of around 25 times for 64 workers (CPUs) and 6 times for 8 workers. This is a satisfactory performance as the problem is P-complete (recall that we showed in Sect. 3 a polynomial time reduction from the P-complete problem of strong bisimulation checking [6] into fixed-point computation on dependency graphs), and hence inherently believed hard to parallelize. Moreover, the distributed algorithm can be used ‘out-of-the-box’ for a number for model verification problems (all those that can be encoded into dependency graphs), instead of designing single purpose distributed algorithms for each individual problem.

Fig. 8.
figure 8

Model verification without and with abstract dependency graphs

Full size image

5 Abstract Dependency Graphs

Dependency graphs have recently been extended in several directions in order to reason about more complex problems. Extended dependency graphs, introduced in [18], add a new type of edge to dependency graphs to handle negation. Another extension with weights, called symbolic dependency graphs [26], extends the value annotation of nodes from the 0–1 domain into the set of natural numbers together with a new type of so-called cover-edges. Recently an extension presented in [14] considers as the value-assignment domain the set of piece-wise constant functions in order to be able to encode weighted PCTL model checking. Because the constructed dependency graphs in these extensions are different, for each problem that we consider we need to implement a single-purpose algorithm to compute the fixed points on such extended dependency graphs, as depicted in Fig. 8a.

In [21] abstract dependency graphs (ADG) are suggested that permit a more general, user-defined domain for the node assignments together with user-defined functions for evaluating the fixed-point assignments. As a result, a number of verification problems can be now encoded as ADG and a single (optimized) algorithm can be used for computing the minimum fixed point as depicted in Fig. 8b.

In ADG the values of node assignments have to form a Noetherian Ordering Relation with least element (NOR), which is a triple \(\mathcal {D}= (D, \sqsubseteq , \bot )\) where \((D, \sqsubseteq )\) is a partial order, \(\bot \in D\) is its least element, and \(\sqsubseteq \) satisfies the ascending chain condition: for any infinite chain \({d_1 \sqsubseteq d_2 \sqsubseteq d_3 \sqsubseteq \dots }\) there is an integer k such that \(d_k = d_{k+j}\) for all \(j > 0\). For algorithmic purposes, we assume that such a domain together with the ordering relation is effective (computable).

Instead of hyperedges, each node in an ADG has an ordered sequence of target nodes together with a monotonic function \(f: D^n \rightarrow D\) of the same arity as the number of its target nodes. The function is used to evaluate the values of the node during an iterative, local fixed-point computation.

An assignment \(A : V \rightarrow D\) is now a function that to each node assigns a value from the domain D and we define a function F as

$$F(A)(v) = \mathcal {E}(v)(A(v_1), A(v_2), \dots , A(v_n))$$

where \(\mathcal {E}(v)\) stands for the monotonic function assigned to node v and \(v_1, v_2, \dots v_n\) are all (ordered) target nodes of v.

The presence of the least element \(\bot \in D\) means that the assignment \(A_\bot \) where \(A_\bot (v) = \bot \) for all \(v \in V\) is the least of all assignments (when ordered component-wise). Moreover, the requirement that \((D, \sqsubseteq , \bot )\) satisfies the ascending chain condition ensures that assignments cannot increase indefinitely and guarantees that we eventually reach the minimum fixed-point assignment as formulated in the next theorem.

Theorem 2

There exists a number i such that \(F^{i} (A_\bot ) = F^{i+1} (A_\bot ) = A_ min \).

Fig. 9.
figure 9

Abstract dependency graphs

Full size image

An example of ADG over the NOR \(\mathcal {D}= (\{0, 1\}, \{(0,1)\}, 0)\) that represents the classical Liu and Smolka dependency graph framework is shown in Fig. 9a. Here 0 (interpreted as false) is below the value 1 (interpreted as true) and the monotonic functions for nodes are displayed as node annotations. In Fig. 9b we demonstrate the fixed-point iterations computing the minimum fixed-point assignment.

A more interesting instance of ADG with an infinite value domain is given in Fig. 9c. The ADG encodes an example of a symbolic dependency graph (SDG) from [26] (with the added node E). The nodes are assigned nonnegative integer values (note that we use the ordering relation in the reverse order here) with the initial value being \(\infty \) and the ‘best’ value (the one that cannot be improved anymore) being 0. The fixed-point computation is shown in Fig. 9d.

The authors in [21] devise an efficient local (on-the-fly) algorithm for ADGs and provide a publicly available implementation in a form of C++ library. The experimental results confirm that the general algorithm on ADGs is competitive with the single-purpose optimized algorithms for the particular instances of the framework.

6 Applications of Dependency Graphs

We shall finish our survey paper with an overview of selected applications of dependency graphs for various verification problems.

Timed Games: In [11] the zone-based on-the-fly reachability algorithm for timed automata implemented in UPPAAL [32] was extended with the synthesis of reachability strategies for timed games. In this application the nodes of the ADG are reachable symbolic states of the form \((\ell ,Z)\) where \(\ell \) is a location and Z is a zone, and the NOR D for such a node are all subsets \(W\subseteq Z\) where W is a finite union of (sub-)zones such that \(W\sqsubseteq W'\) if \(W\subseteq W'\). Informally, the (increasing) set W contains information about the concrete states for which a winning strategy is already known to exist. The resulting on-the-fly algorithm is implemented in UPPAAL TIGA [7].

Weighted CTL: In [25, 26] ADGs—called symbolic DGs at the time of writing of the papers—were used for efficient on-the-fly model checking for weighted Kripke structures with respect to weighted extensions of CTL. Here nodes of the ADG are pairs of the form \((s,\varphi )\) where s a state of the weighted Kripke structure and \(\varphi \) is a WCTL formula. The NOR D for nodes \((s,\varphi )\), where \(\varphi \) is a cost-bounded modality, is \((\mathbb {N} \cup \{\infty \}, \ge , \infty )\). Informally, the (decreasing) values for such nodes provide upper bounds for which the property is known to hold in the associated state s. The resulting on-the-fly algorithm has been implemented in the tool WKToolFootnote 1. In [13], parametric model checking for WCTL has been considered. Here the outcome of the model checking effort is a direct description of the constraints on the parameters that will render the model checking problem true. In this case the NOR D is extended to \((P\rightarrow (\mathbb {N} \cup \{\infty \}), \ge , \infty )\), where P is the set of parameters and \(\ge \) is the pointwise extension of \(\ge \) to functions.

Probabilistic CTL: For model checking Markov reward models (MRM) with respect to probabilistic WCTL, the work in [14, 34] provides an on-the-fly algorithm using ADG. Here nodes are of the form \((s,\varphi )\) where s is a state of the MRM and \(\varphi \) is a property of PWCTL, and where modalities have upper cost-bounds and lower probability bounds. Semantically, the NOR D consists of monotonic functions of the type \(p:\mathbb {R}_{\ge 0}\rightarrow [0,1]\). Informally, assigning a function p to a node \((s,\varphi )\) indicates that for any cost-bound c the property \(\varphi \) holds at least with probability p(c). The Noetherian property of D is ensured by restricting D to piecewise constant functions.

Petri Nets and Games: The CTL model checking engine of the award-winning tool TAPAAL [20] applies dependency graphs with certain-zero optimization [17, 18]. Also for various game engines dependency graphs have been applied. In [27] synthesis for safety games for timed-arc Petri net games have been given demonstrating (and exploiting) equivalence between continuous-time and discrete-time setting. Finally in [8] partial order reduction for synthesis of reachability games on Petri nets has been obtained based on dependency graph framework.

CAAL: Finally we want to point to the educational tool CAAL [4]Footnote 2, which—using dependency graphs— supports a variety of equivalence checking techniques as well as model checking for recursive Hennessy-Milner logic for CCS and timed CCS.