Distributed Computation of Fixed Points on Dependency Graphs

Abstract

Dependency graph is an abstract mathematical structure for representing complex causal dependencies among its vertices. Several equivalence and model checking questions, boolean equation systems and other problems can be reduced to fixed-point computations on dependency graphs. We develop a novel distributed algorithm for computing such fixed points, prove its correctness and provide an efficient, open-source implementation of the algorithm. The algorithm works in an on-the-fly manner, eliminating the need to generate a priori the entire dependency graph. We evaluate the applicability of our approach by a number of experiments that verify weak simulation/bisimulation equivalences between CCS processes and we compare the performance with the well-known CWB tool. Even though the fixed-point computation, being a P-complete problem, is difficult to parallelize in theory, we achieve significant speed-ups in the performance as demonstrated on a Linux cluster with several hundreds of cores.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Formal verification techniques are increasingly applied in industrial development of software and hardware systems, both to ensure safe and reliable behaviour of the final system, and to reduce cost and time by finding bugs at early development stages. In particular industrial take-up has been boosted by the maturing of computer aided verification, where development of a variety of techniques helps in applying verification to critical parts of systems. Heuristics for SAT solving, abstraction, decomposition, symbolic execution, partial order reduction, and other techniques are used to speed up the verification of systems with various characteristics. Still, the problem of automatic verification is hard, and some difficult cases occur frequently in practical experience. For this reason, we aim in this paper at exploiting the computational power of parallel and distributed machine architectures to further enlarge the scope of automated verification.

Automated verification methods contain a large variety of model-checking and equivalence/preorder-checking algorithms. In the former, a system model is (dis-)proved correct with respect to a logical property expressed in a suitable temporal logic. In the latter, the system model is compared with an abstract model of the system with respect to a suitable behavioural equivalence or preorder, e.g. trace-equivalence, weak or strong bisimulation equivalence. Aiming at providing parallel and distributed support to (essentially) all of these problems, we design a distributed algorithm based on the notion of dependency graphs [1, 2]. In particular, dependency graphs have proven a useful and universal formalism for representing several verification problems, offering efficient analysis through linear-time (local and global) algorithms [2] for fixed-point computation of the corresponding dependency graph. The challenge we undertake here is to provide a distributed algorithm for this fixed-point computation. The fact that dependency graphs allow for representation of bisimulation equivalences between system models suggests that we should not expect our distributed algorithm to exhibit linear speed-up in all cases as bisimulation equivalence is known to be P-complete [3]. Our experiments though still document significant speed-ups that together with the on-the-fly nature of our algorithm (where we possibly avoid the construction of the entire dependency graph in situations where it is not necessary) allow us to outperform the tool CWB [4] for equivalence/model checking of processes described in the CCS process algebra [5].

Related Work. Most closely related to our work are those of [6–8] offering parallel algorithms for model-checking systems with respect to the alternation-free modal $\mu$-calculus. The approach in [6] is based on games and tree decomposition but the tool prototype mentioned in the paper is not available anymore. The work in [8] reduces $\mu$-calculus formulae into alternation free Boolean equation systems. Finally [7] uses a global symbolic BDD-based distributed algorithm for modal $\mu$-calculus but does not mention any implementation. We share the on-the-fly technique with some of these works but our framework is more universal in the sense that we deal with the general dependency graphs where the problems above are reducible to. There also exist several mature tools with modern designs like FDR3 [9], CADP [10], SPIN [11] and mCRL2 [12], some of them offering also distributed and/or on-the-fly algorithms. The input language of the tools is however often strictly defined and extensions to these languages as well as the range of verification methods require nontrivial changes in the implementation. The advantage of our approach is that we first reduce a wide range of problems into dependency graphs and then use our optimized distributed implementation on these generic graphs. Finally, we have recently introduced CAAL [13] as a tool for teaching CCS and verification techniques. The tool CAAL, running in a browser and implemented in TypeScript (a typed superset of JavaScript), is also based on dependency graphs but offers only the sequential version of the local algorithm by Liu and Smolka [2]. Here we provide an optimized C++ implementation of the distributed algorithm thus laying the foundation for offering CAAL verification tasks as a cloud service.

2 Definitions

A labelled transition system (LTS) is a triple $(S, A, \rightarrow {})$ where S is a set of states, A is a set of actions that includes the silent action $\tau$, and $\rightarrow \subseteq S \times A \times S$ is the transition relation. Instead of $(s,a,t) \in \rightarrow$ we write . We also write if either $a=\tau$ and , or if $a \not =\tau$ and for some $s',t' \in S$.

A binary relation $R \subseteq S\times S$ over the set of states of an LTS is weak simulation if whenever $(s,t) \in R$ and for some $a \in A$ then also such that $(s',t') \in R$. If both R and $R^{-1} = \{ (t,s) \mid (s,t) \in R \}$ are weak simulations then R is a weak bisimulation.

We say that s is weakly simulated by t and write $s \ll t$ (resp. s and t are weakly bisimilar and write $s \approx t$) if there is a weak simulation (resp. weak bisimulation) relation R such that $(s,t) \in R$.

Fig. 1.

Dependency graph for weak bisimulation

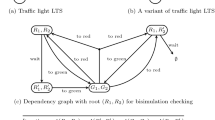
Consider the LTS in Fig. 1a (even though it consists of two disconnected parts, it can still be considered as a single LTS). It is easy to see that $s_1$ weakly simulates $t_1$ and vice versa. For example the weak simulation relation $R = \{(s_1, t_1), (s_2, t_2), (s_3, t_4), (s_4, t_5) \}$ shows that $s_1$ is weakly simulated by $t_1$. However, $s_1$ and $t_1$ are not weakly bisimilar. Indeed, if $s_1$ and $t_1$ were weakly bisimilar, the transition can only be matched by but $s_2$ has a transition under the label b whereas $t_3$ does not offer such a transition.

2.1 Dependency Graphs

A dependency graph [2] is a general structure that expresses dependencies among the vertices of the graph and by this allows us to solve a large variety of complex computational problems by means of fixed-point computations.

Definition 1 (Dependency Graph)

A dependency graph is a pair (V, E) where V is a set of vertices and $E \subseteq V \times 2^V$ is a set of hyperedges. For a hyperedge $(v, T) \in E$, the vertex $v \in V$ is called the source vertex and $T \subseteq V$ is the target set.

Fig. 2.

Dependency graph $G=(\{a,b,c\}, \{ (a, \emptyset ), (b, \{a,b\}), (c, \{b\}), (c, \{a\}) \})$

Let $G=(V,E)$ be a fixed dependency graph. An assignment on G is a function $A: V \rightarrow \{0,1\}$. Let $\mathcal {A}$ be the set of all assignments on G. A fixed-point assignment is an assignment A that for all $(v,T) \in E$ satisfies the following condition: if $A(v')=1$ for all $v' \in T$ then $A(v)=1$.

Figure 2 shows an example of a dependency graph. The hyperedge $(a, \emptyset )$ with the empty target set is depicted by the arrow from a to the symbol $\emptyset$. The figure also denotes a particular assignment A such that vertices with a single circle have the value 0 and vertices with a double circle have the value 1, in order words $A(a)=A(c)=1$ and $A(b)=0$. It can be easily verified that the assignment A is a fixed-point assignment.

We are interested in the minimum fixed-point assignment. Let $A_1, A_2 \in \mathcal {A}$ be assignments. We write $A_1 \sqsubseteq A_2$ if $A_1(v) \le A_2(v)$ for all $v \in V$, where we assume that $0 \le 1$. Clearly $(A, \sqsubseteq )$ is a complete lattice. Let us also define a function $F: \mathcal {A} \rightarrow \mathcal {A}$ such that $F(A)(v) = 1$ if there is a hyperedge $(v,T) \in E$ such that $A(v')=1$ for all $v' \in T$, otherwise $F(A)(v)=A(v)$. Observe that an assignment A is a fixed-point assignment iff $F(A)=A$, and that the function F is monotonic w.r.t. $\sqsubseteq$. By Knaster-Tarski theorem [14] there exists a unique minimum fixed-point assignment, denoted by $A_{min}$. The assignment $A_{min}$ on a finite dependency graph can be computed by a repeated application of the function F on the assignment $A_0$ where $A_0(v)=0$ for all $v \in V$, and we are guaranteed that there is a number m such that $F^m(A_0)=F^{m+1}(A_0)=A_{min}$.

Consider again our example from Fig. 2 and assume that each assignment A is represented by the vector (A(a), A(b), A(c)). We can see that $A_0 = (0,0,0)$, $F(A_0)= (1,0,0)$ and $F^2(A_0)=(1,0,1)=F^3(A_0)$. Hence the depicted assignment (1, 0, 1) is the minimum fixed-point assignment.

2.2 Applications of Dependency Graphs

Many verification problems can be encoded as fixed-point computations on dependency graphs. We shall demonstrate this on the cases of weak simulation and bisimulation, however other equivalences and preorders from the linear/branching-time spectrum [15] can also be encoded as dependency graphs [16] as well as model checking problems e.g. for the CTL logic [17], reachability problems for timed games [18] and the general framework of Boolean equation systems [2], just to mention a few applications of dependency graphs.

Let $T=(S, A, \rightarrow {})$ be an LTS. We define a dependency graph $G_{\approx }(T) = (V, E)$ such that $V = \{(s, t) \mid s, t \in S\}$ and the hyperedges are given by

The general construction is depicted in Fig. 3 and its application to the LTS from Fig. 1a, listing only the pairs of states reachable from $(s_1,t_1)$, is shown in Fig. 1b. Observe that the size of the produced dependecy graph is polynomial with respect to the size of the input LTS.

Fig. 3.

Bisimulation reduction to dependency graph

Proposition 1

Let $T=(S,A,\rightarrow )$ be an LTS and $s,t \in S$. We have $s \approx t$ if and only if $A_{min}((s, t)) = 0$ in the dependency graph $G_{\approx }(T)$.

Proof (Sketch)

“$\Rightarrow$”: Let R be a weak bisimulation such that $(s,t) \in R$. The assignment A defined as $A((s',t')) = 0$ iff $(s', t') \in R$ can be shown to be a fixed-point assignment. Then clearly $A_{min} \sqsubseteq A$ and because $A((s,t))=0$ then also $A_{min}((s,t,))=0$. “$\Leftarrow$”: Let $A_{min}((s,t))=0$. We construct a binary relation $R =\{(s', t') \mid A_{min}((s', t')) = 0 \}$. Surely $(s,t) \in R$ and we invite the reader to verify that R is a weak bisimulation.    $\square$

In our example in Fig. 1b we can see that $A_{min}((s_1,t_1))=1$ and hence $s_1 \not \approx t_1$. The construction of the dependency graph for weak bisimulation can be adapted to work also for the weak simulation preorder by removing the hyperedges that originate by transitions performed by the right hand-side process.

We know that computing $A_{min}$ for a given dependency graph can be done in linear time [19]. By the facts that deciding bisimulation on finite LTS is P-hard [3] and the polynomial time reduction described above, we can conclude that determining the value of a vertex in the minimum fixed-point assignment of a given dependency graph is a P-complete problem.

Proposition 2

The problem whether $A_{min}(v) = 1$ for a given dependency graph and a given vertex v is P-complete.

3 Distributed Fixed-Point Algorithm

We shall now describe our distributed algorithm for computing minimum fixed-points on dependency graphs. Let $G=(V,E)$ be a dependency graph. For the purpose of the on-the-fly computation, we represent G by the function

$$\textsc {Successors}(v) = \{(v, T) \mid (v, T) \in E\}$$

that returns for each vertex $v \in V$ the set of outgoing hyperedges from v.

We assume a fixed number of n workers. Let i, $1 \le i \le n$, denote a worker with id i. Each worker i uses the following local data structures.

• A local assignment function $A^{i}: V \rightharpoonup \{0, 1\}$, which is a partial function mapping each vertex to the values $undefined$, 0 or 1.

• A local dependency function $D^{i}: V \rightarrow 2^E$ returning the current set of dependent edges for each vertex.

• A local waiting set $W^i \subseteq E$ containing edges that are waiting for processing.

• A local request function $R^{i}: V \rightarrow 2^{\{1, \dots , n\}}$ where the worker i remembers who requested the value for a given vertex.

• A local input message set $M^{i} \subseteq \{\,{``value\, of\, v\, needed\, by\, worker\, j''}\, \mid v \in V ,\ 1 \le j \le n\} \cup \{ {``v\, has\, value\, 1''} \mid v \in V\}$. For syntactic convenience, we assume that a worker i can add a message m to $M^j$ of another worker j simply by executing the assignment $M^{j}$ $\leftarrow$ $M^{j} \cup \{ m \}$.

We moreover assume some standard function $\textsc {TerminationDetection}$, computed distributively, that returns true if there are no messages in transit and all waiting sets of all workers are empty, in other words if $\bigcup _{1 \le i \le n}{M^i \cup W^i} = \emptyset$. Finally, we assume a global partitioning function $\delta : V \rightarrow \{1, \dots , n\}$ that partitions vertices to workers.

The distributed algorithm for computing the minimal fixed-point assignment for a given vertex $v_s$ is presented in Algorithm 1. First, all n workers are initialized and the worker that owns the vertex $v_s$ updates its local assignment to 0 and adds the successor edges to its local waiting set. Then the workers start processing the edges on the waiting sets and the messages in their input message sets until they terminate either by one worker announcing that $A_{min}(v_s) = 1$ at line 18 or all waiting edges and messages have been processed and then the workers together claim that $A_{min}(v_s) = 0$ at line 13.

Lemma 1 (Termination)

Algorithm 1 terminates.

Proof

First observe that for each vertex v and each local assignment $A^{i}$ the value of $A^{i}(v)$ is first undefined. Then when v is discovered either as a target vertex of some hyperedge on the waiting set (line 23) or when the value of v gets requested by another worker (line 37), the value $A^{i}(v)$ changes to 0. Finally the value of $A^{i}(v)$ can be upgraded to the value 1 either by the presence of a hyperedge where all target vertices already have the value 1 (line 17) or by receiving a message from another worker (line 33). The point is that for every v, each of the assignments $A^{i}(v)$ $\leftarrow$ 0 and $A^{i}(v)$ $\leftarrow$ 1 is executed at most once during any execution of the algorithm. This can be easily noticed by the inspection of the conditions on the if-commands guarding these assignments.

Next we notice that new hyperedges are added to the waiting set $W^{i}$ only when an assignment of some vertex v gets upgraded from $undefined$ to 0, or from 0 to 1. As argued above, this can happen only finitely many times, hence only finitely many hyperedges can be added to each $W^{i}$. Similarly, new messages to the message sets can be added only at lines 19, 28 and 40. At line 19 a finite number of messages of the form “v has value 1” is added only when a value of $A^{i}(v)$ was upgraded to 1. This can happen only finitely many times. At line 28 the message “value of v’ needed by worker i” is added only when a value of a vertex was upgraded from undefined to 0, hence this can happen only finitely many times. Finally, at line 40 a message is added only when we received the message “value of v needed by worker i” but this message was sent only finitely many times. All together, only finitely many elements can be added to the waiting and message sets and as the main while-loop repeatedly removes elements from those sets, eventually they must become empty and the algorithm terminates at line 13 (unless it terminated earlier at line 18).    $\square$

We can now observe that if a vertex is assigned the value 1 for any worker, then the value of the vertex in the minimal fixed-point assignment is also 1.

Lemma 2 (Soundness)

At any moment of the execution of Algorithm 1 and for all i, $1 \le i \le n$, and all $v \in V$ it holds that

• (a) if $A^{i}(v) = 1$ then $A_{min}(v) =1$, and

• (b) if “v has value 1” $\in M^{i}$ then $A_{min}(v)=1$.

Proof

The invariant holds initially as $A^{i}(v)$ is undefined for all i and all v and all input message sets are empty.

Let us assume that both condition a) and b) hold and that we assign the value 1 to $A^{i}(v)$ for some worker i and a vertex v. This can only happen at lines 17 and 33. In the first assignment at line 17 we know that there is a hyperedge (v, T) such that all vertices $v' \in T$ satisfy that $A^{i}(v')=1$. However, this by our invariant part a) implies that $A_{min}(v')=1$ and then necessarily also $A_{min}(v)=1$ by the definition of fixed-point assignment. Hence the invariant for the case a) is preserved. Similarly, if $A^{i}(v)$ gets the value 1 at line 33, this can only happen if “v has value 1” $\in M^{i}$ and by the invariant part b) this implies that $A_{min}(v)=1$ and hence the invariant for the condition a) is established.

Similarly, let us assume that conditions a) and b) hold and that a message “v has value 1” gets inserted into $M^{j}$ by some worker i. This can only happen at lines 19 and 40. In both situations it is guaranteed that $A^{i}(v)=1$ and hence by the invariant part a) we know that $A_{min}(v)=1$, implying that adding these messages to $M^{j}$ is safe.    $\square$

The next lemma establishes an important invariant of the algorithm.

Lemma 3

For any vertex $v \in V$, whenever during the execution of Algorithm 1 the worker $\delta (v)$ is at line 6 then the following invariant holds: either

• (a) $A^{\delta (v)}(v) = 1$, or

• (b) $A^{\delta (v)}(v)$ is undefined, or

• (c) $A^{\delta (v)}(v) = 0$ and for all $(v, T) \in E$ either

  • (i) $(v, T) \in W^{\delta (v)}$, or

  • (ii) there is $v' \in T$ such that $A^{\delta (v)}(v') = 0$, and $(v, T) \in D^{\delta (v)}(v')$.

Proof

Initially, the invariant is satisfied as $A^{\delta (v)}(v)$ is undefined and the invariant, more specifically the subcase (i), clearly holds also when $v=v_s$ and the worker $\delta (v_s)$ performed the assignments at line 4.

Assume now that the invariant holds. Clearly, if it is by case (a) where $A^{\delta (v)}(v)=1$ then the value of v will remain 1 until the end of the execution.

If the invariant holds by case (b) then it is possible that the value of $A^{\delta (v)}(v)$ changes from $undefined$ to 0. This can happen either at lines 23 or 37. If the assignment took place at line 23 (note that here $v=v'$) then clearly line 26 will be executed too and all successor edges of v will be inserted into the waiting set and hence the invariant subcase (i) will hold once the execution of the procedure is finished. Similarly, if the assignment took place at line 37 then all successors of v are at the next line 38 immediately added to the waiting set, hence again satisfying the invariant subcase (i).

Consider now the case (c). The invariant can be challenged by either removing the hyperedge (v, T) from $W^{\delta (v)}$ hence invalidating the subcase i) or by upgrading the value of the vertex $v'$ in case (ii) such that $A^{\delta (v)}(v')=1$. In the first case where the subcase (i) gets invalidated we can notice that this can happen only at line 9 after which the removed hyperedge (v, T) is processed. There are two possible scenarios now. Either all vertices from T have the value 1 and then the value of $A^{\delta (v)}(v)$ also gets upgraded to 1 at line 17 hence satisfying the invariant (a), or there is a vertex $v' \in T$ such that $A^{\delta (v)}(v')=0$ and then the hyperedge (v, T) is added at line 30 to the dependency set $D^{\delta (v)}(v')$ satisfying the subcase (ii) of the invariant. In the second subcase, we assume that the vertex $v'$ satisfying the subcase (ii) gets upgraded to the value 1. This can happen at line 17 or line 33. In both cases the dependency set $D^{\delta (v)}(v')$ (that by our invariant assumption contains the hyperedge (v, T)) is added to the waiting set (lines 21 and 34) implying that the invariant subpart (i) holds.    $\square$

The following lemmas shows that after the termination, the value 0 for a vertex v in a local assignment of some worker implies the same value also in the assignment of the worker that owns the vertex v. This is an important fact for showing completeness of our algorithm.

Lemma 4

Once all workers in Algorithm 1 terminate at line 13 then for all vertices $v \in V$ and all workers i holds that if $A^{i}(v)=0$ then $A^{\delta (v)}(v)=0$.

Proof

Observe that the assignment of 0 to $A^{i}(v)$ where $i \not = \delta (v)$ can happen only at line 23 (the assignment at line 37 is performed only if $i = \delta (v)$ as the message “value of v is needed by worker i” is sent only to the owner of the vertex v). After the assignment at line 23 done by worker i, the message requesting the value of the vertex is sent to its owner at line 28. Clearly, before the workers terminate, this message must be read by the owner and the value of the vertex is either set to 0 at line 37, or if the value is already known to be 1 the worker i is informed about this via the message “v has value 1” at line 40 and this message will be necessarily read by the worker i before the termination and the value $A^{i}(v)$ will be updated to 1. Otherwise we remember the worker’s id requesting the assignment value at line 42. Should the owner upgrade the value of v to 1 at some moment, all workers that requested its value will be informed about this by a message sent at line 19 and before the termination these workers must read these messages and update the local values for v to 1. It is hence impossible for the algorithm to terminate while the owner of v set its value to 1 and some other worker still has only the value 0 for the vertex v.    $\square$

Lemma 5 (Completeness)

If all workers in Algorithm 1 terminate at line 13 then for all vertices $v \in V$ the fact $A^{\delta (v)}(v) = 0$ implies that $A_{min}(v) = 0$.

Proof

Note that after the termination we have $W^{i} = M^{i} = \emptyset$ for all i. Assume now that $A^{\delta (v)}(v) = 0$. Then by Lemma 3 and the fact that $W^{\delta (v)}=\emptyset$ we can conclude that for all $(v, T) \in E$ there exists $v' \in T$ such that $A^{\delta (v)}(v') = 0$. By Lemma 4 this means that also $A^{\delta (v')}(v')=0$. Let us now define an assignment A such that $A(v)=A^{\delta (v)}(v)$. By the arguments above, A is a fixed-point assignment. As $A_{min}$ is the minimum fixed-point assignment, we have $A_{min} \sqsubseteq A$ and because $A(v)=0$ we can conclude that $A_{min}(v)=0$.    $\square$

Theorem 1 (Correctness)

Algorithm 1 terminates and outputs either

• “$A_{min}(v_s) = 1$” implying that $A_{min}(v_s) = 1$, or

• “$A_{min}(v_s) = 0$” implying that $A_{min}(v_s) = 0$.

Proof

Termination is proved in Lemma 1. The algorithm can terminate either at line 18 provided that $A^{i}(v_s)=1$ but then by Lemma 2 clearly $A_{min}(v_s)=1$. Otherwise the algorithm terminates when all workers reach line 13. This can only happen when $A^{\delta (v_s)}(v_s)=0$ and by Lemma 5 we get $A_{min}(v_s)=0$.    $\square$

Note that the algorithm is proved correct without imposing any specific order by which messages and hyperedges are selected from the sets $W^i$ and $M^i$ or what target vertices are selected in the expressions like $\exists v' \in T$. In the next section we discuss some of the choices we have made in our implementation.

4 Implementation and Evaluation

The distributed algorithm described in the previous section is implemented as an MPI-program in C++, enabling the workers to cooperate not only on a single machine but also across multiple machines. The MPI-program requires a successor generator to explore the dependency graph, a partitioning function and a (de)serialisation function for the vertices (we use LZ4 compression on the generated hyperedges before they leave the successor generator). For our experiments, these functions were implemented for the case of weak bisimulation/simulation on CCS processes but they can be easily replaced with other custom implementations to support other equivalence and model checking problems, without the need of modifying the distributed engine itself.

In our implementation we use hash tables to store the assignments ($A^{i}$) and the dependent edges ($D^{i}$). The algorithm does not constrain specific structures on $W^{i}$ or $M^{i}$. For the waiting list ($W^{i}$) two deques are used, one for the forward propagation (outgoing hyperedges of newly discovered vertexes) and one for the backwards propagation (hyperedges that were inserted due to dependencies). Then the graph can be explored depth-first, or breadth-first, or a probabilistic combination of those, independently for both the forward and backwards propagation. Our experiments showed that it is preferable to prioritize processing of messages rather than hyperedges to free up buffers used by the senders. The distributed termination detection is determined using [20].

The implementation is open-source and available at http://code.launchpad.net/pardg/ in the branch dfpdg-paper that includes also all experimental data. The distributed engine is currently being integrated within the CAAL [13] user interface.

4.1 Evaluation

We evaluate the performance of our implementation on the traditional leader election protocol [21] where we scale the number of processes and on the alternating bit protocol (ABP) [22] where we scale the size of communication buffers. We ask the question whether the specification and implementation (both described as CCS processes) are weakly bisimilar. For both cases we consider a variant where the weak bisimulation holds and where it does not hold (by injecting an error). Finally, we also ask about the schedulability of 180 different task graphs from the well known benchmark database [23] on two processors within a given deadline. Whenever applicable, the performance is compared with the tool Concurrency WorkBench (CWB) [4] version 7.1 using 1 core (there is no parallel/distributed version of CWB). CWB implements the best performing global algorithms for bisimulation checking on CCS processes.

All experiments are performed on a Linux cluster, composed of compute nodes with 1 TB of DDR3 1600 mhz memory, four AMD Opteron 6376 processors (in total 64 cores@2,3 Ghz with speedstep disabled) and interconnected using Intel True Scale InfiniBand (40 Gb/s) for low latency communication. All nodes run an identical image of Ubuntu 14.04 and MPICH 3.2 was used for MPI communication. We use the depth first search order for the forward search strategy and the breadth first search order for the backwards search strategy.

The results for the leader election and ABP are presented in Tables 1 and 2, respectively. For each entry in the tables, four runs were performed and the mean run time and the relative sample standard deviation are reported. We also report on how many microseconds were used (in parallel) per explored vertex of the dependency graph. This measure gives an idea of the speedup achieved when more cores are available. We note that for small instances this time can be very high due to the initialization of the distributed algorithm and memory allocations for dynamic data structures.

Table 1. Time is reported in seconds, RSD is the relative sample standard deviation in percentage and s/tv is the time spend per vertex in micro seconds. The star in RSD column means that only one run finished within the given timeout.

We observe that in the positive cases where the entire dependency graph must be explored, we achieve (with 256 cores) speedups 32 and 52 for leader election with 9 and 10 processes, respectively. For ABP with buffer sizes 3 and 4 the speedups are 102 and 98, respectively. However we do see a relative high standard deviation for 8–32 cores if the run time is short. This is because the scheduler is not configured to ensure locality among NUMA nodes. Compared to the performance of CWB, we observe that on the smallest instances we need up to 64 cores in leader election and 16 cores in ABP to match the run time of CWB. However, on the next instance the run time of CWB is matched already by 8 and 2 cores, respectively. This demonstrates that the performance of our distributed algorithm considerably improves with the increasing problem size.

Table 2. Time is reported in seconds, RSD is the relative sample standard deviation in percentage and s/tv is the time spend per vertex in micro seconds.

In the negative cases, it is often enough to explore only a smaller portion of the dependency graph in order to provide a conclusive answer and here the on-the-fly nature of our distributed algorithm shows a real advantage compared to the global algorithms implemented in CWB. For on-the-fly exploration the search order is very important and we can note that increasing the number of cores does not necessarily imply that we can compute the fixed-point value for the root faster. Even though the algorithm scales still very well and with more cores explores a substantially larger part of the dependency graph, it may (by the combined search strategy of the workers) explore large parts of the graph that are not needed for finding the answer. For example in leader election for 10 processes, two cores produced a very successful search strategy that needed only 7.8 s to find the answer, however, increasing the number of cores led the search in a wrong direction.

Finally, results for checking the simulation preorder on the task graph benchmark can be seen in Table 3. As this is a large number of experiments requiring nontrivial time to run, we tested the scaling only up to 64 cores. We queried whether all the tasks in the task graph (or rather their initial prefixes) can be completed within 25 time units. Out of the 180 task graphs, 61 of them are solvable in one hour (and 34 of them are schedulable while 27 are not schedulable). As CWB does not support simulation preorder, the weaker trace inclusion property is used but CWB cannot solve any of the task graphs within one hour. We achieve an average 25 times speedup using 64 cores, both for the positive and negative cases, showing a very satisfactory performance on this large collection of experiments.

Table 3. Number of solved task graphs within 1 h for all, positive and negative instances. The accumulated average time (AAT) is projected on 9 task graphs that 1 core is able to solve between 20 min and 1 h.

5 Conclusion

We presented a distributed algorithm for computing fixed points on dependency graphs and showed on weak bisimulation/simulation checking between CCS processes that, even though the problem is in general P-hard, we can in many cases obtain reasonable speed-ups as we increase the number of cores. Our algorithm works on-the-fly and hence for the cases where only a small portion of the dependency graphs needs to be explored to provide the answer, we perform significantly better than the global algorithms implemented in the CWB tool. Compared to CWB we also scale better with the increasing instance sizes, even for the cases where the whole dependency graph must be explored. The advantage of our approach based on dependency graphs is that we provide a general distributed algorithm and its efficient implementation that can be directly applied also to other problems like e.g. model checking—most importantly without the need of designing and coding specific single-purpose distributed algorithms for the different applications. In our future work we plan to look into finding better parallel search strategies that will allow for early termination in the cases where the fixed-point value of the root is 1 and also terminating the parallel search of the graph once we know that the exploration is not needed any more.