Keywords

Introduction

Cavitation is a common phenomenon in hydrodynamics and biology [1–6]. Recently, it was recognized that inertial microcavitation rheometry (IMR) can be used to characterize the mechanical behavior of viscoelastic materials since the cavitation bubble collapse is very sensitive to the constitutive equations of the surrounding medium [7–8]. By analyzing the bubble dynamics, the viscoelastic properties of soft materials can be characterized where the strain rates can reach O (103) s−1 ~ O (106) s−1 [10]. Recently, Estrada et al. [7] demonstrated experiments to probe viscoelastic mechanical properties of soft materials using IMR, where time-resolved data for the temporal evolution of bubble radii is fitted to the prediction of the governing equations of bubble dynamics, combined with a neo-Hookean Kelvin-Voigt constitutive model for surrounding soft medium. In the case of polyacrylamide hydrogels, the neo-Hookean Kelvin-Voigt model fitting results show that the shear moduli obtained during cavitation are stiffer than their quasi-static counterparts. This strain stiffening effect, which is a very common feature of soft materials because of structural transitions such as ordering, crystallization, or shear banding under large strain, needs additional consideration and treatment in IMR.

In this paper, we first review the physical model of IMR in Section “Physical model”. We address the issue of strain stiffening by replacing the traditional neo-Hookean spring in the nonlinear Kelvin-Voigt model with a higher order material constitutive relation inspired by the Fung model [9] in Section “Strain Stiffening Effects”. Our experimental setup is introduced in Section “Experımental Setup”. We demonstrate our Fung Kelvin-Voigt model in Section “Results and Dıscussıon”. Finally, we present some conclusions in Section “Conclusıons”.

Physıcal Model

Bubble Dynamics with Viscoelastic Surroundings

We consider the spherical dynamics of a bubble in an infinite viscoelastic medium, where the surrounding medium is assumed to be incompressible in the near field, and compressible in the far field. The bubble dynamics are represented by the Keller-Miksis equation [11]:

$$ \left(1-\frac{\dot{R}}{c}\right)R\ddot{R}+\frac{3}{2}\left(1-\frac{\dot{R}}{3c}\right){\dot{R}}^2=\left(1+\frac{\dot{R}}{c}+\frac{R}{c}\frac{d}{dt}\right)\frac{p-{p}_{\infty }(t)-{\Theta}_{\upsilon e}-\frac{2\gamma }{R}}{\rho }, $$
(30.1)

where R(t) is the bubble radius, and the overdots denote derivatives with respect to time t; ρ and c are the density and sound speed of the surrounding soft materials; γ is the surface tension between bubble inside gas and surroundings; p is the internal bubble pressure given by the sum of the partial pressures of non-condensible gas (p g) and vapor (p v); p ∞(t) is the far-field driving pressure; Θ ve is the viscoelastic stress integral defined as

$$ {\Theta}_{ve}={\int}_R^{\infty}\frac{2}{r}\left({\tau}_{rr}-{\tau}_{\theta \theta}\right) dr. $$
(30.2)

The specifics of the stress integral depend on the constitutive properties of the material at hand. For example, assuming the surrounding material obeys neo-Hookean Kelvin-Voigt formulation, the stress tensor can be expressed as

$$ {\tau}_{rr}=\frac{2}{3}G\left[{\left(\frac{r_0}{r}\right)}^4-{\left(\frac{r}{r_0}\right)}^2\right],\kern1em {\tau}_{\theta \theta}=-\frac{1}{2}{\tau}_{rr}, $$
(30.3)

where \( {r}_0\left(r,t\right)={\left({r}^3-{R}^3+{R}_{\infty}^3\right)}^{1/3} \)is the radial location in the original configuration. The viscoelastic stress integral Θ ve can be further integrated analytically:

$$ {\Theta}_{ve}=\frac{4\mu \dot{R}}{R}+\frac{G}{2}\left[5-4\frac{R_{\infty }}{R}-{\left(\frac{R_{\infty }}{R}\right)}^4\right], $$
(30.4)

where μ is the viscosity of the surrounding soft material, G is the shear modulus, and R ∞ is the bubble radius corresponding to the final equilibrium state.

Strain Stiffening Effects

In addition to a neo-Hookean material model, we also explored strain-stiffening effects and apply a higher order material model inspired by Fung model [9] whose strain energy density is

$$ {\Psi}_{\mathrm{Fung}}\left(\mathbf{F}\right)=\frac{G_{\infty }}{2\alpha}\exp \left(\alpha \left({I}_1-3\right)\right)=\frac{G_{\infty }}{2\alpha}\left[\alpha \left({I}_1-3\right)+\frac{\alpha^2}{2}{\left({I}_1-3\right)}^2\right]+\mathrm{h}.\mathrm{o}.\mathrm{t}, $$
(30.5)

and its stress integral is

$$ {\Theta}_{ve,\mathrm{Fung}}=2{G}_{\infty }{\int}_{R(t)}^{\infty}\left[{\left(\frac{r_0}{r}\right)}^4-{\left(\frac{r}{r_0}\right)}^2\right]\kern0.24em \exp \left[\alpha \left({I}_1-3\right)\right]\frac{dr}{r}. $$
(30.6)

Heat and Mass Transfer at the Bubble Wall

The pressure inside the bubble is assumed to be homobaric. The inclusion of heat and mass transfer [12] modify bubble pressure evolution:

$$ \dot{p}=\frac{3}{R}\left[-\kappa p\dot{R}+\left(\kappa -1\right){K}_w{\left.\frac{\partial T}{\partial r}\right|}_w+\kappa {\mathrm{\mathcal{R}}}_v{T}_w{\dot{m}}_v^{{\prime\prime}}\right], $$
(30.7)

where T(r, t) is the instantaneous, spatially varying temperature, K is the mixture thermal conductivity inside the bubble (K = AT + B), \( {\mathcal{R}}_v \) is the gas constant of vapor, specific heats ratio κ of vapor is assumed equal to that of air, and \( {\dot{m_v}}^{\prime \prime } \) the vapor mass flux across the interface. The subscript w denotes variables evaluated at the bubble wall. The vapor mass flux is related with mass transfer at the bubble wall:

$$ {\dot{m}}_v^{{\prime\prime} }=D\frac{\rho_{m,w}}{1-{C}_w}{\left.\frac{\partial C}{\partial r}\right|}_w, $$
(30.8)

where C is the mass fraction of vapor gas; D is the diffusion coefficient between water vapor and air; ρ m is the mass density of the mixed vapor that satisfies \( p=\mathcal{R}{\rho}_mT \), where \( \mathcal{R}=C{\mathcal{R}}_v+\left(1-C\right){\mathcal{R}}_g \) is the mixture gas constant, \( {\mathcal{R}}_g \) is the gas constant of non-condensible gas, and \( {\mathcal{R}}_v \) if the gas constant of vapor.

Mass diffusion is assumed to follow Fick’s law such that the mass balance equation for vapor reads

$$ \frac{\partial C}{\partial t}+\left(\dot{R}+\frac{{\mathrm{\mathcal{R}}}_v-{\mathrm{\mathcal{R}}}_g}{\mathrm{\mathcal{R}}}\frac{\partial C}{\partial r}\right)\frac{\partial C}{\partial r}=\frac{{\left[\nabla \cdot \left(D{\rho}_m\nabla C\right)\right]}_r}{\rho_m}. $$
(30.9)

To account for heat transfer and energy balance, we apply Fourier’s law both inside and outside the bubble:

$$ \frac{\kappa }{\kappa -1}\frac{p}{T}\left(\frac{\partial T}{\partial t}+\dot{R}\frac{\partial T}{\partial r}\right)-\dot{p}={\left[\nabla \cdot \left(K\nabla T\right)\right]}_r,\kern1em \frac{\partial {T}_s}{\partial t}+\frac{R^2\dot{R}}{r^2}\frac{\partial {T}_s}{\partial r}={D}_s{\left[{\nabla}^2{T}_s\right]}_r+\frac{12\mu }{\rho {C}_p}{\left(\frac{R^2\dot{R}}{r^3}\right)}^2, $$
(30.10)

where T is the temperature inside bubble and T s is the temperature in the outside surroundings; C p = CC p, v + (1 − C)C p, g is the heat capacity at constant pressure where C p, v and C p, g are the constant specific heats at constant pressure for the vapor and non-condensible gas, respectively; D s = K s/(ρC p) is the thermal diffusivity, and K s is the constant thermal conductivity of the soft surrounding medium.

Boundary Conditions

Regarding boundary conditions for the vapor mass fraction and the temperature, at the origin, we have

$$ {\left.\frac{\partial C}{\partial r}\right|}_{r=0}={\left.\frac{\partial T}{\partial r}\right|}_{r=0}=0 $$
(30.11)

due to spherical symmetry. At the bubble wall, we assume that the vapor is in equilibrium with the condensed layer and the vapor partial pressure is equal to its saturation pressure. We also assume that the surrounding material remains isothermal with constant temperature T ∞ everywhere. All the boundary conditions near the wall are summarized as follows:

$$ {T}_s{\left|{}_w=T\right|}_w={T}_{\infty },\kern1em {\left.\frac{\partial {T}_s}{\partial r}\right|}_w={\left.\frac{\partial C}{\partial r}\right|}_w=0,\kern1em {p}_{v,\mathrm{sat}}\left({T}_w\right)={p}_{\mathrm{ref}}\exp \left(-\frac{T_{\mathrm{ref}}}{T_w}\right). $$
(30.12)

where p v, sat(T) is the temperature-dependent saturation pressure of the vapor with empirical constants p ref and T ref.

Experımental Setup

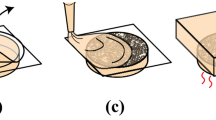
In this study, the experimental setup is the same as in Estrada et al [7] where single bubble inertial cavitation is generated via single pulses of a frequency-doubled Q-switched Nd:YAG 532 nm laser as shown in Fig. 30.1a. We use a Phantom v2511 CCD high speed camera (Vision Research, Wayne, NJ) to take a sequence of images (exposure time of single frame is set to be 2 μs) of bubble growth, collapse and subsequent oscillations as shown in Fig. 30.1b. Bubble images were then fit for their centroid and radius R(t) using a circle fit algorithm (see Figs. 30.1b and 30.2a). Here we tested cavitation experiments using two types (stiff & soft) of polyacrylamide hydrogels, whose quasi-static shear moduli have also been characterized using quasi-static compression indentations [7].

Fig. 30.1
figure 1

Experimental setup and schematic of inertial microcavitation rheometry. (a) A single 6 ns, Q-switched 532 nm Nd:YAG laser pulse of 1–10 mJ passes through a beam expander to fill the back aperture of an objective mounted into an inverted TI-Eclipse microscope, and (inset, star) converges into a cylindrical hydrogel sample. Bright-field illumination is supplied by a condensed halogen lamp. (b) Bubble growth, collapse, and subsequent oscillation are imaged using a Phantom v2511 high speed camera (Vision Research, Wayne, NJ). Image size 512×128 pixels, filmed at 270,000 fps. Scale bar, 200 μm (Image courtesy of Estrada [7])

Full size image
Fig. 30.2
figure 2

IMR characterizes stiff & soft polyacrylamide hydrogels viscoelastic properties using neo-Hookean Kelvin-Voigt model and Fung Kelvin-Voigt model. (a) Bubble radius R-t curve of IMR cavitation experiments inside stiff & soft polyacrylamide hydrogels and water (reference). (b) Characterized viscoelastic properties of the tested stiff & soft polyacrylamide hydrogels using two types of nonlinear material models (neo-Hookean Kelvin-Voigt & Fung Kelvin-Voigt)

Full size image

Results and Discussıon

Following Barajas et al [8], a fifth-order explicit Dormand-Prince Runge-Kutta method with adaptive step-size control is used to evolve the governing equations forward in time. Quantitative values of material parameters for the surrounding medium and the bubble contents used in this study are summarized in Table 30.1. Least squares error (LSE) is defined by minimizing the perpendicular offset between experimental data points and the numerical simulations. Minimizing the discrete LSE in the R-t curves gives the best estimate of the viscoelastic properties for each polyacrylamide gel. Figure 30.2b shows the characterized viscoelastic properties of the tested stiff & soft polyacrylamide hydrogels using neo-Hookean Kelvin-Voigt and Fung Kelvin-Voigt models.

Table 30.1 Material properties used in the present study
Full size table

We find that for both stiff & soft polyacrylamide hydrogels, the nonlinear neo-Hookean Kelvin-Voigt model fitting results show that the shear moduli obtained during cavitation are stiffer than their quasi-static counterparts (see Fig. 30.2b). On the other hand, when we account for strain stiffening by replacing the traditional neo-Hookean spring in the nonlinear Kelvin-Voigt model with a constitutive relation inspired by the Fung model [9], we recover the quasi-static shear modulus at long time scale. We also find that by applying the Fung Kelvin-Voigt model, the accuracy of the measured dynamic material viscosity is also improved compared to the neo-Hookean Kelvin-Voigt formulation.

Conclusions

In this paper, we use inertial microcavitation rheometry (IMR) experiments to characterize viscoelastic properties of stiff & soft polyacrylamide hydrogels undergoing large, finite deformations (|E rr| > 0.05) at strain-rates of up to 106 s−1. We explore the strain stiffening effects of these two types of hydrogels by implementing Fung Kelvin-Voigt model. Compared with our previous neo-Hookean Kelvin-Voigt model, we find the accuracy of the measured dynamic material viscosity (in the order of 10−1 Pa·s) is also improved.