Fast Robot Motor Skill Acquisition Based on Bayesian Inspired Policy Improvement

Abstract

Learning from demonstration with the reinforcement learning (LfDRL) framework has been successfully applied to acquire the skill of robot movement. However, the optimization process of LfDRL usually converges slowly on the condition that new task is considerable different from imitation task. We in this paper proposes a ProMPs-Bayesian-PI$^2$ algorithms to expedite the transfer process. The main ideas is adding new heuristic information to guide optimization search other than random search from the stats of imitation learning. Specifically, we use the result of Bayesian estimation as the heuristic information to guide the PI$^2$ when it random search. Finally, we verify this method by UR5 and compare it with the traditional method of ProMPs-PI$^2$. The experimental results show that this method is feasible and effective.

J. Fu—The author acknowledges the National Natural Science Foundation of China (61773299, 515754112).

1 Introduction

Researchers in the robot have been desiring to make the robot behave like human. Learning from demonstration (LfD) (Schaarschmidt et al. 2018; Havoutis and Calinon 2018) can make robot learn the similar skills as the demonstration action. But it is impossible to learn more complex and dissimilar to demonstration task. So recently, robot learning from demonstration together with reinforcement learning (RL) has attracted significantly increased attention. By means of LfDRL, researchers can autonomously derive a robot controller from merely observing a human’s own performance. Furthermore, the controller could be self-improved ro refine and expand robot motor capability obtained from demonstration to meet with task requirement depicted as a functional criterion. Those advantages indicate that LfDRL might been the promising paradigm to bring the above dream closer to reality.

Usually, LfDRL is built throughout three-phase paradigm sequentially: representation phase, imitation phase and optimization phase. A parametric policy representation is selected on the first phase. Generally, a dynamic model with flexible adjustment sounds good, for the reason that it is easy to modulate online and exhibit robustness. DS (Khoramshahi and Billard 2019; Salehian et al. 2017) and DMPs (Pervez and Lee 2018; Yang et al. 2018) models are current popular dynamic model. DS represent motion scheduling in the form if a nonlinear autonomous dynamic system, which is time-invariance and global/local asympotic stable. Whereas, DMPs models the movement planning as superimposition of a linear dynamic system and a nonlinear term. And there is time-based model like probabilistic movement primitives (ProMPs) (Paraschos et al. 2018; Kroemer et al. 2018). During the imitation phase, the flexible adjustment of model will learn suitable parameters according to the data from demonstration. Various methods including radial basis function networks, regularized kernel least-square, locally weighted regression (Sigaud et al. 2011) and Gaussian process (Deisenroth et al. 2015; Ben Amor et al. 2014) etc. were proposed to present flexible adjustment.

On the optimization stage, the policy parameters learned from the second phase will be constantly adjusted, chosen and updated with respect to a utility function with reinforcement learning until reach the target task.

Although there are many successful achievements int the LfDRL community, many if the existing studies lay emphasis on the innovation in one phase. In our previous research results in Fu et al. (2015a, b), we have developed an effective policy representation which combines a 2nd order critical damping system and a forcing term in the form of Gaussian Mixture Regression (GMR). In previous we proposed a method named PI$^2$-GMR for motor skill learning, with which robot could be board applicable for various task and of good quality for given task simultaneously.

This main contribution of this paper is introduction of a method to learning complex task faster. On the basis of previous research we propose a method named Bayesian-PI$^2$ for the moment, which can improve the efficiency of reinforcement learning on the third stage of LfDRL. Traditional PI$^2$ can explore all space of parameter, so it has lower efficiency for our task scenario. The Bayesian-PI$^2$ can narrow the search space of parameter, and we can call this method a heuristic search.

The paper is organized as follow. Section 2 depicted ProMPs for policy representation and imitation learning. In Sect. 3, we can introduce briefly traditional PI$^2$. At the same time introduce the ProMPs-PI$^2$. Then the heuristic process of Bayesian estimation for parameter search is introduced in detail in Sect. 4. And we can discussed the method of Bayesian-PI$^2$ in combination with imitation learning. In Sect. 5, we present in detail the classical benchmark experiment trajectory planning via prior unknown point(s) using the theory of this article. In addition, detailed experimental settings and results are presented and analyzed. Finally, conclusions are given in Sect. 6.

2 Probabilistic Movement Primitives

In the first stage of LfDRL, we use probabilistic movement primitives as parametric policy representation. This is a method based on probability, so this method is data-drived. This section we could introduce basic concepts of ProMPs.

ProMPs represent a distribution over trajectory that are correlated spatially and temporally. For a single DOF, mark the current position of the joint with a symbol $q_t$. Thus, we denote $y_t=q_t$ as state of joint at time step t, and a trajectory of length T as a sequence $\varvec{y}_{1:T}$. Assuming a smooth trajectory, it can be achieved by linear regression on N Gaussian basis functions, here denoted as $\psi$. Thus,

$$\begin{aligned} y_t=q_t=\varvec{\psi }_t^T\varvec{\omega }+\varepsilon _t \end{aligned}$$

(1)

and,

$$\begin{aligned} p(y_t|\varvec{\omega })=\mathcal {N}(y_t|\varvec{\psi }_t^T\varvec{\omega },\varSigma _t) \end{aligned}$$

(2)

where $\psi _t$ is a time dependent basis matrix and $\varepsilon _t \sim \mathcal {N}(0,\varSigma _t)$. The probability of observing the whole trajectory is then

$$\begin{aligned} p(\varvec{y}_{1:T}|\varvec{\omega })=\prod _1^T\mathcal {N}(y_t|\varvec{\psi }_t^T\varvec{\omega },\varSigma _t) \end{aligned}$$

(3)

In order to decouple movement from time, a phase variable is introduced to replace the time in the Eq. (2). For simplicity, in this article we will assume the phase of the model os identical to the timing of the demonstration such that $z_t=t$ and $\psi _{z_t}=\psi _t$.

For probabilistic models, a large amount of data is needed to learn the parameters. So assume M trajectories are obtained via demonstrations. we can obtain a set of parameter of each trajectory denoted $\varvec{\omega }_m$, and there is sign $W=\{\omega _{1},\cdots ,\omega _{m},\cdots ,\omega _{M} \}$. Define a learning parameter $\varvec{\theta }$ to govern the distribution of $\varvec{\omega }_m$ such that $\varvec{\omega } \sim p(\varvec{\omega };\varvec{\theta })$. A distribution of trajectory is obtained by integrating out $\varvec{\omega }$,

$$\begin{aligned} p(\varvec{y}_{1:T};\varvec{\theta })=\int p(\varvec{y}_{1:T}|\varvec{\omega })p(\varvec{\omega };\varvec{\theta })d\varvec{\omega } \end{aligned}$$

(4)

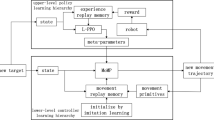
In ProMPs, the relationship between parameters is shown in the Fig. 1.

Fig. 1.

Relationship between parameters of ProMPs

we model $p(\varvec{\omega })$ as a Gaussian with mean $\varvec{\mu } \in \mathbb {R}^N$ and covariance $\varvec{\varSigma } \in \mathbb {R}^{N \times N}$, that is $\varvec{\theta }=\{\varvec{\mu },\varvec{\varSigma }\}$, computed from the training set $\varvec{W}$. The fidelity with which the distribution of trajectories in Eq. (4) captures the true nature of a task clearly depends on how $\varvec{\theta }$ controls the distribution of weights.

3 Path Integral

Although imitation learning can effectively replicate and generalize robot demonstration movement, it maybe not a optimal/suboptimal policy for the task. Furthermore, it can not autonomously fulfill the motion different from demonstration criterion. So we combine imitation learning (policy representation) with path integration (policy improvement) (Theodorou et al. 2010) through stochastic optimal control to meet the requirement. Specifically, we apply Feynman-Kac theorem to derive the state value function based on path integral, and then deduce the optimal control policy. In this way, we solve the Hamilton-Jacobian-Ballman (HJB) equation indirectly.

In Sect. 2, we use the method of ProMPs to parameterize the trajectory of robot joint. The $\varvec{\omega }$ in Eq. (2) is the parameter representation of trajectory. we can use parameter $\varvec{\omega }$ to repeat the demonstration. In this section, we will use a reinforcement learning called Policy Improvement with Path Integrals(PI$^2$) to make robot obtain skill of complex task like via point(s).

Multiple paths of variation $\tau _i$ can be generated by adding random perturbation to the weights($\omega$), and the optimal control quantity of system is the form of weighted average of the path shown as Eq. (5).

$$\begin{aligned} \begin{array}{rl} {\varvec{u}}_{t_i}&{}=-\varvec{R}^{-1}\varvec{B}^{T}_{s_{t_i}}\left( {\nabla }_{\varvec{x}_{t_i}}\varvec{V}_{t_i} \right) \\ &{} = \int \varvec{P}\left( \varvec{\tau _i} \right) \varvec{u_L} \left( \varvec{\tau _i} \right) d\varvec{\tau _i} \end{array} \end{aligned}$$

(5)

where $P\left( \tau _i \right)$ is a softmax function maping the cost $S(\tau _i)$ of ith trajectory to the interval [0,1] shown as Eq. (6), and there is the higher the cost, the lower the probability which can ensure that PI$^2$ converges to the lower cost. And $u_L(\tau _i)$ means the local control based on variation path, the form can be seen as Eq. (7).

$$\begin{aligned} \varvec{P} \left( \varvec{\tau _i} \right) = \frac{e^{-\frac{1}{\lambda }\varvec{S}\left( \varvec{\tau }_{t_i}\right) }}{\int e^{-\frac{1}{\lambda }\varvec{S}\left( \varvec{\tau }_{t_i}\right) }d\varvec{\tau _i}} \end{aligned}$$

(6)

$$\begin{aligned} \varvec{u_L}\left( \varvec{\tau _i}\right) =\frac{\varvec{R}^{-1}\varvec{B}_{s_{t_i}}\varvec{B}^T_{s_{t_i}}}{\varvec{B}_{s_{t_i}}^T R^{-1}\varvec{B}_{s_{t_i}}} (\varvec{\omega +\varepsilon _{t_i}}) \end{aligned}$$

(7)

The most important part for the customized task is the cost function in applying PI$^2$ which limits the convergence direction of algorithm, the form shows as following:

$$\begin{aligned} \begin{array}{rl} \varvec{S}\left( \varvec{\tau _i},k\right) &{}={{\varvec{\phi } _{{t_N,k}}} \!+\! \sum \limits _{j = i}^{N - 1} {{\varvec{q}_{{t_j}}}dt} } +\\ &{}\frac{1}{2}\!\sum \limits _{j = i}^{N - 1}\! \left( \varvec{\omega }+ \varvec{M}_{t_j,k}\varvec{\varepsilon }_{t_j,k}\right) ^T\varvec{R}\left( \varvec{\omega }+ \varvec{M}_{t_j,k}\varvec{\varepsilon }_{t_j,k}\right) \end{array} \end{aligned}$$

(8)

where $\varvec{\phi }_{{t_N,k}}$ means the terminal reward, $\varvec{q}_{{t_j}}$ are a state-dependent variable that the acceleration squared is used in this paper, and $bm{M}_{t_j,k}$ is a projection matrix that can be seen as following:

$$\begin{aligned} \varvec{M}_{t_j,k}=\frac{\varvec{R}^{-1}\varvec{B}_{s_{t_i}}\varvec{B}^T_{s_{t_i}}}{\varvec{B}_{s_{t_i}}^T \varvec{R}^{-1}\varvec{B}_{s_{t_i}}} \end{aligned}$$

(9)

Combining the actual task, the cost of end point present,

$$\begin{aligned} \phi _{t_N}=K_1\sum _{i=t_{N'}}^{t_{N}}\dot{y}^2+K_2\sum _{i=t_{N'}}^{t_{N}}(y-y_{\mathrm{goal}})^2 \end{aligned}$$

(10)

where the y and $\dot{y}$ are the position and velocity respectively. The cost consists of two part, one can ensure the velocity decay to zero in a very short time which is from $t_{N'}$ to $t_{N}$, other make sure that the joint can reach the desired position. $K_1$ and $K_2$ are constants which can be adjusted based on the demand.

In order to via point, we add the three part to cost function.

$$\begin{aligned} R_{\mathrm{viapoint}} = K\sum _{i=1}^N\left( y_{i,t_j}-y_{i,t_j}^*\right) ^2 \end{aligned}$$

(11)

where the $y_{i,t_j}$ and $y_{i,t_j}^*$ are the joint current position and desire position respectively. So, we can get the goal parameter which can achieve via point task.

$$\begin{aligned} \delta \varvec{\omega }_{t_i} = \sum _{k=1}^{K}\left[ \varvec{P}\left( \varvec{\tau }_{i,k}\right) \varvec{M}_{t_i,k}\varvec{\varepsilon }_{t_i,k}\right] \end{aligned}$$

(12)

$$\begin{aligned} \varvec{\omega }^{\mathrm{new}}=\varvec{\omega }^{\mathrm{old}}+\frac{\sum _{i=0}^{N-1}(N-i)w_{t_i}\,\delta \varvec{\omega }_{t_i}}{\sum _{i=0}^{N-1}w_{t_i}(N-i)} \end{aligned}$$

(13)

The way of via point by using ProMPs-PI$^2$ is shown as the Algorithm 1.

When using the method of ProMPs-PI$^2$ to make the robot get new skills, we should use Eq. (14) to generate K roll-outs that is shown the line 4 in Algorithm 1.

$$\begin{aligned} \varvec{\omega }_k=\varvec{\omega }+\varvec{\varepsilon }_k,k=1\cdots K \end{aligned}$$

(14)

where $\varvec{\omega } \in \mathbb {R}^N$, and N is the number of basis. And, $\varvec{\varepsilon }_k \in \mathbb {R}^N$ is the random. $\varvec{\varepsilon }_k^i$ that is the ith component obeys the Gaussian that mean is 0 and the variance is proportional to the order of magnitude of the data.

4 ProMPs-Bayesian-PI$^2$

Random perturbation will be added to the original PI$^2$ in parameter optimization. In other word, original PI$^2$ could search the whole parameter space. So, The efficiency of using traditional PI$^2$ to complete task of via point is relatively lower. In this section, we introduce a method of PI$^2$ combining the Bayesian estimate to compete the task such that via points faster.

Similar to Sect. 3, we assume the current position of joint at time t is $y_t$, desired position is $y^*_t$. Based on ProMPs, we can represent the trajectory as $\varvec{\theta }=\{\varvec{\mu }_{\omega },\varvec{\varSigma }_{\omega }\}$. On the basis of this assumption, we could use Eq. (15) to update the trajectory of via point.

$$\begin{aligned} \begin{array}{rl} \varvec{\mu }^+_{\varvec{{\omega }}} &{}=\varvec{\mu _{\omega }}+\varvec{K}(y^*_t-\varvec{H_t}^T\varvec{\mu _{\omega }})\\ \varvec{\varSigma }^+_{\varvec{\omega }} &{}=\varvec{\varSigma _{\omega }}-\varvec{K}(\varvec{H_t}^T\varvec{\varSigma _{\omega }})\\ \varvec{K} &{} =\varvec{\varSigma _{\omega } H_t}(\varvec{\varSigma _y^*}+\varvec{H_t^T\varSigma _{\omega } H_t})^{-1} \end{array} \end{aligned}$$

(15)

where $\varvec{H_t}=\psi _t$, and the parameter $\varvec{K}$ is called Kalman gain in the algorithm of Kalman filter.

The parameter $\varvec{\theta }^+=\{\varvec{\mu }_{\omega }^+,\varvec{\varSigma }_{\omega }^+\}$ generate trajectory which could via point. This method complete task of via point very fast, because it only needs to be calculated once. But this trajectory isn’t smooth, especially near the time t. Too much acceleration is fatal to the joint damage of robots.

In order to make better use of the advantages of Bayesian estimate and PI$^2$, we can use the results of Bayesian estimate to inspire the parameter search of PI$^2$. Let’s call this method Bayesian-PI$^2$. To be specific, using Bayesian estimation complete the task quickly. Then which is the result of Bayesian estimation can provide a direction for the PI2 search. It can avoid PI$^2$ explore in the whole parameter space. At the same time, in order to ensure the effect of PI2, we could inspire the primary weights of the related task.

Compare the pseudocode in Algorithms 1 and 2, the method proposed in this paper adds heuristic search for PI$^2$ by result target of Bayesian estimate as shown the line 4–6 in the Algorithm 2. The method of heuristic search generate K roll-outs shown in the Eq. (16).

$$\begin{aligned} \begin{array}{rl} \varvec{\omega }_k &{}=\varvec{\omega }+ {\varvec{\eta } '} ^T \cdot \varvec{\varepsilon }_k,k=1\cdots K\\ {\varvec{\eta } '} &{}=[\varvec{1},\varvec{\eta }_{i:i'},\varvec{1}]\\ \end{array} \end{aligned}$$

(16)

where the ${\varvec{\eta } '} \in \mathbb {R}^N$ and the N is the number of basis. Here we recombine the heuristic factory ${\varvec{\eta } '}$ that the part of $\varvec{\eta }_{i:i'}$ is the $[\varvec{\eta }_i \cdots \varvec{\eta }_{i'}]$ and others are the scalar 1. The position of i in the ${\varvec{\eta }}$ and ${\varvec{\eta } '}$ is the same and the option of parameters of i and $i'$ is related with task. Such as the task of via point in this article, we can select the position of the basis with the largest influence for via-point and its left and right five. The $\varvec{\varepsilon }_{i,i'}$ is the positive random and others is the random which obey Gaussian.

As shown in the Algorithm 2 and the Eq. (16), the parameter ${\varvec{\eta } '}$ has been added into heuristic information when PI$^2$ random search by using the result of Bayesian estimation. It can improve learning speed and ability of PI$^2$. The use of this method is described in more detail in the next section.

5 Simulation and Experiments

In this section, we would verify the method of preceding part of the text. At the same time, we would also explain the application scenarios of the theory. In the first experiment we verified the validity and rapidity of the algorithm with actual UR5 robot. Later, more complex tasks will be performed using a simulation robot on the V-REP platform by using Bayesian-PI$^2$.

5.1 Simple Task with Actual UR5

The UR5 is a collaborative robot with six degrees of freedom a repetition accuracy of 0.03 mm. So we can ignore the error of the robot itself in the experiment.

As shown int the table 2, using ProMPs represents the movement of the robot joint firstly. So based on the theory, we do several demonstration actions and record data of joints’ trajectory for the same task. When we say the same task, we mean the same starting point and ending point and the general trend of the trajectory is the same.

In the experiment, we use 31 basis function and evenly distribute over the timeline to fit the trajectory.

Then we randomly put a small landmark in the domain, which the robot can reach (excluding the point of demonstrations trajectories). So the robot is supposed to move passing through this via-point (for example strike) from previous start point to end point with the same duration.

We now proceeded to test the performance of traditional PI$^2$ and Bayesian PI$^2$. Detail results are shown in Fig. 2. The cost function is in the form of

$$\begin{aligned} \begin{aligned}&0.5\!\sum \limits _{j=1}^{6}\!{\sum \limits _{i=1}^{N-1}{\!\!\left[ \!\! {{10^3\!\left( \!\! {\ddot{x}^{\left( j \right) }}\!\!\left( i \right) \!\! \right) }^{2}}\!\!+\!\!{{\left( \!\! a_{f}^{\left( j \right) }\!\!\left( i \right) \!\! \right) }^{2}} \right] }}\!\!+\!\!\sum \limits _{j=1}^{6}\!\!{{{10}^{10}}\!\!\left[ \!\! {{\left( {{x}^{\left( j \right) }}\!\left( m \right) \!\!-\!{{x}^{\left( j \right) }_v} \right) }^{2}} \right] }\\&+\sum \limits _{j=1}^{6}{{{10}^{3}}\left[ {{\left( {{{\dot{x}}}^{\left( j \right) }}\left( N \right) \right) }^{2}}\text {+}{{\left( {{x}^{\left( j \right) }}\left( N \right) -{{x}^{\left( j \right) }_g} \right) }^{2}} \right] } \end{aligned} \end{aligned}$$

(17)

where i indicates the time index from 1 to N, j indicates the joint index from 1 to 3. Besides, $x^{(j)}_g$ denotes the expected position of point j when the task ends. When the time index equals m, $x^{(j)}(m)$ is the position of joint j which is corresponding to the expected via-point $x^{(j)}_v$ of the joint j. Apparently, ${{\ddot{x}}^{\left( j \right) }}$ is an arbitrary state-dependent cost value, $a_{f}^{\left( j \right) }\left( i \right)$ is the acceleration (forcing term) relevant to joint j at the time index i. ${{\dot{x}}^{\left( j \right) }}\left( N \right)$ is the velocity of joint when time index is N.

Fig. 2.

The curve of Bayesian-PI$^2$ and tradition PI$^2$ through via-point in the joint space, Left: Bayesian-PI$^2$, Right: tradition PI$^2$, and the red mark(*) is the via point which is set artificial randomization in the joint space (Color figure online)

Fig. 3.

Compare cost of traditional PI$^2$ and Bayesian PI$^2$

Fig. 4.

Compare the trajectory in space of joint when traditional PI$^2$ and Bayesian PI$^2$ both have the same number of iterations

In this experiment, we set a point which position of joint space is (0.8,-1.14,1.2,-1.0,-0.18,-0.02) and make robot via point at time 1.5s. According to the result as shown in Fig. 2, the traditional PI$^2$ and Bayesian PI$^2$ both complete the task of via point with high accuracy. It can explain that the method mentioned in this paper is effective. But in terms of the rate of convergence of cost, as shown in Fig. 3, Bayesian PI$^2$ has fewer iterations than the methods of traditional PI$^2$.

On the other hand, we use the same number of iterations to compare the results of two methods. The results are shown in the Fig. 4.

Fig. 5.

The actual with UR5, tradition PI$^2$ and Bayesian-PI$^2$ both pass the point

As shown in Fig. 4, dash line is the mean trajectory of multiple demonstration. Dash-dot line and solid line are the curve of traditional PI$^2$ and Bayesian PI$^2$, respectively. In the experiment, we use the UR5 to verify proposed method and the result is shown as Fig. 5.

In this experiment, the result indicate the Bayesian PI$^2$ of this paper is effective and converges faster than traditional PI$^2$.

5.2 Complex Task on V-REP Platform

As shown in Fig. 6(a), we set two points in the joint space which the position in the space of joint are (0.8,1.9,1.2,−1.0,−0.18,−0.22) and (0.55,−1.5,1.34,−0.62,−0.7,0.16) denoted as the mark (*) and (+) respectively. In Fig. 6(b), the mark of red and blue are point set int the Cartesian space which calculate by forward kinematics. Using the method of Bayesian-PI$^2$ make the end of robot via two point at time 1s and 2s, respectively. The result indicates the method has the ability to perform more complex tasks.

Similar to the experiment in the Sect. 5.1, we compare the method tradition PI$^2$ when make robot via two point. The result is shown as Fig. 7. In the Fig. 7(a), the way of traditional PI$^2$ can’t via points accurately. But the method that this paper proposed can via points we set randomly. The result shows the method of Bayesian PI$^2$ has the better performance for complex task such that via two points. As shown in Fig. 7(b), the rate of convergence of Bayesian PI$^2$ is faster than traditional PI$^2$ similarly.

Fig. 6.

Via two points by using the method of Bayesian-PI$^2$ (Color figure online)

Fig. 7.

The result of tradition PI$^2$ and compare the cost with Bayesian PI$^2$

6 Conclusions

This paper present an methods which can make the robot obtain new skills faster on the policy improved stage. The results of Bayesian estimation can provide a heuristic to the search parameters. The search space of policy improved can be reduced by the posterior space of Bayesian estimation. So it can speed up optimization.

At the same time, the article verify the method of Bayesian-PI$^2$ with UR5. As shown in the experiment, it not only complete task but also does converge faster and for the complex task this method has the better performance. Our method is effective for a class of tasks that can predict results such that motion planning of via point(s). In the future, the path planning method with better generalization ability can be explored.