A dynamical system approach to task-adaptation in physical human–robot interaction

Abstract

The goal of this work is to enable robots to intelligently and compliantly adapt their motions to the intention of a human during physical Human–Robot Interaction in a multi-task setting. We employ a class of parameterized dynamical systems that allows for smooth and adaptive transitions between encoded tasks. To comply with human intention, we propose a mechanism that adapts generated motions (i.e., the desired velocity) to those intended by the human user (i.e., the real velocity) thereby switching to the most similar task. We provide a rigorous analytical evaluation of our method in terms of stability, convergence, and optimality yielding an interaction behavior which is safe and intuitive for the human. We investigate our method through experimental evaluations ranging in different setups: a 3-DoF haptic device, a 7-DoF manipulator and a mobile platform.

1 Introduction

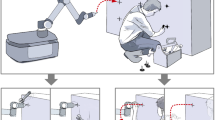
Compliant behavior, ranging from passive (due to the mechanical design) to active (due to the control design), is a key requirement for robots to interact with humans (Billard 2017). Active compliance has been of particular interest to engineers for achieving safe and intuitive physical interaction (De Santis et al. 2008). Most control approaches for pHRI can be formulated as a hierarchical feedback loop as shown in Fig. 1 where the final behavior can exhibit compliance at different levels:

• 1. Compliance at the force-level the robot is designed to fulfill a particular motion, however, it remains compliant toward small perturbations due to the external forces; see Hogan (1988).

• 2. Compliance at the motion-level the robot is designed to execute a particular task, however, it allows for variation of motions that still fulfill the task; see Kronander and Billard (2016).

• 3. Compliance at the task-level the robot switches or adapts to a task that complies with the intention of its human partner; see Bussy et al. (2012a).

As humans, we benefit from compliance at all these levels. Safety is the immediate and fundamental advantage. Moreover, this compliance enables action perception, intention recognition, and adaptation in humans (and potentially robots). Sebanz and Knoblich (2009) suggests that the human follower complies with the actions of others (i.e., compliance at the motion and force-level) which allows intention recognition, and subsequently, action coordination (i.e., compliance at the task-level). Due to the follower’s compliant behavior, the leader is able to communicate his/her intention through interaction-forces (van der Wel et al. 2011; Sawers et al. 2017) and movements (Sartori et al. 2011). Beside compliance, predictive models (Davidson and Wolpert 2003; Vesper et al. 2010) are also required to recognize others’ intention and anticipate their actions. We previously showed that the adaptation of a simple forward predictive model can provide pro-active following behavior (Khoramshahi et al. 2014). In the same line, Noohi et al. (2016) demonstrated that robots can benefit from human-driven predictive models for cooperative tasks with humans. Moreover, Burdet et al. (2001) and Ganesh et al. (2014) suggest that adaptation of such models (at the force-level) improves the motor performance of humans both in solo and interaction scenarios. Even though many works provide compliance and adaptation at the level of force and motion-generation, compliance and adaptation at the task-level has been explored only in limited settings. The goal of this article is to provide a rigorous analysis of this problem and to propose a task-level adaptation mechanism that is smooth and ensures convergence to an intended task. Our previous works (Khansari-Zadeh and Billard 2011; Kronander and Billard 2016) have demonstrate that dynamical systems as motion generators have a great capacity to encode for a task, generate smooth trajectories, and also comply at the level of motion-generation. we complement this body of work by providing adaptation capabilities to these systems, enabling robots to adapt tasks to the intention of the human through physical interaction. More specifically, we contribute to this literature by providing:

$\circ$ :

a dynamical system approach to pHRI that offers:

$\diamond$ :

a strategy for recognizing human intention

$\diamond$ :

stable and smooth task transitions

This approach yields compliant physical interaction between human and the robot in practical settings. We propose an adaptive-control framework based on dynamical systems both as motion-generators (which allows for smooth transitions across tasks) and as predictive models (which allows for efficient human-intention recognition and adaptation). We provide a rigorous analytical evaluation of our approach in terms of stability, convergence and optimality. Experimental evaluations on several scenarios show the efficacy of our approach in terms of prediction of human intention, smooth transition between tasks, stable motion generation, safety during contact, human effort reduction, and execution of the tasks.

2 Related work

The applications of pHRI are multifarious: carrying and installing heavy objects (Kim et al. 2017; Lee et al. 2007), hand-over (Strabala et al. 2013), cooperative manipulation and manufacturing (Peternel et al. 2014; Cherubini et al. 2016), and assistive tele-operation (Peternel et al. 2017). While the field of pHRI is rapidly expanding, the role of most robots in the interaction falls into two extreme cases:

• (1) Passive followers (PF) whereby reducing the interaction-forces and spatial error (i.e., compliance at the force-level), the robot provides a passive following behavior. This approach has the advantage that human can lead the task (i.e., decides on the desired trajectory), however, the robot cannot provide power/effort in the direction of the uncertainties (i.e., due to the human intentions). Carrying heavy loads in collaboration with human (Bussy et al. 2012b) is the rudimentary example where the robot only provides support in the direction of gravity but fails to assist in the human-intended direction of movement where it even increases the total mass.

• (2) Active leaders (AL) where the robot executes a pre-defined task while allowing for safe interactions with environment and tolerating for small perturbations; i.e., achieving compliance at motion and force-level as in Kronander and Billard (2016)), This approach has the advantage of minimizing the human effort. Nonetheless, if the robot is pre-programmed to accomplish only one task, any human efforts to perform a different task (in the course of the interaction) will be rejected.

Evrard and Kheddar (2009) and Li et al. (2015) proposed different control architectures that explicitly modulate the role of the robot (between follower and leader). However, one could aim for approaches that benefit from the advantages of both PF and AL. For example, to reach a pro-active behavior where the robot actively coordinate its actions with the human partner. To do this, many predictive models for human behavior have been proposed. For instance, Petrič et al. (2016) proposed to use Fitts’ law to predict human movements. As another case, Leica et al. (2017) suggested a model based on mechanical-impedance that predicts human motions based on the interaction forces. Other approaches were suggested to learn the dynamics of the collaboration (including control and prediction dynamics) (Rozo et al. 2013; Ghadirzadeh et al. 2016). Moreover, most of the approaches in the literature tackle the prediction problem in the framework of impedance control. From a control perspective, the simplest tool to provide compliance at a force-level is impedance control (Hogan 1988). This controller can be formulated as

$$\begin{aligned} u_r = -K (x_r - x_d) - D (\dot{x}_r - \dot{x}_d) +F_f. \end{aligned}$$

(1)

where $x_r$ and $x_d \in \mathbb {R}^3$ are the real and desired position respectively. K and D indicate the damping and the stiffness of the controller, and $F_f$ represents a feed-forward control force. Based on the advancement of variable impedance control (Vanderborght et al. 2013), many approaches aim for the dynamic optimization of K and D to achieve a desirable compliant behavior during human–robot interaction (Duchaine and Gosselin 2007). To go further and achieve a human-like compliant behavior, Ganesh et al. (2010) proposed an adaptation method based on human motor behavior which was shown to be effective in human–robot interaction settings by Gribovskaya et al. (2011). Beside the optimization of the impedance parameters (K and D), other approaches aim to achieve a desirable behavior by optimization of the impedance setpoints (i.e., $x_d$ and $\dot{x}_d$); see Maeda et al. (2001) and Corteville et al. (2007). To be effective, this approach requires motion estimation and planning under human-induced uncertainties which is tackled in the literature by means of optimal and adaptive control (Medina et al. 2012; Li et al. 2016), machine learning techniques (Calinon et al. 2014; Medina et al. 2011), and more specifically reinforcement learning (Modares et al. 2016). These works, to some extent, rely only on a local anticipation of human motions which, nevertheless, lowers the human effort (Evrard and Kheddar 2009) and increases transparency (Jarrassé et al. 2008). Regarding this literature, human-intention adaptation is only addressed at the motion and force-level (see Fig. 1). However, robotic systems can tremendously benefit from adaptation at the task-level where the robot adapts its task to those intended by the human-user.

Fig. 1

A generic control design approach to physical human–robot interaction where, based on a decided task, corresponding motions are generated, and consequently, corresponding forces are applied. Each block takes proper perceptual input into consideration to achieve a desirable behavior

Fig. 2

Dynamical systems as motion generators. In both cases the dynamical systems in a feedback loop with the controller and the environment. This leads to an active motion generation meaning the generated motion is influenced by the real state of the robot (i.e., the real position $x_r$). a in the static case, the motion generators try to provides desired velocity only corresponding to one dynamical system (i.e., the representation of only one task). b in the adaptive case, the motion generator is capable of combining several dynamical systems to comply to the intention of the human which enables the robot to transit/switch from one task to another). In this schematics, $b_i$ are task-beliefs which are inferred by a similarity check between real velocity $\dot{x}_r$ and the corresponding task velocity ($f_i(x_r)$), and used as output gains to construct the final desired velocity of the motion generator; i.e., $\dot{x}_d$

The amount of previous efforts addressing adaptation at a task level is sparse. Bussy et al. (2012a) employed a velocity threshold to trigger a new task (e.g., switching from “stop” to “walk” while carrying an object). As reported, such hard switching results in abrupt movements which are required to be filtered to reach human-like motions. Pistillo et al. (2011) proposed another framework (based on dynamical systems) where the robot switches between tasks if it is pushed by its human-user to different areas of its workspace. Although this approach leads to a reliable and smooth transition between tasks, such human-intention recognition strategy (i.e., based on the location of the robot in the workspace) is not efficient; e.g., each task needs a considerable volume of the workspace to be functional, and the robot cannot switch between different tasks in the same area of the workspace. Moreover, there has been recent interesting methods to encode several tasks in one model (Ewerton et al. 2015; Calinon et al. 2014; Lee et al. 2015), and disjointly, several works to recognize and learn the intention of the human (Aarno and Kragic 2008; Bandyopadhyay et al. 2012; Wang et al. 2018; Ravichandar and Dani 2015). Only recently, Maeda et al. (2017) proposed a probabilistic model that not only encodes for different tasks, but also acts as an inference tool for intention recognition. However, they do not address the online and physical interaction between the human and the robot.

3 Task-adaptation using dynamical systems

In this section, we propose a novel approach for task-level compliance. Our adaptation scheme is built upon an impedance controller that allows for force-level compliance and a set of dynamical systems (DS) defining the tasks known to the robot as illustrated in Fig. 2.

Definition 1

(DS-based impedance control) The dynamics of the control system are defined as

$$\begin{aligned} M(x_r) \ddot{x}_r + B(x_r,\dot{x}_r) + G(x_r) = F_{inv} + F_{imp} + F_{h} \end{aligned}$$

(2)

where $x_r \in \mathbb {R}^3$ is the real position of the end-effector. $M \in \mathbb {R}^{3\times 3}$ is the mass matrix, $B \in \mathbb {R}^3$ represents the centrifugal forces,and $G \in \mathbb {R}^3$ represent the effects of gravity. $F_{inv} \in \mathbb {R}^3$ is the inverse dynamics forces, $F_{imp} \in \mathbb {R}^3$ is the impedance control forces enabling the robot to track a desirable velocity profile ($\dot{x}_d \in \mathbb {R}^3$), and $F_h \in \mathbb {R}^3$ represents forces applied by human based on his/her intention. Without loss of generality, we assume that $F_{inv}$ compensates for the left side of Eq. 2 yielding dynamics as follows:

$$\begin{aligned} M \ddot{x}_r = F_{imp} + F_{h} \end{aligned}$$

(3)

where

$$\begin{aligned} F_{inv} = B(x_r,\dot{x}_r) + G(x_r) \end{aligned}$$

(4)

Moreover, we use the impedance controller proposed by Kronander and Billard (2016) as follows

$$\begin{aligned} F_{imp} = -D(\dot{x}_r - \dot{x}_d) \end{aligned}$$

(5)

where $\dot{x}_d$ is provided by the motion generator which leads to the final dynamics as:

$$\begin{aligned} M \ddot{x}_r + D(\dot{x}_r - \dot{x}_d) = F_{h} \end{aligned}$$

(6)

Definition 2

(Autonomous non-autonomous modes) Given the dynamics in Eq. (6), we call the condition where the human does not interact with the system (i.e., $F_h=0$) autonomous, and otherwise ($F_h \ne 0$) non-autonomous.

Assumption 1

(Encoded tasks) We further assume that the robot knows a set of N possible tasks represented by first order DS, such that the ith task is given by

$$\begin{aligned} \dot{x}_d = f_i (x_r) \end{aligned}$$

(7)

Moreover, each DS is globally asymptotically stable at either an attractor or a limit cycle under a continuously differentiable Lyapunov function $V_i(x)$.

Fig. 3

Linear combination of two DS allowing for smooth transition from one task to another. a CW and CCW rotations encoded by $f_1$ and $f_2$ where $b_2 = 1-b_1$. The trajectory is a generated motion where $b_1$ is linearly changed from 0 to 1. b The generated motions stay smooth during the transition

Although DS are typically used for motion generation (Eq. 1), they can also be used for task identification; i.e., given a current position and current velocity of the robot, they can evaluate a similarity measure between an arbitrary task and the current velocity, or, equivalently in this context, the result of the interaction between the robot and the human user. We use such similarities in our adaptation mechanism to enforce the task with the highest similarity to the human’s current velocity. To have a smooth transition from one task to another, the desired velocity is specified through a linear combination of DS as follows:

Definition 3

(Task parameterization) Given a set of dynamics systems ($f_1$ to $f_N$) each encoding for a task, we introduce the following linear combination as the motion generator.

$$\begin{aligned} \dot{x}_d = \sum \limits _{i=1}^{N} b_i ~ f_i(x_r) \end{aligned}$$

(8)

where $b_i \in \mathbb {R}$ are corresponding beliefs for each DS ($f_i$) which satisfy the following conditions.

$$\begin{aligned} \sum \limits _{i=1}^{N} b_i =1 ~~~~ \text {and}~~~~ 0 \le b_i \le 1 \end{aligned}$$

(9)

Figure 3 shows a simple example of such linear combination where a continuous transition in $b_i$ parameter leads to a smooth transition from one task to another.

Definition 4

(Adaptation mechanism) We introduce the following adaptation mechanism.

$$\begin{aligned}&\dot{\hat{b}}_i = - \epsilon ~\left( |\dot{x}_r - f_i(x_r)|^2 + 2 \sum \limits _{j\ne i} b_j f_j(x_r)^Tf_i(x_r) \right) \end{aligned}$$

(10)

$$\begin{aligned}&\dot{B} = \varOmega (\dot{\hat{B}})\nonumber \\&b_i \leftarrow b_i + \dot{b}_i ~\varDelta t \nonumber \\&b_i \leftarrow \max (0, \min (1,b_i)) \end{aligned}$$

(11)

where $\dot{\hat{B}}=[\dot{\hat{b}}_1,...,\dot{\hat{b}}_N]$ is a vector of belief-updates, $\epsilon \in \mathbb {R}$ is the adaptation rate, $\varOmega : N \rightarrow N$ represents a winner-take-all process (which adds an offset such that only the maximum update stay positive), and $\varDelta t$ is the sampling time. |.| denotes the norm-2 of a given vector.

In this adaptation mechanism, belief-updates ($\dot{\hat{b}}_i$) are computed based on the similarities between each DS ($f_i$) and the real velocity ($\dot{x}_r$). Broadly speaking, the second term in Eq. (10) accounts for the inner-similarity between DS. In the second step (Eq. 11), the beliefs are modified based on an Winner-Takes-All (WTA) process that ensures only one increasing belief and $N-1$ decreasing one. Finally, the beliefs are updated based on a given sampling-time and saturated between 0 and 1. However to ensure proper convergence behavior the WTA process should satisfy the following properties:

• 1. There is no more than one belief-update with a positive value in $\dot{B}$.

• 2. The pairwise distances are preserved:

  $$\begin{aligned} (\dot{b}_i - \dot{b}_j)/(\dot{\hat{b}}_i - \dot{\hat{b}}_j) \ge 1 ~~~\forall i,j \end{aligned}$$

  (12)

• 3. The update using $\dot{B}$ preserves $\sum \limits _{i=1}^{N} b_i =1$.

Even though WTA can be implemented in several fashions, see “Appendix A.1” for a simple implementation that we use in this work. Moreover, based on the properties of WTA, the adaptation dynamics can be seen as a set of pairwise competitions; see “Appendix A.2”.

4 Optimality, convergence, and stability

In this section, we study the stability and convergence of the proposed adaptive law. We start by showing that our proposed adaptation methods can be considered as a minimization-operator on a cost-function based on the error induced by the human. For simpler notion, we drop the argument of the DS; i.e., we write $f_i$ instead of $f_i(x_r)$.

Theorem 1

(Optimality) The proposed adaptation mechanism in Eq. (10) minimizes the following cost-function.

$$\begin{aligned} J(B) = |\dot{e}|^2 + \sum \limits _{i=1}^{N} b_i (1-b_i) |f_i|^2 \end{aligned}$$

(13)

where $\dot{e} = \dot{x}_r - \dot{x}_d$, and where ${{B}}=[{{b}}_1,...,{{b}}_N]$ is the belief vector.

Proof

see “Appendix A.3”. $\square$

The first term in this cost-function reduces the discrepancy difference between the robot and the human’s intention, and the second term favors the beliefs that are either close to zero or one; i.e., lower uncertainty. It is interesting to note that the error function that the adaptation tries to minimize is similar to the one in the impedance control. However, the difference is that the impedance controller tries to bring $\dot{x}_r$ close to $\dot{x}_d$ whereas in the task-adaptation, the motion generator tries to bring $\dot{x}_d$ (based on possible tasks encoded by the set of $f_i$) close to $\dot{x}_r$ assuming that real trajectory has components induced by human based on his/her intention; see Fig. 4.

Fig. 4

An example of a discrepancy induced by the human guiding the robot away from its current desired trajectory $\dot{x}_d$. The impedance controller (Eq. 5) tries to reduce this error by controlling$\dot{x}_r$ toward $\dot{x}_d$ while the adaptation mechanism (Eq. 10) tries to reduce the same error by adapting$\dot{x}_d$ to a DS that is similar to $\dot{x}_r$ ($f_1$ in this example)

With regard to convergence, in the following, we analyze our adaptation mechanism in two conditions: first, when the user behavior matches the motions encoded in one of the DS, and second, when the user is not exerting any forces and the robot execution becomes autonomous.

Theorem 2

(Convergence to demonstration) Given the real velocity $\dot{x}_r = f_k(x)$, the adaptation converges to $b_k=1$ and $b_i=0$ for all other beliefs if the demonstrated task is distinguishable from others with the following metric.

$$\begin{aligned} |f_k - (f_l + \delta _{kl}) |^2 > 2(b_l - b_k) f_k^T f_l + |\delta _{kl}|^2 ~~~~ \forall l \ne k \end{aligned}$$

(14)

where $\delta _{kl} = \sum \limits _{i \ne k,l} b_i f_i$ is the effect of other DS.

Proof

see “Appendix A.4”. $\square$

Using this condition (Eq. 14), we can study the possibility of switching from one DS to another over the sate-space in the worst case condition. This can be taken into consideration beforehand to design the DS.

Theorem 3

(Convergence in autonomous condition) In the autonomous condition, the belief of a DS ($b_i$) exponentially converges to 1 if $b_i>0.5$

Proof

see “Appendix A.5”. $\square$

Fig. 5

a Geometrical illustration of the adaptation mechanism in the case of two DS. $\dot{x}_r$ is the real velocity vector (assumed to be influenced by human) , and $\dot{x}_d$ is the desired velocity generated by the two DS ($f_1$ and $f_2$) and their corresponding beliefs ($b_1$, $b_2$). b the result of few iterations using $\epsilon =0.4$. c The cost function of the adaptation parametrized over $b_1$ and $b_2$. d The decrease in the cost function for each time step

Now, we investigate the stability of the generated motion due to the linear combination of the DS as introduced in Eq. 8. In our stability analysis, we are concerned with the divergence of the generated motions and spurious attractors/limit-cycles. Here, we only investigate the autonomous case where the human-user does not exert any force. Note that having a stable behavior in the autonomous case provides a satisfactory condition for the stability of the non-autonomous case (where the human is in contact with the robot) for two basic assumptions: First, the human-user increases the passivity of the system (increasing stability margin away from divergent behaviors), and second, our adaptation mechanism is able to adapt to local perturbations of the human-user (rendering void the concept of spurious attractor and limit cycle).

In the following, we assume that each DS ($f_i$) generates stable motions under the Lyapunov function $V_i(x)$.

The stability of generated motion Eq. 8 in the autonomous condition (which can be seen as a Nonlinear Parametrically-Varying System) is not straight-forward (even for linear cases). Nevertheless, one can ensure the stability when all DS ($f_i$) are stable under a same Lyapunov.

Lemma 1

(Convergence set) The following DS

$$\begin{aligned} \dot{x} = \sum \limits _{i=0}^{N} \alpha _i(t) ~ f_i(x) \end{aligned}$$

(15)

where $\alpha _i \in \mathbb {R}$ are a set of positive and arbitrary time-varying values, asymptotically converges to an arbitrarily set $\varXi$ over the state x, if a positive definite function V(x) exists such that

• 1. $V(w) < V(z) ~~~~\forall w,z ~|~ w \in \varXi$  and  $z \notin \varXi$

• 2. $(\partial V/\partial x) ^T f_i < 0 ~~~~ \forall i$  and  $x \notin \varXi$

Although very restrictive in its conditions, Lemma 1 guarantees that the system will not diverge outside $\varXi$. However, in the case of the adaptation, the $b_i(t)$ do not change arbitrarily. Based on the exponential convergence of beliefs (Theorem 3), the stability of the motion generation in the autonomous mode can be formulated as the following theorem.

Theorem 4

((stability of generated motions) In the autonomous condition, the generated motions are stable if a task with $b_i>0.5$ exists.

Proof

see “Appendix A.6”. $\square$

5 Illustrative example with two tasks

For illustrative purposes, we investigate the adaptation mechanism for a simple case with two DS ($f_1$ and $f_2$) encoding two arbitrary tasks. Figure 5a shows a generic example for computation of belief-updates following Eq. (10). It can be seen that the second DS ($f_2$) has a higher similarity to the real velocity ($\dot{x}_r$); i.e., lower norm-2 distance. Inner-similarity terms (i.e., $f_1^Tf_2$) are important in higher number of DS where adaptation favors updates of DS that are less similar to the rest. After few iterations, the motion generator converges to the second DS. Furthermore, regarding the optimality principle (Theorem 1), Fig. 5d shows the decrease in the cost (Eq. 13). Since, in this example $\dot{x}_r$ is fixed, the cost is only a function of $b_1$ and $b_2$ which is illustrated in Fig. 5c. It shows that the beliefs are updated in the direction of the gradient. However, the adaptation mechanism constrains the updates on the $b_1 + b_2 = 1$ manifold.

Moreover, the simplicity of having two DS allows us to have the close formulation of the updates after WTA process. Based on Eq. (25), WTA algorithm in “Appendix A.1”, and the unity constraint ($b_1+b_2=1$), we have

$$\begin{aligned} \begin{aligned} \epsilon ^{-1}~ \dot{b}_1&= (f_1 - f_2)^T\dot{e} + (b_1-0.5)(|f_1|^2+|f_2|^2) \\ \epsilon ^{-1}~ \dot{b}_2&= (f_2 - f_1)^T\dot{e} + (b_2-0.5)(|f_1|^2+|f_2|^2) \\ \end{aligned} \end{aligned}$$

(16)

where $\dot{e} = \dot{x}_r - \dot{x}_d$. Each term in this formulation has an interesting interpretation. The first increases the belief if the error has more similarity (in the form of inner product) to a DS compared to other ones. The second term pushes away the belief from the ambiguous point of 0.5. Therefore, for a belief to go from zero to 1, the similarity (the first term) should be strong enough to overcome the stabilization term (the second term). Moreover, in accordance with Theorem 3, this equations show that, in zero error condition ($\dot{e}=0$), the DS with $b_i>0.5$ tasks over.

Fig. 6

Possible transitions between the two DS shaded in green

Fig. 7

a The simulated results for adaptation across two tasks where the desired behavior changes from the second DS to the first one based on the interactional forces. b The evolution of beliefs and the applied power by the robot and by the human during the simulated example. c The haptic device used to evaluate a simple interaction of our proposed adaptation mechanism with a human-user. d Switching across the two DS induced by the human during the real interaction

We now consider the particular case where the real velocity exactly matches the first DS (i.e., $\dot{x}_r=f_1$); see Theorem 2. This setting takes place when the human demonstrates a task by overriding the motion. By updating the definition of the error in Eq. (16), the dynamics of the adaptation simplifies as

$$\begin{aligned} \begin{aligned} \epsilon ^{-1}~ \dot{b}_1&= 0.5 |f_1-f_2|^2 + (2b_1 - 1) f_1^T f_2 \\ \end{aligned} \end{aligned}$$

(17)

To have a positive update in the worst case scenario ($b_1=0$), the DS should satisfy the following inequality.

$$\begin{aligned} \begin{aligned} |f_1-f_2|^2 > 2 f_1^T f_2 \\ \end{aligned} \end{aligned}$$

(18)

where |.| denotes the absolute value. This inequality can be satisfied by any two vectors with inner angles $>\pi /3$. Therefore, to have a guaranteed transition between DS, their vector fields need to have enough dissimilarity. Figure 6 shows an example where two similar DS bifurcate to different behaviors. The green-shaded area indicates the part of the state-space where transitions are possible (based on Eq. 18). However, is some outer regions, it is still possible to transit between similar DS by exaggerating the motion; e.g., $\dot{x}_r = 1.2f_1 -.2f_2$.

5.1 Simulated interaction

To investigate a simple example with human interaction, we consider the two DS illustrated in Fig. 3 as the motion generators and the DS-based impedance controller in Eq. (5). Figure 7a, b show the result of the simulated interaction. At $t=0$, a simulated agent intends to change the task form $f_2$ to $f_1$ by applying forces with the following equation.

$$\begin{aligned} F_h = -30 (\dot{x}_r - f_1) - (1-b_1) F_{imp} \end{aligned}$$

(19)

However, these forces are only active for 0.5 s and saturated at 15N. Regarding Eqs. (3–5), $M=0.82$ and $D=30$, and adaptation rate ($\epsilon$) is 5. Figure 7a shows how the motion generator adapts with regard to the vector-fields of the DS. It can be seen that only a short demonstration (i.e., the black portion of the trajectory which lasts for 0.3 s) enables the robot to adapt to the intended task. Figure 7b shows the adaptations of the beliefs, and power consumptions of the robot and the simulated agent. Its negative sign indicates that the agent is decelerating the motion as the robot moves in accordance with the undesirable DS.

5.2 Real-world interaction

To test our 2-DS example in a realistic scenario, we implemented our approach on a Falcon Novint haptic device where the human user can drive the robot toward his/her desired trajectory; see Fig. 7c. Hereafter, the robot detects the discrepancy created by the human user and tries to compensate for it by adapting the task to the intention of the human. The results of switching across the two tasks are illustrated in Fig. 7d; i.e., from the first DS to the second one and vice versa. The switching behavior is consistent across different attempts. The switching time (0.5 s which is subjected to the behavior of human-user) is similar to the simulated results (Fig. 7b). However, the profiles are not as linear as in the simulation, and they tend to behave exponentially. This discrepancy can be explained by the difference between the actual and modeled (Eq. 19) behavior of a human-user as well as unmodeled dynamics such as damping and friction. Compared to the power exchanges in the simulation, it can be seen that in the simulated scenario, the simulated human applies abrupt and negative power to quickly decelerate the robot and trigger the adaptation mechanism ($\simeq 0.1$ s). However, in the real scenario, the human user decelerates the robot much slower ($\simeq 0.2$ s) via smaller power benefiting from damping and friction in the hardware. Moreover, after the initial update on the gains ($b_i > 0.4$), no further effort is required from the human. After this phase, the figure shows different arbitrary behaviors from the human; i.e., releasing the device, cooperating with the robot, or trying to switch the DS again.

6 Experimental evaluations

We consider two realistic scenarios (inspired by industrial settings) to evaluate our method in interaction with humans. In the first scenario, the robot and the human-user perform a series of manipulation tasks. In the second scenario, they carry and place heavy objects collaboratively.

Fig. 8

An example of task-adaptation in compliant human–robot interaction. The user and the robot perform a series of manipulation tasks jointly. The robot recognizes the intention of human and adapts its behavior; i.e., switches to the corresponding task. a The human can ask the robot to polish linearly, b leave the workspace , c polish circularly, or d push down on a object

6.1 Scenario 1: manipulation tasks

In this part, we consider a set of collaborative manipulation task. We consider a working station where the robot and the human polish and assemble a wooden structure; see Fig. 8. The robot consists of a 7-DOF KUKA LWR 4+ robot with a flat (plastic) end-effector where a sand-paper is attached. The robot is capable of performing four tasks:

• (A) Linear polish (LP) The robot polishes a surface along a line.

• (B) Circular polish (CP) The robot performs a circular motions as to polish a specific location on an object.

• (C) Push down (PD) The robot pushes down on an object and holds it (e.g., to be glued).

• (D) Retreat The robot retreats and make the workspace fully available to the human-user.

Fig. 9

Motion planning using dynamical systems that encodes for different tasks. Each task can be performed form any point in the robot workspace

Fig. 10

The overall result of the proposed adaptation mechanism for the manipulation tasks using a robot arm. a According the interaction with the human-user, the robot successfully switches from one task to another. b The human-user requires to exchange mechanical power with the robot to demonstrate his/her intention. c The minimization of the adaptation cost (Eq. 13) upon human perturbations. Note that, to have a comparable units, the root-square of the cost in plotted here. d The dynamics of the adaptation (Eq. 10) where the dissimilarity of the real velocity to each task affects its belief and vice versa. e Prediction of the human perturbations based on the dissimilarity of the real velocity with each task. f The performance of the robot for execution of each task after adaptation and in absence of human interaction

As stated in Assumption 1, each tasks is encoded by a DS; see “Appendix B.1.1” for their parameterizations. The generalization provided by the DS enable the robot to perform any of the tasks from any point in its workspace. This is shown in Fig. 9 where the robot is ready to perform any of the task by following the trajectories generated by the DS. From Definition 1, we use the DS-based impedance control to ensure safe and stable interaction between the robot and its environment. For this experiment, D is set 100 to have a practical balance between tracking and compliance. Moreover, this impedance gain (along with DS-generated trajectories) enables the robot to handle the tasks that requires contact with the environment by generating appropriate forces ($F_{imp}$) in both contact and non-contact conditions. For the adaptation rate, we use $\epsilon =1.5$. For discussion on how to tune this parameter, see Sect. 7.1.

Figure 10 shows the overall results of the adaptation in this experiment. We systematically assessed all possible switchings across tasks. The first subplot (Fig. 10a) shows how, upon human perturbation, the beliefs are adapted. Specifically, the previous task loses its beliefs (falling from 1 to 0) while the new one takes over; the changes in the belief of all other tasks being negligible. It roughly takes 1 s for the belief to rise (from 5 to 95%). However, this rise-time depends on the quality of the human-demonstration, distinguishability of the tasks, and the adaptation rate ($\epsilon$). Moreover, the switching behavior is similar to the previous case illustrated in Fig. 7 where the slower adaptation can be explained by lower value for $\epsilon$; 1.5 compared to 3. This conservative choice of $\epsilon$ is to ensure a robust adaptation (i.e., avoiding fluctuations) where the number of possible tasks is higher.

Figure 10b illustrates the power exchange between during the interaction. The human-user spends mechanical power to demonstrate his/her intention. Initially (up to 1 s), the robot rejects the human perturbations when the wining task is still below 0.5. After gaining enough confidence in the new task (i.e., belief higher than 0.5), the robot becomes the active (providing positive effort) and the human the passive partner. The cost of adaptation as formulated in Eq. (13) is depicted in Fig. 10c. It can be seen that, due to human perturbation, the cost [i.e., the first term in Eq. (13)] increases. Before $t=0.5$, in order to reduce this error, the robot increases its effort to fulfill the losing task until the adaptation activates and beliefs are updated ($0.5< t < 1$). This reduces the cost since the winning task complies with the human intention and removes his/her perturbation.

Fig. 11

The demonstration of our proposed mechanism in interaction with a human-user. (Left) After an initial movement induced by the human-user, robot adapt to the “forward” DS and performs the task pro-actively. (Center) After an initial push from the human to the left side, the robot switches form “forward” to “place-left” DS resulting in an active assistance behavior. (Right) The human suddenly decides to place the object on the right, and the robot adapts to this intention

Figure 10d shows the dynamics of our proposed adaptation mechanism (i.e., Eq. 10). Task dissimilarity is computed as the difference between real velocity ($\dot{x}_r$) and generated velocity by each DS ($f_i(x)$)). This graph is averaged over all possible tasks. It can be seen that a low dissimilarity (high similarity) results in a positive update; i.e., a higher belief for a task. Consequently, the task with highest similarity wins the WTA process and reach $b_i=1$. Fig. 10e shows the prediction capability of our method. It can be seen that, on average, the belief of a task with a higher similarity to the real velocity has a higher belief. For example, a task that reaches $b_i=0.9$ has higher similarity to the real velocity compared another task with $b_j=0.1$. Both Fig. 10e, f show that our method adapts the beliefs meaningfully w.r.t. to the real velocity.

Figure 10f shows the performance of the robot during the execution of each task when the belief of the task is 1 and the human is not perturbing the robot. This shows that after adaptation, the robot perform the task satisfactorily in the solo condition. A demonstration of this experiment can be found in “Appendix B.2”.

6.2 Scenario 2: carrying heavy objects

We consider a human–robot collaboration task in a warehouse-like scenario where they carry and place a heavy object across the aisles with shelves on each side. However, the initial and target positions of objects are intended by the human and are unknown to the robot. The robot consists of a Clearpath ridgeback mobile-robot with Universal UR5 robotic-arm mounted on top of the base; see Fig. 11. Using the force-torque sensor (Robotiq FT300) the robot is controlled by the following admittance law.

$$\begin{aligned} \ddot{\tilde{x}}_a= & {} M_a^{-1} \left[ -D_a \dot{\tilde{x}}_a - K_a (x_a - x_e) + F_e + F_c \right] \end{aligned}$$

(20)

$$\begin{aligned} \ddot{\tilde{x}}_p= & {} M_p^{-1} \left[ -D_p \dot{\tilde{x}}_p + R_a^p \left[ D_a \dot{\tilde{x}}_a + K_a (x_a - x_e)\right] \right] \end{aligned}$$

(21)

where $x_a$, $x_e$, $K_a$, and $D_a \in \mathbb {R}^6$ are the position, equilibrium, stiffness, and damping of the arm respectively. $F_e$ denotes the external forces measured by the sensor, and $F_c$ is the control input. $\dot{\tilde{x}}_a$ and $\ddot{\tilde{x}}_a$ are the desired velocity and acceleration computed by the admittance law. The desired velocities are sent to a low-level velocity-controller to be executed on the robot. $M_a$ and $M_p$ are the simulated mass matrices for the arm and platform respectively. $D_p$ denotes the damping of the platform. The rotation matrix $R_a^p \in \mathbb {R}^{6\times 6}$ transforms the arm configuration to the platform frame; see Fig. 12. Upon any force ($F_e$ or $F_c$) the admittance control moves the arm and the platform in order to go back to the equilibrium point (i.e., $x_a = x_e$, $\dot{\tilde{x}} = \ddot{\tilde{x}} =0$). The manner that the admittance control translate the forces into movements of the arm and platform depends on the parameters ($M_p$, $M_a$, $D_a$, $D_p$, $K_a$); the robot can be more responsive to forces by moving either the arm or the platform. See “Appendix.B.1.2” for the parameters used in this experiment.

Fig. 12

Admittance control of the end-effector of the mobile-base robot. The robot is modeled as two virtual admittance in series; i.e., from the arm (end-effector) to the platform, and from the platform to the global coordinate

The motion of the arm can be controlled using $F_c$ in Eq. 20. We use this input for our DS-based impedance-control in Eq. 5. For the DS, we consider four single-attractor dynamics to encode for four different tasks: (1) Move Forward (MP), (2) Move Backward (MB), (3) Place Right (PR), and (4) Place Left (PL); see “Appendix B.1.3” for the parameterization of these tasks. Figure 13 shows the location of these attractor with respect to the equilibrium point of the admittance control. Controlling the arm toward the attractor of MF/MB constantly excites the admittance controller and as the result the robot moves forward/backward. However, due a special parameterization of $K_a$ (the stiffness between the arm and the platform) and placement of the attractors, controlling the arm toward PR/PR does not cause the platform to move. For this experiment, the impedance-control gain D is set 200e. Given the four tasks, we apply our proposed adaptation mechanism (Definition 4) with $\epsilon =4$.

Fig. 13

Tasks are encoded as simple attractors in the workspace of the arm. Generated motion based on “Move forward/backward” excites the admittance control and moves the platform accordingly, whereas, generated motion using “place left/right” only moves the arm

Fig. 14

The overall result of the proposed adaptation mechanism for carrying heavy objects. a According the interaction with the human-user, the robot successfully switches from one task to another. b The human-user requires to exchange mechanical power with the robot to demonstrate his/her intention. c The minimization of the adaptation cost (Eq. 13) upon human perturbations. d The dynamics of the adaptation (Eq. 10) where the dissimilarity of the real velocity to each task affects its belief and vice versa. e Prediction of the human perturbations based on the dissimilarity of the real velocity with each task. f The performance of the robot for execution of each task after adaptation and in absence of human interaction

Figure 14 shows the overall results of the adaptation in this experiment. The results are qualitatively similar to the previous experiment in terms of switching behavior, power exchange, and adaptation performance. It can be seen that due to slower motions and stiffer dynamics, more human-effort and longer time are required to switch between tasks. A demonstration of this experiment can be found in “Appendix B.2”.

7 Discussion

Here, we provide discussion on our experimental results in comparison to theory. Moreover, we shortly discuss limitations, practical issues, and possible improvements for our adaptive mechanism.

7.1 Adaptation rate and convergence speed

As mentioned before, to switch from one task to another, the two tasks need to be "distinguishable". Eq. (14) provides a theoretical condition on tasks dissimilarity. However, this condition is under the assumption that the human is perfectly overriding the target task. This is restrictive assumption in settings where (1) the robot is active at all time and it tries to fulfill its current task, and (2) the human might not know or be able to exactly demonstrate the target task. Thus, it slows down the convergence speed when the robot requires enough dissimilarity to the current task and enough similarity to the target task. If these conditions hold, beliefs are updated proportional to the adaptation rate ($\epsilon$); see “Appendix.A.7” for more details. In short, the speed of convergence depends on: (1) inner-similarity of the tasks, (2) the adaptation rate and (3) the quality of the human perturbations. Therefore, the convergence behavior can be improved by designing the tasks (encoded by DS) to be dissimilar as possible to produce legible motions (Dragan et al. 2013). Moreover, naive users might require a learning phase to be able to express their intention and achieve a better convergence behavior. Finally, one can increase the convergence speed by increasing the adaptation rate cautiously with respect to the noise and undesirable dynamics; see “Appendix.A.7”.

7.2 Robot compliance and human effort

As seen before, switching from one task to another requires human effort. This effort depends on convergence speed and the robot impedance. The longer the adaptation, the more effort the human spends. Moreover, the human effort is proportional to the stiffness and the damping that he/she feels; see “Appendix.A.9”. Therefore, One solution to reduce human effort is to reduce the impedance parameters at the cost of permanently deteriorating the tracking performance of the robot; see “Appendix.A.10”. Nevertheless, this serves as a hint to vary the impedance based on the interaction forces to have a compliant behavior while in contact with human (low damping, to reduce human effort for adaptation) and proper impedance during task-execution (high damping, to increase the tracking performance); see Landi et al. (2017) for such parameters adaptation upon detection of force variations. However, the challenge is to distinguish between the forces intended by human and undesirable disturbances (which requires high stiffness for rejection). Haddadin et al. (2008); Berger et al. (2015); Kouris et al. (2018) propose different approaches to distinguish between intended and unexpected contacts that can be useful in our framework.

Additionally, to improve the compliant and adaptation behavior of the robot, we can consider a DS that only encodes zero-velocities; i.e., null-DS, see “Appendix A.8”. By adapting to this DS, the human-user is able to stop the robot at any time during the interaction. Moreover, this DS can be used as an intermediary step for switching between two tasks since it reduces the final stiffness felt by the user; see “Appendix A.9”.

7.3 Motion versus force-based intention recognition

In this paper, we considered a motion-based intention-recognition strategy. In our adaptation law (Eq. 10), we utilize end-effector velocity directly and its position indirectly; i.e., as the input of the DS. Moreover, a certain level of error is tolerated for the execution of our task which does not lead to task-failures. In future works, we will consider force-based intention recognition which might be more suitable for delicate tasks where a slight deviation from desired trajectories might lead to failure. In such situation, the robot can temporally stays rigid toward external perturbations while interpreting the forces as to recognize the human intention and carefully plans for the switching. Takeda et al. (2005) and Stefanov et al. (2010) propose statistical models for force-based intention recognition that can be used for theses cases.

7.4 Task-adaptation in redundant robot

Our adaptation mechanism is not limited to non-redundant robots and can be applied to any subset of robotic coordinates. In our experiments, the null-space of the robotic robot was set to a specific configuration while the end-effector orientation was set to a fixed angle. Nevertheless, the motion for the end-effector orientation can be embedded into the DS and/or take part in the adaptation. However, a similarity metric that includes both pose and orientation is then necessary.

7.5 Human behavior and task misrecognition

Human behavior has a crucial impact, and in general, on any online algorithm with a human-in-the-loop. For instance, we experienced cases where the human user falsely assumes that the robot recognized his/her intention and stops the demonstration prematurely. This potentially leads to a misrecognition which we impute more to the human-user rather than the algorithm. Nevertheless, this case shows us the importance of transparency where the human user has a precise inference of the robot’s state. In our case, using synthesized speech or a display indicating the dominant task can improve the transparency of the interaction.

8 Conclusion and future work

In this paper, we presented a dynamical-system approach to task-adaptation which enables a robot to comply to the human intention. We extended the DS-based impedance control where, instead of one dynamical system (encoding for one task), several dynamical systems can be considered. We introduced an adaptive mechanism that smoothly switches between different dynamical systems. We rigorously studied the behavior of our method in theory and practice. Experimental results (using Kuka LWR for manipulation task and Ridgeback-UR5 for carrying objects) show that our method allows for smooth and seamless human–robot interaction. This results also prove that our adaptive mechanism is hardware/control-agnostic; i.e., a satisfactory behavior can be achieved with different control architectures (joint-impedance or admittance control), frequency of the control loop (1 kHz for the haptic device, 200 Hz for Kuka LWR, and 125 Hz for the mobile-robot). Moreover, our adaptive mechanism exhibited robustness to real-world uncertainties (e.g., noisy sensors) and deviation from theory (e.g., imperfect tracking).

In this work, we focused only on fixed-impedance control and pro-activity towards human perturbations that are intentional. In our future work, we will consider the general case where the robot can distinguish between human-intended perturbations (to which it needs to comply) and undesirable disturbances (which needs to be rejected). Variable-impedance control appears to a be natural approach toward this problem where impedance varies according to the nature of perturbation (human-intention vs. disturbances). Moreover, our adaptive mechanism has the potential to be extended to an interactive learning algorithm where the robot learns a new task based on a mixture of given dynamical systems. For instance, one can consider dependencies for adaptive parameters ($b_i(x,s)$) on state (x) and other possible contextual signals (s). These dependencies can be learned or approximated while our adaptive mechanism provide an estimation for the parameters. In short, the robot learns to what it adapts. Conversely, the robot can adapt to what it learns. This enables the robot to express what it learns during the interaction and gradually reduces the human supervision and effort. In future, we will focus on this approach for learning by interaction. We expect to achieve a robotic performance that is “behaviorally” accepted by the human; compared to off-line learning methods where the behavior of an optimized model is not necessarily acceptable by the human-user in the real-world.

Appendices

Appendix A: Mathematical details

1.1 A.1 An implementation of Winner-take-all

In the following, we introduce a simple implementation for the Winner-Take-all (WTA) process that is used in this work; see Algorithm 1. This algorithm takes two inputs: a vector for the current beliefs and their updates (computed based on the adaptation mechanism). Here, we assume that beliefs are between 0 and 1 and they sum to unity. In the first step (line 1), the element with the greatest update is detected as the winner. In case of multiple maximums, one can pick the winner randomly. In the following lines (2–5), we handle the case where the winner is already saturated at 1. In this case, no update is necessary. In lines 6–8, we make sure that only the winner has a positive update. This is done by detecting the second-biggest update-value and setting the baseline in the middle. Again, in case of multiple maximums, one can pick randomly. In the rest of the algorithm, we ensure that the belief-updates sum to zero. This guarantees that the sum of the beliefs stays constant. To do this, we compute the sum of the current updates (S). In doing so, we exclude those components that are saturated at zero and have negative updates (line 11) since they do not influence the process. Based on the previous steps (line 6–8), it is guaranteed that S has a non-positive value. By adding this value to the winner component, we ensure that the updates—of active components—sum to zero, thus, sum of the beliefs stays one.

1.2 A.2 Pairwise competitions

The adaptation rule (Eq. 10) can be rewritten as follows:

$$\begin{aligned} \begin{aligned} \epsilon ^{-1}~\dot{\hat{b}}_i&= - |\dot{x}_r - f_i|^2 + 2 \sum \limits _{i\ne j} b_j f_j^Tf_i \\&= - |\dot{x}_r - f_i|^2 + 2 \sum \limits _{j}b_j f_j^Tf_i - 2b_i |f_i|^2 \\&= - |\dot{x}_r - f_i|^2 + 2 ~\dot{x}_d^Tf_i - 2b_i |f_i|^2 \end{aligned} \end{aligned}$$

(22)

A pairwise distance between two arbitrary DS (e.g., k and l) can be considered as follows that takes on values between -1 and 1.

$$\begin{aligned} \begin{aligned} \varDelta b_{kl}&= b_k - b_l \end{aligned} \end{aligned}$$

(23)

Since WTA process preserves the pairwise distances among the beliefs (Eq. 12), the dynamics of the belief after WTA can be approximated by those before WTA (which has slower dynamics).

$$\begin{aligned} \begin{aligned} \varDelta \dot{b}_{kl} =&~ \dot{b}_k - \dot{b}_l \simeq \dot{\hat{b}}_k - \dot{\hat{b}}_l \\ \end{aligned} \end{aligned}$$

(24)

Using Eq. (22), we can write

$$\begin{aligned} \begin{aligned} \epsilon ^{-1} \varDelta \dot{b}_{kl}=&- |\dot{x}_r - f_k|^2 + |\dot{x}_r - f_l|^2 \\&- 2 \dot{x}_d^T (f_k - f_l) + 2b_k |f_k|^2 - 2b_l |f_l|^2\\ =&-f_k^2 + f_l^2 + 2\dot{x}_r^T(f_k - f_l) \\&- 2 \dot{x}_d^T (f_k - f_l) + 2b_k |f_k|^2 - 2b_l |f_l|^2\\ =&~2 \dot{e}^T (f_k - f_l) + (2b_k-1)|f_k|^2 + (1-2b_l)|f_l|^2\\ \end{aligned} \end{aligned}$$

(25)

1.3 A.3 Optimality principle

First, we reformulate the cost function using the expansion of $|\dot{x}_d|^2$.

$$\begin{aligned} |\dot{x}_d|^2 = \sum \limits _{i=1}^{N} b_i^2 |f_i|^2 + \sum \limits _{i \ne j} (b_i f_i)^T (b_j f_j) \end{aligned}$$

(26)

This leads to

$$\begin{aligned} \begin{aligned} J(B) =&|\dot{e}|^2 + \sum \limits _{i=1}^{N} b_i (1-b_i) |f_i|^2 \\ =&|\dot{e}|^2 + \sum \limits _{i=1}^{N} b_i |f_i^2| - |\dot{x}_d|^2 + \sum \limits _{i \ne j} (b_i f_i)^T (b_j f_j) \end{aligned} \end{aligned}$$

(27)

By expanding $|\dot{e}|^2=|\dot{x}_r - \dot{x}_d|^2$, we have

$$\begin{aligned} \begin{aligned} J(B) =&-2 \dot{x}_r^T \dot{x}_d + \sum \limits _{i=1}^{N} b_i (|f_i|^2 + |\dot{x}_r|^2) + \sum \limits _{i \ne j} (b_i f_i)^T (b_j f_j) \end{aligned} \end{aligned}$$

(28)

We can show that the presented adaptive mechanism minimizes this cost-function by moving along its gradient:

$$\begin{aligned} \begin{aligned} \dot{\hat{b}}_i&= -\epsilon ~ \frac{\partial J}{\partial b_i} \\&= -\epsilon ~\left( -2\dot{x}_r^T~ \frac{\partial \dot{x}_d}{\partial b_i} + |f_i|^2 + |\dot{x}_r|^2 + 2 \sum \limits _{j \ne i} (b_j f_j)^T f_i \right) \\&= -\epsilon ~ \left( -2\dot{x}_r^T f_i + |f_i|^2 + |\dot{x}_r|^2 + 2 \sum \limits _{j \ne i} b_j f_j^T f_i \right) \\&= -\epsilon ~ \left( |\dot{x}_r - f_i|^2 + 2 \sum \limits _{j \ne i} b_j f_j^T f_i\right) \end{aligned} \end{aligned}$$

(29)

In this derivation, we assume ${\partial \dot{x}_r}/{\partial b_i}=0$ since the real velocity is the given input to the adaptive mechanism. Moreover, a simple approximation of this cost function (Eq. 26) can be achieved as

$$\begin{aligned} \begin{aligned} \tilde{J}(B)&\simeq |\dot{e}|^2 + |\tilde{f}|^2 \sum \limits _{i=1}^{N} b_i (1-b_i) \\&\simeq |\dot{e}|^2 + (1-b^{\star }) |\tilde{f}|^2 \\ \end{aligned} \end{aligned}$$

(30)

where $|f_i|\simeq |\tilde{f}|$ and the summation is approximated by $1-b^{\star }$, $b^{\star }$ being the maximum $b_i$. To simplify further, we can scale the cost by $|\tilde{f}|$ and remove the offset.

$$\begin{aligned} \begin{aligned} \bar{J}(B) = \tilde{J}(B)/|\tilde{f}|^2 - 1 = |\dot{e}|^2/|\tilde{f}|^2 - b^{\star } \end{aligned} \end{aligned}$$

(31)

which shows the adaptation is a trade-off between minimizing the scaled-error and maximizing the maximum-belief. Moreover, in cases without perturbations (i.e., $\dot{e}=0$ such as the autonomous mode), adaptation maximizes the belief of the most certain task.

1.4 A.4 Convergence to demonstration

By replacing error as $\dot{e} = f_k - \dot{x}_d$, and the definition of $\dot{x}_d$ in Eq. (25), and $\delta _{kl} = \sum \limits _{i \ne k,l} b_i f_i$, we have

$$\begin{aligned} \epsilon ^{-1} \varDelta \dot{b}_{kl}= & {} 2 (f_k - \dot{x}_d)^T (f_k - f_l) + (2b_k-1)|f_k|^2 + (1-2b_l)|f_l|^2\nonumber \\= & {} 2 ( (1-b_k)f_k - b_l f_l - \sum \limits _{i\ne k,l} b_i f_i )^T (f_k - f_l) \nonumber \\+ & {} (2b_k-1)|f_k|^2 + (1-2b_l)|f_l|^2\nonumber \\= & {} |f_k|^2 + |f_l|^2 - 2 (1+b_l-b_k)f_k^Tf_l - 2 \delta _{kl}^T (f_k - f_l)\nonumber \\= & {} |f_k - (f_l + \delta _{kl})|^2 - 2(b_1 - b_k) f_k^T f_l - \delta _{kl}^2\nonumber \\ \end{aligned}$$

(32)

To have a convergence to $b_k=1$, it required to have $\varDelta \dot{b}_{kl} >0$, therefore:

$$\begin{aligned} {[}f_k - (f_l + \delta _{kl})]^2 > 2(b_1 - b_k) f_k^T f_l + \delta _{kl}^2 \end{aligned}$$

(33)

1.5 A.5 Convergence in the autonomous condition

In the absence of human perturbations on the real velocity (i.e., $F_h =0$ in Eq. 3), and with the assumption of perfect tracking (i.e., $\dot{e}=0$), Eq. (25) can be simplified to

$$\begin{aligned} \epsilon ^{-1} \varDelta \dot{b}_{kl} = (2b_k-1)|f_k|^2 + (1-2b_l) |f_l|^2 \end{aligned}$$

(34)

In this case, when the belief of the dominant task ($b_k$) is bigger than 0.5, one can make sure that all other beliefs are less than 0.5 (since $\sum b_i =1$), therefore the terms of the right-hand-side are positive, and consequently, $\varDelta \dot{b}_{kl} >0$. This means that the difference between $b_k$ and $b_l$ increase over time until the saturation points of $b_k=1$ and $b_l=0$. Assuming $|f|^2=min(|f_k|^2,|f_l|^2)$, we have

$$\begin{aligned} \epsilon ^{-1} \varDelta \dot{b}_{kl} > (2b_k-1) |f|^2 + (1-2b_l) |f|^2 = 2 \varDelta b_{kl} |f|^2 \end{aligned}$$

(35)

which shows that the beliefs converge exponentially with rate of $2\epsilon |f|^2$. By assuming $b_k+b_l=1$, we have $\varDelta {b}_{kl} = 2b_k-1$ which changes Eq.(35) to

$$\begin{aligned} \dot{b}_k \simeq 2\epsilon |f|^2 (b_k - 0.5) \end{aligned}$$

(36)

The solution to this equation is

$$\begin{aligned} {b}_k(t) \simeq 0.5 + (b_k(0) - 0.5) exp(2\epsilon |f|^2 t) \end{aligned}$$

(37)

Therefore the convergence time $b_k(T_{auto})=1$ is

$$\begin{aligned} T_{auto} \simeq log(\frac{0.5}{b_k(0)-0.5})/(2 \epsilon |f|^2) \end{aligned}$$

(38)

Moreover, in Eq. (35), the particular case of two tasks with equal beliefs ($b_k=b_l=0.5$) is an unstable equilibrium point for the adaptation where the system generate motions based on $0.5 (f_k+f_l)$. Therefore, the adaptation in the autonomous condition is only guaranteed if there is a task with $b_i>0.5$ which requires the human supervision to ensure that the robot received enough demonstrations before retracting from the physical interaction; e.g., the human retracts only if he/she is confident that the robot switched to the indented task.

1.6 A.6 Stability in the autonomous condition

Assuming there is a task a task with $b_k>0.5$, we can use its Lyapunov function ($V_k(x)$) to investigate the stability of the motion generation in the autonomous condition as follows:

$$\begin{aligned} \begin{aligned} \dot{V}_k&= \left( \frac{\partial V_k}{\partial x}\right) ^T \dot{x}_d = \left( \frac{\partial V_k}{\partial x}\right) ^T (b_k f_k + \sum _{i \ne k} b_i f_i) \\&= b_k \left( \frac{\partial V_k}{\partial x}\right) ^T f_k + \sum _{i \ne k} b_i \left( \frac{\partial V_k}{\partial x}\right) ^T f_i \end{aligned} \end{aligned}$$

(39)

Based on the stability of DS (Assumption 1), $(\frac{\partial V_k}{\partial x})^T f_k <0$. We further assume that the perturbations are bounded $|(\frac{\partial V_k}{\partial x})^T f_i| < \psi (x)$. This boundaries leads to

$$\begin{aligned} \begin{aligned} \dot{V}_k&< -b_k \left( \frac{\partial V_k}{\partial x}\right) ^T f_k + (1-b_k)\psi (x) \end{aligned} \end{aligned}$$

(40)

Due to the exponential convergence of $b_k$ (Eq. 37), for $t>T_{auto}$, the second term vanishes and the stability of kth DS is restored.

1.7 A.7 Convergence speed

To investigate how $\epsilon$ affects the convergence speed, we consider the case where the current task is $\dot{x}_d = f_l$ and the human demonstration is $\dot{x}_r = f_k$. This simplifies Eq. (25) into

$$\begin{aligned} \epsilon ^{-1} \varDelta \dot{b}_{kl} = (1+2b_k)|f_k|^2 + (3-2b_l)|f_l|^2 - 4 f_k^Tf_l \end{aligned}$$

(41)

To reach a simple estimation of convergence speed, we assume $f_k^Tf_l$ (i.e., the two task are distinguishable) and tasks operate at the same speed ($|f_k|^2 =| f_l|^2 = |f|^2$). This yields

$$\begin{aligned} \varDelta \dot{b}_{kl} = \epsilon |f|^2 (4 + 2 \varDelta {b}_{kl}) \end{aligned}$$

(42)

The analytical solution to this equation with initial condition $\varDelta {b}_{kl}=-1$ ($b_l =1$ and $b_k=0$) can be computed as

$$\begin{aligned} \varDelta {b}_{kl}(t) = \exp (2 \epsilon |f|^2 t) -2 \end{aligned}$$

(43)

Then the reaching time $T_{reach}$ to $\varDelta {b}_{kl} = 1$ ($b_l =0$ and $b_k=1$) is

$$\begin{aligned} T_{reach} = \frac{\log (3)}{ 2 \epsilon |f|^2} \end{aligned}$$

(44)

For example, for tasks operating around $|f|^2 = 0.1$ and $\epsilon =4$ as in the Sect. 6.2, we have $T_{reach} = 1.37$ which can be verified in Fig. 14a. In real-world settings, given the time-scale of noises and other undesirable dynamics (approximated by $T_{noise}$), to avoid noise-driven adaptation and chatting between undesirable tasks, one should aim for

$$\begin{aligned} T_{reach}>> T_{noise} \end{aligned}$$

(45)

For example, considering 30 Hz noise ($T_{noise}=1/30$) for a case operating at $|f|^2 = 0.1$ leads to the $\epsilon < 164.7$ as the upper-bound. A better approach to tune $\epsilon$ is to aim for a $T_{reach}$ that correspond to a natural human–robot interaction. For example, expecting the robot to recognize and adapt to the human intention in 1 s leads to $\epsilon = 5.5$. Thereafter, the approximated value can be re-adjusted in the real experiment to achieve the desirable behavior.

1.8 A.8 Null DS

Definition 5

(Null DS) It is possible to include a dynamic DS encoding for zero-velocity (i.e., $f_0(x_r) \equiv 0$) in Eq. (8) with its corresponding belief $b_0$. In this case, the constraints in Eq. (9) should be modified to include $b_0$ as well.

To have the dynamics of the competition between the null-DS and other DS in the autonomous condition, we need to insert $f_0 =0$ in Eq. (34) which results in

$$\begin{aligned} \varDelta \dot{b}_{k0} = (2b_k-1)|f_k|^2 \end{aligned}$$

(46)

This equation shows that any DS with belief lower than 0.5 decreases and saturates at 0. Only the confident task—if exists—converges to 1. Therefore, the human can change the task of the robot to a desired one by providing enough demonstrations as to pass this threshold.

1.9 A.9 Resulting compliance at the force-level

In DS-based impedance control framework (Eq. 6), the observed stiffness for the human-user can be computed as

$$\begin{aligned} K = - \frac{\partial F_h}{\partial x_r} = - D \sum \limits _{i=1}^{N} b_i ~ \frac{\partial f_i(x_r)}{\partial x_r} \end{aligned}$$

(47)

where $K \in \mathbb {R}^{3\times 3}$. It can be seen that the stiffness is not only affected by the control gain D, but also by the properties of the DS (i.e., $\partial f_i(x_r)/\partial x_r$ which denotes the convergence rates of the DS). The stiffness in a particular direction, namely $x_s$ with unit norm, can be calculated by the following Rayleigh quotient.

$$\begin{aligned} K(x_s) = x_s^T K x_s = - D \sum \limits _{i=1}^{N} b_i ~ x_s^T\frac{\partial f_i(x_r)}{\partial x_r} x_s \end{aligned}$$

(48)

Considering that the stiffness of each DS in the $x_s$ direction is $K_i(x_s) = x_s^T K x_s = - D x_s^T {\partial f_i(x_r)}/{\partial x_r} x_s$, we have the following property.

$$\begin{aligned} K(x_s) = \sum \limits _{i=1}^{N} b_i ~ K_i(x_s) \le \sum \limits _{i=1}^{N} b_i ~ K_{max}(x_s) = K_{max}(x_s) \end{aligned}$$

(49)

where $K_{max}(x_s)$ denotes the stiffness of the stiffest DS in $x_s$ direction. This is a conservative upper-bound that shows in transitory states where several DS are active with low $b_i$; the real resulting stiffness of the system would be lower than the most stiff possible candidate. By introducing the null-DS as introduced in “Appendix.A.8”, the resulting stiffness is different since the null-DS has no stiffness ($K_0(x_s)\equiv 0$).

$$\begin{aligned} \begin{aligned} K(x_s)&= \sum \limits _{i=0}^{N} b_i ~ K_i(x_s) = b_0 K_0(x_s) + \sum \limits _{i=1}^{N} b_i ~ K_i(x_s) \\&\le \sum \limits _{i=1}^{N} b_i ~ K_{max}(x_s) = (1-b_0) K_{max}(x_s) \\ \end{aligned} \end{aligned}$$

(50)

This upper-bound shows that the stiffness can be reduced by adapting to the null-DS. The advantage of this property is twofold. First, the lower stiffness (i.e, higher compliance) allows the user to provide demonstration or guidance easier. Second, by sensing this compliance, the user can infer the confidence level of the robot resulting in a richer haptic communication.

Moreover, the observed damping for the human-user (B) can be computed using Eq. (6) as follows.

$$\begin{aligned} B = - \frac{\partial F_h}{\partial \dot{x}_r} = D \end{aligned}$$

(51)

It can be seen that the resulting damping solely depends on the controller. To reduce the human effort in the interaction, lower controller gain should be used.

1.10 A.10 Tracking performance

The tracking performance of the impedance controller for execution of one DS ($f_i(x_r)$) can be investigated using Eq.6 as follows.

$$\begin{aligned} \ddot{e} = - M^{-1} D \dot{e} - f'(x_r)\dot{x}_r + M^{-1} F_h \end{aligned}$$

(52)

where $f'=\partial f(x) / \partial x$. In the first term, $M^{-1} D \succ 0$ guarantees vanishing errors. However, the other terms (especially the external forces) which can be seen as disturbances introduce biases. The control gain (D) can be increased in order to reduce the effect of such disturbances and improve tracking behavior. However, one should note that in discrete control loop, there is upper-bound for the stability of the system. Discretization of Eq. (52) with $\varDelta t$, ignoring the disturbances, and studying the eigenvalues provides us with an approximation of this upper-bound; i.e., $D < 2M \varDelta t^{-1}$

Appendix B: Supplementary materials

1.1 B.1 Technical details

The adaptation and motion generation is running at 300 Hz for both experiments. The control loop of the impedance controller of LWR and the velocity controller of UR5 are running at 200 and 125 Hz respectively. The motion planning for all cases is considered in the Cartesian space i.e, the position and the linear velocity of the end-effector (xyz). The orientation of the end-effector is controlled on a set-point. Moreover, the measured velocities are low-pass-filtered with cutoff frequency around 30 Hz. In both experiment, we set the control gains experimentally to have a practical balance between compliance and tracking.

1.1.1 B.1.1 DS parametrization for manipulation tasks

The linear polish is generated by the following dynamics:

$$\begin{aligned} \begin{aligned} \dot{x}_d&= 0.1 \overrightarrow{p} - 0.8 e^{\perp } \\ \end{aligned} \end{aligned}$$

(53)

first the first term induce a velocity in the direction of the line and the second term generate a velocity (saturated at 0.25 m/s) to correct for deviation from the line. The direction $\overrightarrow{p}$ between two end-points ($[-.54 , .25 , .1 ]$ and $[-.54 , -.25 , 0.1 ]$) switches when one is reached.

The circular polish is encoded in the cylindrical coordinates:

$$\begin{aligned} \begin{aligned} \dot{r}&= -2.7 (r- 0.025) \\ \dot{\theta }&= 2.5 \\ \dot{z}&= -2.7 (z - 0.12) \end{aligned} \end{aligned}$$

(54)

where $r^2 = x^2+ y^2$, and $\theta =atan2(y,x)$, and the center of rotation is $[-.55 ,0 ,.1]$.

The other two tasks (push down and retreat) are created by SEDs (Khansari-Zadeh and Billard 2011) with the following parameters.

$$\begin{aligned} \pi _1= & {} 0.35, ~~\pi _2=0.20, ~~\pi _3=0.45 \nonumber \\ \mu _1= & {} [35.7, -\,5.8, -\,11.4, \,-2.4, 4.3, 18.0]\nonumber \\ \mu _2= & {} [0.6, -\,34.8, 37.4, -\,0.2, 12.9, 3.1]\nonumber \\ \mu _3= & {} [-33.6, 10.9, -\,2.7, 2.6,-\,0.3, 17.8]\nonumber \\ \varSigma _1= & {} \begin{bmatrix} 1.3&-\,0.2&3.0 \\ -\,0.2&0.1&-\,5.4 \\ 3.0&-\,5.4&721.1 \\ -\,0.8&1.2&-\,160.7 \\ -\,0.2&0.5&-\,79.5 \\ -\,0.6&2.0&-\,282.2 \end{bmatrix} ~\varSigma _2=\begin{bmatrix} 22.4&5.4&-\,4.3 \\ 5.4&6.7&21.1 \\ -\,4.3&21.1&136.6 \\ -\,5.1&-\,1.3&0.4 \\ -\,1.7&4.8&33.3 \\ -\,0.7&-\,10.6&-\,58.8 \end{bmatrix}\nonumber \\ ~\varSigma _3= & {} \begin{bmatrix} 1.1&-\,0.3&-\,2.1 \\ -\,0.3&0.2&-\,10.3 \\ -\,2.1&-\,10.3&922.3 \\ -\,0.6&-\,2.4&222.4 \\ 0.2&0.9&-\,89.9 \\ 0.2&4.0&-\,348.4 \\ \end{bmatrix} \end{aligned}$$

(55)

However the attractor of push-down is at $[-.4, 0, .08]$ while the attractor of retreat is at $[-.32, .28, .36]$.

1.1.2 B.1.2 Admittance control parametrization

The parameters used in the admittance control for the mobile-robot are as follows.

$$\begin{aligned} \begin{aligned} M_a&= \text {diag}(1,1,1,.5,.5,.5) \\ D_a&= \text {diag}(25,25,25,5,5,5) \\ K_a&= \text {diag}(10,150,10,5,5,5) \\ M_p&= \text {diag}(100,10,0,0,0,500) \\ D_p&= \text {diag}(500,50,0,0,0,101) \end{aligned} \end{aligned}$$

(56)

diag denotes a diagonal matrix with the given values where coordinate system is $(x,y,z,\theta _x,\theta _y,\theta _z)$.

1.1.3 B.1.3 DS parametrization for carrying task

The four tasks has the same dynamics as $\dot{x}_d=- (x_r - x_{g})$ with saturated velocity at 0.12 m/s. However, the location of the attractor ($x_g$) is set differently for each task as follows.

$$\begin{aligned} \begin{aligned} x_{MF}&= [0.05, 0.47, 0.50]\\ x_{MB}&= [0.05, 0.32, 0.50]\\ x_{PL}&= [-\,0.3, 0.35, 0.1]\\ x_{PR}&= [0.3, 0.35, 0.1]\\ \end{aligned} \end{aligned}$$

(57)

Fig. 15

Snapshots of the task-adaptation in the manipulation task. The robot is initially in the retreat task. Staring around $t=1s$, the human starts to demonstrate the linear polishing task. From $t=4s$ the robot start to perform the linear polish autonomously

Fig. 16

Snapshots of the task-adaptation in the manipulation task. The robot is initially performing the “forwar” task where the human demonstrate a motion that is similar to “place left”. Therefore, the robot switches to this task. The robot performs all the tasks autonomously

1.2 B.2 Videos

The experimental result of the manipulation tasks using Kuka LWR 4+ (Sect. 6.1) can be watched here: https://youtu.be/oqHJ8crB5KY. The snapshots of the interaction for a short period is illustrated in Fig. 15.

The results of the carrying task using the mobile robot (Sect. 6.2) can be viewed here: https://youtu.be/7BjHhV-BkwE The snapshots of the interaction for a short period is illustrated in Fig. 16.

1.3 B.3 Source codes

A C++ implementation of our method can be found at https://github.com/epfl-lasa/task_adaptation.