Eigenvalue Isogeometric Approximations Based on B-Splines: Tools and Results

Abstract

In this note, we focus on the spectral analysis of large matrices coming from isogeometric approximations based on B-splines of the eigenvalue problem

$$ -(a(x)u'(x))'=\lambda b(x) u(x),\quad \quad x\in (0,1), $$

where u(0) and u(1) are given. When considering the collocation case, global distribution results for the eigenvalues are available in the literature, despite the nonsymmetry of the related matrices. Here we complement such results by providing precise estimates for the extremal eigenvalues and hence for the spectral conditioning of the resulting matrices. In the Galerkin setting, the matrices are symmetric and positive definite and a more complete analysis has been conducted in the literature. In the latter case we furnish a further procedure that gives a highly accurate estimate of all the eigenvalues, starting from the knowledge of the spectral distribution symbol. The techniques involve dyadic decomposition arguments, tools from the theory of generalized locally Toeplitz sequences, and basic extrapolation methods.

1 Introduction

In this note we consider the approximation of one-dimensional elliptic eigenvalue problems by using an isogeometric either Galerkin or collocation technique with B-splines [5]. We are interested in the eigenvalues of the large matrices stemming from the considered approximation processes. In particular, we address the problem of estimating the extremal eigenvalues and of providing efficient numerical procedures for computing a good approximation of all the eigenvalues.

In this direction, it has recently been proven that the resulting sequence of matrices, indexed with respect to the matrix size, have a canonical distribution (see [15, 17] and references therein), by using the theory of Generalized Locally Toeplitz (GLT) sequences [16].

We recall that every GLT sequence has an associated function, called the symbol, and that the uniform sampling of the symbol provides an asymptotic approximation of all the eigenvalues, if every matrix of the GLT sequence is Hermitian as it happens in our setting. However, in general the approximation is quite poor and recently some extrapolation techniques have been devised (see [9] and references therein). In the constant coefficient setting, when considering the Galerkin approach, the results presented in [10] are impressive in the sense that machine precision is obtained with very low computational cost, while for the variable coefficients further improvements are needed (see also [17]).

In the current note, when considering the Galerkin setting and variable coefficients, we propose a further numerical scheme for the computation of all the spectrum of large matrices by using the numerical computation of the eigenvalues for small matrices, underlying asymptotic expansions, and extrapolation methods as those in [9]. The numerical results are of the same quality as those produced by the best strategy in [17], especially when the problem coefficients are smooth and at least for low frequencies, which are those of highest interest for understanding the nature of the problem.

On the other hand, when dealing with the collocation approximation we obtain large nonsymmetric matrices. However, the GLT machinery can be employed and the symbol is real-valued and nonnegative [7], as in the symmetric positive definite Galerkin setting [15]. Hence we expect that most of the eigenvalues are real or with negligible imaginary part. Here we start the analysis of the collocation case, by describing a technique based on dyadic decompositions, for estimating the extreme eigenvalues and hence the asymptotic (spectral) conditioning of the involved matrix sequences. The analysis contained in Theorem 1 and Corollary 1 confirms that the conditioning grows at most as $h^{-2}$, h being the fineness parameter, exactly as in the case of the matrices obtained with the Galerkin approximation (see e.g [14]).

Finally, it is not clear if the delicate asymptotic expansions observed in [10, 17] holds also in the collocation setting and indeed this issue will be the subject of future investigations.

2 Preliminaries

In the following we present the notation that we use. In particular we give the definition of eigenvalue distribution, that of rearrangement, and we briefly discuss the informal meaning behind these definitions.

A matrix-sequence is any sequence of the form $\{\mathbf X_n\}_n$, where $\mathbf X_n$ is a square matrix such that $\mathrm{size}(\mathbf X_n)\rightarrow \infty$ as $n\rightarrow \infty$. Let $\mu _d$ be the Lebesgue measure in $\mathbb R^d$ and let $C_c(\mathbb C)$ be the space of continuous complex-valued functions with bounded support defined on $\mathbb C$. If $\mathbf X$ is an $m\times m$ matrix, the eigenvalues of $\mathbf X$ are denoted by $\lambda _1(\mathbf X),\ldots ,\lambda _m(\mathbf X)$. If $\mathbf g:D\subset \mathbb R^d\rightarrow \mathbb C^{s\times s}$ is an $s\times s$ matrix-valued function, we say that $\mathbf g$ is measurable if its $s^2$ components $g_{ij}:D\rightarrow \mathbb C$, $i,j=1,\ldots ,s$, are measurable.

Definition 1

Let $\{\mathbf X_n\}_n$ be a matrix-sequence, let $N_n:=\mathrm{size}(\mathbf X_n)$, and let $\mathbf g:D\subset \mathbb R^d\rightarrow \mathbb C^{s\times s}$ be a measurable $s\times s$ matrix-valued function defined on a set D with $0<\mu _d(D)<\infty$. We say that $\{\mathbf X_n\}_n$ has an (asymptotic) eigenvalue distribution described by $\mathbf g$, and we write $\{\mathbf X_n\}_n\sim _\lambda \mathbf g$, if

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{N_n}\sum _{i=1}^{N_n}F(\lambda _i(\mathbf X_n))=\frac{1}{\mu _d(D)}\int _D\frac{\sum _{i=1}^sF(\lambda _i(\mathbf g(y_1,\ldots ,y_d)))}{s}\mathrm{d}y_1\ldots \mathrm{d}y_d,\ \ \forall \,F\in C_c(\mathbb C), \end{aligned}$$

where $\lambda _i(\mathbf g(y_1,\ldots ,y_d))$, $i=1,\ldots ,s$, are the eigenvalues of the $s\times s$ matrix $\mathbf g(y_1,\ldots ,y_d)$.

The informal meaning behind the eigenvalue distribution $\{\mathbf X_n\}_n\sim _\lambda \mathbf g$ is the following: for all sufficiently large n, the eigenvalues of $\mathbf X_n$ can be subdivided into s different subsets of approximately the same cardinality; and the eigenvalues belonging to the ith subset (except possibly for $o(N_n)$ outliers) are approximated by the samples of the ith eigenvalue function $\lambda _i(\mathbf g(y_1,\ldots ,y_d))$ over a uniform grid in D (the domain of $\mathbf g$). For example, if $d=1,\ N_n=ns$ and $D=[a,b]$, then the eigenvalues of $\mathbf X_n$ are approximately equal to

$$\begin{aligned} \lambda _i\Bigl (\mathbf g\Bigl (a+j\frac{b-a}{n}\Bigr )\Bigr ),\qquad j=1,\ldots ,n,\qquad i=1,\ldots ,s, \end{aligned}$$

for n large enough. Likewise, if $d=2,\ N_n=n^2s$ and $D=[a_1,b_1]\times [a_2,b_2]$, then the eigenvalues of $\mathbf X_n$ are approximately equal to

$$\begin{aligned} \lambda _i\Bigl (\mathbf g\Bigl (a_1+j_1\frac{b_1-a_1}{n},\ a_2+j_2\frac{b_2-a_2}{n}\Bigr )\Bigr ),\qquad j_1,j_2=1,\ldots ,n,\qquad i=1,\ldots ,s, \end{aligned}$$

for n large enough.

Remark 1

(rearrangement) Let $\mathbf g:D\subseteq \mathbb R^d\rightarrow \mathbb C^{s\times s}$ and suppose that D is a rectangle in $\mathbb R^d$, say $D:=[a_1,b_1]\times \cdots \times [a_d,b_d]$. We also assume that the eigenvalues $\lambda _1(\mathbf g(y_1,\ldots ,y_d)),\ldots ,\lambda _s(\mathbf g(y_1,\ldots ,y_d))$ are real for all $(y_1,\ldots ,y_d)\in D$. For each positive integer r, let $\mathcal G_r$ be the uniform grid in D given by

$$\begin{aligned} \mathcal G_r :=\left\{ \Bigl (a_1+\frac{i_1}{r}(b_1-a_1),\ldots ,a_d+\frac{i_d}{r}(b_d-a_d)\Bigr ):\ i_1,\ldots ,i_d=1,\ldots ,r\right\} . \end{aligned}$$

Compute the samples of the eigenvalue functions

$$ \lambda _1(\mathbf g(y_1,\ldots ,y_d)),\ldots ,\lambda _s(\mathbf g(y_1,\ldots ,y_d)) $$

at the points $(y_1,\ldots ,y_d)\in \mathcal G_r$, sort them in increasing order and put them in a vector $(q_1,q_2,\ldots ,q_{sr^d})$. Let $\eta _r:[0,1]\rightarrow \mathbb R$ be the piecewise linear non-decreasing function that interpolates the samples $(q_0:=q_1,q_1,q_2,\ldots ,q_{sr^d})$ over the nodes $(0,\frac{1}{sr^d},\frac{2}{sr^d},\ldots ,1)$, i.e.,

$$\begin{aligned} \eta _r\Bigl (\frac{\ell }{sr^d}\Bigr ):=q_\ell ,\qquad \ell =0,\ldots ,sr^d. \end{aligned}$$

Under certain (normally satisfied) conditions on $\mathbf g$, the function $\eta _r$ converges (a.e.) as $r\rightarrow \infty$ to a non-decreasing function $\eta :[0,1]\rightarrow \mathbb R$, which is referred to as the rearranged version of $\mathbf g$. What is important about $\eta$ is that

$$\begin{aligned} \int _D\frac{\sum _{i=1}^sF(\lambda _i(\mathbf g(y_1,\ldots ,y_d)))}{s}\mathrm{d}y_1\ldots \mathrm{d}y_d = \int _0^1F(\eta (t))\mathrm{d}t,\qquad \forall F\in C_c(\mathbb C). \end{aligned}$$

Therefore, if we have $\{\mathbf X_n\}_n\sim _\lambda \mathbf g$, then we also have $\{\mathbf X_n\}_n\sim _\lambda \eta$.

3 Isogeometric Galerkin Discretization of Variable-Coefficient Eigenvalue Problems

Consider the following one-dimensional variable-coefficient eigenvalue problem:

$$\begin{aligned} \left\{ \begin{array}{ll} -(a(x)u_j'(x))'=\lambda _jb(x)u_j(x), &{} x\in \varOmega ,\\ u_j(x)=0, &{} x\in \partial \varOmega , \end{array}\right. \end{aligned}$$

(1)

where $\varOmega$ is an open interval in $\mathbb R$ and $a,b\in L^1(\varOmega )$ are such that $a,b>0$ a.e. on $\varOmega$. The corresponding weak formulation reads as follows: find eigenvalues $\lambda _j\in \mathbb R^+$ and eigenfunctions $u_j\in H^1_0(\varOmega )$, for $j=1,2,\ldots ,\infty$, such that, for all $v\in H^1_0(\varOmega )$,

$$\begin{aligned} \mathrm{a}(u_j,v)=\lambda _j(b\,u_j,v), \end{aligned}$$

where

$$\begin{aligned} \mathrm{a}(u_j,v):=\int _\varOmega a(x)u_j'(x)v'(x)\mathrm{d}x,\qquad (b\,u_j,v):=\int _\varOmega b(x)u_j(x)v(x)\mathrm{d}x. \end{aligned}$$

In the isogeometric Galerkin method, we assume that the physical domain $\varOmega$ is described by a global geometry map $G:[0,1]\rightarrow \overline{\varOmega }$, which is invertible and satisfies $G(\partial ([0,1]))=\partial \overline{\varOmega }$. We fix a set of basis functions $\{\varphi _1,\ldots ,\varphi _{N_n}\}$ defined on the reference (parametric) domain [0, 1] and vanishing on the boundary $\partial ([0,1])$. We consider the basis functions

$$\begin{aligned} \psi _i(x):=\varphi _i(G^{-1}(x))=\varphi _i(t), \qquad x=G(t),\qquad i=1,\ldots ,N_n, \end{aligned}$$

which are defined on the physical domain $\varOmega$, and we define the approximation space $\mathscr {W}_n:=\mathrm{span}(\psi _1,\ldots ,\psi _{N_n})\subset H^1_0(\varOmega )$. Finally, we find approximations to the exact eigenpairs $(\lambda _j,u_j)$, $j=1,2,\ldots ,\infty$, by solving the following Galerkin problem: find $\lambda _{j,n}\in \mathbb R^+$ and $u_{j,n}\in \mathscr {W}_n$, for $j=1,\ldots ,N_n$, such that, for all $v_n\in \mathscr {W}_n$,

$$\begin{aligned} \mathrm{a}(u_{j,n},v_{n})=\lambda _{j,n}(b\,u_{j,n},v_{n}). \end{aligned}$$

(2)

Assuming that both the exact and numerical eigenvalues are arranged in non-decreasing order, the pair $(\lambda _{j,n},u_{j,n})$ is taken as an approximation of the pair $(\lambda _j,u_j)$ for all $j=1,\ldots ,N_n$. The numbers $\lambda _{j,n}/\lambda _j-1,\ j=1,\ldots ,N_n$, are referred to as the (relative) eigenvalue errors.

In view of the canonical identification of each function $v_{n}\in \mathscr {W}_n$ with its coefficient vector with respect to the basis $\{\varphi _1,\ldots ,\varphi _{N_n}\}$, solving the Galerkin problem (2) is equivalent to solving the generalized eigenvalue problem

$$\begin{aligned} \mathbf K_n(a,G)\mathbf u_{j,n}=\lambda _{j,n}\mathbf M_n(b,G)\mathbf u_{j,n}, \end{aligned}$$

(3)

where $\mathbf u_{j,n}$ is the coefficient vector of $u_{j,n}$ with respect to $\{\varphi _1,\ldots ,\varphi _{N_n}\}$ and

$$\begin{aligned} \mathbf K_n(a,G):=[\mathrm{a}(\psi _j,\psi _i)]_{i,j=1}^{N_n}&=\left[ \int _\varOmega a(x)\psi _j'(x)\psi _i'(x)\mathrm{d}x\right] _{i,j=1}^{N_n}\nonumber \\&=\left[ \int _0^1\frac{a(G(t))}{|G'(t)|}\varphi _j'(t)\varphi _i'(t)\mathrm{d}t\right] _{i,j=1}^{N_n},\end{aligned}$$

(4)

$$\begin{aligned} \mathbf M_n(b,G):=[(b\,\psi _j,\psi _i)]_{i,j=1}^{N_n}&=\left[ \int _\varOmega b(x)\psi _j(x)\psi _i(x)\mathrm{d}x\right] _{i,j=1}^{N_n}\nonumber \\&=\left[ \int _0^1b(G(t))|G'(t)|\varphi _j(t)\varphi _i(t)\mathrm{d}t\right] _{i,j=1}^{N_n}. \end{aligned}$$

(5)

The matrices $\mathbf K_n(a,G)$ and $\mathbf M_n(b,G)$ are, respectively, the stiffness and mass matrices. Due to our assumption that $a,b>0$ a.e. on $\varOmega$, both $\mathbf K_n(a,G)$ and $\mathbf M_n(b,G)$ are always symmetric positive definite, regardless of the chosen basis functions $\varphi _1,\ldots ,\varphi _{N_n}$ and the map G. Moreover, it is clear from (3) that the numerical eigenvalues $\lambda _{j,n}$, $j=1,\ldots ,N_n$, are just the eigenvalues of the matrix

$$\begin{aligned} \mathbf L_n(a,b,G):=(\mathbf M_n(b,G))^{-1}\mathbf K_n(a,G). \end{aligned}$$

(6)

Therefore, if $a, b\in L^1(\varOmega )$ and the basis functions $\varphi _1,\ldots ,\varphi _{N_n}$ are chosen as the B-splines of degree p and global smoothness $C^k$ defined on the interval [0, 1] partitioned into n equal subintervals (see [17, Sect. 2.1]) and denoted by

$$\begin{aligned} B_{2,[p,k]},\ldots ,B_{n(p-k)+k,[p,k]}, \end{aligned}$$

(7)

then

$$\begin{aligned} \mathbf K_n(a,G)&=\left[ \int _0^1\frac{a(G(t))}{|G'(t)|}B_{j+1,[p,k]}'(t)B_{i+1,[p,k]}'(t)\mathrm{d}t\right] _{i,j=1}^{n(p-k)+k-1},\end{aligned}$$

(8)

$$\begin{aligned} \mathbf M_n(b,G)&=\left[ \int _0^1b(G(t))|G'(t)|B_{j+1,[p,k]}(t)B_{i+1,[p,k]}(t)\mathrm{d}t\right] _{i,j=1}^{n(p-k)+k-1}. \end{aligned}$$

(9)

From the *-algebra structure of GLT sequences, as proven in [16, 17], we know that

$$\begin{aligned} \Bigl \{\frac{1}{n}\mathbf K_n(a,G)\Bigr \}_n&\sim _{\lambda }\kappa _{[p,k]},\end{aligned}$$

(10)

$$\begin{aligned} \Bigl \{n\mathbf M_n(b,G)\Bigr \}_n&\sim _{\lambda }\xi _{[p,k]},\end{aligned}$$

(11)

$$\begin{aligned} \Bigl \{\frac{1}{n^2}\mathbf L_n(a,b,G)\Bigr \}_n&\sim _{\lambda }\zeta _{[p,k]}, \end{aligned}$$

(12)

where, according to Remark 1, $\kappa _{[p,k]}$, $\xi _{[p,k]}$, $\zeta _{[p,k]}$ are the rearranged versions of

$$ \frac{a(G(t))}{|G'(t)|}\mathbf f_{[p,k]}(\theta ),\quad b(G(t))|G'(t)|\mathbf h_{[p,k]}(\theta ), \quad \frac{a(G(t))}{b(G(t))|G'(t)|^2}\mathbf e_{[p,k]}(\theta ), $$

respectively, with

$$\begin{aligned} \mathbf f_{[p,k]}(\theta )&:= \mathbf K_{[p,k]}^{[0]}+\sum _{\ell =1}^{\eta -1}\Bigl (\mathbf K_{[p,k]}^{[\ell ]}\mathrm{e}^{\mathbf {i}\ell \theta }+(\mathbf K_{[p,k]}^{[\ell ]})^{\mathrm {T}}\mathrm{e}^{-\mathbf {i}\ell \theta }\Bigr ),\end{aligned}$$

(13)

$$\begin{aligned} \mathbf h_{[p,k]}(\theta )&:= \mathbf M_{[p,k]}^{[0]}+\sum _{\ell =1}^{\eta -1}\Bigl (\mathbf M_{[p,k]}^{[\ell ]}\mathrm{e}^{\mathbf {i}\ell \theta }+(\mathbf M_{[p,k]}^{[\ell ]})^{\mathrm {T}}\mathrm{e}^{-\mathbf {i}\ell \theta }\Bigr ),\end{aligned}$$

(14)

$$\begin{aligned} \mathbf e_{[p,k]}(\theta )&:= (\mathbf h_{[p,k]}(\theta ))^{-1}\mathbf f_{[p,k]}(\theta ), \end{aligned}$$

(15)

where the blocks $\mathbf K_{[p,k]}^{[\ell ]}$ and $\mathbf M_{[p,k]}^{[\ell ]}$, of size $p-k$, are defined in [17]. The analytical predictions of the eigenvalue errors are obtained through the following sampling procedure:

$$\begin{aligned} \frac{\lambda _{j,n}}{\lambda _j}-1\approx \frac{n^2\zeta _{[p,k]}\left( \frac{j}{n(p-k)}\right) }{\lambda _j}-1,\qquad j=1,\ldots ,m, \end{aligned}$$

(16)

where $m:=\min (n(p-k),n(p-k)+k-1)$.

However, such a procedure is not completely satisfactory especially in low frequencies (see [17]), when variable coefficients are considered. More precisely, we recall that the smallest eigenvalues are those related to slowly oscillating modes, that is the related eigenvectors belong to the subspace generated by low frequencies. Since the eigenvalues of the continuous operator appear in the denominator in formula (16), the relative error could be higher even if the absolute approximation is of high precision.

We address this issue in the next section.

For notational completeness, we stress that in the following the geometrical map G is always the identity and hence the matrices we consider are those denoted as $\mathbf L_n(a,b):= \mathbf L_n(a,b,I)$ with $\mathbf L_n(a,b,G)$ as in (6); furthermore, the regularity will be maximal that is $k=p-1$ and hence $e_p(\theta )$, $f_p(\theta )$, $h_p(\theta )$ will denote $\mathbf e_{[p,p-1]}(\theta ), \mathbf f_{[p,p-1]}(\theta ), \mathbf h_{[p,p-1]}(\theta )$, respectively.

4 Global Distribution Results and Extrapolation

As discussed in [17], the mismatch between the analytical predictions and the eigenvalue errors essentially occurs only for small eigenvalues and a way to significantly reduce it has already been illustrated in that paper. Drawing inspiration from [1, 9, 10, 12, 13], we here describe—in the case of an isogeometric Galerkin discretization based on B-splines of the eigenvalue problem (1)—an alternative interpolation–extrapolation procedure to considerably improve the analytical predictions for small eigenvalues. We also illustrate the performance of this procedure by two examples.

• 1. We assume that there exists a function $c_p:[0,\pi ]\rightarrow \mathbb R$, depending only on p and the coefficients a, b of the considered eigenvalue problem (1), such that, when using an isogeometric p-degree $C^{p-1}$ B-spline discretization, the following property holds: independently of the parameter n, all the eigenvalues of the matrix $\frac{1}{n^2}\mathbf L_n(a,b)$, sorted in increasing order, satisfy

  $$\begin{aligned} \frac{\lambda _{j,n}}{n^2}\approx c_p(\theta _{j,n})e_p(\theta _{j,n}),\qquad j=1,\ldots ,\min (n+p-2,n), \end{aligned}$$

  (17)

  where

  $$\begin{aligned} e_p= \frac{f_p(\theta )}{h_p(\theta )}&=\frac{(2-2\cos \theta )h_{p-1}(\theta )}{h_p(\theta )}\\&=\frac{(2-2\cos \theta )\bigl (\phi _{[2p-1]}(p)+2\sum _{\ell =1}^{p-1}\phi _{[2p-1]}(p-\ell )\cos (\ell \theta )\bigr )}{\phi _{[2p+1]}(p+1)+2\sum _{\ell =1}^p\phi _{[2p+1]}(p+1-\ell )\cos (\ell \theta )} \end{aligned}$$

  is defined in [17], and

  $$ \theta _{j,n}=\frac{j\pi }{n},\qquad j=1,\ldots ,n. $$

• 2. Compute the eigenvalues of the matrix $\frac{1}{n_1^{2 {L}}}\mathbf {L}_{n_1}(a,b)$ corresponding to a small value of $n_1$, i.e.,

  $$ \frac{\lambda _{j_1,n_1}}{n_1^2},\qquad j_1=1,\ldots ,n_1+p-2. $$

  Since $n_1$ is small, this computation can be efficiently performed by any standard eigensolver (e.g., the Matlab eig function).

• 3. Under the assumption in item 1,

  $$\begin{aligned} c_p(\theta _{j_1,n_1})\approx \frac{\lambda _{j_1,n_1}}{n_1^2e_p(\theta _{j_1,n_1})},\qquad j_1=1,\ldots ,\min (n_1+p-2,n_1). \end{aligned}$$

  This means that we have an approximation of the unknown function $c_p$ over the coarse uniform grid consisting of the points $\theta _{j_1,n_1}$.

• 4. Interpolate the data

  $$ \left( \theta _{j_1,n_1},\frac{\lambda _{j_1,n_1}}{n_1^2e_p(\theta _{j_1,n_1})}\right) ,\qquad j_1=1,\ldots ,\min (n_1+p-2,n_1), $$

  by using, e.g., the Matlab interp1 function with the ‘spline’ option, so as to obtain an approximation of $c_p$ over the whole interval $[0,\pi ]$. We call this approximation $\tilde{c}_p$. Note that, by construction,

  $$ \tilde{c}_p(\theta _{j_1,n_1})=\frac{\lambda _{j_1,n_1}}{n_1^2e_p(\theta _{j_1,n_1})},\qquad j_1=1,\ldots ,\min (n_1+p-2,n_1). $$

• 5. Given a large n, compute approximations of the numerical eigenvalues $\lambda _{j,n}$ by replacing $c_p$ with $\tilde{c}_p$ in (17):

  $$ \lambda _{j,n}\approx n^2\tilde{c}_p(\theta _{j,n})e_p(\theta _{j,n}),\qquad j=1,\ldots ,\min (n+p-2,n). $$

• 6. Compute analytical predictions for the eigenvalue errors as follows:

  $$ \frac{\lambda _{j,n}}{\lambda _j}-1\approx \frac{n^2\tilde{c}_p(\theta _{j,n})e_p(\theta _{j,n})}{\lambda _j}-1,\qquad j=1,\ldots ,\min (n+p-2,n). $$

The next two examples show that the interpolation–extrapolation algorithm defined by items 1–6 may lead to analytical predictions of the eigenvalue errors which perform better (for small eigenvalues) than the analytical predictions proposed in (16).

Table 1 Example 1 [Linear $C^0$ B-spline discretization with $a(x)=2+0.5\,x$ and $b(x)=1$]: The five smallest eigenvalues and eigenvalue approximations, scaled by $10^2$, for $n=200$, $n'=1500$, $p'=5$, and $r=$ 10000

Fig. 1

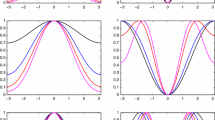
Example 1 [Linear $C^0$ B-spline discretization with $a(x)=2+0.5\,x$ and $b(x)=1$]: analytical predictions $n^2\zeta _r(\frac{j}{n})/\lambda _{j,n'}-1$ and eigenvalue errors $\lambda _{j,n}/\lambda _{j,n'}-1$ versus $j/N_n$, $j=1,\ldots ,N_n$ ($N_n=n-1,\ n=200,\ n'=1500,\ p'=5,\ r=$ 10000)

Fig. 2

Example 1 [Linear $C^0$ B-spline discretization with $a(x)=2+0.5\,x$ and $b(x)=1$]: analytical predictions $n^2\tilde{c}_1(\theta _{j,n})e_1(\theta _{j,n})/\lambda _{j,n'}-1$ and eigenvalue errors $\lambda _{j,n}/\lambda _{j,n'}-1$ versus $j/N_n$, $j=1,\ldots ,N_n$ ($N_n=n-1,\ n=200,\ n'=1500,\ p'=5,\ n_1=10$)

Table 2 Example 2 [p-degree $C^{p-1}$ B-spline discretization for $p=2,3,4,5$ with $a(x)=2.1\cdot 10^9+1.05\cdot 10^9\,x$ and $b(x)=8000$]: The five smallest eigenvalues and eigenvalue approximations, scaled by $10^7$, for $n=200$, $n'=1500$, $p'=5$, and $r=$ 10000

Fig. 3

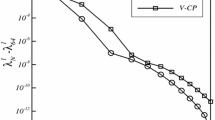
Example 2 [p-degree $C^{p-1}$ B-spline discretization for $p=2,3,4,5$ with $a(x)=2.1\cdot 10^9+1.05\cdot 10^9\,x$ and $b(x)=8000$]: analytical predictions $n^2\zeta _{r,[p,p-1]}(\frac{j}{n})/\lambda _{j,n'}-1$ and eigenvalue errors $\lambda _{j,n}/\lambda _{j,n'}-1$ versus $j/N_n$, $j=1,\ldots ,N_n$ ($N_n=n+p-2$, $n=200$, $n'=1500$, $p'=5$, $r=$ 10000)

Fig. 4

Example 2 [p-degree $C^{p-1}$ B-spline discretization for $p=2,3,4,5$ with $a(x)=2.1\cdot 10^9+1.05\cdot 10^9\,x$ and $b(x)=8000$]: analytical predictions $n^2\tilde{c}_p(\theta _{j,n})e_p(\theta _{j,n})/\lambda _{j,n'}-1$ and eigenvalue errors $\lambda _{j,n}/\lambda _{j,n'}-1$ versus $j/N_n$, $j=1,\ldots ,N_n$ ($N_n=n+p-2$, $n=200$, $n'=1500$, $p'=5$, $n_1=10$)

Example 1

Let $p=1$, $n=200$, $a(x)=2+0.5\,x$ and $b(x)=1$. Let $n'=1500\gg n$, $p'=5$, and take the first $n-1$ eigenvalues of $\mathbf L_{n'}(a,b)$, namely $\lambda _{1,n'},\ldots ,\lambda _{n-1,n'}$, as approximations of the unknown exact eigenvalues $\lambda _1,\ldots ,\lambda _{n-1}$. In Table 1 we report the five smallest eigenvalues and approximated eigenvalues for $p=1$. As is clear the new approximation, $n^2\tilde{c}_1(\theta _{j,n})e_1(\theta _{j,n})$, performs better than $n^2\zeta _{r}\left( \frac{j}{n}\right)$ to approximate $\lambda _{j,n}$, where the function $\zeta _{r}$ introduced in [17, Sect. 3.1] is defined in the following way. Sample $\frac{a(x)}{b(x)}e_1(\theta )$ at the grid points $(x,\theta )\in \mathcal {G}_r$, for a chosen r, where

$$\begin{aligned} \mathcal {G}_r=\left\{ \left( \frac{i}{r},\frac{j\pi }{r}\right) :\quad i,j=1,\ldots ,r\right\} . \end{aligned}$$

The samples are ordered in increasing order in a vector $(z_1,z_2,\ldots ,z_{r^2})$. Let $\zeta _r:[0,1]\rightarrow \mathbb {R}$ be a piecewise linear non-decreasing function that interpolate the samples $(z_0:=z_1,z_2,\ldots ,z_{r^2})$ over the nodes $(0,\frac{1}{r^2},\frac{2}{r^2},\ldots ,1)$.

In Fig. 1 we present the (approximate) analytical predictions $n^2\zeta _r(\frac{j}{n})/\lambda _{j,n'}-1$, with $r=$ 10000, together with the (approximate) eigenvalue errors $\lambda _{j,n}/\lambda _{j,n'}-1$. We note the mismatch for the smallest eigenvalues. In Fig. 2 we plot the (approximate) analytical predictions $n^2\tilde{c}_1(\theta _{j,n})e_1(\theta _{j,n})/\lambda _{j,n'}-1$, obtained from the above interpolation–extrapolation algorithm for $n_1=10$, and the (approximate) eigenvalue errors $\lambda _{j,n}/\lambda _{j,n'}-1$ versus $j/(n-1)$, for $j=1,\ldots ,n-1$. We clearly see that in Fig. 2 the slight mismatch for small eigenvalues observed Fig. 1 has been reduced.

Example 2

Let $p=2,3,4,5$, $n=200$, $a(x)=2.1\cdot 10^9+1.05\cdot 10^9\,x$ and $b(x)=8000$. The approximation parameters $n'$ and $n_1$ have been chosen as $n'=1500$ and $n_1=10$, respectively, and the eigenvalues $\lambda _{j,n'}$ have been chosen correspondingly, in the sense that $\lambda _{j,n'}$ is computed as follows: we compute the eigenvalues $\lambda _{j,n'}$ for a matrix $\mathbf {L}_{n'}(a,b)$ of order $n'=1500$ and B-spline degree $p'=5$. Then we assume that the first $n+p-2$ (for $n=200$) of these eigenvalues, that is $j=1,\ldots ,n+p-2$, are accurate representations of the true eigenvalues $\lambda _j$; see [17] for a motivation and a discussion on this matter.

In Table 2 we present the five smallest eigenvalues and approximated eigenvalues for $p=2,3,4,5$. As is clear the new approximation, $n^2\tilde{c}_p(\theta _{j,n})e_p(\theta _{j,n})$, performs better than $n^2\zeta _{r,[p,p-1]}\left( \frac{j}{n}\right)$ to approximate $\lambda _{j,n}$. Figure 3 shows the comparison between the (approximate) analytical predictions

$$\begin{aligned} \frac{n^2\zeta _{r,[p,p-1]}\left( \frac{j}{n}\right) }{\lambda _{j,n'}}-1,\qquad j=1,\ldots ,n, \end{aligned}$$

and the (approximate) eigenvalue errors

$$\begin{aligned} \frac{\lambda _{j,n}}{\lambda _{j,n'}}-1,\qquad j=1,\ldots ,n+p-2, \end{aligned}$$

whereas Fig. 4 shows the comparison between the (approximate) analytical predictions

$$\begin{aligned} \frac{n^2\tilde{c}_p(\theta _{j,n})e_p(\theta _{j,n})}{\lambda _{j,n'}}-1,\qquad j=1,\ldots ,n, \end{aligned}$$

with the (approximate) eigenvalue errors. We see from Fig. 4 that the mismatch for small eigenvalues observed in Fig. 3 has been lowered.

5 Dyadic Decomposition Argument and Extreme Eigenvalues

While the distribution results are available both in the Galerkin [15] and in the collocation setting [7], the use of extrapolation methods, as those described in the previous section and in [10, 11], has been developed only in the Galerkin setting. The reason is the inherent nonsymmetry of the collocation matrices. However, this issue has to be investigated in the future, even if few preliminary experiments seem quite promising. In this section, we start by analyzing the extreme eigenvalues of the (nonsymmetric) stiffness matrices in the collocation setting. We use a dyadic decomposition argument already employed for symmetric structures in several contexts (see [3, 20] and references therein).

Consider the one-dimensional Poisson problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -u''(x)=\mathrm{f}(x), &{} x\in (0,1),\\ u(x)=0, &{} x\in \{0,1\}, \end{array}\right. } \end{aligned}$$

(18)

where $\mathrm{f}\in C([0,1])$. Suppose we approximate (18) by using the isogeometric collocation method based on uniform B-splines (see [7, Sect. 4] for the details on this method). Then, the resulting discretization matrix is

$$\begin{aligned} n^2\tilde{\mathbf {K}}_n^{[p]}:=\left[ -N_{j,[p]}''(\xi _{i,[p]})\right] _{i,j=2}^{n+p-1}, \end{aligned}$$

(19)

where $\xi _{i,[p]},\ i=2,\ldots ,n+p-1,$ are the Greville abscissae defined in [7, Eq. (4.6)], while $N_{j,[p]},\ j=2,\ldots ,n+p-1,$ are the usual B-spline basis functions of maximal regularity $k=p-1$. In other words, with reference to (7), we have

$$ N_{j,[p]}= B_{j,[p,p-1]},\quad j=2,\ldots ,n+p-1. $$

We denote by $\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})$ the real part of $\tilde{\mathbf {K}}_n^{[p]}$ (the real part of a square complex matrix X [4] is by definition $(X+X^{\mathrm {H}})/2$, $X^{\mathrm {H}}$ being the transpose conjugate). In Theorem 1 we prove for $p=3$ the following result:

$$\begin{aligned} \exists \,c_p>0:\ \mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})\ge c_p\,\tau _{n+p-2}(2-2\cos \theta ),\quad \forall n\ge 2, \end{aligned}$$

(20)

where

$$ \mathfrak {R}(\tilde{\mathbf {K}}_n^{[3]})= \left[ \begin{array}{rrrrrrrrrrr} \frac{11}{2} &{} -\frac{4}{3} &{} -\frac{1}{6} &{} &{} &{} &{} &{} &{} \\ -\frac{4}{3} &{} \frac{5}{2} &{} -1 &{} &{} &{} &{} &{} &{} \\ -\frac{1}{6} &{} -1 &{} 2 &{} -1 &{} &{} &{} &{} &{} \\ &{} &{} -1 &{} 2 &{} -1 &{} &{} &{} &{} \\ &{} &{} &{} \ddots &{} \ddots &{} \ddots &{} &{} &{} \\ &{} &{} &{} &{} -1 &{} 2 &{} -1 &{} &{} \\ &{} &{} &{} &{} &{} -1 &{} 2 &{} -1 &{} -\frac{1}{6} \\ &{} &{} &{} &{} &{} &{} -1 &{} \frac{5}{2} &{} -\frac{4}{3} \\ &{} &{} &{} &{} &{} &{} -\frac{1}{6} &{} -\frac{4}{3} &{} \frac{11}{2} \end{array}\right] $$

and

$$ \tau _{n+1}(2-2\cos \theta )= \left[ \begin{array}{rrrrr} 2 &{} -1 &{} &{} &{} \\ -1&{} \ddots &{} \ddots &{} &{} \\ &{} \ddots &{} &{} \ddots &{} \\ &{} &{} \ddots &{} \ddots &{} -1 \\ &{} &{} &{} -1 &{} 2 \end{array}\right] . $$

Theorem 1

There exists a constant $c_3>0$ such that

$$\mathfrak {R}(\tilde{\mathbf {K}}_n^{[3]})\ge c_3\,\tau _{n+1}(2-2\cos \theta ),\quad \forall n\ge 2.$$

Proof

For $n=2,\ldots ,5$, a direct verification shows that $\mathfrak {R}(\tilde{\mathbf {K}}_n^{[3]})$ is positive definite. Therefore, the theorem is proved if there exists a constant $c>0$ such that

$$\begin{aligned} \mathfrak {R}(\tilde{\mathbf {K}}_n^{[3]})\ge c\,\tau _{n+1}(2-2\cos \theta ),\qquad \forall n\ge 6\text{. } \end{aligned}$$

(21)

For $n\ge 6$ and $c>0$, the matrix $\mathfrak {R}(\tilde{\mathbf {K}}_n^{[3]})-c\,\tau _{n+1}(2-2\cos \theta )$ is explicitly given by

$$\begin{aligned} \, \left[ \begin{array}{rrrrrrrrrr} \frac{11}{2}-2c &{} -\frac{4}{3}+c &{} -\frac{1}{6} &{} &{} &{} &{} &{} &{} \\ -\frac{4}{3}+c &{} \frac{5}{2}-2c &{} -1+c &{} &{} &{} &{} &{} &{} \\ -\frac{1}{6} &{} -1+c &{} 2-2c &{} -1+c &{} &{} &{} &{} &{} \\ &{} &{} -1+c &{} 2-2c &{} -1+c &{} &{} &{} &{} \\ &{} &{} &{} \ddots &{} \ddots &{} \ddots &{} &{} &{} \\ &{} &{} &{} &{} -1+c &{} 2-2c &{} -1+c &{} &{} \\ &{} &{} &{} &{} &{} -1+c &{} 2-2c &{} -1+c &{} -\frac{1}{6} \\ &{} &{} &{} &{} &{} &{} -1+c &{} \frac{5}{2}-2c &{} -\frac{4}{3}+c \\ &{} &{} &{} &{} &{} &{} -\frac{1}{6} &{} -\frac{4}{3}+c &{} \frac{11}{2}-2c \end{array}\right] \end{aligned}$$

and can be decomposed as follows:

In the above decomposition, r, s, and t are arbitrary real numbers, whereas each term of the summation is a $(n+1)\times (n+1)$ matrix whose only nonzero entries are shown in the associated box and are contained in the principal submatrix corresponding to the rows from the superscript to the subscript. For instance,

If each term of the above summation is a nonnegative definite matrix, then $\mathfrak {R}(\tilde{\mathbf {K}}_n^{[3]})-c\,\tau _{n+1}(2-2\cos \theta )$ is nonnegative definite as well. The following conditions ensure that each term of the summation is nonnegative definite:

$$ \left\{ \begin{array}{l} r>0,\ s>0,\ rs\ge \left( \frac{4}{3}-c\right) ^2,\\ \frac{11}{2}-2c-r>0,\ t>0,\ \left( \frac{11}{2}-2c-r\right) t\ge \frac{1}{36},\\ \frac{5}{2}-2c-s>0,\ 1-c-t>0,\\ (\frac{5}{2}-2c-s)(1-c-t)\ge (1-c)^2,\\ c\le 1.\\ \end{array}\right. $$

These conditions are satisfied, for instance, with

$$c=\frac{58}{59},\ \ s=\frac{1}{2},\ \ r=\frac{\left( \frac{4}{3}-c\right) ^2}{s},\ \ t=\frac{\frac{1}{36}}{\frac{11}{2}-2c-r}.$$

Hence, (21) holds with $c=58/59$. $\square$

We verified that the dyadic decomposition argument used in the proof of Theorem 1 can also be used to prove (20) for $p=2,4$. Although this argument becomes quite difficult to apply for $p\ge 5$, we have reason to believe that a careful application of it could prove (20) for any given $p\ge 2$.

The above theorem and the relations in (20) have interesting consequences on the conditioning measured with respect to the induced Euclidean norm as reported in Corollary 1, whose proof requires a technical but interesting in itself lemma.

Lemma 1

Given X square matrix, assuming $\mathfrak {R}(X)$ positive definite, we have

$$ \lambda _{\min }(\mathfrak {R}(X))\le \sigma _{\min }(X). $$

Proof

As a first step define the following matrix $\hat{X}$ of order 2n

$$ \hat{X}=\left[ \begin{array}{ll} 0 &{} X \\ X^{\mathrm {H}} &{} 0 \end{array}\right] . $$

By taking into account the standard singular value decomposition, it is easy to see (and it is well-known) that the singular values $\sigma _j(X)$ of X, $j=1,\ldots ,n$, coincide with the n largest eigenvalues of $\hat{X}$, since the eigenvalues of the Hermitian matrix $\hat{X}$ are $\pm \sigma _j(X)$, $j=1,\ldots ,n$. Therefore, we infer that

$$ \sigma _{\min }(X)=\lambda _{n+1}(\hat{X}), $$

with $\lambda _{1}(\hat{X})\le \lambda _{2}(\hat{X})\le \cdots \le \lambda _{2n}(\hat{X})$. From the minimax characterization (see [4]) of the $(n+1)$-th eigenvalue of $\hat{X}$, we obtain

$$\begin{aligned} \sigma _{\min }(X)=\max _{\mathrm{dim}(U)=n} \min _{u\in U} \frac{u^{\mathrm {H}} \hat{X}u}{u^{\mathrm {H}}u}, \end{aligned}$$

(22)

where the maximum is taken over all subspaces U with codimension n in ${\mathbb {C}}^{2n}$ or, equivalently, over all subspaces U of dimension n. Let $U_*$ be the n-dimensional subspace of ${\mathbb {C}}^{2n}$ made of all vectors y of the form

$$ y=\left( \begin{array}{l} u \\ u \end{array}\right) , \quad u\in {\mathbb {C}}^{n}, \quad u= \left( \begin{array}{l} u_1 \\ u_2 \\ \vdots \\ u_n. \end{array}\right) . $$

If $y\in U_*$ is partitioned into blocks as above, it holds

$$\begin{aligned} \frac{y^{\mathrm {H}} \hat{X}y}{y^{\mathrm {H}} y}= & {} \frac{u^{\mathrm {H}} \mathfrak {R}(X) u}{u^{\mathrm {H}} u}, \end{aligned}$$

(23)

and since $U_*$ is a particular subspace of dimension n, from (22) the thesis follows. $\square$

Corollary 1

Assume that (20) is satisfied for a given p. Then

$$\begin{aligned} \mu _2(\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})) \sim n^2, \end{aligned}$$

(24)

and

$$\begin{aligned} \mu _2(\tilde{\mathbf {K}}_n^{[p]}) \le C_p n^2, \end{aligned}$$

(25)

with $C_p$ a positive constant depending only on p and $\mu (X)=\Vert X\Vert \Vert X^{-1}\Vert$ being the conditioning of an invertible matrix X measured with respect to the induced Euclidean norm $\Vert \cdot \Vert$.

Proof

First of all we observe that both $\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})$ and $\tilde{\mathbf {K}}_n^{[p]}$ are banded matrices with coefficients not depending on the parameter n. Hence we have that their induced Euclidean norm is asymptotic to a a constant not depending on n that is

$$\begin{aligned} \Vert \mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})\Vert \sim 1, \end{aligned}$$

(26)

$$\begin{aligned} \Vert \tilde{\mathbf {K}}_n^{[p]}\Vert \sim 1. \end{aligned}$$

(27)

We first prove (24). By (20) we have

$$ \mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})\ge c_p\,\tau _{n+p-2}(2-2\cos \theta ),\quad \forall n\ge 2, $$

with $c_p>0$ and hence $\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})$ is positive definite and its minimal eigenvalue is bounded from below by

$$ c_p 4\sin ^2\left( \frac{\pi }{2(n+p-1)}\right) , $$

$4\sin ^2\left( \frac{\pi }{2(n+p-1)}\right)$ being the minimal eigenvalue of $\tau _{n+p-2}(2-2\cos \theta )$ (see [19] and references therein). On the other hand, $\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})$ contains as a principal submatrix a Toeplitz matrix of size proportional to n and generated by $f_p$ being nonnegative and having a unique zero of order two (see [7, 14]). Hence such a Toeplitz matrix has the minimal eigenvalue $l_n$ asymptotic to $n^{-2}$ (see again [19] and references therein) and by the Cauchy interlacing theorem the minimal eigenvalue of $\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})$ is bounded from above by $l_n\sim n^{-2}$. Therefore

$$ \lambda _{\min }(\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]}))\sim n^{-2}. $$

But $\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})$ is positive definite and hence

$$ \left\| [\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})]^{-1}\right\| = [\lambda _{\min }(\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]}))]^{-1}\sim n^{2}, $$

from which, using (26), we deduce

$$ \mu _2(\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})) \sim n^2. $$

We now prove (25). Given the known fact $\Vert X^{-1}\Vert =[\sigma _{\min }(X)]^{-1}$, statement (25) is a consequence of (27), of (20), of Lemma 1, and of the fact that the minimal eigenvalue of $\tau _{n+p-2}(2-2\cos \theta )$ is

$$ \sin ^2\left( \frac{\pi }{2(n+p-1)}\right) \sim n^{-2}. $$

$\square$

Furthermore, we have reasons to conjecture that the spectral conditioning of the collocation stiffness matrices grows asymptotically as $n^2$, exactly as in the Galerkin setting [14], since $\tilde{\mathbf {K}}_n^{[p]}$ contains as a principal submatrix a Toeplitz matrix of size proportional to n and generated by $f_p$ having a unique zero of order two (as $\mathfrak {R}(\tilde{\mathbf {K}}_n^{[p]})$, see the proof of Corollary 1).

We finally stress that (20) is also important in a multigrid context for proving the optimality of the related two-grid and multigrid techniques (see [2, 6, 8, 19]), by following the theory reported by Ruge and Stüben in [18].

6 Conclusions

In this note, we have considered the spectral analysis of large matrices coming from the isogeometric approximations based on B-splines of the eigenvalue problem

$$ -(a(x)u'(x))'=\lambda b(x) u(x),\quad \quad x\in (0,1), $$

where u(0) and u(1) are given. In the collocation setting, we complemented global eigenvalue distribution results, available in the literature [7], with precise estimates for the extremal eigenvalues and hence for the spectral conditioning of the resulting matrices. In the Galerkin setting, we have designed an efficient matrix-less procedure (see [9]) that gives a highly accurate estimate of the all the eigenvalues, starting from the knowledge of the spectral GLT distribution symbol. Possible extensions include a more systematic treatment of the collocation case, both via the use of dyadic decomposition arguments and via the use of proper matrix-less extrapolation techniques. This last item is completely new and represents a real challenge, thus it will be the subject of a future investigation.