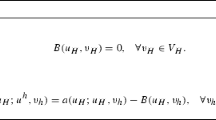Two-grid optimality for Galerkin linear systems based on B-splines

Abstract

A multigrid method for linear systems stemming from the Galerkin B-spline discretization of classical second-order elliptic problems is considered. The spectral features of the involved stiffness matrices, as the fineness parameter h tends to zero, have been deeply studied in previous works, with particular attention to the dependencies of the spectrum on the degree p of the B-splines used in the discretization process. Here, by exploiting this information in connection with $\tau$-matrices, we describe a multigrid strategy and we prove that the corresponding two-grid iterations have a convergence rate independent of h for $p=1,2,3$. For larger p, the proof may be obtained through algebraic manipulations. Unfortunately, as confirmed by the numerical experiments, the dependence on p is bad and hence other techniques have to be considered for large p.

1 Introduction

In this paper we consider the differential problem

(1)

with ${\varOmega }:=(0,1)^d$, $\mathrm{f}\in L^2({\varOmega })$, $\gamma \ge 0$. We are interested in designing a multigrid strategy for the fast numerical solution of large linear systems stemming from the discretization of (1) by the Galerkin B-spline isogeometric analysis (IgA) technique; see [7, 18].

In [16] we studied in detail the spectral properties of the resulting stiffness matrices based on uniform tensor-product B-splines. Not only the spectral localization and the conditioning were investigated, but also the global spectral behavior. This spectral behavior can be described in the Weyl sense (see [24] and the literature therein) in terms of a d-variate trigonometric polynomial $f_{{\varvec{p}}}$, the so-called (spectral) symbol; here, ${{\varvec{p}}}:=(p_1,\ldots ,p_d)$ and $p_i$ is the spline degree in the i-th direction, $i=1,\ldots ,d$. It turns out that the symbol $f_{{{\varvec{p}}}}$ is equivalent to the classical symbol

$$\begin{aligned} z_d({\varvec{\theta }})=z_d(\theta _1,\ldots ,\theta _d):=\sum _{j=1}^d(2-2\cos \theta _j), \end{aligned}$$

(2)

which is obtained when approximating (1) by standard uniform centered second-order Finite Differences (FD) or by piecewise linear Finite Elements (FE) on uniform triangulations. In other words, there exist positive constants $c_{{{\varvec{p}}}}, C_{{{\varvec{p}}}}$ such that

$$\begin{aligned} c_{{{\varvec{p}}}} z_d({\varvec{\theta }}) \le f_{{{\varvec{p}}}}({\varvec{\theta }}) \le C_{{{\varvec{p}}}} z_d({\varvec{\theta }}),\quad \forall {\varvec{\theta }}\in [0,\pi ]^d. \end{aligned}$$

(3)

From (3) we expect that the conditioning of the Galerkin B-spline IgA stiffness matrices grows like $m^{2/d}$, where m is the matrix size, d is the dimensionality of the elliptic problem, and 2 is the order of the elliptic operator in (1). The approximation parameters ${{\varvec{p}}}$ play a limited role, and characterize the constant in the expression $O(m^{2/d})$. We refer the reader to [15, Theorem 4.6] for a rigorous proof of the above statements.¹

Moreover, in view of the equivalence (3) and given the $\tau$-like (resp., Toeplitz-like) structure of the considered stiffness matrices, we expect that a standard multigrid procedure designed for $\tau$ (resp., Toeplitz) linear systems with symbol $z_d$ has to be optimal also in our context. The optimality was predicted and validated through numerical experiments in [9], but a formal proof was not yet given in the literature. In this paper, we formally prove the optimality for the two-grid method and certain values of ${{\varvec{p}}}$, and hence also for the W-cycle and k-grid method (with k independent of the matrix size).

In order to design our optimal multigrid solver, we heavily rely on the spectral and structural information of the coefficient matrices analyzed in detail in [16]. More precisely, the stiffness matrices arising from the Galerkin B-spline IgA discretization of problem (1) are:

• banded in a d-level sense with partial bandwidths proportional to $p_j$, $j=1,\ldots ,d$;

• a small perturbation of a d-level $\tau$-matrix (or Toeplitz matrix) generated by $f_{{{\varvec{p}}}}$, and are spectrally distributed like the symbol $f_{{{\varvec{p}}}}$ in the Weyl sense.

The first item implies that optimal methods should have a total cost which is linear with respect to the matrix size and with a constant proportional to $\Vert {{\varvec{p}}}\Vert _\infty$. The second item suggests to look for optimal methods in the wide literature of multilevel $\tau$ (or Toeplitz) solvers [19]. In this paper, inspired by [12, 22], we follow a sort of ‘canonical procedure’ for creating—on the basis of the symbol—a two-grid method from which we expect optimal convergence properties. The design of the method is based on analogous optimal techniques for $\tau$ and Toeplitz matrices with symbol $f_{{\varvec{p}}}$ or, equivalently, with symbol $z_d$, because of the relation (3). The optimality of the method was already predicted in [9] on the basis of heuristic arguments, but no rigorous proof was given. Here, we provide the formal proof, at least for $p_j\le 3$, $j=1,\ldots ,d$. When proving the optimality result, we arrive at a matrix inequality, see (26), which is useful not only in a multigrid setting, but also in a preconditioning context for designing optimal preconditioners for Krylov-type techniques, in particular for the Conjugate Gradient (CG) method; see Remark 6.

It is worth mentioning that our proof of optimality is based on standard tools from algebraic multigrid analysis [20], applied within the framework of the theory of $\tau$ and Toeplitz matrices [22]. Our choice to consider the formalism of multigrid methods for $\tau$ and Toeplitz matrices instead of the classical Local Fourier Analysis (LFA) is motivated by the possibility to apply directly the results in [16]. Nevertheless, as proved in [8], the convergence analysis based on the symbol of $\tau$ and Toeplitz matrices arising in the discretization of differential problems is equivalent to the LFA. The reader who is familiar with the LFA can follow the proof just being aware of two facts:

• the symbol is not scaled by the discretization step;

• the information on the order of the differential problem survives in the order of the zero of the symbol.

We refer to [8] for further details.

Unfortunately, it turns out that the equivalence constant $c_{{{\varvec{p}}}}$ in (3) tends to 0 when $p_j\rightarrow \infty$ for some j, i.e., when $\Vert {{\varvec{p}}}\Vert _\infty \rightarrow \infty$. Even worse, two further facts occur [9, 11]:

• the convergence to 0 is exponential with respect to each $p_j$, $j=1,\ldots ,d$;

• the values of ${\varvec{\theta }}$ for which $f_{{\varvec{p}}}({\varvec{\theta }})$ tends to 0 exponentially are localized at the frontier of $[0,\pi ]^d$, where at least one variable $\theta _j$ equals $\pi$.

As a consequence, despite the m-independence of the two-grid convergence rate (recalling that m is the matrix size), the method is unsatisfactory when ${{\varvec{p}}}$ has large entries: we have theoretical optimality, but the spectral radius of the two-grid iteration matrix is close to 1. For instance, in the 1D case the spectral radius of the two-grid iteration matrix tends to 1 exponentially as p increases and a similar phenomenon is observed for any dimensionality d. This unpleasant behavior is due to the analytical properties of the symbol $f_{{{\varvec{p}}}}$ and is essentially related to the existence of a subspace of high frequencies associated with very small eigenvalues. This explains the numerical results in [9, 14]. In particular, the considered two-grid and the associated V/W-cycle methods converge very fast in low frequencies, but they are slow, for large ${{\varvec{p}}}$, in high frequencies. This fact is nontrivial, but it can be understood in terms of the theory of multilevel $\tau$-matrices (or Toeplitz matrices) and is related to specific analytic features of the symbol. We refer the reader to [11] for a deeper theoretical insight in these statements.

The above intrinsic difficulty can be addressed by following the multi-iterative idea from [21]. Indeed, the m-independent two-grid/multigrid method was successfully combined in [9, 11] with a ${{\varvec{p}}}$-independent smoother of preconditioned Krylov type (namely a PCG), where the preconditioner was suggested by the symbol. This results in a multi-iterative multigrid solver with m- and ${{\varvec{p}}}$-independent convergence rate. A very similar multi-iterative multigrid solver was also constructed for IgA collocation methods in [10].

The remainder of this paper is organized as follows. In Sect. 2 we detail the considered model problem; we define d-level $\tau$-matrices; and we describe the two-grid method for such kind of matrices. In Sect. 3 we recall the spectral properties obtained in [16] for the matrices arising from the discretization of (1) by IgA based on uniform B-splines. In Sect. 4 the optimality of the two-grid applied to our problem is proved for $p=1,2,3$ in 1D and for $1\le p_1,p_2\le 3$ in 2D. The proof can be trivially extended to any dimensionality for $1\le p_1,\ldots ,p_d\le 3$. In Sect. 5 we provide some numerical examples to support our theoretical analysis. Sect. 6 concludes the work.

2 Preliminaries

We start with a brief description of the Galerkin method applied to (1) in the IgA context. Then, we introduce some auxiliary structures, namely d-level $\tau$-matrices, which are used for designing multigrid algorithms and for studying their convergence features.

2.1 The d-dimensional problem setting

IgA was introduced in [18] aiming to reduce the gap between Finite Element Analysis and Computer-Aided Design (CAD). The main idea in IgA is to use directly the geometry provided by CAD systems—which is usually expressed in terms of tensor-product B-splines or their rational version, the so-called NURBS—and to approximate the unknown solutions of differential equations by the same type of functions. Thanks to the well-known properties of the B-spline basis (see, e.g., [6]), this approach offers some interesting advantages from the geometric, the analytic, and the computational point of view; see [7, 18] and references therein.

Let us now consider our model problem (1). The corresponding weak form reads as follows: find $u\in H^1_0({\varOmega })$ such that

$$\begin{aligned} a(u,v)=\mathrm{F}(v),\quad \forall v\in H^1_0({\varOmega }), \end{aligned}$$

(4)

where $a(u,v):=\int _{{\varOmega }}(\nabla u\cdot \nabla v+\gamma uv)$ and $\mathrm{F}(v):=\int _{{\varOmega }}\mathrm{f}v$. It is well-known that there exists a unique solution u of (4), the so-called weak solution of (1).

In the Galerkin method, we look for an approximation $u_{\mathcal {W}}$ of u by choosing a finite dimensional approximation space ${\mathcal {W}}\subset H^1_0({\varOmega })$ and by solving the following problem: find $u_{\mathcal {W}}\in {\mathcal {W}}$ such that

$$\begin{aligned} a(u_{\mathcal {W}},v)=\mathrm{F}(v),\quad \forall v\in {\mathcal {W}}. \end{aligned}$$

(5)

Let $\dim {\mathcal {W}}=N$, and fix a basis $\{\varphi _1,\ldots ,\varphi _N\}$ for ${\mathcal {W}}$. It is known that problem (5) always has a unique solution $u_{\mathcal {W}}$, which can be written as $u_{\mathcal {W}}=\sum _{j=1}^Nu_j\varphi _j$ and can be computed as follows: find $\mathbf{u } :=(u_1,\ldots ,u_N)^T\in {\mathbb {R}}^N$ such that

$$\begin{aligned} A\mathbf{u } =\mathbf{b } , \end{aligned}$$

(6)

where $A:=\left[ a(\varphi _j,\varphi _i)\right] _{i,j=1}^N\in {\mathbb {R}}^{N\times N}$ is the stiffness matrix and $\mathbf{b } :=\left[ \mathrm{F}(\varphi _i)\right] _{i=1}^N\in {\mathbb {R}}^N$.

In classical FE methods the approximation space ${\mathcal {W}}$ is usually a space of $C^0$ piecewise polynomials vanishing on $\partial {\varOmega }$, whereas in the IgA framework ${\mathcal {W}}$ is a spline space with higher continuity; see [7, 18]. In this paper we only consider the IgA setting without any geometry map.

2.2 d-Level $\tau$-matrices

For every $m\in {\mathbb {N}}$ we denote by ${\mathcal {Q}}_m$ the symmetric unitary discrete sine transform,

$$\begin{aligned} {\mathcal {Q}}_m:=\sqrt{\frac{2}{m+1}}\left[ \sin \left( \frac{\textit{ij}\pi }{m+1}\right) \right] _{i,j=1}^m, \end{aligned}$$

and for every multi-index ${{\varvec{m}}}:=(m_1,\ldots ,m_d)\in {\mathbb {N}}^d$ we set ${\mathcal {Q}}_{{{\varvec{m}}}}:={\mathcal {Q}}_{m_1}\otimes \cdots \otimes {\mathcal {Q}}_{m_d}$.

Definition 1

Given a d-variate function $g:[0,\pi ]^d\rightarrow {\mathbb {R}}$ and a multi-index ${{\varvec{m}}}\in {\mathbb {N}}^d$, the d-level $\tau$-matrix $\tau _{{\varvec{m}}}(g)$ of partial orders $m_1,\ldots ,m_d$ (and order $m_1\cdots m_d$) associated with g is defined as

$$\begin{aligned}&\tau _{{\varvec{m}}}(g):={\mathcal {Q}}_{{\varvec{m}}}\cdot \\&\quad \mathop {\mathrm {diag}}_{j_1=1,\ldots ,m_1} \biggl [\biggr .\biggl .\ldots \biggl [\mathop {\mathrm {diag}}_{j_d=1,\ldots ,m_d}g\biggl (\frac{j_1\pi }{m_1+1},\ldots ,\frac{j_d\pi }{m_d+1}\biggr )\biggr ]\ldots \biggr ]{\mathcal {Q}}_{{\varvec{m}}}. \end{aligned}$$

The function g is called the generating function of the $\tau$-family $\{\tau _{{\varvec{m}}}(g)\}_{{{\varvec{m}}}\in {\mathbb {N}}^d}$.

We denote by $C_c({\mathbb {R}})$ the set of all continuous functions on ${\mathbb {R}}$ with compact support. Given $g:[0,\pi ]^d\rightarrow {\mathbb {R}}$ in $C([0,\pi ]^d)$, one can check that, $\forall F\in C_c({\mathbb {R}})$,

$$\begin{aligned}&\lim _{{{\varvec{m}}}\rightarrow \infty }\frac{1}{m_1\ldots m_d}\sum _{j=1}^{m_1\cdots m_d}F(\lambda _j(\tau _{{\varvec{m}}}(g))) \nonumber \\&\quad =\frac{1}{\pi ^d}\int _{[0,\pi ]^d}F(g(\theta _1,\ldots ,\theta _d))\,\mathrm{d}\theta _1\ldots \mathrm{d}\theta _d, \end{aligned}$$

(7)

where, for a multi-index ${{\varvec{m}}}\in {\mathbb {N}}^d$, ${{\varvec{m}}}\rightarrow \infty$ means that $\min (m_1,\ldots ,m_d)\rightarrow \infty$. Due to the limit relation (7), the function g is called the symbol of the $\tau$-family $\{\tau _{{\varvec{m}}}(g)\}_{{{\varvec{m}}}\in {\mathbb {N}}^d}$.

Note that, for every ${{\varvec{m}}}\in {\mathbb {N}}^d$, if g is a linear d-variate cosine trigonometric polynomial then the d-level $\tau$-matrix $\tau _{{{\varvec{m}}}}(g)$ coincides with the d-level Toeplitz matrix $T_{{{\varvec{m}}}}(g)$ associated with g (see [9, Definition 3.2] for its definition).

2.3 Multigrid methods

Given a linear system of dimension m,

$$\begin{aligned} A_m\mathbf{u } =\mathbf{b } , \end{aligned}$$

(8)

we assume to have a convergent stationary iterative method

$$\begin{aligned} \mathbf{u } ^{(k+1)}=S_m\mathbf{u } ^{(k)}+(I-S_m)A_m^{-1}\mathbf{b } , \end{aligned}$$

called smoother, for the solution of (8), and a full-rank matrix $P_m\in {\mathbb {R}}^{l\times m}$ with $l\le m$, called projector or grid-transfer operator. Moreover, we define the coarse matrix as $P_mA_mP_m^T$, following the Galerkin approach. Then, given an approximation $\mathbf{u } ^{(k)}$ to the solution $\mathbf{u } =A_m^{-1}\mathbf{b }$, the corresponding Two-Grid Method (TGM) for solving (8) computes a new approximation $\mathbf{u } ^{(k+1)}$ by applying a coarse-grid correction and a smoothing iteration as follows:

Algorithm 1

• 1. compute the residual: $\mathbf{r } \leftarrow \mathbf{b } -A_m\mathbf{u } ^{(k)}$;

• 2. project the residual: $\mathbf{r } \leftarrow P_m\mathbf{r }$;

• 3. compute the correction: $\mathbf{e } \leftarrow \left( P_mA_mP_m^T\right) ^{-1}\mathbf{r }$;

• 4. extend the coarse error: $\mathbf{e } \leftarrow P_m^T\mathbf{e }$;

• 5. correct the given approximation: $\mathbf{u } ^{(k+1)}\leftarrow \mathbf{u } ^{(k)}+\mathbf{e }$;

• 6. relax one time: $\mathbf{u } ^{(k+1)}\leftarrow S_m\mathbf{u } ^{(k+1)}+(I-S_m)A_m^{-1}\mathbf{b }$.

The iteration matrix of this two-grid scheme is

$$\begin{aligned} TG(S_m,P_m):=S_m \left( I-P_m^T\left( P_mA_mP_m^T\right) ^{-1}P_mA_m\right) . \end{aligned}$$

Note that Algorithm 1 only considers a single post-smoothing iteration in order to stay in the framework of [20], so as to simplify the presentation of the theoretical analysis, but it is clear that one can add a convergent pre-smoother and/or more smoothing iterations to improve the convergence rate of the TGM.

In practice, the coarser linear system of the TGM could be too large to be solved directly. Hence, the third step in Algorithm 1 is usually replaced by one recursive call, obtaining a multigrid V-cycle algorithm, or by two recursive calls, obtaining a multigrid W-cycle algorithm.

The optimality proofs for the two-grid methods, presented in this paper, heavily rely on a classical result for the two-grid convergence rate, stated in Theorem 2. For its proof, we refer the reader to [20, Theorem 5.2] and [2, Remark 2.2]. Given a Symmetric Positive Definite (SPD) matrix $X\in {\mathbb {R}}^{m\times m}$, we denote by $\Vert \cdot \Vert _{X}$ both the vector-norm and the matrix-norm induced by X, i.e.,

$$\begin{aligned}&\Vert \mathbf{x } \Vert _{X}:=\Vert X^{1/2}\mathbf{x } \Vert _2, \qquad \mathbf{x } \in {\mathbb {R}}^{m},\\&\Vert Y\Vert _{X}:=\Vert X^{1/2}YX^{-1/2}\Vert _2, \qquad Y\in {\mathbb {R}}^{m\times m}, \end{aligned}$$

where $\Vert \cdot \Vert _2$ stands for both the classical 2-norm (the Euclidean norm) and its induced matrix-norm.

Theorem 2

([20]) Let $A_m\in {\mathbb {R}}^{m\times m}$ be SPD, let $S_m\in {\mathbb {R}}^{m\times m}$, and let $P_m\in {\mathbb {R}}^{l\times m}$ be full-rank $(l\le m)$. Assume

• (a) $\exists \, a_m>0:\, \Vert S_m\mathbf{x } \Vert ^2_{A_m}\le \Vert \mathbf{x } \Vert _{A_m}^2-a_m\Vert \mathbf{x } \Vert ^2_{A_m^2}$,

• (b) $\exists \, b_m>0:\, \min _{\mathbf{y } \in {\mathbb {R}}^{l}}\Vert \mathbf{x } -P_m^T\mathbf{y } \Vert _2^2\le b_m\Vert \mathbf{x } \Vert ^2_{A_m}$,

for all $\mathbf{x } \in {\mathbb {R}}^{m}$. Then $b_m\ge a_m$ and

$$\begin{aligned} \rho \left( TG(S_m,P_m)\right) \le \Vert TG(S_m,P_m)\Vert _{A_m}\le \sqrt{1-\frac{a_m}{b_m}}. \end{aligned}$$

The first condition (a) in Theorem 2 is referred to as the smoothing condition, whereas the second condition (b) as the approximation condition. In the following, we discuss the values of the constants $a_m$ and $b_m$ for specific smoothers and projectors. For the smoothers, the discussion will be completely general, independent of the matrix $A_m$ (see Lemma 1), while for the projectors we will restrict our attention to matrices $A_m=A_{{\varvec{m}}}$ (of size $m=m_1\cdots m_d$) that ‘majorize’, in the sense of (13), the $\tau$-matrix $\tau _{{\varvec{m}}}(z_d)$ generated by the trigonometric polynomial (2).

When using the Richardson iteration, the smoothing condition can be easily satisfied and the next lemma can be proved in the same way as [20, Theorem 4.4] (with $D=I$ and $Q=I/\omega$).

Lemma 1

Let $A_m\in {\mathbb {R}}^{m\times m}$ be SPD, let $S_m:=I-\omega A_m$ $(\omega \in {\mathbb {R}})$, and let $\mu _m\ge \rho (A_m)$. If $0<\omega <2/\mu _m$, then the smoothing condition (a) in Theorem 2 holds with $a_m:=\omega (2-\omega \mu _m)>0$ and moreover $\rho (S_m)<1$.

2.4 Multigrid methods for $\tau$-matrices

The definition of multigrid methods for $\tau$-matrices requires a proper choice of the grid-transfer operators, in order to guarantee fast convergence speed and to preserve the same structure of the matrices at the coarser levels [1, 2, 12, 13].

We now define our grid-transfer operator (or projector) $P_{{\varvec{m}}}$ for multi-indices ${{\varvec{m}}}\in {\mathbb {N}}^d$ satisfying certain additional constraints. For any odd $m\ge 3$, let us denote by $U_m$ the cutting matrix of size $\frac{m-1}{2}\times m$ given by

For any ${{\varvec{m}}}\in {\mathbb {N}}^d$ with odd $m_1,\ldots ,m_d\ge 3$, we define $U_{{\varvec{m}}}:=U_{m_1}\otimes \cdots \otimes U_{m_d}$. Then, we set

$$\begin{aligned} P_{{\varvec{m}}}:=U_{{\varvec{m}}}\, \tau _{{\varvec{m}}}(q_d), \end{aligned}$$

(9)

with

$$\begin{aligned} q_d(\theta _1,\ldots ,\theta _d):=\prod _{j=1}^d(1+\cos \theta _j). \end{aligned}$$

By the properties of $\tau$-matrices and Kronecker tensor-products, we have

$$\begin{aligned} P_{{\varvec{m}}}=\bigotimes _{j=1}^d U_{m_j}\,\tau _{m_j}(1+\cos \theta _j), \end{aligned}$$

and

The matrix $P_{{\varvec{m}}}$ has full rank $M:=\prod _{j=1}^d\frac{m_j-1}{2}$ and is the standard restriction operator or the so-called full-weighting projector. Its transpose $P_{{\varvec{m}}}^T$ is the traditional linear interpolation operator.

Let $z_d$ be defined as in (2). Note that $z_d$ is a linear nonnegative d-variate cosine trigonometric polynomial with a unique zero at $(0,\ldots ,0)$ over $[0,\pi ]^d$. The next lemma (Lemma 2) addresses the approximation condition in Theorem 2 when $A_m=A_{{\varvec{m}}}$ is the d-level $\tau$-matrix $\tau _{{{\varvec{m}}}}(z_d)$ (of size $m=m_1\cdots m_d$) and $P_m=P_{{\varvec{m}}}$ is the projector in (9). The lemma is a direct consequence of [22, Lemma 8.2] thanks to the following two properties of $q_d$ and $z_d$: given the set of mirror points of ${\varvec{\theta }}:=(\theta _1,\ldots ,\theta _d)$ as defined in [22, p. 454], namely

$$\begin{aligned}&{\mathcal {M}}({\varvec{\theta }}):=\biggl \{{\widehat{{\varvec{\theta }}}}:=({\widehat{\theta }}_1,\ldots ,{\widehat{\theta }}_d)\in [0,\pi ]^d:\ \biggr .\\&\biggl . \qquad \qquad \qquad {\widehat{\theta }}_i\in \{\theta _i,\pi -\theta _i\},\ \forall i=1,\ldots ,d\biggr \}\setminus \{{\varvec{\theta }}\}, \end{aligned}$$

we have ²

$$\begin{aligned}&\sum _{{\widehat{{\varvec{\theta }}}}\in {\mathcal {M}}({\varvec{\theta }})\cup \{{\varvec{\theta }}\}}q_d^2({\widehat{{\varvec{\theta }}}})>0, \quad \forall {\varvec{\theta }}\in [0,\pi ]^d, \end{aligned}$$

(10)

$$\begin{aligned}&\limsup _{{\varvec{\theta }}\rightarrow \mathbf{0 } }\max _{{\widehat{{\varvec{\theta }}}}\in {\mathcal {M}}({\varvec{\theta }})}\frac{q_d^2({\widehat{{\varvec{\theta }}}})}{z_d({\varvec{\theta }})}<\infty . \end{aligned}$$

(11)

Lemma 2

([22]) For ${{\varvec{m}}}\in {\mathbb {N}}^d$ with odd $m_1,\ldots ,m_d\ge 3$, let $A_{{\varvec{m}}}=\tau _{{\varvec{m}}}(z_d)$ and let $P_{{\varvec{m}}}$ be the full-rank projector given by (9). Then, the matrix $A_{{\varvec{m}}}$ is SPD and the approximation condition (b) in Theorem 2 holds with a constant depending only on d, i.e.,

$$\begin{aligned} \exists \,{{{\widetilde{b}}}}_d>0: \min _{\mathbf{y } \in {\mathbb {R}}^{M}}\Vert \mathbf{x } -P_{{\varvec{m}}}^T\mathbf{y } \Vert _2^2 \le {{{\widetilde{b}}}}_d\Vert \mathbf{x } \Vert ^2_{A_{{\varvec{m}}}}, \end{aligned}$$

(12)

for all $\mathbf{x } \in {\mathbb {R}}^{m_1\cdots m_d}$. Moreover, if $d=1$ then (12) holds with ${{{\widetilde{b}}}}_1=1/2$.

The specific value ${{{\widetilde{b}}}}_1$ has been found by looking carefully at the proof of [22, Lemma 3.2].

From Lemma 2 we deduce the result in Lemma 3. Given $X,Y\in {\mathbb {C}}^{m\times m}$, we write $X\le Y$ if and only if X, Y are both Hermitian and $Y-X$ is nonnegative definite.

Lemma 3

For ${{\varvec{m}}}\in {\mathbb {N}}^d$ with odd $m_1,\ldots ,m_d\ge 3$, let $A_{{\varvec{m}}}\in {\mathbb {R}}^{(m_1\cdots m_d)\times (m_1\cdots m_d)}$ be SPD and let $P_{{\varvec{m}}}$ be given by (9). Let $\delta _{{\varvec{m}}}>0$ such that

$$\begin{aligned} A_{{\varvec{m}}}\ge \delta _{{\varvec{m}}}\,\tau _{{\varvec{m}}}(z_d). \end{aligned}$$

(13)

Then, the approximation condition (b) in Theorem 2 holds, i.e.,

$$\begin{aligned} \exists \, b_{{{\varvec{m}}},d}:=\frac{{{{\widetilde{b}}}}_d}{\delta _{{\varvec{m}}}}>0: \min _{\mathbf{y } \in {\mathbb {R}}^{M}}\Vert \mathbf{x } -P_{{\varvec{m}}}^T\mathbf{y } \Vert _2^2 \le b_{{{\varvec{m}}},d}\Vert \mathbf{x } \Vert ^2_{A_{{\varvec{m}}}}, \end{aligned}$$

for all $\mathbf{x } \in {\mathbb {R}}^{m_1\cdots m_d}$, where ${{{\widetilde{b}}}}_d$ is defined in Lemma 2.

Proof

We use the same monotonicity argument as in [22, proof of Lemmas 4.2 and 9.2]. Assuming (13), we have

$$\begin{aligned} \Vert \mathbf{x } \Vert ^2_{\tau _{{\varvec{m}}}(z_d)}=\mathbf{x } ^T\tau _{{\varvec{m}}}(z_d)\mathbf{x } \le \frac{1}{\delta _{{\varvec{m}}}}\mathbf{x } ^TA_{{\varvec{m}}}\mathbf{x } =\frac{1}{\delta _{{\varvec{m}}}}\Vert \mathbf{x } \Vert _{A_{{\varvec{m}}}}^2, \end{aligned}$$

for all $\mathbf{x } \in {\mathbb {R}}^{m_1\cdots m_d}$. By Lemma 2 we get

$$\begin{aligned} \min _{\mathbf{y } \in {\mathbb {R}}^{M}}\Vert \mathbf{x } -P_{{\varvec{m}}}^T\mathbf{y } \Vert _2^2 \le {{{\widetilde{b}}}}_d\Vert \mathbf{x } \Vert ^2_{\tau _{{\varvec{m}}}(z_d)} \le \frac{{{{\widetilde{b}}}}_d}{\delta _{{\varvec{m}}}}\Vert \mathbf{x } \Vert ^2_{A_{{\varvec{m}}}}, \end{aligned}$$

for all $\mathbf{x } \in {\mathbb {R}}^{m_1\cdots m_d}$, which completes the proof. $\square$

The next corollary follows immediately from Theorem 2 in combination with Lemmas 1 and 3.

Corollary 1

Let ${\mathcal {I}}$ be a set of multi-indices such that ${\mathcal {I}}\subseteq \{{{\varvec{m}}}\in {\mathbb {N}}^d:\,m_1,\ldots ,m_d\ge 3\ \text{ odd }\}$. $\forall {{\varvec{m}}}\in {\mathcal {I}}$, let $A_{{\varvec{m}}}\in {\mathbb {R}}^{(m_1\cdots m_d)\times (m_1\cdots m_d)}$ be SPD, let $S_{{\varvec{m}}}:=I-\omega A_{{\varvec{m}}}$ and let $P_{{\varvec{m}}}:=U_{{\varvec{m}}}\,\tau _{{\varvec{m}}}(q_d)$. Assume that $\mu :=\sup _{{{\varvec{m}}}\in {\mathcal {I}}}\rho (A_{{\varvec{m}}})<\infty$ and that the inequality (13) holds with $\delta :=\inf _{{{\varvec{m}}}\in {\mathcal {I}}}\delta _{{\varvec{m}}}>0$, and take $0<\omega <2/\mu$. Then,

$$\begin{aligned} \rho (TG(S_{{\varvec{m}}},P_{{\varvec{m}}}))\le \sqrt{1-\frac{a\,\delta }{{{{\widetilde{b}}}}_d}},\quad \forall {{\varvec{m}}}\in {\mathcal {I}}, \end{aligned}$$

where $a:=\omega (2-\omega \mu )$ and ${{{\widetilde{b}}}}_d$ is defined in Lemma 2.

In the case where $A_{{{\varvec{m}}}}=\tau _{{{\varvec{m}}}}(z_d)$ and the projector $P_{{\varvec{m}}}$ is taken as in (9), the coarser matrix $P_{{\varvec{m}}}A_{{\varvec{m}}}P_{{\varvec{m}}}^T$ is again a $\tau$-matrix generated by $z_d$ up to a multiplicative constant. More generally, in a multigrid perspective, if we fix multi-indices ${{\varvec{m}}}_0:={{\varvec{m}}}>{{\varvec{m}}}_1>{{\varvec{m}}}_2>\dots >{{\varvec{m}}}_l>0$, where the inequalities are componentwise; if we take at each multigrid level $i=0,\ldots ,l-1$ the projector $P_{{{\varvec{m}}}_i}$, as given by (9) for ${{\varvec{m}}}={{\varvec{m}}}_i$; and if we define the coefficient matrix at level $i+1$ as $A_{{{\varvec{m}}}_{i+1}}:=P_{{{\varvec{m}}}_i}A_{{{\varvec{m}}}_i}P_{{{\varvec{m}}}_i}^T$ for $i=0,\dots , l-1$; then, from the results in [22] or by direct computation, we have $A_{{{\varvec{m}}}_{i}}=\tau _{{{\varvec{m}}}_i}(r_iz_d)$ for all $i=0,\ldots ,l$, where $r_i$ is a positive constant. This observation shows that the $\tau$ structure is preserved on the coarser levels, which is fundamental for the construction of multigrid algorithms with more than one recursion level.

In this regard, we remark that the conditions (10)–(11) are not sufficient to obtain the V-cycle optimality; see [2]. Nevertheless, taking into account the properties of $q_d$ and $z_d$, we see that condition (11) can be replaced by the following stronger version:

$$\begin{aligned} \limsup _{{\varvec{\theta }}\rightarrow \mathbf{0 } }\max _{{\widehat{{\varvec{\theta }}}}\in {\mathcal {M}}({\varvec{\theta }})}\frac{q_d({\widehat{{\varvec{\theta }}}})}{z_d({\varvec{\theta }})}<\infty . \end{aligned}$$

(14)

According to the analysis in [1], conditions (10) and (14) lead to the V-cycle optimality, when the V-cycle algorithm is applied to the $\tau$-matrix $A_{{\varvec{m}}}=\tau _{{\varvec{m}}}(z_d)$. Unfortunately, Lemma 3 does not suffice to extend the optimality proof provided in [1, 2] for $\tau$-matrices (and matrix algebras in general) to more general matrix structures like our matrices in the IgA context. Such a proof will be a (difficult) task to be addressed in future work.

3 Galerkin discretization using B-splines

We now detail the Galerkin discretization based on uniform B-splines of our model problem (1), and we devote special attention to the symbol which describes the spectral behavior of the discretization matrices.

3.1 The 1D setting

In this section we focus on our model problem for $d=1$:

(15)

with $\mathrm{f}\in L^2(0,1)$ and $\gamma \ge 0$. We approximate the (weak) solution u of (15) in the space ${\mathcal {W}}$ of polynomial splines with maximal smoothness represented in the B-spline basis. More precisely, for $p\ge 1$ and $n\ge 2$, let

$$\begin{aligned}&{\mathcal {V}}_n^{[p]}:=\Bigl \{s\in C^{p-1}([0,1]):\,s_{\left| \left[ \frac{i}{n},\frac{i+1}{n}\right) \right. }\in {\mathbb {P}}_p,\ 0\le i< n \Bigr \},\\&{\mathcal {W}}_n^{[p]}:=\Bigl \{s\in {\mathcal {V}}_n^{[p]}:\,s(0)=s(1)=0\Bigr \}\subset H^1_0(0,1). \end{aligned}$$

It is known that $\dim {\mathcal {V}}_n^{[p]}=n+p$ and $\dim {\mathcal {W}}_n^{[p]}=n+p-2$. In the Galerkin method (5) we choose ${\mathcal {W}}={\mathcal {W}}_n^{[p]}$, for some $p\ge 1$ and $n\ge 2$, and for ${\mathcal {W}}_n^{[p]}$ we choose the B-spline basis $\{N_{2,[p]},\ldots ,N_{n+p-1,[p]}\}$, which is defined as follows (see [6] or [16]).

Definition 2

Consider the knot sequence

$$\begin{aligned} t_1= & {} \cdots =t_{p+1}=0<t_{p+2}<\cdots \nonumber \\&\cdots <t_{p+n}<1=t_{p+n+1}=\cdots =t_{2p+n+1}, \end{aligned}$$

(16)

with $t_{p+i+1}:=i/n$, $i=0,\ldots ,n$. The B-splines $N_{i,[p]}:[0,1]\rightarrow {\mathbb {R}}$, $i=1,\ldots ,n+p$, are defined recursively over the knot sequence (16) as follows: for $1\le i\le n+2p$,

and, for $1\le k\le p$, $1\le i\le n+2p-k$,

$$\begin{aligned}&N_{i,[k]}(x)\\&\quad :=\frac{x-t_i}{t_{i+k}-t_i}\,N_{i,[k-1]}(x) +\frac{t_{i+k+1}-x}{t_{i+k+1}-t_{i+1}}\,N_{i+1,[k-1]}(x), \end{aligned}$$

where we assume that a fraction with zero denominator is zero.

With these choices of the approximation space ${\mathcal {W}}_n^{[p]}$ and of the basis functions $\{N_{2,[p]},\ldots ,N_{n+p-1,[p]}\}$, we obtain in (6) the $(n+p-2)\times (n+p-2)$ stiffness matrix $A=A_n^{[p]}$ given by

$$\begin{aligned} A_n^{[p]}=\left[ a(N_{j,[p]},N_{i,[p]})\right] _{i,j=2}^{n+p-1} =nK_n^{[p]}+\frac{\gamma }{n}M_n^{[p]}, \end{aligned}$$

(17)

where

$$\begin{aligned}&nK_n^{[p]}:=\left[ \int _{(0,1)}N'_{j,[p]}N'_{i,[p]}\right] _{i,j=2}^{n+p-1},\end{aligned}$$

(18)

$$\begin{aligned}&\frac{1}{n}M_n^{[p]}:=\left[ \int _{(0,1)}N_{j,[p]}N_{i,[p]}\right] _{i,j=2}^{n+p-1}. \end{aligned}$$

(19)

The above matrices have the following properties.

Lemma 4

[16] For every $p\ge 1$ and $n\ge 2$,

• $K_n^{[p]}$ is SPD and $\Vert K_n^{[p]}\Vert _\infty \le 4p$;

• $M_n^{[p]}$ is SPD, $\Vert M_n^{[p]}\Vert _\infty \le 1$ and $\exists \, C^{[p]}>0$, depending only on p, such that $\lambda _{\min }(M_n^{[p]})>C^{[p]}$.

We now recall the spectral properties of the sequence $\{\frac{1}{n}A_n^{[p]}\}_n$ obtained in [16]. For $p\ge 0$, let $\phi _{[p]}$ be the cardinal B-spline of degree p over the uniform knot sequence $\{0,1,\ldots ,p+1\}$, which is defined recursively as follows:

and

$$\begin{aligned} \phi _{[p]}(t):= \frac{t}{p}\phi _{[p-1]}(t)+\frac{p+1-t}{p}\phi _{[p-1]}(t-1),\quad p\ge 1. \end{aligned}$$

We point out that the ‘central’ basis functions $N_{i,[p]}(x)$, $i=p+1, \ldots , n$, are uniformly shifted and scaled versions of the cardinal B-spline $\phi _{[p]}$, because we have

$$\begin{aligned} N_{i,[p]}(x)=\phi _{[p]}(nx-i+p+1),\quad i=p+1,\ldots ,n. \end{aligned}$$

Let us denote by $\ddot{\phi }_{[p]}(t)$ the second derivative of $\phi _{[p]}(t)$ with respect to its argument t (for $p\ge 3$). For $p\ge 0$, let $h_p:[-\pi ,\pi ]\rightarrow {\mathbb {R}}$,

$$\begin{aligned} h_p(\theta ):=\phi _{[2p+1]}(p+1)+2\sum _{k=1}^p\phi _{[2p+1]}(p+1-k)\cos (k\theta ).\nonumber \\ \end{aligned}$$

(20)

In particular, we have $h_0(\theta )=1$. For $p\ge 1$, let $f_p:[-\pi ,\pi ]\rightarrow {\mathbb {R}}$,

$$\begin{aligned} f_p(\theta ):=-{\ddot{\phi }}_{[2p+1]}(p+1)-2\sum _{k=1}^p{\ddot{\phi }}_{[2p+1]}(p+1-k)\cos (k\theta ).\nonumber \\ \end{aligned}$$

(21)

Let $m_n^{[p]}:=n+p-2$ and fix $p\ge 1$. It has been proved in [16, Theorem 12] that, $\forall F\in C_c({\mathbb {R}})$,

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{m_n^{[p]}}\sum _{j=1}^{m_n^{[p]}}F\left( \lambda _j\left( \frac{1}{n}A_n^{[p]}\right) \right) =\frac{1}{2\pi }\int _{-\pi }^\pi F(f_p(\theta ))\,\mathrm{d}\theta . \end{aligned}$$

(22)

Due to this limit relation, $f_p$ is called the symbol of the sequence of matrices $\{\frac{1}{n}A_n^{[p]}\}_n$. Note that $f_p$ is symmetric on $[-\pi ,\pi ]$, so it is also the symbol of $\{\tau _{n+p-2}(f_p)\}_n$, meaning that (22) holds with $\tau _{n+p-2}(f_p)$ instead of $\frac{1}{n}A_n^{[p]}$.

Remark 1

The symbol $f_p$ is independent of $\gamma$. Moreover, when modifying our problem (15) by adding an advection term $\beta u'$, the resulting symbol is again $f_p$, independent of $\beta$ and $\gamma$; see [16]. The independence of $f_p$ from the advection/reaction terms is not a surprise, as it is known in the literature (see, e.g., [17, 23, 24]) that the symbol has a canonical structure in which only the coefficient of the higher-order operator is present (in our specific case, the higher-order operator is the Laplacian). If $|\beta |$ is very large, however, the fineness parameter n has to be chosen extremely large in order to dampen the effects of the advection term. In such cases, the theoretical spectral distribution (22) is reasonably attained only for very large n. This implies that, for small values of n, the advection term affects significantly the spectrum of $\frac{1}{n}A_n^{[p]}$ (and also the performance of multigrid solvers like the one presented in this paper).

Lemma 5

([16]) For all $p\ge 1$ and $\theta \in [-\pi ,\pi ]$,

$$\begin{aligned} f_p(\theta )=z_1(\theta )h_{p-1}(\theta ), \end{aligned}$$

with $z_1(\theta )=2-2\cos \theta$ as defined by (2) for $d=1$, and $h_{p}$ as defined by (20). Moreover,

$$\begin{aligned} \left( \frac{4}{\pi ^2}\right) ^p\le h_{p-1}(\theta )\le h_{p-1}(0)=1, \end{aligned}$$

and $f_p$ has a unique zero of order two at $\theta =0$ (like the function $z_1$).

The properties in Lemma 5 have been proved in [16, Lemma 7 and Remark 2] for $p\ge 2$, but they can be easily checked for $p=1$ by direct computation. Lemma 5 immediately provides two constants $c_p$ and $C_p$ for the inequalities (3) in the case $d=1$. Figure 1 shows the graph of $f_p$ normalized by its maximum $M_{f_p}$ for $p=1,\ldots ,5$.

Fig. 1

Graph of $f_p/M_{f_p}$ for $p=1,\ldots ,5$

We conclude this section by pointing out that $h_p$ is the symbol of the sequence of matrices $\{M_n^{[p]}\}_n$: $\forall F\in C_c({\mathbb {C}})$,

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{m_n^{[p]}}\sum _{j=1}^{m_n^{[p]}}F(\lambda _j(M_n^{[p]}))=\frac{1}{2\pi }\int _{-\pi }^\pi F(h_p(\theta ))\,\mathrm{d}\theta . \end{aligned}$$

We omit the formal proof of this result; it can be proved using the same arguments as [16, Theorem 12].

3.2 The 2D setting

In this section we focus on our model problem (1) in the case $d=2$, and we follow the same scheme as the 1D setting. Given any two functions $f,g:[a,b]\rightarrow {\mathbb {R}}$, we denote by $f\otimes g$ the tensor-product function

$$\begin{aligned} f\otimes g:[a,b]^2\rightarrow {\mathbb {R}},\quad (f\otimes g)(x,y):=f(x)g(y). \end{aligned}$$

We approximate the weak solution u of (1) by means of tensor-product B-splines. More precisely, we choose ${\mathcal {W}}={\mathcal {W}}_{n_1,n_2}^{[p_1,p_2]}$, for some $p_1,p_2\ge 1$, $n_1,n_2\ge 2$, where

$$\begin{aligned}&{\mathcal {W}}_{n_1,n_2}^{[p_1,p_2]}:=\big \langle N_{j_1,[p_1]}\otimes N_{j_2,[p_2]}:\ \\&\qquad \qquad j_1=2,\ldots ,n_1+p_1-1,\ j_2=2,\ldots ,n_2+p_2-1\big \rangle , \end{aligned}$$

and $N_{j,[p]},\ j=2,\ldots ,n+p-1$, are the basis functions considered in Sect. 3.1 (see Definition 2). We order the tensor-product B-spline basis $\{N_{j_1,[p_1]}\otimes N_{j_2,[p_2]}:\,j_1=2,\ldots ,n_1+p_1-1,\ j_2=2,\ldots ,n_2+p_2-1\}$ in the following way:

$$\begin{aligned} \left[ \left[ N_{j_1,[p_1]}\otimes N_{j_2,[p_2]}\right] _{j_1=2,\ldots ,n_1+p_1-1} \right] _{j_2=2,\ldots ,n_2+p_2-1}. \end{aligned}$$

With these choices of the approximation space and of the basis functions, we obtain in (6) the stiffness matrix $A=A_{n_1,n_2}^{[p_1,p_2]}$ given by

$$\begin{aligned} A_{n_1,n_2}^{[p_1,p_2]}:=K_{n_1,n_2}^{[p_1,p_2]} +\frac{\gamma }{n_1n_2}M_{n_2}^{[p_2]}\otimes M_{n_1}^{[p_1]}, \end{aligned}$$

(23)

where

$$\begin{aligned} K_{n_1,n_2}^{[p_1,p_2]}:=\frac{n_1}{n_2}M_{n_2}^{[p_2]}\otimes K_{n_1}^{[p_1]}+\frac{n_2}{n_1}K_{n_2}^{[p_2]}\otimes M_{n_1}^{[p_1]}, \end{aligned}$$

and the matrices $K_n^{[p]}$, $M_n^{[p]}$ are defined in (18)–(19).

Remark 2

By Lemma 4 and by the fact that $X\otimes Y$ is SPD whenever X, Y are SPD, we know that $A_{n_1,n_2}^{[p_1,p_2]}$ is SPD for all $p_1,p_2\ge 1$ and $n_1,n_2\ge 2$.

We now recall from [16] the spectral properties of the sequence $\{A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}\}_n$. For $p_1,p_2\ge 1$ and $\nu _1,\nu _2\in {\mathbb {Q}}_+:=\{r\in {\mathbb {Q}}:\ r>0\}$, let $f_{p_1,p_2}^{(\nu _1,\nu _2)}:[-\pi ,\pi ]^2\rightarrow {\mathbb {R}}$,

$$\begin{aligned} f_{p_1,p_2}^{(\nu _1,\nu _2)}:=\frac{\nu _1}{\nu _2} h_{p_2}\otimes f_{p_1}+\frac{\nu _2}{\nu _1} f_{p_2}\otimes h_{p_1}, \end{aligned}$$

where $h_p$ and $f_p$ are given in (20)–(21). From now on we assume that $n\in {\mathbb {N}}$ is chosen so that $\nu _1 n, \nu _2 n\in {\mathbb {N}}$. Let us consider the sequence of matrices $\{A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}\}_n$. It was proved in [16, Section 5.2] that, $\forall F\in C_c({\mathbb {R}})$,

$$\begin{aligned}&\lim _{n\rightarrow \infty }\frac{1}{N_n}\sum _{j=1}^{N_n}F\left( \lambda _j\left( A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}\right) \right) \nonumber \\&\quad = \frac{1}{(2\pi )^2}\int _{-\pi }^\pi \int _{-\pi }^\pi F(f_{p_1,p_2}^{(\nu _1,\nu _2)}(\theta _1,\theta _2))\,\mathrm{d}\theta _1\mathrm{d}\theta _2, \end{aligned}$$

(24)

where $N_n:=(\nu _1 n+p_1-2)(\nu _2 n+p_2-2)$ is the size of $A_{\nu _1n,\nu _2n}^{[p_1,p_2]}$. Due to this limit relation, $f_{p_1,p_2}^{(\nu _1,\nu _2)}$ is called the symbol of the sequence $\{A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}\}_{n}$. Since we have $f_{p_1,p_2}^{(\nu _1,\nu _2)}(\pm \theta _1,\pm \theta _2)=f_{p_1,p_2}^{(\nu _1,\nu _2)}(\theta _1,\theta _2)$, the relation (24) continues to hold if $A_{\nu _1n,\nu _2n}^{[p_1,p_2]}$ were replaced by the two-level $\tau$-matrix $\tau _{\nu _2n+p_2-2,\nu _1n+p_1-2}(f_{p_1,p_2}^{(\nu _1,\nu _2)})$. This means that $f_{p_1,p_2}^{(\nu _1,\nu _2)}$ is also the symbol of the sequence of $\tau$-matrices $\{\tau _{\nu _2n+p_2-2,\nu _1n+p_1-2}(f_{p_1,p_2}^{(\nu _1,\nu _2)})\}_n$.

The symbol $f_{p_1,p_2}^{(\nu _1,\nu _2)}$ possesses the following properties, which are consequences of Lemma 5.

Lemma 6

Let $p_1,p_2\ge 1$ and $\nu _1,\nu _2\in {\mathbb {Q}}_+$. Then, for all $(\theta _1,\theta _2)\in [-\pi ,\pi ]^2$,

$$\begin{aligned}&f_{p_1,p_2}^{(\nu _1,\nu _2)}(\theta _1,\theta _2)\ge \left( \frac{4}{\pi ^2}\right) ^{p_1+p_2+1}\min \left( \frac{\nu _2}{\nu _1},\frac{\nu _1}{\nu _2}\right) z_2(\theta _1,\theta _2), \\&f_{p_1,p_2}^{(\nu _1,\nu _2)}(\theta _1,\theta _2) \le \max \left( \frac{\nu _2}{\nu _1},\frac{\nu _1}{\nu _2}\right) z_2(\theta _1,\theta _2), \end{aligned}$$

with $z_2(\theta _1,\theta _2)=\sum _{j=1}^2(2-2\cos \theta _j)$ as defined by (2) for $d=2$. In particular, $f_{p_1,p_2}^{(\nu _1,\nu _2)}$ has a unique zero at $(\theta _1,\theta _2)=(0,0)$ of order two (like the function $z_2$).

Lemma 6 immediately provides two constants $c_{{\varvec{p}}}$ and $C_{{\varvec{p}}}$ for the inequalities (3) in the case $d=2$.

4 TGM for Galerkin B-spline matrices: proof of optimality

In this section we prove that the standard TGM with relaxed Richardson smoother and full-weighting projector (described in Sects. 2.3 and 2.4) is optimal for linear systems with coefficient matrix $\frac{1}{n}A_n^{[p]}$ ($1\le p \le 3$) in the 1D case and $A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}$ ($1\le p_1,p_2 \le 3$) in the 2D case. The results can be easily extended to higher dimensionalities $d>2$, by replicating the argument used in the 2D case.

4.1 Optimality of the TGM for $\frac{1}{n}A_n^{[p]}$

Let us start by giving an intuitive motivation based on the symbol $f_p$ why the proposed TGM with relaxed Richardson smoother and full-weighting projector is expected to be optimal for $\frac{1}{n}A_n^{[p]}$. Because $f_p$ is the symbol of both $\{\frac{1}{n}A_n^{[p]}\}_n$ and $\{\tau _{n+p-2}(f_p)\}_n$, these sequences of matrices share the same spectral distribution. The convergence properties of two-grid/multigrid methods strongly depend on the spectrum of the matrices to which they are applied. Therefore, it is reasonable to use for $\frac{1}{n}A_n^{[p]}$ the same TGM as proposed in [22] which was proved to be optimal for $\tau _{n+p-2}(f_p)$, and to expect that it is optimal also for $\frac{1}{n}A_n^{[p]}$.

Fix $p\ge 1$ and consider the sequence of matrices $\{\frac{1}{n}A_n^{[p]}:\,n\in {\mathcal {I}}_p\}$, with ${\mathcal {I}}_p\subseteq \{n\ge 2:\,n+p-2\ge 3 \text{ odd }\}$ an infinite set of indices. The requirement on the matrix size is due to our projector choice; see (25). We want to solve $\frac{1}{n}A_n^{[p]}\mathbf{u } =\mathbf{b }$, with $n\in {\mathcal {I}}_p$ and $\mathbf{b } \in {\mathbb {R}}^{n+p-2}$, by means of the TGM. As smoother we take the relaxed Richardson method with iteration matrix

$$\begin{aligned} S_n^{[p]}:=I-\omega ^{[p]}\frac{1}{n}A_n^{[p]}, \end{aligned}$$

where $\omega ^{[p]}\in {\mathbb {R}}$ is a relaxation parameter chosen as a function of p and independent of n. The projector is taken to be

$$\begin{aligned} P_n^{[p]}:=U_{n+p-2}\,\tau _{n+p-2}(1+\cos \theta ), \end{aligned}$$

(25)

as defined in (9) for $d=1$ and ${{\varvec{m}}}=n+p-2$.

For the sake of simplicity, we now assume $\gamma =0$, so $\frac{1}{n}A_n^{[p]}=K_n^{[p]}$. Under this assumption and under suitable conditions on the relaxation parameter $\omega ^{[p]}$, we show that, for $p=1,2,3$, the TGM with iteration matrix $TG(S_n^{[p]},P_n^{[p]})$ is optimal, i.e., $\exists \,c_p<1$ such that $\rho (TG(S_n^{[p]},P_n^{[p]}))\le c_p$ for all $n\in {\mathcal {I}}_p$. Corollary 1 can be reformulated in our 1D context as follows.

Corollary 2

Assume that for fixed $p\ge 1$,

$$\begin{aligned} \exists \,\delta ^{[p]}>0:\, K_n^{[p]}\ge \delta ^{[p]}\tau _{n+p-2}(2-2\cos \theta ),\ \ \forall n\ge 2, \end{aligned}$$

(26)

and let $\mu ^{[p]}:=\sup _{n\in {\mathcal {I}}_p}\rho (K_n^{[p]})$. Then, for any $\omega ^{[p]}\in (0,2/\mu ^{[p]})$ it holds that

$$\begin{aligned} \rho (TG(S_n^{[p]},P_n^{[p]}))\le \sqrt{1-2\,a^{[p]}\,\delta ^{[p]}},\quad \forall n\in {\mathcal {I}}_p, \end{aligned}$$

where $a^{[p]}:=\omega ^{[p]}(2-\omega ^{[p]}\mu ^{[p]})$.

From Lemma 4 we know that $\mu ^{[p]}\le 4p$ for all $p\ge 1$. We also have $\mu ^{[1]}=4$ and $\mu ^{[2]}\le 3/2+(1+\sqrt{2})/6$; see [16, Eq. (79)]. Moreover, from some numerical experiments it seems that $\mu ^{[2]}=3/2$ and $\mu ^{[3]}\le 1.80$.

In the next theorem we prove that (26) holds for $p=1,2,3$.

Theorem 3

For $1\le p\le 3$, condition (26) is satisfied with $\delta ^{[1]}=1$, $\delta ^{[2]}=1/3$ and $\delta ^{[3]}=28/465$. Hence, for $1\le p\le 3$ and for any $\omega ^{[p]}\in (0,2/\mu ^{[p]})$, $\exists \,c_p<1$ such that $\rho (TG(S_n^{[p]},P_n^{[p]}))\le c_p$ for all $n\in {\mathcal {I}}_p$.

Proof

Since $K_n^{[1]}=\tau _{n-1}(2-2\cos \theta )$ for any $n\ge 2$, it is obvious that (26) holds for $p=1$ with $\delta ^{[1]}=1$.

In the case $p=2$, for $n\ge 5$ we have

$$\begin{aligned} K_n^{[2]}=\frac{1}{6} \begin{bmatrix} 8&-1&-1&&\\ -1&6&-2&-1&\\ -1&-2&6&-2&-1&\\&\ddots&\ddots&\ddots&\ddots&\ddots&\\&-1&-2&6&-2&-1\\&&-1&-2&6&-1 \\&&-1&-1&8 \end{bmatrix}, \end{aligned}$$

and one can check that the matrix $K_n^{[2]}-\delta \,\tau _n(2-2\cos \theta )$ is nonnegative definite for $\delta =1/3$, thanks to the Gershgorin theorems [5]. As it can be directly verified that $K_n^{[2]}\ge (1/3)\tau _n(2-2\cos \theta )$ for $n=2,\ldots ,4$, we conclude that (26) holds for $p=2$ with $\delta ^{[2]}=1/3$.

In the case $p=3$, for $n\ge 8$ we have

Since

$$\begin{aligned} f_3(\theta )&= (\cos ^2\theta +13\cos \theta +16)(2-2\cos \theta )/30\\&\ge (2/15)(2-2\cos \theta ), \qquad \forall \theta \in [-\pi ,\pi ], \end{aligned}$$

we have $\tau _m(f_3)\ge (2/15)\tau _m(2-2\cos \theta )$, $\forall m\ge 1$. By the Gershgorin theorems we find that $K_n^{[3]}\ge \varepsilon \,\tau _{n+1}(f_3)$ for all $n\ge 8$ with $\varepsilon =14/31$. As a consequence, the inequality $K_n^{[3]}\ge (28/465)\tau _{n+1}(2-2\cos \theta )$ holds for all $n\ge 8$. A direct verification shows that it also holds for $n=2,\ldots ,7$. $\square$

Remark 3

There are at least two reasons why condition (26) is likely to be satisfied for all $p\ge 1$.

• The condition would hold if we had $\tau _{n+p-2}(f_p)$ instead of $K_n^{[p]}$. Indeed, from Lemma 5 it follows that $f_p(\theta )\ge (4/\pi ^2)^p\,(2-2\cos \theta )$, and this implies that $\tau _m(f_p)\ge (4/\pi ^2)^p\,\tau _m(2-2\cos \theta )$, $\forall m\ge 1$. On the other hand, $K_n^{[p]}$ mimics $\tau _{n+p-2}(f_p)$, because these matrices share the same symbol $f_p$ and they differ from each other only by a small-rank correction term [16].

• The matrices $K_n^{[p]}$ and $\tau _{n+p-2}(2-2\cos \theta )$ are both associated with particular approximations of the elliptic problem (15) in the case $\gamma =0$.

Multiplying (26) by $({\tau _{n+p-2}(2-2\cos \theta )})^{-1/2}$ on the left and the right, and observing that

$$\begin{aligned} ({\tau _{n+p-2}(2-2\cos \theta )})^{-1/2}K_n^{[p]}({\tau _{n+p-2}(2-2\cos \theta )})^{-1/2} \end{aligned}$$

is similar to

$$\begin{aligned} ({\tau _{n+p-2}(2-2\cos \theta )})^{-1}K_n^{[p]}, \end{aligned}$$

we obtain that (26) is equivalent to the following:

$$\begin{aligned}&\exists \delta ^{[p]}>0:\nonumber \\&\quad \lambda _{\min }(({\tau _{n+p-2}(2-2\cos \theta )})^{-1}K_n^{[p]}) \ge \delta ^{[p]},\ \ \forall n\ge 2. \end{aligned}$$

(27)

The inequality (27) is certainly satisfied for $p=1$ (with $\delta ^{[1]}=1$), and numerical experiments reveal that (27) is also satisfied for $p=2,\ldots ,6$, with the best value $\delta ^{[p],*}:=\inf _{n\ge 2}\lambda _{\min }(({\tau _{n+p-2}(2-2\cos \theta )})^{-1}K_n^{[p]})$ given by $\delta ^{[2],*}\approx 0.3333$, $\delta ^{[3],*}\approx 0.1333$, $\delta ^{[4],*}\approx 0.0537$, $\delta ^{[5],*}\approx 0.0177$, $\delta ^{[6],*}\approx 0.0054$. Note that the value $\delta ^{[p]}$ obtained in Theorem 3 coincides with $\delta ^{[p],*}$ not only for $p=1$ but also for $p=2$.

Remark 4

From a theoretical viewpoint, the normalized symbol $f_p(\theta )/M_{f_p}$ has a unique zero at $\theta =0$. On the other hand, it has been proved in [11] that the value $f_p(\pi )/M_{f_p}\le 2^{2-p}$ decreases exponentially to zero as $p\rightarrow \infty$. This means that, from a numerical viewpoint, for large p, the normalized symbol $f_p/M_{f_p}$ possesses two zeros over $[0,\pi ]$: one at $\theta =0$ and another at the corresponding mirror point $\theta =\pi$. Because of this, we expect a slow (though optimal) convergence rate, when solving a linear system of the form $\frac{1}{n}A_n^{[p]}\mathbf{u } =\mathbf{b }$ for large p, by means of the TGM described above; see [11] for a rigorous analysis in the case of the $\tau$-matrix $\tau _{n+p-2}(f_p)$. Possible ways to overcome this problem are the choice of a different size reduction at the lower level and/or adopting a multi-iterative strategy, involving a variation of the smoothers. Both approaches have been extensively numerically tested in [9] and the second one turned out to be more efficient, especially for large values of p and higher dimensionalities.

4.2 Optimality of the TGM for $A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}$

Throughout this section, we use the notation $m_{\nu _j n}^{[p_j]}:=\nu _j n+p_j-2$, $j=1,2$. The symbol-based motivation why the TGM with relaxed Richardson smoother and full-weighting projector is expected to be optimal for $A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}$ is essentially the same as in the 1D case: if this TGM were applied to the $\tau$-matrix $\tau _{m_{\nu _2 n}^{[p_2]},\,m_{\nu _1 n}^{[p_1]}}(f_{p_1,p_2}^{(\nu _1,\nu _2)})$, which has the same symbol $f_{p_1,p_2}^{(\nu _1,\nu _2)}$ as $A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}$, then it would be optimal by the results in [22].

Fix $p_1,p_2\ge 1$, $\nu _1,\nu _2\in {\mathbb {Q}}_+$, and consider the sequence of matrices $\{A_{\nu _1 n,\nu _2n}^{[p_1,p_2]}:\,n\in {\mathcal {I}}_{p_1,p_2}^{(\nu _1,\nu _2)}\}$, with

$$\begin{aligned} {\mathcal {I}}_{p_1,p_2}^{(\nu _1,\nu _2)}&\subseteq \Big \{n:\,\nu _1 n\ge 2,\,\nu _2 n\ge 2,\,m_{\nu _1 n}^{[p_1]}\ge 3 \text{ odd },\,\\&\qquad m_{\nu _2 n}^{[p_2]}\ge 3 \text{ odd }\Big \}, \qquad \#{\mathcal {I}}_{p_1,p_2}^{(\nu _1,\nu _2)}=\infty . \end{aligned}$$

The requirements on $m_{\nu _1 n}^{[p_1]}$ and $m_{\nu _2 n}^{[p_2]}$ are due to our projector choice; see (28). We want to solve $A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}\mathbf{u } =\mathbf{b }$, with $n\in {\mathcal {I}}_{p_1,p_2}^{(\nu _1,\nu _2)}$ and $\mathbf{b } \in {\mathbb {R}}^{m_{\nu _1 n}^{[p_1]}\,m_{\nu _2 n}^{[p_2]}}$, by means of the TGM. Like in the 1D setting, we take the relaxed Richardson iteration as smoother,

$$\begin{aligned} S_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}:= I-\omega ^{[p_1,p_2,\nu _1,\nu _2]}A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}, \end{aligned}$$

where $\omega ^{[p_1,p_2,\nu _1,\nu _2]}$ is the relaxation parameter (independent of n). The projector is taken to be

$$\begin{aligned} P_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}:= U_{m_{\nu _2 n}^{[p_2]},m_{\nu _1 n}^{[p_1]}}\,\tau _{m_{\nu _2 n}^{[p_2]},m_{\nu _1 n}^{[p_1]}}(q_2), \end{aligned}$$

(28)

as defined in (9) for $d=2$ and ${{\varvec{m}}}=(m_{\nu _2 n}^{[p_2]},m_{\nu _1 n}^{[p_1]})$.

For the sake of simplicity, we now assume $\gamma =0$, so $A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}=K_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}$. In the bilinear case $p_1=p_2=1$, it can be shown that

$$\begin{aligned} K_{\nu _1 n,\nu _2 n}^{[1,1]}=\tau _{\nu _2 n-1,\nu _1 n-1}(f_{1,1}^{(\nu _1,\nu _2)}), \end{aligned}$$

and the eigenvalues of $K_{\nu _1 n,\nu _2 n}^{[1,1]}$ are given by

$$\begin{aligned} f_{1,1}^{(\nu _1,\nu _2)}\biggl (\frac{j_2\pi }{\nu _2 n},\frac{j_1\pi }{\nu _1 n}\biggr ), \end{aligned}$$

for $j_2=1,\ldots ,m_{\nu _2 n}^{[1]}$, $j_1=1,\ldots ,m_{\nu _1 n}^{[1]}$, and

$$\begin{aligned} \mu ^{[1,1,\nu _1,\nu _2]}:= & {} \sup _{n\in {\mathcal {I}}_{1,1}^{(\nu _1,\nu _2)}}\rho (K_{\nu _1 n,\nu _2 n}^{[1,1]})= \lim _{n\rightarrow \infty }\rho (K_{\nu _1 n,\nu _2 n}^{[1,1]}) \\= & {} \max _{(\theta _1,\theta _2)\in [0,\pi ]^2}f_{1,1}^{(\nu _1,\nu _2)}(\theta _1,\theta _2)=4\max \left( \frac{\nu _1}{\nu _2},\frac{\nu _2}{\nu _1}\right) . \end{aligned}$$

In this case, for any $\omega ^{[1,1,\nu _1,\nu _2]}\in \left( 0,2/\mu ^{[1,1,\nu _1,\nu _2]}\right)$ and $\nu _1,\nu _2\in {\mathbb {Q}}_+$, the optimality of the TGM with iteration matrix $TG(S_{\nu _1 n,\nu _2 n}^{[1,1]},P_{\nu _1 n,\nu _2 n}^{[1,1]})$ was proved in [22] and the optimality of the related V-cycle in [1].

More generally, for $1\le p_1,p_2\le 3$ and $\nu _1,\nu _2\in \mathbb Q_+$, we are going to show that the TGM with iteration matrix $TG(S_{\nu _1 n,\nu _2 n}^{[p_1,p_2]},P_{\nu _1 n,\nu _2 n}^{[p_1,p_2]})$ is optimal under the assumption $\omega ^{[p_1,p_2,\nu _1,\nu _2]}\in (0,2/\mu ^{[p_1,p_2,\nu _1,\nu _2]}),$ with $\mu ^{[p_1,p_2,\nu _1,\nu _2]}:=\sup _{n\in {\mathcal {I}}_{p_1,p_2}^{(\nu _1,\nu _2)}}\rho (K_{\nu _1 n,\nu _2 n}^{[p_1,p_2]})$. From Lemma 4 we know that, $\forall n\ge 2$,

$$\begin{aligned}&\rho (K_{\nu _1 n,\nu _2 n}^{[p_1,p_2]})\nonumber \\&\quad =\Vert K_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}\Vert _2\\&\quad \le \frac{\nu _1}{\nu _2}\Vert M_{\nu _2 n}^{[p_2]}\Vert _2\Vert K_{\nu _1 n}^{[p_1]}\Vert _2+\frac{\nu _2}{\nu _1}\Vert K_{\nu _2 n}^{[p_2]}\Vert _2\Vert M_{\nu _1 n}^{[p_1]}\Vert _2\\&\quad \le \frac{\nu _1}{\nu _2}\Vert M_{\nu _2 n}^{[p_2]}\Vert _\infty \Vert K_{\nu _1 n}^{[p_1]}\Vert _\infty +\frac{\nu _2}{\nu _1}\Vert K_{\nu _2 n}^{[p_2]}\Vert _\infty \Vert M_{\nu _1 n}^{[p_1]}\Vert _\infty \\&\quad \le \frac{4p_1\nu _1}{\nu _2}+\frac{4p_2\nu _2}{\nu _1}, \end{aligned}$$

where we used the fact that if X, Y are normal matrices then $\Vert X\otimes Y\Vert _2=\Vert X\Vert _2\Vert Y\Vert _2$ and $\Vert X\Vert _2\le \Vert X\Vert _\infty$.

In our 2D context, condition (13) reads as

$$\begin{aligned} \exists \,\delta ^{[p_1,p_2,\nu _1,\nu _2]}&>0:\, K_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}\ge \delta ^{[p_1,p_2,\nu _1,\nu _2]}\cdot \nonumber \\&\quad \tau _{m_{\nu _2 n}^{[p_2]},m_{\nu _1 n}^{[p_1]}}(4-2\cos \theta _1-2\cos \theta _2). \end{aligned}$$

(29)

In the next theorem we show that (29) holds for $1\le p_1,p_2\le 3$, yielding the optimality of the TGM with iteration matrix $TG(S_{\nu _1 n,\nu _2 n}^{[p_1,p_2]},P_{\nu _1 n,\nu _2 n}^{[p_1,p_2]})$ for these values of $p_1$ and $p_2$.

Theorem 4

Let $1\le p_1,p_2\le 3$. Then, (29) holds with

$$\begin{aligned} \delta ^{[p_1,p_2,\nu _1,\nu _2]}=\min \left( \frac{\nu _1}{\nu _2}C^{[p_2]}\delta ^{[p_1]},\,\frac{\nu _2}{\nu _1} C^{[p_1]}\delta ^{[p_2]}\right) , \end{aligned}$$

where $C^{[p]}$ is given in Lemma 4 and $\delta ^{[p]}$ is specified in Theorem 3 for $1\le p\le 3$. Hence, the TGM with iteration matrix $TG(S_{\nu _1 n,\nu _2 n}^{[p_1,p_2]},P_{\nu _1 n,\nu _2 n}^{[p_1,p_2]})$ is optimal for $1\le p_1,p_2\le 3$ and for any $\omega ^{[p_1,p_2,\nu _1,\nu _2]}\in (0,2/\mu ^{[p_1,p_2,\nu _1,\nu _2]})$.

Proof

Recall that if $X,X',Y,Y'$ are SPD with $X\ge X'$ and $Y\ge Y'$, then $X\otimes Y$ and $X'\otimes Y'$ are SPD with $X\otimes Y\ge X'\otimes Y'$. Hence, for every $\nu _1 n, \nu _2 n\ge 2$ integer, from Theorem 3 and the properties of $\tau$-matrices we deduce that

$$\begin{aligned}&K_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}\nonumber \\&\quad =\frac{ \nu _1}{\nu _2} M_{\nu _2 n}^{[p_2]}\otimes K_{\nu _1 n}^{[p_1]}+\frac{\nu _2}{\nu _1} K_{\nu _2 n}^{[p_2]}\otimes M_{\nu _1 n}^{[p_1]}\\&\quad \ge \frac{ \nu _1}{\nu _2}C^{[p_2]}I_{m_{\nu _2 n}^{[p_2]}}\otimes \delta ^{[p_1]}\tau _{m_{\nu _1 n}^{[p_1]}}(2-2\cos \theta _1)\\&\qquad +\frac{\nu _2}{\nu _1}\,\delta ^{[p_2]}\tau _{m_{\nu _2 n}^{[p_2]}}(2-2\cos \theta _2)\otimes C^{[p_1]}I_{m_{\nu _1 n}^{[p_1]}}\\&\quad \ge \delta ^{[p_1,p_2,\nu _1,\nu _2]}\,\tau _{m_{\nu _2 n}^{[p_2]},m_{\nu _1 n}^{[p_1]}}\left( \sum _{j=1}^2(2-2\cos \theta _j)\right) . \end{aligned}$$

$\square$

The proof of Theorem 4 can be extended in a straightforward way to higher dimensionalities $d>2$.

Remark 5

The key result that allowed us to prove the optimality of the two-grid methods both in the 1D and 2D setting is the matrix inequality (26). If (26) were true for all $p\ge 1$, then it would be easy to give a proof of optimality for all $p\ge 1$ (in the 1D setting) and for all $p_1,p_2\ge 1$ (in the 2D setting). Indeed, the former would be a direct consequence of Corollary 2, whereas the latter would follow by replicating the argument used in Theorem 4. We point out that the matrix inequality (26) for larger p could be handled by using a dyadic decomposition argument; see [4] and references therein or [25, 26] for further insights on this subject.

Remark 6

The inequality (26) would be also of interest in the context of preconditioning related to the CG method and the GMRES method. Indeed, in the light of the Axelsson–Lindskog theorems [3], it can be shown that (26), which is equivalent to (27) by Remark 3, ensures that $\tau _{n+p-2}(2-2\cos \theta )$ is an optimal CG preconditioner for $K_n^{[p]}$. Hence, for $p=1,2,3$, Theorem 3 ensures $\tau _{n+p-2}(2-2\cos \theta )$ to be an optimal CG preconditioner for $K_n^{[p]}$.

Remark 7

Let $M_{f_{p_1,p_2}^{(\nu _1,\nu _2)}}:=\max _{\varvec{\theta }\in [0,\pi ]^2} f_{p_1,p_2}^{(\nu _1,\nu _2)}(\varvec{\theta })$. It follows from Lemma 6 that the normalized symbol $f_{p_1,p_2}^{(\nu _1,\nu _2)}/M_{f_{p_1,p_2}^{(\nu _1,\nu _2)}}$ has a unique zero at $\varvec{\theta }=\mathbf{0 }$. However, from [11] we know that $f_{p_1,p_2}^{(\nu _1,\nu _2)}(\theta _1,\pi )\le 2^{2-p_1} M_{f_{p_1,p_2}^{(\nu _1,\nu _2)}}$ and $f_{p_1,p_2}^{(\nu _1,\nu _2)}(\pi ,\theta _2)\le 2^{2-p_2} M_{f_{p_1,p_2}^{(\nu _1,\nu _2)}}$. Hence, when $p_1,p_2$ are large, the normalized symbol also has infinitely many small values (they can be seen as numerical zeros) over $[0,\pi ]^2$, located at the edge points

$$\begin{aligned} \{(\theta _1,\pi ):\,0\le \theta _1\le \pi \}\cup \{(\pi ,\theta _2):\,0\le \theta _2\le \pi \}. \end{aligned}$$

Due to this behavior, the TGM described above for the matrix $A_{\nu _1 n,\nu _2 n}^{[p_1,p_2]}$ is expected to show a bad (though optimal) convergence rate for large $p_1,p_2$. A possible way to overcome this problem has been proposed in [9, 11] and consists in adopting a multi-iterative strategy involving a specialized PCG smoother.

5 Numerical examples

Numerical experiments addressing the pure Laplacian ($\gamma =0$) can be found in [9, Sections 6.1 and 7.1]. They confirm the optimality of the TGM analyzed in Sect. 4. However, they also reveal that the spectral radii of the corresponding iteration matrices rapidly approach 1 for increasing $p\ge 2$ (resp., $p_1,p_2\ge 2$). This poor behavior is related to the fact that $f_p(\pi )/M_{f_p}$ (resp., $f_{p_1,p_2}^{(\nu _1,\nu _2)}/M_{f_{p_1,p_2}^{(\nu _1,\nu _2)}}$) converges exponentially to 0 for increasing degree, as discussed in Remarks 4 and 7. Such a worsening was observed in [9] not only in the presence of the relaxed Richardson smoother, but also in the case of the relaxed Gauss-Seidel smoother; in particular, we refer the reader to [9, Table 4]. Actually, this worsening is an intrinsic feature of the problem that arises whenever a classical smoother is employed. So, the proposed TGM can be used only when dealing with small values of p (resp., $p_1,p_2$). Nevertheless, we point out that other techniques can be considered for large p (resp., $p_1,p_2$), as illustrated in [9, 11].

In this section we show that the same conclusions also hold when addressing more general second-order elliptic problems, involving nonzero advection/reaction terms.

5.1 1D Examples

Table 1 shows the results of some numerical experiments for $TG(S_n^{[p]},P_n^{[p]})$ applied to a system with coefficient matrix $\frac{1}{n}A_n^{[p]}$ and $\gamma =1000$. The value of the parameter $\omega ^{[p]}$ for the relaxed Richardson smoother $S_n^{[p]}$ was taken as in [9, Table 2]; it was determined in order to approximately minimize the asymptotic spectral radius in the pure Laplacian case ($\gamma =0$). Then, we computed the spectral radii $\rho _{n}^{[p]}:=\rho (TG(S_n^{[p]},P_n^{[p]}))$ for $p=1,\ldots ,6$ and increasing values of n. In all the considered experiments, the proposed TGM is optimal. Moreover, when $n\rightarrow \infty$, $\rho _{n}^{[p]}$ converges to a limit $\rho _{\infty }^{[p]}$, which is minimal for $p=2$. We also observe that $\rho _{\infty }^{[p]}$ increases for increasing $p\ge 2$, in such a way that even for moderate values of p (such as $p=5,6$) the value $\rho _\infty ^{[p]}$ is not really satisfactory.

Table 1 Values of $\rho _{n}^{[p]}:=\rho (TG(S_n^{[p]},P_n^{[p]}))$ in the case $\gamma =1000$, for the specified parameter $\omega ^{[p]}$

To show that the numerical behavior observed for $TG(S_n^{[p]},P_n^{[p]})$ is common to all classical smoothers, we perform the same test using as smoother the relaxed Gauss-Seidel method, whose iteration matrix is denoted by ${\widehat{S}}_n^{[p]}$. Table 2 illustrates the behavior of the spectral radius ${\widehat{\rho }}_{n}^{[p]}:=\rho (TG({\widehat{S}}_n^{[p]},P_n^{[p]}))$. The relaxation parameter $\omega ^{[p]}$ for ${\widehat{S}}_n^{[p]}$ was chosen as in [9, Table 3], which again approximately minimizes the asymptotic spectral radius in the pure Laplacian case ($\gamma =0$). It follows from Table 2 that, except for the particular case $p=2$, the use of the Gauss-Seidel smoother improves the convergence rate of the two-grid. However, we also observe that ${\widehat{\rho }}_{n}^{[p]}$ presents the same dependence on p as $\rho _{n}^{[p]}$: the scheme is optimal but its asymptotic convergence rate (if existing) attains its minimum for $p=2$ and then worsens as p increases from 2 to 6.

Table 2 Values of ${\widehat{\rho }}_{n}^{[p]}:=\rho (TG({\widehat{S}}_n^{[p]},P_n^{[p]}))$ in the case $\gamma =1000$, for the specified parameter $\omega ^{[p]}$

We also investigated the behavior of the TGM in the case of the diffusion-advection-reaction problem

with $\beta =-30$ and $\gamma =1$. It is known (see Remark 1) that the corresponding sequence of Galerkin B-spline matrices has the same symbol $f_p$ as in (21), which is independent of $\beta$ and $\gamma$. The results of some numerical experiments (with a similar setup as in the previous test) are collected in Tables 3 and 4. We may conclude that the nonzero advection and reaction terms do not have a major influence on the asymptotic spectral radii of the TGM both in the case of the Richardson and the Gauss-Seidel smoother. However, as explained in Remark 1, the presence of a very large $|\beta |$ may affect (negatively) the two-grid convergence rate for relatively small values of n.

Table 3 Values of $\rho _{n}^{[p]}:=\rho (TG(S_n^{[p]},P_n^{[p]}))$ in the case $\beta =-30$ and $\gamma =1$, for the specified parameter $\omega ^{[p]}$

Table 4 Values of ${\widehat{\rho }}_{n}^{[p]}:=\rho (TG({\widehat{S}}_n^{[p]},P_n^{[p]}))$ in the case $\beta =-30$ and $\gamma =1$, for the specified parameter $\omega ^{[p]}$

5.2 2D examples

Table 5 shows the results of some numerical experiments for $TG(S_{n,n}^{[p,p]},P_{n,n}^{[p,p]})$ applied to a system with coefficient matrix $A_{n,n}^{[p,p]}$ and $\gamma =1$; see (23). The value of the relaxation parameter $\omega ^{[p,p]}$ for the relaxed Richardson smoother $S_{n,n}^{[p,p]}$ was taken as in [9, Table 12], and was determined in order to approximately minimize the asymptotic spectral radius in the pure Laplacian case ($\gamma =0$). Then, we computed the spectral radii $\rho _{n,n}^{[p,p]}:=\rho (TG(S_{n,n}^{[p,p]},P_{n,n}^{[p,p]}))$ for $p=1,\ldots ,6$ and increasing values of n. In all the considered numerical experiments, the proposed TGM is optimal. However, for $p\ge 3$, the (asymptotic) spectral radius is very close to 1, and this is not satisfactory for practical purposes.

Table 5 Values of $\rho _{n,n}^{[p,p]}:=\rho (TG(S_{n,n}^{[p,p]},P_{n,n}^{[p,p]}))$ in the case $\gamma =1$, for the specified parameter $\omega ^{[p,p]}$

The numerical experiments in Table 6, obtained as those in Table 5, show a certain improvement in the two-grid convergence rate when using the relaxed Gauss-Seidel smoother instead of Richardson’s, but again the results worsen for increasing p.

Table 6 Values of ${\widehat{\rho }}_{n,n}^{[p,p]}:=\rho (TG({{\widehat{S}}}_{n,n}^{[p,p]},P_{n,n}^{[p,p]}))$ in the case $\gamma =1$, for the specified parameter $\omega ^{[p,p]}$

An effective smoother for large p based on a preconditioned Krylov method has been proposed in [11], whereas an extensive numerical testing can be found in [9].

6 Conclusion and perspectives

In this paper we have proposed two-grid (and multigrid) methods for the solution of linear systems arising from the Galerkin B-spline IgA approximation of 1D and 2D elliptic problems. The optimality of the two-grid scheme, already predicted in [9], has been formally proved for some values of the spline degrees ${{\varvec{p}}}$. It is important to point out that:

• the proposal of the methods is motivated and based on the spectral symbol and on the corresponding techniques for $\tau$-matrices [1, 2, 12, 13, 22]; we could also have opted for Toeplitz matrices;

• the optimality proofs are based on classical tools from algebraic multigrid analysis, applied within the framework of the theory of $\tau$-matrices [20, 22]; again, we could have opted for Toeplitz matrices;

• the spectral properties of the considered matrices, as well as the properties of the associated symbol, were analyzed in a previous work [16].

A plan for future research could include the proof of relation (26) for all $p\ge 1$. It would give at once the optimality proof of the two-grid and—with a little more effort—the optimality proof of the W-cycle multigrid method.