Keywords

1 Introduction

In this work, we investigate the dynamics of a system of two bodies (satellite and stabilizer) connected by a spherical hinge that moves in a central Newtonian force field on a circular orbit using computer algebra methods.

Determining the equilibria for the system of connected bodies on a circular orbit is of practical interest for designing composite gravitational orientation systems of satellites that can stay on the orbit for a long time without energy consumption. The dynamics of various composite schemes for satellite–stabilizer gravitational orientation systems was discussed in detail in [1].

The study of the satellite–stabilizer dynamics under the influence of gravitational torque is an important topic for the practical implementation of attitude control systems of the artificial satellites. The dynamics of a satellite–stabilizer subjected to gravitational torque was considered in many papers indicated in [1]. In [2] and [3], planar equilibrium orientations were found in special cases, when the spherical hinge is located at the intersection of the satellite and stabilizer principal central axis of inertia. In [4], all equilibrium orientations were found in the case of axisymmetric satellite and stabilizer. In paper [5], some classes of spatial equilibrium orientations of the satellite–stabilizer system in the orbital coordinate system were analyzed, using computer algebra methods.

In this paper, we consider the planar equilibria (equilibrium orientations) of the satellite–stabilizer system in the orbital coordinate frame for certain values of the principal central moments of inertia of the bodies when the spherical hinge is located at the intersection of the satellite and stabilizer principal central planes of inertia. The action of the stabilizer on the satellite provides new equilibrium orientations for the two-body system, as well as introduces dissipation into the system. The investigation of satellite equilibria was performed by using the Computer Algebra resultant method. The regions with an equal number of equilibria were specified by using the Meiman theorem [13] for the construction of discriminant hypersurfaces.

The algebraic methods for determining the equilibrium orientations of the two-body system described in this work were successfully used to analyze the dynamics of a satellite–gyrostat system [6, 7] as well as the dynamics of a satellite with an aerodynamic orientation system [8, 9].

In mechanics, computer algebra is widely employed to analyze polynomial systems with the use of symbolic computations. Some computer algebra algorithms for solving these problems were described in [11, 12, 15]. The question of finding regions of parameter space with certain equilibria properties also occurred in relevance to a biology problem was presented at the CASC 2017 Workshop [16].

2 Equations of Motion

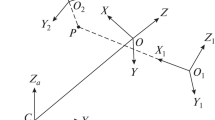
Let us consider the system of two bodies connected by a spherical hinge that moves along a circular orbit [1]. To write equations of motion for two bodies, we introduce the following right-handed Cartesian coordinate systems (Fig. 1). The absolute coordinate system \(CX_aY_aZ_a\) with the origin at the Earth’s center of mass C. The plane \(CX_aY_a\) coincides with the equatorial plane and the \(CZ_a\) axis coincides with the Earth axis of rotation, and OXYZ is the orbital coordinate system. The OZ axis is directed along the radius vector that connects the Earth center of mass C with the center of mass of the two–body system O, the OX axis is directed along the linear velocity vector of the center of mass O. Then, the OY axis is directed along the normal to the orbital plane. The coordinate system for the ith body \((i=1,2)\) is \(Ox_iy_iz_i\), where \(Ox_i\), \(Oy_i\), and \(Oz_i\) are the principal central axes of inertia for the ith body. The orientation of the coordinate system \(Ox_iy_iz_i\) with respect to the orbital coordinate system is determined using the pitch (\({\alpha }_i\)), yaw (\({\beta }_i\)), and roll (\({\gamma }_i\)) angles, and the direction cosines in the transformation matrix between the orbital coordinate system OXYZ and \(Ox_iy_iz_i\) are expressed in terms of aircraft angles using the relations [1]:

$$\begin{aligned} a_{11}^{(i)}= & {} \cos \alpha _i\cos \beta _i,\nonumber \\ a_{12}^{(i)}= & {} \sin \alpha _i\sin \gamma _i-\cos \alpha _i\sin \beta _i\cos \gamma _i,\nonumber \\ a_{13}^{(i)}= & {} \sin \alpha _i\cos \gamma _i+\cos \alpha _i\sin \beta _i\sin \gamma _i,\nonumber \\ a_{21}^{(i)}= & {} \sin \beta _i, \quad a_{22}^{(i)}=\cos \beta _i\cos \gamma _i, \\ a_{23}^{(i)}= & {} -\cos \beta _i\sin \gamma _i, \quad a_{31}^{(i)}=-\sin \alpha _i\cos \beta _i,\nonumber \\ a_{32}^{(i)}= & {} \cos \alpha _i\sin \gamma _i+\sin \alpha _i\sin \beta _i\cos \gamma _i,\nonumber \\ a_{33}^{(i)}= & {} \cos \alpha _i\cos \beta _i-\sin \alpha _i\sin \beta _i\sin \gamma _i.\nonumber \end{aligned}$$
(1)

Suppose that \((a_i, b_i, c_i)\) are the coordinates of the spherical hinge P in the body coordinate system \(Ox_iy_iz_i\), \(A_i, B_i, C_i\) are the principal central moments of inertia; \(M=M_1M_2/(M_1+M_2)\); \(M_i\) is the mass of the ith body; \(p_i\), \(q_i\), and \(r_i\) are the projections of the absolute angular velocity of the ith body onto the axes \(Ox_i\), \(Oy_i\), and \(Oz_i\); and \({\omega }_0\) is the angular velocity for the center of mass of the two-body system moving along a circular orbit. Then, using expressions for kinetic energy and force function, which determines the effect of the Earth gravitational field on the system of two bodies connected by a hinge [1], the equations of motion for this system can be written as Lagrange equations of the second kind by symbolic differentiation in the Maple system [10] in the case when \(b_1=b_2=0\):

(2)

Here

$$\begin{aligned} p_i= & {} (\dot{\alpha _i}+{\omega }_0)a_{21}^{(i)}+\dot{\gamma _i}, \nonumber \\ q_i= & {} (\dot{\alpha _i}+{\omega }_0)a_{22}^{(i)}+\dot{\beta _i}\sin \gamma _i, \\ r_i= & {} (\dot{\alpha _i}+{\omega }_0)a_{23}^{(i)}+\dot{\beta _i}\cos \gamma _i.\nonumber \end{aligned}$$
(3)

In the first three equations of (2), \(i=1\) and \(j=2\); in the next three equations of (2), \(i=2\) and \(j=1\). In (3), \(i=1, 2\). In (2) and (3), the dot denotes the differentiation with respect to time t.

3 Equilibrium Orientations of Satellite-Stabilizer System

Assuming the initial condition \(({\alpha }_i, {\beta }_i, {\gamma }_i)= ({\alpha }_{i0}=\text{ const }, {\beta }_{i0}=\text{ const }, {\gamma }_{i0}= \text{ const })\), also \(A_i~ \ne ~ B_i ~\ne ~ C_i\), and introducing the notations \(a_{ij}^{(1)}=a_{ij}\), \(a_{ij}^{(2)}=b_{ij}\), we obtain from (2) and (3) the equations

$$\begin{aligned}&\big ((C_1-B_1)-Mc_1^2)\big )(a_{22}a_{23} - 3a_{32}a_{33}) - Ma_1c_1(a_{21}a_{22}-3a_{31}a_{32})\nonumber \\&\quad +Mc_1a_{22}(a_2b_{21}+c_2b_{23})-3Mc_1a_{32}(a_2b_{31}+c_2b_{33})=0, \nonumber \\&\big ((A_1-C_1)-M(a_1^2-c_1^2)\big )(a_{23} a_{21} - 3a_{33}a_{31}) - Mc_1a_1((a_{23}^2-a_{21}^2) \nonumber \\&\quad -3(a_{33}^2-a_{31}^2)) - M(c_1a_{21}-a_1a_{23})(a_2b_{21}+c_2b_{23}) \nonumber \\&\quad + 3M(c_1a_{31} - a_1a_{33})(a_2b_{31}+c_2b_{33})=0,\nonumber \\&\big ((B_1-A_1) + Ma_1^2)\big ) (a_{21} a_{22} - 3a_{31}a_{32}) + Ma_1c_1(a_{22}a_{23}-3a_{32}a_{33})\nonumber \\&\quad - Ma_1a_{22}(a_2b_{21}+c_2b_{23})+3Ma_1a_{32}(a_2b_{31}+c_2b_{33})=0, \\&\big ((C_2-B_2)-Mc_2^2)\big )(b_{22} b_{23} -3b_{32}b_{33}) -Ma_2c_2(b_{21}b_{22}-3b_{31}b_{32})\nonumber \\&\quad +Mc_2b_{22}(a_1a_{21}+c_1a_{23})-3Mc_2b_{32}(a_1a_{31}+c_1a_{33})=0, \nonumber \\&\big ((A_2-C_2)-M(a_2^2-c_2^2)\big )(b_{23} b_{21} - 3b_{33}b_{31}) - Mc_2a_2((b_{23}^2-b_{21}^2) \nonumber \\&\quad - 3(b_{33}^2-b_{31}^2)) - M(c_2b_{21}-a_2b_{23})(a_1a_{21}+c_1a_{23}) \nonumber \\&\quad + 3M(c_2b_{31} - a_2b_{33})(a_1a_{31}+c_1a_{33}) = 0,\nonumber \\&\big ((B_2-A_2) + Ma_2^2)\big ) (b_{21} b_{22} - 3b_{31}b_{32})+ + Ma_2c_2(b_{22}b_{23}-3b_{32}b_{33})\nonumber \\&\quad - Ma_2b_{22}(a_1a_{21}+c_1a_{23})+3Ma_2b_{32}(a_1a_{31}+c_1a_{33})=0,\nonumber \end{aligned}$$
(4)

which allow us to determine the equilibrium orientation for the system of two bodies connected by a spherical hinge in the orbital coordinate system. Taking into account the expressions for the direction cosines from (1), system (4) can be considered as a system of six equations with six unknowns \(\alpha _i, \beta _i\), and \(\gamma _i\) \((i=1, 2)\).

Another way of closing Eq. (4) is to add six orthogonality conditions for the direction cosines:

$$\begin{aligned} a^2_{21}+a^2_{22}+a^2_{23} - 1=0,\nonumber \\ a^2_{31}+a^2_{32}+a^2_{33} -1=0,\nonumber \\ a_{21}a_{31}+a_{22}a_{32}+a_{23}a_{33}=0, \\ b^2_{21}+b^2_{22}+b^2_{23} - 1=0,\nonumber \\ b^2_{31}+b^2_{32}+b^2_{33} -1=0,\nonumber \\ b_{21}a_{31}+b_{22}b_{32}+b_{23}b_{33}=0.\nonumber \end{aligned}$$
(5)

For this system, the following problem is formulated: for given 11 parameters, determine all twelve direction cosines. The other six direction cosines \((a_{11}, a_{12}, a_{13}\) and \(b_{11}, b_{12}, b_{13})\) can be obtained from the orthogonality conditions.

The system of Eqs. (4) and (5) was solved only for the following case: \(b_1=b_2=0\), \(c_1=c_2=0\). Equilibrium solutions in this case for the system of two bodies in the orbital plane for \(\beta _{i0} =\gamma _{i0}=0\) and \(\alpha _{i0}\ne 0\) were considered in [2, 3]. In [3], planar oscillations of the two-body system were analyzed, all equilibrium orientations were determined, and sufficient conditions for the stability of the equilibrium orientations were obtained using the energy integral as a Lyapunov function. In [5], for this case the system of 12 algebraic Eqs. (4) and (5) was decomposed using linear algebra methods and algorithms for the Gröbner basis construction. Some classes of spatial equilibrium solutions were obtained from algebraic equations included in the Gröbner basis. The parameter values that cause the change in the number of equilibrium orientations for the satellite–stabilizer system were found.

Construction of the Gröbner basis for the system (4) and (5) of 12 second-order algebraic equations, whose coefficients depend on 11 parameters, is a very complicated algorithmic problem. In general case, the system of algebraic Eqs. (4) and (5) cannot be solved by direct application of the Gröbner basis construction methods. We will solve system (4) and (5) in the special case, when all equilibrium configurations of the two–body system are located in the plane of the circular orbit. In that case, \(\alpha _{10}\ne 0\) and \(\alpha _{20}\ne 0\), \(\beta _{10} = \beta _{20} =\gamma _{10}= \gamma _{20} =0.\)

Substituting the expressions for the direction cosines from (1) in terms of the aircraft angles into Eq. (4) and taking into account the condition \(\beta _{10} = \beta _{20} =\gamma _{10}= \gamma _{20} =0,\) we obtain two equations with two unknowns \(\alpha _{10}\) and \(\alpha _{20}\)

$$\begin{aligned}&d_1\sin \alpha _{10}\cos \alpha _{10}+ a_1c_1(\cos \alpha _{10}^2-\sin \alpha _{10}^2) +a_1a_2\cos \alpha _{10}\sin \alpha _{20}\nonumber \\&\quad -a_1c_2\cos \alpha _{10}\cos \alpha _{20} + a_2c_1\sin \alpha _{10}\sin \alpha _{20} -c_1c_2\sin \alpha _{10}\cos \alpha _{20} =0, \\&d_2\sin \alpha _{20}\cos \alpha _{20}+ a_2c_2(\cos \alpha _{20}^2-\sin \alpha _{20}^2) +a_1a_2\cos \alpha _{20}\sin \alpha _{10}\nonumber \\&\quad -a_2c_1\cos \alpha _{20}\cos \alpha _{10} + a_1c_2\sin \alpha _{20}\sin \alpha _{10} -c_1c_2\sin \alpha _{20}\cos \alpha _{10} =0. \nonumber \end{aligned}$$
(6)

Equations (6) form a closed system of two equations with respect to the two aircraft angles \(\alpha _{10}\) and \(\alpha _{20}\), that determines the flat satellite–stabilizer equilibrium orientations. In (6), we introduce the following designations: , .

Trigonometric system (6) in the \(\alpha _{10}\) and \(\alpha _{20}\) angles cannot be solved directly. Therefore, for this system, we used the universal change of sines and cosines through the half-angle tangent

(7)

where \(t_i=\tan (\frac{\alpha _{i0}}{2})\).

Substituting expressions (7) in terms of half-angle tangent into Eqs. (6) we obtain two algebraic equations with two unknowns \(t_1\) and \(t_2\)

$$\begin{aligned}&a_0t_1^4+a_1t_1^3+a_2t_1^2+a_4=0,\nonumber \\&b_0t_1^2+b_1t_1+b_2=0, \end{aligned}$$
(8)

where

$$\begin{aligned} a_0= & {} a_1(c_1-c_2)t_2^2-2a_1a_2t_2+a_1(c_1+c_2)), \\ a_1= & {} 2(c_1c_2-d_1)t_2^2+4a_2c_1t_2-2(c_1c_2+d_1),\\ a_2= & {} -6a_1c_1(1+t_2^2),\\ a_4= & {} a_1(c_1+c_2)t_2^2+2a_1a_2t_2+a_1(c_1-c_2)),\\ b_0= & {} (1-t_2^2)(a_2c_2(1-t_2^2)+a_2c_1(1+t_2^2 )+2d_2t_2)\\&+ 2c_1c_2t_2(1+t_2^2)-4a_2c_2t_2^2, \\ b_1= & {} 2a_1(1+t_2^2)(a_2(1-t_2^2)+2c_2t_2),\\ b_2= & {} (1-t_2^2)(a_2c_2(1-t_2^2)-a_2c_1(1+t_2^2 )+2d_2t_2)\\&- 2c_1c_2t_2(1+t_2^2)-4a_2c_2t_2^2. \end{aligned}$$

Using the resultant concept we eliminate the variable \(t_1\) from Eq. (8). Expanding the determinant of resultant matrix of Eq. (8) with the help of Maple symbolic matrix function, we obtain the 16th order algebraic equation in \(t_2\) variable

$$\begin{aligned} p_0t_2^{16}&+ p_1t_2^{15}+p_2t_2^{14}+p_3t_2^{13}+p_4t_2^{12}+p_5t_2^{11}+p_6t_2^{10} +p_7t_2^{9}+p_8t_2^{8}\nonumber \\&+ p_9t_2^7+p_{10}t_2^{6}+p_{11}t_2^{5}+p_{12}t_2^{4}+p_{13}t_2^{3}+p_{14}t_2^{2} +p_{15}t_2+p_{16}=0, \end{aligned}$$
(9)

the coefficients of which depend on the parameters \(a_1\), \(a_2\), \(c_1\), \(c_2\), \(d_1\), \(d_2\) in the form

(10)

By the definition of resultant, to every root \(t_2\) of Eq. (9) there corresponds a common root \(t_1\) of system (8). It can easily be shown that to every real root \(t_2\) of Eq. (9), there corresponds one equilibrium solution of the original system (6). Since the number of real roots of Eq. (9) does not exceed 16, the two bodies system satellite–stabilizer in the plane of a circular orbit can have at most 16 equilibrium configurations in the orbital coordinate system.

From the form of the coefficients of the algebraic Eq. (9), it follows that this equation is recurrent. Then dividing Eq. (9) by \(t_2^8\) we will get the equation

$$\begin{aligned}&p_0(t_2^{8}+\frac{1}{t_2^{8}})+p_1(t_2^{7}-\frac{1}{t_2^{7}})+ p_2(t_2^{6}+\frac{1}{t_2^{6}})+p_3(t_2^{5}-\frac{1}{t_2^{5}})+p_4(t_2^{4}+\frac{1}{t_2^{4}})\nonumber \\&\quad + p_5(t_2^{3}-\frac{1}{t_2^{3}})+p_6(t_2^{2}+\frac{1}{t_2^{2}})+p_7(t_2-\frac{1}{t_2})+p_8=0. \end{aligned}$$
(11)

After replacing in (11) \(x=(t_2-\frac{1}{t_2})=(2/\tan \alpha _{i0})\), \((t_2^2+\frac{1}{t_2^2})=x^2+2\), \((t_2^3-\frac{1}{t_2^3})=x^3+3x\) and so on, we will get the equation of the 8th degree

$$\begin{aligned} P(x)= {\bar{p}_0}x^{8}+{\bar{p}_1}x^{7}+{\bar{p}_2}x^{6}+{\bar{p}_3}x^{5}+{\bar{p}_4}x^{4} {\bar{p}_5}x^{3}+{\bar{p}_6}x^2+{\bar{p}_7}x+{\bar{p}_8}=0. \end{aligned}$$
(12)

Here

$$\begin{aligned} {\bar{p}_0}= & {} p_0, \quad {\bar{p}_1}=p_{1},\\ {\bar{p}_2}= & {} p_2+8p_0, \quad {\bar{p}_3}= p_3+ 7p_1,\\ {\bar{p}_4}= & {} p_4+20 p_0 + 6 p_2,\\ {\bar{p}_5}= & {} p_5+14 p_1 + 5 p_3, \\ {\bar{p}_6}= & {} p_6 +16 p_0 + 9 p_2 + 4 p_4,\\ {\bar{p}_7}= & {} p_7+ 7 p_1 + 5 p_3 + 3 p_5,\\ {\bar{p}_8}= & {} p_8+2( p_0 + p_2 + p_4 + p_6). \end{aligned}$$

Using Eqs. (12) and (8), for each set of the system parameters, we can determine numerically the angles \(\alpha _{20}\) and \(\alpha _{10}\), that is, all the planar equilibrium orientations of the satellite–stabilizer system.

4 Investigation of Equilibria

Equations (8) and (12) make it possible to determine all the plane equilibrium configurations of the satellite–stabilizer, due to the action of the gravity torque for the given values of system parameters \(a_1\), \(a_2, c_1, c_2\), and \(d_1, d_2\) of the problem.

In studying the two–body system equilibrium orientations, we determine the domains with an equal number of real roots of Eq. (12) in the space of 6 parameters. To identify these domains, we use the Meiman theorem [13], which yields that the decomposition of the space of parameters into domains with an equal number of real roots is determined by the discriminant hypersurface. It is also possible to calculate the number of real roots of a polynomial by means of ith subdiscriminants using Jacobi theorem [14, 15].

In our case, the discriminant hypersurface is given by the discriminant of polynomial (12). This hypersurface contains a component of codimension 1, which is the boundary of domains with an equal number of real roots. The set of singular points of the discriminant hypersurface in the space of parameters \(a_1\), \(a_2, c_1, c_2\), and \(d_1, d_2\) is given by the following system of algebraic equations:

$$\begin{aligned} P(x) = 0, \quad P^\prime (x) = 0. \end{aligned}$$
(13)

Here the symbol “prime” denotes differentiation with respect to x.

We can eliminate the variable x from system (13) by calculating the determinant of the resultant matrix of Eq. (13) with the help of symbolic matrix functions in Maple. The form of the discriminant of the polynomial P(x) is a very cumbersome expression.

Let us consider a simpler case when \(a_1=a_2=c_1=c_2=a\). Then introducing the new parameters in (6) \(d_{01}=(A_1-C_1))/Ma^2\), \(d_{02}=(A_2-C_2)/Ma^2\), we obtain from (9) a simpler algebraic equation of the 8th degree, whose coefficients depend only on two parameters \(d_{01}\) and \(d_{02}\)

$$\begin{aligned} p_{00}t_2^{8}+p_{01}t_2^{7}+p_{02}t_2^{6}+p_{03}t_2^{5}+p_{04}t_2^{4} +p_{05}t_2^{3}+p_{06}t_2^{2}+p_{07}t_2+p_{08}=0, \end{aligned}$$
(14)

where

$$\begin{aligned} p_{00}= & {} p_{08}=d_{01}^2(d_{02}^2-1)^2-d_{02}^2, \\ p_{01}= & {} -p_{07}=2(d_{02}-2)\big (d_{01}^2(d_{02}^2+d_{02}-2)+2d_{02}^2\big ), \\ p_{02}= & {} p_{06}= d_{01}^2(d_{02}^4 - 20d_{02}^2 + 8d_{02}+20)+ 4d_{02}^2(d_{02}^2-5), \\ p_{03}= & {} -p_{05}=2\big (d_{01}^2(7d_{02}^3 + d_{02}^2 - 28d_{02} -4)+ 2d_{02}^2(7d_{02}+2)\big ),\\ p_{04}= & {} -2\big (d_{01}^2(d_{02}^4 - 27d_{02}^2 - 10d_{02} +13)+ 4d_{02}^4 -13d_{02}^2\big ). \\ \end{aligned}$$

After replacing in (14) \(x=(t_2-\frac{1}{t_2})\), we will obtain the equation of the 4th degree

$$\begin{aligned} P_1(x)= & {} p_{00}x^4+p_{01}x^3+(p_{02}+4p_{00})x^2\nonumber \\&+(p_{03}+3p_{01})x+p_{04}+2(p_{02}+p_{00})=0. \end{aligned}$$
(15)

Now we determine the conditions for the existence of real roots of Eq. (15). To identify these conditions, we use the Meiman theorem [13]. In our case, the discriminant hypersurface is given by the discriminant of polynomial \(P_1(x)\). The boundary of domains with the equal number of real roots on the plane of parameters \(d_{01}\) and \(d_{02}\) is given by the following system of algebraic equations:

$$\begin{aligned} P_1(x) = 0, \quad P_1^\prime (x) = 0. \end{aligned}$$
(16)

We eliminate the variable x from system (16) by calculating the determinant of the resultant matrix of Eqs. (16) and obtain an algebraic equation of the discriminant hypersurface as

$$\begin{aligned} P_2(d_{01}, d_{02})=256d_{02}^{12}P_3(d_{01}, d_{02})P_4(d_{01}, d_{02})P_5(d_{01}, d_{02}) = 0. \end{aligned}$$
(17)

Here

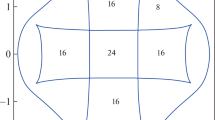
Now we should check the change in the number of equilibria when the curve (17) is intersected. This can be done numerically by determining the number of equilibria at a single point of each domain at the plane \((d_{01}, d_{02})\). This analysis showed that only the curve \( P_4(d_{01}, d_{02})~=~0\) separates the domains with different number of equilibria.

Figure 2 presents an example of the properties and form of the discriminant hypersurface \(P_2(d_{01}, d_{02})= 0\), which are the set of curves on the plane \((d_{01}, d_{02})\). Fig. 2 shows the distributions of domains with equal number of real roots of Eq. (17) and indicates the domains where four and two real solutions exist (8 and 4 equilibrium orientations). In Fig. 2, four branches of two hyperbolas indicate the boundaries \(P_3(d_{01}, d_{02})= 0\), where the number of real roots of Eq. (17) does not change. Therefore, in the case when \(a_1=a_2=c_1=c_2=a\), there exist only 8 and 4 planar equilibrium orientations for the satellite–stabilizer system.

Fig. 1.
figure 1

Basic coordinate systems

Full size image
Fig. 2.
figure 2

The regions with the fixed number of equilibria

Full size image

5 Conclusion

In this paper, we present the study of the dynamics of the rotational motion of the satellite–stabilizer system subject to the gravitational torque in the plane of the orbit. The computer algebra method (based on the resultant approach) of determining all equilibrium orientations of the satellite–stabilizer system in the orbital coordinate system in the plane of a circular orbit was presented. The conditions for the existence of these equilibria were obtained.

We have made an analysis of the evolution of domains of existence of equilibrium orientations in the plane of system parameters \(d_{01}\) and \(d_{02}\) for the special case when the coordinates of the spherical hinge in the satellite body coordinate system \(Ox_1y_1z_1\) and stabilizer body coordinate system \(Ox_2y_2z_2\) are equal. For this case, we have indicated the analytic equation of the discriminant hypersurfaces that limits regions with different number of equilibrium configurations of the satellite–stabilizer system. The hypersurface equation was computed symbolically using the resultant approach.

The obtained results can be used to design gravitational attitude control systems for the artificial Earth satellites.