A Symbolic Investigation of the Influence of Aerodynamic Forces on Satellite Equilibria

Abstract

Computer algebra methods are used to study the properties of a nonlinear algebraic system that determines equilibrium orientations of a satellite moving along a circular orbit under the action of gravitational and aerodynamic torques. An algorithm for the construction of a Gröbner basis is proposed for determining the equilibrium orientations of a satellite with given principal central moments of inertia and given aerodynamic torque in special cases, when the center of pressure of aerodynamic forces is located in one of the principal central planes of inertia of the satellite. The conditions of the equilibria existence are obtained, depending on three dimensionless parameters of the problem. The number of equilibria depending on the parameters is found by the analysis of real roots of algebraic equations from the constructed Gröbner basis. The evolution of domains with fixed number of equilibria from 24 to 8 is investigated in detail. All bifurcation values of the system parameters corresponding to the qualitative change of these domains are determined.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In this work, a symbolic investigation of a satellite dynamics under the influence of gravitational and aerodynamic torques is presented. The gravity orientation systems are based on the result that a satellite with different moments of inertia in the central Newtonian force field in a circular orbit has 24 equilibrium orientations [1]. However, at altitudes from 250 up to 500 km, rotational motion of a satellite is subjected to aerodynamic torque too. Therefore, it is necessary to study the joint action of gravitational and aerodynamic torques and, in particular, to analyse all possible satellite equilibria in a circular orbit. Such solutions are used in practical space technology in the design of attitude control systems of satellites.

The basic problems of satellite dynamics with an aerodynamic attitude control system have been presented in [1]. The problem of determining the classes of equilibrium orientations for general values of aerodynamic torque was considered in [2, 3]. In [4–6], some equilibrium orientations were found in special cases when the center of pressure is located on a satellite principal central axis of inertia and on a satellite principal central plane of inertia. In [7], all equilibrium orientations were found in the case of axisymmetric satellite.

The present work continues the study started in [6]. In this paper, all cases when the center of pressure is located in the satellite principal central plane of inertia are considered. All possible equilibrium orientations are investigated, and their existence conditions are obtained. The equilibrium orientations are determined by real roots of the system of nonlinear algebraic equations. The investigation of equilibria was possible due to application of Computer Algebra Gröbner basis method. The evolution of domains with a fixed number of equilibria is investigated in dependence of three dimensionless system parameters.

2 Equations of Motion

Consider the motion of a satellite subjected to gravitational and aerodynamic torques in a circular orbit. We assume that (1) the gravity field of the Earth is central and Newtonian, (2) the satellite is a triaxial rigid body, (3) the effect of atmosphere on a satellite is reduced to the drag force applied at the center of pressure and directed against the velocity of the satellite center of mass relative to the air, and the center of pressure is fixed in the satellite body. To write the equations of motion we introduce two right-handed Cartesian coordinate systems with origin at the satellite center of mass O. OXYZ is the orbital reference frame. The axis OZ is directed along the radius vector from the Earth center of mass to the satellite center of mass, the axis OX is in the direction of a satellite orbital motion. Oxyz is the satellite body reference frame; Ox, Oy, and Oz are the principal central axes of inertia of the satellite. The orientation of the satellite body coordinate system Oxyz with respect to the orbital coordinate system is determined by means of the aircraft angles of pitch $\alpha$, yaw $\beta$, and roll $\gamma$, and the direction cosines in the transformation matrix between the orbital coordinate system OXYZ and Oxyz are represented by the following expressions:

$$\begin{aligned} a_{11}= & {} \cos (x,X)=\cos \alpha \cos \beta ,\nonumber \\ a_{12}= & {} \cos (y,X)=\sin \alpha \sin \gamma -\cos \alpha \sin \beta \cos \gamma ,\nonumber \\ a_{13}= & {} \cos (z,X)=\sin \alpha \cos \gamma +\cos \alpha \sin \beta \sin \gamma ,\nonumber \\ a_{21}= & {} \cos (x,Y)=\sin \beta ,\nonumber \\ a_{22}= & {} \cos (y,Y)=\cos \beta \cos \gamma , \\ a_{23}= & {} \cos (z,Y)=-\cos \beta \sin \gamma ,\nonumber \\ a_{31}= & {} \cos (x,Z)=-\sin \alpha \cos \beta ,\nonumber \\ a_{32}= & {} \cos (y,Z)=\cos \alpha \sin \gamma +\sin \alpha \sin \beta \cos \gamma ,\nonumber \\ a_{33}= & {} \cos (z,Z)=\cos \alpha \cos \beta -\sin \alpha \sin \beta \sin \gamma .\nonumber \end{aligned}$$

(1)

Then equations of the satellite attitude motion can be written in the Euler form [1, 4]:

$$\begin{aligned} A{\dot{p}}+(C-B)qr -3{\omega }_0^2(C-B)a_{32}a_{33}= {\omega }_0^2( H_2a_{13}-H_3a_{12}),\nonumber \\ B{\dot{q}}+(A-C)rp -3{\omega }_0^2(A-C)a_{31}a_{33}= {\omega }_0^2( H_3a_{11}-H_1a_{13}),\nonumber \\ C{\dot{r}}+(B-A)pq -3{\omega }_0^2(B-A)a_{31}a_{32}= {\omega }_0^2( H_1a_{13}-H_3a_{11}), \\ p=(\dot{\alpha }+{\omega }_0)a_{21}+\dot{\gamma }, \quad q=(\dot{\alpha }+{\omega }_0)a_{22}+\dot{\beta }\sin \gamma ,\nonumber \\ r=(\dot{\alpha }+{\omega }_0)a_{23}+\dot{\beta }\cos \gamma .\nonumber \end{aligned}$$

(2)

Here p, q, and r are the projections of the satellite angular velocity onto the axes Ox, Oy, and Oz; A, B, and C are the principal central moments of inertia of the satellite (without loss of generality, we assume that $B>A>C$); ${\omega }_0$ is the angular velocity of the orbital motion of the satellite center of mass. $H_1=-aQ/{\omega }_0^2$, $H_2=-bQ/{\omega }_0^2$, $H_3=-cQ/{\omega }_0^2$, Q is the atmospheric drug force acting on a satellite; a, b, and c are the coordinates of the center of pressure of a satellite in the reference frame Oxyz. The dot designates differentiation with respect to time t.

3 Equilibrium Orientations of a Satellite

Setting in (2) ${\alpha }={\alpha }_0=\mathrm{const}$, ${\beta }={\beta }_0=\mathrm{const}$, ${\gamma }={\gamma }_0= \mathrm{const}$, we obtain at $A \ne B \ne C$ the equations

$$\begin{aligned} (C-B)(a_{22}a_{23} - 3a_{32}a_{33})= & {} H_2a_{13}-H_3a_{12},\nonumber \\ (A-C)(a_{21}a_{23} - 3a_{31}a_{33})= & {} H_3a_{11}-H_1a_{13}, \\ (B-A)(a_{21}a_{22} - 3a_{31}a_{32})= & {} H_1a_{12}-H_2a_{11},\nonumber \end{aligned}$$

(3)

which allow us to determine the satellite equilibria in the orbital reference frame. Substituting the expressions for the direction cosines from (1) in terms of the aircraft angles and into Eq. (3), we obtain three equations with three unknowns $\alpha$, $\beta$, and $\gamma$. The second procedure for closing Eq. (3) is to add the following six orthogonality conditions for the direction cosines

$$\begin{aligned} a_{i1}a_{j1} + a_{i2}a_{j2} + a_{i3}a_{j3} - \delta _{ij}=0, \end{aligned}$$

(4)

where $\delta _{ij}$ is the Kronecker delta and $i,j=1,2,3$. Equations (3) and (4) form a closed system with respect to the direction cosines, which also specifies the equilibrium solutions of the satellite.

The system (3) and (4) has been solved for general case of the problem when $H_1 \ne 0$, $H_2\ne 0$, $H_3 \ne 0$ [2, 3]. With the help of computer algebra method it was shown that equilibrium orientations are determined by real solutions of algebraic equation of the twelfth degree. The equilibrium orientations and their stability were analysed numerically. The problem has been solved analytically only for some specific cases when the center of pressure is located on a satellite principal central axis of inertia Ox, when $H_1 \ne 0$, $H_2=H_3 = 0$ [4, 5] and for the case of axisymmetric satellite when $A \ne B = C$ [7]. When the pressure center locates in the satellite principal central plane of inertia Oxz of the frame Oxyz, in the case when $H_1 \ne 0$, $H_2= 0$, and $H_3 \ne 0$, very complex analytical study of the system (3) and (4) was conducted, and the equilibria were analysed numerically [6]. In the present work, the problem of determination of the classes of equilibrium orientations for all cases when the pressure center locates in one of satellite principal central planes of inertia of the frame Oxyz, when (1) $H_1 \ne 0$, $H_2 \ne 0$, and $H_3 = 0$, (2) $H_1 \ne 0$, $H_2= 0$, and $H_3 \ne 0$ and (3) $H_1=0$, $H_2 \ne 0$, and $H_3 \ne 0$, with the help of Computer Algebra methods is investigated. The existence of flat solutions in these cases is specified.

4 Investigation of Equilibria

4.1 Equilibria in the Case $H_3=0$ ($H_1 \ne 0$, $H_2 \ne 0$)

We begin by considering the first case $H_1 \ne 0$, $H_2 \ne 0$, and $H_3 = 0$ when the pressure center is located in the plane Oxy. Introducing dimensionless parameters $h_i=H_i/(B-C)$, ${\nu }=(B-A)/(B-C)$, ($0<{\nu }<1$), system (3) takes the form

$$\begin{aligned} a_{22}a_{23}-3a_{32}a_{33}+h_2a_{13}= & {} 0, \nonumber \\ (1- \nu )(a_{23}a_{21}- 3a_{33}a_{31})+h_1a_{13}= & {} 0, \\ \nu (a_{21}a_{22}-3a_{31}a_{32})-h_1a_{12}+h_2a_{11}= & {} 0. \nonumber \end{aligned}$$

(5)

To solve the algebraic system (4), (5) we applied the algorithm of constructing the Gröbner bases [8]. The method of constructing the Gröbner bases is an algorithmic procedure for complete reduction of the problem in the case of the system of polynomials in several variables to the polynomial of one variable. Using the Gröbner[gbasis] Maple 15 package [9] for constructing Gröbner bases, the lexicographic monomial order was chosen. We constructed the Gröbner basis for the system of nine polynomials (4), (5) with nine variables direction cosines $a_{ij}$ $(i, j=1,2,3)$, and in the list of polynomials, we include the polynomials from the left-hand sides $f_i$ $(i=1,2,... 9)$ of the algebraic equations (4), (5):

G:=map(factor,Gröbner[gbasis]([f1, ... f9], plex(a11, ... a33))).

Here we write down the polynomial in the Gröbner basis that depends only on one variable $x=a_{33}$. This polynomial has the form

$$\begin{aligned} P(x) = P_1(x)P_2(x)=0, \end{aligned}$$

(6)

where

$$\begin{aligned} P_1(x)= & {} x(x^2-1),\\ P_2(x)= & {} p_0x^{4}+p_1x^{2}+p_2,\\ p_{0}= & {} 9(1-\nu )^2p_3^2, \\ p_{1}= & {} p_3(h_1^6 -(1-\nu )(6\nu -(3-\nu )h_2^2)h_1^4 \\- & {} (1-\nu )^2((2\nu -3)h_2^4+9\nu ^2(2h_2^2-1))h_1^2+(1-\nu )^4(h_2^2+3\nu )^2), \\ \\ \\ \\ \\ \\ p_{2}= & {} -{\nu }^2h_1^2h_2^2(h_1^6 -(1-\nu )(5\nu +1-(3-\nu )h_2^2)h_1^4 \\- & {} (1-\nu )^2((2\nu -3)h_2^4+2(5\nu ^2-\nu +1)h_2^2-3\nu (2+\nu ))h_1^2\\+ & {} (1-\nu )^4(h_2^2-1)(h_2^2+3\nu )^2), \\ p_3= & {} h_1^4+2(1-\nu )(h_2^2-3\nu )h_1^2 +(1-\nu )^2(h_2^2+3\nu )^2. \end{aligned}$$

It is necessary to consider three cases $a_{33} = 0$, $a^2_{33} =1$, and $P_2(a^2_{33})=0$ to investigate system (4), (5).

In the first case when $a_{33} =0$, system (4), (5) takes the form

$$\begin{aligned} 3{\nu }a_{31}a_{32}+(h_1a_{31}+h_2a_{32})a_{23}= & {} 0, \nonumber \\ a^2_{31}+a^2_{32}= & {} 1,\nonumber \\ a^2_{23}= & {} 1, \\ a_{33}=a_{13}=a_{21}=a_{22}= & {} 0, \nonumber \\ a_{11}=-a_{23}a_{32}, \quad a_{12}= & {} a_{23}a_{21}. \nonumber \end{aligned}$$

(7)

The first two equations of system (7) can be written in a simpler form

$$\begin{aligned} 9{\nu }^2 a^4_{31}+6{\nu }h_2 a^3_{31}+(h_1^2+h_2^2- 9{\nu }^2)a^2_{31} -6{\nu }h_2 a_{31}-h_1^2=0,\\ a_{32}= \mp \frac{h_1a_{31}}{(3{\nu }a_{31}\pm h_2)}. \nonumber \end{aligned}$$

(8)

Having solved system (8) one can determine the remaining direction cosines from the equations of system (7). The first equation of system (7) represents the equations of four hyperbolas. Their two branches pass through the origin of coordinate system ($a_{31} = 0$ and $a_{32} = 0$) in the plane of variables $a_{31}$ and $a_{32}$, while the second equation determines the unit circle in this plane. The number of real solutions to system (7) (and, hence, to system (8)) depends on the character of intersections of the hyperbolas with the circle. It is clear that two branches of the hyperbolas that pass through the origin of coordinates always intersect the circle at four points. If two other branches of the hyperbolas also intersect the circle, we have four more solutions. In the case when hyperbola branches touch the circle four solutions merge into two (there are two pairs of multiple roots) [7]. Thus, system (7), and hence system (8) too, has either eight or four solutions. It follows from the reasoning presented above that bifurcation points are those points of plane $a_{31}$, $a_{32}$, through which the branches of hyperbolas and the circle pass simultaneously, and where tangents to these curves coincide. The condition of coincidence of the tangents to two hyperbola branches and the circle has the following form

$$\begin{aligned} \frac{d(a_{31})}{d(a_{32})}=-\frac{3{\nu }a_{32} \pm h_1}{3{\nu }a_{31} \pm h_2}= -\frac{2a_{31}}{2a_{32}}\\ \end{aligned}$$

or

$$\begin{aligned} 3{\nu }(a^2_{32}-a^2_{31}) \pm h_1 a_{32} \mp h_2 a_{31}=0. \end{aligned}$$

(9)

Substituting the expression for $a_{32}$ from (8) into the second equation of (7) and equation (9), we get the following system of equations

$$\begin{aligned} \frac{h_1^2 a^2_{31}}{(3{\nu }a_{31} + h_2)^2}=1-a^2_{31}, \quad \frac{h_1^2 h_2}{(3{\nu }a_{31} + h_2)^2}=-(3{\nu }a_{31} + h_2). \end{aligned}$$

(10)

Excluding $h_1^2$ from system of equations (10), after some simple transformations we get the relationship $a_{31}=-{(3{\nu })}^{-1/3} h_2^{1/3}$. Finally, substituting the expression for $a_{31}$ into the second equation of (10) we arrive at the equation of astroid

$$\begin{aligned} h_1^{2/3}+h_2^{2/3}=(3{\nu })^{2/3}. \end{aligned}$$

(11)

There are eight solutions inside the region $h_1^{2/3}+h_2^{2/3} < (3{\nu })^{2/3}$; when passing through curve (11) (which is a bifurcation curve), the number of solutions changes to four; there exist four solutions in the region $h_1^{2/3}+h_2^{2/3} > (3{\nu })^{2/3}$.

Now let us consider the second case $a^2_{33} =1$. In this case, system (4), (5) takes the form

(12)

The first two equations of system (12) can be written in the following form:

$$\begin{aligned} {\nu }^2 a^4_{21}+2{\nu }h_2 a^3_{21}+(h_1^2+h_2^2- {\nu }^2)a^2_{21} -2{\nu }h_2 a_{31}-h_1^2=0,\\ a_{22}= \mp \frac{h_1a_{21}}{({\nu }a_{21}\pm h_2)}. \nonumber \end{aligned}$$

(13)

Applying the approach suggested above for investigating system (7) one can demonstrate that for system (12), the bifurcation curve separating the region of existence of eight solutions from the region of existence of four solutions is also the astroid

$$\begin{aligned} h_1^{2/3}+h_2^{2/3}=({\nu })^{2/3}. \end{aligned}$$

(14)

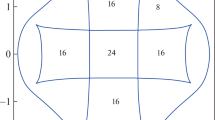
In Figs. 1, 2 and 3, astroids (11) and (14) for the $\nu$ values equal to 0.2, 0.5, and 0.8 are presented, that separate in plane $(h_1, h_2)$ three regions with different numbers of equilibrium orientations of the satellite under the action of gravitational and aerodynamic torques. There exist 8, 6, and 4 real solutions (16, 12, and 8 equilibria) of both Eqs. (8) and (13) for the first and second cases in regions $h_1^{2/3}+h_2^{2/3}<({\nu })^{2/3}$; $({\nu })^{2/3}< h_1^{2/3}~+~h_2^{2/3}~<~({3\nu })^{2/3}$, and $h_1^{2/3}~+~h_2^{2/3}~>~({3\nu })^{2/3}$, respectively.

Let us consider the third case for which the satellite equilibria are determined by the real roots of the biquadratic equation $P_2(x)=0$. The number of real roots of the biquadratic equation (6) is even and not greater than 4. For each solution, one can find from the second polynomial from of the constructed Gröbner base two values of $a_{32}$ and, then, their respective values $a_{31}$. For each set of values $a_{31}$, $a_{32}$, and $a_{33}$, one can unambiguously determine from original system (4) and (5) the respective values of the direction cosines $a_{11}$, $a_{12}$, $a_{13}$ $a_{21}$, $a_{22}$, and $a_{23}$. Thus, each real root of the biquadratic equation (6) is matched with two sets of values $a_{ij}$ (two equilibrium orientations). Since the number of real roots of biquadratic equation (6) does not exceed 4, the satellite in the third case can have no more than 8 equilibrium orientations.

For the variable $t=x^2=a^2_{33}$, we get the quadratic equation

$$\begin{aligned} P_2(t)=p_0t^2+p_1t+p_2=0. \end{aligned}$$

(15)

Equation (15) has two solutions

$$\begin{aligned} t_1= \frac{-p_1-\sqrt{p_1^2 - 4p_0p_2}}{2p_0}; \quad t_2= \frac{-p_1+\sqrt{p_1^2 - 4p_0p_2}}{2p_0}. \end{aligned}$$

(16)

It is possible to show that the discriminant $p_1^2 - 4p_0p_2 \ge 0$ at any values of the system parameters. Thus, in case of the inequality $t_1=a^2_{33} > 0$ satisfaction, Eq. (15) has two real roots $t_1$ and $t_2$ which correspond to four $a_{33}$ values, and system (4), (5) (at $a_{33} \ne 0, a_{33} \ne \pm 1$) has 8 solutions, and these solutions correspond to 8 satellite equilibrium orientations. These equilibria exist in the domain bounded by the curve $t_1(h_1, h_2, \nu )=0$. In Figs. 1, 2 and 3, these curves are marked as $t_1$.

In the domain bounded by the curves $t_1(h_1, h_2, \nu )=0$, $t_2(h_1, h_2, \nu )=1$ for which inequalities $t_1(h_1, h_2, \nu ) < 0$ and $0< t_2(h_1, h_2, \nu ) < 1$ take place, only four equilibria exist, which correspond only to one root $t_2$. Outside the boundary $t_2(h_1, h_2, \nu )=1$, there are no solutions of the third case. In Figs. 1, 2 and 3, these curves are denoted as $t_2$.

The results of the analysis of the equilibria total number in the third case can be summarized as follows. The curves $t_1(h_1, h_2, \nu )=0$, $t_2(h_1, h_2, \nu )=1$ decompose the plane ($h_1, h_2$) into three domains where 8 equilibria, 4 equilibria, and no equilibria exist.

The final decomposition of the plane $(h_1, h_2)$ for all three cases is presented in Figs. 1, 2 and 3 for $\nu =0.2$, $\nu =0.5$, and $\nu =0.8$. Curves (11), (14) and $t_1(h_1, h_2, \nu )~=~0$, $t_2(h_1, h_2, \nu )~=~1$ separate the plane into domains with the fixed number of equilibria equal to 24, 20, 16, 12, and 8.

Fig. 1.

The regions with the fixed number of equilibria for $\nu =0.2$

Fig. 2.

The regions with the fixed number of equilibria for $\nu =0.5$

Fig. 3.

Regions with the fixed number of equilibria for $\nu =0.8$

4.2 Equilibria in the Case $H_1=0$ ($H_2 \ne 0$, $H_3 \ne 0$)

Let us consider the next case $H_1 = 0$, $H_2 \ne 0$, and $H_3 \ne 0$ when the pressure center locates in the plane Oyz. System (3) in that case takes the form

$$\begin{aligned} a_{22}a_{23}-3a_{32}a_{33}+h_2a_{13}-h_3a_{12}= & {} 0, \nonumber \\ (1- \nu )(a_{23}a_{21}- 3a_{33}a_{31})-h_3a_{11}= & {} 0, \\ \nu (a_{21}a_{22}-3a_{31}a_{32})+h_2a_{11}= & {} 0. \nonumber \end{aligned}$$

(17)

Applying the approach suggested above for investigating system (4), (5), we used the algorithm of constructing the Gröbner bases for the polynomials on the left-hand sides of the system (4), (17). The polynomial in the Gröbner basis that depends only on one variable in that case $a_{31}$ has the form

$$\begin{aligned} P_{h1}(a_{31}) = P_3(a_{31})P_4(a_{31})=0, \end{aligned}$$

(18)

where

$$\begin{aligned} P_3(a_{31})= & {} a_{31}(a^2_{31}-1),\\ P_4(a_{31})= & {} p_{40}a^4_{31}+p_{41}a^2_{31}+p_{42},\\ p_{40}= & {} 9{\nu }^2(1-\nu )^2p_{43}^2, \\ p_{41}= & {} p_{43}({\nu }^4h_3^6 +{\nu }^2(1-\nu )(6{\nu }^2-(3\nu -1)h_2^2)h_3^4 \\- & {} {\nu }(1-\nu )^2((2\nu -3)h_2^4+9\nu (2h_2^2-{\nu }^2))h_3^2+(1-\nu )^4h_2^2(h_2^2+3\nu )^2), \\ p_{42}= & {} -h_2^2h_3^2({\nu }^4h_3^6 +{\nu }^2(1-\nu )({\nu }^2(5+\nu )+(1-3\nu )h_2^2)h_3^4 \\+ & {} {\nu }(1-\nu )^2((3\nu -2)h_2^4+2{\nu }(\nu (1-\nu )-5)h_2^2+3{\nu }^3(1+2\nu ))h_3^2\\+ & {} (1-\nu )^4(h_2^2-{\nu }^2)(h_2^2+3\nu )^2), \\ p_{43}= & {} {\nu }^2h_3^4+2{\nu }(1-\nu )(h_2^2-3\nu )h_3^2 +(1-\nu )^2(h_2^2+3\nu )^2. \end{aligned}$$

It is also necessary to consider three cases, $a_{31} = 0$, $a^2_{31} =1$, and $P_{42}(a^2_{31})=0$ to investigate system (4), (17).

In the first case when $a_{31} =0$, using the approach described above in Subsect. 4.1, it is possible to obtain the bifurcation curve

$$\begin{aligned} h_2^{2/3}+h_3^{2/3}=3^{2/3}, \end{aligned}$$

which separates the plane $(h_2, h_3)$ into two regions with eight and four equilibrium orientations of the satellite. In the second case when $a_{31}^2 =1$, applying the above approach one can demonstrate that for system (17), the bifurcation curve separating the region of existence of eight solutions from the region of existence of four solutions is also the astroid

$$\begin{aligned} h_2^{2/3}+h_3^{2/3}=1. \end{aligned}$$

Another two curves separating the regions with an equal number of equilibria can be obtained from the conditions of existence of real roots of the biquadratic equation $P_4(a_{31})=0$. The evolution of domains with a fixed number of equilibrium orientations in the plane of two parameters $(h_2,h_3)$ is very similar to the case described in 4.1.

4.3 Equilibria in the Case $H_2=0$ ($H_1 \ne 0$, $H_3 \ne 0$)

In the last case $H_1 \ne 0$, $H_2 = 0$, and $H_3 \ne 0$ when the pressure center locates in the plane Oxz system (3) takes the form

$$\begin{aligned} a_{22}a_{23}-3a_{32}a_{33}-h_3a_{12}= & {} 0, \nonumber \\ (1- \nu )(a_{23}a_{21}- 3a_{33}a_{31})-h_3a_{11}+h_1a_{13}= & {} 0, \\ \nu (a_{21}a_{22}-3a_{31}a_{32})-h_1a_{12}= & {} 0. \nonumber \end{aligned}$$

(19)

Constructing the Gröbner bases for the polynomials on the left-hand sides of system (4), (19), we will get the polynomial that depends only on one variable $a_{32}$ in the form

$$\begin{aligned} P_{h2}(a_{32}) = P_5(a_{32})P_6(a_{32})=0, \end{aligned}$$

(20)

where

$$\begin{aligned} P_5(a_{32})= & {} a_{32}(a^2_{32}-1),\\ P_6(a_{32})= & {} p_{60}a^4_{32}+p_{61}a^2_{32}+p_{62},\\ p_{60}= & {} 9{\nu }^2p_{63}^2, \\ p_{61}= & {} p_{63}(h_1^6 +{\nu }((2+\nu )h_3^2-6(1-{\nu }))h_1^4 \\+ & {} {\nu }^2((2\nu +1)h_3^4\!-18(1-{\nu })^2h_3^2+9(1-{\nu })^2)h_1^2\!+{\nu }^4h_3^2(h_3^2\!+3(1-\nu ))^2), \\ p_{62}= & {} -h_1^2h_3^2(h_1^6 +{\nu }((2+\nu ))h_3^2+5\nu -6)h_1^4 \\+ & {} {\nu }^2((2\nu +1)h_3^4+2(9\nu -5{\nu }^2-5)h_3^2+3({\nu }^2-4\nu +3))h_1^2 \\+ & {} {\nu }^4(h_3^2-1)(h_3^2+3(1-\nu ))^2), \\ p_{63}= & {} h_1^4+2{\nu }(h_3^2-3(1-\nu ))h_1^2 +{\nu }^2(h_3^2+3(1-\nu ))^2. \end{aligned}$$

It is necessary to consider three cases $a_{32} = 0$, $a^2_{32} =1$, $P_6(a_{32})=0$, to investigate the system (4), (19). In the first case when $a_{32} =0$, using the approach described in Subsect. 4.1, it is possible to obtain the bifurcation curve

$$\begin{aligned} h_1^{2/3}+h_3^{2/3}=(3(1-{\nu }))^{2/3}, \end{aligned}$$

which separates the plane $(h_1, h_3)$ into two regions with eight and four equilibrium orientations of the satellite. In the second case when $a_{32}^2 =1$, the bifurcation curve separating the region of existence of eight solutions from the region of existence of four solutions is also the astroid

$$\begin{aligned} h_1^{2/3}+h_3^{2/3}=(1-{\nu })^{2/3}. \end{aligned}$$

Another two curves separating the regions with an equal number of equilibria can be obtained from the conditions of existence of real roots of the biquadratic equation $P_6(a_{32})=0$.

The evolution of domains with a fixed number of equilibrium orientations in the plane of two parameters $(h_1,h_3)$ is also very similar to the first case. In [6], the sufficient conditions for stability of the equilibrium orientations for the last case $h_1 \ne 0$, $h_2 = 0$, and $h_3 \ne 0$ are obtained using the Lyapunov theorem.

Conditions $a_{31} = 0$, $a^2_{31} =1$; $a_{32} = 0$, $a^2_{32} =1$ and $a_{33} = 0$, $a^2_{33} =1$ define all flat solutions of the problem.

5 Conclusion

In this work, the attitude motion of the satellite under the action of gravitational and aerodynamic torques in a circular orbit has been investigated. The main attention was given to determination of the satellite equilibrium orientation in the orbital reference frame and to the analysis of their evolutions in three cases when the center of pressure of aerodynamic forces is located in one of the principal central planes of inertia of the satellite Oxy, Oxz, and Oyz.

The symbolic method of determination of all the satellite equilibria is suggested in the cases when $h_1 = 0$, or $h_2= 0$, or $h_3 = 0$. The Computer algebra system Maple is applied to reduce the satellite stationary motion system of nine algebraic equations with nine variables to a single algebraic equation with one variable, using the algorithm for the construction of Gröbner basis.

These results permit us to describe the change of the number of equilibrium orientations of the satellite as a function of the parameters $h_i$ and $\nu$. When the aerodynamic torque is small enough, there exist 24 equilibria; when it is large enough, there are 8. The evolution of domains with a fixed number of equilibrium orientations was investigated both analytically and numerically in the plane of two parameters $(h_1,h_2)$ at different values of parameter $\nu$. All bifurcation values of the system parameters corresponding to the qualitative change of domains with fixed number of equilibria were determined. The existence of flat solutions of the problem was specified. The results of the study can be used at the stage of preliminary design of the satellite with aerodynamic control system.