3D Path Network Planning: Using a Global Optimization Heuristic for Mine Water-Inrush Evacuation

Abstract

The evacuation planning for mine water-inrush is of great importance for personal and property security, and the research of this field in 3D scenarios can provide intuition vision for the geographic space and contribute to the evacuation plan and implementation. In this paper, based on 3D mine model, we address a multi-objective optimization problem for evacuation path planning in mine water-inrush scenario, namely the global-optimized multi-path finding problem, which aims to minimize the global evacuation time-consuming and balance the evacuation loads of the emergency exits. Based on the auxiliary graph transformation, we propose a 3-phase heuristic referred to the classical problem, Minimum Weighted Set Cover. We finally conduct extensive experiments to evaluate the performance of the proposed algorithm, whose results indicate the heuristic outperform the existing alternatives in terms of the utilization as well as timeliness.

1 Introduction

With the rise of various hazards and risk raised by the global technology development, disaster avoiding and evacuation planning have drawn much attention due to its huge potential applications. The research on evacuation planning primarily contains risk management [1], escape routes planning [2, 3], emotion mechanism of escape behavior [4, 5] and escape virtual simulation [6, 7].

Escape routes/paths planning is one of the most important problems in evacuation planning for accidents, which is to compute the optimal evacuation paths to minimize the escaping time. The problem in underground mine scenarios has been paid much attention all these years which focused on the cases of fire and explosion [8, 9]. For the escape routes finding problem of coal mines in water-inrush case, the existing research concentrated on 2D mine environment and can be classified into two kinds by the pair of number of the involved evacuators and that of the emergency exits: one is one-source to one-destination model (finding the escape route from one evacuator to one exit) and the other one is one-source to multi-destination (constructing multi-path from one evacuator to several exits). Both of the two kinds has been effectively solved based on the classical algorithms for solving the shortest path problem, the Dijkstra algorithm [10, 11], the Floyd-Warshall algorithm [12], the first k shortest paths [13,14,15], and dynamic programming [16]. For one-source to one-destination, in [13, 14], the authors studied the first k shortest paths problem whose goal is to find another $k-1$ suboptimal paths such that there is an alternative when the shortest one is impassable because of the water spread or congested on account of traffic load. Furthermore, many efforts are made to investigate on one-source to multi-destination in terms of modified or hybrid classical algorithms. In [15], the authors introduced a new variant of k shortest paths problem in a time-schedule network with constraints on arcs and they solved the problem based on the modified Dijkstra algorithm to find shortest paths and enumerate all paths. In [16], the authors considered a path networks with vulnerable links and they proposed a framework based on dynamic programming based on known link disruption probabilities and knowledge of transition probabilities for recovering.

It can be found that a 2D mine laneway model which cannot provide intuition vision for the geographic space and may effect the guideline of evacuation work. Furthermore, in the practical evacuation process, the mine personnel with a certain number locate in different places which may create the congestion on the feasible exits. But the above existing related literatures ignored the critical issue or cannot formally solve it in the problem. In this paper, based on a 3D geological mine model, we introduce an evacuation routes planning problem for the scenarios with a set of mining personnel and a set of feasible escaping exits (multi-source to multi-destination), with the consideration of the traffic load/utilization of the exits in the solution. The objective of the problem is to find multi-path connecting each personnel position and its most suitable exit for the goal of global optimization. The list of our contributions is as follows.

• (i) We introduce a new evacuation path planning problem in 3D mine water-inrush, the global-optimized multi-path finding (GMF) problem, and prove its NP-hardness.

• (ii) We propose a global-optimized strategy to determine the evacuation paths starting at the personnel initial location such that the time consumed by the latest escaped mine worker is minimized and the escaping load of each exit can be balanced.

• (iii) We conduct the simulations and evaluate the performance of the proposed algorithm in terms of utilization and timeliness.

The rest of the paper is organized as follows. Section 2 analyzes modeling of 3D mine laneway model and formulates problem definitions and its hardness proof. Section 3 introduces the framework of the 3-phase solution for GMF problem and describes the related algorithms. Simulation results and corresponding discussions are given in Sect. 4. Section 5 concludes this paper.

2 Modeling of Mine Network Using the Graph Concept and Problem Formulation

2.1 The Spatial Hierarchy Analysis of Mine Network

In this paper, we consider a 3D laneway model in mine water-inrush scenarios, $G = (V, E)$, where $V = V(G) = \{v_1, \cdots , v_n\}$ is the set of predetermined observation vertices, $E = E(G)$ is the set of bidirectional edges, and for each $v_i\in V$, $v_i=(ID_i, x_i, y_i, z_i)$ and for each $e_k\in E$, $e_k=(ID_i, ID_j)$ ($1\le i<j\le n$). For any vertex subset $V^\prime \subseteq V$, $G[V^\prime ]$ is the subgraph of G induced by $V^\prime$. Similarly, $G[E^\prime ]$ is the subgraph of G induced by an edge subset $E^\prime \subseteq E$. Important notations in the vertex set of 3D connected graph G are as follows: (a.) Water-bursting nodes where water-inrush occurred; (b.) Source nodes where the personnel located at the water-inrush moment and will start to escape from; (c.) Destination nodes in mine laneway which are safe for personnel evacuation, e.g. the pithead, the throat of a mine, or mine refuge; (d.) Impassable nodes which cannot be passable for evacuation, i.e. silting-up obstacles or submerged objects raised by water-inrush. Note that the obstacles considered here are a part and do not represent all possible types.

In practice of mining, the laneways are constructed in system structure, i.e. there are several relatively complete and independent components, which are relevant to each other via bend channels (similar to the corridors in a building). Such a mining sub-element of laneways is deployed in certain range of height, e.g., $(-700$ m, $-500$ m). Thus a 3D laneway model G can be regarded as an equivalent multi-layer 3D model via decomposing G into several relatively independent subgraph $G_1,G_2,...,G_L$ based on the spatial geometry speciality, i.e., $G_1$ is composed of the vertices with z-axis value in the range of $(-600$ m, $-500$ m) and those in the range of $(-700$ m, $-600$ m) belong to $G_2$. Thus a given 3D laneway model G can be reformulated into $G=\{<G_1,G_2,E_{1,2}>,<G_2,G_3,E_{2,3}>,...,<G_{L-1},G_L,E_{L-1,L}>\}$. The endpoints in all $E_{l-1,l}$ sets ($2\le l\le L$) are called as turning points.

2.2 The Traffic Capacity Analysis of Mine Network

When the water-inrush happens, the laneway is the main carrier of the trapped workers. And the traffic capacity of the laneway is affected by the following primary influence factors: Laneway types related to the section shape, slope ($\beta _1$), passibility influenced by the obstacles and the vehicle of the escape persons($\beta _2$), water height ($\beta _3$), and geometric length ($length(e_k)$). Here the other influence factors like wind velocity are assumed to be negligible. Then the traffic capacity of laneway can be expressed in term of the equivalent length/edge weight and the calculation of the edge weight is according to the equation: $weight(e_k) = length(e_k)\cdot \beta _1(e_k) \beta _2(e_k) \beta _3(e_k), 1\le k\le |E|$. Thus the mine laneway can be further modeled as a 3D connected and edge-weighted graph $G = (V, E, W)$, and $G_l$ can be rewrote as $G_l= (V_l, E_l, W_l)$, where $1\le l\le L$.

2.3 Problem Definitions and Hardness Results

In this paper, we consider the global evacuation planning problem in mine water-inrush, which is the overall construction of evacuation-paths for all the personnel in mine model. The problem is investigated from two points of view: the one is for each mine worker, to decide its globally ideal escape exit and the escaping path; the other one is for each escape exit, to assign relatively balanced escape count, i.e. to balance the escape loads of all the exits in order to take full advantage of them. Our problem in mine water-inrush evacuation is defined as follows.

Definition 1

(Global-optimized Multi-path Finding (GMF) Problem). Given a 3D mine laneway model, a 3D connected and edge-weighted graph $G = (V, E, W)$, and two vertex subsets, $S\subseteq V$ is the set of source nodes (personnel locations), $D\subseteq V$ is the set of destination nodes (escape exits), the global-optimized multi-path finding problem is to find the evacuation paths from nodes in S to the nodes in D such that the whole evacuation delay can be minimized and the evacuation efficiency can be maximized.

Here the whole evacuation delay is defined as the elapsed time consumed by the latest trapped worker. And the evacuation efficiency is for the evacuation exits (the nodes in D) and is represented by the balance performance among the personnel evacuation to all the exits, i.e. maximizing the evacuation efficiency is equivalent to minimizing the maximal difference between the average personnel evacuation times consumed by the mine workers to any pair of exits.

Based on two important and classical NP-hard problems, Set Cover and Minimum Weighted Set Cover problems, the hardness proof of our problem is given as follows.

Theorem 1

GMF Problem in Mine Water-inrush Evacuation is NP-hard.

Fig. 1.

Bipartite graph transformation of laneway model

Proof

To proof the hardness of GMF Problem, we consider a special case of it: the lengths of the paths between all pair of a root and a leaf are equivalent, $\max _{\forall d_i\in D, \forall s_i\in S} length(d_i,s_j)$, is the same value.

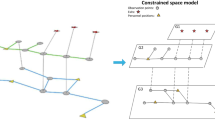
Based on the mathematical formulation of our problem, the forest ${\mathcal {P}}$ to be found has to meet the three conditions except (iii) in this case for the reason that (iii) is a default satisfying condition, i.e. the path lengths between all pair of roots and leaves are equal. Thus via transforming these isometric paths into one-hop edges as shown in Fig. 1, for each node $d_i\in D$, $d_i$ can be used to represent accessible nodes in S, i.e. $S(d_i)\subseteq S$. Thus the problem becomes to finding a conditional (condition (iv)) set cover in the bipartite graph $G^*[D, S]$, i.e. finding a sub-collection ${\mathcal {C}}\subseteq {\mathcal {F}}$ (here ${\mathcal {F}}=\{S(d_1),S(d_2),...,S(d_{|D|})\}$) such that $\bigcup _{d_i\in D} S(d_i)=S$.

This special version of Global-optimized Multi-path Finding Problem is equivalent to Minimum Weighted Set Cover Problem, which is proven to be NP-hard [17]. Therefore, GMF Problem is NP-hard in general. $\square$

3 Global-Optimized Evacuation Paths Algorithm

In this section, we propose the global-optimized algorithm for GMF Problem, which performs three distinct phases to compute evacuation paths from multiple sources to their most suitable destinations: (1.) Transform $G = (V, E, W)$ into a new 2D graph $G^* = (V^*, E^*, W^*)$ via extraction process; (2.) Find a forest ${\mathcal {P}}^*$ in $G^*$ with the root set of ${\mathcal {P}}$ is a subset of $D^*$ and the leaf set of ${\mathcal {P}}^*$ is $S^*$ such that the whole path length between a root and a leaf can be minimized and the leaf numbers of roots can be balanced; (3.) Recover the evacuation network/forest ${\mathcal {P}}$ in G based on ${\mathcal {P}}^*$.

3.1 Auxiliary Graph $G^*$ Induction

In the first phase, we construct a 2D logical graph $G^*$ for the election process of shortest paths from the original graph G, whose details are as follows.

• (i) The vertex set $V^*$: For each $v_i\in V$, $v_i=(ID_i, x_i,y_i, z_i)$, a corresponding node is generated in $V^*$, i.e. $V^*=\{v_i=(ID_i)|\forall v_i\in V, 1\le i\le n\}$. Note that the new node in $V^*$ need not change any properties of the original node $v_i$, thus we continue to adopt $v_i$ denote the new node. The same procedure may be easily adapted to obtain $D^*$ and $S^*$.

• (ii) The edge set and edge-weight set $E^*$ and $W^*$: For each $e_k\in E$, $e_k=(ID_i, ID_j)$, a corresponding edge is generated in $E^{temp}$ and the edge-weight is remained, i.e. $E^{temp}=\{e_k=(ID_i, ID_j)|\forall e_k\in E, 1\le k\le |E|\}$ and $W^{temp}=\{weight(e_k)|\forall e_k\in E^{temp}, 1\le k\le |E^{temp}|\}$.

  Based on the temporary graph $G^{temp}=(V^*, E^{temp}, W^{temp})$ and $D^*$, $S^*$, we operation an extraction process to obtain the set of candidate shortest paths P and $E^*, W^*$. For each pair $(d_i,s_j)$, where $\forall d_i\in D^*$ and $\forall s_j\in S^*$, we find a candidate shortest path, which will be joined into P and all the edges on it (and their corresponding weights) constitute $E^*$ (and $W^*$). The finding process is stated as follows:

  • a. Locate $d_i,s_j$’s layer numbers: $d_i\in G^{temp}_{l_i}$ and $s_j\in G^{temp}_{l_j}$. Here according to the properties of the laneway structure, the assumption that $d_i$’s location is not lower than the position of $s_j$ (i.e. $l_i\le l_j$) can be established.

  • b. If $l_i = l_j$: Dijkstra Algorithm can be executed on $(G^{temp}_{l_i}, d_i, s_j)$ to obtain $SP(d_i,s_j)$.

  • c. If $l_i < l_j$: Firstly determine the turning points in $E^{temp}_{l_j-1, l_j}$ for $s_j$ in its own layer$G^{temp}_{l_j}$; Secondly calculate the shortest paths between $s_j$ to these turning points and choose the shortest one as the segment of $SP(d_i,s_j)$; Thirdly record the destination of the shortest segment as $t_j$, and utilize the similar way to find the second segment of $SP(d_i,s_j)$ in $G^{temp}_{l_j-1}$. Repeat the process until the last segment with the destination $d_i$ is found in the layer $G^{temp}_{l_i}$.

3.2 MWSC-based Strategy to Construct Global Optimized Multi-path in $G^*$

This phase is based on MWSC algorithm and computing global optimized multi-path in $G^*$ between the nodes in $D^*$ and the nodes in $S^*$, as shown in Algorithm 1. In the phase, we firstly sort all the paths of P in the non-decreasing order of their lengths to obtain an ordered path set $P_O= \{path_1, path_2, \cdots , path_q\}$ as shown in step 2 in Algorithm 1. According to the ordered path lengths in $P_O$, we construct a global optimal forest/multi-path to minimize the longest shortest path in the solved forest, which is a binary search process as shown by steps 3–13. The binary search is starting from $Mid = \lfloor \frac{1+q}{2}\rfloor$, and in each iteration, we temporarily remove all the paths $path \in P$ whose length satisfies $length(path_{Mid}) \le length(path)$, and check if the subgraph of $G^*$ induced by P without those edges can still construct a MWSC which is verified by function Greedy-Forest$(G^*[P], D^*, S^*)$ (steps 15–27 in Algorithm 1). If a MWSC can be constructed, we update P and obtain a MWSC Forest on the subgraph of $G^*$ induced by the updated P, and proceed with the decreased Mid. Otherwise, we keep those edges in P and proceed with the increased Mid.

To balance the leaf numbers among all the roots of the solved forest, the criteria of greedy selection of Greedy-Forest$(G^*[P], D^*, S^*)$ is the difference between the leaf number of each root and the average leaf number of all the roots avrNL. Note that in $G^*$, each node $d_i$ in $D^*$ can be regarded as a subset of $S^*$, which is composed of its reachable nodes in $S^*$.

3.3 Paths Reduction for G from the Multi-path in $G^*$

Based on the forest ${\mathcal {P}}^*$ in $G^*$ with the root set $D^*$ and the leaf set $S^*$, we transfer ${\mathcal {P}}^*$ into an equivalent forest ${\mathcal {P}}$ from D to S in original graph G in this phase. In the logical graph, the association information for vertex set V has been restored and the coordinate information for V has been masked, which has not changed any association properties of the original node. Thus the phase is to restore the masked information of forest ${\mathcal {P}}^*$ for the original graph G as follows.

• (i) The vertex set of forest ${\mathcal {P}}$, $V[{\mathcal {P}}]$: For each $v_i=(ID_i)\in V[{\mathcal {P}}^*]$, $V[{\mathcal {P}}]\leftarrow V[{\mathcal {P}}]\bigcup \{v_i=(ID_i, x_i,y_i, z_i)\}$. The same restoring procedure is adapted to obtain D and S as well.

• (ii) The edge set of ${\mathcal {P}}$, $E[{\mathcal {P}}]$: For each $e_k\in E[{\mathcal {P}}^*]$, $E[{\mathcal {P}}]\leftarrow E[{\mathcal {P}}]\bigcup \{e_k\}$.

4 Simulation and Discussion

4.1 Simulation Plan

In this simulation, we will investigate the influence of the following two important parameters on our algorithm: the number of source nodes, m and the number of impassable nodes, o. In particular, we will consider two group of setting for each performance factor: (i) o is fixed as 25 and m varies from 10 to 40 by the step of 5; (ii) m is fixed as 25 and o varies from 10 to 40 by the step of 5. For each parameter setting, we run 50 instances and compute their average for evaluation.

Since the problem is NP-hard, it is unlikely for us to compare an output of the algorithms with an optimal solution. Instead, we employ the theoretical bound of the problem for comparison, which is the performance factor generated by the shortest path(SP) algorithm for each source nodes. And we study the average characteristic behavior of the proposed algorithm and evaluate their average performance in terms of the utilization factor, the average length factor and the global length factor.

• (i) The utilization factor reflects the utilizing balance of each destination, which can be calculated as dividing the sum of the difference between the number of the escaping persons of each escape exit and the average escaping number of all the escape exits by the number of effective destinations, i.e. $\frac{\sum _{d_i\in D^*} |numofleaf(d_i)-avrNL|}{|D^*|}$. For a path-finding algorithm, the lower the utilization factor, the better the performance of the path-finding algorithm.

• (ii) The average length factor stands for the whole shortest property of the planned escaping paths, which is valued as the result of dividing the total sum of all the differences between each planned path and the shortest path with the same source and destination by the number of escaping paths, i.e. $\frac{\sum _{\forall d_i\in D, \forall s_j\in S} (length(d_i, s_j)-SP(d_i, s_j))}{\sum _{\forall d_i\in D, \forall s_j\in S} SP(d_i, s_j)}$, where p is the number of obtained paths by our algorithm, $length(d_i, s_j)$ is the path length between $d_i$ and $s_j$ and $SP(d_i, s_j)$ is the length of shortest path between them.

• (iii) The global length factor stands for the global shortest property of the planned escaping paths, which is valued as the result of the difference between the length of the longest path generated by our algorithm and the length of the longest one among the shortest paths, i.e. $\frac{|\max _{\forall d_i\in D, \forall s_j\in S} length(d_i,s_j) -\max _{\forall d_i\in D, \forall s_j\in S} SP(d_i, s_j)|}{\max _{\forall d_i\in D, \forall s_j\in S} SP(d_i, s_j)}$. For the SP algorithm, the average and global length factors are both 0 which is the lower bound of all the path-finding algorithms.

4.2 Performance of Proposed Algorithms for GMF Problem

Firstly, we focus on the impact of the number of source nodes, m and the number of impassable nodes, o on the the utilization factor in Fig. 2. Overall in the two figures, the utilization factors of our algorithm with the variation of m and o are both obviously lower than those of the SP algorithm. In Fig. 2(a), we can observe that with the increasing of m, the factor of our algorithm stays below that of the SP algorithm and its fluctuation is within the stable and tolerable range, i.e. [0, 0.7]. Furthermore, we also find that the number of personnel has no appreciable impact on the utilization factor of our algorithm, while the poorer performance on the utilization factor of the SP algorithm is more apparent with the growth of the personnel number. Next, we study how the utilization factor is affected by the number of impassable nodes o. As shown in Fig. 2(b), we can learn that the factor of our algorithm has no obvious change as o grows, while the factor of the SP algorithm presents obvious ups and downs with the growth of o. The reason is that the variation of the number of impassable nodes has direct influence on the topological structure of the laneway model, and the utilization factor gained from our algorithm can be guaranteed into a reasonable range for what topological structure the laneway model has.

Fig. 2.

Performance on the utilization factor

Fig. 3.

Performance on the average length factor

Secondly, we investigate the impact of the number of source nodes, m and the number of impassable nodes, o on the the average length factor. From Fig. 3(a) and (b), we can observe that the number of source nodes m has more influence on this factor of our solutions than the number of impassable nodes o. Reasons are as follow: Firstly, the increasing number of obstacles or collapse may lead to the impassability of initial feasible segments. Thus it may raises that the passable segments become longer to some extent, and then it causes the average length of the generated paths becomes larger as well. Secondly, due to the consideration of the balanced utilization of each destination, the path assignment scheme changes with the change of the topological structure of the laneway model. It is worth noting that with the rise of the number of personnel, the gap between the average length of the escaping networks generated by our algorithm and that by SP algorithm tends to be gradually narrowing.

Fig. 4.

Performance on the global length factor

Thirdly, comparing with the variation trend of the average length factor, the trend of the global length factor becomes more apparent as m and o increases. Seen from Fig. 4(a), the difference between the global escaping time-consumption obtained from our solution and that from SP scheme is getting smaller with the rising of the personnel number. And when m is larger than 30, the difference is getting 0 which indicates our strategy can enhance the utilization efficiency of the escaping exits with the minimization guarantee of the global escaping time-consumption. On the contrary, as shown Fig. 4(b), the difference between the global escaping time-consumption obtained from our solution and that from SP scheme is getting larger with the change of the topological structure of the laneway model, and the difference can be controlled in a steady STATE when $o\ge 30$. This reason is similar with that of the influence of o on the average length factor.

To conclude, our algorithm outperforms the SP algorithm on the performance of the escaping exit utilization. Furthermore, the number of personnel has more influence on our algorithm than the number of impassable nodes on the length factor. Although there exists a gap on the global and average path length of the generated escaping network between our algorithm and the SP algorithm, with the rise of the number of personnel, the gap is tending to be gradually narrowing. Therefore, our strategy can enhance the utilization efficiency of the escaping exits and guarantee a tolerable range of the global escaping time-consumption.

5 Conclusions

In this paper, we have proposed a new problem the Global-optimized Multi-path Finding (GMF) Problem in Mine Water-inrush Evacuation, which has two optimization objects, maximizing exit utilization and minimizing the global escaping delay. Based on the classical problem, Minimum Weighted Set Cover (MWSC) Problem, we proposed a 3-phase heuristic algorithm for GMF problem. Based on our simulation results, our algorithm outperforms the shortest path algorithm on one of the most important performance factors, the utilization efficiency of the escaping exits. And our solution can guarantee that the deviation of the global escaping delay from the shortest delay is in a reasonable range.

Future Works. Despite our through studies conducted in this paper, we believe there are lots of room for further investigation. In this paper, we consider one of the multi-objective optimization problems on mine emergency application and we can further take other multi-objective evacuation plan problems, i.e. maximizing the utilization of the prioritized exits’ utilization and minimizing the whole escaping delay. In addition, we plan to investigate intelligent evacuation multi-path plan problems in more application scenarios.