Priority-Oriented Route Network Planning for Evacuation in Constrained Space Scenarios

Abstract

Evacuation planning in three-dimensional (3D) constrained space scenarios is an important kind of emergency management problems. In this paper, we investigate a path planning problem in constrained space evacuation for 3D scenarios, named the Priority-based Route Network Constructing Problem, which has two objectives of maximizing the evacuation exits’ utilization efficiency and minimizing the whole evacuation delay. We propose a 3-phase heuristic to construct a route network based on the Minimum Weighted Set Cover. In the experimental evaluation, we compare the proposed algorithm with the existing algorithms and implement our algorithm in underground mine evacuation, which is a typical kind of constrained space scenarios. Both types of results indicate our strategy can enhance the utilization efficiency of the escaping exits and guarantee a tolerable range of the global escaping time-consumption with a low running time.

1 Introduction

In the wake of the rapid development of science and technology, the demand of energy, chemicals and commodities keeps growing which inevitably raises various hazards and risk, even natural or man-caused disasters. As the most pivotal point of avoiding the potential or great harm of various disasters, evacuation path planning [1, 2] has drawn much attention due to its huge potential applications, e.g., evacuation in open space scenarios and constrained ones. Constrained space work involves in a great range of industries such as urban/factory underground pipeline, tunnel and coal mine. Constrained space is a particular kind of scenario with complex structure and potential risk, i.e., the properties of such spaces include the limitations on entry and exit and the trapping vulnerability in multi obstacles environment. Thus this kind of application scenarios has higher accident occurrence rate and raises more challenges to evacuation and rescue work. To this end, we focus on evacuation path planning in constrained space scenarios in the paper.

Most evacuation planning focused on two-dimensional (2D) scenarios and designed 2D planning algorithms, which cannot provide intuition vision for the geographic space and even adversely effect the planning result. In the practical applications, the evacuation scenarios are 3D spaces and the 2D plane models cannot be directly applied to 3D scenarios due to the missing the geometric properties of the space structure and the influences from the environment and disasters. For example, for an edge in the route network, its endpoints’s heights fail to reflect in a 2D model; in a 3D model, if the endpoints of the edge are at different heights, the edges with same endpoints and reverse directions are definitely different in emergency evacuation for their different passing difficulties. Thus employing a 3D geological model for constrained space will improve the quality of emergency response.

In most of practical applications, the feasible escape exits have different evacuation priorities, e.g., in underground coal mine evacuation, the auxiliary and main shafts have higher priority than chambers or mobile capsules. To avoid congestion in evacuation process, the utilization and efficiency among the exits should be balanced, i.e., the case should be avoided that most evacuees choose a certain exit to evacuate, which results in the exit’s overhigh utilization and even the whole evacuation delay. For the priority-oriented evacuation planning, it must be considered to balance each exit’s utilization and enhance the whole evacuation efficiency. Furthermore, most of the existing evacuation planning algorithms in 2D cannot search paths to enhance the efficiency and minimize the duration of evacuation simultaneously, i.e., they cannot be applied to priority-oriented evacuation planning.

With the above considerations, we consider the scenarios with a set of personnel and a set of feasible escaping exits (multi-source to multi-destination). And we propose a new evacuation route planning problem based on a 3D geological space model, the priority-oriented route network constructing (PRNC) problem, i.e., the problem of finding multi-path connecting each personnel position and its most suitable exit for the goals of maximizing the priority-based evacuation efficiency and minimizing the whole evacuation delay. Based on an important and classical NP-complete problem, Minimum Weighted Set Cover, we propose a priority-oriented strategy to construct the evacuation route network, whose performance will be evaluated by the simulations and instance experiments.

The rest of the paper is organized as follows. Section 2 summarizes the related works. Section 3 proposes the 3D constrained space model, problem definitions and its hardness proof. Section 4 introduces the framework of the 3-phase solution for PRNC problem and describes the related algorithms. Simulation results and corresponding discussions are given in Sect. 5. Section 6 concludes this paper.

2 Related Works

In practical, the timeliness and safety of the planned escape routes are the critical objectives of the evacuation planning, and most existing research work focused on the principle and modeled the problem as the shortest path problem from one source to one destination or from one source to many destinations, the first k shortest paths problem or hybrid path finding problem.

The existing research concentrated on the escape path planning problem can be classified into two kinds: one is one-source-to-one-destination model (finding the escape route from one evacuator to one exit) and the other one is one-source-to-multi-destination (constructing multi-path from one evacuator to several exits). Both kinds have been effectively solved based on the classical algorithms for solving the shortest path problem, the Dijkstra algorithm [3, 4], the Floyd-Warshall algorithm [5], the first k shortest paths [6,7,8], and dynamic programming [9]. For one-source-to-one-destination, in [6, 7], the authors studied the first k shortest paths problem whose goal is to find another $k-1$ suboptimal paths such that there is an alternative when the shortest one is impassable because of the water spread or congested on account of traffic load.

Furthermore, many efforts are made to investigate on one-source-to-multi-destination based on modified or hybrid classical algorithms in operational research. Based on the k shortest paths problem, the authors introduced a new variant of the classical problem in a time-schedule network with constraints on arcs, and they solved the problem based on the modified Dijkstra algorithm to find shortest paths in [8]. Based on the dynamic programming problem, the authors considered a path network with vulnerable links and they proposed a framework based on known link disruption probabilities and knowledge of transition probabilities for recovering in [9]. Based on the network flow problem, [10] summerized a systematic collection of network flow models applied to emergency evacuation and their applications, e.g., max flows and min cost flows, lexicographic flows, quickest flows, and earliest arrival flows; [11] proposed greedy algorithms for building evacuation problems which were modeled as the maximum flow, minimum cost flow, and minimax flow problems; [12] proposed a corridor-based emergency evacuation system based on contraflow design.

Furthermore, another part of researchers focused on the evacuation model studies in evacuation and disaster management [13,14,15]. Vogiatzis et al. [13] studied a large-scale optimization problem and proposed a clustering technique via divide-and-conquer method; [14] and [15] considered the evacuation betweenness centrality and evacuation centrality and proposed algorithms to make the evacuation routes sufficiently safe. In application scenarios, indoor scenarios [16] implemented the agent-based indoor evacuation simulations based on volunteered geographic information from OpenStreetMap for multiple users scenarios. Tang and Ren [17] and Adjiski et al. [18] concerned about the fire evacuation. Tang and Ren [17] modeled pre-evacuation activities as rule-based behavior based on geographic information system and adopted the rule-based behavior modeling to the indoor fire evacuation; the authors in [18] developed a model for the planning system for evacuation and rescue in underground mines fire, which is utilized for training, research and practical purposes.

Most researches focused on the 2D planning algorithms design, which cannot provide intuition vision for the geographic space, and the 2D planning strategies cannot be directly applied to 3D scenarios due to the omitting of some important properties. And the feasible escape exits have different evacuation priorities in practical, which may be ignored in the existing literatures. Thus we will research on a new evacuation routes problem based on a 3D geological space model and design the solutions.

3 3D Constrained Space Model and Problem Definitions

In this section, we firstly present the formulation of the 3D constrained space model. Secondly we introduce the calculation of the equivalent length based on the traffic capacity and the passing complexity. Then we formally define the problem we consider and give its NP-hardness proofs as well as the problem decomposition.

3.1 3D Constrained Space Model

The emergency evacuation scenario we consider is a densely populated constrained space (e.g., underground mine, cabin), which can be modeled as a 3D connected graph $G:=(V, E)$, where V is the set of n predetermined observation vertices in the space, E is the set of directional edges. For each $v_i\in V$, $v_i:=(ID_i, x_i, y_i, z_i)$ where $ID_i$ is $v_i$’s identifier, $x_i, y_i, z_i$ are its 3D coordinate. And for each $e_k\in E$, $e_k:=<v_i, v_j>$ ($1\le i < j\le n$). Note that any pair of directional edges $<v_i, v_j>$ and $<v_j, v_i>$ are definitely different in G for the reason that their geometric characteristic and vector elements are different.

There are three kinds of important vertex set in G: a. The source set $S\subseteq V$ is composed of the personnel initial positions, i.e., the collection of evacuee sources; b. The destination set $D\subseteq V$ consists of the feasible exits or temporary shelters, which have their escaping priorities $priority(d_j)$ ($\forall d_j\in D$). We denote the priority set as priority(D) and the escaping priority of an exit/a shelter is assumed as an integer; c. The obstacle set O includes the hollow parts in space and other obstructive. And note that the edges adjoint to obstacles are regarded as an impassable ones.

In practical applications, a constrained space is generally constructed in system structure, i.e., there are several relatively independent connected components, which are relevant to each other via transferring links, e.g., the corridors in a building, or the aisles between upper and lower coal beds. Such a connected component of the original space is deployed in certain range of height which is decided by the application requirement. Thus a 3D space model G can be regarded as an equivalent multilayer 3D model via the following transformation.

Phase 1::

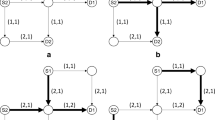
Divide the vertex set V of G into several subset $V_1,V_2,\ldots ,V_L$, where L is the layer number of the space. Note that L is decided by the structure of the specific space and assumed to be predetermined on the basis of the height or z-axis value of the vertex, as shown in Fig. 1. The division of vertex set can be realized in a polynomial time.

Phase 2::

Decompose G into several vertex-induced subgraph $G_1,G_2,\ldots ,G_L$ based on the division of V, i.e., $G_l:=G[V_l]$ is the subgraph of G induced by $V_l$, where $1\le l\le L$.

Phase 3::

Denote the transferring links between each pair of adjacent subgraphs as $E_{l,l+1}$, i.e., the edges in E which connect a pair of upper and lower adjacent subgraphs $G_l$ and $G_{l+1}$, where $1\le l\le L-1$. Finally G could be transformed into a multilayer 3D graph which is composed of the subgraphs $G_1,G_2,\ldots ,G_L$ jointed by the transferring links $E_{l,l+1}$($\subseteq E$), where $1\le l\le L-1$. And we define the endpoints in all $E_{l,l+1}$ sets ($1\le l\le L-1$) as transferring vertices which can be considered as stair corners in a building. Thus a given 3D model G can be reformulated into $G:=\{<G_1,G_2,E_{12}>,<G_2,G_3,E_{23}>,\cdots ,<G_{L-1},G_L,E_{L-1,L}>\}$.

Fig. 1

Hierarchical model transformation instance: the exit vertices form $V_1$, the vertices with z-axis value in the range of (− 10 m, − 20 m) belong to $V_2$, and those in the range of (− 20 m, − 30 m) belong to $V_3$

3.2 Equivalent Length of the Edge

In the evacuation process, the edges in the space are the main carrier of the evacuees and the edges’ traffic capacities are affected by several influence factors, which need to be considered in the decision of the most reliable evacuation paths. We list the main influence factors in Table 1, and based on these influence factors, the traffic capacity on edge $e_k$ can be expressed in terms of the equivalent length/the edge weight: $weight(e_k):= length(e_k)\cdot \beta _1(e_k)\cdot \beta _2(e_k)\cdot \alpha (e_k), 1\le k\le |E|$. Thus the original space model can be transformed into a 3D edge-weighted graph $G:= (V, E, W)$, in which each $G_l$ can be further denoted as $G_l:= (V_l, E_l, W_l)$, where $1\le l\le L$.

Table 1 Influence factors of the traffic capacity

3.3 Problem Definitions and Hardness Results

We consider the global evacuation planning problem in a constrained space, which is to construct a evacuation path network from all the personnel to the proper exits or shelters in G. The problem is investigated from two perspectives: 1. For each evacuee, we aim at deciding its globally ideal escape exit based on evacuation priority and the escaping paths. The goal is measured as the whole evacuation delay, which is defined as the path length of the latest evacuee; 2. For each escape exit, we intend to enhance the utilization rate of each exit, i.e., assign relatively balanced count of evacuees to the exit such that the congestion in some an overdrawn exit can be avoided. It is measured as the priority-oriented evacuation efficiency, which can be valued as the reciprocal of the maximum distance between the priority efficiency of any pair of exits. The problem is defined as follows.

Definition 3.1

Priority-oriented Route Network Constructing (PRNC) Problem

Input: :

Given a 3D constrained space model, graph $G:= (V, E, W)$, source set S and destination set D with its priority set priority(D).

Find: :

Find the path network from S to D with the goals of maximizing the priority-oriented evacuation efficiency and minimizing the longest escaping path length.

Before the analysis of the hardness of our problem, we review an important and classical NP-hard problem, Set Cover Problem. The mathematical formulation of it is as follows:

Definition 3.2

Set Cover (SC) Problem

Given a set $\mathcal {X}$ composed of n elements, and a collection $\mathcal {F}$ of m subsets of $\mathcal {X}$ ($\mathcal {F}:=\{X_1,X_2,\ldots ,X_m\}$), the problem is to find a sub-collection $\mathcal {C}\subseteq \mathcal {F}$ such that $\bigcup _{X_i\in \mathcal {C}} X_i:= \mathcal {X}$ and $|\mathcal {C}|$ is minimized.

If each subset is assigned a cost/weight in the problem, it becomes Minimum Weighted Set Cover Problem which is NP-hard as well.

Definition 3.3

Minimum Weighted Set Cover (MWSC) Problem

Given a set $\mathcal {X}$ composed of n elements, a collection $\mathcal {F}$ of m subsets of $\mathcal {X}$ ($\mathcal {F}:=\{X_1,X_2,\ldots ,X_m\}$), and each $X_i\subseteq \mathcal {X}$ ($1\le i\le m$) has a weight $w(X_i)$, the problem is to find the minimum weighted sub-collection $\mathcal {C}\subseteq \mathcal {F}$ such that $\bigcup _{X_i\in \mathcal {C}} X_i:= \mathcal {X}$ and $\sum _{X_i\in \mathcal {C}} w(X_i)$ is minimized.

To solve MWSC Problem, we introduce a classical approximation algorithm with the ratio of $\ln (n+1)$. The main idea of the greedy algorithm for MWSC problem is: Select a subset $\mathcal {T}\in \mathcal {F}$ that minimizes $\frac{w(\mathcal {T})}{|\mathcal {T}\bigcap \mathcal {U}|}$ in each loop, where $\mathcal {U}$ stands for the uncovered elements in $\mathcal {X}$; repeat the greedy selection until the set of $\mathcal {T}$s cover $\mathcal {X}$. Based on the two classical problems, the hardness proof of our problem is given as follows.

Theorem 3.1

PRNC Problem in constrained space evacuation is NP-hard.

Proof

In order to prove the hardness of PRNC Problem, we rewrite our problem into a mathematical formulation: Given a 3D connected and edge-weighted graph $G:= (V, E, W)$, two subsets S and D of V, and D’s priority set of priority(D), PRNC Problem is to find a forest $\mathcal {P}$ such that

• (i) the root set of $\mathcal {P}$ is a subset of D: $Root(\mathcal {P})\subseteq D$,

• (ii) the leaf set of $\mathcal {P}$ is S: $Leaf(\mathcal {P}):=S$,

• (iii) the maximum value among the differences between any pair of roots’ weights, $\max _{d_p,d_q\in D} |\frac{priority(d_p)}{numofleaf(d_p)}-\frac{priority(d_q)}{numofleaf(d_q)}|$, can be minimized, where $numofleaf(d_p)$ stands for the number of leaves on the tree rooted at $d_p$,

• (iv) the longest path length among any pair of a root and a leaf, $\max _{\forall d_i\in D, \forall s_j\in S} length(d_i,s_j)$, can be minimized.

We consider a special case of it: (1) In condition (iii) all the $priority(d_i)$s are assigned as 1, i.e., $\forall d_i\in D$, $priority(d_i):= 1$; (2) In condition (iv) the lengths of the paths between all root-leaf pairs are equivalent, i.e., $\forall d_i\in D, \forall s_j\in S$, $length(d_i,s_j):= UL$.

Based on the mathematical formulation of our problem, condition (iv) is a default satisfying one, i.e., the path lengths between all pair of roots and leaves are equal. Via transforming these isometric paths into one-hop edges, for each node $d_i\in D$, $d_i$ can be used to represent accessible nodes in S, i.e., $S(d_i)\subseteq S$. When each $d_i$ is assigned the weight of $\frac{\frac{|S|}{|D|}}{|S(d_i)-\frac{|S|}{|D|}|}$, the problem becomes to a set cover problem, i.e., finding a sub-collection $\mathcal {C}\subseteq \mathcal {F}$ (here $\mathcal {F}:=\{S(d_1),S(d_2),\ldots ,S(d_{|D|})\}$) such that $\bigcup _{d_i\in D} S(d_i):=S$ and the total weight of $d_i$ in $\mathcal {C}$ is maximized.

Since this special version of PRNC Problem is equivalent to MWSC Problem, which is proven to be NP-hard [19], PRNC Problem is NP-hard in general. $\square$

4 Priority-Oriented Route Network Constructing Algorithm

In this section, we propose a heuristic algorithm for PRNC problem, which performs the following three phases to compute evacuation paths from multiple sources to their most suitable destinations. Firstly, we transform the 3D connected and edge-weighted graph $G:= (V, E, W)$ into a 2D logical graph $G^*:= (V^*, E^*, W^*)$, which includes the candidate shortest paths. Secondly, based on $G^*$, we find a forest $\mathcal {P}^*$ with the root set $Root(\mathcal {P}^*)\subseteq D^*$ and the leaf set $Leaf(\mathcal {P}^*):=S^*$, with the goals of shortening the longest path among the root-and-leaf pairs and balancing the ratios between the leaf number and the priority value among all roots. Thirdly, $\mathcal {P}^*$ is recovered into the evacuation network $\mathcal {P}$ in G.

4.1 Phase 1: Auxiliary Graph $G^*$ Induction

The original space model G has the information of the vertices’ positions and spatial relationships, which are useful for the route planning. To efficiently construct a forest rooted from D, we can extract the effective information based on an equivalent transformation, which is a preliminary election process of the candidate shortest paths. And G can be transformed into a 2D logical graph $G^*$ which only contains the effective information in the following.

• (i) The vertex set$V^*$: For each $v_i:=(ID_i, x_i,y_i, z_i)\in V$, there is a corresponding node $v_i:=(ID_i)$ in $V^*$, i.e., $V^*:=\{v_i:=(ID_i)|\forall v_i\in V, 1\le i\le n\}$. Note that the new node in $V^*$ omits the position information, which does not change any properties of the original node $v_i$; thus, we continue to adopt $v_i$ to denote the new node. $D^*$ and $S^*$ can be obtained in the same way.

• (ii) The temporary edge set and edge-weight set  $E^{temp}$ and $W^{temp}$: For each $e_k:=(v_i, v_j)\in E$, $e_k$, there is an edge $e_k$ in $E^{temp}$, which remains the incidence relations in E, and the edge-weights are assigned in two cases:

  a. $D^*$-incident edge set: we gather the edges whose endpoint belongs to $D^*$ into $E^{temp}_D$, and $W^{temp}\leftleftarrows W^{temp}\bigcup \{\frac{weight(e_k)}{priority(d_p)}|\forall e_k\in E^{temp}_D$, and $endpoint(e_k)\bigcap D^*\ne \emptyset \}$;

  b. $D^*$-independent edge set: $W^{temp}\leftleftarrows W^{temp}\bigcup \{weight(e_k)|\forall e_k\in E^{temp}\setminus E^{temp}_D\}$.

• (iii) The edge set and edge-weight set $E^*$ and $W^*$: Based on the temporary graph $G^{temp}=(V^*, E^{temp},$$W^{temp})$ and $D^*$, $S^*$, we operate an extraction process to obtain the set of candidate shortest paths P and $E^*, W^*$, as shown in Algorithm 1. The process constructs the shortest segments in relevant layers based on transferring vertices, i.e., each shortest path between a root-and-leaf pair $(d_i,s_j)$ is constructed by the segments from $s_j$’s layer $G^{temp}_{l_j}$ to $d_i$’s layer $G^{temp}_{l_i}$. Finally for each pair $(d_i,s_j)$, we find a candidate shortest path, which will be joined into P and $E^*$ is composed of all the edges in P.

4.2 Phase 2: MWSC-Based Strategy to Construct Priority-Oriented Route Network in $G^*$

This phase is a MWSC-based strategy to compute global optimized multi-path in $G^*$ between $S^*$ and $D^*$, as shown in Algorithm 2. The strategy is based on a binary search manner: The sequenced collection is the non-decreasing order of the path lengths, which belong to all the paths of P, i.e., $P_O:= \{path_1, path_2, \cdots , path_q\}$ as shown in Step 2 in Algorithm 2. And the minimum, maximum and middle cursors are chosen from the range $\{1,2,\ldots ,q\}$. In each iteration of the binary search, for each $path_i \in P_O$, starting from $Mid :=\lfloor \frac{1+q}{2}\rfloor$, we temporarily remove all the paths $path \in P$ whose length satisfies $length(path) > length(path_{Mid})$, denoted as $P\setminus P_{temp}$ in Step 3.2 in Algorithm 2. And in Step 3.3, we check if the subgraph of $G^*$ induced by $P\setminus P_{temp}$ can still construct a feasible forest which is verified by Function: Greedy-Forest$(G^*[P], D^*, S^*)$ elaborated later. If Greedy-Forest$(G^*[P], D^*, S^*)$ succeeds, we obtain the forest on the subgraph of $G^*$ induced by $P\setminus P_{temp}$, and proceed with the decreased Mid. Otherwise, we restore $P_{temp}$ and proceed with the increased Mid in Step 3.4 in Algorithm 2.

The binary search aims at minimizing the longest shortest path in the forest, and Function: Greedy-Forest $(G^*[P], D^*, S^*)$ in each iteration is designed to construct a balanced forest. Thus we apply the greedy algorithm based on the Minimum Weighted SetCover(MWSC) problem as stated in the latter part of Algorithm 2. The main idea of the function is to balance the leaf numbers among all the roots in the final forest and the criteria of greedy selection is the difference between the leaf number of each root and the average leaf number of all the roots avrNL.

4.3 Phase 3: Paths Reduction for G from the Multi-path in $G^*$

Based on the forest $\mathcal {P}^*$ in $G^*$ with the root set $D^*$ and the leaf set $S^*$ obtained in Phase 2, we explain how to transfer $\mathcal {P}^*$ into an equivalent forest $\mathcal {P}$ from D to S in G, which is the final output of our strategy. In the logical graph, the association information for vertex set V has been restored and the coordinate information for V has been masked, which has not changed any association properties of the original node. Thus the phase is to restore the masked information of forest $\mathcal {P}^*$ for the original graph G as follows.

• (i) The vertex set of forest $\mathcal {P}$, $V[\mathcal {P}]$: For each $v_i:=(ID_i)\in V[\mathcal {P}^*]$, $V[\mathcal {P}]\leftleftarrows V[\mathcal {P}]\bigcup \{v_i=(ID_i, x_i,y_i, z_i)\}$. The same restoring procedure is adopted to obtain D and S as well.

• (ii) The edge set of $\mathcal {P}$, $E[\mathcal {P}]$: For each $e_k\in E[\mathcal {P}^*]$, $E[\mathcal {P}]\leftleftarrows E[\mathcal {P}]\bigcup \{e_k\}$.

Finally, based on the auxiliary graph transformation, forest construction and the original graph restoring, we obtain the route network $\mathcal {P}$ as the output of the 3-phase strategy.

5 Simulation Results and Discussion

In this section, we firstly present a series of simulation experiments and analyze their results. Secondly, the same type of experiments will be performed on an instance of the 3D laneway model for a coal mine area in Zhangjiakou, Hebei Province of China, which is a representative kind of constrained space applications.

5.1 Simulation Experiments and Analysis

The parameters and their variation modes are described as follows: (i) $n:=|V|$: the number of observation nodes which are randomly deployed for a constrained space. Note that the edge set E is also randomly generated based on the deployment of observation nodes, which satisfies the condition of graph connectivity; (ii) $s:=|S|$: the number of source nodes; (iii) $d:=|D|$: the number of destination nodes; (iv)$o:=|O|$: the number of obstacle nodes; (v) Influence factor: For the parameters of traffic capacity, we decide edge type $\beta _1(e_k)$ based on the slope of edge; Passibility $\beta _2(e_k)$ is assumed to be uniform in walking mode, i.e., $\beta _2:=1$; Transiting length ($length(e_k)$) is calculated as the Euclidean distance; (vi) $\alpha (e_k)$: the priorities of destinations are randomly valued in the range of [1, |D|], whose relevant edge has the priority of $\frac{1}{priority(d_i)}$. We will investigate the influence of all the relevant parameters on our algorithm according to the following four groups of setting:

• (a) n varies from 200 to 500 by the step of 50 and $s:=30$, $d:=6$, $o:=20$;

• (b) s varies from 10 to 40 by the step of 5 and $n:=300$, $d:=6$, $o:=20$;

• (c) d varies from 2 to 12 by the step of 2 and $n:=300$, $s:=30$, $o:=20$;

• (d) o varies from 10 to 40 by the step of 5 and $n:=300$, $s:=30$, $d:=6$.

Based on the above parameters and their variation modes, we study the characteristic behavior of the proposed algorithm and evaluate their average performance in terms of three aspects:

• (i) The priority factor is the evaluating indicator of each destination’s evacuation priority utilization, which can be calculated as the maximal difference between any pair’s priority utilization, $\max |\frac{priority(d_p)}{numofleaf(d_p)}-\frac{priority(d_q)}{numofleaf(d_q)}|$ ($\forall d_p, d_q\in D$), where the priority utilization of a destination is the result of dividing the leave number of the destination by its priority.

• (ii) The average length factor stands for the whole shortest property of the planned escaping paths, which is defined as the difference ratio of all the planned paths and all the shortest paths,

  $\frac{\sum (length(d_i, s_j)-SP(d_i, s_j))}{\sum SP(d_i, s_j)}$ ($\forall d_i\in D, \forall s_j\in S$), where $length(d_i, s_j)$ and $SP(d_i, s_j)$ are the path length and the shortest path length between $d_i$ and $s_j$.

• (iii) The global length factor is utilized to evaluate the minimization of the whole evacuation delay for the planned route network, which is valued as the difference ratio of the length of the longest path generated by our algorithm and that among the shortest paths, i.e., $\frac{|\max length(d_i,s_j) -\max SP(d_i, s_j)|}{\max SP(d_i, s_j)}$ ($\forall d_i\in D, \forall s_j\in S$).

• (iv) The running time is adopted to measure the time complexity of the algorithms.

For each parameter setting, we run 50 instances and compute their average for evaluation. Since all of the problem is NP-hard, it is unlikely for us to compare an output of the algorithms with an optimal solution. Instead, we employ the theoretical bound of the problem for comparison, which is the performance factor generated by the shortest path algorithm (SP Algorithm) for each source node. Since the classical algorithm solves the problems in 2D plane scenarios, we apply it on the transformed 2D logical graph $G^*$ and compare the performance with ours. Note that for SP Algorithm, the planned paths are the shortest paths between each pair of source and destination. Thus the average length factor is  0 which can be regarded as the lower bound of all the path-finding algorithms, as well as the global length factor. We discuss about the average behavioral characteristics of our proposed strategy (denoted as PRNC Algorithm) as well as compare the performance with the bound value for SP Algorithm.

Fig. 2

Performance on the priority factor. a The priority factor versus n. b The priority factor versus s. c The priority factor versus d. d The priority factor versus o

(i) We first observe the impact of n, s, d and o on the the priority factor. Overall in the first two subfigures, the priority factors of our algorithm with the variation of n and s are both obviously lower than those of SP Algorithm. In Fig. 2a, we can observe that with the increasing of n, the factor’s fluctuation in SP Algorithm is more obvious than that in PRNC Algorithm and they are both with the peak value at $n:=350$. When $n>500$, the difference between priority factors of the two algorithms is gradually lessened and tends to be 0. It is because with the increasing of the vertex density in the deployment, the connectivity of the candidate route network can be improved. In a network with high connectivity, the number of the feasible paths becomes larger, which makes more shortest paths be chosen in the priority-oriented route network. As shown in Fig. 2b, we also find that the number of personnel s raises the fluctuation in the two algorithms with the peak values at $s:=30$ in SP Algorithm and $s:=35$ in PRNC Algorithm. When s is larger than 35, the variation trends for the two algorithms become similar and our algorithm maintains the advantage. From Fig. 2c, we can learn that the factor of SP Algorithm presents obvious leap when $d<6$ and continues fluctuation when $d>6$, while the priority factor gained from our algorithm can be guaranteed into a reasonable range [1, 2]. Finally, we can find that the number of obstacles o has no appreciable impact on the priority factor of our algorithm in Fig. 2d, while the poorer performance on the priority factor of SP Algorithm is still apparent with the growth of o.

As shown by the performance under the four parameters’s variation, we can draw the conclusions: a. our algorithm outperforms SP Algorithm in terms of priority factor when the scale of a constrained space is moderate; b. when the scale of evacuating personnel becomes larger, the evacuation priority advantage of our algorithm maintains signification; c. the count of feasible exits has unconspicuous influence on priority factor performance to our algorithm, which shows the remarkable difference between performances of the two algorithms; d. the changes of topology structure of the constrained space have insignificant influence on the priority performance of our algorithm.

Fig. 3

Performance on the average length factor. a The average length factor versus n. b The average length factor versus s. c The average length factor versus d. d The average length factor versus o

(ii) Secondly, we investigate the impact of n, s, d and o on the the average length factor. Based on Fig. 3a, the average length factor of our algorithm is in slow growth along with the raise of n. It is because with the enlarging of the scale of constrained space, the global lengths of paths between each pair of source and destination will be increased. From Fig. 3b, c, we can observe that the number of source nodes s has more influence on this factor of our solutions than the number of destination nodes d. With the increasing of s, the factor of PRNC Algorithm presents parabolic shape in the range [10, 35] and the gap between the two algorithms tends to be gradually narrowing when $s>35$. And with the growth of d, the factor of PRNC Algorithm shows a milder parabolic in a reasonable range [0, 0.35]. According to Fig. 3d, the factor of our algorithm significantly rises when increasing the number of obstacles. Reasons are as follow: Firstly, the increasing number of obstacles may raises that the passable segments become longer to some extent, i.e., circuitous segments, and then, it causes the average length of the generated paths becomes larger as well. Secondly, due to the consideration of the evacuation priority of each destination, the path assignment scheme changes with the change of the topological structure of the space model.

Fig. 4

Performance on the global length factor. a The global length factor versus n. b The global length factor versus s. c The global length factor versus d. d The global length factor versus o

(iii) Thirdly, comparing with the variation trend of the average length factor, the trend of the global length factor becomes more relaxative as the parameters increase. Seen from Fig. 4a, c, the difference between the global escaping time-consumption obtained from our solution and that from SP scheme is getting smaller with the enlarging of space scale or the rising of the personnel number. And when n is larger than 450, the difference is approaching to 0 which indicates our strategy can enhance the priority utilization efficiency of the escaping exits with the complication of the space structure. On the contrary, as shown Fig. 4b, d, the difference between the two algorithms is getting larger with the growth of s and o, which is also caused by circuitous segments. And the difference can be controlled in a steady state when $s\ge 35$.

Fig. 5

Performance on the running time. a The running time versus n. b The running time versus s. c The running time versus d. d The running time versus o

(iv) Finally, to measure the time complexity of the algorithms, we investigate the running time results of the two algorithm, which is measured in seconds. Seen from the figure group in Fig. 5, we can find that the two algorithm have unconspicuous difference, i.e., the running time PRNC Algorithm is equal to or a litter more than that of SP Algorithm in the range from 0 second to 0.3 second, and they have similar variation tendency in terms of the running time. Among the four subfigures, the numbers of sources and obstacles do not have apparent effects on the running times, i.e., with the change of s or o, the running times of two algorithms have little fluctuations as shown in Fig. 5b, d; the numbers of observation nodes and destinations have obvious influence on the running time, especially d, i.e., with the increasing of n and d, two algorithms both have growing running times as shown in Fig. 5a, c.

Fig. 6

The visualization results of PRNC Algorithm and SP Algorithm. a PRNC-exit1. b SP-exit1. c PRNC-exit2. d SP-exit2. e PRNC-exit3. f SP-exit3. g PRNC-exit4. h SP-exit4. i PRNC-exit5. j SP-exit5

5.2 Application Instance Experiments and Analysis

In order to evaluate the performance of PRNC Algorithm, we further operate instance experiments on a representative kind of constrained space application scenarios, evacuation planning in underground coal mine water inrush. Here we adopt the 3D model data of a mine area in Zhangjiakou, Hebei Province of China from Kailuan Group Company. The model data is a preprocessing result of the original spatial data, i.e., the vertex set in the laneway model is composed of all the traverse points, and the edge set maintains consistent direction with the original laneway. Disaster spreading status ($\beta _3$) are obtain by the data of all the water level observation points in the worst case, i.e., the water level data at the most tolerant survival time. According to practical requirements, the priorities of five feasible exits, auxiliary shaft(exit1), main shaft(exit2), air shaft(exit3), mine chamber(exit4) and mobile capsule(exit5), are valued as follows: $priority(exit1):=5$, $priority(exit2):=2$, $priority(exit3):=1.5$, $priority(exit4):=priority(exit5):=1$. Note that in the experiment results, we denote the number of paths reaching to these exits as PN1, PN2, PN3, PN4, PN5, respectively. And the evaluation criterions, priority factor, average length factor and global length factor are represented by Factor1, Factor2, Factor3 in short.

Table 2 Instance experiments results

Based on the contrast of the results obtained by two algorithm on each escaping exit in Fig. 6, the observations from the visualization results in the parameter setting $n:=517$, $s:=30$, $d:=5$ and $o:=25$, reaffirm that our algorithm for PRNC problem outperforms SP Algorithm in terms of the escaping exits’ priority utilizations: our algorithm takes full advantage of the exits’s evacuation priority, i.e., the number of effectively used exits is 4 and the four exits obtain balanced utilization based on their evacuation priority. But there is 3 exits utilized by SP Algorithm which have 5, 12, 8 paths getting to, the utilization of these exits present serious imbalance, which leads to disadvantaged performance on priority factor. For the length factors, the average length of the route network in our algorithm increases 13.208% of that of SP Algorithm, which appears as two circuitous paths reaching to exit 1 as shown in Table 2. It is worth mentioning that the global length shows less gap, i.e., 2.4979%.

To conclude, our algorithm is far ahead of SP Algorithm on the performance of the escaping exit priority utilization. Furthermore, the parameter, the number of personnel, has more influence on our algorithm than the number of exits on the length factor. Although there exists a gap on the global and average path length of the generated escaping network between our algorithm and SP Algorithm, with the rise of the space scale or the personnel count, the gap is tending to be gradually narrowing. Furthermore, the running time of our algorithm is at a relatively low level and approaches that of SP Algorithm. Therefore, our strategy can enhance the priority utilization efficiency of the escaping exits and guarantee a tolerable range of the global escaping time-consumption.

6 Conclusions

In this paper, we concentrated on the evacuation planning in the constrained space and proposed a problem Priority-oriented Route Network Constructing (PRNC). The problem is a multi-objective optimization problem with the goals of maximizing the utilization efficiency and minimizing the escaping delay. We solved the problem in 3D scenarios and proposed a 3-phase heuristic algorithm based on the logical auxiliary graph transformation and the Minimum Weighted Set Cover (MWSC) Problem. The simulation results reveal that firstly our algorithm has advantages on enhancing the priority utilization efficiency of the escaping exits; secondly, our algorithm can decrease the global escaping delay gradually to the shortest delay in constrained spaces with large scales; thirdly, the running time of our algorithm is at a relatively low level and approaches theoretical lower bound. Despite our throughout studies conducted in this paper, we plan to investigate intelligent evacuation network planning problems in constrained space application scenarios and design dynamic strategies to organize route network in real time.