Some Lessons from Two Simple Approaches to Model the Impact of Harvest Timing on Seasonal Populations

Abstract

Using two different discrete-time models for seasonal populations, we review the potential effects of harvesting in regard to population abundance, stability, and extinction, and we emphasize how these effects strongly depend on harvest timing. We also stress the fact that census timing is crucial, and populations should be measured as many times as a discrete event occurs during the year cycle.

1 Introduction

An important challenge in harvesting and management theory is predicting population responses to the removal of individuals. In seasonal populations, for which population growth is controlled by a combination of density-dependent processes during different periods of the annual cycle, the timing of harvesting not only influences the impact of captures on population abundance, but also can alter stability properties and extinction risk.

Recently, we have addressed this problem for discrete-time population models, assuming proportional harvesting and using two different approaches. Both lead to one-dimensional discrete dynamical systems, which makes the mathematical analysis simpler than with other approaches. The first model was introduced by Seno in 2008 [12], and assumes that there is a specific season during which population accumulates energy for reproduction. Harvesting is assumed to be a discrete event that can occur at any moment within the season. The second model follows the ideas introduced by Jonzén and Lundberg in 1999 [6] (see also [10]), and assumes that there are a breeding and a nonbreeding season in the annual cycle, and harvesting is considered as a new event that can take place after or before the breeding season.

In this note, we review some potential effects of harvesting, emphasizing how these effects strongly depend on harvest timing. Of particular interest is the hydra effect, defined as a paradoxical increase in population size in response to an increasing mortality [1]. In a recent paper, McIntire–Juliano [9] found strong evidence that timing of mortality contributes to overcompensation and the hydra effect in mosquitoes.

We also stress the fact that census timing is crucial, and populations should be measured as many times as a discrete event occurs during the year cycle.

The paper is based on Refs. [3, 7], although it contains new insight concerning analogies and differences between the two mentioned models; the role of harvest timing in models with Allee effects; and how to choose harvest time based on different criteria, such as sustainability or maximizing the yield. Paper [3] has recently won the Bellman Prize, awarded every two years for the best paper published in the journal Mathematical Biosciences over the preceding two years [2].

2 Seno’s Model

For many species, births occur in well-defined breeding seasons in the annual cycle, and their life stories are usually described by discrete-time models. We consider a seasonal population subject to some form of harvesting (e.g., fishing, hunting, control). The simplest models assume only two processes in each generation: reproduction and harvesting. If harvesting is proportional to population stock, so that a percentage $\gamma x$ of the population size x is harvested every year, the between-year dynamics is defined by the simple model

$$\begin{aligned} x_{n+1}=(1-\gamma )f(x_n), \end{aligned}$$

(1)

$n=0,1,2,\ldots$, starting at an initial population size $x_0\ge 0$. Here, $x_n$ is the population size after n generations and f is the production function. For a review of some potential effects of harvesting in this simple model, we refer to [8] and references therein. One important remark is that even in this situation, census time is relevant for management decisions. Indeed, if population is censused after reproduction, the model reads

$$\begin{aligned} x_{n+1}=f((1-\gamma )x_n), \end{aligned}$$

(2)

$n=0,1,2,\ldots$. Although Eqs. (1) and (2) are topologically conjugated, and therefore they exhibit the same dynamics, in case of overcompensatory dynamics (usually represented by a unimodal map f), Eq. (2) can exhibit hydra effects.

A manager who only measures population after reproduction and before harvesting, may have the impression that increasing harvesting intensity can be beneficial for population abundance, while if census takes place after harvesting, the message can be the opposite; see [5] for more details.

Since we are interested in the influence of harvest timing, we need to consider a more sophisticated model. Seno [12] suggested a model in which it is assumed that there is a prereproductive season of length T, and harvesting can take place at any moment $\tau =\theta T$, $0\le \theta \le 1$, during this season. The intraspecific density effect on reproduction is then divided in two parts: one depending on $x_n$, and the other on $(1-\gamma )x_n$. For a recruitment map f and proportional harvesting, Seno’s model writes

$$\begin{aligned} x_{n+1}=\theta (1-\gamma )f(x_n)+(1-\theta )f((1-\gamma )x_n). \end{aligned}$$

(3)

In mathematical terms, the right-hand side of (3) is a convex combination of the right-hand sides of models (1) and (2). Seno showed that, for stable overcompensatory populations, the earlier we harvest, the most the population size is increased. In [3], we extended the mathematical analysis to study how harvest time may determine the stability of the equilibrium, and to analyze models with Allee effect [4], where there is a higher risk of population extinction. In these models, overharvesting leads population to extinction when the equilibrium $x=0$ becomes globally asymptotically stable after a tangent bifurcation occurs. The main conclusions from Seno’s model are the following:

• (i) In models without Allee effects:

  • (1) the critical value of $\gamma$ leading to extinction does not depend on harvest time;

  • (2) later harvesting leads to a decrease in population size at the equilibrium, so early harvest is better for conservation purposes;

  • (3) in the presence of dynamical instabilities, intermediate harvest times can help to stabilize the positive equilibrium, sometimes preventing population extinction due to stochastic perturbations.

• (ii) In the presence of Allee effects, mid-season harvesting can induce extinction.

In Fig. 1, we represent these effects for the Ricker map $f(x)=x e^{2.5(1-x)}$ (without Allee effects), and for the Ricker–Schreiber map $f(x)=0.5 x^2 e^{4(1-x)}/(1+0.5 x)$, which exhibits a strong Allee effect [11].

Fig. 1

Bifurcation diagrams for Seno’s model (3) as harvesting rate $\gamma$ is increased, with different harvest times. a For a Ricker map, the critical value of $\gamma$ leading to extinction does not depend on $\theta$, but intermediate values of $\theta$ help to stabilization; b For a Ricker–Schreiber map with Allee effect, intermediate values of $\theta$ may increase the risk of extinction. In both cases, a hydra effect is observed for early harvesting. Dashed lines correspond to unstable equilibria

3 The Seasonal Model of Jonzén and Lundberg

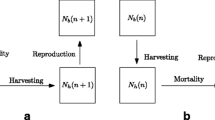
There are species subject to harvesting whose annual cycle is divided into a breeding season (typically, summer) and a nonbreeding season (typically, winter), and a harvesting season is only allowed either in spring or in autumn; see, e.g., [7]. For these populations, the main lesson that we could learn from Seno’s model is that autumn harvest is preferable to increase average population abundance. Perhaps, the main drawback of Seno’s model is that it predices similar qualitative behavior for very early and very late harvest within the season, because the cases $\theta =0$ and $\theta =1$ are equivalent in Eq. (3). Hence, in regard to stability and bifurcations, it would not show any difference between autumn and spring harvest; see Fig. 2.

Fig. 2

Representation of the different seasons in the Jonzén–Lundberg model, where reproduction (R) occurs in summer, mortality during winter, and the harvest season is either autumn or spring. In Seno’s model (3), autumn harvest would correspond to early harvest within the specific season (small $\theta$), and spring harvest would correspond to late harvest within the specific season ($\theta$ close to 1)

The discrete-time Jonzén–Lundberg model [6, 7] consists of a composition of three discrete events during the annual cycle: density-dependent breeding, that we represent by a Ricker map $R(x)=x e^{r(1-x)}$, $r>0$; density-dependent mortality represented by $M(x)=x e^{-a x}$, $a>0$; and proportional harvesting, given by $H(x)=(1-\gamma )x$, $\gamma \in (0,1)$. In this way, spring harvest is represented by equation

$$\begin{aligned} x_{n+1}=R(H(M(x_n))), \end{aligned}$$

(4)

$n=0,1,2,\ldots$, while autumn harvest is governed by

$$\begin{aligned} x_{n+1}=R(M(H(x_n))), \end{aligned}$$

(5)

$n=0,1,2,\ldots$.

In both models, population is sampled after reproduction, but the relative order of the three discrete events is different, which can dramatically affect the size and dynamics of populations [10]. Regarding permanence, it is easy to prove that the critical value of $\gamma$ leading to extinction does not depend on harvest time, and it is the same value predicted by Seno’s model.

Proposition 1

(Extinction) Assume that $R(x)=x e^{r(1-x)}$, $M(x)=x e^{-a x}$, $H(x)=(1-\gamma )x$, with $r>0$, $a>0$, $0<\gamma <1$. Then Eqs. (4) and (5) have at least one positive equilibrium if and only if $\gamma <\gamma ^*:=1-e^{-r}$. If $\gamma \ge \gamma ^*$, then all solutions converge to zero.

Regarding stability, Jonzén–Lundberg [6] argued that increasing harvesting is stabilizing, and the stability effect is stronger for autumn harvest. However, a further analysis shows that this effect depends strongly on the mortality rate a. Roughly speaking, the effect is stronger for autumn harvest only if a is large enough. Notice that mortality rates also influence which harvest season is better for population size, and again (5) is better for higher mortalities [7]; see Fig. 3a, b.

Fig. 3

Bifurcation diagrams for the Jonzén–Lundberg model as harvesting rate $\gamma$ is increased, with blue color for spring harvest and black color for autumn harvest. Dashed lines correspond to unstable equilibria. a $R(x)=x e^{3(1-x)}$, $M(x)=x e^{-0.2 x}$; b $R(x)=x e^{3(1-x)}$, $M(x)=x e^{-2 x}$; c $R(x)=2x^2 e^{3(1-x)}/(1+2x)$, $M(x)=x e^{-2 x}$

As far as we know, the Jonzén–Lundberg model has not been studied when the recruitment function R exhibits Allee effects. As in Seno’s model, there is a critical value $\gamma ^*$ of the harvesting rate parameter for which a saddle–node bifurcation occurs. This value is different for spring harvest and autumn harvest. Numerical simulations suggest that autumn harvest can be beneficial to prevent sudden collapses; see Fig. 3c. This issue deserves further study.

An important feature of the seasonal models (4) and (5) that it is not present in Seno’s model is that, for large growth rates r (a necessary condition is $r>4$), the reproduction function R(x) can have 3 critical points and 3 positive equilibria. This property opens the possibility for the coexistence of two nonzero attractors, and increasing harvesting can either promote or prevent bistability. Moreover, other phenomena such as non-smooth hydra effects, hysteresis and stability switches are possible; see [7] for more details.

4 The Importance of Census Time

Another difference between Seno’s model and the approach of Jonzén–Lundberg is that in the latter census can take place in three different moments, namely, after every discrete event occurs in the annual cycle. As we have mentioned, even in simple models with only two discrete events, census time is important for management decisions. Although this aspect has been emphasized in previous work (e.g., [5, 7, 10]), we give an illustrative example and propose two criteria to choose between spring and autumn harvest.

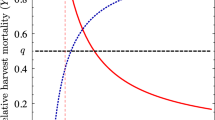
In Fig. 4, we plot the positive equilibrium of models (4) and (5), with $R(x)=xe^{3(1-x)}$, $M(x)=xe^{-0.3x}$, $H(x)=(1-\gamma )x$. We denote by $N_b$, $N_{nb}$, and $N_h$ the population sizes at the end of the breeding, the nonbreeding, and the harvesting seasons, respectively. A manager looking at panel (b) (census after winter mortality) would say that spring harvest is preferable for conservation purposes, but panel (c) sends the opposite message.

Fig. 4

Population size at equilibrium as harvesting intensity is increased, with blue color for spring harvest and black color for autumn harvest. a Census after reproduction; b Census after natural mortality; c Census after harvesting

We suggest two criteria for choosing between autumn harvest and spring harvest. Having in mind the diagrams in Fig. 5, we arrive at the following conclusions:

• (i) looking at census with lower population densities: if the target is sustainability, it seems autumn harvest is preferable;

• (ii) looking at the yield: if the target is maximizing yield, again autumn harvest seems to be better.

Fig. 5

Comparison between spring harvest (blue color) and autumn harvest (black color). a Low population densities are attained censusing after harvesting in the first case, and after natural mortality in the second one; b The yield is obtained as the difference between the number of individuals just after the harvesting season and just before it

5 Discussion

Theoretical and experimental results indicate that the size of seasonal populations depends strongly on harvest time. Using two different approaches based on discrete-time population models, we aimed to contribute to the understanding of the influence of harvest time and census time in the management of exploited populations. In summary, we list the following main conclusions:

• (i) Extinction: for globally persistent models, harvest timing does not change the critical harvest intensity leading to extinction. In models with Allee effects, a suitable harvest timing could prevent population collapses.

• (ii) Stability: harvest timing has a strong influence on the stability properties of the population. However, choosing a suitable harvest season depends on other population parameters (birth rate, mortality rate).

• (iii) Hydra effects: population can increase in response to an increasing mortality. Harvesting seasonal populations can lead to new forms of this paradoxical effect.

• (iv) Census time: seasonal models emphasize the importance of sampling the population after every discrete event occurs during one cycle.