Heuristic Homogenization of Euler and Pantographic Beams

Abstract

In the present contribution, we address the following problem: is it possible to find a microstructure producing, at the macro-level and under loads of the same order of magnitude, a beam which can be both extensible and flexible? Using an asymptotic expansion and rescaling suitably the involved stiffnesses, we prove that a pantographic microstructure does induce, at the macro-level, the aforementioned desired mechanical behavior. Thus, in an analogous fashion to that of variational asymptotic methods, and following a mathematical approach resembling that used by Piola, we have employed asymptotic expansions of kinematic descriptors directly into the postulated energy functional and a heuristic homogenization procedure is presented and applied to the cases of Euler and pantographic beams.

Introduction

While in the standard finite deformation Euler beam theory the energy functional depends only on the material curvature, i.e., the normalized projection of the second gradient of the placement on the normal vector to the current configuration, the energy functional for the nearly inextensible pantographic beam model depends also on the projection of the second gradient of the placement on the tangent vector to the current configuration. Thus, the full decomposition of the second gradient of the placement is present in the latter model. In order to analyze this fact, a heuristic homogenization procedure is presented and applied to the cases of Euler (in section “Euler Beams”) and pantographic (in section “Pantographic Beams”) beams.

Pantographic structures belong to the class of metamaterials that have to be treated as non-standard (or generalized) continua. Generalized continua (Alibert et al. 2003; Carcaterra et al. 2015; Abali et al. 2017; Pietraszkiewicz and Eremeyev 2009; Altenbach and Eremeyev 2009), and in particular higher gradient theories, see dell’Isola et al. (2016b) or dell Isola et al. (2015) for a comprehensive review, are able to describe behaviors which cannot be accounted for in classical Cauchy theories (dell’Isola et al. 2015b, 2016a, e; Reiher et al. 2016; Boutin et al. 2017; Seppecher et al. 2011; Cuomo et al. 2016; Placidi et al. 2016c). In the literature, several examples can be found motivating the importance of generalized continua: electromechanical (Enakoutsa et al. 2015) and biomechanical (Placidi et al. 2016a; Giorgio et al. 2015; Andreaus et al. 2013, 2014) applications, elasticity theory (Andreaus et al. 2010; Giorgio et al. 2017; Turco et al. 2017; Placidi et al. 2015; dell’Isola et al. 2015a; Abali et al. 2015), capillary fluids analysis (Auffray et al. 2015), granular micromechanics (Yang and Misra 2012; Misra and Poorsolhjouy 2015; Misra and Singh 2015), robotic systems analysis (Della Corte et al. 2016; Del Vescovo and Giorgio 2014), damage theory (Rinaldi and Placidi 2014; Placidi 2015; Madeo et al. 2014c; Misra 2002; Misra and Singh 2013; Yang and Misra 2010), and wave propagation analysis (Madeo et al. 2014a; Bersani et al. 2016; Placidi et al. 2008; Madeo et al. 2014b, 2016). Furthermore, second gradient continuum models always appear when the considered micro-system is a pantographic structure (Giorgio 2016; dell’Isola et al. 2016c, d; Scerrato et al. 2016; Giorgio et al. 2016; Rahali et al. 2015; Alibert and Della Corte 2015; Eremeyev et al. 2017). A comprehensive review of the modeling of pantographic structures can be found in Placidi et al. (2016b), Barchiesi and Placidi (2017). Several results of numerical investigations can be found in Turco et al. (2016a, b, c, d), Spagnuolo et al. (2017), Andreaus et al. (2010), Battista et al. (2015, 2016), Greco et al. (2016), and Turco and Rizzi (2016), while for an outline of recent experimental results we refer to dell’Isola et al. (2015c) and Ganzosch et al. (2016).

Euler Beams

Introduction

Customarily, the theory of nonlinear beams is either postulated by means of a suitable least action principle in the so-called “direct way” or is deduced, by means of a more or less rigorous procedure, starting from a three-dimensional elasticity theory. The first example of direct model can be found in the original paper by Euler (Euler and Carathéodory 1952). Many epigones of Euler used this approach: a comprehensive account for this procedure can be found in Antman Antman (1995). On the other hand, by following the procedure described by De Saint-Venant, one can try to identify the constitutive equation of a Euler type (1D) model in terms of the geometrical and mechanical properties, at microlevel, of the considered mechanical systems. This is done, in more modern textbooks, using a more or less standard asymptotic micro–macro identification procedure, which generalizes the one used by De Saint-Venant for bodies with cylindrical shape (see, for instance, Placidi et al. 2017). It can be rigorously proven, under a series of well-precised assumptions, that only flexible and inextensible beams can be obtained (Murat and Sili 1999; Mora and Müller 2004; Jamal and Sanchez-Palencia 1996; Pideri and Seppecher 2006; Allaire 1992; Bensoussan et al. 1978).

Long fibers are often modeled as Euler beams. Here, we will define a Euler beam from a continuum point of view for the extensible and for the inextensible cases. A discrete model for the same beam will be also introduced and a heuristic homogenization procedure, see, e.g., dell’Isola et al. (2016d), applied. A rescaling law will be derived for the extensible and for the inextensible cases.

Continuous Euler Beams

Kinematics

At each point S of $\mathcal {C}_{0}$, see Fig. 3.1, is associated a copy of the rigid section $\mathcal {R}$ through O such that $\mathcal {C}_{0}$ and $\mathcal {R}$ are orthogonal. $\mathcal {B}_{0}$ is the reference configuration of a beam. $\mathcal {B}$ is the present configuration, which is defined as

Fig. 3.1

Reference configuration $\mathcal {B}_{0}$. $q_{0}\left( S\right)$ is the position of the origin O of the section $\mathcal {R}$

• (i) A vector function $\chi \left( S\right)$ that gives the present position of $q_{0}\left( S\right)$.

• (ii) An orthogonal tensor field $R\left( S\right)$ that gives the rotation of $\mathcal {R}$ from the reference to the present configuration.

The kinematics is therefore defined by the following fields (Fig. 3.2):

$$\begin{aligned} \chi \left( S\right) ,R\left( S\right) . \end{aligned}$$

(3.1)

The admissible motion is, e.g., for a cantilever, those kinematic fields such that

$$ \chi \left( 0\right) =0,\qquad R\left( 0\right) =0. $$

Fig. 3.2

Definition of the fundamental kinematical fields, where the rotation $\varphi$ defines the rotation matrix R, in the two-dimensional case via Eq. (3.7)

Action

Physical intuition and definition of the action functional

$$ \mathcal {A}=\left[ \int _{0}^{L}W\left( \chi ,R,\chi ',R'\right) -W^{ext}\left( \chi ,R\right) \right] -\left. W_{S}^{ext}\right| _{S=0,S=L}, $$

where W is the strain energy that is assumed to depend upon the fundamental kinematical fields and their derivative. $W^{ext}$ is the energy of the distributed forces and $W_{S}^{ext}$ that of the concentrated ones.

Objectivity and Representation of the Invariants

Let us assume that the fundamental kinematical fields in one frame of reference are represented in (3.1). In another frame of reference they are as

$$\begin{aligned} \widetilde{\chi }=U+Q\chi ,\qquad \widetilde{R}=QR, \end{aligned}$$

(3.2)

where U and Q are the translation and the rotation of the second frame of reference with respect to the first one. The derivative of (3.2) yields

$$\begin{aligned} \widetilde{\chi }'=Q\chi ',\qquad \widetilde{R}'=QR'. \end{aligned}$$

(3.3)

Let us define the following two fields in the first frame of reference

$$\begin{aligned} E=R^{T}R'\end{aligned}$$

(3.4)

$$\begin{aligned} e=R^{T}\chi '-q_{0}'\left( S\right) . \end{aligned}$$

(3.5)

In the second frame of reference, they are from (3.2) to (3.5)

$$\begin{aligned} \tilde{E}=\widetilde{R}^{T}\tilde{R}'=R^{T}Q^{T}QR'=R^{T}R'=E\\ \tilde{e}=\widetilde{R}^{T}\tilde{\chi }'-q_{0}'\left( S\right) =R^{T}Q^{T}Q\chi '-q_{0}'\left( S\right) =R^{T}\chi '-q_{0}'\left( S\right) =e, \end{aligned}$$

which means that they are invariant. In order to represent E and e, we assume a Cartesian frame of reference. The origin of such a frame of reference is $q_{0}\left( 0\right)$with basis

$$ D_{1}=q_{0}',\qquad D_{2}\qquad D_{3}. $$

If S is a curvilinear abscissa of straight frame of reference

$$ q_{0}=S\, D_{1} $$

that yields

$$ q_{0}'=D_{1}=\left( \begin{array}{c} 1\\ 0\\ 0 \end{array}\right) . $$

The 2D assumption is

$$ \chi \in span\left\{ D_{1},D_{2}\right\} . $$

We define the displacement vector field

$$ u=\chi -q_{0}, $$

and therefore its derivative

$$ u'=\chi '-D_{1}\quad \Rightarrow \quad u'=\left( \begin{array}{c} u_{1}'\\ u_{2}' \end{array}\right) =\left( \begin{array}{c} \chi _{1}'-1\\ \chi _{2}' \end{array}\right) , $$

so that the derivative of the placement is

$$ \chi '=\left( \begin{array}{c} \chi _{1}'\\ \chi _{2}' \end{array}\right) =\left( \begin{array}{c} 1+u_{1}'\\ u_{2}' \end{array}\right) $$

and its squared modulus,

$$ \left\| \chi '\right\| ^{2}=\left( 1+u_{1}'\right) ^{2}+u_{2}'^{2}. $$

A representation of R is given in terms of the rotation angle $\varphi$,

$$\begin{aligned} R=&\cos \varphi D_{1}\otimes D_{1}-\sin \varphi D_{1}\otimes D_{2}+\sin \varphi D_{2}\otimes D_{1}+\cos \varphi D_{2}\otimes D_{2}\end{aligned}$$

(3.6)

$$\begin{aligned}&=\left( \begin{array}{cc} \cos \varphi &{} -\sin \varphi \\ \sin \varphi &{} \cos \varphi \end{array}\right) . \end{aligned}$$

(3.7)

Thus, the two invariants are represented as follows:

$$\begin{aligned} E= & {} R^{T}R'= \left( \begin{array}{cc} \cos \varphi &{} \sin \varphi \\ -\sin \varphi &{} \cos \varphi \end{array}\right) \left( \begin{array}{cc} -\sin \varphi &{} -\cos \varphi \\ \cos \varphi &{} -\sin \varphi \end{array}\right) \varphi '\\&=\left( \begin{array}{cc} 0 &{} -\varphi '\\ \varphi ' &{} 0 \end{array}\right) =\left( \begin{array}{cc} 0 &{} -\kappa \\ {{\kappa }} &{} 0 \end{array}\right) \nonumber \\ e= & {} \left( \begin{array}{c} \varepsilon \\ \gamma \end{array}\right) =R^{T}\chi '-q_{0}'\left( S\right) = \end{aligned}$$

(3.8)

$$\begin{aligned}&=\left( \begin{array}{cc} \cos \varphi &{} \sin \varphi \\ -\sin \varphi &{} \cos \varphi \end{array}\right) \left( \begin{array}{c} 1+u_{1}'\\ u_{2}' \end{array}\right) -\left( \begin{array}{c} 1\\ 0 \end{array}\right) \nonumber \\&=\left( \begin{array}{c} \left( 1+u_{1}'\right) \cos \varphi +u_{2}'\sin \varphi -1\\ -\left( 1+u_{1}'\right) \sin \varphi +u_{2}'\cos \varphi \end{array}\right) ,\nonumber \end{aligned}$$

(3.9)

which means in terms of $\kappa$, $\varepsilon$, and $\gamma$. A representation of the internal energy W that is compatible with the indifference frame principle is given by the function g

$$ W\left( \chi ,R,\chi ',R'\right) =g\left( \kappa ,\varepsilon ,\gamma \right) . $$

Let us give a representation for $\kappa$ and$\varepsilon$ whether the beam is assumed to be shear un-deformable, i.e., with $\gamma =0$. Thus, from the second equation of (3.9) we have

$$\begin{aligned} \left( 1+u_{1}'\right) \sin \varphi =u_{2}'\cos \varphi ,\quad \Rightarrow \quad \tan \varphi =\frac{u_{2}'}{1+u_{1}'}, \end{aligned}$$

(3.10)

that means

$$\begin{aligned} \varphi =\arctan \frac{u_{2}'}{1+u_{1}'}=\arctan \frac{\chi _{2}'}{\chi _{1}'}. \end{aligned}$$

(3.11)

Besides from the first equation of (3.9), we have

$$\begin{aligned} \varepsilon =-1+\left( 1+u_{1}'\right) \cos \varphi +u_{2}'\sin \varphi \end{aligned}$$

(3.12)

Keeping in mind that

$$ \tan ^{2}\varphi =\frac{\sin ^{2}\varphi }{\cos ^{2}\varphi }=\frac{1-\cos ^{2}\varphi }{\cos ^{2}\varphi }=\frac{1}{\cos ^{2}\varphi }-1 $$

that yields

$$ 1+\tan ^{2}\varphi =\frac{1}{\cos ^{2}\varphi }, $$

we have from (3.10)

$$ \cos ^{2}\varphi =\frac{1}{1+\tan ^{2}\varphi }=\frac{1}{1+\left( \frac{u_{2}'}{1+u_{1}'}\right) ^{2}}=\frac{\left( 1+u_{1}'\right) ^{2}}{\left( 1+u_{1}'\right) ^{2}+u_{2}'^{2}}, $$

that yields

$$\begin{aligned} \cos \varphi =\frac{1+u_{1}'}{\sqrt{\left( 1+u_{1}'\right) ^{2}+u_{2}'^{2}}} \end{aligned}$$

(3.13)

and

$$\begin{aligned} \sin \varphi =\tan \varphi \cos \varphi =\frac{u_{2}'}{1+u_{1}'}\frac{1+u_{1}'}{\sqrt{\left( 1+u_{1}'\right) ^{2}+u_{2}'^{2}}}=\frac{u_{2}'}{\sqrt{\left( 1+u_{1}'\right) ^{2}+u_{2}'^{2}}}. \end{aligned}$$

(3.14)

Therefore, from (3.12), (3.13), and (3.14)

$$\begin{aligned} 1+\varepsilon =\left( 1+u_{1}'\right) \frac{1+u_{1}'}{\sqrt{\left( 1+u_{1}'\right) ^{2}+u_{2}'^{2}}}+u_{2}'\frac{u_{2}'}{\sqrt{\left( 1+u_{1}'\right) ^{2}+u_{2}'^{2}}}=\end{aligned}$$

(3.15)

$$\begin{aligned} =\frac{\left( 1+u_{1}'\right) ^{2}+u_{2}'^{2}}{\sqrt{\left( 1+u_{1}'\right) ^{2}+u_{2}'^{2}}}=\sqrt{\left( 1+u_{1}'\right) ^{2}+u_{2}'^{2}}=\left\| . \chi '\right\| \end{aligned}$$

(3.16)

Besides, the derivative of (3.11) is

$$\begin{aligned} \kappa =\varphi '=\frac{1}{1+\left( \frac{\chi _{2}'}{\chi _{1}'}\right) ^{2}}\frac{\chi _{2}''\chi _{1}'-\chi _{2}'\chi _{1}''}{\chi _{1}'^{2}}=\frac{\chi ''\cdot \left( *\chi '\right) }{\left\| \chi '\right\| ^{2}}, \end{aligned}$$

(3.17)

where the $90^{\circ }$ rotation matrix is defined as follows:

$$ *=\left( \begin{array}{cc} 0 &{} -1\\ 1 &{} 0 \end{array}\right) , $$

so that

$$\begin{aligned} \chi ''\cdot \left( *\chi '\right) =\left( \begin{array}{cc}\chi ''_{1}&\chi ''_{2}\end{array}\right) \left( \begin{array}{cc} 0 &{} -1\\ 1 &{} 0 \end{array}\right) \left( \begin{array}{c} \chi '_{1}\\ \chi '_{2} \end{array}\right) \end{aligned}$$

(3.18)

$$\begin{aligned} \quad =\left( \begin{array}{cc} \chi ''_{1}&\chi ''_{2}\end{array}\right) \left( \begin{array}{c} -\chi '_{2}\\ \chi '_{1} \end{array}\right) =-\chi _{2}'\chi _{1}''+\chi _{2}''\chi _{1}'. \end{aligned}$$

(3.19)

Let us call

$$\begin{aligned} \hat{e}=\frac{\chi '}{\left\| \chi '\right\| },\quad \tilde{c}=\frac{\chi ''}{\left\| \chi '\right\| }. \end{aligned}$$

(3.20)

Thus, the curvature (3.17) is

$$\begin{aligned} \kappa =\varphi '=\left( *\hat{e}\right) \cdot \tilde{c}. \end{aligned}$$

(3.21)

Macroscopic Strain Energy for the General Case

A quadratic form of the strain energy in terms of the two invariants $\kappa$, from (3.21), and $\varepsilon$, from (3.16), is

$$\begin{aligned} U_{macro}=\int _{0}^{l}\left[ \frac{1}{2}K_{b}\kappa {}^{2}+\frac{1}{2}k_{e}\varepsilon {}^{2}\right] dS\end{aligned}$$

(3.22)

$$\begin{aligned} =\int _{0}^{l}\left[ \frac{1}{2}K_{b}\left( \frac{\chi ''\cdot \left( *\chi '\right) }{\left\| \chi '\right\| ^{2}}\right) ^{2}+\frac{1}{2}K_{e}\left( \left\| \chi '\right\| -1\right) {}^{2}\right] dS. \end{aligned}$$

(3.23)

It is worth to be noted that the strain energy is of second gradient type only for the normal component $\left( *\hat{e}\right) \cdot \chi ''$. The tangential component $\hat{e}\cdot \chi ''$ do not have any contribution in the strain energy. In pantographic structures, we will see that also this tangential contribution is able to accumulate strain energy.

Macroscopic Strain Energy for the Inextensible Case

For inextensible beams, $\chi '$ is the unit vector $\hat{e}$,

$$\begin{aligned} \left\| \chi '\right\| ^{2}=1=\chi '\cdot \chi ' \end{aligned}$$

(3.24)

that means

$$ \chi ''\cdot \chi '+\chi '\cdot \chi ''=0\qquad \Longrightarrow \qquad \chi '\cdot \chi ''=0, $$

and

$$\begin{aligned} \left\| \chi ''\right\| ^{2}=\chi ''\cdot \chi ''=\chi ''\cdot \left[ \left( \left( *\chi '\right) \cdot \chi ''\right) *\chi '+\left( \left( \chi '\right) \cdot \chi ''\right) \chi '\right] =\nonumber \\ =\chi ''\cdot \left[ \left( \left( *\chi '\right) \cdot \chi ''\right) *\chi '\right] =\left[ \chi ''\cdot \left( *\chi '\right) \right] ^{2}. \end{aligned}$$

(3.25)

Thus, from (3.24) and (3.25), the strain energy (3.23) for the inextensible case is

$$\begin{aligned} U_{macro}=\int _{0}^{l}\left[ \frac{1}{2}K_{b}\left( \frac{\chi ''\cdot \left( *\chi '\right) }{\left\| \chi '\right\| ^{2}}\right) ^{2}\right] dS=\int _{0}^{l}\frac{1}{2}K_{b}\left\| \chi ''\right\| ^{2}dS. \end{aligned}$$

(3.26)

Discrete Henky-Type Beam

Microscopic models for the inextensible Euler beams in the reference configuration are plotted in Fig. 3.3 (bottom). The bars are rigid and of length $\varepsilon$

Fig. 3.3

Microscopic models for the inextensible Euler beams in (bottom) the reference configuration. Definition (top) of the angle $\theta _{i}$

Piola’s Ansatz

$$\begin{aligned} p_{i}=\chi \left( P_{i}\right) , \end{aligned}$$

(3.27)

Thus, the position of the other points is

$$\begin{aligned} p_{i+1}=\chi \left( P_{i+1}\right) =\chi \left( P_{i}\right) +\varepsilon \chi '\left( P_{i}\right) +\frac{1}{2}\varepsilon ^{2}\chi ''\left( P_{i}\right) .\end{aligned}$$

(3.28)

$$\begin{aligned} p_{i-1}=\chi \left( P_{i}\right) -\varepsilon \chi '\left( P_{i}\right) +\frac{1}{2}\varepsilon ^{2}\chi ''\left( P_{i}\right) , \end{aligned}$$

(3.29)

so that the cosine of the angle $\theta _{i}$ is defined, in the inextensible case (3.24), by

$$\begin{aligned} \cos \theta _{i}= & {} \frac{\left( p_{i+1}-p_{i}\right) \cdot \left( p_{i-1}-p_{i}\right) }{\left\| p_{i+1}-p_{i}\right\| \left\| p_{i-1}-p_{i}\right\| }\end{aligned}$$

(3.30)

$$\begin{aligned}= & {} \frac{\left[ \varepsilon \chi '\left( P_{i}\right) +\frac{1}{2}\varepsilon ^{2}\chi ''\left( P_{i}\right) \right] \cdot \left[ -\varepsilon \chi '\left( P_{i}\right) +\frac{1}{2}\varepsilon ^{2}\chi ''\left( P_{i}\right) \right] }{\varepsilon ^{2}},\end{aligned}$$

(3.31)

$$\begin{aligned}= & {} \frac{-\varepsilon ^{2}\left\| \chi '\right\| ^{2}+\frac{1}{2}\varepsilon ^{3}\chi '\cdot \chi ''-\frac{1}{2}\varepsilon ^{3}\chi '\cdot \chi ''+\frac{1}{4}\varepsilon ^{4}\chi ''\cdot \chi ''}{\varepsilon ^{2}}\end{aligned}$$

(3.32)

$$\begin{aligned}= & {} -1+\frac{1}{4}\varepsilon ^{2}\chi ''\cdot \chi ''. \end{aligned}$$

(3.33)

Discrete energy in the inextensible case is defined as

$$ U_{micro}=\sum _{i=1}^{N}k_{b}\left( 1+\cos \theta _{i}\right) =\sum _{i=1}^{N}\frac{1}{4}k_{b}\varepsilon ^{2}\left\| \chi ''\right\| ^{2}. $$

With the homogenization formula,

$$\begin{aligned} \sum _{i=1}^{N}\varepsilon \left( \cdot \right) \longrightarrow \int _{0}^{l}\left( \cdot \right) dS, \end{aligned}$$

(3.34)

we have

$$\begin{aligned} U_{micro}=\int _{0}^{l}\frac{1}{4}k_{b}\varepsilon \left\| \chi ''\right\| ^{2}dS. \end{aligned}$$

(3.35)

An identification of (3.26) and (3.35) implies

$$\begin{aligned} k_{b}\varepsilon =2K_{b}. \end{aligned}$$

(3.36)

Thus, in order to have a finite macro-energy, even in the limit $\varepsilon \rightarrow 0$, we need to impose the scaling law (3.36). This means that, if one wants a finite macro-energy, then the lower the size of the cell, the higher is the rigidity of the rotational spring. Besides, in the limit of $\varepsilon \rightarrow 0$, $k_{b}$ should be infinite, i.e., $k_{b}\rightarrow \infty$.

For extensible beams, the distance between internal hinges is not fixed to be equal to $\varepsilon$. The extensible bar at the right-hand side of $P_{i}$ has the following length:

$$\begin{aligned} \left\| p_{i+1}-p_{i}\right\| =\sqrt{\left[ \varepsilon \chi '\left( P_{i}\right) +\frac{1}{2}\varepsilon ^{2}\chi ''\left( P_{i}\right) \right] \cdot \left[ \varepsilon \chi '\left( P_{i}\right) +\frac{1}{2}\varepsilon ^{2}\chi ''\left( P_{i}\right) \right] }\end{aligned}$$

(3.37)

$$\begin{aligned} =\sqrt{\varepsilon ^{2}\left\| \chi '\right\| ^{2}+\frac{1}{2}\varepsilon ^{3}\chi '\cdot \chi ''+\frac{1}{2}\varepsilon ^{3}\chi '\cdot \chi ''+\frac{1}{4}\varepsilon ^{4}\chi ''\cdot \chi ''}\end{aligned}$$

(3.38)

$$\begin{aligned} =\varepsilon \sqrt{\left\| \chi '\right\| ^{2}+\varepsilon \chi '\cdot \chi ''+\frac{1}{4}\varepsilon ^{2}\chi ''\cdot \chi ''}=\varepsilon \left\| \chi '\right\| +\varepsilon ^{2}\frac{\chi '\cdot \chi ''}{2\left\| \chi '\right\| }. \end{aligned}$$

(3.39)

The extensible bar on the left-hand side of $P_{i}$ has the following length:

$$\begin{aligned} \left\| p_{i-1}-p_{i}\right\| =\sqrt{\left[ -\varepsilon \chi '\left( P_{i}\right) +\frac{1}{2}\varepsilon ^{2}\chi ''\left( P_{i}\right) \right] \cdot \left[ -\varepsilon \chi '\left( P_{i}\right) +\frac{1}{2}\varepsilon ^{2}\chi ''\left( P_{i}\right) \right] }\\ =\sqrt{\varepsilon ^{2}\left\| \chi '\right\| ^{2}-\frac{1}{2}\varepsilon ^{3}\chi '\cdot \chi ''-\frac{1}{2}\varepsilon ^{3}\chi '\cdot \chi ''+\frac{1}{4}\varepsilon ^{4}\chi ''\cdot \chi ''}\\ =\varepsilon \sqrt{\left\| \chi '\right\| ^{2}-\varepsilon \chi '\cdot \chi ''+\frac{1}{4}\varepsilon ^{2}\chi ''\cdot \chi ''}=\varepsilon \left\| \chi '\right\| -\varepsilon ^{2}\frac{\chi '\cdot \chi ''}{2\left\| \chi '\right\| }. \end{aligned}$$

The representation of the cosine of the angle $\theta _{i}$ in the extensible case, from (3.31) to (3.33), is

$$\begin{aligned} \cos \theta _{i}= & {} \frac{\left( p_{i+1}-p_{i}\right) \cdot \left( p_{i-1}-p_{i}\right) }{\left\| p_{i+1}-p_{i}\right\| \left\| p_{i-1}-p_{i}\right\| }\end{aligned}$$

(3.40)

$$\begin{aligned}= & {} \frac{\left[ \varepsilon \chi '\left( P_{i}\right) +\frac{1}{2}\varepsilon ^{2}\chi ''\left( P_{i}\right) \right] \cdot \left[ -\varepsilon \chi '\left( P_{i}\right) +\frac{1}{2}\varepsilon ^{2}\chi ''\left( P_{i}\right) \right] }{\left( \varepsilon \left\| \chi '\right\| +\varepsilon ^{2}\frac{\chi '\cdot \chi ''}{2\left\| \chi '\right\| }\right) \left( \varepsilon \left\| \chi '\right\| -\varepsilon ^{2}\frac{\chi '\cdot \chi ''}{2\left\| \chi '\right\| }\right) }\end{aligned}$$

(3.41)

$$\begin{aligned}= & {} \frac{-\varepsilon ^{2}\left\| \chi '\right\| ^{2}+\frac{1}{4}\varepsilon ^{4}\chi ''\cdot \chi ''}{\varepsilon ^{2}\left\| \chi '\right\| ^{2}-\frac{1}{4}\varepsilon ^{4}\left( \frac{\chi '\cdot \chi ''}{\left\| \chi '\right\| }\right) ^{2}}=\frac{-\left\| \chi '\right\| ^{2}+\frac{1}{4}\varepsilon ^{2}\chi ''\cdot \chi ''}{\left\| \chi '\right\| ^{2}-\frac{1}{4}\varepsilon ^{2}\left( \frac{\chi '\cdot \chi ''}{\left\| \chi '\right\| }\right) ^{2}}. \end{aligned}$$

(3.42)

The Taylor series expansion of the function $f\left( x\right)$ around $x=0$

$$\begin{aligned} f\left( x\right) =\frac{-a+bx}{a-cx}=-1+f'\left( 0\right) x,\end{aligned}$$

(3.43)

$$\begin{aligned} f'\left( x\right) =\frac{b\left( a-cx\right) -\left( -a+bx\right) \left( -c\right) }{\left( a-cx\right) ^{2}},\end{aligned}$$

(3.44)

$$\begin{aligned} f'\left( 0\right) =\frac{ba-ac}{a^{2}}=\frac{b-c}{a} \end{aligned}$$

(3.45)

that imply

$$\begin{aligned} \cos \theta _{i}=-1+\frac{\chi ''\cdot \chi ''-\left( \frac{\chi '\cdot \chi ''}{\left\| \chi '\right\| }\right) ^{2}}{4\left\| \chi '\right\| ^{2}}\varepsilon ^{2}. \end{aligned}$$

(3.46)

Discrete energy for the extensible case is therefore

$$ U_{micro}=\sum _{i=1}^{N}\frac{k_{e}}{2}\left( \left\| p_{i+1}-p_{i}\right\| -\varepsilon \right) ^{2}+k_{b}\left( 1+\cos \theta _{i}\right) , $$

that, because of (3.39) and (3.46)

$$\begin{aligned} U_{micro}=\sum _{i=1}^{N}\frac{k_{e}}{2}\left( \left\| p_{i+1}-p_{i}\right\| -\varepsilon \right) ^{2}+k_{b}\left( 1+\cos \theta _{i}\right) \end{aligned}$$

(3.47)

$$\begin{aligned} =\sum _{i=1}^{N}\frac{k_{e}}{2}\varepsilon ^{2}\left( \left\| \chi '\right\| -1\right) ^{2}+k_{b}\frac{\chi ''\cdot \chi ''-\left( \frac{\chi '\cdot \chi ''}{\left\| \chi '\right\| }\right) ^{2}}{4\left\| \chi '\right\| ^{2}}\varepsilon ^{2}. \end{aligned}$$

(3.48)

The last addend, because of the definitions (3.20), is rearranged as

$$\begin{aligned} \frac{\chi ''\cdot \chi ''-\left( \frac{\chi '\cdot \chi ''}{\left\| \chi '\right\| }\right) ^{2}}{\left\| \chi '\right\| ^{2}}=\tilde{c}\cdot \tilde{c}-\left( \tilde{c}\cdot \hat{e}\right) ^{2}\end{aligned}$$

(3.49)

$$\begin{aligned} =\tilde{c}\cdot \left( \tilde{c}-\hat{e}\left( \tilde{c}\cdot \hat{e}\right) \right) =\tilde{c}\cdot \tilde{c}_{\bot }=\tilde{c}_{\bot }\cdot \tilde{c}_{\bot }=\left[ \tilde{c}\cdot \left( *\hat{e}\right) \right] ^{2}, \end{aligned}$$

(3.50)

which imply another form of the discrete strain energy

$$\begin{aligned} U_{micro}=\sum _{i=1}^{N}\frac{k_{e}}{2}\varepsilon ^{2}\left( \left\| \chi '\right\| -1\right) ^{2}+\frac{1}{4}k_{b}\left[ \frac{\chi ''\cdot \left( *\chi '\right) }{\left\| \chi '\right\| ^{2}}\right] ^{2}\varepsilon ^{2}. \end{aligned}$$

(3.51)

With the homogenization formula (3.34), the equation (3.51) yields

$$ U_{micro}=\int _{0}^{l}\frac{1}{2}\varepsilon k_{e}\left( \left\| \chi '\right\| -1\right) ^{2}+\frac{1}{4}k_{b}\varepsilon \left[ \frac{\chi ''\cdot \left( *\chi '\right) }{\left\| \chi '\right\| ^{2}}\right] ^{2}dS. $$

Thus, in order to have a finite macro-energy, we need to impose the following rescaling law:

$$\begin{aligned} k_{b}\varepsilon =2K_{b},\qquad \varepsilon k_{e}=K_{e}. \end{aligned}$$

(3.52)

Thus, in order to have a finite macro-energy, even in the limit $\varepsilon \rightarrow 0$, we need to impose the scaling laws (3.52). This means that, if one wants a finite macro-energy, then the lower the size of the cell, the higher is the rigidity of the tensional and of the rotational springs. Besides, in the limit of $\varepsilon \rightarrow 0$, $k_{b}$ should be infinite, i.e., $k_{b}\rightarrow \infty$.

Pantographic Beams

Introduction

In this section, we discuss the discrete micro-mechanical model which is employed throughout this paper. We begin giving a geometrical description and then we give a mechanical characterization, by choosing a deformation energy. It is a Hencky-type spring model with the geometrical arrangement of a pantographic strip. Once the energy of the micro-model is chosen in its general form, we assume a particular asymptotic behavior for some relevant kinematic quantities, i.e., the elongation of oblique springs, as will be clear in the sequel. We consider the quasi-inextensibility case, i.e., the relative elongation of the oblique springs is small. As a further specialization, the inextensibility case is considered. Finally, after having defined a micro–macro identification, we express the energy of the micro-system in terms of macroscopic kinematic descriptors to prepare the field to the homogenization procedure which will be discussed in details in the next section.

Discrete Micro-model

Geometry

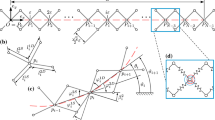
In the spirit of dell’Isola et al. (2016d), Alibert and Della Corte (2015), and Alibert et al. (2017), in this section, we introduce a discrete-spring model (also referred to as the micro-model, since it resembles the features of a specific microstructure). The topology and features of the undeformed and deformed discrete-spring system are summarized in Figs. 3.4 and 3.5, respectively. In the undeformed configuration, $N+1$ material particles are arranged upon a straight line at positions $P_{i}$’s, $i\in \left[ 0;N\right]$, with a uniform spacing $\varepsilon$. The basic ith unit cell centered in $P_{i}$ is formed by four springs joined together by a hinge placed at $P_{i}$. Between two oblique springs, belonging to the same cell and lying on the same diagonal, a rotational spring opposing to their relative rotation is placed. Rotational springs are colored in Fig. 3.4 in blue and red.

Fig. 3.4

Undeformed spring system resembling the microstructure

Fig. 3.5

Deformed spring system resembling the microstructure

We denote with $p_{i}$ the position in the deformed configuration corresponding to position $P_{i}$ in the reference one. In order to completely describe the kinematics of the micro-model, we have to introduce other descriptors. At this end, the length of the oblique deformed springs, indicated with $l_{i}^{\alpha \beta }$, is introduced, the indices $\alpha$ and $\beta$ belonging, respectively, to the sets $\{1,2\}$ and $\{D,S\}$ and referring to the first and second diagonal and left and right, respectively. Referring to Fig. 3.5, we consider the ith node, notwithstanding that the same quantities can be defined for each node. We define $\alpha _{i}$ as the angle between the vectors $p_{i}-p_{i-1}$ and $p_{i}-p_{i+1}$, respectively. We define as $\vartheta _{i}^{\alpha }$ the angle measuring the deviation of two opposite oblique springs from being collinear. In order to illustrate the definition of $\varphi _{i}^{\alpha \beta }$, we consider the case $\alpha =1$ and $\beta =D$. The quantity $\varphi _{i}^{1D}$ is the angle between the vector $p_{i+1}-p_{i}$ and the upper oblique spring hinged at $p_{i}.$ By means of elementary geometric considerations, we have that

$$\begin{aligned}&\vartheta _{i}^{1}=\alpha _{i}+\varphi _{i}^{1D}-\varphi _{i}^{1S}\nonumber \\&\vartheta _{i}^{2}=\alpha _{i}+\varphi _{i}^{2S}-\varphi _{i}^{2D},\ i\in \left[ 0;N\right] . \end{aligned}$$

(3.53)

In the undeformed configuration, see Fig. 3.4, we have

$$\begin{aligned}&l_{i}^{\alpha \beta }=\frac{\sqrt{2}}{2}\varepsilon ,\ \alpha =1,2\quad \beta =D,\ S\quad i\in \left[ 0;N\right] \nonumber \\&\vartheta _{i}^{1}=\vartheta _{i}^{2}=0\nonumber \\&\Vert p_{i}-p_{i-1}\Vert =\varepsilon ,\ i\in \left[ 0;N\right] . \end{aligned}$$

(3.54)

Considering that $\varphi _{i}^{\alpha D},\varphi _{i}^{\alpha S}\in \left[ 0,\pi \right]$, by means of the law of cosines, we get

$$\begin{aligned}&\varphi _{i}^{1D}=\cos ^{-1}\left( \frac{\Vert p_{i+1}-p_{i}\Vert ^{2}+\left( l_{i}^{1D}\right) ^{2}-\left( l_{i+1}^{2S}\right) ^{2}}{2l_{i}^{1D}\Vert p_{i+1}-p_{i}\Vert }\right) \nonumber \\&\varphi _{i}^{2D}=\cos ^{-1}\left( \frac{\Vert p_{i+1}-p_{i}\Vert ^{2}+\left( l_{i}^{2D}\right) ^{2}-\left( l_{i+1}^{1S}\right) ^{2}}{2l_{i}^{2D}\Vert p_{i+1}-p_{i}\Vert }\right) \nonumber \\&\varphi _{i}^{1S}=\cos ^{-1}\left( \frac{\Vert p_{i}-p_{i-1}\Vert ^{2}+\left( l_{i}^{1S}\right) ^{2}-\left( l_{i-1}^{2D}\right) ^{2}}{2l_{i}^{1S}\Vert p_{i}-p_{i-1}\Vert }\right) \nonumber \\&\varphi _{i}^{2S}=\cos ^{-1}\left( \frac{\Vert p_{i}-p_{i-1}\Vert ^{2}+\left( l_{i}^{2S}\right) ^{2}-\left( l_{i-1}^{1D}\right) ^{2}}{2l_{i}^{2S}\Vert p_{i}-p_{i-1}\Vert }\right) . \end{aligned}$$

(3.55)

Mechanical Model

The micro-model energy, written as a combination of the elastic energy contributions of the springs, is defined as

$$\begin{aligned} \mathcal {M}&= \sum _{i}\sum _{\alpha ,\beta }\frac{k_{\alpha \beta ,i}^{e}}{2}\left( l_{i}^{\alpha \beta }-\frac{\sqrt{2}}{2}\varepsilon \right) ^{2}+\sum _{i}\sum _{\alpha }\frac{k_{\alpha ,i}^{f}}{2}\left( \vartheta _{i}^{\alpha }\right) ^{2}+\nonumber \\&+\sum _{i}\frac{k_{i}^{m}}{2}\left( \Vert p_{i+1}-p_{i}\Vert -\varepsilon \right) ^{2}. \end{aligned}$$

(3.56)

Reminding that $\vartheta _{i}^{\alpha }=\alpha _{i}+\left( -1\right) ^{\alpha }\left( \varphi _{i}^{\alpha S}-\varphi _{i}^{\alpha D}\right)$, then (3.56) recasts as

$$\begin{aligned}&\mathcal {M}=\sum _{i}\sum _{\alpha ,\beta }\frac{k_{\alpha \beta ,i}^{e}}{2}\left( l_{i}^{\alpha \beta }-\frac{\sqrt{2}}{2}\varepsilon \right) ^{2}\\&+\sum _{i}\sum _{\alpha }\frac{k_{\alpha ,i}^{f}}{2}\left[ \alpha _{i}+\left( -1\right) ^{\alpha }\left( \varphi _{i}^{\alpha S}-\varphi _{i}^{\alpha D}\right) \right] ^{2}+\nonumber \\&+\sum _{i}\frac{k_{i}^{m}}{2}\left( \Vert p_{i+1}-p_{i}\Vert -\varepsilon \right) ^{2}.\nonumber \end{aligned}$$

(3.57)

In the next subsections, we will specialize this form of the energy by means of assumptions on the properties of the micro-system. In particular, we will discuss in detail the representation of the micro-energy for the quasi-inextensibility assumption that will be made clear next and, subsequently, for the (complete) inextensibility cases.

Toward the Continuum Model

Asymptotic Expansion and Quasi-inextensibility Assumption

We postulate that the following asymptotic expansion holds for $l_{i}^{\alpha \beta }$:

$$\begin{aligned}&l_{i}^{\alpha \beta }=\varepsilon \tilde{l}_{i1}^{\alpha \beta }+\varepsilon ^{2}\tilde{l}_{i2}^{\alpha \beta }+o\left( \varepsilon ^{2}\right) , \end{aligned}$$

(3.58)

where the constant (with respect to $\varepsilon$) term is not present. We now turn to what we refer to as the quasi-inextensibility case. It consists in fixing the value of the first-order term in (3.58) as $\tilde{l}_{i1}^{\alpha \beta }=\frac{\sqrt{2}}{2}$. Moreover, to lighten the notation, we drop the subscript “2” of $\tilde{l}_{i2}^{\alpha \beta }$, i.e., $\tilde{l}_{i}^{\alpha \beta }=\tilde{l}_{i2}^{\alpha \beta }$. Hence, (3.58) reads as

$$\begin{aligned}&l_{i}^{\alpha \beta }=\frac{\sqrt{2}}{2}\varepsilon +\varepsilon ^{2}\tilde{l}_{i}^{\alpha \beta }+o\left( \varepsilon ^{2}\right) . \end{aligned}$$

(3.59)

Piola’s Ansatz

The reference shape of the macro-model is a one-dimensional straight segment $\mathcal {S}$ and we introduce on it an abscissa $s\in [0,B]$ – where $B=N\varepsilon$ is the length of $\mathcal {S}$ which labels each position in $\mathcal {S}$. Proceeding as in the pioneering works of Gabrio Piola, an Italian mathematician and physicist who lived in the 1800s (see Dell’Isola et al. 2015 for a historical review), we introduce the so-called kinematical maps, i.e., some fields in the macro-model that uniquely determine $p_{i}$ and $\tilde{l}_{i}^{\alpha \beta }$:

$$\begin{aligned}&\chi :\ \left[ 0,B\right] \rightarrow \mathcal {E}\nonumber \\&\tilde{l}^{\alpha \beta }:\ \left[ 0,B\right] \rightarrow \mathbb {\mathbb {R}}^{+}, \end{aligned}$$

(3.60)

with $\mathcal {E}$ the Euclidean space on $\mathbb {V\equiv \mathbb {R}}^{2}$. We choose $\chi$ to be the placement function of the 1D continuum and, hence, it has to be injective. The current shape can be regarded as the image of the (sufficiently smooth) curve $\varvec{\chi }:\ [0,B]\rightarrow \mathcal {E}$ and, unlike the reference shape, it is not parameterized by its arc length and it is not a straight line in general. In order for these fields to uniquely determine the kinematical descriptors of the micro-model (i.e., $p_{i}$ and $\tilde{l}_{i}^{\alpha \beta }$), we use the Piola’s Ansatz and impose

$$\begin{aligned}&\chi \left( s_{i}\right) =p_{i}\nonumber \\&\tilde{l}^{\alpha \beta }\left( s_{i}\right) =\tilde{l}_{i}^{\alpha \beta },\ \forall i\in \left[ 0;N\right] . \end{aligned}$$

(3.61)

Micro-model Energy as a Function of Macro-model Descriptors

In this subsection, we obtain the micro-model energy for the quasi-inextensibility case in terms of the macroscopic kinematical maps. Assuming that $\chi$ is at least twice continuously differentiable with respect to the space variable in $s_{i}$’s, we have

$$\begin{aligned}&\chi \left( s_{i+1}\right) =\chi \left( s_{i}\right) +\varepsilon \chi ^{\prime }\left( s_{i}\right) +\frac{\varepsilon ^{2}}{2}\chi ^{\prime \prime }\left( s_{i}\right) +o\left( \varepsilon ^{2}\right) \nonumber \\&\chi \left( s_{i-1}\right) =\chi \left( s_{i}\right) -\varepsilon \chi ^{\prime }\left( s_{i}\right) +\frac{\varepsilon ^{2}}{2}\chi ^{\prime \prime }\left( s_{i}\right) +o\left( \varepsilon ^{2}\right) . \end{aligned}$$

(3.62)

Plugging (3.61) in (3.59) and (3.62), we get the following expressions:

$$\begin{aligned}&l_{i}^{\alpha \beta }=\frac{\sqrt{2}}{2}\varepsilon +\varepsilon ^{2}\tilde{l}^{\alpha \beta }\left( s_{i}\right) +o\left( \varepsilon ^{2}\right) \nonumber \\&p_{i+1}-p_{i}=\varepsilon \chi ^{\prime }\left( s_{i}\right) +\frac{\varepsilon ^{2}}{2}\chi ^{\prime \prime }\left( s_{i}\right) +o\left( \varepsilon ^{2}\right) \nonumber \\&p_{i-1}-p_{i}=-\varepsilon \chi ^{\prime }\left( s_{i}\right) +\frac{\varepsilon ^{2}}{2}\chi ^{\prime \prime }\left( s_{i}\right) +o\left( \varepsilon ^{2}\right) . \end{aligned}$$

(3.63)

Substituting (3.63) into (3.55) and expanding $\varphi _{i}^{\alpha S}-\varphi _{i}^{\alpha D}$ up to first order with respect to $\varepsilon$, we get

$$\begin{aligned}&\varphi _{i}^{\alpha S}-\varphi _{i}^{\alpha D}=\nonumber \\&\frac{\frac{\sqrt{2}}{4}\left[ \Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{2}\right] ^{\prime }+\left[ \tilde{l}^{\left( 3-\alpha \right) D}\left( s_{i-1}\right) -\tilde{l}^{\left( 3-\alpha \right) S}\left( s_{i+1}\right) \right] }{\Vert \chi ^{\prime }\left( s_{i}\right) \Vert \sqrt{1-\frac{\Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{2}}{2}}}\varepsilon +\nonumber \\&+\frac{\left[ \Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{2}-1\right] \left[ \tilde{l}^{\alpha S}\left( s_{i}\right) -\tilde{l}^{\alpha D}\left( s_{i}\right) \right] }{\Vert \chi ^{\prime }\left( s_{i}\right) \Vert \sqrt{1-\frac{\Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{2}}{2}}}\varepsilon +o\left( \varepsilon \right) . \end{aligned}$$

(3.64)

Finally, substituting (3.64) in (3.57) yields the micro-model energy $\mathcal {M}$ as a function of the kinematical descriptors $\chi$ and $\tilde{l}^{\alpha \beta }$ of the macro-model

$$\begin{aligned}&\mathcal {M}=\sum _{i}\sum _{\alpha ,\beta }\frac{k_{\alpha \beta ,i}^{e}\varepsilon ^{4}}{2}\left( \tilde{l}_{i}^{\alpha \beta }\right) ^{2}+\sum _{i}\frac{k_{i}^{m}\varepsilon ^{2}}{2}\left( \Vert \chi _{i}^{\prime }\Vert -1\right) ^{2} \\&\nonumber +\sum _{i}\sum _{\alpha }\frac{k_{\alpha ,i}^{f}\varepsilon ^{2}}{2}\biggl \{\vartheta ^{\prime }\left( s_{i}\right) \\&+\left( -1\right) ^{\alpha }\frac{\frac{\sqrt{2}}{4}\left[ \Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{2}\right] ^{\prime }+\left[ \tilde{l}_{i}^{\left( 3-\alpha \right) D}\left( s_{i-1}\right) -\tilde{l_{i}}^{\left( 3-\alpha \right) S}\left( s_{i+1}\right) \right] }{\Vert \chi ^{\prime }\left( s_{i}\right) \Vert \sqrt{1-\frac{\Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{2}}{2}}}+\nonumber \\&+\left( -1\right) ^{\alpha }\frac{\left[ \Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{2}-1\right] \left[ \tilde{l}_{i}^{\alpha S}\left( s_{i}\right) -\tilde{l_{i}}^{\alpha D}\left( s_{i}\right) \right] }{\Vert \chi ^{\prime }\left( s_{i}\right) \Vert \sqrt{1-\frac{\Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{2}}{2}}}\biggr \}^{2}, \nonumber \end{aligned}$$

(3.65)

where $\alpha _{i}=\varepsilon \vartheta ^{\prime }\left( s_{i}\right)$ has been used and

$$ \vartheta ^{\prime }=\frac{\chi _{\perp }^{\prime }\cdot \chi ^{\prime \prime }}{\Vert \chi ^{\prime }\Vert ^{2}}, $$

with $\chi _{\perp }^{\prime }$ the 90$^{\circ }$ anticlockwise rotation of $\chi ^{\prime }$, is the material curvature, i.e., rate of change with respect to the reference abscissa of the orientation of the tangent $\chi ^{\prime }\left( s\right) =\rho \left( s\right) \left[ \cos \vartheta \left( s\right) \mathbf {e}_{1}+\sin \vartheta \left( s\right) \mathbf {e}_{2}\right]$ to the deformed centerline. We remark that the micro-model energy, when written in terms of macroscopic fields, contains already a contribution from the second gradient of $\chi (s)$. Finally, it is worth to be noticed that, for a fixed $\varepsilon$, Eq. (3.65) provides an upper bound for $||\chi '||$, i.e., $\Vert \chi ^{\prime }\Vert <\sqrt{2}$, even if no kinematic restrictions directly affect $||\chi '||$.

The Case of Inextensible Fibers

We consider now the case of inextensible oblique springs. This translates in considering $\tilde{l}_{i}^{\alpha \beta }=0$ and it is referred as the inextensibility case. Moreover, for the sake of simplicity, we consider the elastic constants of the rotational springs to satisfy $k_{F,i}^{1}=k_{F,i}^{2}:= k_{F,i}$, $\forall i\in [1;N]$. We remark that $\tilde{l}_{i}^{\alpha \beta }=0$ implies, through a purely geometric argument, that $\varphi _{i+1}^{S1}=\varphi _{i+1}^{S2}=\varphi _{i}^{D1}=\varphi _{i}^{D2}:=\varphi _{i}$. Once the kinematic restrictions implied by the inextensibility assumption have been presented, we are ready to define the micro-model energy (3.57) as

$$\begin{aligned} \mathcal {I}= & {} \sum _{i}k_{i}^{f}\sum _{\alpha }\frac{\left[ \alpha _{i}+\left( -1\right) ^{\alpha }\left( \varphi _{i}-\varphi _{i-1}\right) \right] ^{2}}{2} \\&+\sum _{i}\frac{k_{i}^{m}}{2}\left( \Vert p_{i+1}-p_{i}\Vert -\varepsilon \right) ^{2}.\nonumber \end{aligned}$$

(3.66)

Proceeding in analogy with the previous construction, we introduce the kinematical map

$$\begin{aligned}&\varphi :\ \left[ 0,B\right] \rightarrow \left[ 0,\frac{\pi }{2}\right] \end{aligned}$$

and, then, we perform the Piola’s Ansatz by imposing

$$\begin{aligned}&\varphi \left( s_{i}\right) =\varphi _{i},\ \forall i\in \left[ 0;N\right] . \end{aligned}$$

(3.67)

Assuming both $\chi$ and $\varphi$ to be at least one time continuously differentiable with respect to the space variable in $s_{i}$ and taking into account the Piola’s Ansatz (3.67), we have

$$\begin{aligned}&p_{i+1}-p_{i}=\varepsilon \chi ^{\prime }\left( s_{i}\right) +o(\varepsilon )\nonumber \\&\varphi _{i-1}-\varphi _{i}=-\varepsilon \varphi ^{\prime }\left( s_{i}\right) +o(\varepsilon ). \end{aligned}$$

(3.68)

Substituting (3.68) into (3.66) yields the micro-model energy for the inextensibility case in terms of the kinematical quantities of the macro-model

$$\begin{aligned}&\mathcal {I}=\nonumber \\&\sum _{i}k_{i}^{f}\varepsilon ^{2}\left[ \vartheta ^{\prime }{}^{2}\left( s_{i}\right) +\varphi _{i}^{\prime }{}^{2}\left( s_{i}\right) \right] +\sum _{i}\frac{k_{i}^{m}\varepsilon ^{2}}{2}\left( \Vert \chi _{i}^{\prime }\Vert -1\right) ^{2}. \end{aligned}$$

(3.69)

We now impose the so-called internal connection constraint:

$$\begin{aligned} \sqrt{2}\varepsilon \cos \varphi \left( s_{i}\right) =\Vert \chi \left( s_{i+1}\right) -\chi \left( s_{i}\right) \Vert , \end{aligned}$$

(3.70)

which, up to $\varepsilon$-terms of order higher than one, reads

$$\begin{aligned} \sqrt{2}\cos \varphi =\Vert \chi ^{\prime }\Vert . \end{aligned}$$

(3.71)

This constraint ensures that, in the deformed configuration, the upper-left spring of the ith cell is hinge joint with the upper-right spring of the $(i-1)$th cell, and the lower-left spring of the ith cell is hinge joint with lower-right spring of the $(i-1)$th cell. Due to this constraint, the maps $\varphi$ and $\chi$ are not independent and it is possible to rewrite the expression of the micro-model energy in terms of the placement field $\chi (s)$ only. Indeed, deriving (3.71) with respect to the space variable yields

$$\begin{aligned} -\sqrt{2}\varphi ^{\prime }\left( s_{i}\right) \sin \varphi \left( s_{i}\right) =\Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{\prime }, \end{aligned}$$

(3.72)

which, in turn, implies

$$ \varphi ^{\prime }\left( s_{i}\right) =-\frac{\Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{\prime }}{\sqrt{2}\sin \varphi \left( s_{i}\right) }. $$

Reminding $\varphi \in \left[ 0,\pi \right]$ and taking into account (3.71), we get

$$\begin{aligned}&\varphi _{i}^{\prime }=-\frac{\Vert \chi _{i}^{\prime }\Vert ^{\prime }}{\sqrt{2}\sqrt{1-\text{ cos }^{2}\varphi \left( s_{i}\right) }}=\\&=-\frac{\Vert \chi _{i}^{\prime }\Vert ^{\prime }}{\sqrt{2-\Vert \chi _{i}^{\prime }\Vert ^{2}}}. \end{aligned}$$

Hence, in the inextensibility case, the micro-model energy (3.69) can be recast, as a function of the macro-model descriptor $\chi$ only, as

$$\begin{aligned}&\mathcal {I}= \\&\sum _{i}k_{i}^{f}\varepsilon ^{2}\left[ \left[ \vartheta ^{\prime }\left( s_{i}\right) \right] ^{2}+\left( \frac{\Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{\prime }}{\sqrt{2-\Vert \chi ^{\prime }\left( s_{i}\right) \Vert ^{2}}}\right) ^{2}\right] +\sum _{i}\frac{k_{i}^{m}\varepsilon ^{2}}{2}\left( \Vert \chi ^{\prime }\left( s_{i}\right) \Vert -1\right) ^{2}. \nonumber \end{aligned}$$

(3.73)

Clearly, since the inextensibility case is just a special case of the quasi-inextensibility case, it is possible to show that this expression can be also obtained in a more direct way from (3.65) by setting $\tilde{l}^{\alpha S}\left( s_{i}\right) =0$ and $k_{F,i}^{1}=k_{F,i}^{2}:= k_{F,i}$.

Continuum-Limit Macro-model

In this section, by performing the final steps of the heuristic homogenization procedure presented throughout this paper, we derive a 1D continuum model, also referred to as the macro-model, associated to the aforementioned microstructure. Besides, we analyze the quasi-inextensibility and inextensibility cases and we obtain the corresponding macro-model energies in terms of the displacement field $\chi$.

Rescaling of Stiffnesses and Heuristic Homogenization

The preliminary step to perform the homogenization procedure consists of the definition of the quantities $\mathbb {K}_{\alpha \beta ,i}^{e}$, $\mathbb {K}_{\alpha ,i}^{f}$, and $\mathbb {K}_{i}^{m}$. These quantities are scale-invariant, meaning that they do not depend on $\varepsilon$. Their role is to keep track of the asymptotic behavior of the stiffnesses $k_{\alpha ,\beta ,i}^{e}$, $k_{\alpha ,i}^{f},$ and $k_{i}^{m}$ of the micro-model springs. More explicitly, we assume

$$\begin{aligned}&k_{\alpha \beta ,i}^{e}(\varepsilon )=\frac{\mathbb {K}_{\alpha \beta ,i}^{e}}{\varepsilon ^{3}};\qquad k_{\alpha ,i}^{f}(\varepsilon )=\frac{\mathbb {K}_{\alpha ,i}^{f}}{\varepsilon };\qquad k_{i}^{m}(\varepsilon )=\frac{\mathbb {K}_{i}^{m}}{\varepsilon }. \end{aligned}$$

(3.74)

We remark that in this rescaling, as $\varepsilon$ approaches zero, the ratio between the stiffness $k_{\alpha \beta ,i}^{e}$ of the oblique springs and the stiffness $k_{\alpha ,i}^{f}$ will approach infinity with a rate of divergence in $\varepsilon$ equal to two, i.e., $\frac{k_{\alpha \beta ,i}^{e}}{k_{\alpha ,i}^{e}}\sim \varepsilon ^{2}$. Now, we are ready to perform the homogenization procedure. First, we consider the more general quasi-inextensibility case. For simplicity, let us set

$$\begin{aligned}&\mathbb {K}_{1D,i}^{e}=\mathbb {K}_{1S,i}^{e}=\mathbb {K}_{2D,i}^{e}=\mathbb {K}_{2S,i}^{e}:=\mathbb {K}_{i}^{e};\qquad \mathbb {K}_{1,i}^{f}=\mathbb {K}_{2,i}^{f}:=\mathbb {K}_{i}^{f}. \end{aligned}$$

(3.75)

Let us introduce the kinematical maps

$$\begin{aligned}&\mathbb {K}^{e}:\ \left[ 0,B\right] \rightarrow \mathbb {R}^{+};\qquad \mathbb {K}^{f}:\ \left[ 0,B\right] \rightarrow \mathbb {R}^{+};\qquad \mathbb {K}^{m}:\ \left[ 0,B\right] \rightarrow \mathbb {R}^{+} \end{aligned}$$

such that they satisfy the following Piola’s Ansatz:

$$\begin{aligned}&\mathbb {K}^{e}\left( s_{i}\right) =\mathbb {K}_{i}^{e};\qquad \mathbb {K}^{f}\left( s_{i}\right) =\mathbb {K}_{i}^{f};\qquad \mathbb {K}^{m}\left( s_{i}\right) =\mathbb {K}_{i}^{m}. \end{aligned}$$

(3.76)

Substituting (3.74) in (3.65), taking into account (3.75) and (3.76), and letting $\varepsilon \rightarrow 0$ yield

$$\begin{aligned}&\mathcal {E}=\nonumber \\&\int _{\mathcal {S}}\frac{\mathbb {K}^{e}}{2}\left( \tilde{l}^{1S}\right) ^{2}\text{ ds } +\int _{\mathcal {S}}\frac{\mathbb {K}^{e}}{2}\left( \tilde{l}^{1D}\right) ^{2}\text{ ds } \nonumber \\&+\int _{\mathcal {S}}\frac{\mathbb {K}^{e}}{2}\left( \tilde{l}^{2S}\right) ^{2}\text{ ds } +\int _{\mathcal {S}}\frac{\mathbb {K}^{e}}{2}\left( \tilde{l}^{2D}\right) ^{2}\text{ ds }+\nonumber \\&+\int _{\mathcal {S}}\frac{\mathbb {K}^{f}}{2} \left\{ \vartheta ^{\prime } \right. \nonumber \\&\left. +\frac{-\sqrt{2}\left( \Vert \chi ^{\prime }\Vert ^{2}\right) ^{\prime }-4\left[ \left( \tilde{l}^{2D}-\tilde{l}^{2S}\right) -\left( \Vert \chi ^{\prime }\Vert ^{2}-1\right) \left( \tilde{l}^{1D}-\tilde{l}^{1S}\right) \right] }{\Vert \chi ^{\prime }\Vert \sqrt{2-\Vert \chi ^{\prime }\Vert ^{2}}}\right\} ^{2} \text{ ds }+\nonumber \\&+\int _{\mathcal {S}}\frac{\mathbb {K}^{f}}{2}\left\{ \vartheta ^{\prime }\right. \nonumber \\&+\left. \frac{\sqrt{2}\left( \Vert \chi ^{\prime }\Vert ^{2}\right) ^{\prime }+4\left[ \left( \tilde{l}^{1D}-\tilde{l}^{1S}\right) +\left( \Vert \chi ^{\prime }\Vert ^{2}-1\right) \left( \tilde{l}^{2S}-\tilde{l}^{2D}\right) \right] }{\Vert \chi ^{\prime }\Vert \sqrt{2-\Vert \chi ^{\prime }\Vert ^{2}}}\right\} ^{2} \text{ ds }+\nonumber \\&+\int _{\mathcal {S}}\frac{\mathbb {K}^{m}}{2}\left( \Vert \chi ^{\prime }\Vert -1\right) ^{2}\text{ ds }, \end{aligned}$$

(3.77)

which is the continuum-limit macro-model energy for a 1D pantographic beam under the hypothesis of quasi-inextensible oblique micro-springs. It is worth to remark that, when $\mathbb {K}^{m}=0$, $\tilde{l}^{\alpha \beta }=0$ and $\chi \left( s\right) =Cs\mathbf {e}_{1}$, with $C\in \mathbb {R}$, the beam undergoes a floppy mode, i.e., (3.77) vanishes. Thus, under the above conditions, the configuration $\chi \left( s\right) =Cs\mathbf {e}_{1}$ is isoenergetic to the undeformed configuration for any C. For a fixed $\varepsilon ,$ considering $k_{i}^{m}=0$ and $\tilde{l_{i}}^{\alpha \beta }=0$ in the micro-model energy (3.65), we have that $\chi (s_{i})=Cs_{i}{\mathbf{e }_{1}}$ is a floppy mode for the micro-model as well. This means that the homogenization procedure that we have carried out has preserved a key feature of the micro-model. Up to now, the expression of the continuum-limit homogenized energy depends both on the kinematical maps $\chi$ and $\tilde{l}.$ In the next section, we show that, at equilibrium, it is possible to write the macro-energy in terms of the placement field only.

Macro-model Energy as a Function of the Placement Field

We now equate to zero the first variations of (3.77) with respect to $\tilde{l}^{\alpha \beta }$’s, i.e., we look for stationary points, with respect to $\tilde{l}^{\alpha \beta }$, of (3.77). This is a necessary first-order condition for optimality. In the continuum limit homogenized energy, no spatial derivatives of $\tilde{l}^{\alpha \beta }$ appear. Such energy depends only by linear and quadratic contributions in $\tilde{l}^{\alpha \beta }$. Hence, this process yields four algebraic linear equations in $\tilde{l}^{\alpha \beta }$. Solving these equations gives $\tilde{l}^{\alpha \beta }$ at equilibrium

$$\begin{aligned}&\tilde{l}^{1D}=\frac{\sqrt{2}}{2}\mathbb {K}^{f}\left( \chi ^{\prime \prime }\cdot C+\vartheta ^{\prime }D\right) \nonumber \\&\tilde{l}^{2D}=\frac{\sqrt{2}}{2}\mathbb {K}^{f}\left( \chi ^{\prime \prime }\cdot C-\vartheta ^{\prime }D\right) \nonumber \\&\tilde{l}^{1S}=\frac{\sqrt{2}}{2}\mathbb {K}^{f}\left( -\chi ^{\prime \prime }\cdot C-\vartheta ^{\prime }D\right) \nonumber \\&\tilde{l}^{2S}=\frac{\sqrt{2}}{2}\mathbb {K}^{f}\left( -\chi ^{\prime \prime }\cdot C+\vartheta ^{\prime }D\right) \end{aligned}$$

(3.78)

with

$$\begin{aligned}&C=\frac{\chi ^{\prime }}{2\mathbb {K}^{f}\Vert \chi ^{\prime }\Vert ^{2}-\frac{1}{2}\left( \mathbb {K}^{e}\Vert \chi ^{\prime }\Vert ^{2}+8\mathbb {K}^{f}\right) }\\&D=\frac{\Vert \chi ^{\prime }\Vert \sqrt{4\tilde{L}^{2}-\Vert \chi ^{\prime }\Vert ^{2}}}{\mathbb {K}^{e}\tilde{L}^{2}\left( \Vert \chi ^{\prime }\Vert ^{2}-2\right) -2\mathbb {K}^{f}\Vert \chi ^{\prime }\Vert ^{2}}. \end{aligned}$$

From (3.78), we can get, in some particular cases, interesting information about the properties of the pantographic beam. First, let us notice that $\tilde{l}^{1D}=-\tilde{l}^{1S}$ and $\tilde{l}^{2D}=-\tilde{l}^{2S}$. Moreover, we also notice that when $\chi ^{\prime }=\rho \mathbf {e}_{1}$, with $\rho$ independent of the abscissa s, then, as $\chi ^{\prime \prime }$ vanishes, $\tilde{l}^{\alpha \beta }=0$, i.e., the fibers undergo no elongation. Instead, when $\chi ^{\prime }\left( s\right) =\rho \left( s\right) \mathbf {e}_{1}$, with $\rho$ depending on s, then $\tilde{l}^{1D}=\tilde{l}^{2D}=-\tilde{l}^{1S}=-\tilde{l}^{2S}$. This remarkable and counterintuitive feature can be used as a possible benchmark test to validate, as $\varepsilon$ approaches zero, a numerical scheme based on the discrete micro-model. Let us consider the case of nonzero bending curvature, i.e., $\vartheta ^{\prime }\ne 0$, when $\chi ^{\prime \prime }\cdot C<<\vartheta ^{\prime }D$, which implies that $\tilde{l}^{1D}=-\tilde{l}^{2D}=-\tilde{l}^{1S}=\tilde{l}^{2S}$. If $\vartheta ^{\prime }>0$ then $\tilde{l}^{1D},\tilde{l}^{2S}>0$ and $\tilde{l}^{2D},\tilde{l}^{1S}<0$ while, if $\vartheta ^{\prime }<0$ then $\tilde{l}^{1D},\tilde{l}^{2S}<0$ and $\tilde{l}^{2D},\tilde{l}^{1S}>0$. We are now ready to express the macro-model energy $\overline{\mathcal {E}}\left( \chi \right)$ as a function of the placement $\chi$ only, by substituting (3.78) in (3.77):

$$\begin{aligned}&\overline{\mathcal {E}}\left( \chi \left( \cdot \right) \right) =\min _{\tilde{l}^{\alpha \beta }\left( \cdot \right) }\mathcal {E}= \\&\int _{\mathcal {S}}\mathbb {K}^{e}\mathbb {K}^{f}\left\{ \frac{\left( \rho ^{2}-2\right) }{\rho ^{2}\left( \mathbb {K}^{e}-4\mathbb {K}^{f}\right) -2\mathbb {K}^{e}} \vartheta ^{\prime 2}\right. \nonumber \\&\left. +\frac{\rho ^{2}}{\left( 2-\rho ^{2}\right) \left[ \rho ^{2}\left( \mathbb {K}^{e}-4\mathbb {K}^{f}\right) +8\mathbb {K}^{f}\right] }\rho ^{\prime 2}\right\} \text{ ds }+\nonumber \\&+\int _{\mathcal {S}}\frac{\mathbb {K}^{m}}{2}\left( \rho -1\right) ^{2}\text{ ds }=\nonumber \\&=\int _{\mathcal {S}}\frac{\mathbb {K}^{e}\mathbb {K}^{f}\left( \Vert \chi ^{\prime }\Vert ^{2}-2\right) }{\Vert \chi ^{\prime }\Vert ^{4}\left[ \Vert \chi ^{\prime }\Vert ^{2}\left( \mathbb {K}^{e}-4\mathbb {K}^{f}\right) -2\mathbb {K}^{e}\right] }\left( \chi _{\perp }^{\prime }\cdot \chi ^{\prime \prime }\right) ^{2}\text{ ds }+\nonumber \\&+\int _{\mathcal {S}}\frac{\mathbb {K}^{e}\mathbb {K}^{f}}{\left( 2-\Vert \chi ^{\prime }\Vert ^{2}\right) \left[ \Vert \chi ^{\prime }\Vert ^{2}\left( \mathbb {K}^{e}-4\mathbb {K}^{f}\right) +8\mathbb {K}^{f}\right] }\left( \chi ^{\prime }\cdot \chi ^{\prime \prime }\right) ^{2}\text{ ds }+\nonumber \\&+\int _{\mathcal {S}}\frac{\mathbb {K}^{m}}{2}\left( \Vert \chi ^{\prime }\Vert -1\right) ^{2}\text{ ds }.\nonumber \end{aligned}$$

(3.79)

We observe that, for $0<\rho <\sqrt{2}$ and for any choice of the positive macro-stiffnesses $\mathbb {K}^{e}$, $\mathbb {K}^{f}$, and $\mathbb {K}^{m}$, (3.79) is positive definite. Moreover, not only we can classify this homogenized model as a second gradient theory, but we notice that the full second gradient $\chi ^{\prime \prime }$ of $\chi$ contributes to the strain energy. Indeed, beyond the usual term $\bigl (\chi _{\perp }^{\prime }\cdot \chi ^{\prime \prime }\bigr )$ related to the Lagrangian curvature, also the term $\bigl (\chi ^{\prime }\cdot \chi ^{\prime \prime }\bigr )$, deriving from the presence of the oblique springs, appears. There is a remarkable feature in this model which deserves to be discussed. From (3.79), it is clear that in the limit $||\chi ^{\prime }||\rightarrow \sqrt{2}$ the model exhibits a so-called phase transition: it locally degenerates into the model of an uniformly extensible cable, notwithstanding that $\sqrt{2}$ is an upper bound for $\rho$. Indeed,

$$\begin{aligned}&\frac{\left( \rho ^{2}-2\right) }{\rho ^{2}\left( \mathbb {K}^{e}-4\mathbb {K}^{f}\right) -2\mathbb {K}^{e}}\rightarrow 0\\&\frac{\rho ^{2}}{\left( 2-\rho ^{2}\right) \left[ \rho ^{2}\left( \mathbb {K}^{e}-4\mathbb {K}^{f}\right) +8\mathbb {K}^{f}\right] }\rightarrow +\infty , \end{aligned}$$

so that no deformation energy is stored for finite bending curvature and, in order for the energy to be bounded for bounded deformations, $\rho ^{\prime }$ must approach zero, meaning that the elongation must be locally uniform. Further developments of this model could consist in contemplating a phase transition to a model that, for finite bending curvature, entails a nonzero stored deformation energy.

Nondimensionalization

In order to handle more easily the model in the numerical implementation and in the interpretation of the corresponding results, we turn to the use of nondimensional quantities. Therefore, we introduce the following nondimensional fields:

$$\begin{aligned}&s=B\overline{s};\quad \chi =B\overline{\chi };\quad \mathbb {K}^{e}=K\overline{\mathbb {K}}^{e};\quad \mathbb {K}^{f}=K\overline{\mathbb {K}}^{f};\quad \mathbb {K}^{m}=K^{m}\overline{\mathbb {K}}^{m}. \end{aligned}$$

In terms of these new quantities, we can recast (3.79) as

$$\begin{aligned}&\frac{K}{B}\int _{0}^{1}\frac{\overline{\mathbb {K}}^{e}\overline{\mathbb {K}}^{f}\left( \Vert \overline{\chi }^{\overline{\prime }}\Vert ^{2}-2\right) }{\Vert \overline{\chi }^{\overline{\prime }}\Vert ^{4}\left[ \Vert \overline{\chi }^{\overline{\prime }}\Vert ^{2}\left( \overline{\mathbb {K}}^{e}-4\overline{\mathbb {K}}^{f}\right) -2\overline{\mathbb {K}}^{e}\right] }\left( \overline{\chi }_{\perp }^{\overline{\prime }}\cdot \overline{\chi }^{\overline{\prime \prime }}\right) ^{2}\text{ d }\overline{\text{ s }}+\nonumber \\&+\frac{K}{B}\int _{0}^{1}\frac{\overline{\mathbb {K}}^{e}\overline{\mathbb {K}}^{f}\left( \overline{\chi }^{\overline{\prime }}\cdot \overline{\chi }^{\overline{\prime \prime }}\right) ^{2}}{\left( 2-\Vert \overline{\chi }^{\overline{\prime }}\Vert ^{2}\right) \left[ \Vert \overline{\chi }^{\overline{\prime }}\Vert ^{2}\left( \overline{\mathbb {K}}^{e}-4\overline{\mathbb {K}}^{f}\right) +8\overline{\mathbb {K}}^{f}\right] }\text{ d }\overline{\text{ s }}+\nonumber \\&+K^{m}B\int _{0}^{1}\frac{\overline{\mathbb {K}}^{m}}{2}\left( \Vert \overline{\chi }^{\overline{\prime }}\Vert -1\right) ^{2}\text{ d }\overline{\text{ s }}, \end{aligned}$$

(3.80)

where the symbol $^{\overline{\prime }}$ denotes differentiation with respect to the dimensionless abscissa $\overline{s}$.

The Inextensibility Case

Let us focus now on the inextensibility case. The homogenization procedure follows the same lines of the previous case. Indeed, keeping in mind (3.75) and (3.76), letting $\varepsilon \rightarrow 0$ in (3.73) yields the continuum-limit macro-model energy for the inextensibility case

$$\begin{aligned}&\int _{\mathcal {S}}\left\{ \mathbb {K}^{f}\left[ \vartheta ^{\prime 2}+\frac{\rho ^{\prime 2}}{2-\rho ^{2}}\right] +\frac{\mathbb {K}^{m}}{2}\left( \rho -1\right) ^{2}\right\} \text{ ds }=\nonumber \\&=\int _{\mathcal {S}}\left\{ \mathbb {K}^{f}\left[ \frac{\left( \chi _{\perp }\cdot \chi ^{\prime \prime }\right) ^{2}}{\Vert \chi ^{\prime }\Vert ^{4}}+\frac{\left( \chi \cdot \chi ^{\prime \prime }\right) ^{2}}{\Vert \chi ^{\prime }\Vert ^{2}\left( 2-\Vert \chi ^{\prime }\Vert ^{2}\right) }\right] +\frac{\mathbb {K}^{m}}{2}\left( \Vert \chi ^{\prime }\Vert -1\right) ^{2}\right\} \text{ ds }.\nonumber \\ \end{aligned}$$

(3.81)

This result is consistent with the quasi-inextensibility case. Indeed, we could have found (3.81) also by letting $\mathbb {K}^{e}\rightarrow +\infty$ in (3.79). Let us remark that, also in this case, the homogenized continuum model, due to the richness of the microstructure, gives rise to a full second gradient theory.

Linearization

An interesting connection can be traced with the existing literature on the formulation of 1D continuum homogenized model for microstructured media and, in particular, for pantographic ones. Indeed, this connection is traced by considering a linearization of the pantographic beam energy in the (complete) inextensibility case. We set $\chi \left( s\right) =\begin{pmatrix}s\\ 0 \end{pmatrix}+\eta \tilde{u}$, with $\tilde{u}$ independent of $\eta$, i.e., we linearize with respect to the displacement $u=\chi \left( s\right) -\begin{pmatrix}s\\ 0 \end{pmatrix}$, and $\mathbb {K}^{m}=0$. By means of simple algebra manipulations, it is possible to derive the deformation energy in Eq. (5) (with $K^{+}=K^{-}$) of Alibert et al. (2003) (see also Seppecher et al. 2011):

$$\begin{aligned} \int _{\mathcal {S}}\mathbb {K}^{f}\Vert u^{\prime \prime }\Vert ^{2} \text{ ds }. \end{aligned}$$

(3.82)

We remark that in the linearized energy (3.82) the transverse displacement and the axial one decouple.

Numerical Simulations of the Continuous Model

Preliminaries

Using the so-obtained 1D continuum model, we show some equilibrium shapes exhibiting highly non-standard features, essentially related to the complete dependence of the homogenized continuum energy density functional on the second gradient of the placement field.

In the sequel, $\mathbb {K}^{m}=0$ will be considered, which means that the standard quadratic additive elongation/shortening contribution to the deformation energy will be turned off. This is made in order to better highlight some non-standard features of the nearly inextensible pantographic beam model. In this section, we show numerical results for the quasi-inextensible and inextensible pantographic beam model and for the geometrically nonlinear Euler model. We remind that these cases stand for $\mathbb {K}^{e}<+\infty$ and $\mathbb {K}^{e}\rightarrow +\infty$, respectively. Two benchmark tests are exploited in order to illustrate peculiar and non-standard features of the pantographic beam model. Convergence of the quasi-inextensible pantographic beam model to the completely inextensible one is shown, by means of a numerical example, as the macro-stiffness $\mathbb {K}^{e}$ related to elongation of the oblique springs approaches $+\infty$. This is due to the fact that, as it is clear from Eq. (3.77), if $\mathbb {K}^{e}\rightarrow +\infty$, then $\tilde{l}^{\alpha \beta }\rightarrow 0$. Of course, the same discussion and simulations can be made for the micro-model and this could be the subject of a further investigation. For the sake of self-consistence, we recall that the deformation energy of the geometrically nonlinear Euler model employed in the following simulations is the following:

$$\begin{aligned}&\int _{\mathcal {S}}\left\{ \frac{K^{e}}{2}\left( \Vert \chi ^{\prime }\Vert -1\right) ^{2}+\frac{K^{b}}{2}\left[ \frac{\chi ^{\prime \prime }\cdot \chi ^{\prime \prime }}{\Vert \chi ^{\prime }\Vert ^{2}}-\left( \frac{\chi ^{\prime }\cdot \chi ^{\prime \prime }}{\Vert \chi ^{\prime }\Vert ^{2}}\right) ^{2}\right] \right\} \text{ ds }=\\&=\int _{\mathcal {S}}\left\{ \frac{K^{e}}{2}\left( \rho -1\right) ^{2}+\frac{K^{b}}{2}\vartheta ^{\prime 2}\right\} \text{ ds }, \end{aligned}$$

and we notice that, while in the nearly inextensible pantographic beam model both $\rho$ and $\vartheta$ can be enforced at the boundary, for the nonlinear Euler model it can be done for $\vartheta$ only, as no spatial derivative of $\rho$ appears in the energy.

Fig. 3.6

Semi-circle test. Deformed shapes for the nearly inextensible pantographic beam model and for the geometrically nonlinear Euler beam model (GNEM). (left) Elongation $\rho -1$ versus the reference abscissa for the nearly inextensible pantographic beam model and for the geometrically nonlinear Euler beam model (GNEM) (right). Numbers in the legends stand for different dimensionless values of $\rho _{0}$

Semi-circle Test

We consider for both the nearly inextensible pantographic beam model and the geometrically nonlinear Euler beam model the reference domain to be the interval $\left[ 0,2\pi \right]$. We enforce the following boundary conditions for both models

$$\begin{aligned}&1.\ \chi \left( 0\right) =\mathbf {0};\quad 2.\ \chi \left( 2\pi \right) =2\mathbf {e}_{1;}\quad 3.\ \vartheta \left( 0\right) =-\frac{\pi }{2};\quad 4.\ \vartheta \left( 2\pi \right) =\frac{\pi }{2} \end{aligned}$$

and, for the nearly inextensible pantographic beam model, we also have the following two additional constraints:

$$\begin{aligned}&5.\ \rho \left( 0\right) =\rho _{0};\quad 6.\ \rho \left( 2\pi \right) =\rho _{0}. \end{aligned}$$

In Fig. 3.6 (up), the deformed shapes for the nearly inextensible pantographic beam model and for the geometrically nonlinear Euler beam model (GNEM) are shown for different values of $\rho _{0}$ reported in the legend. In Fig. 3.6 (down), the elongation $\rho -1$ for the nearly inextensible pantographic beam model and for the geometrically nonlinear Euler beam model (GNEM) is shown for different values of $\rho _{0}$ reported in the legend. It is remarkable that passing from $\rho _{0}>1$ to $\rho <1$, there is a change of concavity in the elongation for the pantographic beam model. In Fig. 3.7 (up), the deformed shapes for the nearly inextensible pantographic beam model (blue) and for the inextensible pantographic beam model (green) with $\rho _{0}=1.4$ are compared. Of course, the area spanned by the quasi-inextensible pantographic beam includes that of the (completely) inextensible one. In Fig. 3.7 (down), it is numerically shown that the energy of the nearly inextensible pantographic beam model (ordinate) asymptotically tends to the energy of the inextensible pantographic beam model (asymptote) as $\mathbb {K}^{e}\text { (abscissa)}\rightarrow +\infty$.

Fig. 3.7

Semi-circle test. Deformed shapes for the nearly inextensible pantographic beam model (blue) and for the inextensible pantographic beam model (green) with $\rho _{0}=1.4$ (left). Energy of the nearly inextensible pantographic beam model (ordinate) asymptotically tends to the energy of the inextensible pantographic beam model (asymptote) as $\mathbb {K}^{e} \text { (abscissa)}\rightarrow +\infty$ (right)

Three-Point Test

We consider for both the quasi-inextensible pantographic beam model and the geometrically nonlinear Euler beam model the reference domain to be the interval $\left[ 0,2\right]$. We enforce the following boundary conditions for both models:

$$\begin{aligned} 1.\ \chi \left( 0\right)= & {} \mathbf {0}; \quad 2.\ \chi \left( 1\right) \cdot \mathbf {e}_{2}=\overline{u};\quad 3.\ \chi \left( 2\right) =\mathbf {0};\\&\quad 4.\ \vartheta \left( 0\right) =0;\quad 5.\ \vartheta \left( 2\right) =0. \end{aligned}$$

In Fig. 3.8, the deformed shapes for the nearly inextensible pantographic beam model (red, light blue) and for the geometrically nonlinear Euler beam model (blue, green) are shown for different values of $\overline{u}$ in the legend. Figure 3.9 shows, for different values of the parameter $\overline{u}$, the elongation $\rho -1$ versus the reference abscissa for the nearly inextensible pantographic beam model. The parameter $\overline{u}$ is increasing from bottom to top. We observe that, as $\overline{u}$ increases, at some point, there is a concavity change in the elongation plot and, increasing further the parameter $\overline{u}$, curves start to intersect. This means that, for some points of the beam, an increase of the prescribed displacement $\overline{u}$ implies a decrease in the elongation. Figure 3.10 shows the pulling force, i.e., Lagrange multiplier associated to the weak constraint $\chi \left( 1\right) \cdot \mathbf {e}_{2}=\overline{u}$, changed of sign, applied at the midpoint in order to vertically displace it of an amount $\overline{u}$. In the nearly inextensible pantographic beam model (blue) negative stiffness property, also known as elastic softening, is observed, while in the geometrically nonlinear Euler beam model (green) elastic softening is not observed. Figure 3.11 shows the plot of $\tilde{l}^{1D}$ versus reference abscissa for different values of $\overline{u}$ in the legend. Analogous plots hold for $\tilde{l}^{2D}$, $\tilde{l}^{1S}$, and $\tilde{l}^{2S}$.

Fig. 3.8

Three-point test. Deformed shapes for the nearly inextensible pantographic beam model (red, light blue) and for the geometrically nonlinear Euler beam model (blue, green) for different values of $\overline{u}$ in the legend

Fig. 3.9

Three-point test. Elongation $\rho -1$ versus the reference abscissa for the nearly inextensible pantographic beam model. The parameter $\overline{u}$ is increasing from bottom to top. We observe that, while increasing $\overline{u}$, there is a concavity change at some point. Increasing further the parameter $\overline{u}$, curves start to intersect

Fig. 3.10

Three-point test. Pulling force (i.e., Lagrange multiplier associated to the weak constraint $\chi \left( 1\right) \cdot \mathbf {e}_{2}=\overline{u}$), changed of sign, applied at the midpoint in order to vertically displace it of an amount $\overline{u}$ (abscissa). In the nearly inextensible pantographic beam model (blue) elastic softening is observed, while in the geometrically nonlinear beam model (green) elastic softening is not observed

Fig. 3.11

Three-point test. Plot of $\tilde{l}^{1D}$ versus reference abscissa for different values of $\overline{u}$ in the legend. Analogous plots hold for $\tilde{l}^{2D}$, $\tilde{l}^{1S}$ and $\tilde{l}^{2S}$

Modified Three-Point Test

We consider for both the quasi-inextensible pantographic beam model and the geometrically nonlinear Euler beam model the reference domain to be the interval $\left[ 0,2\right]$. We enforce the three-point test boundary conditions for both models

$$\begin{aligned} 1.\ \chi \left( 0\right)= & {} \mathbf {0};\quad 2.\ \chi \left( 1\right) \cdot \mathbf {e}_{2}=\overline{u};\quad 3.\ \chi \left( 2\right) =\mathbf {0};\\&4.\ \vartheta \left( 0\right) =0;\quad 5.\ \vartheta \left( 2\right) =0 \end{aligned}$$

with the additional condition, at the midpoint $s=1$,

$$\begin{aligned}&6.\ \rho \left( 1\right) \simeq \sqrt{2}. \end{aligned}$$

Figure 3.12 shows the deformed configuration for the nearly inextensible pantographic beam model, while in Fig. 3.13 the elongation $\rho -1$ versus the reference abscissa for the nearly inextensible pantographic beam model is shown.

Fig. 3.12

Modified three-point test. Deformed configuration for the nearly inextensible pantographic beam model

Fig. 3.13

Modified three-point test. Elongation $\rho -1$ versus reference abscissa for the nearly inextensible pantographic beam model