Keywords

1 Introduction

Modular robot manipulators have attracted wildly attentions in robotics community since they are possessed of better structural adaptability and flexibility than conventional robot manipulators. An MRM is composed by standardized robotic modules, which consist of actuators, speed reducers, sensors and communication units. These modules can be assembled to desired configurations via standard mechanical interfaces according to the requirements of various tasks. Benefitting from the advantages above, MRMs are often utilized in dangerous and complex environments. Correspondingly, appropriate control systems are required to guarantee the robustness and precision of MRMs with uncertain environments.

In order to seek out appropriate control for MRMs, joint torque feedback techniques have attached attentions of both robotic researchers and industrial manufacturers. JTF technique can not only eliminate the necessity of contact model in motion control of robot-environment interactive tasks, it also facilitates in suppressing the effect of uncertain contact force created between the end-effector and payloads [1,2,3]. However, the existed JTF-based motion/force control methods have not considered the issue of optimal implementation between the error performance of joint motion and the output torque of actuator. Indeed, an ideal controllers for MRMs should be possessed of the properties that ensure the robustness of the robotic systems, and simultaneously take into account the optimal realization of the composite of error performance and output power.

Adaptive dynamic programming methodology is considered as one of the key directions to address the optimal control problems in complex systems. Some investigations reported the latest research progress of ADP-based optimal control methods for robot manipulators systems [4,5,6]. These strategies both follow the premise that the dynamic models of the robotic systems are completely unknown, thus the application of these methods are limited to address the optimal control problems of specific classes of robotic systems without implementing dynamic compensation. Dong et al. address the optimal control problems of MRMs by combining the model-based compensation control with ADP-based learning control [7], and their researches are further expanded to deal with the optimal tracking control issues of MRMs with uncertain environments [8]. However, the existing methods consider the disturbance torques, which are introduced by environmental contacts, as a class of dynamic uncertainties, and ignoring the intractability of decomposing the effects of model uncertainties and environmental contact disturbance targetedly. Indeed, there is less discussion on ADP-based robust optimal control for robot manipulators with both dynamic decomposition and optimal compensation, especially, for MRMs with uncertain environmental contact.

In this paper, a novel decentralized robust zero-sum neuro-optimal control method is presented for MRMs with uncertain environments. First, the dynamic model of the MRM systems is formulated via JTF technique, and a model-based compensation controller is designed by effectively utilizing the local dynamic information of each joint module. Second, a decentralized robust controller is proposed to deal with the compensation control issue of model uncertainties. Then, the robust optimal control problem of uncertain environment-contacted MRMs is transformed into a two-player zero-sum optimal control one. The ADP algorithm is employed to solve the HJI equation, in which the cost function, optimal control policy and worst disturbance can be approximated by constructing one critic NN and two action NNs, and then the decentralized robust zero-sum neuro-optimal control is developed. Finally, experiments are performed to verify the effectiveness of the proposed method.

2 Dynamic Model Formulation

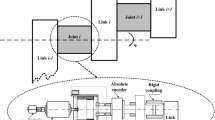
We consider the MRMs comprise n joint modules installed in series, and each integrated with a DC motor, a speed reducer, two encoders and a joint torque sensor. By referencing the modelling methods of JTF-based robot manipulators with multi-degree of freedom (DOF) [9, 10], we formulate the dynamic model of the MRM system as a synthesis of interconnected robotic joint subsystems, in which the ith joint subsystem dynamic model is represented as:

$$\begin{aligned} {{I}_{mi}}{{\gamma }_{i}}{{\ddot{q}}_{i}}+{{f}_{i}}\left( {{q}_{i}},{{{\dot{q}}}_{i}} \right) +{{z}_{i}}\left( q,\dot{q},\ddot{q} \right) +\frac{{{\tau }_{si}}}{{{\gamma }_{i}}}+{{d}_{i}}\left( {{q}_{i}} \right) ={{\tau }_{i}}, \end{aligned}$$
(1)

where the subscript “i” indicates the ith subsystem; \({{I}_{mi}}\) is the moment of inertia of actuator rotor about the rotation axis; \({{\gamma }_{i}}\) denotes the gear ratio; \({{q}_{i}},{{\dot{q}}_{i}}\) and \({{\ddot{q}}_{i}}\) are the joint angular position, velocity and acceleration respectively; \({{f}_{i}}\left( {{q}_{i}},{{{\dot{q}}}_{i}} \right) \) represents the joint lumped frictional torque; \({{z}_{i}}\left( {{q}_{i}},{{{\dot{q}}}_{i}},{{{\ddot{q}}}_{i}} \right) \) denotes the interconnected dynamic coupling (IDC) among the joint subsystems; \({{\tau }_{si}}\) represents the coupling torque at the torque sensor location; \({{d}_{i}}\left( {{q}_{i}} \right) \) is the disturbance torque and \({{\tau }_{i}}\) indicates the control torque.

(1) Joint friction

The friction term can be defined as a function with respect to joint angular position and velocity, which is given as:

$$\begin{aligned} \begin{aligned} {{f}_{i}}({{q}_{i}},{{{\dot{q}}}_{i}}) \approx&{{{\hat{f}}}_{bi}}{{{\dot{q}}}_{i}}+\left( {{{\hat{f}}}_{si}}{{e}^{(-{{{\hat{f}}}_{\tau i}}\dot{q}_{i}^{2})}}+{{{\hat{f}}}_{ci}} \right) \mathop {\mathrm {sgn}}({{{\dot{q}}}_{i}}) +{{f}_{pi}}({{q}_{i}},{{{\dot{q}}}_{i}})+Y({{{\dot{q}}}_{i}}){{{\tilde{F}}}_{i}} \\ \end{aligned}, \end{aligned}$$
(2)

where indicates the parametric uncertainty of the friction; \({{f}_{bi}}\), \({{f}_{si}}\), \({{f}_{\tau i}}\) and \({{f}_{ci}}\) represent the ideal parameters of the friction model; \({{f}_{pi}}\left( {{q}_{i}},{{{\dot{q}}}_{i}} \right) \) denotes the position dependency of friction and the other friction modeling errors; \(\mathop {\mathrm {sgn}} \left( {\dot{q}} \right) \) is a classical sign function; \({{\hat{f}}_{bi}}\), \({{\hat{f}}_{si}}\), \({{\hat{f}}_{\tau i}}\) and \({{\hat{f}}_{ci}}\) are estimated parameters of the friction model and \(Y\left( {{{\dot{q}}}_{i}} \right) \) is defined as:

(3)

(2) Interconnected dynamic coupling

The IDC term \({{z}_{i}}\left( {q},{{\dot{q}}},{{{\ddot{q}}}} \right) \), which is considered a complex nonlinear function, can be defined with respect to the positions, velocities and accelerations of the lower joint modules (from joint 1 to \(i-1\)), that is given as:

$$\begin{aligned} \begin{aligned}&{{z}_{i}}\left( q,\dot{q},\ddot{q} \right) ={{I}_{mi}}\sum \limits _{j=1}^{i-1}{D_{j}^{i}}{{{\ddot{q}}}_{j}}+{{I}_{mi}}\sum \limits _{j=2}^{i-1}{\sum \limits _{k=1}^{j-1}{\varTheta _{kj}^{i}}{{{\dot{q}}}_{k}}{{{\dot{q}}}_{j}}} ={{U}_{zi}}+{{V}_{zi}}, \\&{{U}_{zi}}={{\sum \limits _{j=1}^{i-1}{\left[ \begin{matrix} {{I}_{mi}}\hat{D}_{j}^{i} &{} {{I}_{mi}} \\ \end{matrix} \right] \left[ \begin{matrix} {{{\ddot{q}}}_{j}} &{} \tilde{D}_{j}^{i}{{{\ddot{q}}}_{j}} \\ \end{matrix} \right] }}^{T}}, {{V}_{zi}}={{\sum \limits _{j=2}^{i-1}{\sum \limits _{k=1}^{j-1}{\left[ \begin{matrix} {{I}_{mi}}\hat{\varTheta }_{kj}^{i} &{} {{I}_{mi}} \\ \end{matrix} \right] \left[ \begin{matrix} {{{\dot{q}}}_{k}}{{{\dot{q}}}_{j}} &{} \tilde{\varTheta }_{kj}^{i}{{{\dot{q}}}_{k}}{{{\dot{q}}}_{j}} \\ \end{matrix} \right] }}}^{T}}, \\ \end{aligned} \end{aligned}$$
(4)

where \(D_{j}^{i}\) and \(\varTheta _{kj}^{i}\) are given as \(D_{j}^{i}=z_{mi}^{T}{{z}_{lj}}\) and \(\varTheta _{kj}^{i}=z_{mi}^{T}\left( {{z}_{lk}}\times {{z}_{lj}} \right) \) respectively, \({{z}_{mi}}\), \({{z}_{lj}}\) and \({{z}_{lk}}\) are the unity vectors along the axis of rotation of the ith robot, jth joint and kth joint respectively. Moreover, we have the relations \(\hat{D}_{j}^{i}=D_{j}^{i}-\tilde{D}_{j}^{i}\) and \(\hat{\varTheta }_{kj}^{i}=\varTheta _{kj}^{i}-\tilde{\varTheta }_{kj}^{i}\), where \(\tilde{D}_{j}^{i}\) and \(\tilde{\varTheta }_{kj}^{i}\) are the alignment errors.

(3) Joint torque and disturbance torque

The coupled joint torques \({{\tau }_{si}}\), which are measured by using the embedded torque sensors, can be represented as the following form:

$$\begin{aligned} {{\tau }_{si}}={{\tau }_{sri}}+{{\tau }_{sci}}, \end{aligned}$$
(5)

where \({{\tau }_{sri}}\) indicates the joint torque that is obtained in free space and \({{\tau }_{sci}}\) denotes the torque produced by environmental contact in constrained space. Besides, the disturbance torque term \({{d}_{i}}\left( {{q}_{i}} \right) \) can be defined as:

$$\begin{aligned} {{d}_{i}}\left( {{q}_{i}} \right) ={{d}_{is}}\left( {{q}_{i}} \right) +{{d}_{ic}}\left( {{q}_{i}} \right) , \end{aligned}$$
(6)

where \({{d}_{is}}\left( {{q}_{i}} \right) \) represents the disturbance of torque sensor and \({{d}_{ic}}\left( {{q}_{i}} \right) \) indicates unmeasured environmental contact torque in joint space.

Assumption 1

The uncertainty term \({{\tilde{F}}_{i}}\) is bounded by \(\left| {{{\tilde{F}}}_{i}} \right| \le {{\rho }_{Fin}}\), the friction modeling error is bounded by \(\left| Y\left( {{{\dot{q}}}_{i}} \right) {{{\tilde{F}}}_{i}} \right| \le Y\left( {{{\dot{q}}}_{i}} \right) {{\rho }_{Fin}}\) and \({{f}_{pi}}\left( {{q}_{i}},{{{\dot{q}}}_{i}} \right) \) is bounded by \(\left| {{f}_{pi}}\left( {{q}_{i}},\!{{{\dot{q}}}_{i}} \right) \right| \!\le \! {{\rho }_{fpi}}\).

Assumption 2

The terms \({{U}_{zi}}\) and \({{V}_{zi}}\) are bounded by \(\left| {{U}_{zi}} \right| \le {{\rho }_{Ui}}, \left| {{V}_{zi}} \right| \le {{\rho }_{Vi}}\).

Assumption 3

The disturbance \({{d}_{is}}\left( {{q}_{i}} \right) \) is bounded by \(\left| {{d}_{is}}\left( {{q}_{i}} \right) \right| \le {{\rho }_{dsi}}\) and the unmeasured environmental contact torque \({{d}_{ic}}\left( {{q}_{i}} \right) \) is bounded by \(\left| {{d}_{ic}}\left( {{q}_{i}} \right) \right| \le {{\rho }_{dci}}\).

Then, define \({{B}_{i}}={{\left( {{I}_{mi}}{{\gamma }_{i}} \right) }^{-1}}\in {{R}^{+}}\) and the state vector \({{x}_{i}}={{\left[ \begin{matrix} {{x}_{i1}} &{} {{x}_{i2}} \\ \end{matrix} \right] }^{T}}={{\left[ \begin{matrix} {{q}_{i}} &{} {{{\dot{q}}}_{i}} \\ \end{matrix} \right] }^{T}}\in {{R}^{2\times 1}}\) and the control input \({{u}_{i}}={{\tau }_{i}}\in {{R}^{1\times 1}},i=1,2,\ldots n\), the state space of ith subsystem can be formulated as

$$\begin{aligned} {{S}_{i}}=\left\{ \begin{aligned}&{{{\dot{x}}}_{i1}}={{x}_{i2}} \\&{{{\dot{x}}}_{i2}}={{\phi }_{i}}\left( {{x}_{i}} \right) +{{\upsilon }_{i}}\left( x \right) +{{p}_{i}}\left( {{x}_{i}} \right) +{{B}_{i}}{{u}_{i}} \\&y={{x}_{i1}} \\ \end{aligned} \right. , \end{aligned}$$
(7)

where \({{\phi }_{i}}\left( {{x}_{i}} \right) \), \({{\upsilon }_{i}}\left( x \right) \) and \({{p}_{i}}\left( {{x}_{i}} \right) \) are represented as follows:

$$\begin{aligned} \begin{aligned}&{{\phi }_{i}}\left( {{x}_{i}} \right) ={{B}_{i}}\left( \begin{aligned}&-\left( {{{\hat{f}}}_{si}}{{e}^{\left( -{{{\hat{f}}}_{\tau i}}\dot{q}_{i}^{2} \right) }}+{{{\hat{f}}}_{ci}} \right) \mathop {\mathrm {sgn}} \left( {{{\dot{q}}}_{i}} \right) \\&-{{{\hat{f}}}_{bi}}{{{\dot{q}}}_{i}}-\frac{{{\tau }_{si}}}{{{\gamma }_{i}}} \\ \end{aligned} \right) \\&{{\upsilon }_{i}}\left( x \right) ={{B}_{i}}\left( -{{U}_{zi}}\!-{{V}_{zi}}-{{f}_{pi}}\left( {{q}_{i}},{{{\dot{q}}}_{i}} \right) \!-\!Y\left( {{{\dot{q}}}_{i}} \right) {{{\tilde{F}}}_{i}} \right) \\&{{p}_{i}}\left( {{x}_{i}} \right) ={{B}_{i}}\left( -{{d}_{is}}\left( {{q}_{i}} \right) -{{d}_{ic}}\left( {{q}_{i}} \right) \right) \\ \end{aligned}. \end{aligned}$$
(8)

Next, a decentralized robust zero-sum optimal control method is presented for MRMs to ensure that both position and velocity of the closed-loop robotic systems are asymptotically stable.

3 Decentralized Robust Zero-Sum Neuro-Optimal Control Based on ADP

Consider the MRM systems with the dynamic model formulation (1) and the state space description (7), if the contact disturbance \({{p}_{i}}\left( {{x}_{i}} \right) \) is viewed as a system control input, the robust optimal control problem can be transformed into a two-player zero-sum optimal control issue, in which the continuously differentiable infinite horizon local cost function can be defined as follows:

$$\begin{aligned} {{J}_{i}}\left( {{s}_{i0}}\left( {{e}_{i}} \right) \right) =\int _{0}^{\infty }{\left\{ \begin{aligned}&{{s}_{i}}{{\left( {{e}_{i}}\left( \tau \right) \right) }^{T}}{{Q}_{i}}{{s}_{i}}\left( {{e}_{i}}\left( \tau \right) \right) +{{u}_{i}}{{\left( \tau \right) }^{T}}{{R}_{i}}{{u}_{i}}\left( \tau \right) \\&-\gamma _{pi}^{2}{{p}_{i}}{{\left( {{x}_{i}}\left( \tau \right) \right) }^{T}}{{p}_{i}}\left( {{x}_{i}}\left( \tau \right) \right) \end{aligned} \right\} }d\tau , \end{aligned}$$
(9)

where

$$\begin{aligned} {{s}_{i}}\left( {{e}_{i}} \right) ={{\dot{e}}_{i}}+{{\alpha }_{ei}}{{e}_{i}} \end{aligned}$$
(10)

is a filtered error function with the initial filtered error \({{s}_{i0}}\left( {{e}_{i}} \right) ={{s}_{i}}\left( 0 \right) \); \({{e}_{i}}={{x}_{i1}}-{{x}_{id}}\) and \({{\dot{e}}_{i}}={{x}_{i2}}-{{\dot{x}}_{id}}\) indicate the position and velocity tracking error of the ith joint module respectively; \({{x}_{id}}\), \({{\dot{x}}_{id}}\) and \({{\ddot{x}}_{id}}\) represent the desired angular position, velocity and acceleration that are known and bounded reference states. \(Q_{i}^{T}={{Q}_{i}}\), \(R_{i}^{T}={{R}_{i}}\) denote the positive constant matrixes; \({{\alpha }_{ei}}\) and \({{\gamma }_{pi}}\) are determined positive constants.

According to (9), one can define the local Hamiltonian as:

$$\begin{aligned} \begin{aligned}&{{H}_{i}}\left( {{s}_{i}},{{u}_{i}},{{p}_{i}},\nabla {{J}_{i}} \right) =s_{i}^{T}{{Q}_{i}}{{s}_{i}}+u_{i}^{T}{{R}_{i}}{{u}_{i}} \\&+\nabla J_{i}^{T}\left( {{s}_{i}} \right) \left( {{\phi }_{i}}+{{\upsilon }_{i}}+{{p}_{i}}+{{\alpha }_{ei}}{{{\dot{e}}}_{i}}+{{B}_{i}}{{u}_{i}}-{{{\ddot{x}}}_{id}} \right) -\gamma _{pi}^{2}p_{i}^{T}{{p}_{i}} \\ \end{aligned}, \end{aligned}$$
(11)

where \(\nabla {{J}_{i}}\left( {{s}_{i}} \right) =\left( {\partial {{J}_{i}}\left( {{s}_{i}} \right) }/{\partial {{s}_{i}}} \right) \) denotes the partial derivative of \({{J}_{i}}\left( {{s}_{i}} \right) \) with regard of \({{s}_{i}}\). Define the utility function as

$$\begin{aligned} {{\varOmega }_{i}}\left( {{s}_{i}},{{u}_{i}},{{p}_{i}} \right) =s_{i}^{T}{{Q}_{i}}{{s}_{i}}+u_{i}^{T}{{R}_{i}}{{u}_{i}}-\gamma _{pi}^{2}p_{i}^{T}{{p}_{i}}. \end{aligned}$$
(12)

Then, one obtain that the optimal local cost function \(J_{i}^{*}\) satisfies:

$$\begin{aligned} \begin{aligned} J_{i}^{*}\left( {{s}_{i}} \right)&=\underset{{{u}_{i}}}{\mathop {\min }}\,\underset{{{p}_{i}}}{\mathop {\max }}\,\int _{0}^{\infty }{{{\varOmega }_{i}}\left( {{s}_{i}},{{u}_{i}},{{p}_{i}} \right) d\tau } =\underset{{{p}_{i}}}{\mathop {\max }}\,\underset{{{u}_{i}}}{\mathop {\min }}\,\int _{0}^{\infty }{{{\varOmega }_{i}}\left( {{s}_{i}},{{u}_{i}},{{p}_{i}} \right) d\tau } . \end{aligned} \end{aligned}$$
(13)

According to (11) and (13), the local optimal control pair (\(u_{i}^{*},p_{i}^{*}\)) satisfies the following HJI equation:

$$\begin{aligned} \begin{aligned} 0\,=\,&\nabla J_{i}^{*T}\left( {{s}_{i}} \right) \left( {{\phi }_{i}}+{{\upsilon }_{i}}+{p_{i}^{*}}+{{\alpha }_{ei}}{{{\dot{e}}}_{i}}+{{B}_{i}}{u_{i}^{*}}-{{{\ddot{x}}}_{id}} \right) +{{\varOmega }_{i}}\left( {{s}_{i}},{u_{i}^{*}},{p_{i}^{*}} \right) . \end{aligned} \end{aligned}$$
(14)

On the basis of the principle of optimality, the local optimal control pair (\(u_{i}^{*},p_{i}^{*}\)) can be represented as follows:

$$\begin{aligned} \begin{aligned} u_{i}^{*}=-\frac{1}{2}R_{i}^{-1}B_{i}^{T}\nabla J_{i}^{*}, \quad p_{i}^{*}=\frac{1}{2\gamma _{pi}^{2}}\nabla J_{i}^{*} \end{aligned}. \end{aligned}$$
(15)

Rewriting the optimal control law \(u_{i}^{*}\) of the ith subsystem as:

$$\begin{aligned} u_{i}^{*}={{u}_{i1}}+{{u}_{i2}}+u_{i3}^{*} \end{aligned}$$
(16)

to deal with modeled dynamic term \({{\phi }_{i}}\), model uncertainty term \({{\upsilon }_{i}}\) and contact disturbance term \({{p}_{i}}\) respectively, then, the HJI equation can be modified as:

$$\begin{aligned} 0\,=\,\nabla J_{i}^{*}\left( \begin{aligned}&{{\phi }_{i}}+{{\upsilon }_{i}}+{p_{i}^{*}}+{{\alpha }_{ei}}{{{\dot{e}}}_{i}}-{{{\ddot{x}}}_{id}} \\&+{{B}_{i}}{{u}_{i1}}+{{B}_{i}}{{u}_{i2}}+{{B}_{i}}u_{i3}^{*} \\ \end{aligned} \right) +{{\varOmega }_{i}}\left( {{s}_{i}},u_{i}^{*},p_{i}^{*} \right) . \end{aligned}$$
(17)

Therefore, the zero-sum optimal control problem has been transformed into the one of obtaining the decentralized control laws \({{u}_{i1}}\), \({{u}_{i2}}\) and \(u_{i3}^{*}\) respectively, and therefore, to realize the optimal compensation of model uncertainty and environmental contact disturbance of the MRM system.

First, we can design control law \({{u}_{i1}}\), that is given as:

$$\begin{aligned} {{u}_{i1}}=-\left( \begin{aligned}&\!-\left( \!{{{\hat{f}}}_{si}}{{e}^{\!\left( \!-{{{\hat{f}}}_{\tau i}}x_{i2}^{2}\right) }}+{{{\hat{f}}}_{ci}}\right) \mathop {\mathrm {sgn}} \left( {{x}_{i2}}\!\right) \!-{{{\hat{f}}}_{bi}}{{x}_{i2}}-B_{i}^{-1}{{{\ddot{x}}}_{id}}-\frac{{{\tau }_{si}}}{{{\gamma }_{i}}}+B_{i}^{-1}{{\alpha }_{ei}}{{{\dot{e}}}_{i}} \\ \end{aligned}\! \right) . \end{aligned}$$
(18)

Second, we consider that the MRM systems, which work in free space, is possessed of accurate joint torque sensing. Thus, substituting (18) into (17), one obtains:

$$\begin{aligned} 0={{\varOmega }_{i}}\left( {{s}_{i}},u_{i}^{*},p_{i}^{*} \right) \!+\nabla J_{i}^{*}\left( {{\upsilon }_{i}}\!+p_{i}^{*}\!+{{B}_{i}}{{u}_{i2}}+{{B}_{i}}u_{i3}^{*} \right) . \end{aligned}$$
(19)

Note that we have \(p_{i}^{*}=u_{i3}^{*}=0\) when the MRM system works in free space, therefore, combining the time derivative of (10) and the model-based compensation control (18), one obtains

$$\begin{aligned} \begin{aligned} {{{\dot{s}}}_{i}}&={{B}_{i}}\left( \begin{aligned}&-{{f}_{pi}}\left( {{x}_{i1}},{{x}_{i2}} \right) -{{U}_{zi}} -Y\left( {{x}_{i2}} \right) {{{\tilde{F}}}_{i}}-{{V}_{zi}} \\ \end{aligned} \right) +{{B}_{i}}{{u}_{i2}} \\ \end{aligned}. \end{aligned}$$
(20)

Here, we introduce the decentralized robust control \({{u}_{i2}}\) to compensate the effects of model uncertainties. For the unmodeled friction in (2), we decomposed \({{\tilde{F}}_{i}}\) as the summation of constant part and variable part, which is given as:

$$\begin{aligned} {{\tilde{F}}_{i}}={{\tilde{F}}_{ic}}+{{\tilde{F}}_{iv}}, \end{aligned}$$
(21)

where \({{\tilde{F}}_{ic}}\) indicates an unknown constant vector and \({{\tilde{F}}_{iv}}\) denotes an unknown variable vector that is bounded as:

$$\begin{aligned} \left| {{{\tilde{F}}}_{iv}} \right| \le {{\rho }_{Fivn}},n=1,2,3,4, \end{aligned}$$
(22)

in which \({{\rho }_{Fivn}}={{[\begin{matrix} {{\rho }_{Fiv1}} &{} {{\rho }_{Fiv2}} &{} {{\rho }_{Fiv3}} &{} {{\rho }_{Fiv4}} \\ \end{matrix}]}^{T}}\) is a determined constant vector. Then, one can design the robust control law \({{u}_{i2f}}\), which is given as:

$$\begin{aligned} {{u}_{i2f}}={{u}_{i2fu}}+Y\left( {{x}_{i2}} \right) \left( {{u}_{i2fc}}+{{u}_{i2fv}} \right) , \end{aligned}$$
(23)

where \({{u}_{i2fu}}\) is designed to compensate friction term \({{f}_{pi}}\left( {{x}_{i1}},{{x}_{i2}} \right) \); \({{u}_{i2fc}}\), \({{u}_{i2fv}}\) are used to compensate the effect of uncertainties \({{\tilde{F}}_{ic}}\) and \({{\tilde{F}}_{iv}}\) respectively:

$$\begin{aligned} {{u}_{i2fu}}=\left\{ \begin{aligned}&\begin{matrix} -{{\rho }_{fpi}}\frac{{{s}_{i}}}{\left| {{s}_{i}} \right| } &{} if\ \left| {{s}_{i}} \right| >{{\varepsilon }_{ifu}} \\ \end{matrix} \\&\begin{matrix} -{{\rho }_{fpi}}\frac{{{s}_{i}}}{{{\varepsilon }_{ifu}} } &{} if\ \left| {{s}_{i}} \right| \le {{\varepsilon }_{ifu}} \\ \end{matrix} \\ \end{aligned} \right. , \end{aligned}$$
(24)
$$\begin{aligned} {{u}_{i2fc}}=-{{\varepsilon }_{ifc}}\left( \int _{0}^{t}{Y{{\left( {{x}_{i2}} \right) }}{{s}_{i}}}d\tau +s_{i} \right) , \end{aligned}$$
(25)
$$\begin{aligned} \begin{aligned} {{u}_{i2fv}}&\!=\!\left\{ \begin{aligned}&\begin{matrix} -{{\rho }_{Fivn}}\frac{Y{{\left( {{x}_{i2}} \right) }}{{s}_{i}}}{\left| Y{{\left( {{x}_{i2}} \right) } }{{s}_{i}} \right| } &{} if\ \left| Y{{\left( {{x}_{i2}} \right) } }{{s}_{i}} \right| >{{\varepsilon }_{ifvn}} \\ \end{matrix} \\&\begin{matrix} -{{\rho }_{Fivn}}\frac{Y{{\left( {{x}_{i2}} \right) }}{{s}_{i}}}{ {{\varepsilon }_{ifvn}} } &{} if\ \left| Y{{\left( {{x}_{i2}} \right) } }{{s}_{i}} \right| \le {{\varepsilon }_{ifvn}} \\ \end{matrix} \\ \end{aligned} \right. , n&=1,2,3,4 \end{aligned} \end{aligned}$$
(26)

where \({{\varepsilon }_{ifu}}\), \({{\varepsilon }_{ifc}}\) and \({{\varepsilon }_{ifvn}}\) are determined positive parameters. Moreover, we decomposed the terms of \({{U}_{zi}}\) and \({{V}_{zi}}\) as:

$$\begin{aligned} \begin{aligned} {{U}_{zi}}={{U}_{zic}}+{{U}_{ziv}},\quad {{V}_{zi}}={{V}_{zic}}+{{V}_{ziv}} \end{aligned}, \end{aligned}$$
(27)

where \({{U}_{zic}}\) and \({{V}_{zic}}\) are with known up-bounds; \({{U}_{ziv}}\) and \({{V}_{ziv}}\) are bounded as:

$$\begin{aligned} \begin{aligned} \left| {{U}_{ziv}} \right| \le {{\rho }_{Uiv}}, \quad \left| {{V}_{ziv}} \right| \le {{\rho }_{Viv}} \end{aligned}, \end{aligned}$$
(28)

where \({{\rho }_{Uiv}}\) and \({{\rho }_{Viv}}\) are constant up-bounds to be determined.

Then, by adopting the decomposition-based analysis of the uncertainties, we can design the robust control law \({{u}_{i2h}}\), which is formulated as:

$$\begin{aligned} {{u}_{i2h}}={{u}_{i2hU}}+{{u}_{i2hV}}, \end{aligned}$$
(29)

where \({{u}_{i2hU}}\) is used to compensate the effect of the term \({{U}_{zi}}\), that is given as:

$$\begin{aligned} \begin{aligned}&{{u}_{i2hU}}={{u}_{i2hUc}}+{{u}_{i2hUv}}, \\&{\!{u}_{i2hUc}}=-{{\varepsilon }_{iUs}}\left( \!\int _{0}^{t}{{{\varepsilon }_{iUs}}{{s}_{i}}d\tau }+s_{i}\!\right) , {{u}_{i2hUv}}\text {=}\left\{ \!\begin{aligned}&\begin{matrix} -{{\rho }_{Uiv}}\frac{{{\varepsilon }_{iUs}}{{s}_{i}}}{\left| {{\varepsilon }_{iUs}}{{s}_{i}}\!\right| } &{} if\ \left| {{\varepsilon }_{iUs}}{{s}_{i}} \right| \!>\!{{\varepsilon }_{iUB}} \\ \end{matrix} \\&\begin{matrix} -{{\rho }_{Uiv}}\frac{{{\varepsilon }_{iUs}}{{s}_{i}}}{ {{\varepsilon }_{iUB}}} &{} if\ \left| {{\varepsilon }_{iUs}}{{s}_{i}} \right| \!\le \! {{\varepsilon }_{iUB}} \\ \end{matrix} \\ \end{aligned} \right. \\ \end{aligned}, \end{aligned}$$
(30)

where \({{\varepsilon }_{iUs}}\) and \({{\varepsilon }_{iUB}}\) are positive parameters to be determined. Moreover, one can design the control law \({{u}_{i2hV}}\) to compensate the effect of the term \({{V}_{zi}}\):

$$\begin{aligned} \begin{aligned}&{{u}_{i2hV}}={{u}_{i2hVc}}+{{u}_{i2hVv}} \\&{{u}_{i2hVc}}\!=\!-{{\varepsilon }_{iVs}}\left( \!\int _{0}^{t}{{{\varepsilon }_{iVs}}{{s}_{i}}d\tau }+s_{i}\!\right) , {{u}_{i2hVv}}\!=\!\left\{ \begin{aligned}&\begin{matrix} -{{\rho }_{Viv}}\frac{{{\varepsilon }_{iVs}}{{s}_{i}}}{\left| {{\varepsilon }_{iVs}}{{s}_{i}} \right| } &{}\! if\ \! \left| {{\varepsilon }_{iVs}}{{s}_{i}} \right| \!>\!{{\varepsilon }_{iVB}} \\ \end{matrix} \\&\begin{matrix} -{{\rho }_{Viv}}\frac{{{\varepsilon }_{iVs}}{{s}_{i}}}{ {{\varepsilon }_{iVB}} } &{} \!if\ \! \left| {{\varepsilon }_{iVs}}{{s}_{i}} \right| \le {{\varepsilon }_{iVB}} \\ \end{matrix} \\ \end{aligned} \right. \\ \end{aligned}, \end{aligned}$$
(31)

where \({{\varepsilon }_{iVs}}\) and \({{\varepsilon }_{iVB}}\) are positive parameters to be determined. Then, by combining (23) with (29), one obtain the decentralized control law \({{u}_{i2}}\), which is given as follows:

$$\begin{aligned} {{u}_{i2}}={{u}_{i2f}}+{{u}_{i2h}}. \end{aligned}$$
(32)

Then, we introduce the critic NN, u-action NN and p-action NN to approximate the performance index function \({{J}_{i}}\left( {{s}_{i}} \right) \), the optimal control law \(u_{i3}^{*}\) and the worst contact disturbance \(p_{i}^{*}\) respectively.

By employing RBF NNs, the ideal critic NN is represented as:

$$\begin{aligned} {{J}_{i}}\left( {{s}_{i}} \right) =w_{ci}^{T}{{\sigma }_{ci}}\left( {{s}_{i}} \right) +{{\varepsilon }_{ci}}, \end{aligned}$$
(33)

where \({{w}_{ci}}\) is the unknown ideal NN weight, \({{\varepsilon }_{ci}}\) represent the finite approximation error of the critic NN, \({{\sigma }_{ci}}\left( {{s}_{i}} \right) \) indicates a standard activation function. Besides, the gradient of the approximated cost function is given as:

$$\begin{aligned} \nabla {{J}_{i}}\left( {{s}_{i}} \right) =\nabla {{\sigma }_{ci}}{{\left( {{s}_{i}} \right) }^{T}}{{w}_{ci}}+\nabla \varepsilon _{ci}^{T}, \end{aligned}$$
(34)

where \(\nabla {{\sigma }_{ci}}\left( {{s}_{i}} \right) ={\partial {{\sigma }_{ci}}\left( {{s}_{i}} \right) }/{\partial {{s}_{i}}}\;\) indicates the gradients of the activation function and \(\nabla {{\varepsilon }_{ci}}\) is the gradient error. Then, one can rewrite the Hamiltonian and obtain the following relation:

$$\begin{aligned} \begin{aligned} {{H}_{i}}\left( {{s}_{i}},{{u}_{i}},{{p}_{i}},{{w}_{ci}} \right) = {{\varOmega }_{i}}\left( {{s}_{i}},{{u}_{i}},{{p}_{i}} \right) +\left( w_{ci}^{T} \nabla {{\sigma }_{ci}}\left( {{s}_{i}} \right) \right) {{{\dot{s}}}_{i}}-{{e}_{cHi}} = 0 \end{aligned}, \end{aligned}$$
(35)

where \({{e}_{cHi}}\) denotes the approximation error of the critic NN:

$$\begin{aligned} {{e}_{cHi}}={{\varOmega }_{i}}+\left( w_{ci}^{T}\nabla {{\sigma }_{ci}} \right) {{\dot{s}}_{i}}. \end{aligned}$$
(36)

Let \({{\hat{w}}_{ci}}\) be the estimated weight vector of \({{w}_{ci}}\), therefore, one obtains:

$$\begin{aligned} {{\hat{J}}_{i}}\left( {{s}_{i}} \right) =\hat{w}_{ci}^{T}{{\sigma }_{ci}}\left( {{s}_{i}} \right) . \end{aligned}$$
(37)

Then, one can define the approximate Hamilton function as:

$$\begin{aligned} \begin{aligned} {{\hat{H}}_{i}}\left( {{s}_{i}},{{u}_{i}},{{p}_{i}},{{{\hat{w}}}_{ci}} \right) = {{\varOmega }_{i}}\left( {{s}_{i}},{{u}_{i}},{{p}_{i}} \right) +\left( \hat{w}_{ci}^{T}\nabla {{\sigma }_{ci}}\left( {{s}_{i}} \right) \right) {{\dot{s}}_{i}}. \end{aligned} \end{aligned}$$
(38)

Define the weight approximation error \({{\tilde{w}}_{ci}}={{w}_{ci}}-{{\hat{w}}_{ci}}\), then, one obtains:

$$\begin{aligned} {{e}_{ci}}={{e}_{cHi}}-\tilde{w}_{ci}^{T}\nabla {{\sigma }_{ci}}\left( {{s}_{i}} \right) {{\dot{s}}_{i}}. \end{aligned}$$
(39)

Define the residual error function \({{E}_{ci}}=\frac{1}{2}e_{ci}^{2}\), which is minimized to adjust the weight vector of the critic NN, that is updated by

$$\begin{aligned} {{\dot{\hat{w}}}_{ci}}=-{{\alpha }_{ci}}\left( \frac{\partial {{E}_{ci}}}{\partial {{{\hat{w}}}_{ci}}} \right) =-{{\alpha }_{ci}}\frac{{{p}_{ci}}\left( p_{ci}^{T}{{{\hat{w}}}_{ci}}+{{\varOmega }_{i}} \right) }{{{\left( p_{ci}^{T}{{p}_{ci}}+1 \right) }^{2}}}, \end{aligned}$$
(40)

where \({{\alpha }_{ci}}>0\) is the learning rate of the critic NN, and \({{p}_{ci}}\text {=}\nabla {{\sigma }_{ci}}\left( {{s}_{i}} \right) {{\dot{s}}_{i}}\).

Then, we employ the action NNs to approximate \(u_{i3}^{*}\) and \(p_{i}^{*}\) respectively. The ideal u- and p-action NNs are given as follows:

$$\begin{aligned} u_{i3}^{*}=w_{ai}^{T}{{\sigma }_{ai}}\left( {{s}_{i}} \right) +{{\varepsilon }_{ai}}, \quad p_{i}^{*}=w_{pi}^{T}{{\sigma }_{pi}}\left( {{s}_{i}} \right) +{{\varepsilon }_{pi}}, \end{aligned}$$
(41)

where \({{w}_{ai}}\), \({{w}_{pi}}\) represent the ideal weight vectors, \({{\sigma }_{ai}}\), \({{\sigma }_{pi}}\) denote the activation functions and \({{\varepsilon }_{ai}}\), \({{\varepsilon }_{pi}}\) are the finite approximation errors of u- and p-action respectively. Let \({{\hat{w}}_{ai}}\) and \({{\hat{w}}_{pi}}\) be the estimation weight vectors of \({{w}_{ai}}\) and \({{w}_{pi}}\), then we have:

$$\begin{aligned} {{\hat{u}}_{i3}}=\hat{w}_{ai}^{T}{{\sigma }_{ai}}\left( {{s}_{i}} \right) , \quad {{\hat{p}}_{i}}=\hat{w}_{pi}^{T}{{\sigma }_{pi}}\left( {{s}_{i}} \right) . \end{aligned}$$
(42)

Since \(\left( {\partial {{{\hat{H}}}_{i}}\left( {{s}_{i}},{{{\hat{u}}}_{i}},{{{\hat{p}}}_{i}},{{{\hat{w}}}_{ci}} \right) }/{\partial {{{\hat{u}}}_{i}}}\; \right) =0\) and \(\left( {\partial {{{\hat{H}}}_{i}}\left( {{s}_{i}},{{{\hat{u}}}_{i}},{{{\hat{p}}}_{i}},{{{\hat{w}}}_{ci}} \right) }/{\partial {{{\hat{p}}}_{i}}}\; \right) =0\), so that \({{\hat{u}}_{i3}}\) and \({{\hat{p}}_{i}}\) can be further described as follows:

$$\begin{aligned} {{\hat{u}}_{i3}}=-\frac{1}{2}R_{i}^{-1}B_{i}^{T}\nabla \sigma _{ci}^{T}\left( {{s}_{i}} \right) {{\hat{w}}_{ci}},\quad {{\hat{p}}_{i}}=\frac{1}{2\gamma _{pi}^{2}}\nabla \sigma _{ci}^{T}\left( {{s}_{i}} \right) {{\hat{w}}_{ci}}, \end{aligned}$$
(43)

where the update laws for u- and p-action NN weights are given as:

$$\begin{aligned} {{\dot{\hat{w}}}_{ai}}=-{{\alpha }_{ai}}{{\sigma }_{ai}}\left( {{s}_{i}} \right) \cdot {{\left( \! \begin{aligned}&\hat{w}_{ai}^{T}{{\sigma }_{ai}}\left( {{s}_{i}} \right) +\frac{1}{2}R_{i}^{-1}B_{i}^{T}\nabla \sigma _{ci}^{T}\left( {{s}_{i}} \right) {{{\hat{w}}}_{ci}} \\ \end{aligned}\! \right) }^{T}}, \end{aligned}$$
(44)
$$\begin{aligned} {{\dot{\hat{w}}}_{pi}}=-{{\alpha }_{pi}}{{\sigma }_{pi}}\left( {{s}_{i}} \right) \cdot {{\left( \begin{aligned}&\hat{w}_{pi}^{T}{{\sigma }_{pi}}\left( {{s}_{i}} \right) -\frac{1}{2\gamma _{pi}^{2}}\nabla \sigma _{ci}^{T}\left( {{s}_{i}} \right) {{{\hat{w}}}_{ci}} \\ \end{aligned} \right) }^{T}}, \end{aligned}$$
(45)

where \({{\alpha }_{ai}}\) and \({{\alpha }_{pi}}\) are the positive learning rates of u- and p-action NNs.

Then, by combining (18), (32) with (43), the proposed decentralized robust zero-sum neuro-optimal control law \(u_{i}^{*}\) is given as:

$$\begin{aligned} \begin{aligned} u_{i}^{*}=&-\left( \begin{aligned}&-{{{\hat{f}}}_{bi}}{{x}_{i2}}-B_{i}^{-1}{{{\ddot{x}}}_{id}}-\frac{{{\tau }_{si}}}{{{\gamma }_{i}}}+B_{i}^{-1}{{\alpha }_{ei}}{{{\dot{e}}}_{i}} \\&-\left( \! {{{\hat{f}}}_{si}}{{e}^{\left( -{{{\hat{f}}}_{\tau i}}x_{i2}^{2} \right) }}+{{{\hat{f}}}_{ci}} \right) \mathop {\mathrm {sgn}} \left( {{x}_{i2}} \right) \\ \end{aligned}\! \right) -\left( -{{u}_{i2hU}}-{{u}_{i2hV}} \right) \\&-\left( -{{u}_{i2fu}}-Y\left( {{x}_{i2}} \right) \left( {{u}_{i2fc}}+{{u}_{i2fv}} \right) \right) -\frac{1}{2}R_{i}^{-1}B_{i}^{T}\nabla \sigma _{ci}^{T}{{{\hat{w}}}_{ci}} \\ \end{aligned}. \end{aligned}$$
(46)

Theorem 1

Consider an n-DOF modular robot manipulator, with the dynamic model of the ith joint subsystem formulated in (1); the model uncertainties existed in (2), (4) and the environmental contact disturbance given in (6). The closed-loop robotic system is asymptotically stable under the decentralized robust zero-sum neuro-optimal control law proposed by (46).

Proof

A Lyapunov function candidate is selected as:

$$\begin{aligned} \begin{aligned} {{V}_{g}}\left( t \right)&=\sum \limits _{i=1}^{n}{{{V}_{gi}}}\left( t \right) =\sum \limits _{i=1}^{n}{\left( \begin{aligned}&{{\delta }_{si}}s_{i}^{T}{{s}_{i}}+{{\delta }_{\varOmega i}}{{J}_{i}}\left( {{s}_{i}} \right) \\&+{{\delta }_{pi}}\int _{t}^{\infty }{\gamma _{pi}^{2}p_{i}^{T}\left( \tau \right) {{p}_{i}}\left( \tau \right) d\tau } \\ \end{aligned} \right) } \\ \end{aligned}, \end{aligned}$$
(47)

where \({{\delta }_{si}}>0\) and \({{\delta }_{pi}}\ge {{\delta }_{\varOmega i}}>0\) are determined positive definite constants. Then, one obtains the time derivative of (47) that is given as:

$$\begin{aligned} \begin{aligned}&{{{\dot{V}}}_{g}}\left( t \right) \!\le \!\sum \limits _{i=1}^{n}{\left( 2{{\delta }_{si}}\left( {{\left\| {{s}_{i}} \right\| }^{2}}\!+\!\frac{1}{2}{{\left\| {{B}_{i}} \right\| }^{2}} {{\left\| u_{i3}^{*} \right\| }^{2}} \right) \right) }\!-\!\sum \limits _{i=1}^{n}{\left( -{{\delta }_{si}}\!-\!\left( \!{{\delta }_{\varOmega i}}-{{\delta }_{pi}}\!\right) \gamma _{pi}^{2} \right) } {{\left\| {{p}_{i}} \right\| }^{2}} \\&-\sum \limits _{i=1}^{n}{{{\delta }_{\varOmega i}}\left( \begin{aligned}&{{\lambda }_{\min }}\left( {{Q}_{i}} \right) {{\left\| {{s}_{i}} \right\| }^{2}}+{{\lambda }_{\min }}\left( {{R}_{i}} \right) {{\left\| {{u}_{i1}} \right\| }^{2}} \\&+{{\lambda }_{\min }}\left( {{R}_{i}} \right) {{\left\| {{u}_{i2}} \right\| }^{2}}+{{\lambda }_{\min }}\left( {{R}_{i}} \right) {{\left\| u_{i3}^{*} \right\| }^{2}} \\ \end{aligned} \right) } \\ =&-\sum \limits _{i=1}^{n}{\left( {{\delta }_{\varOmega i}}{{\lambda }_{\min }}\left( {{Q}_{i}} \right) -2{{\delta }_{si}} \right) {{\left\| {{s}_{i}} \right\| }^{2}}} -\sum \limits _{i=1}^{n}{\left( {{\delta }_{\varOmega i}}{{\lambda }_{\min }}\left( {{R}_{i}} \right) \right) {{\left\| {{u}_{i1}} \right\| }^{2}}} \\&-\sum \limits _{i=1}^{n}{\left( {{\delta }_{\varOmega i}}{{\lambda }_{\min }}\left( {{R}_{i}} \right) \right) {{\left\| {{u}_{i2}} \right\| }^{2}}} -\sum \limits _{i=1}^{n}{\left( {{\delta }_{\varOmega i}}{{\lambda }_{\min }}\left( {{R}_{i}} \right) -{{\delta }_{si}}{{\left\| {{B}_{i}} \right\| }^{2}} \right) } {{\left\| u_{i3}^{*} \right\| }^{2}} \\&-\sum \limits _{i=1}^{n}{\left( -{{\delta }_{si}}-\left( {{\delta }_{\varOmega i}}-{{\delta }_{pi}} \right) \gamma _{pi}^{2} \right) } {{\left\| {{p}_{i}} \right\| }^{2}} \\ \end{aligned}. \end{aligned}$$
(48)

Therefore, we know that \({{\dot{V}}_{g}}\left( t \right) \le 0\) when the following condition holds:

$$\begin{aligned} \begin{aligned} {{\lambda }_{\min }}\left( {{Q}_{i}} \right) \ge \frac{2{{\delta }_{si}}}{{{\delta }_{\varOmega i}}},\quad {{\lambda }_{\min }}\left( {{R}_{i}} \right) \ge \frac{{{\delta }_{si}}}{{{\delta }_{\varOmega i}}I_{mi}^{2}\gamma _{i}^{2}},\quad {{\delta }_{pi}}\ge {{\delta }_{\varOmega i}}+\frac{{{\delta }_{si}}}{\gamma _{pi}^{2}} \\ \end{aligned} . \end{aligned}$$
(49)

Besides, from (48), one obtains that if (49) is satisfied, then \({{\dot{V}}_{g}}\left( t \right) <0\) for any \({{s}_{i}}\ne 0\). Therefore, by the Lyapunov theory, the closed-loop robotic system is asymptotically stable under the proposed decentralized robust zero-sum neuro-optimal control (46). This completes the proof of the Theorem 1.

4 Experimental Results

In this section, the experimental results are presented based on the experimental platform as illustrated in [8], and the experimental results are collected to verify the effectiveness of the proposed control method. We consider the environmental contact as a kind of instantaneous collision between the MRM link and the collision object that may create instantaneous contact forces.

Table 1. Parameters setting
Full size table
Fig. 1.
figure 1

Error curves under the collision contact, (a) position errors, (b) velocity errors.

Full size image
Fig. 2.
figure 2

Control torque and weight adjustment curves, (a) control torque, (b) weight adjustment.

Full size image

The parameter definition is represented as follows: The critic NN is chosen as 2-5-1 with 2 input neurons, 5 hidden neurons and 1 output neuron, and the weight vectors are selected as for joint 1 and for joint 2, with the initial values \({{\hat{w}}_{c1}}={{\hat{w}}_{c2}}=\left[ 0 \right] \). The NN structures and initial weight values of the and action NNs are selected as the same of the critic NNs. The other model parameters, uncertainty up-bound parameters and control parameters are given in Table 1.

Figure 1 illustrate the position and velocity error curves under the situation of instantaneous collision contact. In this figure, obvious position and velocity deviations are captured, which are due to the effect of collision force. Moreover, we also observe that the error values decreased to normal ranges with very short time periods, which may attribute to the performance of the proposed zero-sum neuro-optimal controller that realized the optimal compensation of unknown contact disturbance.

Figure 2(a) illustrate the control torque curves under the situation of instantaneous collision contact. From this figure, the reliable control torque outputs are obtained, in which the instant increase of control torques keep in safe limits. This is attribute the contribution of the proposed optimal control that realizes the optimization of tracking errors and output torques.

Figure 2(b) illustrate the variations of the estimated critic NN weights under the proposed method. From this figure, one obtain that the critic NN weights may converge in certain ranges for each isolated joint subsystem. With the critic NN weight estimations, the HJI equation and the optimal control law can be solved and derived respectively.

5 Conclusion

In this paper, we develop a decentralized robust zero-sum neuro-optimal control scheme for MRMs. Based on local dynamic information of each joint module and the JTF technique, a model-based compensation controller and an uncertainty decomposition-based robust controller are designed for controlling MRM systems. Based on ADP algorithm, the HJI equation is solved by constructing the action-critic NNs, and then the decentralized robust zero-sum neuro-optimal control is developed. Finally, experimental results are illustrated to verify the effectiveness and advantages of the proposed method.