1 Introduction

Physical human–robot interaction (pHRI) as a hotspot research area makes the design of robotic configuration and control strategy developing towards human-centered criterion [1]. As the collaborative robots (cobots) develops, the collaboration between the human and the robot has turned into a nontrivial research project, such as manufacturing [2], robotic adjuvant therapy (surgery robot [3], habilitation robot [4]) and so on. Although the traditional cobot is with superior security and accuracy, its large size and difficult assembly limit further application. Modular robot manipulator (MRM) is a kind of robot with standard modules and interfaces that can be recombined and assembled its configuration according to different task requirements. Owing to the unique modular reconfigurability, structural flexibility and environment adaptability of MRM, it is with great significance to study the interactive control method of the human and the modular robot.

Human robot collaboration refers to the continuous contact or interaction between bilateral participants (human and robot) to achieve common goals in the same workspace [5]. Therefore, it is with great value for both participants to optimize personal goal by using available self-information [6]. However, in the process of collaboration, each participant needs to consider the decisions of other participants and make corresponding interactive actions [7]. Game theory can be traced back to 1944 [8] as a description of the rational decision-making process between participants [9], and describes the interaction behavior among participants as well as their corresponding strategies as game [10]. For the moment, game theory has been widely applied in large-scale networks [11], unmanned vehicles [12], multi-robot systems [13] and other fields. In the interaction process between a human and an MRM, bilateral participants can be regarded as players in game theory, and the interaction behavior can be described with different cost functions (tasks) and control strategies (optimization criteria) [14]. Cooperative game as a branch of game theory, multiple participants collaborate to optimize their own goals in a dynamic system, and all players need to consider the joint cost function while minimizing their own costs simultaneously, that is Pareto equilibrium, which fits well with the control objective of pHRI [15]. To obtain the optimal strategy for each participant, the Pareto equilibrium solution is attained by solving the coupled Hamilton–Jacobi–Bellman (HJB) equation of the system [16]. However, it is not always feasible to derive the optimal solution of the equation by analytically method for complex issues such as pHRI due to the occurrence of dimension disaster [17]. Therefore, the researchers utilize adaptive dynamic programming (ADP)-based learning method to approximate the ideal equilibrium results.

ADP, as a branch of reinforcement learning, is increasingly popular in the field of optimal control. It employs approximation structures such as neural networks (NNs) to approach nonlinear unknown functions through iterative learning [18]. Optimal control has already been with a wide range of applications, such as discrete-time [19,20,21], continuous-time [22,23,24], data-driven [25,26,27], robotic systems with input/output constraints [28,29,30], uncertainties disturbances [31,32,33] and multiple sensor failures [34,35,36]. It is with great importance to select an appropriate control mechanism to satisfy the requirements of system stability and performance for human-MRM collaboration, which involves interconnected or coupling among participants and affects subsystems as well as the whole system. Decentralized control effectively mitigates the computation burden and avoids the problem of data acquisition as well as communication blocking caused by subsystem failure, which only utilizes the local feedback information of each subsystem controller instead of the overall system information [37], and has been widely applied in ADP, such as large-scale system [38], unmanned autonomous vehicle tracking [39], robotic control [40], etc. In the application of MRM, decentralized control strategy is with the ability of decomposing the complex robot system dynamic model into several subsystems with dynamic coupling. The derivation of the local controller is capable to compensate the uncertainty and coupling of the subsystem model that can simplify the complexity of the controller as well as improve the speed of the operation simultaneously.

As noted previously, MRM is particularly appropriate for pHRI tasks. In different implementation phases among interaction tasks, the analysis of a human and a robot bilateral interaction behavior is complicated. In accordance with this issue, cooperative game approach is introduced into pHRI, as well as a human and an MRM are regarded as two participants, that is propitious to pHRI control. Simultaneously, decentralized control strategy fits well with the MRM system due to utilizing only local information of the corresponding subsystem for reducing the complexity of the controller design and ensuring the stability of the robot system. Cooperative game-based decentralized optimal control approach describes the interaction behavior via cost function and control strategy respectively, and then, the coupling effect between the human and the robot has been solved. However, the dynamic coupling effect exists not only between the human and the robot, but also in the MRM subsystem itself, that still affects the control performance and even makes the system unstable, for increases the difficulty of solving the HJB equation, when cooperative game-based decentralized optimal control approach is applied to solve Pareto equilibrium solution of human-MRM cooperative system.

Motivated by above, a cooperative game-based decentralized optimal control approach of MRMs is assessed for pHRI. The coupled MRM subsystem is handled by using local desired control including control input matrix and local tracking error. Therefore, the assumptions on the upper bound of coupling effect and matching condition are relaxed. The main contribution of this paper is summarized as follow:

  1. 1.

    Unlike the distributed control mechanism in cooperative game [41], a novel decentralized cooperative game-based pHRI control approach is proposed in this paper, which not only solves the coupling effect between the human and the robot, but also deals with the intense coupling of MRM subsystem itself, and obtains the Pareto equilibrium solution of the system by solving the coupled HJB equation. Besides, the strict assumption on satisfying the norm-boundness of IDC is relaxed.

  2. 2.

    Unlike only considering the cooperative relation in MRM [41], a joint cooperative game concerning with human and the robot as well as MRM subsystem itself approximate optimal control method is proposed. The control torque of each module as well as the interaction torque both guarantee optimality via adaptive dynamic programming-based decentralized optimal control approach, which solves the approximate optimal interaction control problem of modular robot system under pHRI.

2 Dynamic analysis and problem formulation

2.1 Dynamic model of MRM

By considering an MRM using the joint torque feedback (JTF) technique, the ith subsystem dynamic model is:

$$\begin{aligned}&{{I}_{im}}{{\gamma }_{i}}{{\ddot{q}}_{i}}+\frac{{{\tau }_{is}}}{{{\gamma }_{i}}}+{{f}_{ir}}({{q}_{i}},{{\dot{q}}_{i}})+{{I}_{i}}(q,\dot{q},\ddot{q})\nonumber \\&\quad ={{\tau }_{i}}+{{\left[ J_{i}^{T}f \right] }_{i}}, \end{aligned}$$
(1)

where \({{I}_{im}}\) indicates the motor’s moment of inertia, subscript i is the ith joint module subsystem, \({{\gamma }_{i}}\) represents the gear ratio, \({{q}_{i}}\) denotes the joint position, \({{\tau }_{is}}\) is the coupled joint torque, \({{f}_{ir}}({{q}_{i}},{{\dot{q}}_{i}})\) represents the lumped joint friction, \({{I}_{i}}(q,\dot{q},\ddot{q})\) denotes the IDC effect among subsystems, \({{\tau }_{i}}\) is the control torque, \(J_{i}\) denotes the Jacobi matrix, f represents the human force input that the interaction force exert on the end-effector, and \({{\left[ \centerdot \right] }_{i}}\) means the ith element of the vector. The analysis of the properties is summarized as follows:

  1. (1)

    The lumped joint friction

The lumped friction term \({{f}_{ir}}({{q}_{i}},{{\dot{q}}_{i}})\) mainly includes friction of harmonic drive speed reducer and the motor friction in each joint module, that is expressed as:

$$\begin{aligned} {{f}_{ir}}\left( {{q}_{i}},{{{\dot{q}}}_{i}} \right)&={{f}_{ib}}{{\dot{q}}_{i}}+\left( {{f}_{ic}}+{{f}_{is}}{{e}^{\left( -{{f}_{i\tau }}{{{\dot{q}}}_{i}}^{2} \right) }} \right) {\textit{sgn}} \left( {{{\dot{q}}}_{i}} \right) \nonumber \\&\quad +{{f}_{ip}}\left( {{q}_{i}},{{{\dot{q}}}_{i}} \right) \nonumber \\ {{f}_{ir}}({{q}_{i}},{{\dot{q}}_{i}})&\approx {{\hat{f}}_{ib}}{{\dot{q}}_{i}}+({{\hat{f}}_{is}}{{e}^{(-{{{\hat{f}}}_{i\tau }}\dot{q}_{i}^{2})}}+{{\hat{f}}_{ic}})sgn ({{\dot{q}}_{i}})\nonumber \\&\quad +{{f}_{ip}}({{q}_{i}},{{\dot{q}}_{i}})+{{Y}_{i}}({{\dot{q}}_{i}}){{\tilde{F}}_{ir}}, \end{aligned}$$
(2)

in which

$$\begin{aligned} {{Y}_{i}}({{\dot{q}}_{i}})={{[{{f}_{ib}}-{{{\hat{f}}}_{ib}},{{f}_{ic}}-{{{\hat{f}}}_{ic}},{{f}_{is}}-{{{\hat{f}}}_{is}},{{f}_{i\tau }}-{{{\hat{f}}}_{i\tau }}]}^{T}}, \end{aligned}$$
(3)

where \({{f}_{ip}}({{q}_{i}},{{\dot{q}}_{i}})\) is the position dependency friction term, \({{f}_{ib}},{{f}_{i\tau }}\) are viscous and Stribect friction effect, \({{f}_{is}},{{f}_{ic}}\) are static and Coulomb friction parameters, \({{\tilde{F}}_{ir}}\) is parameter uncertainty term. Furthermore, \({{\hat{f}}_{ib}},{{\hat{f}}_{ic}},\) \({{\hat{f}}_{is}},{{\hat{f}}_{i\tau }}\) are the estimated values of \({{f}_{ib}},{{f}_{ic}},\) \({{f}_{is}},{{f}_{i\tau }}\), respectively. \({{\tilde{F}}_{ir}}\) is the uncertain friction. \({{f}_{ib}},{{f}_{ic}},{{f}_{is}},{{f}_{i\tau }}\) and estimations are bounded because of all physical parameters of practical significance, so that \({{\tilde{F}}_{ir}}\) is bounded as \(\left| {{{\tilde{F}}}_{ir}} \right| \le {{b}_{iFrm}}(m=1,2,3,4)\), and \({{b}_{iFrm}}\) is a known positive constant. Accordingly, one can obtain \({{Y}_{i}}({{\dot{q}}_{i}}){{\tilde{F}}_{ir}}\) which is given as \(\left| {{Y}_{i}}({{{\dot{q}}}_{i}}){{{\tilde{F}}}_{ir}} \right| \le {{Y}_{i}}({{\dot{q}}_{i}}){{b}_{iFrm}}\). Besides, \(\left| {{f}_{ip}}({{q}_{i}},{{{\dot{q}}}_{i}}) \right| \le {{b}_{iFp}}\), in which \({{b}_{iFp}}\) is a known positive constant bound.

  1. (2)

    The interconnected dynamic coupling

The derivation of interconnected dynamic coupling mainly comes from robot reconfiguration, such as misalignment of the axes. If the IDC effect is ignored, it will reduce the tracking performance of the robot system or even lead the MRM unstable. For \(i\ge 3\), IDC can be expressed as:

$$\begin{aligned} {{I}_{i}}(q,\dot{q},\ddot{q})&={{I}_{im}}\sum \limits _{j=1}^{i-1}{v_{mi}^{T}{{v}_{lj}}}{{{\ddot{q}}}_{j}}\nonumber \\&\quad +{{I}_{im}}\sum \limits _{j=2}^{i-1}{\sum \limits _{k=1}^{j-1}{v_{mi}^{T}({{v}_{lk}}\times {{v}_{lj}})}}{{{\dot{q}}}_{k}}{{{\dot{q}}}_{j}} \nonumber \\&={{I}_{im}}\sum \limits _{j=1}^{i-1}{D_{j}^{i}}{{{\ddot{q}}}_{j}}+{{I}_{im}}\sum \limits _{j=2}^{i-1}{\sum \limits _{k=1}^{j-1}{\Theta _{kj}^{i}}}{{{\dot{q}}}_{k}}{{{\dot{q}}}_{j}} \nonumber \\&=\sum \limits _{j=1}^{i-1}{\left[ {{I}_{im}}\hat{D}_{j}^{i},{{I}_{im}} \right] {{\left[ {{{\ddot{q}}}_{j}},\tilde{D}_{j}^{i}{{{\ddot{q}}}_{j}} \right] }^{T}}} +\sum \limits _{j=2}^{i-1}\nonumber \\&\quad \times \sum \limits _{k=1}^{j-1}\left[ {{I}_{im}}\hat{\Theta }_{kj}^{i},{{I}_{im}} \right] \left[ {{{\ddot{q}}}_{j}},\tilde{\Theta }_{kj}^{i}{{{\dot{q}}}_{k}}{{{\dot{q}}}_{j}} \right] ^{T}, \end{aligned}$$
(4)

in which \({{v}_{mi}},{{v}_{lj}},{{v}_{lk}}\) represent the unit vectors along with the ith, jth and kth joint rotation axes, respectively. Accordingly, one can define \(D_{j}^{i}=v_{mi}^{T}{{v}_{lj}}\) and \(\Theta _{kj}^{i}=v_{mi}^{T}({{v}_{lk}}\times {{v}_{lj}})\). Moreover, we also have the relations that \(\hat{D}_{j}^{i}=D_{j}^{i}-\tilde{D}_{j}^{i}\) and \(\hat{\Theta }_{kj}^{i}=\Theta _{kj}^{i}-\tilde{\Theta }_{kj}^{i}\), in which \(\hat{D}_{j}^{i},\hat{\Theta }_{kj}^{i}\) denote the estimated values of \(D_{j}^{i},\Theta _{kj}^{i}\) as well as \(\tilde{D}_{j}^{i},\tilde{\Theta }_{kj}^{i}\) are alignment errors. If \(i\le 2\), the IDC term can be referenced in [42]. According to the definition of \({{v}_{mi}},{{v}_{lk}},{{v}_{lj}}\) in (4), we obtain that the vector products are bounded by \(\left| D_{j}^{i} \right| = \left| v_{mi}^{T}{{v}_{lj}} \right| <1\) and \(\left| \Theta _{kj}^{i} \right| \text {=}\left| v_{mi}^{T}({{v}_{lk}}\times {{v}_{lj}}) \right| <1\). Moreover, we also conclude that \({{I}_{i}}(q,\dot{q},\ddot{q})\) is bounded and the up-bound is given as \(\left| {{I}_{i}}(q,\dot{q},\ddot{q}) \right| \le {{b}_{iI}}\).

Define state vector \({{x}_{i}}={{[{{x}_{i1}},{{x}_{i2}}]}^{T}}={{[{{q}_{i}},{{\dot{q}}_{i}}]}^{T}}\) and the control input \({{u}_{i}}={{\tau }_{i}}\), \({{h}_{i}}={{\left[ J_{i}^{T}f \right] }_{i}}\). One has the ith subsystem state space:

$$\begin{aligned} \left\{ \begin{array}{l} {{{\dot{x}}}_{i1}}={{x}_{i2}} \\ \\ {{{\dot{x}}}_{i2}}={{\ell }_{i}}(x)+{{g}_{i}}{{u}_{i}}+{{h}_{i}} \\ \end{array} \right. , \end{aligned}$$
(5)

where

$$\begin{aligned} {{g}_{i}}&={{({{I}_{im}}{{\gamma }_{i}})}^{-1}} \nonumber \\ {{\ell }_{i}}(x)&=-{{g}_{i}}\left( \begin{array}{l} ({{{\hat{f}}}_{is}}{{e}^{(-{{{\hat{f}}}_{i\tau }}\dot{x}_{i1}^{2})}}+{{{\hat{f}}}_{ic}}){\textit{sgn}} ({{x}_{i2}})\\ \quad +{{f}_{ip}}({{x}_{i1}},{{x}_{i2}}) +{{{\hat{f}}}_{ib}}{{x}_{i2}}\\ \quad +{{Y}_{i}}({{x}_{i2}}){{{\tilde{F}}}_{ir}}+\frac{{{\tau }_{is}}}{{{\gamma }_{i}}}+{{I}_{i}}(x,\dot{x},\ddot{x}) \\ \end{array}\right) . \end{aligned}$$
(6)

2.2 Human limb model and motion intention estimation

In physical human robot interaction, the human force is considered as the only external force exerting on the robot end-effector [43]. The pHRI control transfers the human force input into the motion commands of the robot manipulator:

$$\begin{aligned} -{{C}_{H}}\dot{z}+{{G}_{H}}({{z}_{Hd}}-z)={{f}_{}}, \end{aligned}$$
(7)

where \({{C}_{H}}\), \({{G}_{H}}\) are the damper, spring unknown diagonal matrices of the human, z is the robot actual position in Cartesian space which can be calculated as \(z(t)=\xi (q)\), \(q(t)={{\left[ {{q}_{1}},\ldots ,{{q}_{i}},\ldots ,{{q}_{n}} \right] }^{T}}\) is the position vector in the joint space, \(\xi (\cdot )\) is a mapping matrix from joint space to Cartesian space, \({{z}_{Hd}}\) denotes the trajectory planned in the human which is referred to as the motion intention of the human and robot.

Remark 1

The up-bound of interaction force f is \(b_{f}\) which guarantees that, once a feasible pHRI is determined, it is possible to guarantee that the MRM will converge to its goal. If the human interaction force is without a finite bound, it is not possible to guarantee the convergence that the position tracking error is UUB.

The human motion intention while interacting with a robot \({{z}_{Hd}}\) can be expressed as [44]:

$$\begin{aligned} {{z}_{Hd}}=\Lambda (f,z,\dot{z}), \end{aligned}$$
(8)

where \(\Lambda (\cdot )\) is taken into account as an unknown nonlinear function.

Furthermore, it is known that \({{z}_{Hd}}\) is difficult to obtain since the human may change its limb during the collaboration task. Considering the concept of radial basis function NN, the human motion intention while interacting with a robot and its estimation are given by as follows:

$$\begin{aligned} {{z}_{Hd}}=W_{x}^{T}S(f,z,\dot{z})+\varepsilon , {{{\hat{z}}}_{Hd}}=\hat{W}_{x}^{T}S(f,z,\dot{z}), \end{aligned}$$
(9)

where \(\varepsilon \) is the estimation error, \({{\hat{W}}_{x}}\) denotes the estimated value of ideal weight \({{W}_{x}}\), and S represents the Gaussian function.

The gradient descent algorithm is used to obtain \({{\hat{W}}_{x}}\) in (9). In order to make the MRM actively and easily move toward its human’s intended position and the interaction force f is small, \({{\hat{W}}_{x}}\) is adjusted online using the following cost function \(E=\frac{1}{2}\left\| f^{2} \right\| .\)

$$\begin{aligned} {{{\dot{\hat{W}}}}_{x}}=-{\alpha }^{\prime }\frac{\partial E}{\partial {{{\hat{W}}}_{x}}}=-{\alpha }^{\prime }{{f}}{{G}_{H}}S=-{{\alpha }_{A}}{{f}}S, \end{aligned}$$
(10)

where \({\alpha }'\) is a positive scalar, \({{\alpha }_{A}}={{\alpha }^{\prime }}{{G}_{H}}\). As \({{G}_{H}}\) is the parameter of human limb dynamics and unknown, it is absorbed by \({{\alpha }_{A}}\) [45].

We can get \({{\hat{W}}_{x}}\) as

$$\begin{aligned} {{\hat{W}}_{x}}\left( t \right) ={{\hat{W}}_{x}}\left( 0 \right) -{{\alpha }_{A}}\int _{0}^{t}{\left( {{f}}\left( v \right) S(v ) \right) d}v. \end{aligned}$$
(11)

Therefore, one can obtain \({{\hat{z}}_{Hd}}\) in (9).

The control object consists that optimally ensuring tracking error of MRM systems under pHRI is UUB. Therefore, a cooperative game-based decentralized optimal control approach is presented in next section.

3 Cooperative game-based decentralized optimal control approach of MRMs

3.1 Problem transformation

In this work, a cooperative game-based decentralized optimal control approach is developed to guarantee that the end-effector of MRM can actively move toward human’s planned intention under pHRI task. In addition, in the cooperative game, the object consists in ensuring the minimization of overall performance index for all the modules as well as the interaction torque between the human and the robot. Therefore, each module in the manipulator forms cooperative game and then cooperates with the human. Hence, in order to facilitate the design of the controller, n modules can be deemed as n players.

We consider that the overall performance situation, in which all players cannot be improved simultaneously with at least one player being proved, as the Pareto equilibrium (cf. [46]).

The estimated joint space motion intention \(\hat{q}\) is defined as \(\hat{q}={{\xi }^{-1}}({{z}_{Hd}})\). The augmented subsystem of the state space dynamic is:

$$\begin{aligned} \left\{ \begin{array}{l} {{{\dot{x}}}_{1}}={{x}_{2}} \\ \\ {{{\dot{x}}}_{2}}=\ell (x)+\sum _{p=1}^{n}{{{G}_{p}}{{u}_{p}}+}H(x) \\ \end{array} \right. , \end{aligned}$$
(12)

where \(x={{[x_{1}^{T},x_{2}^{T}]}^{T}}\in {{R}^{2n}}\) is the global state of the MRM system, in which the vectors \({{x}_{1}},{{x}_{2}}\) are given by \({{x}_{1}}=[{{x}_{11}},\ldots ,{{x}_{i1}},\ldots ,{{x}_{n1}}]^{T}\in {{R}^{n}}\) and \({{x}_{2}}=[{{x}_{12}},\ldots ,{{x}_{i2}},\ldots ,{x}_{n2}]^{T}\in {{R}^{n}}\). Moreover, we have \(\ell (x)=[{\ell }_{1}(x),\ldots ,{\ell }_{i}(x), \ldots ,{\ell }_{n}(x)]^{T}\), \({{G}_{p}}=[0,\ldots ,0,{{g}_{p}},0,\ldots ,0]^{T}\), \({{H(x)}}=[{h}_{1},\ldots ,{{h}_{i}},\ldots , {h}_{n}]^{T}\), where \({{g}_{p}}=\left( {{I}_{pm}}{{\gamma }_{p}} \right) ^{-1},p=1,\ldots ,n\). The terms \(\ell (x),{{G}_{p}}\) and H(x) are the augment of the drift dynamic, control input matrix and interaction torque, respectively.

Then, the optimal control problem of MRM system with pHRI can be transformed into a cooperative game issue, which the joint cost function is defined as follows:

$$\begin{aligned} {{V}_{p}}(\dot{E},U,H)&=\int _{t}^{\infty }{\!\left( \!{{{\dot{E}}}^{T}}{{Q}_{b}}\dot{E}+{{U}^{T}}{{R}_{M}}U+{{H}^{T}}{{P}_{M}}H\! \right) }d\tau \nonumber \\&=\int _{t}^{\infty }{\Gamma (\dot{E},U,H)}d\tau , \end{aligned}$$
(13)

where the position error is \(E={{x}_{1}}-{{x}_{d}}\) and the velocity error vector means \(\dot{E}={{x}_{2}}-{{\dot{x}}_{d}}\), \({{x}_{d}}=\hat{q}(t)\) denotes the estimated human motion vectors in joint space, \({{Q}_{b}}, {{R}_{M}}={\textit{diag}}[{{R}_{1}},{{R}_{2}},\ldots ,{{R}_{n}}], {{P}_{M}}={\textit{diag}}[{{P}_{1}},{{P}_{2}},\ldots , {{P}_{n}}]\) are determined positive definite matrixes, and \(\Gamma (\dot{E},U,H)\) represents the utility function, \(U=[{{U}_{1}},{{U}_{2}},\ldots ,{{U}_{n}}]\).

Remark 2

The cooperation game issue represented in (13) is considered, where each joint subsystem is responsible for the minimization of the joint cost function. By defining \(G=[{{G}_{1}},{{G}_{2}},\ldots ,{{G}_{n}}]\), the cooperation differential game is equivalent to solving the joint cost function (13).

The mentioned MRM system is a second-order system. For obtaining the Hamiltonian function related to the control torque, we select velocity error instead of position error. Then, using the infinitesimal version of (13) with (1) and (12), the Hamiltonian function is expressed as:

$$\begin{aligned} H_{am}(\dot{E},U,H)&={{(\nabla {{V}_{p}})}^{T}}\left( \ell (x)+GU+H-{{{\ddot{x}}}_{d}} \right) \nonumber \\&\quad +\Gamma (\dot{E},U,H), \end{aligned}$$
(14)

where \(\nabla {{V}_{p}}(\dot{E})=\frac{\partial {{V}_{p}}(\dot{E})}{\partial \dot{E}}\) is the partial derivative of \({{V}_{p}}(\dot{E})\). Moreover, the optimal cost function can be defined as:

$$\begin{aligned} V_{p}^{*}(\dot{E},U,H)=\underset{U,H}{\mathop {\min }}\,\int _{t}^{\infty }{\Gamma (\dot{E},U,H)}d\tau . \end{aligned}$$
(15)

According to the stationary condition \(\frac{\partial H_{am}}{\partial U}=0,\frac{\partial H_{am}}{\partial H}=0\), the local decentralized optimal control policy and interaction torque \(U^{*},H^{*}\) are given by:

$$\begin{aligned} U^{*}&=-\frac{1}{2}R_{M}^{-1}G^{T}\nabla V_{p}^{*},\end{aligned}$$
(16)
$$\begin{aligned} H^{*}&=-\frac{1}{2}P_{M}^{-1}\nabla V_{p}^{*}. \end{aligned}$$
(17)

Afterwards, by substituting (13), (16) and (17) into the Hamiltonian function (14), the coupled HJB equation is:

$$\begin{aligned} 0&={{(\nabla V_{p}^{*})}^{T}}\left( \ell (x)-{{{\ddot{x}}}_{d}} \right) -\frac{1}{4}{{(\nabla V_{p}^{*})}^{T}}GR_{M}^{-1}G^{T}(\nabla V_{p}^{*}) \nonumber \\&\quad -\frac{1}{4}{{(\nabla V_{p}^{*})}^{T}}P_{M}^{-1}(\nabla V_{p}^{*})+{{{\dot{E}}}^{T}}{{Q}_{b}}\dot{E}. \end{aligned}$$
(18)

As (18) can be deduced to obtain \(\nabla V_{p}^{*}\), the required Pareto optimal solution can be derived. However, in the framework of the cooperative game, the control issue is transformed to optimally ensure MRM position tracking under the pHRI task and the end-effector can actively move toward its human partner’s intended position. As the coupled HJB equation with other players is difficult to solve, we use critic NN approach to deal with it.

3.2 Approximate solution of the cooperative game-based decentralized optimal control via the implementation of critic NN

Dynamic compensation is a significant part in robotic control. In this study, a compensator controller which comprises dynamic information-based model, local desired control and cooperative game-based optimal control is designed.

$$\begin{aligned} u_{i}^{*}=u_{i1}+u_{ib}+u_{i2}^{*}, \end{aligned}$$
(19)

where \(u_{i1}\) is dealt with the dynamic model \(\ell _{i}({{x}_{}})\), \(u_{ib}\) denotes local desired control that deals with the coupled term of MRM, and \(u_{i2}^{*}\) is the optimal compensation issue of the uncertainties as well as pHRI tasks.

According to (5), \(u_{i1}\) can be designed as:

$$\begin{aligned} u_{i1}=-\left( \begin{array}{l} -\left( {{{\hat{f}}}_{is}}{{e}^{\left( -{{{\hat{f}}}_{i\tau }}x_{i2}^{2} \right) }}+{{{\hat{f}}}_{ic}} \right) sgn ({{x}_{i2}}) \\ -{{{\hat{f}}}_{ib}}{{x}_{i2}}-g_{i}^{-1}{{{\ddot{x}}}_{id}}-\frac{{{\tau }_{is}}}{{{\gamma }_{i}}} \\ \end{array} \right) . \end{aligned}$$
(20)

The optimal compensation control problem is then transformed into a cooperative game-based decentralized optimal control approach.

The critic NN is developed to approximate the cost function (15):

$$\begin{aligned} {{V}_{p}}^{*}(\dot{E})=W_{c}^{T}{{\phi }_{c}}(\dot{E})+{{\varepsilon }_{c}}, \end{aligned}$$
(21)

where \({{W}_{c}}\) is the critic NN vector, \({{\varepsilon }_{c}}\) is the finite approximate error, and \({{\phi }_{c}}(\dot{E})\) represents activation function.

The gradient of the approximated cost function can be obtained as:

$$\begin{aligned} \nabla {{V}_{p}}^{*}(\dot{E})=\nabla {{\phi }_{c}}(\dot{E})W_{c}+\nabla {{\varepsilon }_{c}}, \end{aligned}$$
(22)

where \(\nabla {{\phi }_{c}}(\dot{E})=\partial {{\phi }_{c}}(\dot{E})/\partial \dot{E}\) is the gradient of the activation function, and \(\nabla {{\varepsilon }_{c}}\) means gradient error.

By substituting (22) into (16) and (17), the optimal control policy and interaction torque are given by:

$$\begin{aligned} {{U}^{*}}&=-\frac{1}{2}R_{M}^{-1}G^{T}\left( \nabla \phi _{c}^{T}(\dot{E}){{W}_{c}}+\nabla {{\varepsilon }_{c}} \right) , \end{aligned}$$
(23)
$$\begin{aligned} {{H}^{*}}&=-\frac{1}{2}P_{M}^{-1}\left( \nabla \phi _{c}^{T}(\dot{E}){{W}_{c}}+\nabla {{\varepsilon }_{c}} \right) . \end{aligned}$$
(24)

According to (23) and (24), we have:

$$\begin{aligned} u_{i}^{*}&=-\frac{1}{2}R_{i}^{-1}G_{i}^{T}\left( \nabla \phi _{c}^{T}(\dot{E}){{W}_{c}}+\nabla {{\varepsilon }_{c}} \right) , \end{aligned}$$
(25)
$$\begin{aligned} h_{i}^{*}&=-\frac{1}{2}P_{i}^{-1}\left( \nabla \phi _{c}^{T}(\dot{E}){{W}_{c}}+\nabla {{\varepsilon }_{c}} \right) . \end{aligned}$$
(26)

Substituting (22), (23), (24) into (14), we have:

$$\begin{aligned} H_{am}(\dot{E},U,H)&=\left( \!{{{\dot{E}}}^{T}}{{Q}_{b}}\dot{E}+{{U}^{T}}{{R}_{M}}U+{{H}^{T}}{{P}_{M}}H\! \right) \nonumber \\&\quad +{{(\nabla {{V}_{p}})}^{T}}\left( \ell (x)+GU+H-{{{\ddot{x}}}_{d}} \right) \nonumber \\&\quad -{{e}_{cH}}=0, \end{aligned}$$
(27)

where \({{e}_{cH}}\) denotes the residual error.

In order to remove the norm-boundness assumption on interconnections for decentralized control, the desired states of coupled subsystems are employed to substitute their actual ones. Thus, the interconnection term \(\ell _{i} (x)\) can be expressed as follows:

$$\begin{aligned} \ell _{i} (x)&={{\ell }_{i}}({{x}_{i}},{{x}_{bd}})+\Delta {{\ell }_{i}}(x,{{x}_{bd}}), \nonumber \\ {{u}_{bd}}&=G_{b}^{-1}({{{\dot{x}}}_{b2d}}-{{\ell }_{b}}({{x}_{d}})),b\ne i. \end{aligned}$$
(28)

where \({{x}_{bd}}\) is the desired state of the coupled subsystems with \(b=1,\ldots ,i-1,i+1,\ldots ,n,\) and \(\Delta {{\ell }_{i}}(x,{{x}_{bd}})\) denotes the substitution error. Since the interconnection satisfies the global Lipschitz condition, it thus implies:

$$\begin{aligned} \left\| \Delta {{\ell }_{i}}(x,{{x}_{bd}}) \right\| \le \sum \limits _{b=1,b\ne i}^{n}{{{c}_{ib}}{{B}_{b}},} \end{aligned}$$
(29)

where \({{B}_{b}}=\left\| {{x}_{b}}-{{x}_{bd}} \right\| ,\) and \({{c}_{ib}}\ge 0\) is an unknown global Lipschitz constant.

The estimated optimal cost function is given by:

$$\begin{aligned} \hat{V}_{p}^{*}(\dot{E})=\hat{W}_{c}^{T}{{\phi }_{c}}(\dot{E}). \end{aligned}$$
(30)

Based on (25), (26) and (30), the approximate optimal control is expressed as:

$$\begin{aligned}{} & {} \hat{u}_{i2}^{*}=-\frac{1}{2}R_{i}^{-1}G_{i}^{T}\nabla \phi _{c}^{T}(\dot{e_{i}}){{\hat{W}}_{c}}. \end{aligned}$$
(31)
$$\begin{aligned}{} & {} \hat{h}_{i}^{*}=-\frac{1}{2}P_{i}^{-1}\nabla \phi _{c}^{T}(\dot{e_{i}}){{\hat{W}}_{c}}. \end{aligned}$$
(32)

Remark 3

According to (28), the interconnected MRM is decoupled via the substitute technique. This facilitates the smooth implementation of the decentralized control via removing the norm-boundness assumption on interconnections. Therefore, the term \({{\phi }_{c}}(\dot{E})\) in (25) and (26) is converted to \({{\phi }_{c}}({{\dot{e}}_{i}})\) in (31) and (32). The similar technique can be referenced in [47].

Remark 4

[48] As the interaction torque H can be obtained by the measurable human force input via six-axis force sensor, the difference between \(h_{i}\) and \(\hat{h}_{i}^{*}\) in (32) is able to assess the conflict of the goal between the robot and the human, such as the clash with MRM and human in coordinate operation task.

Denote \(L(x)=[{{\ell }_{1}}({{x}_{1}},{{x}_{bd}}),{{\ell }_{2}}({{x}_{2}},{{x}_{bd}}),\ldots {{\ell }_{n}} ({{x}_{n}},{{x}_{bd}})]\). According to (27), the approximated Hamiltonian function is given by:

$$\begin{aligned} \hat{H}_{am}(\dot{E},\hat{U},\hat{H})&=\left( \! {{{\dot{E}}}^{T}}{{Q}_{b}}\dot{E}+{{{\hat{U}}}^{T}}{{R}_{M}}\hat{U}+{{{\hat{H}}}^{T}}{{P}_{M}}\hat{H}\! \right) \nonumber \\&\quad +{{(\nabla {{V}_{p}})}^{T}}\left( L(x)+G\hat{U}+\hat{H}-{{{\ddot{x}}}_{d}} \right) \nonumber \\&={{e}_{c}}. \end{aligned}$$
(33)

The approximated Hamiltonian error function \({{e}_{c}}\) is defined as follows:

$$\begin{aligned} {{e}_{c}}={{\hat{H}}_{{am}}}-{{H}_{{am}}}, \end{aligned}$$
(34)

where \({{e}_{c}}=\hat{H}_{am}\) is obtained using (27), (33).

When defining the vector estimate error \({{\tilde{W}}_{c}}={{W}_{c}}-{{\hat{W}}_{c}},\) it can be deduced that \({{e}_{c}}={{e}_{cH}}-\tilde{W}_{c}^{T}\nabla {{\phi }_{c}}(\dot{E})\ddot{E}\), by combining (27), (33) with (34). Base on gradient decent algorithm, define residual error function \({{E}_{c}}=\frac{1}{2}e_{c}^{2}\), which is minimized for adjusting the critic NN weights. The update law is designed as:

$$\begin{aligned} {{{\dot{\hat{W}}}}_{c}}&=-\varsigma \frac{1}{{{\left( {{\xi }^{T}}\xi +1 \right) }^{2}}}\frac{\partial {{E}_{c}}}{\partial {{{\hat{W}}}_{c}}}. \nonumber \\&=-\varsigma \frac{\xi }{{{\left( {{\xi }^{T}}\xi +1 \right) }^{2}}}\left( {{e}_{cH}}-{{\xi }^{T}}{{{\tilde{W}}}_{c}} \right) , \end{aligned}$$
(35)

where \(\varsigma \) is the updated rate of the critic NN. \(\xi \) is denoted as \(\nabla {{\phi }_{c}}(\dot{E})\ddot{E}\), and a positive constant \({{\xi }_{L}}\) and \(\left\| \xi \right\| \le {{\xi }_{L}}\) is assumed.

Assumption 1

(Persistently exciting condition [49]) Signal \(\bar{\xi }=\frac{1}{{{\left( {{\xi }^{T}}\xi +1 \right) }^{2}}}\) is persistently excited, for \(\forall t\in [0,\infty )\), then, there are with positive constants \({{\kappa }_{1}},{{\kappa }_{2}},T\), such that following equation is satisfied:

$$\begin{aligned} {{\kappa }_{1}}I\le \int _{t}^{t+T}{{\bar{\xi }}}{{\bar{\xi }}^{T}}dz\le {{\kappa }_{2}}I. \end{aligned}$$
(36)

Theorem 1

Considered the selected cost function which is approximated by (21), with an ideal weight \({{W}_{c}}\), and the estimated cost function given by (30) with approximated weight \({{\hat{W}}_{c}}\), if the update law of critic NN is denoted as (35), then the weight approximation error is UUB.

Proof

Choose the Lyapunov function:

$$\begin{aligned} {{L}_{a}}=\frac{1}{2}\tilde{W}_{c}^{T}\tilde{W}_{c}. \end{aligned}$$
(37)

The time derivative of \({{L}_{a}}(t)\) is:

$$\begin{aligned} {{{\dot{L}}}_{a}}&=\tilde{W}_{c}^{T}\dot{\tilde{W}}_{c}=\varsigma \tilde{W}_{c}^{T}\frac{\xi }{{{\left( {{\xi }^{T}}\xi +1 \right) }^{2}}}\left( {{e}_{cH}}-{{\xi }^{T}}{{{\tilde{W}}}_{c}} \right) \nonumber \\&=\frac{\varsigma \tilde{W}_{c}^{T}\xi {{e}_{cH}}}{{{\left( {{\xi }^{T}}\xi +1 \right) }^{2}}}-\frac{\varsigma \tilde{W}_{c}^{T}\xi {{\xi }^{T}}\tilde{W}_{c}}{{{\left( {{\xi }^{T}}\xi +1 \right) }^{2}}} \nonumber \\&\le -\left( \varsigma -\frac{1}{4} \right) \frac{{{\lambda }_{\min }}\left( \xi {{\xi }^{T}} \right) {{\left\| \tilde{W}_{c} \right\| }^{2}}}{{{\left( {{\xi }^{T}}\xi +1 \right) }^{2}}}+\frac{{{\varsigma }^{2}}e_{cH}^{2}}{{{\left( {{\xi }^{T}}\xi +1 \right) }^{2}}}, \end{aligned}$$
(38)

when \(\varsigma >\frac{1}{4}\) and \(\tilde{W}_{c}\) is outside the compact set \({{\Omega }_{a}}=\left\{ \tilde{W}_{c}:\left\| \tilde{W}_{c}\right\| \le \sqrt{\frac{e_{cH}^{2}}{\left( \varsigma -\frac{1}{4} \right) {{\lambda }_{\min }}\left( \xi {{\xi }^{T}} \right) }} \right\} \), the weight approximation error of critic NN is UUB. This completes the proof. \(\square \)

Based on the compensation-based control policy (20), desired control policy (28) and the optimal control policy (31), \(\hat{u}_{i}^{*}\) is given by:

$$\begin{aligned} \hat{u}_{i}^{*}&=u_{i1}+{u}_{id}+\hat{u}_{i2}^{*} \nonumber \\&=-\left( \begin{array}{l} -\left( {{{\hat{f}}}_{is}}{{e}^{\left( -{{{\hat{f}}}_{i\tau }}x_{i2}^{2} \right) }}+{{{\hat{f}}}_{ic}} \right) sgn ({{x}_{i2}}) \\ -{{{\hat{f}}}_{ib}}{{x}_{i2}}-g_{i}^{-1}{{{\ddot{x}}}_{id}}-\frac{{{\tau }_{is}}}{{{\gamma }_{i}}} \\ \end{array} \right) \nonumber \\&\quad +G_{i}^{-1}({{{\dot{x}}}_{i2d}}-{{\ell }_{i}}({{x}_{d}}))-\frac{1}{2}R_{ii}^{-1}G_{i}^{T}\nabla \phi _{ic}^{T}(\dot{e}){{{\hat{W}}}_{ic}}. \end{aligned}$$
(39)

Remark 5

The proposed decentralized approximated optimal control fits well with the MRM due to utilize only local information of the corresponding subsystem for reducing the complexity of the controller design and ensuring the stability of the robot system. The developed scheme not only solves the coupling effect between the human and the robot, but also in the MRM itself.

The algorithm of human motion intention estimation-based decentralized optimal control is shown as below.

Algorithm 1 Human motion intention estimation-based decentralized optimal control

1: Calculate the robot actual position in Cartesian space

using \(z(t)=\xi (q)\).

2: Obtain the human motion intention via

\({{\hat{z}}_{Hd}}=\hat{W}_{x}^{T}S(f,z,\dot{z})\).

3: Calculate the position tracking error by

\(E={{x}_{1}}-{{\xi }^{-1}}({\hat{z}_{Hd}})\).

4: Obtain the decentralized approximate optimal control according to the update law

\({{\dot{\hat{W}}}_{c}}=-\varsigma \frac{\xi }{{{\left( {{\xi }^{T}}\xi +1 \right) }^{2}}}\left( {{e}_{cH}}-{{\xi }^{T}}{{{\tilde{W}}}_{c}} \right) .\)

Theorem 2

Given an MRM joint subsystem dynamic model developed in (1), and the state space shown in (12), the position tracking error of the closed-loop robot manipulator system is UUB under the pHRI task, by the presented cooperative game-based decentralized optimal control policy derived in (39).

Fig. 1
figure 1

Experimental platform setup

Full size image

Proof

Choose \(V_{p}^{*}(\dot{E})={{L}_{b}}(t)\) as Lyapunov function, then derivative it as follows:

$$\begin{aligned} {{\dot{L}}_{b}}(t)={{(\nabla V_{p}^{*})}^{T}}\left( L(x)+GU+H-{{{\ddot{x}}}_{d}} \right) . \end{aligned}$$
(40)

By considering the coupled HJB equation formulated in (18), it yields:

$$\begin{aligned} {{(\nabla V_{p}^{*})}^{T}}\left( L(x)-{{{\ddot{x}}}_{d}} \right)&=\frac{1}{4}{{(\nabla V_{p}^{*})}^{T}}GR_{M}^{-1}G^{T}(\nabla V_{p}^{*}) \nonumber \\&\quad +\frac{1}{4}{{(\nabla V_{p}^{*})}^{T}}P_{M}^{-1}(\nabla V_{p}^{*})\nonumber \\&\quad -\dot{E}^{T}{{Q}_{b}}\dot{E}. \end{aligned}$$
(41)

Combining (41) into (40), we obtain:

$$\begin{aligned} {{{\dot{L}}}_{b}}(t)&=-\dot{E}^{T}{{Q}_{b}}\dot{E}+\frac{1}{4}{{(\nabla V_{p}^{*})}^{T}}GR_{M}^{-1}G^{T}(\nabla V_{p}^{*}) \nonumber \\&\quad +\frac{1}{4}{{(\nabla V_{p}^{*})}^{T}}P_{M}^{-1}(\nabla V_{p}^{*})+{{(\nabla V_{p}^{*})}^{T}}(GU+H). \end{aligned}$$
(42)

Considering (42), one obtains:

$$\begin{aligned} {{{\dot{L}}}_{b}}(t)&=-\dot{E}^{T}{{Q}_{b}}\dot{E}-{{(\nabla V_{p}^{*})}^{T}}\nonumber \\&\quad \times \left( G\left( U^{*}-U \right) +\left( H^{*}-H \right) \right) \nonumber \\&\quad +\frac{1}{4}{{(\nabla V_{p}^{*})}^{T}}GR_{M}^{-1}G^{T}(\nabla V_{p}^{*})\nonumber \\&\quad +\frac{1}{4}{{(\nabla V_{p}^{*})}^{T}}P_{M}^{-1}(\nabla V_{p}^{*}). \end{aligned}$$
(43)

Then, substituting (40) into (43), one yields:

$$\begin{aligned} {{{\dot{L}}}_{b}}(t)&=-\dot{E}^{T}{{Q}_{b}}\dot{E}+\frac{1}{4}{{(\nabla V_{p}^{*})}^{T}}\left( \begin{array}{l} GR_{M}^{-1}G^{T}(\nabla V_{p}^{*}) \\ \quad +P_{M}^{-1}(\nabla V_{p}^{*}) \\ \end{array} \right) \nonumber \\&\quad +\frac{1}{2} {{\left( \nabla \phi _{c}^{T}{{W}_{c}}(\dot{E})+\nabla {{\varepsilon }_{c}} \right) }^{T}}\nonumber \\&\quad \times \left( \begin{array}{l} GR_{M}^{-1}\left( G^{T}\nabla \phi _{c}^{T}{{{\tilde{W}}}_{c}}+G^{T}\nabla {{\varepsilon }_{c}} \right) \\ \quad +P_{M}^{-1}\left( \nabla \phi _{c}^{T}{{{\tilde{W}}}_{c}}+\nabla {{\varepsilon }_{c}} \right) \\ \end{array} \right) \nonumber \\&=-\dot{E}^{T}{{Q}_{b}}\dot{E}+{{\Pi }_{J}}, \end{aligned}$$
(44)

in which \({{\Pi }_{J}}\) has up-bound:

$$\begin{aligned} {{\Pi }_{J}}\le \left\| \begin{array}{l} \frac{1}{4}{{(\nabla V_{p}^{*})}^{T}}\left( \begin{array}{l} GR_{M}^{-1}G^{T}(\nabla V_{p}^{*}) \\ \quad +P_{M}^{-1}(\nabla V_{p}^{*}) \\ \end{array} \right) \\ \quad +\frac{1}{2}{{\left( \begin{array}{l} \nabla \phi _{c}^{T}{{W}_{c}}(\dot{E})+\nabla {{\varepsilon }_{c}} \\ \end{array} \right) }^{T}} \\ \left( \begin{array}{l} GR_{M}^{-1}\left( G^{T}\nabla \phi _{c}^{T}{{{\tilde{W}}}_{c}}+G^{T}\nabla {{\varepsilon }_{c}} \right) \\ \quad +P_{M}^{-1}\left( \nabla \phi _{c}^{T}{{{\tilde{W}}}_{c}}+\nabla {{\varepsilon }_{c}} \right) \\ \end{array} \right) \\ \end{array} \right\| \le {{\pi }_{J}}, \end{aligned}$$
(45)

where \({{\pi }_{J}}\) denotes computable constant.

With (45), \({{{\dot{L}}}_{b}}(t)\) has upper bound by:

$$\begin{aligned} {{{\dot{L}}}_{b}}(t)\le -{{{\dot{E}}}^{T}}{{Q}_{b}}\dot{E}+{{\pi }_{J}}\le -{{\lambda }_{\min }}({{Q}_{b}}){{\left\| {\dot{E}} \right\| }^{2}}+{{\pi }_{J}}. \end{aligned}$$
(46)

If \(\dot{E}\) lies outside:

$$\begin{aligned} \Omega =\left\{ \dot{E}:\left\| {\dot{E}} \right\| \le \sqrt{\frac{{{\pi }_{J}}}{{{\lambda }_{\min }}({{Q}_{b}})}} \right\} , \end{aligned}$$
(47)

Equation (40) is negative. Hence, we have \({{{\dot{L}}}_{b}}(t)<0\) for any \(\dot{E}\ne 0\) when (47) is satisfied. The position tracking error under pHRI task is proved to be UUB under (39). This completes the proof. \(\square \)

4 Experiments

4.1 Experiment setup

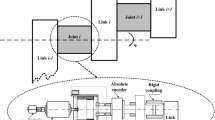
The proposed control method is verified by two degrees of freedom MRM experimental platform (see Fig. 1). The situation of pHRI that is handshaking as well as writing-aid tasks with MRM is considered for simulating robotic adjuvant therapy and aided daily life (cf. Fig. 2). An experiment is performed to determine if the requirements of position tracking performance and control torque as well as interaction torque optimization are met under pHRI. The related dynamic model and control design are given by Table 1.

Table 1 Parameter definition
Full size table
Fig. 2
figure 2

Experimental with physical human robot interaction a handshaking tasks b writing-aid tasks

Full size image

4.2 Experimental results

The experimental results demonstrate the performance of position tracking, tracking error, control torque, interaction torque and critic NN weight. Two types of control methods are used to verify the validity of the proposed method: the existed learning-based optimal control without cooperative game method (e.g. critic only policy iteration-based zero-sum neuro-optimal control [50], compensator-critic-based non-zero-sum optimal control [51], discounted guaranteed cost control [52]), and the proposed cooperative game-based decentralized optimal control approach. The two control methods are both used in handshaking as well as writing-aid pHRI tasks.

Table 2 Performance comparisons
Full size table
Fig. 3
figure 3

Motion intention estimation and position tracking curves under handshaking tasks via the proposed control approach a joint one b joint two

Full size image
Fig. 4
figure 4

Motion intention estimation and position tracking curves under writing-aid tasks via the proposed control approach a joint one b joint two

Full size image
Fig. 5
figure 5

Position tracking error curves in joint space under handshaking tasks via the existed and the proposed control method a joint one b joint two

Full size image
Fig. 6
figure 6

Position tracking error curves in joint space under writing-aid tasks via the existed and the proposed control method a joint one b joint two

Full size image
Fig. 7
figure 7

Control torque curves under handshaking tasks via the existed and the proposed control method a joint one b joint two

Full size image
Fig. 8
figure 8

Control torque curves under writing-aid tasks via the existed and the proposed control method a joint one b joint two

Full size image
Fig. 9
figure 9

Interaction torque curves under handshaking tasks via the existed and the proposed control method a joint one b joint two

Full size image
Fig. 10
figure 10

Interaction torque curves under writing-aid tasks via the existed and the proposed control method a joint one b joint two

Full size image
Fig. 11
figure 11

NN curves under handshaking tasks via the proposed cooperative game-based decentralized optimal control approach a joint one b joint two

Full size image
Fig. 12
figure 12

NN curves under writing-aid tasks via the proposed cooperative game-based decentralized optimal control approach a joint one b joint two

Full size image
  1. (1)

    Position tracking performance

Figures 3 and 5 present the position tracking and tracking error curves in joint space under handshaking tasks, obtained by the existed learning-based optimal control and proposed cooperative game-based decentralized optimal control approach, respectively. It can be seen that the amplitude of position tracking error under the proposed cooperative game-based decentralized optimal control approach is fairly smaller than the one under the existed control method, as the proposed cooperative game-based decentralized optimal control approach accurately solves the human motion intention estimation problem. Figures 4 and 6 are the position tracking and error curves in joint space under the writing-aid tasks. The similar results can be obtained.

  1. (2)

    Control torque

Figure 7 shows the control torque curves under handshaking tasks using the existed learning-based optimal control method and the proposed cooperative game-based decentralized optimal control approach. Furthermore, the control torque curves show serious chattering effects under the existed control method, which may reduce the precision of the position tracking. The control torque curves of the writing-aid tasks are illustrated in Fig. 8. The effectiveness of the proposed cooperative game-based decentralized optimal control approach is demonstrated, which is attributed to the approximate optimal control that realizes output torque optimization.

  1. (3)

    Interaction torque

Figure 9 shows the interaction torque curves under handshaking tasks by the existed learning-based optimal control method and the proposed cooperative game-based decentralized optimal control approach. The existed learning-based optimal control method is without coupling compensation, therefore the interaction torque is a touch of quavering and massive than the proposed method. It can be seen that the interaction torque is less than or equal to 0.25 Nm for both joints, under the cooperative game-based decentralized optimal control approach, and without strong chattering phenomenon. This facilitates the accurate implementation of the cooperative game technique, which guarantees the comfort and security of the human demonstrated from the interaction torque. Figure 10 provides the interaction torque curves under writing-aid tasks via the proposed cooperative game-based decentralized optimal control approach. Making the full use of cooperative game and decentralized control mechanism, the coupling effect between the MRM and the human has been worked out faultlessly. The writing process for human perceives gentle and effortless. Besides, on account of the approximate optimal control approach, the interaction torque is minor than the existed learning-based optimal control method.

  1. (4)

    Critic NN weight

Figures 11 and 12 show the critic NN weight curves under handshaking and writing-aid tasks obtained by the proposed cooperative game-based decentralized optimal control approach, respectively. The cooperative game-based decentralized optimal control approach can be obtained using the converged weights (cf. Figs. 7 and 8). Thus, the weight can reflect the human intention in real time.

Based on the experimental results, the closed-loop MRM systems under the pHRI task have better performance than the existed methods in terms of position tracking, control torque, and interaction torque under the proposed cooperative game-based decentralized optimal control approach (cf. Table 2).

5 Conclusions

This paper proposed a cooperative game-based decentralized optimal control approach for MRMs under pHRI tasks. Based on the differential game strategy, the optimal control problem of closed-loop robotic systems is transformed into a cooperative game issue between the human and the MRM. Using the ADP algorithm, the cost function is developed by critic NN and implemented to solve the coupled HJB equation, which facilitates the acquisition of Pareto equilibrium solutions. The position tracking error is UUB under the pHRI task. Finally, the performed experiments demonstrate the efficiency of the proposed method. In pHRI, human’s comfort via subjective scales is with great importance. Inspired by [53, 54], the quantification of human’s comfort will be our future work.