Keywords

1 Introduction

The most difficult and responsible stage in the calculation and development of new elements and devices, machines and mechanisms, drives and control systems is the development of the mathematical models of the nonstationary workflows occurring in them [1,2,3,4]. It is very important not to allow excessive unjustified complication of the mathematical models as they may not be suitable for practical use. At the same time, neglecting phenomena that significantly affect the work processes can make the model too rough, not providing the required accuracy and also not reflecting the main features of the ongoing processes.

The nonstationary hydromechanical processes refer to the complex physical phenomena in which unsteady fluid flows arise with changes in velocities and pressures not only in time but also in the space occupied by flow [5,6,7,8]. The direct description of such processes leads to the systems of nonlinear equations in partial derivatives, and the boundary conditions necessary for the solution of these equations are often themselves differential equations describing the dynamic processes in those devices with which fluid flows interact. The use of such complex models requires the implementation of labor-intensive calculations, which may not yield visible results.

The important parameter in calculations of hydromechanical processes is the force of viscous fluid friction, which is characterized by the shearing stress arising in the working medium contacting the surface of the moving element of the actuating, regulating, distributing, or auxiliary hydraulic devices [9,10,11,12,13,14]. In the presence of a gap between the surfaces of the elements, the shearing stresses arise when relative motion of these surfaces and the motion of the medium are affected by the pressure difference.

2 Literature Review

The traditional approaches [5, 15,16,17,18,19,20] to the development of mathematical models of nonstationary hydromechanical processes are mainly based on the fact that real flows are replaced by a successive sequence of flows with a quasi-stationary distribution of hydrodynamic quantities over the live flow cross-section. This allows us to introduce into account the coefficients and characteristics obtained for stationary flows. In fact, the structure of nonstationary flows differs from the quasi-stationary flow [1, 5, 8], and it is not always known how and under what conditions such a difference can affect the change in hydrodynamic characteristics.

In real devices, the gap is small in such a way that the flow is considered as a laminar plane between parallel walls (Fig. 1), and the velocity distribution (Fig. 2) has the form [6, 7, 21, 22]

Fig. 1
figure 1

Laminar flow between parallel planes. a Flow scheme; b velocity distribution in the absence of a pressure gradient (Couette flow); c velocity distribution for fixed boundary planes (flow in a flat channel)

Full size image
Fig. 2
figure 2

Dimensionless velocity profiles for the general case of fluid flow between parallel walls \((p_{*} = - \delta^{2} {\text{d}}p/{\text{d}}x/(2\rho \nu u_{0} ))\)

Full size image
$$\frac{u}{{u_{0} }} = \frac{{\delta^{2} }}{2\rho \nu }\frac{{{\text{d}}p}}{{{\text{d}}x}}\frac{y}{\delta }\left( {1 - \frac{y}{\delta }} \right) + \frac{y}{\delta },$$
(1)

where x, y—coordinates; u—velocity of the fluid in the gap; u0—speed of movement of the moving element (or relative speed of motion of the surfaces); δ—size of the gap; \({\text{d}}p/{\text{d}}x\)—pressure gradient; and ρ, ν—density and kinematic viscosity of the fluid.

The shearing stress is calculated on the basis of the velocity distribution (1) according to the Newton’s law of viscous friction [7, 19, 21].

The aim of the paper is to obtain dependencies for calculating the shearing stress in nonstationary fluid friction, considering the inertia of the change in the flow structure in the gap, and also estimating the boundaries of the quasi-stationary approach for calculating the forces of nonstationary viscous friction on the moving elements of hydraulic devices.

3 Research of Shearing Stress in Nonstationary Fluid Friction

Let the speed of motion of the moving element (or the relative speed of motion of surfaces) be nonstationary

$$u_{0} = V(t).$$
(2)

Then, for a quasi-stationary approach, the shearing stress on the moving surface (quasi-stationary shearing stress), taking (1) into account,

$$\tau_{qs}^{0} = \rho \nu \frac{{{\text{d}}u}}{{{\text{d}}y}} = - \frac{\delta }{2}\frac{{{\text{d}}p}}{{{\text{d}}x}} + \frac{\rho \nu }{\delta }V(t).$$
(3)

We transform (3) by the Laplace [23,24,25] and establish the transfer functions for the quasi-stationary shearing stress with respect to the velocity of the moving element and the pressure gradient

$$W_{{\tau V.{\text{qs}}}} (s) = \frac{{\tau_{\text{qs}}^{0} (s)}}{V(s)} = k_{\tau V} .$$
(4)
$$W_{{\tau p.{\text{qs}}}} (s) = \frac{{\tau_{\text{qs}}^{0} (s)}}{{\frac{{{\text{d}}p}}{{{\text{d}}x}}(s)}} = k_{\tau p} .$$
(5)

where s—Laplace variable and transfer coefficients kτV = ρν/δ, kτp = –δ/2.

In order to obtain the transfer functions for the shearing stress, considering the influence of the inertia of the flow structure, we consider the nonstationary laminar motion of incompressible fluid in the gap between fixed and moving elements in the Cartesian coordinate system (Fig. 1). Assuming the flow is plane, the equation of fluid motion is represented in the known form [6]

$$\frac{\partial u}{\partial t} = - \frac{1}{\rho }\frac{\partial p}{\partial x} + \nu \frac{{\partial^{2} u}}{{\partial y^{2} }}.$$
(6)

For the fluid velocity u, which is the function of time t and the coordinate y, we define the boundary conditions:

$$\left\{ {\begin{array}{*{20}l} {u = 0,\quad y = 0;} \hfill \\ {u = V(t),\quad y = \delta .} \hfill \\ \end{array} } \right.$$
(7)

To simplify the mathematical calculations, we make the change of variables

$$z = y - \delta ,$$
(8)

and also consider that for the flow under consideration

$$\frac{\partial p}{\partial x} = \frac{{{\text{d}}p}}{{{\text{d}}x}}.$$
(9)

Taking (8, 9) into account, in place of (6, 7) we have:

$$\frac{\partial u}{\partial t} = - \frac{1}{\rho }\frac{{{\text{d}}p}}{{{\text{d}}x}} + \nu \frac{{\partial^{2} u}}{{\partial z^{2} }},$$
(10)
$$\left\{ {\begin{array}{*{20}l} {u = 0,\quad z = - \delta ;} \hfill \\ {u = V(t),\quad z = 0.} \hfill \\ \end{array} } \right.$$
(11)

Applying the one-dimensional Laplace transform under zero initial conditions, we obtain instead of the partial differential equation (10) the equation in ordinary derivatives

$$\frac{{{\text{d}}^{2} u(s)}}{{{\text{d}}z^{2} }} - \frac{s}{\nu }u(s) = \frac{p(s)}{\rho s},$$
(12)

where u(s), p(s)—Laplacian image of velocity u and the pressure gradient dp/dx.

The solution of Eq. (12) has the form

$$u(s) = A_{1} \exp \left( {z\sqrt {s/\nu } } \right) + A_{2} \exp \left( { - z\sqrt {s/\nu } } \right) - \frac{p(s)}{\rho s},$$
(13)

where A1, A2—integration constants.

The shearing stress on the surface of the moving element is found according to the Newton’s law of viscous friction

$$\tau^{0} (s) = \left. {\rho \nu \left( {\frac{\partial u(s)}{\partial y}} \right)} \right|_{y = \delta } = \left. {\rho \nu \left( {\frac{\partial u(s)}{\partial z}} \right)} \right|_{z = 0} .$$
(14)

Substituting (13) into (14), we have

$$\tau^{0} (s) = \rho \nu \sqrt {s/\nu } \left( {A_{1} - A_{2} } \right).$$
(15)

The value A1 − A2 is determined using the boundary conditions (11) and the obtained solution (13):

$$\left\{ {\begin{array}{*{20}l} {0 = A_{1} \exp \left( { - \sqrt {\delta^{2} s/\nu } } \right) + A_{2} \exp \left( {\sqrt {\delta^{2} s/\nu } } \right) - \frac{p\left( s \right)}{\rho s};} \hfill \\ {V(s) = A_{1} + A_{2} - \frac{p\left( s \right)}{\rho s}.} \hfill \\ \end{array} } \right.$$
(16, 17)

We multiply (17) by \(\exp \left( { - \sqrt {\delta^{2} s/\nu } } \right)\) and subtract (16), then we have

$$V(s)\exp \left( { - \sqrt {\delta^{2} s/\nu } } \right) = - 2A_{2} {\text{sh}}\left( {\sqrt {\delta^{2} s/\nu } } \right) + \frac{p\left( s \right)}{\rho s}\left( {1 - \exp \left( { - \sqrt {\delta^{2} s/\nu } } \right)} \right).$$
(18)

The subtraction (16) from (17), multiplied by \(\exp \left( {\sqrt {\delta^{2} s/\nu } } \right)\), gives

$$V(s)\exp \left( {\sqrt {\delta^{2} s/\nu } } \right) = - 2A_{1} {\text{sh}}\left( {\sqrt {\delta^{2} s/\nu } } \right) + \frac{p(s)}{\rho s}\left( {1 - \exp \left( {\sqrt {\delta^{2} s/\nu } } \right)} \right).$$
(19)

We summarize (18) and (19)

$$2V(s){\text{ch}}\left( {\sqrt {\delta^{2} s/\nu } } \right) = 2(A_{1} - A_{2} ){\text{sh}}\left( {\sqrt {\delta^{2} s/\nu } } \right) + \frac{2p(s)}{\rho s}\left( {1 - {\text{ch}}\left( {\sqrt {\delta^{2} s/\nu } } \right)} \right),$$
(20)

and hence, we obtain

$$A_{1} - A_{2} = \frac{p(s)}{\rho s}\frac{{{\text{ch}}\left( {\sqrt {\delta^{2} s/\nu } } \right) - 1}}{{{\text{sh}}\left( {\sqrt {\delta^{2} s/\nu } } \right)}} + V(s){\text{cth}}\left( {\sqrt {\delta^{2} s/\nu } } \right).$$
(21)

We substitute (21) into (15), then we transform to the form

$$\tau^{0} (s) = - \frac{\delta }{2}p(s)\frac{2}{{\sqrt {\delta^{2} s/\nu } }}\frac{{{\text{ch}}\left( {\sqrt {\delta^{2} s/\nu } } \right) - 1}}{{{\text{sh}}\left( {\sqrt {\delta^{2} s/\nu } } \right)}} + \frac{\rho \nu }{\delta }V(s)\left[ {\sqrt {\delta^{2} s/\nu } {\text{cth}}\left( {\sqrt {\delta^{2} s/\nu } } \right)} \right].$$
(22)

This expression is the nonstationary shearing stress on the surface of the moving element in the operator form.

According to Eq. (22), we obtain the transfer function for the nonstationary shearing stress with respect to the velocity of the moving element

$$W_{\tau V} (s) = \frac{{\tau^{0} (s)}}{V(s)} = k_{\tau V} \sqrt {Ts} {\text{cth}}\sqrt {Ts} ,$$
(23)

where kτV—transfer coefficient, introduced according to the expression (4); \(T = \delta^{2} /\nu\)—time constant.

Consider the dimensionless transfer function

(24)

where \(\bar{s} = sT\)—dimensionless Laplace variable. By the function (24), we determine the amplitude-frequency characteristic

$$\overline{A}_{\tau V}^{{}} (\bar{\omega }) = \bmod \left[ {\overline{W}_{\tau V} (j\bar{\omega })} \right],$$
(25)

where \(j = \sqrt { - 1} ;\bar{\omega } = \omega T\)—dimensionless frequency.

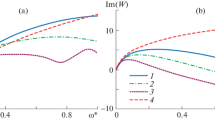
The graph \(\overline{A}_{\tau V} (\bar{\omega })\), shown in Fig. 3a, shows, that for \(\bar{\omega } < 0.81\), the nonstationary of motion leads to an increase in the amplitude of the shearing stresses fluctuations by no more than 5%. Therefore, in this range, it is permissible to use the quasi-stationary transfer function (4) to calculate the frequency characteristics. Thus, this frequency value can be considered as the boundary of a quasi-stationary approach for calculating the viscous friction forces for vibrations of the moving element.

Fig. 3
figure 3

Shearing stress characteristic. a Dimensionless amplitude-frequency shearing stress characteristic (for vibrations of the moving element); b dimensionless amplitude-frequency shear stress characteristic (for the pressure gradient vibrations)

Full size image

Also, by expression (22), we establish the transfer function for the nonstationary shearing stress with respect to the pressure gradient

$$W_{\tau p} (s) = \frac{{\tau^{0} (s)}}{p(s)} = k_{\tau p} \frac{2}{{\sqrt {Ts} }}\frac{{{\text{ch}}\sqrt {Ts} - 1}}{{{\text{sh}}\sqrt {Ts} }},$$
(26)

where kτp—transfer coefficient, introduced according to the expression (5).

By the dimensionless transfer function

(27)

determine the dimensionless amplitude-frequency characteristic

$$\bar{A}_{\tau p} (\bar{\omega }) = \bmod \,\left[ {\bar{W}_{\tau p} (j\bar{\omega })} \right].$$
(28)

The graph \(\overline{A}_{\tau \rho } (\bar{\omega })\), shown in Fig. 3b, shows, that for \(\bar{\omega } < 3.34\) the decrease in amplitude of the shearing stresses fluctuations by no more than 5%. Therefore, in this range, it is permissible to use the quasi-stationary transfer function (5) to calculate the frequency characteristics. Thus, this frequency value can be considered as the boundary of a quasi-stationary approach for calculating viscous friction forces for the pressure gradient vibrations.

A good approximation of the transfer functions (23, 26) gives their approximation by the following functions:

$$W_{\tau v} (s) \approx k_{\tau v} \left( {1 + 0.387Ts} \right);\quad W_{\tau p} (s) \approx \frac{{k_{\tau p} }}{0.098Ts + 1}.$$
(29)

4 Conclusions

Thus, the dependence in the operator form for the shearing stress for nonstationary fluid friction is obtained. The transfer functions for the shearing stress with respect to the velocity of the moving element and the pressure gradient are determined. Based on the analysis of amplitude-frequency characteristics, the boundaries of a quasi-stationary approach for calculating the forces of nonstationary viscous friction on the moving elements are established. The approximate transfer functions for the nonstationary shearing stress are proposed, which allow to establish the connection between the originals in the form of ordinary linear differential equations.