The viscoelastic properties of non-Newtonian fluids affect significantly the hydraulic characteristics of flow. In transporting highly viscous and heavy oils and oil products at large distances and in drilling mud circulation in the well, one of the important problems is the development of the efficient method for reducing hydraulic resistance of streams. The experimental investigations showed that both the drilling muds processed by highly-molecular polymers and the oils with high content of asphaltene-tarry substances possess the relaxation properties and can be related to viscoelastic liquids [1–4]. In many technological processes the fluid stream is pulsating or oscillatory and its characteristics can significantly differ from those of usual streams. In such streams the regime of variation in the pressure or the behavior of fluid has the oscillatory nature. Such streams are widely used in various technological processes, together with those noted above, in the chemical technology, food industry, physiology, and acoustics.

The mathematical description of the processes of non-Newtonian fluids is directly connected with the choice of the rheological model which can adequately describe the flow of such liquids. From the above it follows that the hydrodynamic resistance is the most important characteristic of fluid flow when investigating various technological processes. The hydrodynamic resistance for non-Newtonian fluids and the tangential stress for shear flows are determined in different ways for various rheological models. In this case the tangential shear stress can have specific features which are not distinctive characteristic for ordinary viscous fluids. Therefore, the study of the tangential shear stress in non-Newtonian fluid flow, together with other flow characteristics, is of great importance [5–7].

Many investigations are devoted to studying the pulsating motion of non-Newtonian fluids in tubes, in particular, viscoelastic fluids. In [8] the fluid velocity field developed in oscillatory laminar flow through a long circular pipe under the action of a periodic pressure gradient was studied experimentally. In the case of Newtonian fluid the experimental results demonstrate that the amplitude of the periodic longitudinal velocity as a function of the radial coordinate and the frequency is in good agreement with the theoretical results. It is shown that at low frequencies the velocity distribution is approximately parabolic with a maximum on the pipe axis. At the higher frequencies the maximum velocity is reached between the axis and the pipe wall and this peak is displaced towards the wall with increase in the frequency. In [9, 10] some investigations of periodic streams were also considered.

In [11] the motion of a viscoelastic fluid through a long pipe under the action of an oscillatory pressure gradient was studied and the distinctive features of this motion as compared with the case of the corresponding motion of a Newtonian fluid were demonstrated.

In [12] the instantaneous velocity profiles over the circular pipe cross-section and the corresponding streamwise pressure gradients in inertialess oscillatory and pulsating flows of a nonlinear viscoelastic polymeric solution were investigated. It was shown that in oscillating flow the longitudinal velocity profiles are symmetric and there exists a considerable phase shift between the pressure gradient and the velocity. In pulsating flows, there was actually no phase shift and the axial velocity varied asymmetrically with respect to its period-average value.

In [13] laminar oscillatory flow of viscoelastic Maxwell and Oldroyd-B fluids was studied. The oscillatory behavior of flow was classified in two wide classes which corresponded to “wide” and “narrow” systems.

In Poiseuille flow of a viscoelastic Maxwell fluid with a relaxation time spectrum the instantaneous flow velocities can significantly increase at certain frequencies of the oscillating pressure gradient [14]. Rather large increases can be reached at the resonance frequencies even if the amplitude of an additional oscillatory pressure gradient is very low.

In [15] pulsating Green–Rivlin fluid flow in straight tubes of an arbitrary cross-section was investigated. The principal conclusion of the study consists in the fact that the effect of velocity enhancement in tubes of arbitrary shape cannot be predicted using the first-order analysis. In [16] unsteady axial viscoelastic pipe flows of an Oldroyd B fluid through an infinite pipe of circular cross-section was analyzed. The fluid moves under the action of a time-dependent pressure gradient in three following cases: 1) the pressure gradient varies with time in accordance with the exponential law; 2) the pressure gradient is pulsating; 3) the pressure gradient is constant. The fluid velocity distributions with the pulsating behavior are obtained.

Recently, the differential rheological models with fractional derivatives came into use in the theory of viscoelasticity [17–19]. This can be considered as the natural generalization of classical models. In [20] it was noted that very good description of the experimental data was reached using the fractional-order Maxwell models. Certain exact analytical solutions were obtained for the class of unsteady flows for a generalized second-grade fluid with fractional derivatives between two parallel plates [21]. Unstable flows were created by pulse motion or periodic oscillation of one of the plates. In [22] unsteady viscoelastic fluid flow is described for the Maxwell model with fractional derivatives. The effect of the fractional parameters and material constants on the velocity field and the tangential shear stress is analyzed.

It should be noted that studying the pulsating unsteady motion of non-Newtonian fluids in pipes and channels is of importance in investigating the stability of flow and pipe itself [23, 24]. In this case, the establishment of the stability and absolute instability criteria as functions of the rheological properties of fluid and pipe material, as well as of the flow regimes, is of the same importance.

In the above-mentioned papers, the fluid velocity field is mainly studied in various regimes of change in the pressure. The stress fields and the tangential and normal stresses developed in the motion of viscoelastic fluids were investigated to the relatively small extent. In the majority of cases, in the hydrodynamic models of unsteady fluid flows the real streams were replaced by a succession of streams with a quasi-stationary distribution of hydrodynamic quantities [25]. However, the structure of unsteady flows differs from the structure of steady flows and such a replacement of flow should be justified in each particular case. At present, the question of legitimacy of using the quasi-stationary approach in determining the tangential stress field even for unsteady flows of ordinary viscous fluid, without mentioning viscoelastic fluids, is far from being settle to the end. It is natural that for such conditions it is necessary to use the hydrodynamic models of unsteady processes that take into account variations in the flow characteristics and the hydrodynamic parameters as functions of time. In particular, in the generic case the friction resistance in unsteady fluid pipe flow cannot be determined from the characteristics that correspond to the stationary flow conditions.

In the present study, the theoretical method for determining the generalized resistance law in the periodic motion of a viscoelastic Maxwell fluid in the cylindrical pipe is proposed. The transfer function that expresses the generalized friction resistance law is constructed and formulas for the frequency function are derived. The dependence of the pipe wall unsteady tangential shear stress on the oscillation frequency, the acceleration, and the relaxation properties of fluid is studied using these formulas. The role of flow unsteadiness in the resistance law is estimated and the difference between the results obtained and those found on the basis of the quasi-stationary approach is demonstrated.

1 FORMULATION OF THE PROBLEM

We will consider the problem of determination of the tangential shear stress \({{\tau }_{{{\text{ons}}}}}(t) = \tau (R,t)\) on the wall of a circular cylindrical pipe of radius R under the periodic motion of fluid. The rheological equation of state of fluid is taken in the form [5, 7]:

$$\left( {1 + \lambda \frac{\partial }{{\partial t}}} \right)\tau \left( {r,t} \right) = - \mu \frac{{\partial u}}{{\partial r}},$$
(1.1)

where r is the radial coordinate reckoned from the axis of pipe (\(0 \leqslant r \leqslant R\)), \(t\) is time, u is the fluid velocity, μ is dynamic viscosity, τ is the tangential shear stress, and λ is the relaxation time. In (1.1) when λ = 0 we obtain the Newton viscous friction law and when λ > 0—the model of the viscoelastic Maxwell medium. Substituting (1.1) in the equation of motion

$$\rho \frac{{\partial u}}{{\partial t}} = - \frac{{\partial p}}{{\partial z}} - \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\tau } \right)$$

for the fluid velocity u(r, t), we obtain

$$\rho \left( {1 + \lambda \frac{\partial }{{\partial t}}} \right)\frac{{\partial u}}{{\partial t}} = - \left( {1 + \lambda \frac{\partial }{{\partial t}}} \right)\frac{{\partial p}}{{\partial z}} + \mu \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial u}}{{\partial r}}} \right),$$
(1.2)

where \(\partial p{\text{/}}\partial z\) is the gradient of the pressure p along the Oz axis that coincides which the axis of pipe and ρ is the fluid density. At the initial instant of time the fluid is assumed to be at rest and, in accordance with the no-slip condition, the velocity is equal to zero on the pipe wall. Then the initial and boundary conditions take the form:

$$u(r,0) = 0,\quad \frac{{\partial u(r,0)}}{{\partial t}} = 0,\quad 0 \leqslant r \leqslant R;\quad u(0,t) < + \infty ,\quad u(R,t) = 0,\quad \tau (R,0) = 0.$$
(1.3)

Equations (1.1) and (1.2) and conditions (1.3) express the mathematical model of the process considered.

We introduce the following dimensionless quantities:

$$r' = \frac{r}{R},\quad t' = \frac{U}{R}t,\quad \lambda ' = \frac{U}{R}\lambda ,\quad u' = \frac{u}{U},$$
(1.4)

where U is a certain characteristic velocity.

In dimensionless variables (1.4) equations (1.1) and (1.2) take the form:

$$\left( {1 + \lambda '\frac{\partial }{{\partial \bar {t}}}} \right)\tau ' = - \frac{{\partial u'}}{{\partial r'}},$$
(1.5)
$$\frac{1}{{\operatorname{Re} }}\frac{1}{{r'}}\frac{\partial }{{\partial r'}}\left( {r'\frac{{\partial u'}}{{\partial r'}}} \right) - \left( {1 + \lambda '\frac{\partial }{{\partial t'}}} \right)\frac{{\partial u'}}{{\partial t'}} = \left( {1 + \lambda '\frac{\partial }{{\partial t'}}} \right){{P}_{z}}(t'),$$
(1.6)

where \(\operatorname{Re} = UR\rho {\text{/}}\mu \), \(\tau ' = \tau R{\text{/}}(U\mu )\) is the dimensionless tangential shear stress, \({{P}_{z}}(t') = \partial p'{\text{/}}\partial z'\) = \(R(\partial p{\text{/}}\partial z){\text{/}}(\rho {{U}^{2}})\) is the dimensionless pressure gradient, \(p' = p{\text{/}}(\rho {{U}^{2}})\), and \(z = Rz'\).

In dimensionless quantities the initial and boundary conditions take the form:

$$\begin{gathered} \hfill u'(r',t') = 0,\quad \frac{{\partial u'(r',0)}}{{\partial t'}} = 0,\quad 0 \leqslant r' \leqslant 1; \\ \hfill u'(0,t') < + \infty ,\quad u'(1,t') = 0,\quad \tau '(1,t') = 0. \\ \end{gathered} $$
(1.7)

2 SOLUTION OF THE PROBLEM

Using the integral Laplace transformation [26]

$${{u}_{ * }}(r',s) = \int\limits_0^{ + \infty } {u'{{e}^{{ - st'}}}dt',\quad {{\tau }_{ * }}\left( {r',s} \right) = \int\limits_0^{ + \infty } {\tau '{{e}^{{ - st'}}}dt',\quad {{P}_{{z \text{*} }}}\left( s \right) = \int\limits_0^{ + \infty } {{{P}_{z}}(t'){{e}^{{ - st'}}}dt'} } } $$

for solving Eqs. (1.5) and (1.6) with the boundary conditions (1.7), we obtain

$$\frac{1}{{r'}}\frac{d}{{dr'}}\left( {r'\frac{{d{{u}_{ \text{*} }}}}{{dr'}}} \right) - \operatorname{Re} {{k}^{2}}{{u}_{ * }} = \frac{{{{k}^{2}}\operatorname{Re} }}{s}{{P}_{{z\text{*}}}}(s),$$
(2.1)
$${{u}_{ * }}(1,s) = 0,\quad {{u}_{ * }}(0,s) < + \infty ,$$
(2.2)
$$\left( {1 + \lambda 's} \right){{\tau }_{ * }} = - \frac{{d{{u}_{ * }}}}{{dr'}}.$$
(2.3)

The solution of Eq. (2.1) with the boundary conditions (2.2) takes the form:

$${{u}_{ \text{*} }}\left( {r',s} \right) = - \frac{{{{P}_{*}}(s)}}{s}\left[ {1 - \frac{{{{J}_{0}}(iakr')}}{{{{J}_{0}}(iak)}}} \right].$$
(2.4)

Substituting (2.4) in (2.3), we obtain the following formula for the tangential shear stress:

$${{\tau }_{ * }}(r',s) = - \frac{{\operatorname{Re} }}{{iak}}\frac{{{{J}_{1}}(iakr')}}{{{{J}_{0}}(iak)}},$$
(2.5)

where \(k = \sqrt {s(1 + \lambda 's)} \), \(a = \sqrt {\operatorname{Re} } \), and \({{J}_{0}}(x)\) and J1(x) are the zeroth- and first-order Bessel functions of the first kind.

The pipe wall friction resistance is determined by the tangential shear stress \({{\tau }_{{{\text{ons}}}}}(t) = \tau (R,t)\) whose dimensionless form in the case under consideration takes the form:

$$\tau _{{{\text{ons}}}}^{'}(t') = \frac{R}{{U\mu }}{{\tau }_{{{\text{ons}}}}}(t).$$

By setting \(r' = 1\) in (2.5), we can find the Laplace transform of the dimensionless time-dependent tangential shear stress on the pipe wall

$${{\tau }_{{{\text{ons*}}}}}(s) = {{\tau }_{ * }}(1,s) = - \frac{{\operatorname{Re} }}{{iak}}\frac{{{{J}_{1}}(iak)}}{{{{J}_{0}}(iak)}}{{P}_{{z\text{*}}}}(s).$$
(2.6)

For the quasi-stationary velocity distribution, the tangential shear stress on the pipe wall \({{\tau }_{{{\text{oks}}}}}\) is determined as follows [27, 28]:

$${{\tau }_{{{\text{oks}}}}} = \frac{4}{R}\mu {{{v}}_{{{\text{ks}}}}},$$
(2.7)

and in dimensionless form as

$$\tau _{{{\text{oks}}}}^{'} = 4{v}_{{{\text{ks}}}}^{'},$$
(2.8)

where \({{{v}}_{{ks}}}\) is the quasi-stationary pipe-cross-section-average velocity, \(\tau _{{{\text{oks}}}}^{'} = R{{\tau }_{{{\text{oks}}}}}{\text{/}}(U\mu )\), and \({v}_{{{\text{ks}}}}^{'} = {{{v}}_{{{\text{ks}}}}}{\text{/}}U\).

In accordance with (2.7), the quasi-stationary tangential shear stress on the pipe wall \({{\tau }_{{{\text{oks}}}}}\) is the function of the pipe-cross-section-average velocity. In order to find the dependence of the time-dependent tangential shear stress on the pipe wall on the pipe-cross-section-average velocity \({v}(t)\) of unsteady flow in dimensionless quantities, we eliminate the image of the dimensionless pressure gradient \({{P}_{{z\text{*}}}}(s)\) from formula (2.6). For this purpose, we multiply Eq. (1.6) by \(2\pi r'\) and integrate over the segment [0, 1]

$$2\pi \int\limits_0^1 {\frac{\partial }{{\partial r'}}\left( {r'\frac{{\partial u'}}{{\partial r'}}} \right)dr'} - 2\pi {\text{Re}}\int\limits_0^1 {\left( {1 + \lambda '\frac{\partial }{{\partial t'}}} \right)\frac{{\partial u'}}{{\partial t'}}r'dr' = 2\pi \operatorname{Re} \left( {1 + \lambda '\frac{\partial }{{\partial t'}}} \right){{P}_{z}}(t')\int\limits_0^1 {r'dr'} } ,$$

hence

$$2{{\left. {\left[ {\frac{{\partial u'}}{{\partial r'}}} \right]} \right|}_{{\bar {r} = 1}}} - {\text{Re}}\left( {1 + \lambda '\frac{d}{{dt'}}} \right)\frac{{d{v}'}}{{dt'}} = \operatorname{Re} \left( {1 + \lambda '\frac{d}{{dt'}}} \right){{P}_{z}}(t').$$
(2.9)

Going over to the image in (2.9) with regard to (2.3), we obtain

$${{P}_{{z\text{*}}}}(s) = - 2{{\tau }_{{{\text{ons*}}}}}(s){\text{/}}\operatorname{Re} \; - s{{{v}}_{ * }}(s),$$

where \({v}'(t') = 2\int_0^1 {u'r'dr'} \) is the dimensionless pipe-cross-section-average velocity and \({{{v}}_{ * }}(s) = \int_0^{ + \infty } {{v}'{{e}^{{ - st'}}}dt'} \) is its Laplace transform. Substituting the expression obtained for \({{P}_{{z\text{*}}}}(s)\) in (2.6) and using the property of Bessel functions \(2{{J}_{1}}(x){\text{/}}x - {{J}_{0}}(x) = {{J}_{2}}(x)\), we obtain

$${{\tau }_{{{\text{ons*}}}}}(s) = - s{{{v}}_{ * }}(s)\frac{{\operatorname{Re} {{J}_{1}}(iak)}}{{iak{{J}_{2}}(iak)}},$$
(2.10)

where J2(x) is the second-order Bessel function of the first kind.

Relation (2.10) establishes a link between the dimensionless values of the Laplace transform of the tangential shear stress on the pipe wall and the pipe-cross-section-average fluid velocity for unsteady fluid flow. In terms of the automatic control theory it can be represented in the form of the transfer function:

$$W(s) = \frac{{{{\tau }_{{{\text{ons*}}}}}(s)}}{{{{{v}}_{ * }}(s)}} = - s\frac{{\operatorname{Re} {{J}_{1}}(iak)}}{{iak{{J}_{2}}(iak)}}.$$
(2.11)

In the generic case the transfer function is determined by the ratio of the “force” factor (the voltage, the force, or the pressure) to the “velocity” factor (the electric current, the velocity, or the volume flow rate) in the complex form. The mechanical transfer function (2.11) expresses the ratio of the complex quantities that describe the law of variation in the tangential shear stress on the pipe wall and the pipe-cross-section-average velocity. It is valid for any perturbations initiating unsteady laminar motion in the pipe and, therefore, describes the generalized friction resistance law. A particular case of this law is the dependence of the pipe wall tangential shear stress on the velocity under steady-state motion of fluid which is well-known in hydraulics in the form of relation (2.7). The function \(W(i\omega )\), where ω is the oscillation frequency, is called the frequency function. Studies [25, 27, 28] are devoted to construction of the transfer and frequency functions for the tangential shear stress on the pipe wall under laminar periodic motion of viscous fluid.

In order to clarify the character of variation in the time-dependent tangential shear stress on the pipe wall we will consider the definition of the dimensionless tangential shear stress on the pipe wall \(\tau _{{{\text{ons}}}}^{'}(t')\) under the harmonic oscillations of fluid

$${v}'(t') = {{a}_{{v}}}{\text{sin}}\omega 't'{\text{,}}$$
(2.12)

where \({{a}_{{v}}}\) is the amplitude of the dimensionless pipe-cross-section-average velocity and \(\omega ' = \omega R{\text{/}}U\) is the dimensionless angular frequency of fluid oscillations.

Considering the steady-state harmonic oscillations, we can represent \(\tau _{{{\text{ons}}}}^{'}(t')\) in the form of the following function:

$$\tau _{{{\text{ons}}}}^{'}(t') = {{a}_{\tau }}\sin (\omega 't' + {{\varphi }_{\tau }}),$$
(2.13)

where aτ is the amplitude of the dimensionless tangential shear stress on the pipe wall and \({{\varphi }_{\tau }}\) is the phase shift between the quantities \(\tau _{{{\text{ons}}}}^{'}(t')\) and \({v}'(t')\). Taking (2.12) into account, equality (2.13) can be reduced to the form:

$$\tau _{{{\text{ons}}}}^{'}(t') = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}{v}'\cos {{\varphi }_{\tau }} + \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\frac{1}{{\omega '}}\sin {{\varphi }_{\tau }}\frac{{d{v}'}}{{dt'}}.$$
(2.14)

Applying the Laplace transform to (2.14), we have

$${{\tau }_{{{\text{ons*}}}}}(s) = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}{{{v}}_{ * }}(s)\cos {{\varphi }_{\tau }} + \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\frac{s}{{\omega '}}{{{v}}_{ * }}(s)\sin {{\varphi }_{\tau }}.$$

Hence and from (2.11) there follows

$$W(s) = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}{\text{cos}}{{\varphi }_{\tau }} + \frac{s}{{\omega '}}\frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}{\text{sin}}{{\varphi }_{\tau }}.$$
(2.15)

The frequency function that corresponds to (2.15) takes the form:

$$W(i\bar {\omega }) = \operatorname{Re} \left( {W(i\omega ')} \right) + i\operatorname{Im} \left( {W(i\omega ')} \right) = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\cos {{\varphi }_{\tau }} + i\frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\sin {{\varphi }_{\tau }},$$

where \(\operatorname{Re} \left( {W(i\omega ')} \right)\) and \(\operatorname{Im} \left( {W(i\omega ')} \right)\) are the real and imaginary parts of the expression for \(W(i\omega ')\).

Hence it follows that

$$\operatorname{Re} \left( {W(i\omega ')} \right) = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\cos \varphi ,\quad \operatorname{Im} \left( {W(i\omega ')} \right) = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\sin {{\varphi }_{\tau }}.$$

Taking this fact into account, we can represent (2.15) in the form:

$$\tau _{{{\text{ons}}}}^{'}(t') = \operatorname{Re} \left( {W(i\omega ')} \right){v}'(t') + \frac{1}{{\omega '}}\operatorname{Im} \left( {W(i\omega ')} \right)\frac{{d{v}'}}{{dt'}}.$$
(2.16)

The function (2.16) determines the time-dependent tangential shear stress on the pipe wall in dimensionless variables at any instant of time under the steady-state harmonic oscillations of fluid. It provides insight into the main feature of its unsteadiness consisting in the fact that its value varies as a function of both the velocity and the acceleration of fluid, in addition the oscillation frequency of fluid in the pipe and the viscoelastic properties of fluid affecting its value. Based on the quasi-stationary velocity distribution over the clear area of the stream, such a character of variation in the tangential shear stress on the pipe wall will be neglected under unsteady motion of the medium. In the last case the stress on the wall pipe can be determined from relation (2.7) which, being nondimensionalized, takes form (2.8).

The use of formula (2.16) is related with the problem of determination of the real and imaginary parts of the frequency function \(W(i\omega ')\). In [27] the corresponding formulas were obtained for viscous fluid by means of the Kelvin functions. The asymptotic formulas were used for large values of \(\omega '\). We will now derive the formulas \(\operatorname{Re} \left( {W(i\omega ')} \right)\) and \(\operatorname{Im} \left( {W(i\omega ')} \right)\) for the viscoelastic fluid considered here which are valid for any \(\omega '\). For this purpose, we introduce the following function of the complex variable

$$f(z) = \frac{{{{J}_{1}}(z)}}{{z{{J}_{2}}(z)}}.$$

We can show that \({{z}^{2}}f(z) \to 4\) as\(z \to 0\). For this reason, the point z = 0 is the removable singular point for the function

$$F(z) = f(z) - \frac{4}{{{{z}^{2}}}}.$$
(2.17)

When \(z \ne 0\) this function is bounded and has simple poles at the points ±z1, \( \pm {{z}_{2}}, \ldots , \pm {{z}_{n}}\), …, where zn are positive roots of the equation \({{J}_{2}}(z) = 0\), \(n = 1,2, \ldots \). Consequently, F(z) does satisfy all the conditions of the Cauchy theorem on expansion of the meromorphic function in simple fractions [29]. Consequently, the formula holds

$$F(z) = \sum\limits_{n = 1}^\infty {\left[ {\frac{1}{{{{z}_{n}}(z - {{z}_{n}})}} + \frac{1}{{{{z}_{n}}(z + {{z}_{n}})}}} \right] = 2\sum\limits_{n = 1}^\infty {\frac{1}{{{{z}^{2}} - z_{n}^{2}}}} } .$$

Hence, with regard for (2.17) we obtain

$$\frac{{{{J}_{1}}(z)}}{{z{{J}_{2}}(z)}} = \frac{4}{{{{z}^{2}}}} + 2\sum\limits_{n = 1}^\infty {\frac{1}{{{{z}^{2}} - z_{n}^{2}}}} .$$
(2.18)

Using formula (2.18), we can expand the function W(s) into the series

$$W(s) = \frac{{4s}}{{{{k}^{2}}}} + 2s\sum\limits_{n = 1}^\infty {\frac{1}{{{{k}^{2}} + z_{n}^{2}}} = } \frac{4}{{1 + \lambda {\kern 1pt} '{\kern 1pt} s}} + 2s{\text{Re}}\sum\limits_{n = 1}^\infty {\frac{1}{{s{\text{Re}}(1 + \lambda 's) + z_{n}^{2}}}} .$$

Setting here \(s = i\omega '\), we find the expansion for the frequency function

$$W(i\omega ') = \frac{{4(1 - \lambda '\omega 'i)}}{{1 + {{\lambda }^{{'2}}}{{\omega }^{{'2}}}}} + 2{\text{Re}}\omega '\sum\limits_{n = 1}^\infty {\frac{{{\text{Re}}\omega ' + i(z_{n}^{2} - \lambda '{{\omega }^{{'2}}}{\text{Re}})}}{{{{{(z_{n}^{2} - \lambda '{{\omega }^{{'2}}}{\text{Re}})}}^{2}} + {{\omega }^{{'2}}}{\text{R}}{{{\text{e}}}^{2}}}}} .$$

Hence we obtain the following formulas for the real and imaginary parts of the frequency function:

$$\operatorname{Re} \left( {W(i\omega ')} \right) = \frac{4}{{1 + {{\lambda }^{{'2}}}{{\omega }^{{'2}}}}} + 2{\text{R}}{{{\text{e}}}^{2}}{{\omega }^{{'2}}}\sum\limits_{n = 1}^\infty {\frac{1}{{{{{(z_{n}^{2} - \lambda '{{\omega }^{{'2}}}{\text{Re}})}}^{2}} + {{\omega }^{{'2}}}{\text{R}}{{{\text{e}}}^{2}}}}} ,$$
(2.19)
$$\operatorname{Im} \left( {W(i\omega ')} \right) = - \frac{{4\omega '\lambda '}}{{1 + {{\lambda }^{{'2}}}{{\omega }^{{'2}}}}} + 2{\text{Re}}\omega '\sum\limits_{n = 1}^\infty {\frac{{z_{n}^{2} - \lambda '{{\omega }^{{'2}}}{\text{Re}}}}{{{{{(z_{n}^{2} - \lambda '{{\omega }^{{'2}}}{\text{Re}})}}^{2}} + {{\omega }^{{'2}}}{\text{R}}{{{\text{e}}}^{2}}}}} .$$
(2.20)

In particular, for viscous fluid we have

$${\text{Re}}\left( {W(i\omega ')} \right) = 4 + 2{\text{R}}{{{\text{e}}}^{2}}{{\omega }^{{'2}}}\sum\limits_{n = 1}^\infty {\frac{1}{{z_{n}^{4} + {{\omega }^{{'2}}}{{{\operatorname{Re} }}^{2}}}}} ,\quad {\text{Im}}\left( {W(i\omega ')} \right) = 2{\text{Re}}\omega '\sum\limits_{n = 1}^\infty {\frac{{z_{n}^{2}}}{{z_{n}^{4} + {{\omega }^{{'2}}}{\text{R}}{{{\text{e}}}^{2}}}}} .$$

In order to compare \(\tau _{{{\text{ons}}}}^{'}\) and \(\tau _{{{\text{oks}}}}^{'}\) in the same instants of time we take \({v} = {{{v}}_{{{\text{ks}}}}}\) and, by dividing (2.15) term-by-term by \(\tau _{{{\text{oks}}}}^{'} = 4{v}_{{{\text{ks}}}}^{'}\), we find the ratio

$$\frac{{\tau _{{{\text{ons}}}}^{'}}}{{\tau _{{{\text{oks}}}}^{'}}} = \frac{1}{4}\operatorname{Re} \left( {W(i\omega ')} \right) + \frac{1}{{4\omega '}}{{K}_{n}}\operatorname{Im} \left( {W(i\omega ')} \right).$$
(2.21)

Here, the parameter \({{K}_{n}} = (1{\text{/}}{v}')d{v}'{\text{/}}dt'\) serves as the criterion that reflects the effect of the fluid acceleration on the time-dependent tangential shear stress on the pipe wall in the instant of time considered. Substituting (2.18) and (2.19) in (2.20), we obtain

$$\frac{{\tau _{{{\text{ons}}}}^{'}}}{{\tau _{{{\text{oks}}}}^{'}}} = \frac{{{{\tau }_{{{\text{ons}}}}}}}{{{{\tau }_{{{\text{oks}}}}}}} = \frac{{1 - {{K}_{n}}\lambda '}}{{1 + {{\lambda }^{{'2}}}{{\omega }^{{'2}}}}} + \frac{{\operatorname{Re} }}{2}\sum\limits_{n = 1}^\infty {\frac{{{{\omega }^{{'2}}}{\text{Re}} + {{K}_{n}}(z_{n}^{2} - \lambda '{{\omega }^{{'2}}}{\text{Re}})}}{{{{{(z_{n}^{2} - \lambda '{{\omega }^{{'2}}}{\text{Re}})}}^{2}} + {{\omega }^{{'2}}}{\text{R}}{{{\text{e}}}^{2}}}}} .$$
(2.22)

In particular, for viscous fluid

$$\frac{{\tau _{{{\text{ons}}}}^{'}}}{{\tau _{{{\text{oks}}}}^{'}}} = \frac{{{{\tau }_{{{\text{ons}}}}}}}{{{{\tau }_{{{\text{oks}}}}}}} = 1 + \frac{{\operatorname{Re} }}{2}\sum\limits_{n = 1}^\infty {\frac{{{\text{Re}}\omega {{'}^{2}} + {{K}_{n}}z_{n}^{2}}}{{z_{n}^{4} + {{\omega }^{{'2}}}{\text{R}}{{{\text{e}}}^{2}}}}} .$$
(2.23)

From formulas (2.22) and (2.23) it can be seen that with increase in the acceleration (parameter Kn) the time-dependent tangential shear stress increases for the viscous fluid, while for the viscoelastic fluid it also depends on the relaxation parameter \(\lambda \).

3 NUMERICAL EXPERIMENTS AND CONCLUSIONS

Using the formulas obtained, we have carried out the numerical experiments on investigation of the effect of the oscillation frequency, the acceleration (criterion Kn), and the viscoelastic properties of fluid on the time-dependent tangential shear stress distribution over the pipe wall under the periodic motion of fluid. In our calculations we used the following dimensional quantities for the initial data of the problem: R = 0.08 m, U = 0.2 m/s, \(0 \leqslant \omega \leqslant 2.5\) s–1, and λ = 0; 0.5; 1; 2 s. The corresponding dimensionless values of the oscillation frequency and the relaxation parameter are as follows: \(0 \leqslant \omega ' \leqslant 1\) and \(\lambda ' = 0\); 1.25; 2.50; 5. For the density \(\rho = 1200\) kg/m3 and the viscosity \(\mu = 0.030\) Pa s the value of the parameter Re = \(\rho RU{\text{/}}\mu \) is Re = 640.

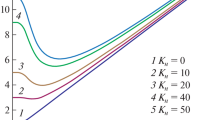
In Fig. 1 we have plotted the graphs of the dependence of the real and imaginary parts of the frequency function on the dimensionless frequency \(\omega '\). It can be seen that for viscous fluid both the parts increase with the dimensionless frequency. For viscoelastic fluid they can decrease at high frequencies. With enhancement of the elastic properties of fluid (with increase in \(\lambda '\)) the graphs take the oscillatory character.

Fig. 1.
figure 1

Dependences of the real and imaginary parts of the frequency function ((a, b), respectively) on the dimensionless oscillation frequency at Re = 640: curves 1–4 correspond to \(\lambda ' = 1.25,\;2.5,\;5,\;0\), respectively.

Full size image

The graphs of the amplitude-phase frequency characteristic of the oscillatory motion considered as the dimensionless frequency \(\omega '\) increases from 0 to 1 (Fig. 2) show that for the viscoelastic fluid the wall tangential shear stress under the harmonic oscillations of fluid in the pipe differs radically from the case of viscous fluid, especially with enhancement of the relaxation properties. For large values of the relaxation time reverse flows can be formed. This is typical for the viscoelastic fluids.

Fig. 2.
figure 2

Amplitude–phase frequency characteristics of the tangential shear stress on the pipe wall under the laminar flow of a viscoelastic fluid with increase in the dimensionless oscillation frequency from 0 to 1 at Re = 640; curves 1–4 are the same as in Fig. 1.

Full size image

In Fig. 3 we have plotted the graphs of the dimensionless time-dependent tangential shear stress on the pipe wall \(\tau _{{{\text{ons}}}}^{'}{\text{/}}\tau _{{{\text{oks}}}}^{'}\) as a function of the dimensionless frequency \(\omega '\) for Re = 640 and the following values of the criterion Kn: 0, 0.01, and 0.05. It can be seen that at \(\omega ' = 0\) and low frequencies (\(0 \leqslant \omega ' \leqslant 0.2\)) the sharp growth in the tangential shear stress is observed with increase in the acceleration (parameter Kn). At high frequencies the profiles differ only slightly. With increase in \(\lambda '\) (for example, at \(\lambda ' = 5\)) the graph has the oscillatory character.

Fig. 3.
figure 3

Variation in the unsteady tangential shear stress on the pipe wall as a function of the dimensionless frequency at Re = 640: (a–c) correspond to Kn = 0, 0.01, and 0.05 and curves 1–4 are the same as in Fig. 1.

Full size image

At low frequencies the profiles are restructured with increase in the acceleration. A minimum is formed at the low frequencies with further increase in the parameter Kn = 0.1 and 0.3 (Figs. 4a and 4b). With strengthening of the relaxation properties this minimum is displaced to the right along the axis of frequencies. With further increase in the acceleration (parameter Kn) the profiles flatten out and the minimum disappears (Fig. 4c).

Fig. 4.
figure 4

Variation in the unsteady tangential shear stress on the pipe wall as a function of the dimensionless frequency at Re = 640: (a–c) correspond to Kn = 0.1, 0.3, 0.5, respectively, and curves 1–4 are the same as in Fig. 1.

Full size image

The plots of \(\tau _{{{\text{ons}}}}^{'}{\text{/}}\tau _{{{\text{oks}}}}^{'}\) as a function of \(\omega '\) show (Fig. 5) that with increase in the Re number (Re = 1000) the time-dependent tangential shear stress on the pipe wall increases at the low frequencies and the minimum on the graphs is manifested already at \({{K}_{n}} = 0.05\) (Fig. 5a). With increase in the acceleration (at Kn = 0.1) a significant modification of the profiles occurs mainly at the low frequencies \(0 \leqslant \omega ' \leqslant 0.4\). At the higher oscillation frequencies, when \(\lambda ' = 5\), the tangential shear stress decreases sharply.

Fig. 5.
figure 5

Variation in the unsteady tangential shear stress on the pipe wall as a function of the dimensionless frequency at Re = 1000: (a, b) correspond to Kn = 0.05 and 0.1; respectively, and curves 1–4 are the same as in Fig. 1.

Full size image

Note that the obvious result on increase in the time-dependent tangential shear stress on the pipe wall with increase in the viscosity cannot be obtained when using formula (2.22), since in the ratio \({{\tau }_{{{\text{ons}}}}}{\text{/}}{{\tau }_{{{\text{oks}}}}}\) both the numerator and the denominator depend on the viscosity. In addition, with increase in the viscosity this ratio decreases. At the first glance, this can lead to the contradictory conclusion on reduction in the time-dependent tangential shear stress on the pipe wall with increase in the viscosity. In fact, let \({{\tau }_{{{\text{ons}}}}}\) and \({{\tau }_{{{\text{oks}}}}}\) be the values of the unsteady and quasi-stationary tangential shear stresses for the viscosity \(\mu \) and \(\tau _{{{\text{ons}}}}^{*}\) and \(\tau _{{{\text{oks}}}}^{*}\) be their values for the viscosity \(\mu {\text{*}} = 2\mu \). From the equilibrium relation (2.7) it follows that when the viscosity increases by two times the quasi-stationary tangential shear stress also increases by two times. Due to the non-equilibriumness of relation (1.1), the time-dependent tangential shear stress (as a result of time delay) increases lesser than by two times at various instants of time of the transition interval, for example, by α times, where \(1 < \alpha < 2\). Then

$$\tau _{{{\text{oks}}}}^{*} = \frac{{4\mu {\text{*}}}}{R}{{{v}}_{{{\text{ks}}}}} = 2 \times \frac{{4\mu }}{R}{{{v}}_{{{\text{ks}}}}} = 2{{\tau }_{{{\text{oks}}}}};\quad \tau _{{{\text{ons}}}}^{*} = \alpha {{\tau }_{{{\text{ons}}}}};\quad \frac{{\tau _{{{\text{ons}}}}^{*}}}{{\tau _{{{\text{oks}}}}^{*}}} = \frac{\alpha }{2}\frac{{{{\tau }_{{{\text{ons}}}}}}}{{{{\tau }_{{{\text{oks}}}}}}} < \frac{{{{\tau }_{{{\text{ons}}}}}}}{{{{\tau }_{{{\text{oks}}}}}}},$$

i.e., the ratio \({{\tau }_{{{\text{ons}}}}}{\text{/}}{{\tau }_{{{\text{oks}}}}}\) decreases with increase in the viscosity.

It seems that when investigating the effect of viscosity on the time-dependent tangential shear stress it is better to use the formula

$${{\tau }_{{{\text{ons}}}}} = \frac{{4\mu {{{v}}_{{{\text{ks}}}}}}}{R}\frac{{\tau _{{{\text{ons}}}}^{'}}}{{\tau _{{{\text{oks}}}}^{'}}},$$
(3.1)

where the second multiplier on the right-hand side can be calculated from formula (2.22). The calculations carried out using the formula (3.1) showed that increase in the fluid viscosity leads to a significant increase in the tangential shear stress everywhere. Significant change in the profiles occurs only for viscoelastic fluid, especially with increase in the relaxation time.

SUMMARY

It is established that the unsteady tangential shear stress on the pipe wall increases with the acceleration of fluid, particularly at low oscillation frequencies, and the significant dependence on the relaxation parameter of viscoelastic fluid is observed. As the relaxation parameter increases, the difference between the profiles also increases with the fluid velocity oscillation frequency. For certain accelerations of fluid the unsteady tangential stress has a minimum at low frequencies. As the acceleration grows, this minimum is displaced to the right along the frequency axis and the difference between the profiles of viscous and viscoelastic fluids increases. For the viscoelastic fluid this minimum depends also on the relaxation parameter. As the parameter Re increases, the minimum on the graphs is manifested at relatively small acceleration and the oscillatory nature strengthens. With increase in the acceleration the minimum disappears and the profiles become decreasing.

As a whole, an increase in the relaxation time decreases both the relative and the absolute stresses on the pipe wall. The oscillatory nature of the stress is caused by both the given oscillatory regime of the fluid velocity and the relaxation properties of fluid that lead to the nonuniform oscillatory distribution of the fluid velocity field over the pipe cross-section even in the non-oscillatory regime of fluid motion. The last fact is known from numerous studies devoted to the motion of viscoelastic fluids in pipes. The results obtained show that the relaxation properties of fluid serve as the limiting factor in using the quasi-stationary approach for determining both the unsteady tangential stress on the pipe wall and the acceleration of fluid.