Designed Examples as Mediating Tools: Introductory Algebra in Two Norwegian Grade 8 Classrooms

Abstract

A critical element in the introduction of algebra is to focus student attention on the basic ideas of algebraic reasoning including the use of concepts such as variable and algebraic expression. In the Norwegian classrooms, representing a student-centered instructional philosophy, the teachers utilized examples and problems that they themselves had designed, and the examples involved resources such as concrete objects and body movements in order to make algebra accessible to students. When designing these examples, teachers thus used their own previous experiences of teaching algebra in an attempt to articulate the passage from arithmetic to algebra.

Introduction

The teachers Kari and Ola are introducing algebra in two Grade 8 classrooms. Kari holds up a set of large playing cards and she writes on the blackboard what is written in the corner of the cards. Ola gets the attention of the students and carefully starts walking in one direction in the classroom, asking the students to describe what he is doing. These are the starting points of two examples that each teacher has designed as a tool for communicating and explaining new algebraic ideas in their respective classrooms.

The aim of this chapter is to investigate two introductory algebra lessons. The passage from arithmetic to algebra in school mathematics is known to be challenging for students as has been pointed out repeatedly in this volume. The learning of algebra includes new symbols, new concepts and also new ways of thinking (Berg, 2009). In the two lessons, the teachers are presenting algebraic concepts through examples, using them as mediating devices, bridging between new concepts, on the one hand, and familiar situations and prior knowledge of the students, on the other hand. The purpose of our analysis is to capture how the teachers approach the complexity students meet in such learning situations and how they support learning. Both teachers introduce and illustrate the concepts of variable and algebraic expression and demonstrate processes of simplification and substitution in the introductory lesson. The topics coincide with the textbook; however, the teachers have chosen to design their own examples in order to engage the students in algebra.

Examples play a central role in the teaching and learning of mathematics as described by, among others, Bills et al. (2006) and Rowland (2008). Paying attention to how examples are used offers both a practical and a theoretical perspective on the design of teaching activities and on the professional development of mathematics teachers. The whole point of giving worked out examples is that students appreciate them as generic, and even internalize them as templates so that they have general tools for solving classes of problems (Bills et al., 2006).

Bills et al. (2006) give a historical account and a categorization of the use of examples from the perspective of the mathematics teacher. They refer to Rissland-Michner’s (1978) four epistemological classes of examples (not necessarily entirely separate): (a) start-up examples, which help motivate basic definitions and results; (b) reference examples, which are mentioned repeatedly in different situations; (c) model examples, which are generic examples, indicative of the general case; and, finally, (d) counterexamples. These classes represent what Rowland (2008) refers to as inductive examples for the purpose of abstraction. “Exercises”, on the other hand, are examples used for practicing and rehearsal.

The worked out examples in this study have features that the literature points out as important. They provide an opportunity for the students to experience the mathematization of familiar situations (Bills et al., 2006; see also Chap. 4), including transactions with semiotic means such as spoken language, inscriptions (e.g. numbers, words, and items belonging to the algebraic symbol system), and gestures, to interpret and express mathematical meaning (Fried, 2009; Radford, 2003). They have epistemological qualities as they motivate basic definitions and concepts, they model central ideas in algebra, and they are referred to more than once and in different situations. Both are inductive examples in Rowland’s (2008) sense, and mainly start-up and reference examples, and to a certain extent model examples applying Rissland-Michener’s (1978) epistemological classes.

The concepts of mediation and mediating tool (Carlsen, 2010; Säljö, 2006; Wertsch, 1991; cf. Chap. 3, this volume) are central for the analysis of our empirical material. Leont’ev (1981) considers the use of artifacts and tools as mediational means and emphasizes that tools connect “humans not only with the world of objects but also with other people” (p. 56). The theoretical term of mediating tool facilitates our analysis in making a distinction between, on the one hand, the tools (designed examples, concretes and semiotic means) that the teachers employ in their interaction with the students and, on the other hand, the educational goals of the lessons (including the mathematical objects of variable and algebraic expressions).

In this chapter, we will use the term semiotic mediation , introduced by Vygotsky (1978), when we discuss the teachers’ use of semiotic means in the designed examples. John-Steiner and Mahn (1996) refer to semiotic mediation as one of three major themes¹ in Vygotsky’s theory regarding the interrelationship between the social and individual processes of knowledge co-construction. The semiotic means play a central role in the designed example as they are physical links (can be seen or heard) between the students and the mathematical objects that the teachers are trying to explain. The semiotic means are not neutral but add meaning to the activity; however, they are also given meaning through the activity.

In the following, the reader is invited into two Norwegian Grade 8 classrooms to observe the practices of two colleagues; how they start their lesson, how they approach introductory algebra, and how they interact with their students. The purpose is to make visible the complexity of the learning situation and teachers’ ingenuity in trying to make algebra accessible to their students. Our attempt to show this important interactive and instructional work has guided the organization and presentation of the empirical material. The object of inquiry is the teachers’ introduction of algebra, and we focus our analysis on how the teachers mediate the new concepts through their designed examples. More specifically, we ask: Which approaches do the teachers use to introduce the concept of algebraic expressions ?

National Curriculum, Classroom Environment and Textbook

Compulsory schooling in Norway starts at the age of six. Algebra enters the curriculum as part of the main subject area, Numbers and algebra, in grades 5–7. This continues to be a subject area throughout primary education, where algebra in school is described as generalized arithmetic. The curriculum lists specific educational goals in each subject area after 2nd, 4th, 7th and 10th grade. The goals referring to algebra state that the students shall be able to:

• explore and describe structures and changes in simple geometric patterns and number patterns (Grade 7)

• process and factor simple algebraic expressions , and carry out calculations with formulas, parentheses and fraction expressions with a single term in the denominator (Grade 10)

• solve equations and inequalities of the first order and simple equation systems with two unknowns (Grade 10)

• use, with and without digital aids, numbers and variables in exploration, experimentation, practical and theoretical problem solving and technology and design projects (Grade 10)

  (The Ministry of Education and Research, 2013)

In Norway, most students go to comprehensive school until the age of 16 (Grade 10) and are taught in mixed-ability groups. According to Pepin (2011) there appears to be particular “customary ways” of conducting the teaching of mathematics in Norwegian classrooms. For example, most teachers ask their students to work on exercises from the textbook for a considerable amount of time during a lesson, so that the students can practice what has been explained, and the teacher can monitor the students’ understanding. The textbook used in the classroom and at home is chosen by the school, which furthermore provides a copy for each student.

There are many textbooks available in the market, and they differ with respect to the grade in which algebra is introduced and also on the number of pages dedicated to this topic. Many textbook series only produce textbooks for grades 1–7 or 8–10, which mirrors a shift in the Norwegian educational system, in teachers’ education and in the classroom culture. Although letters appear as variables, mainly in geometry chapters, in 6th grade textbooks, they are often not introduced as such. Some of the 7th grade textbooks have algebra as a specific topic but vary in the extent to which it is covered, from only a few pages to a whole chapter. It is more common to find an algebra chapter in 8th grade textbooks, though there are exceptions.

The two Grade 8 classrooms presented in this chapter are from the same junior high school (“ungdomsskole”, grades 8–10). The textbook used by all mathematics teachers in the school is Faktor (Hjardar & Pedersen, 2006), which is widely used in Norway. Faktor 1 (the book for Grade 8) has a separate chapter called Numbers and Algebra. The title reflects the subject area introduced in the National Curriculum. In the textbook analysis done by Reinhardtsen (2012), Faktor is interpreted as reflecting the traditional view of learning by instruction. Each subchapter first presents a kernel (definitions, procedures, etc.), an example and then tasks that are similar to the one presented in the example. This is a teaching and learning cycle that is common in many educational systems.

The goals for the teachers’ presentations in this study concern processing simple algebraic expressions and carrying out calculations with formulas, as formulated in the second point in the National Curriculum, and treated in the first section on algebra in the textbook Faktor 1. The teachers follow the textbook in this respect.

Methods

In order to accomplish the aims of this study, we use a qualitative approach to collect and analyze the empirical data grounded in a sociocultural perspective on learning. The data have been collected according to the VIDEOMAT design (see Chap. 3, this volume): as in the other countries, we observed the first five algebra lessons in each classroom (videotaping), interviewed the teachers after the fifth lesson (audiotaping) and collected written material used in the classrooms (teacher and student materials). As a first analytical approach to the collected data, lesson graphs for each lesson were produced, and the first lesson in all classrooms was transcribed.

In this chapter, we have used an inductive approach to the video analysis as defined by Derry et al. (2010, p. 9), which is suitable when: “a minimally edited video corpus is collected and/or investigated with broad questions in mind but without a strong orienting theory.” The two episodes presented and analyzed in this chapter were chosen from the lesson graphs and after several viewings of the video material. The designed examples stood out as unique in the international video material. In addition, the examples used are referred to in later lessons by the teachers, and they therefore play an important role in the introduction of algebra in these two classrooms.

The episodes, as part of the first lesson in each classroom, have been transcribed in their entirety. The national curriculum and the textbook are viewed as integrated parts of the classroom practice, and the designed examples are analyzed and related to these important didactical documents.

Participants and Context of Research

The two Norwegian Grade 8 classrooms (A and B), as mentioned earlier, are from the same junior high school. It is the main school at this level in the local community and has about 500 students. The school is located at the center of this community, which is situated outside a larger city. The main income in the area is from industries, trade and services.

In classroom A there are 21 students (age 13–14), 11 girls and 10 boys (the class holds 29 students but eight were not present at the time of the observation). The teacher is an experienced female teacher (with 9 years of experience). She has a master’s degree in pedagogy and a specialization in mathematics. In classroom B there are 25 students, 14 girls and 11 boys (27 in the class, with two students not present at the time of the observation). The male teacher has 4 years of experience and was at the time when the recordings were made taking additional courses in mathematics. He has been educated as a general teacher (4 years, including half a year of mathematics).

Analytical Framework

According to the theoretical and methodological constructs used for analyzing talk-in-interaction, Linell (1998) identifies two building blocks of a dialog, namely turns and idea units. A turn is basically a period of time when one speaker holds the floor, while an idea unit refers to, as the name indicates, a specific idea within a turn. A turn can include several idea units. In line with the sequential organization of a dialog, each turn should be interpreted and understood in relation to the prior discourse, as well as being seen as creating conditions for the ongoing dialog.

A number of turns form larger units, which Linell (1998) refers to as topical episodes. We choose to call these units “episodes”, and we divide an episode into fragments.

Each episode in this chapter contains all the turns in a period of time (which are numbered chronologically), and each fragment constitutes a continuous flow of turns and idea units as methodological constructs used for structuring the data. The analysis performed does not focus on the constructs of the dialog. However, the ideas emerging in the classroom discussion are understood and presented within the analytical framework of Linell. The unit of analysis is the introductory algebra example as realized in the interaction between teacher and students.

Findings: The First Minutes of Algebra

The data is organized in two episodes taken from Classroom A and Classroom B, respectively. Each episode starts with the lesson graph from the first lesson, and is divided into fragments with headings that characterize the content. We have chosen to present the complete dialog of the episodes intertwined with short descriptions and limited analyses in order to preserve for the reader a more genuine experience of the teachers’ examples. Further analyses will follow at the end of each episode. The chapter ends with a comparison between the two episodes.

Episode 1: Classroom A

This episode is chosen from the very beginning of the first lesson on variable expression in classroom A. The teacher, Kari, uses playing cards to introduce the idea of using letters for numbers. The rest of the lesson is dedicated to an algebra game (see Table 5.1). The teacher returns to the playing cards in lessons 2 and 4. In the lesson graph (Table 5.1) the flow of the entire lesson 1 is presented.

Table 5.1 Lesson graph showing classroom A (lesson 1, 40 min)

In Fragments 1 to 7 we will present the full teacher-student conversation that takes place during the first 13 min of the lesson.

Fragment 1: Introduction of the Lesson

1.

T:

I know that you have been a little excited, because I have said that no , we will not begin with algebra before this week. Now we will start. But I have been asking whether anyone has had any experience with algebra before. There have been no hands raised, but perhaps you have some experience, only you don’t know that it is algebra. And, among other things, we have indeed started ahead a little, for you have been doing some algebra, probably a lot, but at least one lesson, that we had two weeks ago. Do you remember? I think it was two weeks ago, that you brought some playing cards, and then we worked with those cards. We worked with positive and negative numbers first, then you got some cards and counted how many points you had. And the ones who got the highest number won. Do you remember that? (.) And then, afterwards, we played with the black cards as positive numbers and the red cards as negative numbers. And then you were to find out who came closest to zero when you added them together. Do you remember that? Yes, but then there was something else we also had to do when we were calculating with the cards…

The teacher starts the lesson by relating algebra to prior activities in the classroom. She reminds the students that they used playing cards in a game where they performed calculations with negative and positive numbers. The teacher emphasizes the new topic, saying the word algebra four times. At the same time, she initiates the use of playing cards as a tool to appropriate algebra. She connects the word algebra to their work with whole numbers and operations with such numbers. In this way, she connects the word algebra with arithmetic, using playing cards as a mediating tool. The teacher does not explicitly mention her goals for the lesson, but implicitly she follows those of the textbook.

Fragment 2: Numbers and Letters in Playing Cards

1.	T:	… When we added the cards, I don’t know if you at the back [of the classroom] can see, but here I have [showing the cards] an eight, or we can begin with a two, and then I have a four, and then I have an A , and then I have an eight, and then I have a K [writes on the blackboard: 2 4 A 8 K]. Do you see that? Here we operated [referring to a prior lesson] with both numbers and letters. We have an A , and we have a K . How did you do it, when you calculated how much you had altogether? Does anyone remember? Ola?
2.	S:	The A was one.
3.	T:	We said that the A was equal to one, yes. Great! So A is equal to one, [writes: A = 1] we said. Really, the A was one or fourteen. We could choose, but then everyone wanted to use A equal to one. I don’t know if it is because it is easier to calculate with one or if that is the most common, that A equals one. Anyway, we used A equal to one. What about this K then? Alf?
4.	S:	Thirteen.
5.	T:	We said it was equal to thirteen, yes. The king was equal to thirteen [writes: K = 13]…

The teacher shows a hand of five large playing cards and asks the students what is written in the corner of each card. Some of the cards have numbers and some have letters. With the help of the students, the teacher reveals the hidden numbers behind the letters. The teacher carefully writes it all on the blackboard.

Fragment 3: Numerical Expression and Calculation

5.	T:	… And then , when you calculated [referring to the prior lesson], what did you do then to find out how many you had altogether? Do you remember that? What did you do to count them together? Ina?
6.	S:	We added all the numbers.
7.	T:	We added them all together. So we took two plus four plus A ?
8.	S	We had said that it was one, so therefore we added one.
9.	T:	Great! So instead of A we put one, plus eight and then plus K ? And that was thirteen. So instead of K we put in the number thirteen. Good! And then we calculated how much it was. Two plus four plus one plus eight plus thirteen [writes: 2 + 4 + 1 + 8 + 13]. It is? Kim?
10.	S:	It is (…) twenty-five.
11.	T:	Yes, seven, fifteen, it will be more.
12.	S:	I mean twenty-six.
13.	T:	Even more.
14.	S:	Twenty-seven.
15.	T:	He, he, he, even more.
16.	S:	Twenty-eight.
17.	T:	Yes, work it through one more time and see if you don’t get twenty - eight (…) it could be that I’m also doing some wrong calculations, you know.
18.	S:	Twenty - six then.
19.	T:	Did you say twenty - six? Two plus four is six, plus one is seven.
20.	S	Twenty-eight.
21.	T:	Yes, plus eight is fifteen, plus thirteen is twenty - eight [writes: = 28]. Good! So then you see, when you added together, you put in, you replaced A with one. You replaced K with thirteen. Look here. You replaced a letter with a number. Good! We will erase this and then we will do another one…

In the dialogues in Fragments 2 and 3, the teacher identifies letters and numbers on the cards. Then she assigns fixed values (hidden numbers) to the letters and thus makes a correspondence between letters and numbers (see Fig. 5.1). The numbers and hidden numbers are arranged in a numerical expression, for which the sum is calculated.

Fig. 5.1

Overview of what the teacher has written on the blackboard in Fragments 2 and 3 (letter K referring to King)

Fragment 4: Algebraic Expression

21.	T:	… Let’s see if we can find some new cards here. Let’s see, I think I will choose these cards [showing the cards]. Here I have, for those of you who cannot see, I have a six, then I have two queens and then I have two kings. Mmm. A six, two queens and two kings. So I have six plus queen plus queen plus king plus king. [Writes: 6 + D + D + K + K] If you are to calculate how much this is altogether, how should we calculate this? (.) Six plus queen plus queen plus king plus king. Ina?
22.	S:	The queen is twelve.
23.	T:	Great! The queen is twelve. So we write [writes: D = 12], we replace the queen with twelve. Good!
24.	S:	Then you add six plus twelve plus twelve, and then comes thirteen plus thirteen.
25.	T:	[writes: 6 + 12 + 12 + 13 + 13] Great! Good! …

The teacher picks a new set of cards and creates an algebraic expression. With the help of the students the letters are given values and the algebraic expression is made into a numerical expression without solving the addition task (see Fig. 5.2).

Fig. 5.2

Overview of what the teacher has written on the blackboard in Fragment 4 (letters D referring to Queen [Dame in Norwegian] and K to King)

Fragment 5: Simplification of an Algebraic Expression

25.	T:	… If we now were to simplify these, now we are looking at the top one again, okay? Six plus D plus D plus K plus K . If we only were to add those, what would we get then? Tor?
26.	S:	Fifty-six.
27.	T:	Yes, and if we added, or if we add these together, a little more, but if we look at, if we have the number six [writes: = 6], and then we are to add queen and queen. Can we write it differently than D plus D ? Ina?
28.	S:	D2
29.	T:	Right, two times queen, for there are two queens [writes: + 2·D]. Good. Plus…
30.	S	Two times king.
31.	T:	Two times king, oi. Good! Two times king [writes: + 2 · K]. It is, do you agree that twelve plus twelve is the same as if we now put it in here then, equals six plus two times twelve plus two times thirteen [writes: = 6 + 2 · 12 + 2 · 13]. Do you see that I replaced the queen with twelve and the king with thirteen? Do you see here that twelve plus twelve, do you agree that it is two times twelve? It is twelve two times. And thirteen plus thirteen, another way of writing that is two times thirteen. Right? It is the same that we are writing. But if we are to calculate this now, six plus two times twelve plus two times thirteen. Do you remember the order of operations when we were to calculate with addition, subtraction, multiplication and division in one expression? Arne?
32.	S:	(…) the multiplications first.
33.	T:	You have to do the multiplications first. And here we see clearly that the two queens belong together, because there are two of them. And the two kings belong together, because there are two of them. So we do the multiplications first. So it equals six plus, two times twelve, that is? Twenty-four, good, plus two times thirteen, yes. Six plus twenty-four plus twenty-six [writes: = 6 + 24 + 26], it equals?
34.	S:	Fifty-six.
35.	T:	Fifty-six. [writes: = 56] That is good. Great! Mm. So this was a little repetition, right. That we do the multiplication and the division first, and then the addition afterwards. And here we see clearly that the two queens belong together. The two kings belong together. Okay…

The teacher returns to the algebraic expression created in Fragment 4 and prepares a simplification. One student, Tor, responds to the teacher’s question regarding how to simplify (25) by calculating the sum of the numerical expression, which is fifty six (26). The teacher does not follow up this response and instead starts to add the letters.

The teacher and the students replace the letters in the simplified algebraic expression with numbers, and simultaneously the teacher makes the link between addition and multiplication explicit (31). So, the teacher makes clear that the numerical expression (31) is the same as the one developed in Fragment 4 (25). They calculate the sum (33, 34, 35) and get the same answer as Tor gave in (26) (see Fig. 5.3).

Fig. 5.3

Overview of what the teacher has written on the blackboard in Fragments 4 and 5

The choice of cards in Fragment 4, which includes two queens and two kings, gives an expression with two Ds and two Ks. The teacher follows the same approach of substituting the letters with fixed numbers as in fragments 2 and 3, but, in addition, she introduces an intermediate step of simplifying the algebraic expression. In doing both a vertical (on the blackboard, see Fig. 5.3) translation from an algebraic to a numerical expression and a horizontal translation to a simplified algebraic expression, the teacher sets the stage for showing the relationship between addition and multiplication and between the different numerical and algebraic expressions.

Fragment 6: Variables (on Sheets of Paper)

35.	T:	… Now I’m wondering, if I now had, instead, these are not playing cards [Shows two sheets of paper]. But if I, instead of D and D and K and K , which represent king and queen, if I now had an a and a b , do you see it, no perhaps you don’t see it. But we have an a here and a b here.
36.	S:	Yes, we know that a is one (…) and b could be any number.
37.	T:	Great! You do know, good. If we now are to add these two cards, an a and a b [writes: a + b], then yes, we have said here that a is one, but letters can be variables and we can replace them with any number. So a is not always one. We can choose the numbers we want to replace the letters. So if I now say that we have the expression a plus b and then I erase this [erase: A = 1, K = 13, D = 12]. And now I put in that, for example, now we want a equals three, and b equals two [writes: a = 3 b = 2]. Can I now calculate how, what a plus b equals? If we have a plus b , and then I say that a equals three and b equals two, can you do this calculation? Ann?
38.	S:	Five.
39.	T:	You replaced a with, instead of a you put in?
40.	S:	Three.
41.	T:	Great, and you replaced b with two, and then you found that it was equal to five [writes: 3 + 2 = 5]. Good. Great. But if I now choose that a will equal 4, and then, oh, I want b to equal five [writes: a = 4 b = 5]. What do we get now? If a equals four and b equals five? Ulf?
42.	S:	Nine.
43.	T:	Because you replaced a with?
44.	S:	Four.
45.	T:	And what did you replace b with? And then, four plus five equals nine [writes 4 + 5 = 9]. Good…

The teacher shows two sheets of paper with the letter a on one of them and the letter b on the other. The teacher writes the expression a + b on the blackboard, and introduces the term variables (37). She explains variables in this manner: ...letters can be variables and we can replace them with any number (37). Rather than further elaborating the concept of variable, she continues by giving the letters different values (a = 3, b = 2 and a = 4, b = 5) and calculates the sum in both cases (see Figs. 5.4 and 5.5).

Fig. 5.4

Overview of what the teacher has written on the blackboard in Fragment 6

Fig. 5.5

Overview of what the teacher has written on the blackboard in the last part of Fragment 7

Fragment 7: Different Algebraic Expressions

45.	T:	… Great! What if I changed the expression to b minus a ? [writes: b - a] b minus a . Ina?
46.	S:	Then b is five, so then (…) minus four, and that is one.
47.	T:	Great. b was equal to five, and a was equal to four. Five minus four equals one [writes: 5 – 4 = 1]. Good. If we did the opposite then, and used a minus b , how do we calculate that? Per?
48.	S:	Four minus five.
49.	T:	Yes. Then we get a , we replace a with four, and we replace b with five [writes: 4 – 5 =]. And four minus five, what is that? Ole?
50.	S:	Minus one.
51.	T:	It is minus one, yes [writes: -1]. Do you see that we have more negatives than we have positives? So then the answer has to be negative. It was the same with the cards, right? We added together, how many black we had, and how many red [the teacher uses her hands]... And the red was negative. So when we had most of those, we knew that the answer had to be negative. Good. Do you think this seems okay, or what? It wasn’t so difficult to calculate with letters anyway. Was it difficult to calculate with letters, yes? Fortunately we will try this out now, because it is important to see how much of this you are able to do, and what I need to tell you more about.

At the end, the teacher varies the algebraic expressions and evaluates each one for the same set of values. It does not seem to confuse the students that the teacher again refers to the earlier use of the playing cards in relation to negative numbers. By introducing the two sheets of paper, the teacher extracts the letters a and b from the context of the cards. At this point she operates with independent letters and refers to them explicitly as variables.

The teacher continues the lesson by introducing the algebra game (see Table 4.1). The variables a and b, which have been replaced by different numbers, are now given additional meaning in the sense that they are explicitly connected to the number of eyes on the white and the red dice, respectively. The expressions on the game board determine how many steps a player can move in one turn. The evaluations of the expressions vary and depend on each throw of the dice.

Analysis: Classroom A

Our object of inquiry has been the teacher’s introduction of algebra. More specifically, we asked: Which are the teacher’s approaches when introducing the concept of algebraic expression? Although the teacher does not mention the textbook in the introduction, it is evident that she has considered it as she planned the first lesson in algebra. The algebra chapter opens with a repetition of numerical expressions with a focus on the order of operations, and it continues with an introduction to variables, algebraic expressions and then to equations. In line with the textbook’s sequencing of algebraic topics, the teacher started by introducing the concepts of variable and algebraic expression, including demonstrations of simplification and substitution. But how she did this deviates from the activity in the textbook. Her mediating tool is a designed example, and we will focus our analysis on four concerns: (a) the manner in which the teacher introduces her lesson, (b) how she mediates her designed example, (c) what semiotic means she uses to introduce the concept of variable, and (d) how she interacts with the students.

Introduction of the Lesson

In the very beginning (Fragment 1), the teacher repeats the word algebra four times in order to emphasize the coming topic. Then she reminds the students that they have done algebra before (maybe without knowing it) in connection with an activity of adding positive and negative whole numbers by using playing cards. So, she brings the word algebra, calculation with whole numbers (arithmetic), and playing cards to the forefront of the students’ attention. These are central elements in the coming activity with the designed example.

Mediating Function of Designed Example

The activity is based on a carefully designed example which is not taken from the textbook, but created by the teacher herself. Fragments 2 to 7 illustrate how the designed example is operationalized as a mediating tool for the teacher and the students in the learning situation. As well-known artifacts, the teacher uses playing cards and sheets of paper to bridge numerical and algebraic expressions. The approach used by the teacher to introduce algebraic expressions is intended to present the different components which constitute such expressions (numbers, letters as variables, operational signs) one by one. She is all the time linking the algebraic expressions with the numeric ones by substituting values for the variables and calculating the numerical expressions. So, together with the students she develops the concept of algebraic expression from numerical ones, as it is done in the textbook. The example plays several roles in the classroom, and we use Rissland-Michner’s (1978) epistemological classes of examples to examine those. It is a start-up example as it motivates the basic algebraic ideas of performing operations on letters and that a letter can represent any number. The teacher’s choice of designing an example to introduce the topic of algebra is also an effort to get the students’ attention and a way of marking the shift from arithmetic to algebra.

In the first five fragments, the mediating tool of playing cards is used and the activity including them can work as a model example for letters representing numbers and the activity of developing expressions including letters. However, the letters on the playing cards are not variables but hidden numbers, and therefore the activity involving those cannot function as a model example for the notion of a variable. The teacher changes her mediating tool to sheets of paper featuring an a and a b, respectively, before discussing the concept of a variable which is first mentioned in Fragment 6. A student response shows that the transition from the playing cards and hidden numbers to letters as variables is not trivial (36): Yes, we know that a is one (…) and b could be any number. The teacher answers (37): then yes, we have said here that a is one, but letters can be variables and we can replace them with any number. The activity with the sheets of paper can play the role as a model example for the notion of variable as long as the difference between the two mediating tools is made clear. However, the shortcomings of playing cards as a model example may inhibit the conceptual development of students.

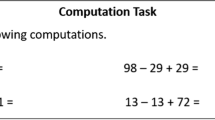
The designed example also plays the role of a reference example in the classroom as the teacher has used playing cards as the basis for an earlier activity. The cards are used again and in different contexts at the beginning of lessons 2 and 4. In lesson 2, the word variable is not mentioned in relation to the playing cards and the letters are assigned their numbers by the teacher: We know now, I’m certain that you remember this now, but I write it anyway. J equals 11 and D equals 12. The teacher then focuses on the rules of operations. In lesson 4, the cards are used to write an expression and again assigned their numbers however this time the teacher emphasizes that: but such letters we call variables, right, we can put in almost what we want normally for letters, so that varies. She lifts up the playing cards as a special case where the letters are assigned specific numbers. It is again clear that the activity with the playing cards does not function as a model example as it is not indicative of the general case.

Semiotic Mediation: Concrete Materials—Numbers—Variables

To interpret the steps taken by the teacher in a form of dialog when introducing variables, we use the concept of semiotic mediation to explain the passage between arithmetic and algebra, from numbers to variables. First of all she introduces playing cards, including letters and numbers, as a mediating tool. The material is suitable, as numbers and letters are part of the semiotic repertoire from algebra. Secondly, the teacher makes the values explicit for every letter (for example: K=13) as if the numbers are hidden. Thirdly, she introduces numerical expressions including numbers and operation signs and, then, fourthly, she calculates the sum. Only at the fifth step does she introduce algebraic expressions including both numbers and letters. Next, the teacher simplifies, adding similar terms and turning repeated addition into multiplication. Finally, she picks two sheets of paper with letters on (one a, and one b). She uses letters as independent entities. She substitutes a and b with different sets of values, objectifying in this way the idea of variables. And, at the very end, she varies the algebraic expressions as well. The teacher does not publicly elaborate on the concept of variable. In this example, the teacher is using numbers in a purely mathematical context. The variables a and b are substituted with numbers when first introduced in the classroom, but later, in relation to the algebra game, the variables are connected to quantities, i.e. the number of dots on the red and the white dice. Variables are, in this sense, therefore introduced in the classroom in an abstract, mathematical context and only later given a more concrete meaning for the algebra game.

Student-Teacher Interaction

Focusing on the teacher’s role in the classroom interaction, we have identified the following steps:

• The teacher presents (verbally and visually) playing cards and two blank sheets of paper with only a and b written on them, respectively.

• She writes numbers, letters, operations and equal signs on the blackboard.

• The teacher poses mostly checking and controlling questions to the students.

• The students give short answers.

• The teacher writes the students’ answers on the blackboard only if they are correct and proposed in a timely manner in order not to interrupt the flow of her presentation.

• The teacher openly asks (at the end): was it or wasn’t it difficult to calculate with letters? And she announces that there are more exercises to come, so that she can see how much they can do themselves and what she needs to say more about.

We did not observe students taking notes or the teacher encouraging them to do so.

The teacher seems to follow her plan for the presentation, and she keeps the students’ attention by asking checking and controlling questions that mostly are returned with yes/no answers or facts. Even when a student gives an unexpected (but relevant) answer (as in turn 26), she neither comments on it nor follows up the possibilities it offers. Questions that require answers that the teacher has thought out in advance are, by Myhill and Dunkin (2005), referred to as closed questions, facilitating a procedurally oriented approach to teaching.

Episode 2: Classroom B

This episode is chosen from the very start of the first lesson on algebra in classroom B. The teacher, Ola, introduces the students to algebraic expressions and variables using body movements. The teacher continues the lesson with other examples involving expressions, and then the students work with tasks from the textbook. The textbook exercises will not be presented here. The flow of the lesson is described in the lesson graph (Table 5.2).

Table 5.2 Lesson graph showing classroom B (lesson 1, 42 min)

In fragments 1 to 8 we will present the full teacher-student discourse that takes place during the first 17 min of the lesson.

Fragment 1: Introduction of the Lesson

1.

T:

First of all, before I forget, you see that you have got a red folder on your desk, in front of you, everyone. You are to use that instead of your workbook this week, and you can write everything you do in school in it, and you can also take it home as a workbook and do homework in it. And then there are some cameras in here, but we are having a regular mathematics lesson, so nothing special besides that. And today we will start with a new topic, and that is Chap. 6 , and it is called algebra. It is a chapter that we skipped that we are now going back to. If you turn to page one hundred and eighty-one, the one that looks like this, numbers and algebra it says. Then we will have a brief look at the goals for the chapter before we get started. In algebra we use letters as symbols for numbers. The value for the symbols can vary. Therefore we name the symbols variables. This may sound unfamiliar now, but we will talk a lot about variables in this chapter and what that means. Numbers that vary. And the goal for this chapter is that you will learn about simple, algebraic expressions , calculations with expressions or formulas and solutions of equations. This is the goal of the chapter. And here there were probably many unfamiliar words, but we will work with them in the following lessons this week, and I think we will use three or four weeks on this. Now everyone must pay attention to me and see what I’m doing now. It is a little, I will do it with my legs, but you have to see what I’m doing anyway. And then you will need to describe it afterwards. If I do this. Now you can see well enough. Are you ready?

The teacher starts the lesson with practical information regarding artifacts to be used (notebook, textbook), and he also informs the students to expect a regular lesson in spite of the cameras present. He introduces the new topic, algebra, by referring the students to Chap. 6, Numbers and algebra, in the textbook. He proceeds to talk about variables and introduces the term as follows: In algebra we use letters as symbols for numbers. The value for the symbols can vary. This is why we call symbols variables. Then the teacher again turns to the textbook and reads out aloud the goals for the chapter (see Fig. 5.6).

Fig. 5.6

The goals for Chap. 6 in textbook Factor 8

The teacher attempts to defuse the unfamiliar words by saying that they will be working with them over the next three or four weeks. The teacher continues by introducing an activity, which we will follow in the next seven fragments. He informs the students that he is going to use his legs and that they need to follow closely what he does.

Fragment 2: Bodily Number Line; Unit (Step) and Direction

2.	S:	Yes!
3.	T:	What did I do now? Per?
4.	S:	You walked.
5.	T:	Yes, I walked. How did I walk?
6.	S:	Forward.
7.	T:	Forward. Yes?
8.	S	And then you first took three steps, and then two.
9.	T:	First I took three steps. Now I write exactly what you said. First three steps, and then two. Can I write plus then? [writes: 3 skritt + 2 skritt]. Will it be the same?
10.	S:	Yes.
11.	T:	I can write plus two steps…

The teacher performs a demonstration of body movements in the classroom. He walks three steps along a line in parallel with the blackboard, stops, walks two steps forward and stops again. Then he asks the students to describe what he did. The teacher formulates it as an expression on the blackboard. “Step” (“skritt”) is the quantitative unit he is using, and he writes out the word in his expression. Thus, the teacher is constructing an imaginary number line indicating unit and direction with his body.

Fragment 3: Doing and Speaking Algebra; Expression in Words (One Unit)

11.	T:	… Now you have to pay attention. Now I will do the same again. Now I will do exactly what it says there [walks]. What did I do in addition now? (…) what happened? Pia?
12.	S:	You took one step back.
13.	T:	Yes. First I did that, and then I took one step back. Can I write it as minus? [writes: 3 skritt + 2 skritt – 1 skritt]
14.	S:	Yes.
15.	T:	Now you have done algebra. Now I speak algebraically. Three steps plus two steps minus one step…

The teacher performs the same body movements again and adds one more step. He walks three steps forward, stops, walks two steps forward, stops, and walks one step back. Then he asks the students to describe what he did. The teacher adds another element to the former walking procedure and also includes it in the expression he is developing on the blackboard. He comments that now they have done algebra, and that he is talking algebra.

Fragment 4: Expression in Words (Two Units, Step and Foot)

15.	T:	… Did everyone follow what I have done now? Now I will do one more thing. (…) Now I first walked like this, and then I made it to here. And then I will do something quite smart here, but I will count aloud. One, two, three, and then I’m moving all the way up to the camera, four. What did I do now then? Was there any difference now?
16.	S:	(…) four.
17.	T:	I took four, what was it?
18.	S:	Steps!
19.	T:	Yes, but was it steps like before?
20.	S:	Half.
21.	T:	Half steps?
22.	S:	Feet? Foot lengths?
23.	T:	Feet? Mouse steps? Can I call it a foot? That was a nice example. Plus four feet. [writes: 3 skritt + 2 skritt – 1 skritt + 4 fot] Write it in your notebook. When you have written it, that expression, I call it an expression now. We can call every calculation task an expression…

The teacher makes exactly the same body movements as earlier and then takes some additional steps, and finally he takes some small steps in which he places one foot in front of the other (feet). He walks three steps, stops, walks two steps forward, stops, walks one step back, and walks four feet forward. Then he asks the students to describe what he did. The teacher again adds to the walking procedure and models it in the expression he is developing on the blackboard. The units he is using are “steps” and “feet”² (“skritt” and “fot”). The teacher then asks the students to write the expression in their notebooks. He elaborates on the notion of an expression by explaining that We can call every calculation task an expression.

Fragment 5: Simplification of Expressions; Letters for Words

23.	T:	… When you have written that expression, then you look at it and see if you can do something with it, so that it becomes a little shorter. Is it possible to shrink it so that it doesn’t take up so much space? Write it differently? It is really another description so that I arrive at exactly the same position. Very open question. (…) Has everyone written it down? Good. Now I will walk down here, because there was not enough room here. Now I’m walking. First the three steps, two more, three plus two steps, one step back, and then four feet. One, two, three, four. Now I ended up about here. Ida, are you watching to make sure that it was right next to that stool?
24.	S:	Yes!
25.	T:	Three steps, plus two steps, minus one step. Is that the same distance as something else? Can I say that it is four steps?
26.	S:	Yes!
27.	T:	Three plus two steps, that is five steps total, minus the one [He gestures an equal sign after the expression 3 skritt + 2 skritt – 1 skritt + 4 fot]. Then I say that I have walked four steps and four feet. [writes: 4 skritt + 4 fot]. I start at the same place. One two three four one two three four. So, roughly, Ida. What is it?
28.	S:	You moved a little further.
29.	T:	I think I started a little further out. I should have marked where I started. But you agree that if I take four steps at once, or if I take five steps forward and then go back one, then I should end up at the same position. It is a little difficult to make exactly the same steps every time. Four feet, is it possible to shorten that expression? (…) Yes.
30.	S:	You can make feet into something else.
31.	T:	Is it possible to make feet into something else? Perhaps four feet are one step. It could be, but I don’t know that. I have not measured it. So I don’t know it. So I cannot do that. Perhaps I could have done it this way [writes: 4s + 4f]. But in addition I don’t know how long a step is, or I don’t know how long a foot is. Now I write down the equal signs [writes: = (after the expression 3 skritt + 2 skritt – 1 skritt + 4 fot); writes: = (between the expressions 4 skritt + 4 fot and 4s + 4f)], because now I see that this expression is equal to that expression. So, if you haven’t written down the two expressions, then write them down in your notebook (…) It becomes a treasure hunt. One could have used a map, right? Then I could have said: four steps and then four feet and then you would end up where the treasure is, and then dig it out. I could have made infinite variations with this as long as the total was four steps in the end…

The teacher asks if the expression can be written differently, shorter. He then demonstrates the body movement again, now along a new “imaginary number line” between two rows of student desks, and takes note of where he ends up in the classroom. He simplifies the expression and then demonstrates that he ends up at the same place. He writes it on the blackboard. Then “steps” and “feet” are shortened to s and f (see Fig. 5.7).

Fig. 5.7

Overview of what the teacher has written on the blackboard in Fragments 2 to 5

The teacher simplifies the first expression (the first expression in the second line in Fig. 5.7). As a second step, he abbreviates the terms using only their first letters. The result is an expression that looks algebraic; however, the letters are still connected to the teacher’s “steps” and “feet”, and the expression is a mathematization of his movements in the classroom related to a specific distance. On the other hand, “steps” and “feet” are general terms which vary in lengths in relation to different people, and they can be talked about and operated on without first knowing their exact lengths. In this way, Ola develops the concept of variable from the students’ everyday life. The teacher uses treasure hunt as a metaphor to explain the equivalent expressions. He does not comment on the contradiction the metaphor is to the development of the concept of variable; such a map is supposed to lead the readers to the same position i.e. all steps and feet are of equal length.

Fragment 6: Expression as Recipe; Variable and Constant

31.	T:	… Would it be the same if I do it as if… eh, Kai, if you do it? Would we end up at the same spot?
32.	S:	No.
33.	T:	Why not?
34.	S:	Your steps are longer than mine.
35.	T:	Are my steps longer than yours? Yes, Mia, would we end up in the same spot?
36.	S:	No.
37.	T:	Odd, me and you then? You are pretty tall.
38.	S:	Yes, that could be.
39.	T:	Could you say approximately?
40.	S:	Yes…
41.	S:	You and Pål.
42.	T:	Perhaps me and Pål, yes. And it is like this, someone might be walking a little like this, while another person takes shorter steps. And feet also, perhaps different shoe sizes. So that number, it can vary. Right? This number and this number, we call them a variable. [writes: variable] Because it doesn’t need to be the same every time. It depends who is doing it, whether it is Kai, Mia, Oda or Pål, so it will never be exactly the same. A little different. But that, it is a constant. It is the same every time. The recipe is four steps plus four feet, no matter what…

The teacher asks the students whether, if one of them had done the walking, they would end up in the same position (31), and they answer No (32). The teacher asks for an explanation (33), and one student answers that the teacher’s steps are longer than his (34). The teacher elaborates on the variations of the length of peoples’ steps (35), and ends the discussion by labeling s and f as variables and 4 as a constant (see Fig. 5.8).

Fig. 5.8

Overview of what the teacher has written on the blackboard in Fragments 2 to 6

The teacher approaches the concept of variable by comparing steps and feet of students with his own. The students agree that the length of steps and feet varies among different people. To further exemplify the unique characteristic of variables, i.e. that they can take on different values, he points to the number 4 and names it a constant . He also makes an analogy between the expression and a recipe to further explain what remains the same and what varies; the constant and the algebraic expression in its entirety stay the same, while the variables s and f vary with the person who walks. Again, Ola relates expressions to a known concept from students’ everyday life.

Fragment 7: From Algebraic to Numerical Expression; Letters to Values

42.	T:	… And then we will end up at different positions because the variables , which are the length of legs or lengths of the steps, are different for each of us. I could have made calculations if I say that one step for me was seventy centimeters, and one foot was twenty centimeters [writes: s = 70cm f = 20cm].
43.	S:	You need to know the shoe size?
44.	T:	The shoe size?
45.	S:	It is different.
46.	T:	Yes, but it is not marked in centimeters.
47.	S:	It is!
48.	T:	It is?
49.	S:	Yes!
50.	T:	Now I will not look so carefully at it. Twenty centimeters, I say that it is twenty centimeters, I have not measured, but yes, it is probably not enough.
51.	S:	It is forty-two.
52.	T:	If we say four steps plus four feet [writes: 4s + 4f], four, then I must multiply by seventy, right? Because I take four steps which are seventy centimeters plus four feet which are twenty centimeters [writes: 4 · 70cm + 4 · 20cm]. And then we have really made a calculation task of it. We have replaced the variables, replaced the s , because we know that one step was seventy centimeters for me. If it had been Mia, it would have been something different. Perhaps it would have been sixty, fifty.(…) Do you follow so far? Now I write an equal sign (.). Write it down in your book (…). [writes: 280cm + 80cm = 360cm] Two hundred and eighty centimeters. I walked with the four steps, plus the eighty centimeters I walked with the four feet. Did you follow that, the distance from here and down became about three hundred and sixty centimeters? Any questions? …

The teacher suggests approximate lengths of his “steps” and “feet” in centimeters (cm) and writes these on the blackboard. This provokes a student to request further accuracy and he suggests using the size of the teacher’s shoe (43). Ola explains that the shoe size is not marked in centimeters but fails to convince the student. The teacher continues by substituting s and f for the given values in the expression. He bridges the algebraic and the numerical expressions by connecting the values to his prior walk. He also underlines that s is a variable by saying that the value would have been different if Mia had been walking (52). Ola calculates the numerical expression in two steps and continues by making explicit the connections between the numbers on the blackboard, the lengths of his steps and feet, and the previously marked distance in the classroom. The distance that was previously measured in steps and feet (Fragment 5, 25) is now described by the standard unit cm (see Fig. 5.9).

Fig. 5.9

Overview of what the teacher has written on the blackboard in Fragments 2 to 7

For the first time the teacher is not waiting for the students to respond to his question: Any questions? (52). He continues the lesson, introducing a new example presented in Fragment 8.

Fragment 8: From Expression and Recipe to Formula—Same Approach

52.	T:	… Now I’m starting to erase this, but you have written it down, so that will be fine. I have a little sister. She is seven years younger than me. Does anyone remember how old I am? Last time you guessed that I was about thirty-five, which was pretty rude. Do you remember?
53.	S:	Twenty-six.
54.	T:	Yes, that was rather young, which was nice of you. But I’m a little older. I’m twenty-seven.
55.	S:	Big difference!
56.	T:	Big difference. But I said that she is seven years younger than me. If I say that I’m twenty-seven, then you can easily calculate that she is…?
57.	S:	Twenty.
58.	T:	Twenty. Yes. Twenty-seven minus seven. Next year, how old am I then? You can also calculate that. Tonje?
59.	S:	Twenty-eight.
60.	T:	Yes, how old is she then?
61.	S:	Twenty-one.
62.	T:	Yes, twenty-eight minus seven. So, it is really my age minus seven [writes: min alder - 7]. Do you agree? This is the formula all the time. The expression is like this. And then I get my sister’s age as an answer [writes: = søsters alder]. If you didn’t know how old she was - now you knew approximately - then we could have said that my age was unknown, you don’t know what it is, we could have called it x [writes: x ]. Mister x . x is the, eh, letter we normally use in algebra, most often, when we have an unknown, something that we don’t know the value of. So really it just means that we don’t know that number. We only know that it is a number. But we know that my sister was seven years younger than me [writes: -7], and then you are able to calculate anyway. Should we put in twenty-eight? That becomes twenty-eight minus seven. Now I’m fifty, fifty minus seven. (…) Now you will get the next task. That one you will (…), now you are sitting two and two. You can turn around to the person sitting next to you also. I have a neighbor, a good neighbor; we live right next to each other. He is five years older than me. Can you try, two and two, to write down an expression like the one here which describes that my neighbor is five years older than me? You can talk across to each other here. You will not get much time.

This example is chosen from the textbook and mathematizes the relationship between the ages of two people. It is a regular paper and pencil problem that the teacher personalizes by using his own and his sister’s ages as variables. He first models the relationship with an equation including words (“min alder”, “søsters alder”), naming the expression on the left side of the equal sign a formula for his sister’s age (see Fig. 5.10), which he then expresses in terms of the letter x. However, he first establishes a constant relationship between the ages by performing calculations with specific values for his own age. Then the lesson continues with the students working, in groups of two, on modeling a proposed problem of the same nature.

Fig. 5.10

Overview of what the teacher has written on the blackboard in Fragment 8 (my age—7 = sister’s age)

The teacher reconnects with the textbook by discussing one of its examples. There is a correspondence between the two introductory examples. Again, Ola writes the algebraic expression rhetorically before using letters as variables. And here, too, the variables represent quantities, which in this case have the inherent quality of changing with time. However, the two examples conceptualizes algebraic expressions differently. In the latter example, the two quantities are connected by a constant, and if one of them is given, the other can be found. This example features a special kind of algebraic expression in the context of an equation. The teacher also briefly talks about the x as an unknown, even though the task is focused on writing expressions. There is also a difference in how the two examples are mediated. In the latter example, Ola goes from the specific by comparing specific ages, to the general, writing an algebraic expression. While in the first example he did the opposite, moving from the general to the specific.

Analysis: Classroom B

Our object of inquiry has been the teacher’s introduction of algebra. As was the case in the analysis of classroom A, we asked more specifically: Which are the teacher's approaches when introducing the concept of algebraic expression? Unlike Kari, Ola starts the lesson by having the students open the textbook to the new chapter called Numbers and algebra, and then he reads aloud the learning goals written there. He proceeds by introducing the same topics as Kari: the concepts variable and algebraic expression , and he also provides demonstrations of simplification and substitution. And, as Kari did, he designs his own example as a mediating tool. In order to compare the two designed examples, we will look at the same analytical concerns as previously presented: (a) the manner in which the teacher introduces his lesson, (b) how he mediates his designed example, (c) what semiotic means he uses to introduce the concept of variable, and (d) and how he interacts with the students.

Introduction of the Lesson

The teacher starts his lesson by giving practical information. He reminds the students about writing notes in the special folders handed out, and he urges them to write down everything done in school for later use, e.g. when doing homework. He also reassures the students regarding the cameras present, emphasizing that it is a regular lesson. He then continues by announcing that they will start with a new topic called algebra, and refers to the page and chapter in the textbook where the topic is presented. He points to the goals for the chapter, but before reading them aloud he explains the role of letters in algebra and why they are called variables. Reading the goals in the textbook aloud, he lists the contents to be dealt with in the coming three to four weeks, that is simple algebraic expressions, calculations with expressions or formulas, and equation solving. Finally, he asks for the students’ attention, telling them that he will move his legs and that he expects them to observe carefully so that they can describe what he did subsequently. In short, the teacher prepares the students for his introduction of algebra in the coming weeks and finally for the lesson of the day. He shows consideration for the students’ feelings as they are asked to participate in a new domain of mathematics, and he is explicit about what he expects from them, both in taking notes and in interacting with him in a specific way. The textbook has a clear role in the classroom and dictates the content of the lesson. However, the teacher adds what he thinks is important and his designed example shows an attempt to facilitate learning by relating to everyday experiences.

Mediating Function of Designed Example

The activity presented in fragments 2–7 is based on a designed example, which is not taken from the textbook, but created by the teacher himself. The teacher uses walking procedures to establish successively more extensive expressions, as he moves along an imaginary number line. These algebraic expressions are developed in interaction with the students, verbally and by writing the expressions in words (the units “step” and “foot”) on the board and in their notebooks. In the same manner, a simplification of the final expression is also completed before the words are shortened to letters (s, f). Finally, in Fragment 7, the letters are given values, bridging algebraic and numerical expressions. The teacher uses the terms expression, recipe, and formula synonymously.

In moving along an imaginary number line, using his steps and feet to designate distance, the teacher operates with quantities and develops an understanding of variables and operations without using numbers and numerical expressions as motivators. Instead, he models the distance walked in the classroom with an algebraic expression that builds on relationships between quantities. He is therefore touching what Davydov, Gorbov, Mikulina, and Savaleva (1999) do in their approach to algebra in school, where algebra is introduced through working with quantities. The Russian curriculum developed by Davydov and his colleagues introduces algebra and its symbolism from first grade with numbers following as concrete applications of algebraic generalizations (Schmittau & Morris, 2004).

After having presented the concept of algebraic expression in terms of quantities, the teacher shows that numerical expressions are special cases of these. At the very end (Fragment 8), the teacher connects his way of introducing algebraic expressions with how it is done in a standard textbook problem, and thus bridges his own presentation and that of the textbook.

As Kari’s designed example, Ola’s example plays several roles in the classroom. It is a start-up example that motivates the use of the concepts algebraic expression and variable. The example signals a shift in the mathematics classroom in modes of working where numbers no longer have the central role and are replaced by letters as variables. The activity with the mediating tools of steps and feet can work as a model example for the concept of variable and also for building algebraic expressions and operating with letters. The image of how the length of steps and feet vary between different people is a very tangible reference for the meaning of variable. The movements of the teacher in the classroom are described and written down as an expression of physical length in the classroom. The teacher walking a simplified version of the expression, and showing that it corresponds to the same length as the first one, is a physical demonstration that one can operate with letters (quantities). The example is also a reference example as the teacher uses this example again in Lesson 3, having a student perform the movements this time. The teacher marks the length in the classroom which corresponds to his own movements, and then he does the same for the student and shows that the lengths are different even though they made the same movements. The activity thus becomes a model example also in the sense that an algebraic expression can represent different lengths.

Semiotic Mediation: Body Movements—Quantities—Variables

To interpret the steps taken by the teacher in a form of dialog when introducing variables, we use the concept of semiotic mediation to explain the passage from body movement to variable. Firstly, the teacher demonstrates, by a walking procedure, an imaginary number line with direction (forward) and a unit (step). Movement (walking), is thus the first semiotic element that emerges. Secondly, the teacher repeats the students’ description of his movement, and he formulates it as an expression on the blackboard (inscription). The semiotic means are spoken and written words, numbers, quantity (step), and plus and minus signs. Thirdly, the teacher adds a new unit (foot) first in his walking procedure and then on the blackboard. Fourthly, the teacher starts to operate with all the symbols and signs in order to simplify the algebraic expression. At this point the teacher abbreviates step and foot with the letters s and f. Fifthly, he points out s and f as variables. The teacher makes a connection between the concept of variable and letters in algebraic expressions through his inscriptions on the blackboard. So, altogether, he has made a passage from steps and feet as measuring units to seeing these units as variables, i.e. step, foot →s, f→ variables, mediated through body movements, spoken and written words, and inscriptions. At the end the teacher attributes values to letters/variables (measured in cm), showing that a numerical expression is a special case of an algebraic expression.

Student-Teacher Interaction

The teacher’s way of interacting with the students goes through the following steps:

• The teacher walks back and forth along an imaginary number line indicating direction and units (step and foot).

• The teacher poses checking and controlling questions to the students.

• The students answer the specific questions from the teacher, and they describe the teacher's movements.

• The teacher writes the students’ description of his walking procedure on the blackboard.

• The teacher and the students interact in dialogical modus at the end of the lesson (from Fragment 6).

• The students copy in their notebooks what the teacher has written on the board.

• The teacher summarizes and concludes what they have achieved together.

The teacher keeps the students’ attention by asking checking and controlling questions and by challenging them to describe his movements. The last part of the episode is more like a dialog. They are asking and answering each other’s questions. The teacher is specifically following up some of the students’ responses (30, 43), but only for a short time before he brings the class back on track again. Only once does the teacher rush on to the next task without waiting for the students’ response (52), which he had invited them to give. Following Myhill and Dunkin (2005), Ola used both closed questions, mostly returned with yes/no answers or facts, and open questions that invite the students to explore and investigate, the latter type facilitating a conceptual approach to teaching.

Comparison

From the interviews with the teachers, it is obvious that both teachers are interested in developing their mathematical competencies. They are also concerned with having a practical approach to the teaching and learning of mathematics, i.e. connecting mathematics to the everyday life of students. The female teacher, Kari, has 9 years of experience, and she is a coordinator between the leadership and the mathematics teachers in the school. The male teacher, Ola, has 4 years of experience, and he was at the time of data collection taking additional courses in mathematics. Ola was also involved in a national project which focuses on low-performing students in mathematics. Both teachers refer to professional development courses they have attended when explaining their viewpoints. In their mathematics teaching, they use the textbook, but often also other resources such as games, booklets, books, internet and digital tools (spreadsheets and GeoGebra).

Our focus has been on how the teachers introduce and mediate algebra through their designed examples. Their introductions of algebra have been analyzed with specific focus on four issues: introduction of the lesson, the mediating functions of designed examples, semiotic mediation in relation to the concept of variables and student-teacher interaction. In this section, the two approaches to introduce the concepts of variable and algebraic expression are compared.

Introduction of the Lesson

The two teachers introduce their lessons quite differently. Kari (the female teacher in classroom A) brings the word algebra, calculation with whole numbers, and playing cards to the forefront of the students’ attention, providing only the information they need in order to follow the planned activity based on her designed example. Ola (the male teacher in classroom B) has a broader approach in his starting lesson. He introduces the new terms the students are expected to become acquainted with in the coming weeks by reading the goals of the algebra chapter, before narrowing down and focusing on the concepts for the actual lesson of the day.

Kari does not mention the textbook in the introduction of the lesson, and she does not bring it up after presenting the designed example. Instead, she provides copies of an algebra game as a group activity where the students work with the new concepts. Ola introduces his lesson by showing the students where they are in the textbook, and he points out what the students are expected to learn in the coming lessons by referring to the learning goals provided there. After the activity based on his designed example, he returns to the textbook by presenting one of its examples, and then the students work individually with tasks in the textbook. Although Kari does not use the textbook directly in her lesson, the content is the same as in Ola’s lesson, and the same as the first algebraic topic in the textbook. In the interviews, the teachers do not refer to the national curricula when commenting on their teaching of algebra. The textbook is therefore interpreted as the enacted curriculum in the two lessons.

The role of affective factors in the learning of mathematics has been documented in research. It has been consistently shown that while confidence has a positive correlation with mathematical performance, mathematical anxiety has a negative effect (Schoenfeld, 1989). In the introductions of a new topic, both teachers address this aspect of learning. Kari only articulates a positive emotion when she says that she knows the students have been excited (Classroom A, Fragment 1) to start with algebra. However, as she continues it becomes clear that she has been preparing the students for this coming topic, i.e. she has previously asked them whether anyone has had any experiences with algebra. And now she reassures them that they probably have done a lot of algebra before without knowing it. She then proceeds to mention a specific example related to cards and negative numbers. In this manner, she attempts to address the feelings of anxiety students may have when a new branch of mathematics is introduced in the classroom. Ola also shows awareness about the issue of students’ anxiety when encountering new concepts and terms. He says that now these words may appear unfamiliar but assures them that they will work a lot with them in the coming weeks.

Kari moves ahead with her designed example without making explicit her expectations about the students’ role in the activity. Ola, however, explains what he is expecting from the students: they should take notes during the activity and observe, in order to describe afterwards, his exact movements as he walks in the classroom.

The Mediating Function of Designed Examples

Both teachers have chosen to follow the topical sequencing of the algebra chapter in the textbook and to introduce variables and algebraic expressions during the first lesson. However, they do not follow how this is done in the algebra chapter. Instead, they design their own examples as mediating tools in their presentations.

Kari has chosen playing cards, which the students are familiar with (she has used them earlier for adding whole numbers), in order to illustrate that letters can stand for numbers and be included in mathematical operations. The playing cards and two sheets of paper with the letters a and b respectively, are used to carefully develop algebraic expressions from numerical ones. Therefore, Kari’s introduction is interpreted as an inductive approach to algebra that reflects the textbook's view of algebra as generalized arithmetic.

In the interview, Kari justifies her way of introducing algebra by underlining the importance of a practical approach. So basically, I always think that I will follow the textbook, but this time I found the textbook’s presentation of the algebraic concepts problematic. She continues by explaining that she wanted to be more practical, as opposed to being theoretical, in her approach, especially since it is the students’ first encounter with algebra: … I said in the beginning also that I felt like, as a first approach [to algebra; as done in the textbook], that it was perhaps not the one I would have chosen, that it is very theoretical… in a way a little abstract in that they had not put it in an everyday context… but then again algebra [as a subject] is abstract. It is (.) but still I think the way it is done [in the textbook] is perhaps too theoretical and abstract in the way they have presented it. This is my initial impression.

Kari explains that she therefore looked elsewhere for ideas: and therefore I used something I have found in mathematics journals. She mentions Tangenten, a Norwegian journal for mathematics teachers, as the inspirational source for using playing cards as concrete objects in her designed example: When I read it I thought it looked like a nice approach and I decided to test it to see if it works. Kari says that she does this a lot: I have used ideas from different professional courses and from the specializing in mathematics (.) ... if I have learned something new I test it out and use it.

Ola carefully establishes an imaginary number line with direction and two different units (step and foot), which allows him to introduce addition and subtraction of these quantities without using numbers. In their responses, the students appear to be able to follow the rather complex reasoning of the teacher, and we conjecture that this is facilitated by his pedagogical choices of mediating his ideas. That is, choosing the familiar activity of walking, involving the students in describing his movements, and writing their responses on the blackboard. In addition, he encourages the students to copy from the blackboard into their notebooks. Thus, Ola introduces algebraic expressions directly in terms of mathematizing a situation involving distance without first involving numerical expressions. At the end of his presentation he shows that numerical expressions are special cases of algebraic expressions. Ola’s designed example is therefore interpreted as a deductive approach. In the last fragment from classroom B, Ola presents a new example inspired by the textbook as a part of his introduction. In this way he connects his designed example to the textbook’s presentation of variables and algebraic expressions.

In the interview, Ola (like Kari) justifies his way of introducing algebra by underlining the importance of a practical approach. I try to use examples that are realistic and that they can understand (.) Present examples that they can associate with daily life.

Ola did not use any of the introductory examples in the textbook as he thinks they are too theoretical and artificial: When I’m planning to teach a topic I tend to look in the textbook (.) I look at how it is organized, and I look through the examples to see if they are good (.) and decide whether I want to use any of them (.) This time I chose not to do it as in the textbook (.) I slightly rearranged the sequencing of concepts as I felt it would be a more appropriate way of doing it (.) Eh, additionally I have tried to use several other examples that are not in Faktor (.) I think the examples are too theoretical and artificially constituted, and they did not work for me as I wanted to find something that students can understand and that involves algebra, which is often a difficult and somewhat vague topic for them.

Following the epistemological classification of Rissland-Michner (1978), both examples play several roles in the classroom; as start-up examples in which they introduce the definitions of variable and algebraic expression; and as reference examples since they are referred to in different contexts. However, the activity with the mediating tool of playing cards, in which the letters represent fixed numbers, cannot work as a model example for the concept of variable. The activity with the sheets of paper, which could play this role, seems to lack permanence (in the classroom) as they are only brought out briefly and not mentioned again. In contrast, the playing cards are familiar objects to the students; they are used repeatedly in the classroom, and have a central role in the designed example. Thus, the designed example dominated by the playing cards may not work effectively as a model example for the concept of variable. Ola’s movements in the classroom, and the descriptive quantities of step and foot, which vary between different people, have qualities that correspond with variables and algebraic expressions. When used in the third lesson as a reference example, in which a student also walks in the classroom, it is used to deepen the understanding of algebraic expressions. Ola’s designed example has the qualities of a model example in that it is indicative of the general nature of variables and algebraic expressions. This can be summarized by Mason’s (1996) well-cited phrase of “seeing the general through the particular.”

Semiotic Mediation of the Concept of Variable

The paths the teachers follow in order to develop the concept of variable are quite different. Kari starts by introducing playing cards, a concrete object, including letters and numbers, as a mediating tool. On the other hand, Ola walks along an imaginary number line, and it is the body movement that are intended to mediate the algebraic concept. The mediating tools the teachers use, concrete objects and the body, have different representational qualities involving affordances and constraints; in Kari’s example the playing cards are only an entry point and the letters are not truly variables but hidden numbers (that do not vary); in Ola’s example the movements in the classroom remain a visual demonstration of the work done on the blackboard, and the units step and foot used to describe the movements are variables from the very beginning. As we can see, the teachers use different semiotic means as starting points.

Secondly, Kari identifies hidden numbers represented by the letters in the cards. Immediately following this, she introduces numerical expressions from the hand of cards and then calculates the sum. Ola writes an expression on the blackboard related to his walking procedure. He introduces two units (step and foot). Ola takes account of the semiotic elements of an algebraic expression and operates with the letters (simplification). At this point Ola abbreviates step and foot as s and f, and then calls them variables (he also writes variable on the blackboard). He has made a passage of units: step, foot → s, f → variables. However, Kari follows the opposite approach, introducing the semiotic elements one by one, and develops algebraic expressions from the numerical ones.

Kari introduces algebra using playing cards, substituting letters for numeric values. The example works for evaluating expressions and for combining terms. However, the letters in this case are known values that do not vary. As an introductory example, they have the potential to create misconceptions among students if the teacher does not reflect on the concept of variable. There seems to be very little effort made by the teacher to address this possibility. In Fragment 6 (37), the teacher explains that we have said here that a is one, but letters can be variables and we can replace them with any number. This is a critical clarification in need of further elaborations.

As we have seen, these two teachers follow different semiotic pathways to introduce variables. Kari goes from the elements to the expression using an inductive approach, while Ola takes into account the whole expression, not pointing out the various elements until the end. We can characterize this as a deductive approach. Another difference is that while Kari’s designed example only operates with numbers as mathematical objects in themselves, Ola operates with quantities and numbers that have a meaning.

Student-Teacher Interaction

When we compare these two lessons, some interactional features emerge clearly. For example, in the case of Kari, she made a lesson plan, and followed it carefully, using checking and controlling questions which require yes/no answers. Meanwhile, Ola also follows his plan and questioning mode. However, in addition, he also asks students to describe his movements, and they do that. In this way Ola goes further in the interaction by asking questions which require a more descriptive answer. He involves the students in the sense of stimulating them to find adequate words and to intuitively grasp the number line idea (including direction and units).

Both teachers use the blackboard for their inscriptions. Kari shows large playing cards and writes the numbers and letters included in the illustrations on the board. She asks the students what the hidden values of the letters are, and, after a brief discussion, she writes them in a separate place on the blackboard. She adds algebraic signs to the row of numbers and letters in order to create a numerical expression and then calculates the sum. Ola writes the students’ answers systematically on the blackboard, thus acknowledging their contributions, and he also asks them to write what he has written on the blackboard in their notebooks. In Kari’s class, the students are not required to make notes.

Both teachers initiate their lesson by speaking at length, leading and monitoring the discourse (an asymmetric interactional pattern). In Kari’s case, this pattern continues throughout the whole episode. However, Ola changes his pattern by inviting more student input (transforming the relation into a more symmetric one) towards the end.

Conclusion

The aim of this analysis has not been to propose how algebra should be introduced in the classroom, but to carefully study how it is done in two specific cases. The analysis illuminates the complexity students meet when facing introductory algebra in school, and the challenge it is for teachers to make algebra accessible for all students. The main approach of the teachers has been to design and use examples, mediating the passage from the students’ real world experiences, as well as the school mathematics they know, to algebra. There are similarities and differences in these teachers’ ways of introducing algebra. We would like to close this chapter by answering the research question and pointing out implications for teaching: Which approaches do the teachers use when introducing the concept of algebraic expression ?

The two teachers both design introductory examples that are used as their central means for explaining the same mathematical concepts (variable and algebraic expression). The examples are easily distinguishable in their use of concrete materials (playing cards versus the body); however, there are more fundamental differences in the example structures. Kari starts with numbers, number operations, and numerical expressions, and, based on their prior work in class, she makes generalizations introducing algebraic expressions. She continually connects the numerical and the algebraic elements, and explains variables as numbers. She goes from the specific to the general, and follows an inductive approach to introduce algebraic expressions (which adheres to the way it is done in the textbook). Ola, on the other hand, establishes an algebraic expression directly from the imaginary number line with given direction and units (first step, then foot) without using numbers. He builds the algebraic expression through a transformation chain following this path: bodily movement—words—abbreviations—variables, and he sees variables as quantities. We are instantly immersed in algebra in general, with very little abstraction. Later he shows that numerical expressions are specific examples of more general algebraic expressions (Classroom B, Fragment 7). In this manner, he moves from the general to the specific. Therefore, Ola is following a deductive approach when introducing algebraic expressions.

In a summary of research addressing the teaching and learning of algebra in the elementary grades, Kieran (2007a) points out that the majority of this work is situated within the curricular approach of developing algebra from the experience of numbers and their operations. This body of work is mainly concerned with issues of how to engage students in the early grades in algebra thinking, with or without introducing formal algebraic notations. The Russian curriculum developed by Davydov and his colleagues represents an alternative position in which the study of algebra precedes the study of numbers and introduces algebraic notations in first grade. Schmittau and Morris, reporting on their study of Davydovs’ curriculum and their adaption and implementation of it in a US school setting, explain that “algebra is developed from an exploration of quantitative relationships” (Schmittau & Morris, 2004, p. 61). As mentioned earlier, it is in this aspect that Ola in his designed example (unknowingly) touches the ideas of Davydov as he develops the algebraic concepts from quantities and not from numbers. In addition, introducing concepts by going from the general to the specific is also a trademark of the Russian curriculum, which is what Ola does in this specific example. The implications for student learning later in the curriculum are beyond the scope of this chapter but certainly in need of further exploration.

The teachers’ strategy of designing their own examples as a first introduction to algebra has specific implications for their teaching. The teachers’ use of concrete objects and body movements can make introductory algebra accessible to students by linking students’ observations of real world activities to school mathematics. The examples themselves are well thought through. The teachers do not run into unforeseen limitations regarding their use of concrete objects and body movements, as is illustrated in the chapter from Sweden (see Chap. 4). Even if the presentations of the examples are well prepared, the teachers’ flexibility is challenged when meeting the students’ questions/answers. In her interaction with the students’, Kari mainly uses questions that emphasize a procedurally oriented approach to teaching, and Ola mainly uses questions that emphasize a conceptually oriented approach.

Bills et al. (2006, p. 10) point out that “the art of constructing an explanation for teaching is a highly demanding task.” In order to create the designed examples, it is evident that the teachers have reflected on the content they are about to teach and what they want the students to learn. The strength of Kari’s example is the familiarity of the playing cards as she connects to the prior experiences of the students. While Ola’s insistence on involving the students in developing his example is important as he directs the attention of the students to the creative process of building an algebraic expression and the meaning of its elements. Our data show that these examples become anchor points for the teaching of algebra in the sense that the teachers return to the examples in the following lessons. This in turn may be a product of the teachers’ personal investment in the examples.

Our analysis is a response to what stood out as characteristic of the Norwegian classrooms in the international data of algebra teaching. We have discussed in detail the elements of the designed examples. The analysis has provided insights into the complexity of introducing algebra in the classroom. However, the phenomenon of teachers designing their own examples especially fitted for their classrooms deserves further attention from the research community: the role of this activity in the professional development of teachers; and which role these types of examples, with specific epistemological qualities as in start-up, model and reference examples, should play in student’s concept formation. Discussing and comparing the epistemological underpinnings of examples as mediating tools in the learning process seem to be critical for advancing a shared understanding among teachers of how algebraic concepts can be made accessible to students.