Abstract
We present the ArAl project, conceived as an integrated system of teacher education and classroom innovation, aiming at renewing the teaching of arithmetic in an early algebra perspective, guiding pupils towards the discovery of letters to express generalities. We focus on some theoretical key points (KP) and on the main language constructs (LC). Through excerpts of class-discussions, we show the incidence of KP and LC on the progressive construction and refinement of pupils’ early algebraic thinking . Finally we discuss the difficulties met by teachers at the K–8 levels when they reflect upon their knowledge, beliefs, attitudes, and ways of relating with the pupils.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
- Early algebra
- Algebraic thinking
- Algebraic babbling
- Metacognitive teaching
- Noticing
- Professional development of teachers
- Linguistic approach to early algebra
1 Epistemological Roots of Early Algebra
Early algebra can be considered the result of a long process of teaching innovation, started in the 1960s after the modern mathematics movement, which rejected the conception of mathematics as an abstract, static, and isolated discipline in favor of a dynamic and evolutionary vision of it, rooted in the concrete world and open to interactions with different disciplines and contexts. Moreover, a methodological revolution shifted the attention from the passive learning of mathematical facts towards problem solving and mathematical discovery.
According to these new visions, there is a widespread awareness of the importance of investing in studies dedicated to the problems of teaching and learning, and of improving the culture of teachers to cope with the novelties. As far as the teaching of algebra is concerned, the first studies were diagnostic, looking for the most widespread, erroneous performance in students, for example, Küchemann’s study under the heading of Algebra in Hart (1981). Particularly meaningful have been Kieran’s surveys (1989, 1992), which clearly show how the difficulties with algebra are mainly due to the traditional teaching of arithmetic, teaching that completely disregards relational aspects and the control of meanings implied by calculation processes. Other studies have concentrated on projects of curricular innovation. The pioneering work in this area includes the English projects on the teaching of mathematics in Grades 6–10 (e.g., Bell et al. 1985; Harper 1987), which promoted an approach to algebra centered, from the very beginning, on problem solving, generalization, and modeling. In this context it is important to recall the new perspectives on algebra in the early grades that were proposed at ICME-5 (in Adelaide in 1984) inside the Working Group (WG) on algebra teaching and learning (Davis 1985).
In those years, scholars had different opinions regarding the relationship between arithmetic and algebra in education. Some scholars underlined the epistemological rupture between the two areas (e.g., Filloy and Rojano 1989; Herscovics and Linchevski 1994); others looked at them with a perspective of continuity, stressing their mutual synergies (e.g., Chevallard 1989, 1990). Nevertheless, there was general agreement on the need to set the foundations of the teaching of arithmetic within a relational perspective with respect to algebra. The main objectives were: (a) to overcome stereotypes such as the directional equal sign, or the lack of closure in arithmetic expressions; (b) to induce a structural vision of arithmetical expressions, detecting equivalences or similarities; and (c) to open the way to generalization and modeling for the genesis of the objects of algebra.
The acknowledgement of the importance of these issues was highlighted at the WG on algebra at ICME-7 (in Quebec City in 1992), where a specific area of teaching called pre-algebra was identified as a bridge between arithmetic and algebra. In that context, it was stressed that “Within primary-school arithmetic there is ample opportunity for the development of algebraic thought” and that “letters could be used within children’s arithmetic experience in order to facilitate their understanding of the meaning and significance of letters in later, formal algebra” (Linchevski 1995, p. 114). At that time, moreover, the activities of syntactic transformation were no longer seen as isolated, but rather in their relationship with activities of representation and interpretation: Bell (1996) has spoken of the essential algebraic cycle, unifying in a whole the triad representing, transforming, interpreting, and their reciprocal interrelationships. Other scholars (e.g., Arcavi 1994; Arzarello et al. 1993; Boero 2001; Mason 1996) have taken into consideration also the metacognitive dimension, shifting the attention towards the control of the properties that legitimate the processes of syntactic transformation and the activation of anticipatory thinking. This control is seen as the ability to foresee (without carrying out syntactic transformations) new possible forms of an expression, by checking its meanings with reference to a given aim, or to hypothesize formal writings to be reached in order to achieve specific results. Arcavi (1994) summarizes all these aspects in the symbol sense construct. With reference to generalization, Mason (1996) maintains that pupils should be led to conquer the double awareness of seeing the general in the particular and seeing the particular in the general (p. 21) and, most of all, to become aware of the plurality of cases contained in a general statement.
In the second half of the 1990s there was a flourishing of studies on these aspects, mainly targeted at pupils aged 11–13. Some of the studies stood out for theorizing, within the framework of a linguistic vision of algebra , models of conceptual development of a socio-constructive type (e.g., Da Rocha Falcão 1995; Meira 1996; Radford 2000). In the USA there was widespread agreement on the idea that primary school syllabuses should be re-arranged in this perspective for the social needs of the 21st century (Kaput 1998).
In the international arena scholars have assumed different positions about the early usage of letters. Carraher and Schliemann (2007) have distinguished two different lines of thinking, one that focuses on “pre-algebra” as a transition between arithmetic and algebra and which postpones the use of letters until arithmetical learning has reached the upper grades, and the other, usually referred to as “early algebra,” which can include the early introduction of letters to promote relational thinking and the coordination of different registers of representations . Thus, the label Early Algebra has been introduced to refer to the initiation towards (a) generalizations of relationships or properties through the observation of similarities in various numerical cases, (b) the verbal formulation in general terms of observed relationships, and (c) the symbolic translation of verbal sentences and the approach to algebraic reasoning through syntactically guided actions on the formulae obtained. With the evolution that has taken place with the various studies related to early algebra , that corpus has been legitimized as a specific subject area by the international scientific community, as documented by: (a) the many interventions devoted to this theme at international conferences since the 12th ICMI study “The future of the teaching and learning of algebra” (Chick et al. 2001); (b) the production of specific monographs (Cai et al. 2005; Cai and Knuth 2011; Kaput et al. 2008); and (c) the collective studies on Early Algebra, such as the research forum at PME 25 (Ainley et al. 2001), the Early Algebra Conference organized by David Carraher (in Evron, France, in 1998), and more recently the Early Algebra Topic Study Group at ICME-13 (in Hamburg in 2016). Several of these studies have also dealt with the problem of suitable teacher education with focused intervention on professional development (see, e.g., Blanton and Kaput 2003; Carpenter et al. 2003; Russell et al. 2011).
Our research places itself within this frame and has developed a project for Grades K-8 (5–14 years of age) called the ArAl Project: paths in arithmetic to favor pre-algebraic thinking (Malara and Navarra 2003). We used the expression ‘pre-algebraic thinking’ according to the original meaning of the term ‘pre-algebra’ (as discussed at the ICME-7 WG on algebra). In our view, pre-algebraic thinking concerns not only the development of relational arithmetic, but also the progressive construction of the algebraic language and the development of the habits of mind that will allow pupils to use algebraic language as a tool for thinking. Pre-algebraic thinking occurs in all the activities aimed at building in pupils an attitude to look for regularities, relationships, and properties, and to express them first in natural, and then in algebraic, language. In this way, pupils acquire the experiential ground–layer to activate the essential algebraic cycle. This view fits with the characterization of ‘early algebraic thinking’ given by Kieran et al. (2016, p. 10). Then, (later) algebraic thinking is characterized by students’ achievement of a robust algebraic understanding (Schoenfeld 2013) that allows them to deal with non-trivial tasks. Therefore, we can say that early algebra develops pre-algebraic thinking or that it promotes algebraic thinking . However, to avoid misunderstandings associated with the term pre-algebra, we will now speak of our approach as one focused on ‘early algebraic thinking’.
2 Early Algebra Within the ArAl Project: The Main Key Points
The ArAl project proposes a socio-constructive approach to early algebra and is structured as an integrated system of teacher education that merges early algebra teaching experiments with teachers’ educational processes based on teachers’ practice. The schools involved are spread throughout all regions of Italy. The activities are realized within the frame of institutional programs of teacher professional development . The practices of sharing and reflecting with teachers on the classroom transcripts are realized via web (e-mail, Skype, forum, etc.) and in apposite meetings in the schools or at the university.
The main idea on which the project is based is that the algebraic language can be learned in analogy with the learning modalities of natural language. In our view, the algebraic language should be built right from the earliest years of primary school, having pupils face pre-algebraic activities and the use of letters to codify relationships. The discussions of comparison of the short sentences they produce—and the constant, collective reflections on the meanings of each expression—progressively bring them to master the syntactical rules of the algebraic language. By analogy with a young child’s babbling when she starts to learn the natural language, we call algebraic babbling this process of construction/interpretation/refinement of ‘raw’ algebraic sentences. To better understand the meaning of this construct, it must be considered together with the other theoretical points of the project that we now present.
In the ArAl project, the image of early algebra is expressed through a set of key words and concepts that refer both to arithmetic and algebra, but the two disciplines are seen as evolving towards a different and original identity. We can consider the combined two disciplines as a meta-discipline, concerning not so much objects, processes, and properties of arithmetic and algebra, but rather the genesis of a unifying language, that is, a meta-language. In order to control the meta-disciplinary knowledge of early algebra , we bring the teachers to command the meaning of words and linguistic constructs that represent new conceptions of intertwining between arithmetic and algebra. Later we discuss some of these terms, that turn out to be fundamental in order to generate—both in teachers and in pupils—ways of seeing that are suitable to the development of algebraic thinking . In this sense we speak of ‘epistemological issues in early algebra.’
In order to facilitate teachers’ acculturation, we have conceived and shared with them a set of glossaries that concern: theoretical frame, mathematical topics, methodological-didactic and social issues, and linguistic issues related to the managing of discussions with the class. The theoretical constructs, made explicit by suitable keywords, become a cultural patrimony for teachers, who are about to carry out an authentic Copernican revolution in their being and acting in the class: they become aware that social interaction, argumentation, and verbalization are key elements in the construction of knowledge and that a stable acquisition of meanings happens through activities that emphasize metacognitive and metalinguistic aspects. We stress that the aim of the project is to prepare metacognitive students. In order to achieve it, we need to educate metacognitive teachers.
We present now the main key points (KP) underpinning our project:
-
KP.1. The socio-constructive aspects of knowledge, which are typical of ‘doing mathematics,’ nurtured by collective activity in the class. The social construction of knowledge, that is, the shared construction of new meanings, is negotiated on the basis of the cultural tools and skills available to pupils and teachers; the contents of arithmetic and algebra are central, they emerge and condense through the teacher’s orchestration of the individual contributions.
-
KP.2. The aspects of generalization and interplay between arithmetic and algebra, with the shift of attention—in the teaching of arithmetic—from the procedural point of view to the relational one, the construction of arithmetical sentences—the recognition of those that are equivalent and their transformation through the basic arithmetical properties—as well as the approach to letters as a means to express in general terms observed numerical regularities.
-
KP.3. Identifying and making explicit the algebraic thinking often ‘hidden’ in concepts and representations of arithmetic. The genesis of the generalizing language can be located in this ‘unveiling’—when a pupil starts to describe a sentence like 4 × 2 + 1 = 9 no longer (not only) as the result of a procedural reading, ‘I multiply 4 times 2, add 1 and get 9’, but rather as the outcome of a relational reading, such as ‘The sum of the double of 4 and 1 is equal to 9’. Pupils talk about mathematical language using natural language and do not focus on numbers, but rather on relations and the structure of the sentence.
-
KP.4. The central role of natural language as the main didactical mediator within the slow construction of syntactic and semantic aspects of algebraic language. Verbalization, argumentation , discussion, and exchange promote understanding and critical review of ideas. We foster the relational point of view that brings pupils to elaborate complete and coherent argumentations , to compare them in their meanings, and to deal with the translation of verbal sentences expressing observed relationships into formal terms. To motivate pupils to face this task, we have conceived of a character—Brioshi—a Japanese virtual pen friend who loves to exchange mathematical questions by e-mail and to communicate through mathematical sentences (Malara and Navarra 2001). The mathematical language becomes a tool for communication. In this process letters are introduced to represent unknowns or variables , and their meanings are shared by pupils through collective discussions in class. In the production of representations in algebraic language, natural language also plays a meta-language role because it allows discussion at a meta-level of the meanings of the choices made by individual pupils and of the naive sentences they produce. The progressive mastering of the use of letters throughout the translation between verbal and formal sentences, which is sharply linked with interpretative aspects, characterizes the core process of algebraic babbling .
-
KP.5. The devolution Footnote 1 to pupils of the generation/interpretation of formulas and the progressive construction/refining of algebraic language. This aspect represents an important moment of condensation in the evolution of algebraic babbling. The pupils, during a collective exploration of a thought-provoking task, are guided towards the detection of a rule and the individual phrasing of a verbal sentence that represents it. This is an important step that facilitates the pupil’s assumption of the task to translate the sentence into algebraic language and, vice versa, to interpret a formula in verbal terms. In this way pupils become producers of genuine mathematical thought, overcoming the role of passive performers (examples are shown later).
-
KP.6. The metacognitive aspects. We promote the shifting from concrete generative situations to the construction of concepts through reflective activities in class; for instance, this is done for the purpose of reifying the properties of the arithmetical operations , but also for becoming aware of their role in counting strategies. We promote the detection of similarities in figural patterns or arithmetical/algebraic sentences and the recognition of structural analogies, the identification and verbalization of the reasons underlying syntactic transformations of formulas, and the generation and interpretations of new formulas from the perspective of the development of formal reasoning. We also favor the interpretation of a given formula in different contexts, so that it can be conceived as an object representing all its possible interpretations in different words. We extend the attention to other languages (iconic, graphic, …), bringing pupils to face questions about the coordination of different types of representation.
-
KP.7. Problematizing the activities. In the ArAl project each activity is posed as an exploratory situation. We illustrate this issue through two episodes.
First episode: The writing 42 + 15 = 11 + 42 emerges in a class; the teacher problematizes the situation asking the pupils to assess its correctness without calculating, reasoning on both sides of the equal sign and looking at relationships between the terms. These are some of the pupils’ justifications drawn from the classroom transcripts: (A) “It is not true that they are equal and I explain it in two ways: 42 + 15 ≠ 11 + 42 and 42 + 15 > 11 + 42”; (B) “42 is in both sides, 15 is bigger than 11, then 42 + 15 is bigger than 11 + 42”; (C) “I have written the sentence putting a question mark on the equal sign,Footnote 2 so Brioshi understands: 42 + (11 + 4) =?= 11 + 42 → 42 + 11 + 4 − 11 =?= 11 + 42 − 11 → 42 + 4 =?= 42 → 46 ≠ 42”.
Second episode: The core of the well-known ‘pyramid of numbers’ activity is the ‘mini-pyramid’, that is, two side-by-side bricks upon which there is another brick. On the visible side of each brick a number is written; the rule is that the sum of the numbers on the two bricks below is shown on the top brick. A 1st grade teacher proposes a mini-pyramid where there are: on the top brick 18, on the left brick 7 and on the right one a spot of ice cream that hides the number. She assigns the task : “Represent in algebraic language this situation so that Brioshi can find the number below the spot”. In this formulation the unknown number is no longer the result to be found, but one of the terms used to express, in several ways, the relationships between them; that is, 7 +
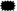 = 18; 18 = 7 +
= 18; 18 = 7 +  ;
; 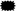 + 7 = 18; 18 =
+ 7 = 18; 18 = 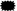 + 7; 18 − 7 =
+ 7; 18 − 7 = 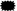 ;
; 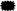 = 18 − 7; 18 −
= 18 − 7; 18 − 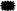 = 7; 7 = 18 −
= 7; 7 = 18 − 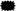 . Then the coded sentences are interpreted in natural language and reflections on the relational view of the equal sign are made. In this way what we call
equations
for fun, solvable without particular formal transformations, are generated (we propose them at 1st and 2nd grade).
. Then the coded sentences are interpreted in natural language and reflections on the relational view of the equal sign are made. In this way what we call
equations
for fun, solvable without particular formal transformations, are generated (we propose them at 1st and 2nd grade). -
KP.8. The algebraic verbal problems, the construction of equations, and their naïve solutions. The problematization of situations, like the ones described above, allows an early approach to verbal problems with one unknown and not immediately solvable. Algebraic verbal problems constitute the topic of the ArAl Unit 6Footnote 3: From scales to equations, for pupils of 4th–6th grade. It presents a connected set of teaching episodes, each based on a problem on the use of a pair of scales, to favor the shift from manipulation of known and unknown weights to a reflection on the actions made. The representation of the relationships expressed by the text of the problem leads to the construction of the equation , and the reflection on the actions made leads to reifying the principles of equivalence of an equation and to formalizing the steps to solve it. More recently in 3rd grade we have carried out some teaching experiments involving additive verbal problems with an unknown datum that can be modeled by an equation such as 7 + 9 + a = 11 + 12. For solving these problems, we adopt a strategy we call ‘dynamic scenes,’ based on the use of a short video-clip. In the first scene, a visualization of the quantities at play and their relationships is carried out through different strips of paper. In the successive scenes, the manipulation of strips of paper, strategic cuts, and shifts of the strips are showed. Interpreting the meaning of the scenes, one arrives at the formalization of the problem and then discovers the additive cancellation rule and its role in determining the value of the unknown.
3 The Main ArAl Language Constructs
In early algebra, content knowledge is shown by identifying and progressively refining keywords or phrases and the relationships among them, with the aim to condense with increasing precision their crucial aspects, refining their clarity and consistency. In this perspective, some language constructs (LCs) of our theoretical framework have proven to be fundamental in order to generate among both teachers and pupils new ways to see arithmetic, suitable to generalization and algebraic representation. Now we summarize the main constructs and classify them according to their reciprocal links. Through some excerpts of classroom discussions we show how, from the beginning of primary school, the introduction of these LCs brings pupils to progressively reach habits of mind that promote algebraic thinking . We present three sets of LCs conceived respectively: (a) to foster the shift of attention from the result to the process; (b) to relate several representations of a natural number to a relational view of the equal sign; (c) to favor socio-constructive classroom practices that enhance the role of natural language.
3.1 Promoting the Shift of Attention from the Result to the Process
We analyze three dualities, sharply intertwined, that allow pupils to shift from the action plane to that of reflection: (LC.1) Representing versus solving, (LC.2) Process versus product, (LC.3) Transparent versus opaque.
-
LC.1. Representing versus solving. A widespread belief among pupils, favored by the traditional teaching of arithmetic, is that the solution of a problem coincides with the identification of the result. This means that their attention is focused on operations . This prevents the exploration of mental paths that could generate algebraic thinking. In our case instead, pupils are slowly driven to shift from the cognitive level to the metacognitive one, where the solver interprets the structure of the problem and represents it through mathematical language. In this way the operational point of view is minimized in favor of the relational one.
-
LC.2. Process versus product: The previous duality is strictly linked with one of the most important aspects of the epistemological gap between arithmetic and algebra: whilst arithmetic requires an immediate search of a solution, algebra postpones it and begins with a formal trans-positioning from natural language to a specific system of representation. When a pupil is guided to overcome his/her worry about the result (the product), he/she reaches a higher level of thinking, substituting the calculations with the observation of him/herself reasoning, controlling the structure of the problem (the process).
-
LC.3. Transparent versus opaque representation. A representation in mathematical language consists of symbols that communicate meanings whose understanding depends both on the representation itself and on the ability of those who interpret them. Let us consider the so-called canonical form of a number, that is, the symbol related to its name (see later LC.4): we can say that it is poorer in meaning in comparison to other (non-canonical) representations of the number. For an extreme example: the non-canonical form 21 × 33 × 52 provides more information on the divisors of 1350 than the canonical form. Regarding its divisibility, we can speak of the greater opacity of the writing 1350 versus the greater transparency of 21 × 33 × 52. In general, transparency fosters the understanding of processes, that is, the ways in which a certain product is obtained; it highlights the strategies adopted, the possible mistakes, and the misconceptions underlying the solution to that particular problem.
Example 1 (4th grade): It is part of an activity aimed at approaching the distributive property. The teacher presents the following situation (see Fig. 3.1):
Marina collects red and green marbles and places them inside the boxes as shown below. Represent the situation in mathematical language so as to find the number of marbles.
The following pupils’ translations are transcribed on the Interactive Whiteboard (IWB):
$$\begin{aligned} ({\text{a}})\;16 \times 40 = n; \quad ({\text{b}})\;2 \times 4 + 5 \times 4;\quad ({\text{c}})\;n = 5 \times 8\quad n = 2 \times 8;\\ \quad ({\text{d}})\;2 \times 8 = n\quad5 \times 8 = n \quad n = 2 \times 8 + 5 \times 8; \quad ({\text{e}})\;\;2 \times 8 + 5 \times 8 = n; \\ \quad ({\text{f}})\;(2 \times 8) + (5 \times 8) = n;\quad ({\text{g}})\;n = (2 \times 8) + (5 \times 8) \hfill \\ \end{aligned}$$- Melania::
-
The translation (a) is opaque for me.
- Teacher::
-
What do you mean?
- Bruno::
-
(a) is opaque because they have already found the number of marbles.
- Clara::
-
We didn‘t have to find this number, but to write a translation for Brioshi. They have already solved the problem.
- Bruno::
-
It’s true, they didn’t represent the situation. They found the product and not the process.
- Melania::
-
[author of (b)] I forgot something. I wrote 2 × 4 + 5 × 4 because I saw the separate lines of boxes. Now I realize that my representation is not complete, I must add × 2. (She writes: 2 × 4 × 2 + 5 × 4 × 2 = n).
- Franco::
-
Melania wrote (e), like me, (c) and (f) are equal because 4 × 2 is 8.
- Teacher::
-
Now can you choose a translation for Brioshi?
Among the sentences written on the IWB, the pupils choose n = 2 × 8 + 5 × 8. Later the teacher proposes a new organization of the marbles putting in each box 2 reds and 5 greens, and asks the class to represent the new situation. Among the sentences, n = (2 + 5) × 8 and n = 7 × 8 show up.
- Miriam::
-
What I have written, (2 + 5) × 8, is more transparent; Alessandro’s writing (n = 7 × 8) is opaque. Opaque means it is not very clear; transparent means it is clear, you understand the process.
Later in the class, the equality 2 × 8 + 5 × 8 = (2 + 5) × 8 is made explicit, favoring the recognition of the structural equality of the two sentences. In our project, activities like this are spread out; they allow the pupils to construct the experiential undertone for the reification of the distributive property.Footnote 4 (For more, see Malara and Navarra 2009).
This transcript shows how the class is familiar with mathematical discussion: the pupils express good argumentations and draw on important theoretical constructs (the dualities opaque/transparent and process/product). They are brought to compare representations and, reflecting on the employed symbols, they interpret the sentences and explain their differences.
Example 2 (4th grade): The task is: Translate the sentence 3 × b × h into natural language. The class is comparing Lorenzo’s proposal (I multiply 3 by an unknown number, then I multiply it also by another unknown number) with Rita’s (The triple of the product of two unknown numbers).
- Lorenzo: :
-
Rita has explained what 3 × b × h is , whereas I have said what you do.
Lorenzo evaluates the two translations focusing on the distinction between the operational and relational aspects related to the duality representing/solving. He recognizes in his sentence the operational point of view and in Rita’s, the meaning of the sentence arising from a relational reading of it. The metacognitive control achieved by the pupil is high and it can be seen as a fruit of the type of teaching received.
3.2 Relating the Representations of a Number to a Relational View of the Equal Sign
-
LC.4. Canonical and non-canonical representation of a number. Faced with the question, “Is 3 × (11 + 7) ÷ 9 a number?”, students or teachers usually answer: “They are operations”; “It is an expression”; “They are calculations.” In order to promote reflection on this aspect, we resort to the strategy of transcribing some information about a pupil—son of, friend of, desk mate of, etc. The class understands that those are different ways to describe the pupil: one is his/her name, whereas all the other representations expand the knowledge about him by adding information that the first name does not provide. The teacher then explains that, similarly, each number can be represented in different ways, through any expression equivalent to it. For example: 12 is his name, the so-called canonical form, all the other forms (3 × 4, (2 + 2) × 3, 36 ÷ 3, 10 + 2, 3 × 2 × 2, …) are non-canonical, each of which has a meaning in relation to the context and the underlying processes that generate them. This experience leads to the conclusion that 3 × (11 + 7) ÷ 9 is one of the many non-canonical forms of the number 6. The concept of canonical/non-canonical form also has crucial implications (for both pupils and teachers) in order to reflect on the meanings attributed to the equal sign . It becomes a kind of ‘semantic ferry’ towards generalization.
Example 3 (1st grade): The task is: Given the number 8 + 4, the pupils have to choose equivalent forms from among the following representations: A. 7 + 2; B. 6 + 5 + 2; C. 8 + 3 + 1; D. 9 + 0 + 4; minimizing the calculations.
- Michele::
-
I know it! 8 plus 3 plus 1. You see that 3 plus 1 is the non-canonical form of 4. (Others confirm.)
- Teacher::
-
Have you understood what Michele and others observed? Nicola, what kind of comparison can you do here?
- Nicola::
-
They said that 8 plus 4 is the same as 8 plus 3 plus 1, because 8 remains equal and then, after 3, I put 1 and it still is 4 (he shows the numbers with his fingers).
- Teacher::
-
But what a good pupil! Look now. (She writes on the IWB: 39 + 4, 39 + 3 + 1, 39 + 3 + 2).
The pupils are amazed by such ‘large’ numbers; however, many are able to read them.
- Teacher::
-
What number is equal to 39 plus 4? (Many hands go up.) Is it necessary to make calculations?
- Many::
-
No!
- Teacher::
-
You have to wise up!
- Alexandra::
-
The number is 39 plus 3 plus 1, because 39 is in all three expressions, 3 plus 1 is equal to the non-canonical form of 4, and 3 plus 2 is the non-canonical form of 5.
This episode shows that since the beginning the pupils are educated to compare number sentences reflecting on the relationships between their addends. They learn to compare sentences without calculating their results. The number sentences 39 + 4, 39 + 3 + 1, 39 + 3 + 2 are proposed to favor the transfer between the two situations and to plant the seeds of relational thinking . These comparisons provide a foundation for the gradual, smooth transition to algebra (e.g., a + 4, a + 3 + 1, a + 3 + 2).
-
LC.5. Equal sign . To reflect upon the meanings of the equal sign has crucial implications both for pupils and teacher. In (6 + 11) − 2 = 15, for example, both often ‘see’ operations on the left side and a result on the right side of the equal sign. The main idea is: ‘I sum up 6 and 11, then take away 2 and get 15’. The usual teaching of arithmetic imprints in the pupils a meaning of the equal sign as a directional operator: it has a space-time characterization. In moving to algebra the pupils must learn to move around in a conceptual universe where they have to overcome the familiar space-time characterization: an equality like 2a − 6 = 2(a − 3) has a relational meaning; it states the equivalence between two representations of the same quantity. A consequence of the received imprinting is that the request ‘Write down 14 plus 23’ very often in primary school gets the answer ‘14 + 23 =’ or ‘37’. The equal sign is viewed as an indicator of a conclusion and expresses the implicit belief that the conclusion will sooner or later be required by the teacher; ‘14 + 23’ is viewed as an event waiting for its realization. The pupil is a victim of a lack (or rather a poverty) of control over meanings. In our approach this misconception is bypassed.
Example 4 (2nd grade):
- Piero::
-
It is correct to say that 5 plus 6 ‘makes’ 11, but you cannot say that 11 ‘makes’ 5 plus 6. So it is better to say that 5 plus 6 ‘equals’ 11, because then the contrary is also true.
Piero’s phrase expresses in a naïve, but convincing, way his relational view of the sign ‘=’. Piero argues correctly, highlighting the differences in the meanings of the two sentences: the verbal term ‘equals’ has a symmetric connotation; the verbal term ‘makes’ does not, it has a directional connotation. Piero’s reflection shows the metacognitive character of the teaching he receives.
3.3 Fostering Socio-constructive Classroom Practices Enhancing the Role of Natural Language
-
LC.6. Algebraic babbling. In the learning of the native language, a child acquires little by little its meanings and the rules supporting it, gradually developing to its formal study in school, when he learns to read and reflect on the structural aspects of language. As we have already sketched, we believe that the mental models of algebraic thinking should be similarly organized from the early years of primary school, constructing algebraic language in a dense interlace with arithmetic, starting from its meanings. For this reason, we create an environment that stimulates the pupil’s autonomous processing of encodings of verbal sentences into formulas alongside with their collective comparison within the class. The appropriation of the new language therefore occurs experimentally, and its rules mature gradually within a didactic contract that tolerates initial moments of syntactical inaccuracy. A key aspect in this frame is to help pupils understand the importance of respecting the rules of algebraic language. While students soon start interiorizing the importance of respecting the rules of natural language in order to facilitate communication, it is difficult to make them develop a similar awareness in relation to algebraic language. Therefore, it is necessary to help them understand that algebraic language, too, is a finite set of arbitrary symbols that can be combined according to specific functional rules to be respected (see points LC.8 and LC.9).
Example 5 (5th grade): The teacher poses a story problem concerning the council approval of several car parks that have to be built along the tree-lined roads of the town according to the rule ‘two cars between two trees’ (see Fig. 3.2): Having the car parks to be made with the same pattern but different number of car spaces, the mayor asks that the approval be summarized in a formula which expresses, for all the car parks, the number of car spaces according to the number of trees.
The pupils explore various numerical cases through drawings, collect their data, analyze them, and arrive at the following rule: ‘The number of car spaces can be found by multiplying by 2 the number of trees and subtracting 2’. The teacher begins a discussion to lead the pupils to reformulate the rule in a relational way.
- Teacher::
-
Instead of saying ‘multiplying …’ how might we write the rule?
- Many::
-
It is equal to.
- Teacher::
-
Well, let us rewrite it. ‘The number of car spaces is equal to …’ to what? We cannot write ‘is equal multiplying’.
- Simone::
-
… is equal to ‘the number of trees multiplied by 2’.
- Laura::
-
… and then ‘taking away 2’.
- Teacher::
-
(writing the sentence) May we say the same thing using instead of ‘multiplied by 2’ a little word …?
- Giuseppe::
-
‘The number of car spaces is equal to the double of the number of trees minus 2’.
- Teacher::
-
(writes the last sentence) Now translate it to send it to the mayor.
Each pupil translates the phrase. Translations are listed on the IWB (t = number of trees, cs = number of car spaces)
$$({\text{a}})\;(2 \times t) - 2 = cs\quad ({\text{b}})\;t \times 2 - 2\quad ({\text{c}})\;(cs \times 2) - 2\quad ({\text{d}})\;(2 \times t)(2 - 2)$$The teacher opens the discussion.
- Mauro::
-
(c) is wrong, we must multiply the number of trees, not that of parking spaces.
- Renato::
-
I would remove (d), (2 − 2) is not involved.
Two sentences remain: (a) (2 × t) − 2 = cs (b) t × 2 − 2.
- Teacher::
-
Do you think it’s really necessary to write ‘cs’, indicating what?
- Andrea::
-
I wanted to indicate the car spaces … the number of parking spaces.
- Teacher::
-
Do we have to use two letters ‘cs’? You used t to indicate the number of trees.
- Valentina::
-
We can use c alone!
- Teacher::
-
Do you agree that we use only c to indicate the number of car spaces? Ok. Now: for you, which is the most correct, (a) or (b)? The sentence to be translated was: ‘The number of car spaces is equal to the double of the number of trees minus 2’.
- Irene::
-
The sentence (a) is opposite.
- Andrea::
-
In (b) the number of car spaces is missing.
- Teacher::
-
Let us complete the sentence. (She marks the sentence in parts with brackets and asks the pupils to translate each part into the corresponding symbol .)
This leads to the comparison between the verbal and formal sentence:
The number of parking spaces is equal to the double of the number of trees minus 2

The most meaningful pupils’ interventions that characterize the algebraic babbling are: (i) the answer given by many pupils, “it is equal to,” which reflects a shift towards a relational wording of the rule that had started with the operational wording, “it can be found multiplying by 2”; (ii) Giuseppe’s adding “the double of the number of trees,” which is a conceptual and linguistic refinement in a relational sense of the expression “multiplying by 2”; (iii) the interpretation of the formulas (c) and (d) by Mauro and Renato and their accurate expression of the reasons why they are wrong; (iv) the teacher’s question about the usage of ‘cs’ that favors the pupils’ understanding of the opportunity to reduce it to one letter; (v) Irene’s intervention—where she compares the verbal sentence and its algebraic translation, observing the different positions of the subject—highlights her sensitivity towards the structural aspects of a sentence and the coordination of different representations ; and (vi) Andrea’s intervention underlines the sentence incompleteness because the subject does not appear.
For the refinement of the algebraic babbling , a key moment is the collective comparison of verbal and algebraic formulations of the rule where corresponding parts are underlined. This metacognitive activity allows the pupils to harmonize syntactic and semantic aspects.
-
LC.7. Argumentation. A fundamental aspect in our approach to early algebra is the recognition of the potential role played by the relationship between argumentation and generalization in the social construction of knowledge. Only when argumentation becomes a shared cultural tool in the class can this relationship be made explicit and can students understand the role played by verbalization in the development of their capability to reflect on what they are saying. We could say that the power of argumentation is related to the fact that often those who start developing it are not completely aware of their ideas before they try to express them. As argumentation becomes a habit, the student understands its value and becomes aware of its role in comparing facts and in making their similarities gradually emerge.
Example 6 (6th grade): The class is working to find a rule that gives the number of black triangles according to the numerical position of a Fig. 3.3.
- Ylenia::
-
On the line where the pyramids lie… for example, in the fourth pyramid the black triangles are four and the white are three… my pyramid of six floors has six black triangles and five white triangles on its base… The white (triangles) are always one less than the black ones. Maybe a pyramid with any number of floors has a number of black triangles on its base which is equal to the number of floors and as many white triangles as the black ones minus one.
The teacher writes the following comment in her transcript: “Before her intervention, Ylenia wasn’t aware of her conclusions but, as she was verbalizing, she started deducing and expressing the general rule”.
This episode shows how pupils’ implicit algebraic reasoning and generalizing emerge when argumentation and justification are central to teaching.
-
LC.8. Syntax and Semantics. Control of the syntactical aspects of a new language occurs through its semantic control. In the traditional learning of mathematics, formulas are generally ‘given’ to pupils, thus losing their social value; it is necessary to lead them to understand that they are appropriating a new language that develops according to precise syntactical rules. As we sketched above, to highlight the value of mathematical language for communication, we invite teachers to propose an exchange of messages in formal language with either real or virtual correspondents (pupils, classes, teachers, Brioshi) engaged in the solution of the same problem. The collective comparison of formal sentences produced by the pupils and their interpretative analysis allow pupils to learn that algebraic language also has a syntax (which enables them to detect whether a sentence is correctly expressed or not) and a semantics (which enables them to detect whether it is true or false). So pupils acquire competencies in interpreting formulas and begin to conceive of the translation between these languages as the core of algebraic activity. Notwithstanding that natural language is systematically used in doing mathematics, it is necessary that pupils understand that algebraic language possesses a specific character, which creates an element of rupture with natural language. In our project the pupils are led to discuss these differences while becoming aware of the possible referents of mathematical terms and symbols. We offer two examples.
Example 7 (7th grade): Thomas represents the relationship between two variables as follows: a = b + 1 × 4 and explains his writing.
- Thomas::
-
The number of oranges, a, is quadruple the number of apples, b, plus 1.
- Katia::
-
It’s not correct, because this would mean that the number of oranges is the number of apples plus 4. You have to put the brackets: a = (b + 1) × 4.
Thomas and Katia exchange their views on their translations between natural and algebraic language, and on the semantic and syntactic aspects of mathematical writing. Katia intervenes at a metacognitive level and her argumentation is very articulated: she detects Thomas’s syntactical mistake and correctly translates the verbal sentence. This episode shows how a metacognitive and socio-constructive teaching allows the pupils to assume an appropriate attitude for both early algebraic thinking and arguing.
Example 8 (5th grade): The class is given the task to represent in mathematical language the statement, The double of the sum of 5 and its successive number. As soon as the pupils’ proposals are written on the IWB, Diana steps into justify her writing.
- Diana::
-
Filippo has written 2 × (5 + 6), and it is correct. But I have written 2 × (5 + 5 + 1) because this way it is more evident that the number following 5 is bigger by a unit.
Diana is explaining how her translation is clearer and more transparent because it considers the functional relationship between a number and its successor. Diana recognizes the syntactic correctness of Filippo’s sentence, but considers it opaque: it does not make explicit the relationship between the addends. This episode shows that Diana has acquired either early algebra linguistic constructs or the attitude to make explicit all the relationships in play.
All these examples show that the teaching we promote generates not only an early algebraic thinking but also a wide range of linguistic, logical, and metacognitive abilities related to generalization, argumentation, and justification.
4 Teachers and Early Algebra: The Multicommented Transcripts Methodology
The early algebra approach requires a deep change of perspective in teachers. Their main difficulties concern the revision of their mathematical knowledge and beliefs that condition their teaching actions. They should learn to manage socio-constructive processes in the classroom, drawing on appropriate theoretical frameworks, comparing them to their own epistemology,Footnote 5 thus fruitfully and significantly enriching both culture and work in the classroom. The coordination of a mathematical discussion requires methodological skills that go beyond mere disciplinary competence. Teachers should foresee the development of classroom actions and form hypotheses about pupils’ conceptual constructs and possible strategies to help them modify such constructs. From a social point of view, they should be able to create a good interactional environment, stimulating participation and mutual listening, avoiding judgment and leading the class to validate the arguments, and asking questions at a metacognitive level so that pupils can internalize the processes carried out.
In order to develop these skills—in tune with other scholars (e.g., Jaworski 2004; Mason 2002, 2008; Potari 2013; Schoenfeld 2013; Sowder 2007; Thames and Van Zoest 2013)—we enact educational processes with/for teachers that combine theoretical study, self-observation, and shared critical reflections on their practice. The glossaries allow the teachers to gradually attain a global vision of early algebra . As to teachers’ ability to interpret signals when they are in the classroom, improvement can be obtained through the increasing awareness with which they learn to transform the recurring occasional observations and reflections into a personal methodology. The latter should result from the interlacing of observational skills, motivation to action, and knowledge of how it would be appropriate to intervene. Our aim is that teachers approaching early algebra become trainers of their own development, gradually sharing their experiences to generate a new forma mentis, that becomes a firm base for their autonomous development. Our hypothesis is that a fruitful exchange between theory and praxis can make teachers’ competence evolve in two directions: first, in recognizing signals that their role is at stake either on the spot or in the organization of their theoretical tools; secondly, in processing the received signals so as to convert them into their own cultural patrimony.
Regarding the teaching methodology, we believe that observation and critical-reflective study of socio-constructive classroom processes are necessary conditions to foster teachers’ development of awareness about the roles they must play in the class, the dynamics that characterize the mathematical collective construction, and the variables involved (Cusi and Malara 2015). In the perspective of constituting a community of inquiry, the teachers are organized into groups according to the topics they are working on, and each group is coordinated by a researcher-mentor, who often goes into the classrooms to support the teachers’ actions and frequently has face-to-face and web exchanges with them (Skype, e-mail). Periodically, work-sessions are held by the project leader and also joint meetings with all the teachers and mentors involved in the studies. A crucial aim of the teachers’ educational process lies in leading them to perceive on which aspects they should concentrate and helping them understand how to intervene. Therefore we encourage the teachers involved in ArAl teaching experiments to observe their pupils’ activity according to some key principles, as suggested by other scholars (e.g., Llinares et al. 2016): attending to childrens’ utterances and strategies, interpreting them and appropriately deciding when to intervene to support them, but also observing the effectiveness of their actions (ways of listening, speaking, acting, reacting, …). One important method through which we try to promote these attitudes is the construction of what we call Multicommented Transcripts (MTs), which develops in various steps: the teachers transcribe meaningful classroom episodes, send them by e-mail with their own comments to the mentor who makes his/her own comments, and then the mentor sends them back to the authors and other members of the team who can add further comments. So the MTs become important objects for the education of the teachers (Malara 2008), leading them to critically analyze their didactic interventions through the ‘theoretical glasses’ acquired in the project.
The comments in MTs highlight not only the positive aspects, but also often erroneous beliefs and behaviors. Frequently, they underline that teachers need to have better control of linguistic operative terms (calculate, solve, find the result, it gives …), as well as that of algebraic terms (connect, translate, represent, interpret), the absence of which inhibit the development of a relational view in arithmetic. Furthermore, the comments give suggestions on how to guide the translation from natural to symbolic language, and vice versa. Particular care is devoted to helping teachers reflect on their actions in the face of ‘false discussions,’ that is, dialogues between teacher and only a few pupils where she rhetorically suggests the answers. Another weakness to be signaled would be closing the discussion through questions such as: “Is everything clear?” “Do you understand?” “Do you agree?”, and not allowing pupils to re-examine the situation or not checking whether the conclusion has been effectively reached. Usually in the comments the project leader or mentors recommend that pupils be educated to argue thoroughly and coherently, with an appropriate use of language, underlining that the comprehension of mathematics occurs also through its collective and correct use. Moreover, they suggest that teachers promote a peer-dialogue interaction and limit their role as much as possible, stimulating questions in the classroom and drawing back during the answer phase: if the teacher is the constant pivot of the discussion, the social aspects of knowledge construction are weakened (for more on these aspects, see Cusi et al. 2011; Cusi and Malara 2015; Malara and Navarra 2011, 2016).
The fruits of this methodology, and in particular of the joint reflection on the MTs, strongly influence the development of the theoretical, methodological, and instrumental aspects of our project. In fact, meaningful excerpts of MTs become part of ArAl Units and are discussed in reports or transformed into learning objects (Malara and Navarra in press). In this way they become educational tools for early algebra, offering teachers the possibility to develop the capability and sensitivity to act differently in the classroom (see Fig. 3.4).
In this cycle, the teachers learn to manage the socio-cognitive processes, comparing their epistemology about teaching arithmetic and algebra with the reference frames that they are offered and gradually internalizing the outcomes of the process, so as to consolidate them as a steady cultural patrimony about early algebra. Particularly effective are the occasions (meetings at school, university, the sharing via web of MTs among teachers) where collective debates develop on the classroom actions of teachers dealing with the same activity. Through these cross comparisons, the actions of one teacher can become a model of good practice for his/her colleagues. The following example offers a good model of a teacher’s interactions while leading a discussion.
Example 9 (4th grade): Question: What is the color of the 27th pearl in this sequence (see Fig. 3.5)?
Students propose the following expressions:
The teacher starts the discussion.
- Samuele::
-
In my opinion Brioshi doesn’t understand (a) because he does not know what are 9 and 3, and (b) because 6 × 4 − 1 is not equal to 27 but to 23.
- Francesco::
-
It’s true, I got confused. I counted 3 white pearls and 3 black ones until I got to 27.
- Giovanni::
-
The module is formed by 6 pearls, 3 white and 3 black. You were wrong. The 27th pearl is the 3rd white of the 5th module because 27, which is the number we have to find, divided by 6, is equal to 4 with remainder 3. We need to look at the remainder to establish the 27th pearl.
- Mattia::
-
In my opinion they’re both right, because the remainder 3 means that the 5th module started on. (d) is more correct than Giovanni’s (c).
- Teacher::
-
Do you understand what Mattia said?
- Giuliana::
-
Emanuele (d) used the same numbers as Giovanni (c), but wrote a multiplication and an addition: 6 × 4 + 3 = 27.
- Teacher::
-
Who wants to explain better?
- Giovanni::
-
6 is the number of pearls of the module, 4 is the number of times that the module is repeated, and 3 is the number that I must add to 24, which is the product of 6 by 4 to get to 27.
- Marta::
-
I understand: 6 is the divisor, 4 is the quotient, 3 is the remainder and 27 is the dividend. Emanuele used the same numbers in the division as Giovanni.
The pupils shift from the operative plane to the relational one and learn to appreciate the role of the Euclidean representation of the division. The episode shows how the effectiveness of the teacher’s actions—paradoxically—consists in her marginality in the discussion: she limits herself to follow and carefully observe the development of the pupils’ argumentations; she avoids giving indications or answers, but poses on the spot reflective questions. She induces virtuous behaviors in the pupils: they are encouraged to deepen or rephrase their argumentations and to intervene so as to clarify some claims of their classmates. Very often the MTs show instead how teachers have difficulty in promoting collective discussions with the result that the classroom interactions shrink into short fragmented dialogues between the teacher and the pupils.
In the long run, the MTs allow for ascertaining whether the classroom-leading strategies have changed, and how, during the training. Indications of the effectiveness of the training and of the teacher’s professional growth are provided by the answers to the following questions: Does he/she modify his/her initial points of view or does he/she seem unaware of meaningful changes in his/her initial attitude? Is the teacher able to assume the appropriate roles in order to promote reflection on mathematical processes or objects? Does he/she foster linguistic interactions by encouraging verbalization, argumentation, and collective discussion? Does he/she negotiate and share with the pupils the ArAl theoretical framework? (on these aspects, see Malara and Navarra 2016).
Regarding the last point, we stress that a real and potentially effective sharing of the ArAl theoretical frame with the pupils occurs only if the teacher constantly communicates with the class by using the LCs. However, it is not sufficient to use such terms: the analysis of the MTs shows that teachers often forget to make sure that pupils also use them with a conscious control of the conceptual meanings that they condense. The consequence is ambiguity: the teacher uses them; the pupils seem to understand them, but actually don’t use them during the discussions. The teacher doesn’t notice it and goes along without checking whether the pupils acquire and use the terms with an authentically shared meaning.
The teacher should therefore not only get acquainted with the meaning of the LCs with the aim of stabilizing, conceptualizing, and mastering the meta-disciplinary knowledge of early algebra , but also improve and refine their use in a constant negotiation with the pupils. The acquisition of the key words of the discipline should be achieved through patient teacher-pupils cooperation, during which not only are the terms themselves important, but also the relationships that connect them.
In order to allow the terminology to settle in and improve, it is however necessary that the mathematical discussions be effective, that they promote communication and the sharing of meanings, and that they favor a thorough comparison among the sentences, expressed both in natural and in symbolic language. In other words: a stimulating discussion promotes the use of an advanced terminology, whereas an exchange of short sentences and word phrases generates poor terminology and syntactically mediocre or incomplete sentences, because the pupils delegate to the teacher the task of organizing the whole discourse. This completely blocks the functioning of the devolution, while the teacher gives up his role of guiding the pupils towards assuming their responsibility for the construction of their own knowledge. Let us consider an example. It concerns the interpretation of three formal sentences related to the same problematic situation. The pupils have to choose the correct one and justify the reasons for their choice.
Example 10 (5th grade):
In a pet store showcase there are 11 puppies. Some are visible, others not, because they are inside the house (see Fig. 3.6). Which of the following phrases represents this situation correctly?
The pupils write their explanations, which are then copied on the IWB and discussed.
- Besmala::
-
B tells you that the 7 puppies together with the ones inside are 11 overall.
- Martina::
-
I chose B because it is more transparent.
- Daniele::
-
B, because it summed all the dogs and gives a result of 11. A is wrong because the task wants us to find the suitable non-canonical form to find 11. C is not the answer, because if you do d minus 7 you cannot obtain 11, because we have to sum up all the dogs.
- Clark::
-
B is correct, because 7 plus d, which is the small house, corresponds to 11.
- Sofia::
-
Representation B is the right one, because the puppies are 11 altogether, that is the sum of the visible ones and of the ones that are in the small house.
The teacher considers the pupils’ explanations, reported above, to be correct since they favor phrase B (the correct answer); so she doesn’t analyze them in detail. This excerpt shows how a teacher can miss precious opportunities to test and consolidate important skills from an early algebra perspective. We stress the importance of taking care not only of formalization, but also of interpretation, based on a constant activity of relational reading of the formulas. The pupils resort to terms such as ‘representation,’ ‘transparent,’ and ‘canonical form’; however, the teacher doesn’t express the necessary sensitivity towards what their arguments express or their level of awareness in using such terms.
Besmala could be invited to reformulate her sentence in a relational sense, for example: “The sum between the number of the outside puppies and of the inside puppies is equal to their overall number.” It would have then become evident that it is the translation of 7 + d = 11.
It would be important to understand which meaning Martina gives to the concept of transparent: it seems closer to ‘comprehensible,’ that is, that the sentence can also be seen from a traditional point of view, based on operations (left of the equal sign) and result (on the right). Reflecting on the meaning of a term would allow for scrutinizing important conceptual aspects, as well as the meaning of the equal sign —thus favoring the shift from an operational to a relational perspective.
Not only does the teacher accept Daniele’s and Sofia’s statements about summing ‘animals’ and not ‘numbers of animals,’ but she doesn’t even notice that Daniele’s three justifications are cues to his operational viewpoint: “[B] ‘gives a result’ of 11,” “the task wants us to find the suitable non-canonical form ‘to find’ 11,” and “if you do C minus 7 you cannot ‘obtain’ 11”. When Daniele speaks of ‘canonical form,’ he actually thinks of the operation that allows him to ‘find 11’. Therefore, instead of fostering the pupils’ relational view among the entities at play, the teacher allows (without noticing it) a hidden operational attitude.
Clark could be invited to reconsider his sentence; a frequent error of inexperienced pupils facing letters in algebra consists in associating them with the initial of the name of the object, not to the number of objects that it represents.
This analysis provides evidence that, even if a teacher actively takes part in a co-learning environment, it is not always easy for him/her to react appropriately to support/refine children’s mathematical thinking. As documented in many of our research studies, the conquest of these capabilities requires a long time, an intentional self-monitoring on the part of the teachers, and a constant sharing of their own practices in the realm of teacher education programs focused on the critical analysis of such practice (see, for instance, Cusi et al. 2011; Cusi and Malara 2015; Malara and Navarra 2011, 2016).
5 Concluding Remarks
Leading 5- to 14-year-old pupils to approach early algebra essentially means leading them—through purposely-created problematic situations addressed in a socio-constructive way—towards a new language, with its semantics and syntax. Therefore, respecting its rules becomes essential for treating activities such as translating, arguing, interpreting, predicting, and communicating as mathematical activities. Carrying out calculations is still present, but is subordinated to ‘higher’ purposes: it is the groundwork for reasoning, argumentations, refutations, and corrections. As soon as the algebra that pupils deal with grows in complexity, they will be led to understand that the manipulation of symbolic forms is not self-referential, such understanding helping them mathematize, explore, reason, deduce, and achieve new knowledge.
What we have described shows educational aspects that we believe should be constantly developed in pupils, since these aspects support the growth of their algebraic thinking , promoting metalinguistic and metacognitive competencies, and consequently reflection on: (1) language, which promotes abilities to construct argumentations , to translate natural language into algebraic language, and to produce original thought; (2) the relationship between individual intuitions or productions and the social construction of shared knowledge; (3) passing from concrete generative situations to the conceptual condensation of the underlying mathematical facts and to the construction of the related concepts; and (4) some basic mathematical aspects, such as the evolution of counting strategies and the progressive recognition of the structural equivalence between sentences or, in the case of unknown and variable data, the generation of equations and functions.
Our report in this chapter should make clear that pupils can develop algebraic thinking as long as they are taught as metacognitive students. But in order to achieve this goal, it is necessary that teachers, in turn, learn to be metacognitive teachers . To promote metacognition in teachers we have conceived tools and enacted strategies involving them in a strict intertwining of reflections upon the knowledge in question (theory) and action in the classroom (practice). Our experience and our research studies have made us aware that changing teaching towards the perspective of early algebra requires a conversion of the teachers’ professionalism: this is a slow process that must be supported through appropriate developmental programs.
Working in an early algebraic perspective means, for teachers, to become aware of the fact that arithmetic and algebra must be considered as interlaced disciplines right from the very beginning of primary school. In order to keep this perspective alive in classroom activity, teachers must improve their sensitivity to recognize the continuous micro-situations in which it is possible to contrast/compare the pupils’ (and one’s own) operational point of view to the relational one. We believe that on this basis pupils can experience, from the first school years, a conscious approach to algebraic language and thinking and, in general, a positive attitude towards mathematics. Our research shows that, in order to help pupils reach this goal and gradually and consciously build mathematical skills, it is necessary for pupils and teachers to share the specific terms of the theoretical frame for early algebra, using them constantly when they discuss, reflecting on their meaning, and letting their connections emerge.
Notes
- 1.
‘Devolution’ is a term introduced by Brousseau (1997) in his Theory of Didactical Situations in Mathematics (Didactique des Mathématiques 1970–1990). It indicates a process between the teacher and her students where she, in presenting a problematic situation, brings them to assume the responsibility to deal with it. The devolution is fulfilled when the students actually accept the uncertainty implied in this assumption and they take on the commitment.
- 2.
For typing questions, here we have written “=?=”. In our teaching experiments, the teachers put the question mark on top of the equal sign to stress that they are in front of a hypothetical equality; the pupils then have to express the reasons that support or refute it.
- 3.
The ArAl Units (at the moment there are 12 of them)—supported by the theoretical frame and the glossary—can be seen as models of teaching pathways for arithmetic in an algebraic perspective. They are structured in such a way as to make the teaching process transparent in relation to the problem situation being examined (methodological choices, activated class dynamics, key elements of the process, extensions, potential behavior of pupils, and difficulties they may encounter).
- 4.
The ArAl Unit 11 is devoted to the construction of this property.
- 5.
This term unifies a set of teacher’s characteristics, such as knowledge, beliefs, orientations, goals, and ways of being inside the classroom.
References
Ainley, J., Carraher, D. W., Schliemann, A. D., Brizuela, B. M., Linchevski, L., Radford, L., Tall, D., et al. (2001). Research forum on early algebra. In M. van den Huevel-Panhuizen (Ed.), Proceedings of the 25th Annual Conference of the International Group for the Psychology of Mathematics Education (Vol. 1, pp. 128–159). Utrecht: PME.
Arcavi, A. (1994). Symbol sense: Informal sense-making in formal mathematics. For the Learning of Mathematics, 14(3), 24–35.
Arzarello, F., Bazzini, L., & Chiappini, G. (1993). Cognitive processes in algebraic thinking: Towards a theoretical framework? In I. Hirabayashi, N. Nohda, K. Shigematsu, & F. L. Lin (Eds.), Proceedings of 17th Annual Conference of the International Group for the Psychology of Mathematics Education, (Vol. 1, pp. 138–145). Tsukuba: PME.
Bell, A. (1996). Problem solving approaches to algebra: Two aspects. In N. Bednarz, C. Kieran, & L. Lee (Eds.), Approaches to algebra: Perspectives for research and teaching (pp. 167–187). Dordrecht: Kluwer Academic.
Bell, A. W., Onslow, B., Pratt, K., Purdy, D., & Swan, M. B. (1985). Diagnostic teaching: Teaching from long term learning (Report of ESRC project 8491/1). Nottingham: Shell Centre for Mathematical Education.
Blanton, M., & Kaput, J. (2003). Developing elementary teachers’ algebra eyes and ears. Teaching Children Mathematics, 10(2), 70–77.
Boero, P. (2001). Transformation and anticipation as key processes in algebraic problem solving. In R. Sutherland, T. Rojano, A. Bell, & R. Lins (Eds.), Perspectives on school algebra (pp. 99–119). Dordrecht: Kluwer Academic.
Brousseau, G. (1997). Theory of didactical situations in mathematics (ed. and trans. by N. Balacheff, M. Cooper, R. Sutherland, & V. Warfield). Dordrecht: Kluwer Academic.
Cai, J., & Knuth, E. (Eds.). (2011). Early algebraization: A global dialogue from multiple perspectives. Berlin: Springer.
Cai, J., Lew, H. C., Morris, A., Moyer, J. C., Ng, S. F., & Schmittau, J. (2005). The development of students’ algebraic thinking in earlier grades: A cross-cultural comparative perspective. ZDM The International Journal of Mathematics Education, 37(1), 5–15.
Carpenter, T. P., Franke, M. L., & Levi, L. (2003). Thinking mathematically: Integrating arithmetic and algebra in the elementary school. Portsmouth, NH: Heinemann.
Carraher, D. W., & Schliemann, A. D. (2007). Early algebra and algebraic reasoning. In F. K. Lester, Jr. (Ed.), Second handbook of research on mathematics teaching and learning (Vol. 2, pp. 669–705). Charlotte, NC: Information Age.
Chevallard, Y. (1989). Le passage de l’arithmétique à l’algèbre dans l’enseignement des mathématiques au collège [The passage from arithmetic to algebra in the teaching of mathematics at the high school level—second part]. Petit X, 19, 43–72.
Chevallard, Y. (1990). Le passage de l’arithmétique à l’algèbre dans l’enseignement des mathématiques au collège [The passage from arithmetic to algebra in the teaching of mathematics at the high school level—third part], Petit X, 23, 5–38.
Chick, H., Stacey, K., Vincent, J. L., & Vincent, J. N. (Eds.). (2001). Proceedings of the 12th ICMI Study: The future of the teaching and learning of algebra. Melbourne: University of Melbourne.
Cusi, A., & Malara, N. A. (2015). The intertwining between theory and practice: Influences on ways of teaching and teachers’ education. In L. English & D. Kirshner (Eds.), Handbook of international research in mathematics education (3rd ed., pp. 504–522). London: Taylor & Francis.
Cusi, A., Malara, N. A., & Navarra, G. (2011). Early algebra: Theoretical issues and educational strategies for promoting a linguistic and metacognitive approach to the teaching and learning of mathematics. In J. Cai & E. Knuth (Eds.), Early algebraization: A global dialogue from multiple perspectives (pp. 483–510). Berlin: Springer.
Da Rocha Falcão, J. T. (1995). A case study of algebraic scaffolding: From balance to algebraic notation. In L. Meira & D. Carraher (Eds.), Proceedings of the 19th Annual Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 66–73). Recife: PME.
Davis, R. B. (1985). ICME-5 report: Algebraic thinking in the early grades. Journal of Mathematical Behavior, 4, 195–208.
Filloy, E., & Rojano, T. (1989). Solving equations: The transition from arithmetic to algebra. For the Learning of Mathematics, 9(2), 19–25.
Harper, E. (Ed.). (1987). NMP Mathematics for Secondary School. Essex: Longman.
Hart K. (Ed.). (1981). Children’s understanding of mathematics: 11–16. London: Murray.
Herscovics, N., & Linchevski, L. (1994). A cognitive gap between arithmetic and algebra. Educational Studies in Mathematics, 27(1), 59–78.
Jaworski, B. (2004). Grappling with complexity: Co-learning in inquiry communities in mathematics teaching development. In M. J. Hoines & A. B. Fuglestad, (Eds.), Proceedings of the 28th Annual Conference of the International Group for the Psychology of Mathematics Education (Vol. 1, pp. 17–36). Bergen: PME.
Kaput, J. J. (1998). Transforming algebra from an engine of inequity to an engine of mathematical power by “algebrafying” the K–12 curriculum. In S. Fennell (Ed.), The nature and role of algebra in the K–14 curriculum: Proceedings of a national symposium (pp. 25–26). Washington, DC: National Academy Press.
Kaput, J. J., Carraher, D. W., & Blanton, M. L. (Eds.). (2008). Algebra in the early grades. New York: Lawrence Erlbaum.
Kieran C. (1989). The early learning of algebra: A structural perspective. In S. Wagner & C. Kieran (Eds.), Research issues in the learning and teaching of algebra (pp. 33–56). Reston VA: NCTM.
Kieran C. (1992). The learning and teaching of school algebra. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 390–419). New York: Macmillan.
Kieran, C., Pang, J. S., Schifter, D., Ng, S. F. (2016). Early algebra. Research into its nature, its learning, its teaching. Berlin: Springer.
Linchevski, L. (1995). Algebra with numbers and arithmetic with letters: A definition of pre-algebra. Journal of Mathematical Behavior, 14, 113–120.
Llinares, S., Fernandez, C., & Sanchez-Matamoros, G. (2016). Changes in how prospective teachers anticipate secondary students’ answers. Eurasia Journal of Mathematics, Science & Technology Education, 12(8), 2155–2170.
Malara, N. A. (2008). Methods and tools to promote a socio-constructive approach to mathematics teaching in teachers. In B. Czarnocha (Ed.), Handbook of teaching research (pp. 89–102). Rzeszów: University of Rzeszów.
Malara, N. A., & Navarra, G. (2001). “Brioshi” and other mediation tools employed in a teaching of arithmetic with the aim of approaching algebra as a language. In E. Chick, K. Stacey, Jl. Vincent, & Jn. Vincent (Eds.), Proceedings of the 12th ICMI Study: The Future of the Teaching and Learning of Algebra (Vol. 2, pp. 412–419). Melbourne: University of Melbourne.
Malara, N. A., & Navarra, G. (2003). ArAl project: Arithmetic pathways towards favouring pre-algebraic thinking. Bologna: Pitagora.
Malara, N. A., Navarra, G. (2009). Approaching the distributive law with young pupils, PNA Revista de Investigacíon en Didáctica de la Matematica, 3(2), 73–85.
Malara, N. A., Navarra G. (2011). Multicommented transcripts methodology as an educational tool for teachers involved in early algebra. In M. Pytlak & E. Swoboda, (Eds.). Proceedings of 7th Congress of the European Society for Research in Mathematics Education (pp. 2737–2745). Rzezsow: CERME.
Malara, N. A., & Navarra, G. (2016). Principles and tools for teachers’ education and the assessment of their professional growth. In K. Krainer & N. Vondrova (Eds.), Proceedings of 9th Congress of the European Society for Research in Mathematics Education (pp. 2854–2860). Prague: CERME.
Malara, N. A., & Navarra, G. (in press), Integrating teachers institutional and informal mathematics education: The case of ‘project ArAl’ group in Facebook. In T. Dooley (Ed.), Proceedings of 10 th Congress of the European Society for Research in Mathematics Education. Dublin: CERME.
Mason, J. (1996). Future for arithmetic & algebra: Exploiting awareness of generality. In J. Gimenez, R. Lins, & B. Gomez (Eds.), Arithmetic and algebra education: Searching for the future (pp. 16–33). Barcelona: Universitat Rovira y Virgili.
Mason, J. (2002). Researching your own practice: The discipline of noticing. London: Falmer Press.
Mason, J. (2008). Being mathematical with and in front of learners. In B. Jaworski & T. Wood (Eds.), The mathematics teacher educator as a developing professional (pp. 31–55). Rotterdam: Sense Publishers.
Meira, L. (1996). Students’ early algebraic activity: Sense making and production of meanings in mathematics. In L. Puig & A. Gutierrez (Eds.), Proceedings of the 19 th Annual Conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 377–384). Valencia: PME.
Potari, D. (2013). The relationship of theory and practice in mathematics teacher professional development: An Activity Theory perspective. ZDM The International Journal of Mathematics Education, 45(4), 507–519.
Radford L. (2000). Signs and meanings in students’ emergent algebraic thinking: A semiotic analysis. Educational Studies in Mathematics, 42(3), 237–268.
Russell, S. J., Schifter, D., & Bastable, V. (2011). Connecting arithmetic to algebra. Portsmuth: Heinemann.
Schoenfeld, A. H. (2013). Classroom observations in theory and practice. ZDM The International Journal of Mathematics Education, 45(4), 607–621.
Sowder, J. T. (2007). The mathematical education and development of teachers. In F. K. Lester, Jr. (Ed.), Second handbook of research on mathematics teaching and learning (Vol. 1, pp. 157–223). Charlotte, NC: Information Age.
Thames, M., & Van Zoest, L. (2013). Building coherence in research on mathematics teacher characteristics by developing practice-based approaches. ZDM International Journal of mathematics Education, 45(4), 583–594.
Sitography
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this chapter
Cite this chapter
Malara, N.A., Navarra, G. (2018). New Words and Concepts for Early Algebra Teaching: Sharing with Teachers Epistemological Issues in Early Algebra to Develop Students’ Early Algebraic Thinking. In: Kieran, C. (eds) Teaching and Learning Algebraic Thinking with 5- to 12-Year-Olds. ICME-13 Monographs. Springer, Cham. https://doi.org/10.1007/978-3-319-68351-5_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-68351-5_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-68350-8
Online ISBN: 978-3-319-68351-5
eBook Packages: EducationEducation (R0)


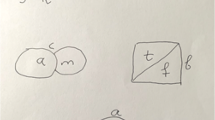


 = 18; 18 = 7 +
= 18; 18 = 7 +  ;
;  + 7 = 18; 18 =
+ 7 = 18; 18 =  + 7; 18 − 7 =
+ 7; 18 − 7 =  ;
;  = 18 − 7; 18 −
= 18 − 7; 18 −  = 7; 7 = 18 −
= 7; 7 = 18 −  . Then the coded sentences are interpreted in natural language and reflections on the relational view of the equal sign are made. In this way what we call
equations
for fun, solvable without particular formal transformations, are generated (we propose them at 1st and 2nd grade).
. Then the coded sentences are interpreted in natural language and reflections on the relational view of the equal sign are made. In this way what we call
equations
for fun, solvable without particular formal transformations, are generated (we propose them at 1st and 2nd grade).





