Abstract
Group signatures allow members of a group to anonymously produce signatures on behalf of the group. They are an important building block for privacy-enhancing applications, e.g., enabling user data to be collected in authenticated form while preserving the user’s privacy. The linkability between the signatures thereby plays a crucial role for balancing utility and privacy: knowing the correlation of events significantly increases the utility of the data but also severely harms the user’s privacy. Therefore group signatures are unlinkable per default, but either support linking or identity escrow through a dedicated central party or offer user-controlled linkability. However, both approaches have significant limitations. The former relies on a fully trusted entity and reveals too much information, and the latter requires exact knowledge of the needed linkability at the moment when the signatures are created. However, often the exact purpose of the data might not be clear at the point of data collection. In fact, data collectors tend to gather large amounts of data at first, but will need linkability only for selected, small subsets of the data. We introduce a new type of group signature that provides a more flexible and privacy-friendly access to such selective linkability. When created, all signatures are fully unlinkable. Only when strictly needed or desired, should the required pieces be made linkable with the help of a central entity. For privacy, this linkability is established in an oblivious and non-transitive manner. We formally define the requirements for this new type of group signatures and provide an efficient instantiation that provably satisfies these requirements under discrete-logarithm based assumptions.
L. Garms—Work done as an intern at IBM Research – Zurich.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Group signatures are a powerful and well-studied primitive that allow members of a group to sign messages on behalf of the group in an anonymous way [2, 4, 9, 10, 21, 22, 28, 32,33,34]. That is, a verifier of a group signature is assured that it was signed by a valid member of the group, but it does not learn anything about the identity of the signer, or even whether two signatures stem from the same user. This makes group signatures highly suited whenever data is collected that needs to be authenticated while, at the same time, the privacy of the data sources must be respected and preserved. In particular when data is collected from users, the protection of their privacy is of crucial importance, and sees increased attention due to the recently introduced General Data Protection Regulation (GDPR) [1], Europe’s new privacy regulation. In fact, the GDPR creates strong incentives for data collectors to thoroughly protect users’ data and implement the principle of data minimization, as data breaches are fined with up to 4% of an enterprises annual turnover.
When aiming to implement such techniques for privacy and data protection, one needs to find a good balance with utility though: data gets collected in order to be analysed and to generate new insights. For these processes it is usually necessary to know the correlation among different data events, as they carry a crucial part of the information. For instance, when a group of users measure and upload their blood pressure via wearable activity trackers, several high value measurements are not critical when they are distributed over many participants, but might be alarming when originating from a single user.
Often the exact purpose of the data might not be clear at the point of data collection. In fact, given the rapid advancements in machine learning and the ubiquitously available and cheap storage, data collectors tend to gather large amounts of data at first, and will only use small subsets for particular applications as they arise. A famous example are the Google Street View cars that inadvertently recorded public Wi-Fi data like SSID information, which later got used to improve Google’s location services.
Ideally, the data should be collected and stored in authenticated and unlinkable form, and only the particular subsets that are needed later on should be correlated in a controlled and flexible manner.
Linkability in Group Signatures. To address the tension between privacy and utility, group signatures often have built-in measures that control linkability of otherwise anonymously authenticated information. Interestingly, despite the long line of work on this subject, none of the solutions provides the functionality to cater for the flexibility needed in practice: They either recover linkablity in a privacy-invasive way or offer control only in a static manner.
Group Signatures with Opening. Standard group signatures [4, 5, 9, 10, 22, 34] guarantee full unlinkability of signatures, except to the group manager (or dedicated opening authority) that owns a so-called opening key. The opening key allows the group manager, when given a signature, to recover the signer’s identity. Originally, the opening was intended to prevent abuse of anonymity, and rather meant to be used in extreme situations. Clearly, the opening capability can also be leveraged to determine the linkability of various data events, but at high costs for privacy: every request for linkability will recover the full identity of the signer, and the central group manager learns the (signed) data of the data collectors and their correlation.
Group Signatures with Controlled Linkability. A more suitable solution are group signatures with controlled linkability [29, 30, 37]. In these schemes, signatures are unlinkable except to a dedicated linking authority with a secret key: on input two signatures it tells whether they stem from the same user or not. This is much better then revealing the identity of the user, but still relies on a fully trusted entity that will learn the collectors’ signed data. Further, this approach does not scale well for applications where a data collector is interested in the correlations within a large data set. To link a data set of n signed entries, each pair of signatures would have to be compared, which would require \(n(n-1)/ 2\) requests to the linking authority. Another related concept are traceable group signatures [31] where a dedicated entity can generate a tracing trapdoor for each user which allows to trace this user’s signatures. This approach is not suitable for our use case of controlled data linkage either, as it requires knowledge of the users’ identities behind the anonymous group signatures or trapdoors for all users, and also needs every signature to be tested for every trapdoor.
Group Signatures with User-Controlled Linkability. Finally, schemes with user-controlled linkability exist, mostly in the context of Direct Anonymous Attestation (DAA) [6, 11, 12, 14, 15] or anonymous credentials [19, 35]. For linkability, a so-called basename is chosen alongside the message and all signatures with the same basename can easily be linked, but signatures for different basenames remain unlinkable. In contrast to solutions with opening or linking authorities, the linkability here can be publicly verified: a signature in such schemes contains a pseudonym that is deterministically derived from the user’s secret key and the basename. Thus, the user re-uses the same pseudonym whenever he wants to be linkable. On the downside, this linkage is immediate and static. That is, the users have to choose at the beginning whether they want to disclose their data in a fully unlinkable manner, or linked w.r.t. a context-specific pseudonym. There is no option to selectively correlate the data after it has been disclosed. Therefore, users, or rather the data collectors allowing the use of such protocols, will hesitate to choose the option of unlinkability, as they fear to lose too much information by the irreversible decorrelation.
Our Contributions. In this work we overcome the aforementioned limitations by introducing a new type of group signatures that allows for flexible and selective linkability. We achieve that functionality by combining ideas from the different approaches discussed above: Group signatures are associated with pseudonyms, but pseudonyms are all unlinkable per default. Only when needed, a set of signatures – or rather the pseudonyms – can be linked in an efficient manner through a central entity, the converter. The converter receives a batch of pseudonymous data and transforms them into a consistent representation, meaning that all pseudonyms stemming from the same user will be converted into the same value. To preserve the privacy of the users and their data, the converter correlates the data in a fully blind way, i.e., not learning anything about the pseudonyms he transforms. We term these new form of group signatures \(\textsf {CLS}\), which stands for convertably linkable (group) signatures.
Security and Privacy for CLS. A crucial property that we want from pseudonym conversions is that they establish linkability only strictly within the queried data, i.e., linked pseudonyms from different queries should not be transitive. Otherwise, different re-linked data sets with overlapping input data could be pieced together, thereby gradually eroding the user’s privacy. Aiming for such non-transitivity has an immediate impact on the overall setting: we need to channel both, the pseudonyms and messages, blindly through the converter, as transforming pseudonyms without the messages would require linkability between the in- and outputs of the conversion query, which in turn allows to correlate outputs from different queries.
We formally define the security of \(\textsf {CLS}\) through a number of security games, strongly inspired by the existing work on group signatures and DAA [4, 5, 15]. That is, we want signatures to be fully anonymous and unlinkable bearing in mind the information that is revealed through the selective linkability. We discuss that the classic anonymity notion adapted to our setting won’t suffice, as it cannot guarantee the desired non-transitivity. In fact, capturing the achievable privacy and non-transitivity property in the presence of adaptive conversion queries was one of the core challenges of this work, and we formalize this property through a simulation-based definition. If the converter is corrupt, then unlinkability of signatures no longer holds, but the adversary should neither be able to trace signatures to a particular user, nor harm the obliviousness of queries which is captured in the conversion blindness and join anonymity properties. The guarantees in terms of unforgeability are captured through non-frameability and traceability requirements. The former says that corrupt users should not be able to impersonate honest users, and the latter guarantees that the power of an adversary should be bounded by the number of corrupt users he controls.
From a corruption point of view, we assume the data collector to be at most honest-but-curious towards the converter, i.e., even a corrupt data collector will only query pseudonym-message pairs that it has received along with a valid signature. We consider this a reasonable assumption, as data collectors that will use such a \(\textsf {CLS}\) scheme do so in order to implement the principle of data minimization on their own premises, and don’t have an incentive to cheat themselves.
Efficient Instantiation. We propose an efficient construction of such \(\textsf {CLS}\) schemes, following the classical sign-and-encrypt paradigm that underlies most group signatures. Roughly, we use BBS+ signatures [3] for attesting group membership, i.e., a user will blindly receive a BBS+ signature from the group issuer on a secret key y chosen afresh by the user. To sign a message m on behalf of the group, the user computes a signature-proof-of-knowledge (SPK) for m where he proves knowledge of such an issuer’s signature on its secret key and also encrypts it’s user key (or rather its “public key” version \(h^y\)) under the converter’s public key. The ciphertext that encrypts \(h^y\) serves as the pseudonym \(nym\).
When the converter is asked to recover the correlations for a set of k pseudonym-message pairs \((nym_1, m_1), \dots (nym_k,m_k)\), it blindly decrypts each pseudonym and blindly raises the result to the power of r which is chosen fresh for every conversion query, but used consistently within. That is, all pseudonyms belonging to the same user will be mapped to the same query-specific DDH tuple \(h^{yr}\) which allows for linkage of data within the query, but guarantees that converted pseudonyms remain unlinkable across queries. To achieve obliviousness and non-transitivity of conversions, we encrypt all pseudonyms and messages with a re-randomisable (homomorphic) encryption scheme under the blinding key of the data collector. The re-randomisation is applied by the converter before he returns the transformed values, which ensures that the data collector cannot link the original and the converted pseudonyms by any cryptographic value. Clearly, if the associated messages are unique, then the data collector can link in- and outputs anyway, but our scheme should not introduce any additional linkage. Given that the pseudonyms are encryptions under the converter’s public key, we need to add the second layer of encryption in a way that it doesn’t interfere with the capabilities of the inner ciphertext. Using a nested form of ElGamal encryption [23] gives us these properties as well as the needed re-randomisability.
Finally, we prove that our instantiation satisfies the desired security and privacy requirements under the DDH, q-SDH and DCR assumption in the random oracle model. Our construction relies on type-3 pairings and performs most of the work in \(\mathbb {G}_1\) which comes with significant efficiency benefits. In fact, we show that our construction is reasonably efficient considering the increased flexibility when establising the linkability in such a selective and controlled manner.
Other Related Work. A number of results exist that establish convertible pseudonyms in the setting of distributed databases and have inspired our work. Therein, the data gets created and maintained in a distributed manner. For privacy, related data is stored under different, database-specific pseudonyms that are seemingly unlinkable and can only be correlated by a central entity that controls the data flow. While the initial approach by Galindo and Verheul [26] required the converter to be a trusted third party, Camenisch and Lehmann [17, 18] later showed how the converter can operate in an oblivious manner. However, none of these solutions supports authenticated data collection and [26] and [17] even let the (trusted) converter establish all pseudonyms. The pseudonym system in [18] bootstraps pseudonyms in a blind way from a user secret, but for every new pseudonym that requires the user, converter and targeted data base to engage in an interactive protocol. Clearly, this is not practical for a setting where users frequently want to upload data. Further, all schemes re-use the same pseudonym for a user within a database, whereas our solution creates fresh and unlinkable pseudonyms for every new data item.
2 Preliminaries
This section presents all building blocks and assumptions that are needed for our CLS construction. We use ElGamal encryption as re-randomisable and homomorphic encryption scheme that is chosen plaintext secure, BBS+ signatures [3], and standard proof protocols.
Bilinear Maps & q-SDH Assumption. Let \(\mathbb {G}_1\), \(\mathbb {G}_2\), \(\mathbb {G}_T\) be cyclic groups of prime order p. A map \(e: \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) must satisfy the following conditions: bilinearity, i.e., \(e(g_1^x, g_2^y) = e(g_1, g_2)^{xy}\); non-degeneracy, i.e., for all generators \(g_1 \in \mathbb {G}_1\) and \(g_2 \in \mathbb {G}_2\), \(e(g_1, g_2)\) generates \(\mathbb {G}_T\); and efficiency, i.e., there exists an efficient algorithm \(\mathcal {G}(1^{\tau })\) that outputs a bilinear group \((p,\mathbb {G}_1\), \(\mathbb {G}_2\), \(\mathbb {G}_T, e, g_1, g_2)\), and an efficient algorithm to compute e(a, b) for all \(a \in \mathbb {G}_1\), \(b \in \mathbb {G}_2\).
We use type-3 pairings [25] in this work, i.e., we do not assume \(\mathbb {G}_1 = \mathbb {G}_2\) or the existence of an isomorphism between both groups in our scheme and security proofs. The advantage of type-3 pairings is that they enjoy the most efficient curves.
q-Strong Diffie Hellman Assumption (q-SDH). There are two versions of the q-Strong Diffie Hellman Assumption. The first version, given by Boneh and Boyen in [7], is defined in a type-1 or type-2 pairing setting. We use their second version of that definition that supports type-3 pairings and was stated in the journal version of their paper [8].
Given \(( g_1, g_1^{\chi }, g_1^{(\chi )^2}, ..., g_1^{(\chi )^q}, g_2, g_2^{\chi })\) such that \(g_1 \in \mathbb {G}_1, g_2 \in \mathbb {G}_2\), output \((g_1^{\frac{1}{\chi +x}}, x) \in \mathbb {G}_1 \times \mathbb {Z}_p \backslash \{-\chi \} \).
BBS+ Signatures. Our scheme will make use of BBS+ signatures given by Au et al. [3], and inspired by BBS group signatures introduced in [9].
- Key Generation::
-
Take
 ,
,  , \(w \leftarrow g_2^x\), and set \(sk = x\) and \(pk = (w, h_1, h_2)\).
, \(w \leftarrow g_2^x\), and set \(sk = x\) and \(pk = (w, h_1, h_2)\). - Signature::
-
On input a message \(m \in \mathbb {Z}_p\) and secret key x, pick
 and compute \(A \leftarrow (g_1 h_1^s h_2^{m})^{\frac{1}{e+x}}\). Output signature \(\sigma \leftarrow (A, e, s)\).
and compute \(A \leftarrow (g_1 h_1^s h_2^{m})^{\frac{1}{e+x}}\). Output signature \(\sigma \leftarrow (A, e, s)\). - Verification::
-
On input a public key \((w, h_1, h_2) \in \mathbb {G}_2 \times \mathbb {G}_1^{2}\), message \(m \in \mathbb {Z}_p\), and purported signature \((A, e, s) \in \mathbb {G}_1 \times \mathbb {Z}_p^2\), check \(e(A, w g_2^e) = e(g_1 h_1^s h_2^{m}, g_2)\).
When proving the unforgability of our scheme (called traceability in our setting), we will make use of techniques from [14] which prove the unforgeability of BBS+ signatures in the type-3 setting. Originally, Au et al. [3], proved the BBS+ signature secure under the first version of the q-SDH assumption given in [7], making use of the isomorphism between the groups in the security proof.
Re-randomisable ElGamal Encryption. We use the ElGamal encryption scheme [23] with public parameters \((\mathbb {G}_1, g, p)\), such that the DDH problem is hard with respect to \(\tau \), i.e p is a \(\tau \) bit prime.
- Key Generation::
-
Choose
 , \(pk \leftarrow g^{sk}\), and output (pk, sk).
, \(pk \leftarrow g^{sk}\), and output (pk, sk). - Encryption::
-
On input (pk, m), choose
 , and output \(c \leftarrow ( g^{r}, pk^r m)\).
, and output \(c \leftarrow ( g^{r}, pk^r m)\). - Decryption::
-
On input \((sk,(c_1, c_2))\), output \( m \leftarrow c_2 c_1^{-sk}\).
ElGamal encryption is chosen-plaintext secure under the DDH assumption. In our construction, we will use the homomorphic property of ElGamal, i.e., if \(C_1 \in \textsf {Enc}(pk, m_1)\), and \(C_2 \in \textsf {Enc}(pk, m_2)\), then \(C_1 \odot C_2 \in \textsf {Enc}(pk, m_1 \cdot m_2)\).
We further use that ElGamal ciphertexts  are publicly re-randomisable in the sense that a re-randomised version \(c'\) of c looks indistinguishable from a fresh encryption of the underlying plaintext m. The following procedure clearly satisfies this:
are publicly re-randomisable in the sense that a re-randomised version \(c'\) of c looks indistinguishable from a fresh encryption of the underlying plaintext m. The following procedure clearly satisfies this:
- Re-randomisation::
-
On input \((pk, (c_1, c_2))\), get
 and output \((c_1 g^{r'}, c_2 pk^{r'})\).
and output \((c_1 g^{r'}, c_2 pk^{r'})\).
2.1 Proof Protocols
We follow the notation defined in [16] when referring to zero-knowledge proofs of knowledge of discrete logarithms. For example \(\textsf {PK}\{(a, b, c): y = g^a h^b \wedge \tilde{y} = \tilde{g}^a \tilde{h}^c \}\) denotes a zero knowledge proof of knowledge of integers a, b and c such that \(y = g^a h^b\) and \( \tilde{y} = \tilde{g}^a \tilde{h}^c\) hold. \(\textsf {SPK}\) denotes a signature proof of knowledge, that is a non-interactive transformation of a proof \(\textsf {PK}\), e.g., using the Fiat-Shamir heuristic [24] in the random oracle. Using the Fiat-Shamir heuristic, the witness can be extracted from these proofs by rewinding the prover and programming the random oracle. Alternatively, these proofs can be extended to be online-extractable, by verifiably encrypting the witness to a public key defined in the common reference string. Clearly this requires a trusted common reference string. We underline the values that we need to be online-extractable in our proofs.
We require the proof system to be simulation-sound and zero-knowledge. The latter roughly says that there must exist a simulator that can generate simulated proofs which are indistinguishable from real proofs from the view of the adversary. The simulation-soundness is a strengthened version of normal soundness and guarantees that an adversary, even after having seen simulated proofs of false statements of his choice, cannot produce a valid proof of a false statement himself.
3 Definition & Security Model for \(\textsf {CLS}\)
In this section we first introduce the syntax and generic functionality of \(\textsf {CLS}\) and then present the desirable security and privacy properties for such schemes.
The following entities are involved in an \(\textsf {CLS}\) scheme: an issuer \(\mathcal {I}\), a set of users \(\mathcal {U}=\{uid_i\}\), a Verifier \(\mathcal {V}\) and a converter \(\mathcal {C}\). The issuer \(\mathcal {I}\) is the central entity that allows users to join the group. Once joined, a user can then sign on behalf of the group in a pseudonymous way. That is, a verifier \(\mathcal {V}\) can test the validity of a signature w.r.t the group’s public key but does not learn any information about the particular user that created the signature. Most importantly, we want the pseudonymously signed data to be linkable in a controlled yet blind manner. Such selected linkability can be requested through the converter \(\mathcal {C}\) that can blindly transform tuples of pseudonym-message pairs into a consistent representation.
3.1 Syntax of CLS
Our notation closely follows the definitional framework for dynamic group signatures given in [5]. We stress that our algorithms (and security notions) are flexible enough to cover settings where multiple verifiers and converters exist. For the sake of simplicity, however, we focus on the setting where there is only one entity each.
Definition 1
(CLS). A convertably linkable group signature scheme \(\textsf {CLS}\) consists of the following algorithms:
Setup & Key Generation. We model key generation individually per party, and refer to \((\textsf {\textsf {param}}, ipk, cpk)\) as the group public key \(gpk\).
- \(\textsf {Setup}(1^{\tau }) \rightarrow \textsf {\textsf {param}}\)::
-
on input a security parameter \(1^{\tau }\), outputs param, the public parameters for the scheme.
- \(\textsf {IKGen}(\textsf {\textsf {param}}) \rightarrow (ipk, isk)\)::
-
performed by the issuer \(\mathcal {I}\), outputs the issuer secret key isk, and the issuing public key ipk.
- \(\textsf {CKGen}(\textsf {\textsf {param}}) \rightarrow (cpk, csk)\)::
-
performed by the Converter \(\mathcal {C}\), outputs the converter secret key csk, and the converter public key cpk.
- \(\textsf {BKGen}(\textsf {\textsf {param}}) \rightarrow (bpk, bsk)\)::
-
performed by the verifier \(\mathcal {V}\)Footnote 1, outputs a blinding secret key, bsk, and blinding public key, bpk. As the key is only used for blinding purposes, (bpk, bsk) can be ephemeral. We write \(\mathcal {BPK}\) as the public key space induced by \(\textsf {BKGen}\).
Join, Sign & Verify. As in standard dynamic group signatures we have a dedicated join procedure that a user has to complete with the issuer. All users that have successfully joined the group can then create pseudonymous signatures on behalf of the group, i.e., that verify w.r.t. the group public key \(bpk\). For ease of expression we treat the pseudonym \(nym\) as a dedicated part of the signature.
- \(\langle \textsf {Join}( gpk), \textsf {Issue}(isk, gpk) \rangle \)::
-
a user \(uid\) joins the group by engaging in a interactive protocol with the Issuer \(\mathcal {I}\). The user uid and Issuer \(\mathcal {I}\) perform algorithms \(\textsf {Join}\) and \(\textsf {Issue}\) respectively. These are input a state and an incoming message respectively, and output an updated state, an outgoing message, and a decision, either cont, accept, or reject. The initial input to \(\textsf {Join}\) is the group public key, gpk, whereas the initial input to \(\textsf {Issue}\) is the issuer secret key, isk, and the issuer public key ipk. If the user uid accepts, \(\textsf {Join}\) has a private output of \(\mathbf gsk [uid]\).
- \(\textsf {Sign}(gpk, \mathbf gsk {[uid]}, m) \rightarrow (nym, \sigma )\)::
-
performed by the user with identifier uid, with input the group public key gpk, the user’s secret key \(\mathbf gsk [uid]\), and a message m. Outputs a pseudonym nym and signature \(\sigma \).
- \(\textsf {Verify}(gpk, m, nym, \sigma ) \rightarrow \{0,1\}\)::
-
performed by the Verifier \(\mathcal {V}\). Outputs 1 if \(\sigma \) is a valid signature on m for pseudonym nym under the group public key \(gpk\), and 0 otherwise.
Blind Conversion. Finally, we want our pseudonymous group signatures to be blindly convertable. Thus, we introduce a dedicated \(\textsf {Blind}\) and \(\textsf {Unblind}\) procedure for the verifier and a \(\textsf {Convert}\) algorithm that requires the converter’s secret key. The latter transforms the unlinkable pseudonyms in a consistent manner, i.e., outputting converted pseudonyms that are consistent whenever the input pseudonyms belong to the same user.
- \(\textsf {Blind}(gpk, bpk, (nym, m)) \rightarrow (cnym, c) \)::
-
performed by the verifier \(\mathcal {V}\) on input a pseudonym-message pair (nym, m) and blinding public key \(bpk\), group public key gpk. Outputs a blinded pseudonym and message.
- \(\textsf {Convert}(gpk, csk, bpk, \{(cnym_i, c_i)\}_{k}) \rightarrow \{(\overline{cnym}_i, \overline{c}_i)\}_{k}\)::
-
performed by the converter \(\mathcal {C}\), on input k blinded pseudonym-message tuples \(\{(cnym_i, c_i)\}_{k}= ((cnym_1, c_1), ..., (cnym_k, c_k))\), and the public blinding key \(bpk\) used. Outputs converted pseudonyms \(\{(\overline{cnym}_i, \overline{c}_i)\}_{k}= ((\overline{cnym}_1, \overline{c}_1), ..., (\overline{cnym}_k, \overline{c}_k))\)
- \(\textsf {Unblind}(bsk, (\overline{cnym},\overline{c})) \rightarrow (\overline{nym}, \overline{m}) \)::
-
performed by the Verifier \(\mathcal {V}\) on input a converted pseudonym-message tuple, and the blinding secret key \(bsk\). Outputs an unblinded converted pseudonym-message tuple \((\overline{nym}, \overline{m}) \).
We sometimes make the randomness r used in these algorithms explicit, and e.g. write \(\textsf {Blind}(gpk, bpk, (nym, m); r)\).
3.2 Security Properties
We want that CLS schemes enjoy roughly the same security and privacy properties as group signatures when taking the added linkability into account. Defining these properties when pseudonyms can be selectively and adaptively converted is very challenging, though, as it requires a lot of care to avoid trivial wins while keeping the adversary as powerful as possible.
In a nutshell, we require the following guarantees from convertably linkable group signatures, where (join) anonymity and non-transitivity capture the privacy-related properties and non-frameability and traceability formalize the desired unforgeability.
- (Join) Anonymity::
-
Pseudonymous signatures should be unlinkable and untraceable (to a join session) even when the issuer and verifier are corrupt. When the converter is honest, unlinkability holds for all signatures for which the associated pseudonyms have not been explicitly linked through a conversion request. If the converter is corrupt and also controlled by the adversary, unlinkability is no longer possible, yet the anonymity of joins must remain.
- Non-transitivity::
-
Converted pseudonyms should be non-transitive, i.e., the verifier should not be able to link the outputs of different convert queries. Otherwise, a corrupt verifier would be able to gradually link together all pseudonyms that have ever been queried to the converter.
- Conversion Blindness::
-
The converter learns nothing about the pseudonyms (and messages) it receives and the transformed pseudonyms it computes.
- Non-frameability::
-
An adversary controlling the issuer and some corrupt users, should not be able to impersonate other honest users, i.e., create pseudonymous signatures that would be linked to a pseudonym of an honest user.
- Traceability::
-
An adversary should not be able to create more signatures that remain unlinkable in a conversion than he controls corrupt users.
Clearly, any re-linked subset of the originally anonymous data increases the risk of re-identification. Thus, the converter could enforce some form of access control to the re-linked data, e.g., only converting a certain amount of pseudonyms at once. The non-transitivity requirement then ensures that a corrupt verifier cannot further aggregate the individually learned data. We stress that our security properties only formalize the achievable privacy for the pseudonyms and signatures. They do not and cannot capture information leakage through the messages that the users sign. This is the case for all group signatures though, and not special to our setting.
Oracles & State. The security notions we formalize in the following make use a number of oracles which keep joint state, e.g., keeping track of queries and the set of corrupted parties. We present the detailed description of all oracles in Fig. 1 and an overview of them and their maintained records below.
-
ADDU (join of honest user & honest issuer) Creates a new honest user for \(uid\) and internally runs a join protocol between the honest user and honest issuer. At the end, the honest user’s secret key \(\mathbf gsk [uid]\) is generated and from then on signing queries for \(uid\) will be allowed.
-
SNDU (join of honest user & corrupt issuer) Creates a new honest user for \(uid\) and runs the join protocol on behalf of \(uid\) with the corrupt issuer. If the join session completes, the oracle will store the user’s secret key \(\mathbf gsk [uid]\).
-
SNDI (join of corrupt user & honest issuer) Runs the join protocol on behalf of the honest issuer with corrupt users. For joins of honest users, the ADDU oracle must be used.
-
SIGN This oracle returns signatures for honest users that have successfully joined (via \(\textsf {ADDU}\) or \(\textsf {SNDU}\), depending on the game).
-
CONVERT The oracle returns a set of converted pseudonyms along with their messages. To model that conversion is triggered by an at most honest-but-curious verifier, we request \(\mathcal {V}\) to provide the unblinded set of pseudonyms along with signatures. The conversion will only be done when all signatures are valid. The oracle then internally blinds the pseudonym-message pairs and returns the blinded input, the randomness used for the blinding along with the converted output. When this oracle is used in the anonymity game, it further checks that the input does not allow the adversary to trivially win by converting the challenge pseudonym together with pseudonyms from either of the challenge users.
All oracles have access to the following records maintained as global state:
- HUL :
-
List of \(uid\)’s of honest users, initially set to \(\varnothing \). New honest users can be added by queries to the \(\textsf {ADDU}\) oracle (when the issuer is honest) or \(\textsf {SNDU}\) oracle (when the issuer is corrupt).
- CUL :
-
List of corrupt users that have (requested) to join the group. Initially set to \(\varnothing \), new corrupt users can be added through the \(\textsf {SNDI}\) oracle if the issuer is honest. If the issuer is corrupt, we do not keep track of corrupt users.
- SL :
-
List of
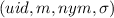 tuples requested from the \(\textsf {SIGN}\) oracle.
tuples requested from the \(\textsf {SIGN}\) oracle.
Helper Algorithms. We introduce two additional algorithms for notational simplicity in our security games: \(\textsf {Identify}\) and \(\textsf {UnLink}\). Roughly, \(\textsf {Identify}\) allows to test whether a pseudonym belongs to a certain \(uid\) by exploiting the convertability of pseudonyms. That is, we create a second signature for \(\mathbf gsk [uid]\) and use the converter’s secret key to test whether both are linked. If so, \(\textsf {Identify}\) returns 1. This algorithm already uses our second helper algorithm \(\textsf {UnLink}\) internally, which takes a list of (correctly formed) pseudonym-message pairs and returns 1 if they are all unlinkable and 0 otherwise.

For even more simplicity we often omit the keys for the algorithms (as they are clear from the context). That is, we write \(\textsf {Identify}(uid, nym)\) which will indicate whether the pseudonym \(nym\) belongs to the user with identity \(uid\) or not. Likewise we write \(\textsf {UnLink}(nym_1,\dots , nym_k)\) to test whether all pseudonyms are uncorrelated or not.
Correctness. \(\textsf {CLS}\) signatures should be correct and consistent when being produced by honest parties. More precisely, we formulate correctness via three requirements: Correctness of sign guarantees that signatures formed using the \(\textsf {Sign}\) algorithm with a user secret key generated honestly will verify correctly. Correctness of conversion guarantees that after blinding, converting and then unblinding correctly, the output will be correctly linked messages/pseudonyms. Consistency is a stronger variant of conversion-correctness and requires that the correlations of pseudonyms established through the conversion procedure must be consistent across queries. More precisely, if a conversion query reveals that two pseudonym \(nym_1\) and \(nym_2\) are linked, and another one that \(nym_2\) and \(nym_3\) are linked, then it must also hold that a conversion query for \(nym_1\) and \(nym_3\) returns linked pseudonyms. We require that this property even holds for maliciously formed pseudonyms, which will be a helpful property in some of our security proofs. For space reasons, the detailed correctness definitions are deferred to the full paper [27].
Anonymity (Corrupt Issuer & Verifier). This security requirement captures the desired anonymity properties when both the issuer and verifier are corrupt. Just as in conventional group signatures, we want that the signatures of honest users are unlinkable and cannot be traced back to a user’s join session with the corrupt issuer. To model this property, we let the adversary output uid’s of two honest users together with a message and return a challenge  that is created either by user \(uid_0\) or \(uid_1\). For anonymity, the adversary should not be able to determine the user’s identity better than by guessing.
that is created either by user \(uid_0\) or \(uid_1\). For anonymity, the adversary should not be able to determine the user’s identity better than by guessing.
In our setting, this property must hold when the corrupt verifier has access to the conversion oracle where it can obtain linked subsets of the pseudonymous data. To avoid trivial wins, the adversary is not allowed to make conversion queries that link the challenge pseudonym \(nym^*\) to another pseudonym belonging to one of the two honest challenge users.
Definition 2
(Anonymity). A CLS scheme satisfies anonymity if for all polynomial time adversaries  the following advantage is negligible in \(\tau :\)
the following advantage is negligible in \(\tau :\)


Non-transitivity (Corrupt Issuer & Verifier). The second privacy-related property we want to guarantee when both the issuer and verifier are corrupt, is the strict non-transitivity of conversions. This ensures that the outputs of separate convert queries cannot be linked together, further than what is already possible due the messages queried. For example if \(\overline{nym}_1\) and \(\overline{nym}_2\) are outputs by two separate convert queries, the adversary should not be able to decide whether they were derived from the same pseudonym or not. Otherwise the verifier could gradually build lists of linked pseudonyms, adding to these during every convert query and eventually recover the linkability among all pseudonymous signatures.
To model non-transitivity of conversions we use a simulation-based approach, requiring the indistinguishability of an ideal and a real world. In the real world, all convert queries are handled normally through the \(\textsf {CONVERT}\) oracle defined in Fig. 1. Whereas in the ideal world, the converted pseudonyms are produced by a simulator \(\textsf {SIM}\) through the \(\textsf {CONVSIM}\) oracle defined below. For a conversion request of input  the simulator will only learn which of the messages belong together, i.e., are associated to pseudonyms that belong to the same user \(uid\). For honest users this can be looked up through the records of the signing oracle that stores tuples \((uid, m_i, nym_i, \sigma _i)\) for each signing query. Thus, we let the simulator mimic the conversion output for all pseudonyms stemming form honest users, and convert pseudonyms from corrupt users normally (as there is no privacy to guarantee for them anyway). Finally, the \(\textsf {CONVSIM}\) oracle outputs a random shuffle of the correctly converted pseudonyms of corrupt users, and the simulated ones for honest users. As mentioned before, we assume the verifier to be honest-but-curious, which we enforce by requesting the adversary to output valid signatures along with the pseudonyms to be converted and handle the blinding step within the conversion oracle.
the simulator will only learn which of the messages belong together, i.e., are associated to pseudonyms that belong to the same user \(uid\). For honest users this can be looked up through the records of the signing oracle that stores tuples \((uid, m_i, nym_i, \sigma _i)\) for each signing query. Thus, we let the simulator mimic the conversion output for all pseudonyms stemming form honest users, and convert pseudonyms from corrupt users normally (as there is no privacy to guarantee for them anyway). Finally, the \(\textsf {CONVSIM}\) oracle outputs a random shuffle of the correctly converted pseudonyms of corrupt users, and the simulated ones for honest users. As mentioned before, we assume the verifier to be honest-but-curious, which we enforce by requesting the adversary to output valid signatures along with the pseudonyms to be converted and handle the blinding step within the conversion oracle.
Definition 3
(Non-transitivity). A CLS scheme satisfies non-transitivity if for all polynomial time adversaries  there exists an efficient simulator \(\textsf {SIM}\) such that the following advantage is negligible in \(\tau \):
there exists an efficient simulator \(\textsf {SIM}\) such that the following advantage is negligible in \(\tau \):


Anonymity vs. Non-transitivity. Note that non-transitivity is not covered by the anonymity notion defined before: A scheme that satisfies anonymity could output the converted pseudonyms in the exact same order as the input ones, allowing trivial linkage between the in- and output of each conversion request. Thus, whenever the same pseudonym is used as input to several conversion queries, this would enable the linkability of the transformed pseudonyms across the different conversions, which is exactly what non-transitivity aims to avoid. On the first glance, it might seem odd that having transitive conversions does not harm our anonymity property. However, transitivity is only useful when several pseudonyms belonging to the same user appear in each conversion request with one pseudonym being re-used in all these sessions. In the anonymity game, the challenge pseudonym is not allowed to be used in combination with any other pseudonym stemming from either of the challenge users (as this would make the definition unachievable), and thus the transitivity of conversions can not be exploited.
Conversion Blindness (Corrupt Issuer & Converter). A crucial property of our signatures is that they can be converted in an oblivious manner, i.e., without the converter learning anything about the pseudonyms or messages it converts. In particular, this blindness property ensures the unlinkability of blinded inputs across several conversion requests. Conversion blindness should hold if both the issuer and converter are corrupt, but the verifier is honest. We formalize this property in a classic indistinguishability style: the adversary outputs two tuples of pseudonym-message pairs and receives a blinded version of either of them. Given that blinding of pseudonyms is a public-key operation we don’t need an additional blinding oracle. In fact, we don’t give the adversary any oracle access at all in this game. He already corrupts the issuer and converter, and this property does not distinguish between honest and corrupt users, thus we simply assume that the adversary has full control over all users as well.
Definition 4
(Conversion Blindness). A CLS scheme satisfies conversion blindness if: for all polynomial time adversaries  the following advantage is negligible in \(\tau \):
the following advantage is negligible in \(\tau \):


Join Anonymity (Corrupt Issuer & Converter & Verifier). The final privacy related property we require from a CLS is the anonymity of joins even if all central entities are corrupt. Here the challenge is that the adversary, controlling the issuer, converter and verifier, should not be able to link signatures of an honest user back to a particular join session. This is the best one can hope for in this corruption setting as unlinkability of signatures (as guaranteed by our anonymity property) is no longer possible: the corrupt converter can simply convert all signatures/pseudonyms into a consistent representation. Such a property does not exist in conventional group signatures, as therein a corrupt opener can always reveals the join identity. In our setting, signatures can only be linked instead of being opened and thus anonymity of the join procedure can and should be preserved.
To model this property we let the adversary output two identities of honest users \(uid_0, uid_1\) that have successfully joined. We then give the adversary access to a signing oracle for one them. This is done by adding the challenge user \(uid^*\) (where \(uid^*\) stands for a dummy handle) to the list of honest users \(\textsf {HUL}\) with user secret key \(\mathbf gsk [uid_b]\). Thus, in the second stage of the game, the adversary can invoke the \(\textsf {SIGN}\) oracle on \(uid^*\) to receive signatures of messages of his choice for the challenge user. The adversary wins if he can determine the bit b better than by guessing. To avoid trivial wins, the adversary is not allowed to see any signature directly from \(uid_0\) or \(uid_1\).
Definition 5
(Join Anonymity). A CLS scheme satisfies join anonymity if: for all polynomial time adversaries  the following advantage is negligible in \(\tau \):
the following advantage is negligible in \(\tau \):


Non-frameability (Corrupt Issuer & Converter & User). This notion captures the desired unforgeability properties when the issuer, converter and some of the users are corrupt, and requires that an adversary should not be able to impersonate an honest user. Our definition is very similar to the non-frameability definitions in standard group signature or DAA schemes [4,5,6]. Roughly, the only part we have to change is how we detect that an honest user has been framed. In group signatures, non-frameability exploits the presence of the group manager that can open signatures and requests that an adversary cannot produce signatures that will open to an honest user who hasn’t created said signature. Here we have the converter instead of the group manager (or dedicated opening authority), and thus express non-frameability through the linkage that is created in a conversion. More precisely, an adversary should not be able to produce a valid signature  that within a conversion request would falsely link to a signature of an honest user. For generality (and sake of brevity), we use our helper function \(\textsf {Identify}\) that we introduced at the beginning of this section to express that the adversary’s signature should not be recognized as a signature of an honest user.
that within a conversion request would falsely link to a signature of an honest user. For generality (and sake of brevity), we use our helper function \(\textsf {Identify}\) that we introduced at the beginning of this section to express that the adversary’s signature should not be recognized as a signature of an honest user.
Definition 6
(Non-frameability). A CLS scheme satisfies non-frameability if for all polynomial time adversaries  , the advantage
, the advantage  is negligible in \(\tau \).
is negligible in \(\tau \).

Traceability (Corrupt Converter & User). Our final requirement formalizes the unforgeability properties when only the converter and some users are corrupt. In this setting, an adversary should not be able to output more pseudonymous signatures that remain unlinkable in a conversion than the number of users it has corrupted. This is again an adaptation of the existing traceability notions for group signatures with an opening authority [4, 5] or user-controlled linkability [6]. Interestingly, in the latter work (that is closer to our setting than standard group signatures), two traceability notions where introduced: While one is similar in spirit to our notion, a second property guarantees that all signatures of corrupt users can be traced back to the exact signing key that the corrupt user has established in the join protocol with the honest issuer. This seems a bit of an odd requirement, as it is not noticeable in the real world. In fact, we do not limit the strategy of the adversary in that way and only require his power to be bounded by the amount of corrupt users he controls.
Our definition stated below uses our helper algorithm \(\textsf {UnLink}\) that we introduced at the beginning of this section and that internally uses the \(\textsf {Convert}\) algorithm to detect whether pseudonyms are unlinkable or not. Note that \(\textsf {UnLink}\) returns 1 only if all inputs are mutually unlinkable, i.e., there is not a single tuple of input pseudonyms that got converted to the same value.
Definition 7
(Traceability). A CLS scheme satisfies traceability if for all polytime adversaries  the advantage
the advantage  is negligible in \(\tau \).
is negligible in \(\tau \).

4 Our \(\textsf {CLS}\) Construction
We now present our construction that securely realizes such \(\textsf {CLS}\) group signatures. Our scheme follows the classical sign-and-encrypt paradigm: we use BBS+ signatures [3] for attesting group membership, i.e., a user will blindly receive a BBS+ signature from the group issuer on the user’s secret key y. To sign a message m on behalf of the group, the user computes a \(\textsf {SPK}\) for m where he proves knowledge of a BBS+ signature on y and also encrypts \(h^y\) under the converter’s public key. The ElGamal ciphertext that encrypts \(h^y\) serves as the associated pseudonym \(nym\).
To blind a set of k pseudonym-message pairs \((nym_1, m_1), \dots (nym_k,m_k)\) for conversion, the verifier encrypts each value under its own ElGamal public key. As the pseudonyms are already ElGamal ciphertexts themselves, this results in a nested double-encryption of \(h^y\) being encrypted under both keys. The converter then decrypts the “inner” part of the ciphertext and blindly raises the result to a random value r. This r is chosen fresh for every conversion query, but used consistently within. That is, all pseudonyms belonging to the same user will be mapped to the same query-specific DDH tuple \(h^{yr}\). Finally, the converter re-randomises all ciphertexts and shuffles them to destroy any linkage between the in- and output tuples—this is crucial for achieving the desired non-transitivity property. The verifier then simply decrypts the received tuples and can link correlated data via the converted pseudonyms \(\overline{cnym}_i\).
4.1 Detailed Description of CLS–DDH
Setup & Key Generation. We use a bilinear group \((p,\mathbb {G}_1\), \(\mathbb {G}_2\), \(\mathbb {G}_T, e, g_1, g_2)\) with \(g_1\) and \(g_2\) being generators of \(\mathbb {G}_1\) and \(\mathbb {G}_2\) respectively. Further, we need four additional generators g, h and \(h_1,h_2\) in \(\mathbb {G}_1\), where \(h_1, h_2\) are used for the BBS+ part, and g, h will be used for the ElGamal encryption.

Join. To join the group, users perform an interactive protocol with the issuer to obtain their user secret key and group credential. Roughly, the \(\mathbf gsk [uid]\) of a user consists of a secret key \(y \in \mathbb {Z}^*_p\) and a BBS+ signature (A, x, s) of \(\mathcal {I}\) on y, where \(A= (g_1 h_1^y h_2^s)^{1 / (isk+x)}\). The detailed protocol of \(\langle \textsf {Join}( gpk), \textsf {Issue}(isk, gpk) \rangle \) is given in Fig. 2.
Sign & Verify. To sign a message m under \(\mathbf gsk [uid] = (A,x,y,s)\), the user proves knowledge of a BBS+ credential (A, x, s) on its secret key y and also encrypts \(h^y\) under the converter’s public key \(cpk\). The proof \(\pi \) then proves knowledge of the BBS+ credential and asserts that the encryption contains the same value y. From \(\pi \) we only need the value y to be online extractable. We use the improved \(\textsf {SPK}\) from Camenisch et al. [14] who have shown how to move most of the work from \(\mathbb {G}_T\) to \(\mathbb {G}_1\) and thus yield a much faster instantiation than the original proof by Au et al. [3]. For verification, one verifies the proof \(\pi \) and some correctness properties of the re-randomised versions of A that are sent along with the proof. In more detail, \(\textsf {Sign}\) and \(\textsf {Verify}\) are defined as follows:

Blind Conversions. When the verifier wants to learn which of the pseudonymously received messages belong together, it sends a batch of pseudonym-message pairs in blinded form to the converter. That is, it encrypts the messages and pseudonyms using ElGamal encryption. The pseudonyms are ElGamal ciphertexts itself and we roughly wrap them in another encryption layer. The converter then blindly decrypts the pseudonyms, i.e., decrypts the “inner” part of the ciphertext, which yields \(h^y\) encrypted under the verifiers blinding key \(bpk\). To ensure non-transitivity, i.e., restrict the linkage of pseudonyms to hold only within the queried batch, the converter blindly raises the encrypted \(h^y\) to a random exponent r. This value is chosen afresh for every batch but used consistently within the query, i.e., all pseudonyms that belong to the same user with secret key y will be mapped consistently to \(h^{yr}\). To ensure that the ciphertexts and their order cannot leak any additional information, we let the converter re-randomize and shuffle all ciphertexts before he returns them to the verifier. Both the verifier and the converter are assumed to be at most honest-but-curious, and so proofs that they have performed \(\textsf {Blind}\) and \(\textsf {Convert}\) correctly are not needed.

4.2 Security of CLS–DDH
We now show that our scheme satisfies all security properties defined in Sect. 3. More precisely, we show that the following theorem holds (using the type-3 pairing version of the q-SDH assumption given in [8]).
Theorem 1
The CLS–DDH construction presented in Sect. 4.1 is a secure \(\textsf {CLS}\) as defined in Sect. 3 if the DDH assumption holds in \(\mathbb {G}_1\), the q-SDH assumption holds, and the \(\textsf {SPK}\) is simulation-sound, zero-knowledge and online extractable (for the underlined values).
In the following we focus on the proof of non-transitivity which was the most challenging property to define and prove. For the other properties we provide short proof sketches and refer for the detailed proofs to the full paper [27].
Lemma 1
The CLS–DDH construction presented in Sect. 4.1 satisfies anonymity if the DDH assumption holds in \(\mathbb {G}_1\), and the \(\textsf {SPK}\) is unbounded simulation-sound, zero knowledge and online extractable (for the underlined values).
Proof
(sketch). Roughly, anonymity follows from the unlinkability property of BBS+ signatures, the CPA-security from ElGamal (used to compute the pseudo-nyms under \(cpk\)), and the DDH assumption (for showing that the conversion doesn’t leak any information). Recall that in this setting, the converter is honest, i.e.,  does not know \(csk\) but is given access to the \(\textsf {CONVERT}\) oracle. Thus, the surprising part might be that CPA encryption is sufficient, despite the converter having to decrypt the blinded pseudonyms. However, in the security proof we can simulate decryption queries by computing the converted pseudonyms from scratch and returning fresh encryptions of them (under \(bpk\)) to the adversary. That is, here we use that the convert algorithm returns re-randomised ciphertexts which, for ElGamal encryption, are distributed as fresh encryptions. To recover the plaintext, i.e., \(h^y\) that needs to be encrypted under \(bpk\), we either look up \(h^y\) from our internal records (when the pseudonyms stem from honest users) or extract y from \(\pi \) (when the pseudonym belongs to a corrupt user). Thus, for each tuple
does not know \(csk\) but is given access to the \(\textsf {CONVERT}\) oracle. Thus, the surprising part might be that CPA encryption is sufficient, despite the converter having to decrypt the blinded pseudonyms. However, in the security proof we can simulate decryption queries by computing the converted pseudonyms from scratch and returning fresh encryptions of them (under \(bpk\)) to the adversary. That is, here we use that the convert algorithm returns re-randomised ciphertexts which, for ElGamal encryption, are distributed as fresh encryptions. To recover the plaintext, i.e., \(h^y\) that needs to be encrypted under \(bpk\), we either look up \(h^y\) from our internal records (when the pseudonyms stem from honest users) or extract y from \(\pi \) (when the pseudonym belongs to a corrupt user). Thus, for each tuple  sent to the \(\textsf {CONVERT}\) we check if an entry
sent to the \(\textsf {CONVERT}\) we check if an entry  in the list of created signatures \(\textsf {SL}\) exist, and if so we look up the \(h^{y_i}\) value we have chosen when mimicking the join protocol for this honest user \(uid_i\). For computing the converted pseudonyms, we then simply compute
in the list of created signatures \(\textsf {SL}\) exist, and if so we look up the \(h^{y_i}\) value we have chosen when mimicking the join protocol for this honest user \(uid_i\). For computing the converted pseudonyms, we then simply compute  for a fresh r. Note that in the case of pseudonyms from corrupt users it is not sufficient to extract just \(h^y\), which would be much more efficient than extracting y: When we have to embed a DDH challenge in the converted output, we won’t be privy of the converter’s exponent r that is supposed to be used in all converted pseudonyms \(h^{y_i r}\). Knowing y we can simply compute \(R^y\) for \(R=g^r\) being a part of the DDH challenge. \(\square \)
for a fresh r. Note that in the case of pseudonyms from corrupt users it is not sufficient to extract just \(h^y\), which would be much more efficient than extracting y: When we have to embed a DDH challenge in the converted output, we won’t be privy of the converter’s exponent r that is supposed to be used in all converted pseudonyms \(h^{y_i r}\). Knowing y we can simply compute \(R^y\) for \(R=g^r\) being a part of the DDH challenge. \(\square \)
Lemma 2
The CLS–DDH construction presented in Sect. 4.1 satisfies non-transitivity if the DDH assumption holds in \(\mathbb {G}_1\), and the \(\textsf {SPK}\) is unbounded simulation-sound, zero knowledge and online extractable (for the underlined value).
Proof
For proving non-transitivity, we have to show that there exists an efficient simulator \(\textsf {SIM}\) that makes the real and simulated game indistinguishable. We start by describing the simulator and then explain why the real and simulated conversion oracles \(\textsf {CONVERT}\) and \(\textsf {CONVSIM}\) are indistinguishable.

We assume that an adversary \(\mathcal {A}\) exists, that makes q queries to the \(\textsf {SNDU}\) oracle for distinct user identifiers, that guesses b correctly in the non-transitivity game with \(\textsf {SIM}\) given above and wins with probability \(\epsilon + 1/2\).
We will stepwise make the real-world (b=0) and the simulated world (b=1) equivalent, using a sequence of Games \(\mathcal {H}_j\) for \(j=0, \dots , q\). The idea is that in Game \(\mathcal {H}_j\) we will not use simulated conversions for all users \(uid_1, \dots , uid_j\) in order of when they were queried to \(\textsf {SNDU}\). More precisely, we define Game \(\mathcal {H}_j\) to be as given in Fig. 3 with all other oracles identical to in the non-transitivity experiment. Let \(S_j\) be the event that \(\mathcal {A}\) guesses b correctly in Game \(\mathcal {H}_j\), with the simulator given above. Game \(\mathcal {H}_j\) keeps track of the queries to \(\textsf {SNDU}\), adding the first j queries \(uid\) to a set \(\textsf {UL}\). Then during queries to \(\textsf {CONVSIM}\), if a signature of a user in \(\textsf {UL}\) is queried, these are treated in the same way as pseudonyms for corrupted users, i.e., they are normally converted using the \(\textsf {Convert}\) algorithm.
Game \(\mathcal {H}_0\) is identical to the non-transitivity game, because \(\textsf {UL}\) is empty. Therefore, \(\Pr [S_0] =\epsilon + 1/2\). In Game \(\mathcal {H}_q\), \(\textsf {UL}\) contains all honest users, and so the \(\textsf {CONVSIM}\) oracle is now identical to the \(\textsf {CONVERT}\) oracle, and inputs to the adversary are now independent of b, therefore \(\Pr [S_q] = 1/2\).
We now show that if an adversary can distinguish Games \(\mathcal {H}_j\) and \(\mathcal {H}_{j+1}\), we can turn this into a distinguisher \(\mathcal {D}_j\) that can break the DDH assumption. We describe the reduction and the additional simulation that is needed therein in Figs. 4 and 5.
We now argue that when a DDH tuple \((D_1, D_2,D_3,D_4)\) is input to \(\mathcal {D}_j\), the inputs to \(\mathcal {A}\) are distributed identically to in Game \(\mathcal {H}_{j+1}\); when a DDH tuple is not input, the inputs to \(\mathcal {A}\) are distributed identically to in Game \(\mathcal {H}_j\). That is for \(D_1 =h, D_2 = h^a, D_3 = h^b, D_4 = h^c\), the oracles provided by \(\mathcal {D}_j\) will be exactly as in \(\mathcal {H}_{j+1}\) when \(c=ab\), and as in \(\mathcal {H}_j\) otherwise.
First, note that gpk, csk, isk are distributed identically as to the non-transitivity game, as \(\chi \) is chosen randomly and independently when setting \(h_1 \leftarrow h^{\chi }\).
Simulating the SNDU Oracle. The \(\textsf {SNDU}\) oracle only differs from the oracle in the non-transitivity experiment during the \((j+1)\)-th query by embedding \(D_2\) of the DDH challenger into the user’s “public key” H using knowledge of \(\chi \). Clearly, H is distributed identically as when computed normally, and \(\pi _H\) can be simulated due to the zero-knowledge property of the proof system. Note that y is not defined for this honest user, but this is not output to \(\mathcal {A}\), or used in the next stage of the protocol.
Simulating the SIGN Oracle. The \(\textsf {SIGN}\) oracle is identical to the oracle in the non-transitivity experiment, when \(uid \ne uid'\) is queried. When \(uid'\) is queried, we simply encrypt \(D_2\) instead of \(h^y\).
This is consistent with \(\textsf {SNDU}\), as \(H = D_2^{\chi } \). Further, \(A', d'\) are chosen randomly and independently, and \(\hat{A} = A'^{isk}\) and so these are distributed identically to in \(\textsf {Sign}\). The SPK \(\pi \) can be simulated due to the zero knowledge property of the proof system.
Simulating the CONVSIM Oracle. What remains to be shown is that the \(\textsf {CONVSIM}\) oracle created by \(\mathcal {D}_j\) either behaves identical to the \(\textsf {CONVSIM}\) oracle in Game \(\mathcal {H}_j\) or as in \(\mathcal {H}_{j+1}\), depending on whether its input was a DDH tuple or not. We know that \(D_3 = h^{\tilde{r}}\) for some \(\tilde{r}\) and thus it must hold that \(D_3^{yr} = h^{\tilde{r}r y}\). Finally, we derive \(\overline{cnym}\) by encrypting \(D_3^{yr}\) from scratch under \(bpk\), which is not noticeable to the adversary due to the re-randomisation that is applied in the conversion algorithm.
If \((D_1, D_2, D_3, D_4)\) is a DDH tuple, then \( D_4^r = h^{\tilde{r} r \tilde{y}}\). Therefore as \(\tilde{y} = y_{uid'}\), the inputs to \(\mathcal {A}\) are also distributed identically to in Game \(\mathcal {H}_{j+1}\). Whereas if \((D_1, D_2, D_3, D_4)\) is not a DDH tuple, then \( D_4^r \), is distributed identically to \(nym'\), which was chosen randomly and independently. Therefore the inputs to \(\mathcal {A}\) are distributed identically to in Game \(\mathcal {H}_{j}\).
Reduction to the DDH problem. Therefore the probability that \(\mathcal {D}_j\) outputs 1 if it was given a valid DDH tuple as input is \( \Pr [S_{j+1}]\), and \(\Pr [S_j]\) is the probability that \(\mathcal {D}_j\) outputs 1 when the input was not a DDH tuple. The advantage of \(\mathcal {D}_j\) is then \( | \Pr [S_{j}] -\Pr [S_{j+1}] |\), therefore \( | \Pr [S_j] -\Pr [S_{j+1}] | = \epsilon _{\mathsf {DDH}}\).
Overall, for our sequence of games \(\mathcal {H}_0\) to \(\mathcal {H}_q\) it holds that \(|\Pr [S_0] - \Pr [S_q] | \leqslant q \epsilon _{\mathsf {DDH}}\) and thus \(\epsilon \leqslant q \epsilon _{\mathsf {DDH}}\) is negligible. This concludes our proof that the CLS–DDH construction satisfies non-transitivity. \(\square \)
Lemma 3
The CLS–DDH construction presented in Sect. 4.1 satisfies conversion blindness if the DDH assumption holds in \(\mathbb {G}_1\).
Proof
(sketch). Given that all a corrupt converter sees are ElGamal ciphertexts that are encrypted under a key \(bpk\) for which \(bsk\) is not known to the adversary, the proof for conversion blindness is a straightforward reduction to the CPA-security of ElGamal which holds under the DDH assumption. \(\square \)
Lemma 4
The CLS–DDH construction presented in Sect. 4.1 satisfies join anonymity if the DDH assumption holds in \(\mathbb {G}_1\), and the \(\textsf {SPK}\) is zero knowledge.
Proof
(sketch). For proving that adversary  cannot break the join anonymity of our CLS–DDH construction we have to show that it is infeasible to link a join session of an honest user to the user’s signatures. In this setting the adversary controls both the converter and issuer. The only value the corrupt issuer learns during the join protocol from an honest user is \(H = h_1^y\) for the user’s secret y and \(\pi _H\), the proof of knowledge of y. When receiving signatures from the user, the adversary can use the converter’s secret key to recover \(h^y\) from \(nym\) and also sees \(\pi \), the proof-of-knowledge of a BBS+ signature on y. By the zero-knowledge property of the proof system, neither \(\pi \) nor \(\pi _H\) leak any information about y. It is easy to see that an adversary that can link \(h_1^y\) and \(h^y\) for the independent generators \(h_1\) and h can be turned into an adversary breaking the DDH assumption. \(\square \)
cannot break the join anonymity of our CLS–DDH construction we have to show that it is infeasible to link a join session of an honest user to the user’s signatures. In this setting the adversary controls both the converter and issuer. The only value the corrupt issuer learns during the join protocol from an honest user is \(H = h_1^y\) for the user’s secret y and \(\pi _H\), the proof of knowledge of y. When receiving signatures from the user, the adversary can use the converter’s secret key to recover \(h^y\) from \(nym\) and also sees \(\pi \), the proof-of-knowledge of a BBS+ signature on y. By the zero-knowledge property of the proof system, neither \(\pi \) nor \(\pi _H\) leak any information about y. It is easy to see that an adversary that can link \(h_1^y\) and \(h^y\) for the independent generators \(h_1\) and h can be turned into an adversary breaking the DDH assumption. \(\square \)
Lemma 5
The CLS–DDH construction presented in Sect. 4.1 satisfies non-frameability if the DL assumption holds in \(\mathbb {G}_1\), and the \(\textsf {SPK}\) is simulation-sound and zero knowledge.
Proof
(sketch). If an adversary  exists that can break the non-frameability of our CLS–DDH scheme, then we can build an adversary
exists that can break the non-frameability of our CLS–DDH scheme, then we can build an adversary  that breaks the discrete logarithm assumption. Recall that non-frameability ensures that an adversary should not be able to create a valid signature that \(\textsf {Convert}\) will falsely link to signatures of an honest user. In the proof we embed re-randomized versions of a DL challenge \(D = h^y\) in the join protocol for all users, i.e., using \(D^r\) instead of H when receiving the BBS+ signature from the corrupt issuer. We also set the public parameters such that \(h_1=h^z\) for a random exponent z. For signature queries we use the knowledge of z to compute proper looking pseudonyms, and then mimic the SPK by choosing \(A', d'\) randomly, setting \(\hat{A} \leftarrow A'^{isk}\), and simulating \(\pi \). If the adversary outputs his forgery
that breaks the discrete logarithm assumption. Recall that non-frameability ensures that an adversary should not be able to create a valid signature that \(\textsf {Convert}\) will falsely link to signatures of an honest user. In the proof we embed re-randomized versions of a DL challenge \(D = h^y\) in the join protocol for all users, i.e., using \(D^r\) instead of H when receiving the BBS+ signature from the corrupt issuer. We also set the public parameters such that \(h_1=h^z\) for a random exponent z. For signature queries we use the knowledge of z to compute proper looking pseudonyms, and then mimic the SPK by choosing \(A', d'\) randomly, setting \(\hat{A} \leftarrow A'^{isk}\), and simulating \(\pi \). If the adversary outputs his forgery  we extract y from \(\pi ^*\) contained in
we extract y from \(\pi ^*\) contained in  . Clearly, this also relies on the simulation soundness and zero-knowledge property of the proof system. \(\square \)
. Clearly, this also relies on the simulation soundness and zero-knowledge property of the proof system. \(\square \)
Lemma 6
The CLS–DDH construction presented in Sect. 4.1 satisfies traceability if the q-SDH assumption holds, and the \(\textsf {SPK}\) is simulation-sound, zero knowledge and online extractable.
Proof
(sketch). We show that if an adversary  can break traceability for the CLS–DDH construction then we can build an adversary
can break traceability for the CLS–DDH construction then we can build an adversary  that breaks the q-SDH assumption. Roughly, to win the traceability game the adversary must be able to create more signatures that remain unlinkable in \(\textsf {Convert}\) than users he controls, which requires
that breaks the q-SDH assumption. Roughly, to win the traceability game the adversary must be able to create more signatures that remain unlinkable in \(\textsf {Convert}\) than users he controls, which requires  to forge BBS+ signatures. Our proof closely follows the revised proof of the unforgeability of BBS+ signatures given in [14]. Note that this uses the newer version of the q-SDH assumption [8] that supports type-3 pairings, which in turn allows to prove the unforgeability of BBS+ signatures in the type-3 pairing setting. \(\square \)
to forge BBS+ signatures. Our proof closely follows the revised proof of the unforgeability of BBS+ signatures given in [14]. Note that this uses the newer version of the q-SDH assumption [8] that supports type-3 pairings, which in turn allows to prove the unforgeability of BBS+ signatures in the type-3 pairing setting. \(\square \)
4.3 Instantiation of \(\textsf {SPK}\) and Efficiency
We now discuss how to securely instantiate the online-extractable \(\textsf {SPK}\)’s used in our CLS–DDH construction and state the computational cost and lengths of signatures and pseudonyms.
Instantiation of \(\textsf {SPK}\)’s. We have two non-interactive zero-knowledge proofs of knowledge in our scheme: \(\pi _H\) used in the join protocol for proving knowledge of y in \(H = h_1^{y}\), and \(\pi \) proving knowledge of a BBS+ signature on y and that \(nym\) encrypts the same y. In both cases we need the witness y to be online extractable. For this, we additionally encrypt y under a public key that needs to be added to \(\textsf {\textsf {param}}\) (and to which in security proof we will know the secret key for), and extend \(\pi \) and \(\pi _H\) to prove that the additional encryption contains the same y that is used in the rest of the proof. For the verifiable encryption of y we use Paillier encryption [20], that is secure under the DCR assumption [36].
For transforming interactive into non-interactive zero-knowledge proofs we rely on the Fiat-Shamir heuristic that ensures security in the random oracle model. Due to this, we can now state Corollary 1.
Corollary 1
The CLS–DDH construction presented in Sect. 4.1, with the \(\textsf {SPK}\) instantiated as above, is a secure \(\textsf {CLS}\) as defined in Sect. 3 under the DDH, q-SDH and DCR assumption in the random oracle model.
Computational Cost. We give the operations required for the entities involved in the scheme in the table below. We denote k exponentiation in group \(\mathbb {G}_i\) by \(k\textsf {exp}_{\mathbb {G}_i}\), k hash function calls by \(k\textsf {hash}\), and k pairing operations by \(k \textsf {pair}\). We denote k exponentiations in \(\mathbb {Z}_{n^2}^*\) due to the Paillier encryption used, by \(k\textsf {exp}_{\mathbb {Z}_{n^2}^*}\).
Entity | Algorithm | Computational Cost |
|---|---|---|
User | Sign | \(16 \textsf {exp}_{\mathbb {G}_1} + 15\textsf {exp}_{\mathbb {Z}_{n^2}} + 1 \textsf {hash}\) |
Verifier | Verify | \(12 \textsf {exp}_{\mathbb {G}_1} + 11\textsf {exp}_{\mathbb {Z}_{n^2}} + 1 \textsf {hash} + 2 \textsf {pair} \) |
Blind | \(6 \textsf {exp}_{\mathbb {G}_1}\) | |
Unblind | \(2 \textsf {exp}_{\mathbb {G}_1}\) | |
Converter | Convert(k pseudonyms input) | \(7 k \textsf {exp}_{\mathbb {G}_1}\) |
Pseudonym & Signature Length. We give the sizes of pseudonyms and signatures in terms of the amount of group elements below. We denote the length required to represent k elements in \(\mathbb {G}_1\) as \(k \mathbb {G}_1\), k outputs of a hash function as kH, and k elements in \(\mathbb {Z}_{n^2}^*\), due to the Paillier encryption used, as \(k\mathbb {Z}_{n^2}^*\).
Pseudonym | Signature | |||
|---|---|---|---|---|
Original | Blinded | Converted | Unblinded Converted | |
nym | cnym | \(\overline{cnym}\) | \(\overline{nym}\) | \(\sigma \) |
\(2\mathbb {G}_1\) | \(3\mathbb {G}_1\) | \(2\mathbb {G}_1\) | \(1\mathbb {G}_1\) | \(3\mathbb {G}_1\) \(6\mathbb {Z}_p\) 1H \(6 \mathbb {Z}^*_{n^2}\) |
5 Conclusion and Future Work
In this work we have introduced a new form of group signatures that support flexible and controlled linkability: data can be collected in authenticated and fully unlinkable form, whilst still allow the data to be obliviously relinked by queries to a central entity. We have formalized the required security properties in a dynamic model, i.e., users are able to join the scheme, and proposed an efficient scheme that satisfies these requirement under discrete logarithm and Paillier assumptions in the random oracle model.
There are a number of open problem we consider to be interesting avenues for future work: Compared with the anonymity requirements of conventional dynamic group signatures, our anonymity notions are somewhat weaker as we do not allow the adversary to corrupt the two challenge users after it received the challenge signature. This means that our privacy related requirements do not yield forward anonymity. Given the conversion functionality that is inherent in our setting, achieving such stronger notion seems challenging, if not even impossible. In fact, for the related problem of group signatures with user-controlled linkability with signature-based revocation, forward anonymity has not been achieved by any of the existing schemes either.
Another direction for further work would be to investigate how to achieve security against fully malicious verifiers. On a high level, this will require to forward blinded versions of the users’ signatures to the converter, allowing him to check the validity of the blinded inputs. The challenge is to do this while preserving the converter’s capability to blindly decrypt and transform the inputs.
In a similar vein, we have considered the verifier to be both the data collector and data processor so far. However, our blind and unblind algorithms already cater for a more flexible setting, as they are specified in the public-key setting. That is, the verifier could blind and push the data to be linked towards a dedicated data processor holding the secret unblinding key. This has the advantage that data storage and processing can be strictly separated. For such a setting it might be desirable to preserve the authenticity of the data throughout the process, i.e., the blind conversion must also take the signatures as input and transform them into valid signatures for the re-linked pseudonyms.
Notes
- 1.
For sake of simplicity we state the algorithms for the setting where the requester and receiver of conversions is the same party, namely the verifier. However, our algorithms work in a public key setting to facilitate more general settings as well.
References
EU general data protection regulation. https://gdpr-info.eu
Ateniese, G., Camenisch, J., Joye, M., Tsudik, G.: A practical and provably secure coalition-resistant group signature scheme. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 255–270. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_16
Au, M.H., Susilo, W., Mu, Y.: Constant-size dynamic k-TAA. In: De Prisco, R., Yung, M. (eds.) SCN 2006. LNCS, vol. 4116, pp. 111–125. Springer, Heidelberg (2006). https://doi.org/10.1007/11832072_8
Bellare, M., Micciancio, D., Warinschi, B.: Foundations of group signatures: formal definitions, simplified requirements, and a construction based on general assumptions. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 614–629. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_38
Bellare, M., Shi, H., Zhang, C.: Foundations of group signatures: the case of dynamic groups. In: Menezes, A. (ed.) CT-RSA 2005. LNCS, vol. 3376, pp. 136–153. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30574-3_11
Bernhard, D., Fuchsbauer, G., Ghadafi, E., Smart, N.P., Warinschi, B.: Anonymous attestation with user-controlled linkability. Int. J. Inf. Secur. 12(3), 219–249 (2013)
Boneh, D., Boyen, X.: Short signatures without random oracles. In: Cachin and Camenisch [13], pp. 56–73
Boneh, D., Boyen, X.: Short signatures without random oracles and the SDH assumption in bilinear groups. J. Cryptol. 21(2), 149–177 (2008)
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_3
Bootle, J., Cerulli, A., Chaidos, P., Ghadafi, E., Groth, J.: Foundations of fully dynamic group signatures. In: Manulis, M., Sadeghi, A.-R., Schneider, S. (eds.) ACNS 2016. LNCS, vol. 9696, pp. 117–136. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-39555-5_7
Brickell, E.F., Camenisch, J., Chen, L.: Direct anonymous attestation. In: Atluri, V., Pfitzmann, B., McDaniel, P. (eds.) ACM CCS 2004, pp. 132–145. ACM Press, October 2004
Brickell, E., Li, J.: A pairing-based DAA scheme further reducing TPM resources. In: Acquisti, A., Smith, S.W., Sadeghi, A.-R. (eds.) Trust 2010. LNCS, vol. 6101, pp. 181–195. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13869-0_12
Cachin, C., Camenisch, J.L. (eds.): EUROCRYPT 2004. LNCS, vol. 3027. Springer, Heidelberg (2004). https://doi.org/10.1007/b97182
Camenisch, J., Drijvers, M., Lehmann, A.: Anonymous attestation using the strong Diffie Hellman assumption revisited. In: Franz, M., Papadimitratos, P. (eds.) Trust 2016. LNCS, vol. 9824, pp. 1–20. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45572-3_1
Camenisch, J., Drijvers, M., Lehmann, A.: Universally composable direct anonymous attestation. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9615, pp. 234–264. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49387-8_10
Camenisch, J., Kiayias, A., Yung, M.: On the portability of generalized schnorr proofs. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 425–442. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_25
Camenisch, J., Lehmann, A.: (Un)linkable pseudonyms for governmental databases. In: Ray, I., Li, N., Kruegel, C. (eds.) ACM CCS 2015, pp. 1467–1479. ACM Press, October 2015
Camenisch, J., Lehmann, A.: Privacy-preserving user-auditable pseudonym systems. In: 2017 IEEE European Symposium on Security and Privacy (EuroS&P), pp. 269–284. IEEE (2017)
Camenisch, J., Lysyanskaya, A.: An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 93–118. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_7
Camenisch, J., Shoup, V.: Practical verifiable encryption and decryption of discrete logarithms. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 126–144. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_8
Camenisch, J., Stadler, M.: Efficient group signature schemes for large groups (extended abstract). In: Kaliski Jr., B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 410–424. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052252
Chaum, D.: Some weaknesses of “weaknesses of undeniable signatures” (rump session). In: Davies, D.W. (ed.) EUROCRYPT 1991. LNCS, vol. 547, pp. 554–556. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-46416-6_54
ElGamal, T.: On computing logarithms over finite fields. In: Williams, H.C. (ed.) CRYPTO 1985. LNCS, vol. 218, pp. 396–402. Springer, Heidelberg (1986). https://doi.org/10.1007/3-540-39799-X_28
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Galbraith, S.D., Paterson, K.G., Smart, N.P.: Pairings for cryptographers. Discrete Appl. Math. 156(16), 3113–3121 (2008)
Galindo, D., Verheul, E.R.: Microdata sharing via pseudonymization. Joint UNECE/Eurostat work session on statistical data confidentiality (2007)
Garms, L., Lehmann, A.: Group signatures with selective linkability (2019). https://eprint.iacr.org/2019/027
Groth, J.: Fully anonymous group signatures without random oracles. In: Kurosawa, K. (ed.) ASIACRYPT 2007. LNCS, vol. 4833, pp. 164–180. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76900-2_10
Hwang, J.Y., Lee, S., Chung, B.H., Cho, H.S., Nyang, D.: Short group signatures with controllable linkability. In: 2011 Workshop on Lightweight Security & Privacy: Devices, Protocols and Applications (LightSec), pp. 44–52. IEEE (2011)
Hwang, J.Y., Lee, S., Chung, B.H., Cho, H.S., Nyang, D.: Group signatures with controllable linkability for dynamic membership. Inf. Sci. 222, 761–778 (2013)
Kiayias, A., Tsiounis, Y., Yung, M.: Traceable signatures. In: Cachin and Camenisch [13], pp. 571–589
Kiayias, A., Yung, M.: Group signatures with efficient concurrent join. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 198–214. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_12
Libert, B., Ling, S., Nguyen, K., Wang, H.: Zero-knowledge arguments for lattice-based accumulators: logarithmic-size ring signatures and group signatures without trapdoors. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 1–31. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_1
Libert, B., Peters, T., Yung, M.: Scalable group signatures with revocation. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 609–627. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_36
Lysyanskaya, A., Rivest, R.L., Sahai, A., Wolf, S.: Pseudonym systems. In: Heys, H., Adams, C. (eds.) SAC 1999. LNCS, vol. 1758, pp. 184–199. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-46513-8_14
Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 223–238. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_16
Slamanig, D., Spreitzer, R., Unterluggauer, T.: Adding controllable linkability to pairing-based group signatures for free. In: Chow, S.S.M., Camenisch, J., Hui, L.C.K., Yiu, S.M. (eds.) ISC 2014. LNCS, vol. 8783, pp. 388–400. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-13257-0_23
Acknowledgments
The first author is supported by the UK Government as part of the CDT in Cyber Security program at Royal Holloway University of London (EP/K035584/1). The second author was supported by the European Union’s Horizon 2020 research and innovation program under Grant Agreement Number 768953 (ICT4CART).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Garms, L., Lehmann, A. (2019). Group Signatures with Selective Linkability. In: Lin, D., Sako, K. (eds) Public-Key Cryptography – PKC 2019. PKC 2019. Lecture Notes in Computer Science(), vol 11442. Springer, Cham. https://doi.org/10.1007/978-3-030-17253-4_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-17253-4_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17252-7
Online ISBN: 978-3-030-17253-4
eBook Packages: Computer ScienceComputer Science (R0)





 ,
,  ,
,  and compute
and compute  ,
,  , and output
, and output  and output
and output 
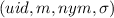 tuples requested from the
tuples requested from the 



