Abstract
Direct Anonymous Attestation (DAA) is a cryptographic protocol for privacy-protecting authentication. It is standardized in the TPM standard and implemented in millions of chips. A variant of DAA is also used in Intel’s SGX. Recently, Camenisch et al. (PKC 2016) demonstrated that existing security models for DAA do not correctly capture all security requirements, and showed a number of flaws in existing schemes based on the LRSW assumption. In this work, we identify flaws in security proofs of a number of qSDH-based DAA schemes and point out that none of the proposed schemes can be proven secure in the recent model by Camenisch et al. (PKC 2016). We therefore present a new, provably secure DAA scheme that is based on the qSDH assumption. The new scheme is as efficient as the most efficient existing DAA scheme, with support for DAA extensions to signature-based revocation and attributes. We rigorously prove the scheme secure in the model of Camenisch et al., which we modify to support the extensions. As a side-result of independent interest, we prove that the BBS+ signature scheme is secure in the type-3 pairing setting, allowing for our scheme to be used with the most efficient pairing-friendly curves.
This work has been supported by the ERC under Grant PERCY #321310.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Direct anonymous attestation (DAA) is a cryptographic authentication protocol that lets a platform, consisting of a secure element and a host, create anonymous attestations. These attestations are signatures on messages and convince a verifier that the message was signed by a authorized secure element, while preserving the privacy of the platform. DAA was designed for the Trusted Platform Module (TPM) by Brickell, Camenisch, and Chen [9] and was standardized in the TPM 1.2 specification in 2004 [34]. Their paper inspired a large body of work on DAA schemes [4, 10, 11, 13, 15, 22–24, 26], including more efficient scheme using bilinear pairings as well as different security definitions and proofs. One result of these works is the recent TPM 2.0 specification [31, 35] that includes support for multiple pairing-based DAA schemes, two of which are standardized by ISO [30].
DAA is widely used in the area of trusted computing. Over 500 million TPMs have been soldFootnote 1, making DAA probably the most complex cryptographic scheme that is widely implemented. Additionally, an extension of DAA is used in the Intel Software Guard Extensions (SGX) [27], the most recent development in the area of trusted computing.
A number of functional extensions to DAA have been proposed. Brickell and Li [12, 14] introduced Enhanced Privacy ID (EPID), which extends DAA with signature-based revocation. This extension allows one to revoke a platform based on a previous signature from that platform. This is an improvement over the private key revocation used in DAA schemes, where a TPM cannot be revoked without knowing its secret key.
Chen and Urian [25] introduced DAA with attributes (DAA-A), in which the membership credential can also contain attributes. These attributes might include more information about the platform, such as the vendor or model, or other information, such as an expiration date of the credential. When signing, the platform can selectively disclose attributes, e.g., reveal that the signature was created by a TPM of a certain manufacturer, or create more advanced proofs, such as proving that the expiration date of the credential lies in the future.
Unfortunately, in spite of being used in practice, many of the existing schemes are not provably secure. Recently, Camenisch et al. [15] showed that previous security definitions of DAA are not satisfactory, meaning that security proofs using these security models do not guarantee security. They further point out that many of the DAA schemes based on the LRSW assumption [32] are flawed. They finally provide a comprehensive security model and provide a LRSW-based scheme that is provably secure in their model. However, there is to date no scheme based on the qSDH assumption [6] that is secure in their model.
Indeed, in this work we show that also many of the DAA schemes based on the qSDH assumption are flawed. The most efficient qSDH-based schemes [13, 22, 25] use a credential which is not provably secure against adaptive chosen message attacks, leaving room for an attacker to forge credentials. Moreover, these schemes use a flawed proof-of-knowledge of credentials, which in fact does not prove possession of such a credential. Finally, the security of all existing qSDH-based schemes has only been analyzed in the type-2 pairing setting [29]. However, these schemes are often used in the more efficient type-3 setting, where there is no efficient isomorphism from \(\mathbb {G}_2\) to \(\mathbb {G}_1\), As the security proofs rely on such an isomorphism, they do not apply to a type-3 setting, meaning there is no evidence of security.
Apart from pointing out flaws in the existing qSDH-based DAA schemes, this paper provides two more main contributions. Second, we fix the issues and present a qSDH-based DAA scheme with support for attributes and signature-based revocation. Like previous work, we use the BBS+ signature [1] for credentials, but unlike previous work we move to the more efficient and flexible type-3 pairing setting. Third, we extend the security model by Camenisch et al. [15] to capture signature-based revocation and support attributes, and rigorously prove our scheme secure in this model.
2 Flaws in Existing qSDH-based Schemes
The first DAA scheme by Brickell et al. [9] is based on the strong RSA assumption. Due to the large keys required for RSA, this protocol was inefficient and hard to implement. A lot of research has gone into designing more efficient DAA schemes using bilinear pairings and improving the security model of DAA. The work on efficient DAA schemes can be split in two chains of work, one based on the LRSW assumption [32], and one on the qSDH assumption [6]. The schemes based on the LRSW assumption have recently been studied by Camenisch et al. [15]. In this section we now discuss the existing qSDH-based schemes and their proofs of security. We start by giving an overview of existing security models for DAA and DAA with extensions, and then show that none of the existing qSDH-based are efficient and provably secure.
2.1 Security Models for DAA
One of the most challenging tasks in cryptography is to formally define a security model that allows for rigorous security proofs. Before we discuss security models, we give some intuition on the required security properties of DAA. First, signatures must be unforgeable, meaning only platforms that the issuer allowed to join can create signatures. Second, signatures must be anonymous. A basename is used to control anonymity, and an adversary given two signatures valid with respect to two distinct basenames must not be able to decide whether the signatures were created by the same platform. Third, we require non-frameability. When a platform signs with respect to the same basename multiple times, a verifier can link these signatures, meaning it realizes both signatures stem from the same platform. No adversary should be able to frame a platform, meaning it cannot create a signature on a message m that links to some platform’s signatures, while that platform never signed m.
There are multiple ways to define a security model. Property-based definitions are a set of security games, where every game defines a security property, and a scheme is secure when every property holds. Simulation-based definitions consist of a trusted third party. In a so-called ideal world, every protocol participant hands their inputs to the trusted third party rather than executing the protocol, and outputs are generated by the trusted third party. As the trusted third party performs the task in a way secure by design, the ideal world performs the desired task securely. A protocol is considered secure if the real world, in which protocol participants execute the protocol, is as secure as the ideal world.
The first security model for DAA as introduced by Brickell et al. [9] follows the simulation-based paradigm. Therein, signature generation and verification is modeled as an interactive process, meaning a signature must always be verified immediately and cannot be used further. Camenisch et al. [15] define a simulation-based security model for DAA that outputs signatures and allows them to be used in any way.
In an attempt to simplify the security model of DAA, Brickell et al. [11] introduce a property-based definition for DAA. Unfortunately, this definition does not cover non-frameability, and the notion for unforgeability allows forgeable schemes to be proven secure: A scheme in which one value is a signature on every message can fulfill the security model, while clearly being insecure. Chen [22] extends this definition with a property for non-frameability, but the other issues remain. Brickell and Li create a property-based security model for enhanced privacy ID (EPID) [14] very similar to the model of Brickell et al. [11], and containing the same flaws.
Camenisch et al. [15] give a more detailed overview of the security models for DAA.
2.2 qSDH-Based DAA Schemes and Proofs
Chen and Feng [26] introduce the first DAA scheme based on the qSDH assumption. The scheme requires the TPM to work in the target group \(\mathbb {G}_T\), which is inefficient and makes implementation more involved. Chen [22] improves the efficiency of the previous schemes by removing one element of the membership credential. Brickell and Li [13] further improve the efficiency by changing the distribution of work between the host and TPM such that the TPM only performs computations in \(\mathbb {G}_1\). Being the most efficient scheme, it is supported by the TPM 2.0 standard and ISO standardized [30].
All three schemes come with proofs of security using the security models by Brickell et al. [11] and Brickell and Li [14]. However, as these models allow one to prove insecure schemes secure, proofs in these models are not actual evidence of security. Furthermore, the proofs of the two most efficient schemes [13, 22] are invalid, as the membership credential is not proven to be existentially unforgeable against adaptive chosen message attacks. The proof aims to reduce a credential forgery to breaking the qSDH assumption, meaning that the issuer private key is an unknown value defined by the qSDH instance. They start by using the Boneh-Boyen trick [6] to create \(q-1\) weak BB signatures under the issuer key, on previously chosen \(e_i\) values. From every weak BB signature, one membership credential on a (potentially adversarial) platform key can be created. For one randomly selected honest platform joining, it returns a credential on a key chosen during the parameter selection of the scheme. It can create this credential without consuming a BB04 signature due to the special selection of parameters. Since the key is chosen like an honest platform would, this simulation is valid for honest platforms. Finally, the authors claim that when a credential forgery occurs that reuses part of an issued credential, with probability \(\frac{1}{q}\), it is reusing part of the specially crafted credential. This is not true, as there may not even be honest platforms joining, or the adversary may disregard credentials issued to honest platforms. To fix the proof, one must be able to issue the special credential also to corrupt platforms, i.e., on a key chosen by the adversary, but this does not seem possible.
Related to this issue, the proofs of knowledge proving knowledge of a credential in these schemes do not prove the correct statement. The prover proves knowledge of TPM secret \( gsk \) and of values a, b. The proof only proves knowledge of a valid credential when \(b = a \cdot gsk \), but this structure of b is not proven. This means that from a signature that passes verification, one cannot always extract a valid signature, which prevents proving unforgeability. This could be fixed by also proving \(b = a \cdot gsk \) in zero knowledge.
Finally, the security proofs of all the pairing-based schemes mentioned here make use of an isomorphism from \(\mathbb {G}_2\) to \(\mathbb {G}_1\) in the security proof. This prevents the schemes from being used with the more efficient type-3 curves [29]. However, the TPM 2.0 standard [31, 35], designed to support the DAA scheme by Brickell and Li [13], uses such type-3 curves. As there is no efficient isomorphism in this setting, any security proof requiring an isomorphism is not applicable, leaving the security of the scheme unproven.
DAA with Extensions. Two extensions of DAA have been proposed. Brickell and Li [14] present EPID based on the qSDH assumption. This extends DAA with signature-based revocation, allowing revocation of platforms based on a signature from that platform. Unfortunately, they do not show how the work of the platform can be split between a TPM and host. Chen and Urian [25] introduce DAA with attributes (DAA-A), where the membership credential does not only contain the TPM key, but also attribute values. This allows for many new use cases, such as showing that a signature was created by a platform of a certain vendor, or adding expiration dates to credentials. The authors present two instantiations, one based on the LRSW assumption and one based on the qSDH assumption. Unfortunately, the schemes do not come with security proofs. The qSDH scheme suffers from the same flaws as the most recent qSDH DAA schemes discussed above, i.e., the credential is not proven to be unforgeable. Worse, the LRSW scheme is forgeable using the trivial credential \(A = B = C = D = E_1 = \ldots = E_L = 1_{\mathbb {G}_1}\) that signs all attributes and keys, so anyone can sign with respect to any desired set of attributes.
3 A New Security Model for DAA with Extensions
In this section we present our security model for DAA with attributes and signature-based revocation, which is defined as an ideal functionality  in the UC framework [21]. In UC, an environment \(\mathcal {E}\) passes inputs and outputs to the protocol parties. The network is controlled by an adversary \(\mathcal {A}\) that may communicate freely with \(\mathcal {E}\). In the ideal world, the parties forward their inputs to the ideal functionality
in the UC framework [21]. In UC, an environment \(\mathcal {E}\) passes inputs and outputs to the protocol parties. The network is controlled by an adversary \(\mathcal {A}\) that may communicate freely with \(\mathcal {E}\). In the ideal world, the parties forward their inputs to the ideal functionality  , which then (internally) performs the defined task and creates outputs that the parties forward to \(\mathcal {E}\). Roughly, a real-world protocol \(\varPi \) is said to securely realize a functionality
, which then (internally) performs the defined task and creates outputs that the parties forward to \(\mathcal {E}\). Roughly, a real-world protocol \(\varPi \) is said to securely realize a functionality  , if the real world is indistinguishable from the ideal world, meaning for every adversary performing an attack in the real world, there is an ideal world adversary (often called simulator) \(\mathcal {S}\) that performs the same attack in the ideal world.
, if the real world is indistinguishable from the ideal world, meaning for every adversary performing an attack in the real world, there is an ideal world adversary (often called simulator) \(\mathcal {S}\) that performs the same attack in the ideal world.
3.1 Ideal Functionality 
We now formally define our ideal functionality  , which is a modification of
, which is a modification of  as defined by Camenisch et al. [15]. The modifications extend the functionality to support signature-based revocation and attributes.
as defined by Camenisch et al. [15]. The modifications extend the functionality to support signature-based revocation and attributes.
The UC framework allows us to focus our analysis on a single protocol instance with a globally unique session identifier sid. Here we use session identifiers of the form \( sid = (\mathcal {I}, sid')\) for some issuer \(\mathcal {I} \) and a unique string \( sid '\). To allow several sub-sessions for the join and sign related interfaces we use unique sub-session identifiers \( jsid \) and \( ssid \). Our ideal functionality  is parametrized by a leakage function \(l : \{0,1\}^* \rightarrow \{0,1\}^*\), that we need to model the information leakage that occurs in the communication between a host \(\mathcal {H} _i\) and TPM \(\mathcal {M} _j\). As our functionality supports attributes, we have parameters L and \(\{\mathbb {A}_i\}_{0 < i \le L}\), where L is the amount of attributes every credential contains and \(\mathbb {A}_i\) the set from which the i-th attribute is taken. A parameter \(\mathbb {P}\) is used to describe which proofs over the attributes platforms can make. This generic approach lets the functionality capture both simple protocols that only support selective disclosure and more advanced protocols that support arbitrary predicates. Every element \( p \in \mathbb {P}\) is a predicate over the attributes: \(\mathbb {A}_1 \times \ldots \times \mathbb {A}_L \rightarrow \{0, 1\}\).
is parametrized by a leakage function \(l : \{0,1\}^* \rightarrow \{0,1\}^*\), that we need to model the information leakage that occurs in the communication between a host \(\mathcal {H} _i\) and TPM \(\mathcal {M} _j\). As our functionality supports attributes, we have parameters L and \(\{\mathbb {A}_i\}_{0 < i \le L}\), where L is the amount of attributes every credential contains and \(\mathbb {A}_i\) the set from which the i-th attribute is taken. A parameter \(\mathbb {P}\) is used to describe which proofs over the attributes platforms can make. This generic approach lets the functionality capture both simple protocols that only support selective disclosure and more advanced protocols that support arbitrary predicates. Every element \( p \in \mathbb {P}\) is a predicate over the attributes: \(\mathbb {A}_1 \times \ldots \times \mathbb {A}_L \rightarrow \{0, 1\}\).
The full definition of  is presented in Figs. 1 and 2. Two macros are used to simplify the presentation of the functionality:
is presented in Figs. 1 and 2. Two macros are used to simplify the presentation of the functionality:


Camenisch et al. [15] give an extensive argumentation of why their functionality guarantees the desired properties. We now argue that our changes indeed allow for attributes and signature-based revocation and that they do not have a negative impact on the other properties guaranteed by the functionality.
Attributes. The issuer is in charge of the attributes, and must explicitly allow a platform to be issued certain attributes with the  output and input. The verification interface now checks whether the signer has the correct attributes, fulfilling the attribute predicate (Check (xii)). This guarantees that no platform can create valid signatures with respect to attribute predicates that do not hold for the attributes of this platform.
output and input. The verification interface now checks whether the signer has the correct attributes, fulfilling the attribute predicate (Check (xii)). This guarantees that no platform can create valid signatures with respect to attribute predicates that do not hold for the attributes of this platform.
Signature-based Revocation. The sign interface now takes a signature-based revocation list \(\texttt {SRL} \) as input. The functionality does not sign for platforms that are revoked by \(\texttt {SRL} \), which it enforces via Check (vi). Further, the verification interface will reject signatures from platforms revoked in \(\texttt {SRL} \) by checking whether any of those signatures is based on the key \( gsk \) from the signature being verified.
Our functionality enforces that every signature matches to only one \( gsk \) value. To ensure this also for the signatures specified in \(\texttt {SRL} \), Check (v) has been added and the \(\texttt {CheckGsk}\) macros have been extended to also take the \(\texttt {SRL} \) values into consideration.
4 Building Blocks
In this section we introduce the building blocks used by our construction. In addition to the standard building blocks such as bilinear pairings and the qSDH assumption, we introduce the BBS+ signature without requiring an isomorphism between the bilinear groups. Up to now, this signature has only been proven secure using such an isomorphism, limiting the settings in which the signature can be used.
4.1 Bilinear Maps
Let \(\mathbb {G}_1\), \(\mathbb {G}_2\), and \( \mathbb {G}_T\) be groups of prime order p. A map \(e: \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) must satisfy bilinearity, i.e., \(e(g_1^x,g_2^y)=e(g_1,g_2)^{xy}\); non-degeneracy, i.e., for all generators \(g_1 \in \mathbb {G}_1\) and \(g_2 \in \mathbb {G}_2\), \(e(g_1,g_2)\) generates \( \mathbb {G}_T\); and efficiency, i.e., there exists an efficient algorithm \(\mathcal {G}(1^\tau )\) that outputs the bilinear group \((p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e,g_1,g_2)\) and an efficient algorithm to compute e(a, b) for any \(a \in \mathbb {G}_1\), \(b \in \mathbb {G}_2\).
Galbraith et al. [29] distinguish three types of pairings: type-1, in which \(\mathbb {G}_1 = \mathbb {G}_2\); type-2, in which \(\mathbb {G}_1 \ne \mathbb {G}_2\) and there exists an efficient isomorphism \(\psi : \mathbb {G}_2 \rightarrow \mathbb {G}_1\); and type-3, in which \(\mathbb {G}_1 \ne \mathbb {G}_2\) and no such isomorphism exists.
Type-3 pairings currently allow for the most efficient operations in \(\mathbb {G}_1\) given a security level using BN curves with a high embedding degree [2]. Therefore it is desirable to describe a cryptographic scheme in a type-3 setting, i.e., without assuming \(\mathbb {G}_1 = \mathbb {G}_2\) or the existence of an efficient isomorphism from \(\mathbb {G}_2\) to \(\mathbb {G}_1\).
4.2 q-Strong Diffie-Hellman Assumption
The q-Strong Diffie-Hellman (qSDH) problem has two versions. The first version by Boneh and Boyen is defined in a type-1 and type-2 pairing setting [6]. This version, to which we refer as the Eurocrypt version, is informally stated as follows:
Given a q+2-tuple \((g_1, g_2, g_2^x, g_2^{(x^2)}, \ldots , g_2^{(x^q)}) \in \mathbb {G}_1\,\times \,\mathbb {G}_2^{q+1}\) with \(g_1 = \psi (g_2)\), output a pair \((c, g_1^{1/(x+c)}) \in \mathbb {Z} _p^* \times \mathbb {G}_1\).
Boneh and Boyen created a new version of the qSDH problem to support type-3 settings [7]. The so-called JOC version is informally stated as follows:
Given a q+3-tuple \((g_1, g_1^x, g_1^{(x^2)}, \ldots , g_1^{(x^q)}, g_2, g_2^x) \in \mathbb {G}_1^{q+1} \times \mathbb {G}_2^2\), output a pair \((c, g_1^{1/(x+c)}) \in \mathbb {Z} _p \setminus \{-x\} \times \mathbb {G}_1\).
4.3 BBS+ Signatures
We recall the BBS+ signature, as described by Au et al. [1], which is inspired by the group signature scheme by Boneh et al. [8].
-
Key Generation. Take
 ,
,  , \(w \leftarrow g_2^x\), and set \(sk = x\) and \(pk = (w, h_0, \ldots , h_L)\).
, \(w \leftarrow g_2^x\), and set \(sk = x\) and \(pk = (w, h_0, \ldots , h_L)\). -
Signature. On input message \((m_1, \ldots , m_L) \in \mathbb {Z} _p^L\) and secret key x, pick
 and compute \(A \leftarrow (g_1 h_0^s \prod _{i = 1}^{L} h_i^{m_{i}})^{\frac{1}{e+x}}\). Output signature \(\sigma \leftarrow (A, e, s)\).
and compute \(A \leftarrow (g_1 h_0^s \prod _{i = 1}^{L} h_i^{m_{i}})^{\frac{1}{e+x}}\). Output signature \(\sigma \leftarrow (A, e, s)\). -
Verification. On input a public key \((w, h_0, \ldots , h_L) \in \mathbb {G}_2 \times \mathbb {G}_1^{L+1}\), message \((m_1, \ldots , m_L) \in \mathbb {Z} _p^L\), and purported signature \((A, e, s) \in \mathbb {G}_1 \times \mathbb {Z} _p^2\), check \(e(A, w g_2^e) = e(g_1 h_0^s \prod _{i = 1}^{L} h_i^{m_{i}}, g_2)\).
Au et al. prove the BBS+ signature secure under the Eurocrypt version of the qSDH assumption, making use of the isomorphism between the groups in the security proof. As in type-3 pairings no such isomorphism exists, this means the proof is not valid when this isomorphism does not exist and we do not know whether the signature is secure in this setting. We modify the proof by Au et al. to use the JOC version of the qSDH assumption and no longer rely on an isomorphism in the proof, allowing us to use BBS+ signatures with type-3 pairings.
Theorem 1
The BBS+ signature scheme is existentially unforgeable against adaptive chosen message attacks under the JOC version of the qSDH assumption and the DL assumption, in particular in pairing groups where no efficient isomorphism between \(\mathbb {G}_2\) and \(\mathbb {G}_1\) exists.
Due to space contraints, the proof is presented in the full version of the paper [16].
4.4 Proof Protocols
When referring to the zero-knowledge proofs of knowledge of discrete logarithms and statements about them, we will follow the notation introduced by Camenisch and Stadler [19] and formally defined by Camenisch, Kiayias, and Yung [17].
For instance, \( PK \{(a, b, c): y=g^a h^b \wedge \tilde{y}=\tilde{g}^a \tilde{h}^c \}\) denotes a “zero-knowledge proof of knowledge of integers a, b and c such that \(y=g^{a}h^{b}\) and \(\tilde{y}=\tilde{g}^{a}\tilde{h}^{c}\) holds,” where \(y, g, h, \tilde{y}, \tilde{g}\) and \(\tilde{h}\) are elements of some groups \(\mathbb {G}=\langle {g}\rangle =\langle {h}\rangle \) and \(\tilde{\mathbb {G}}=\langle \tilde{g} \rangle =\langle \tilde{h} \rangle \). Given a protocol in this notation, it is straightforward to derive an actual protocol implementing the proof [17]. Indeed, the computational complexities of the proof protocol can be easily derived from this notation: for each term \(y=g^{a}h^{b}\), the prover and the verifier have to perform an equivalent computation, and to transmit one group element and one response value for each exponent.
\( SPK \) denotes a signature proof of knowledge, that is a non-interactive transformation of a proof with the Fiat-Shamir heuristic [28] in the random oracle model [3]. From these non-interactive proofs, the witness can be extracted by rewinding the prover and programming the random oracle. Alternatively, these proofs can be extended to be online-extractable, by verifiably encrypting the witness to a public key defined in the common reference string (CRS). A practical instantiation is given by Camenisch and Shoup [18] using Paillier encryption, secure under the DCR assumption [33].
5 Construction
In this section, we present our DAA protocol with attributes and signature-based revocation called  . On a high level, it is similar to previous work on qSDH-based DAA. A platform, consisting of a TPM and a host, must once run the join protocol before it can create signatures. In the join protocol, the TPM authenticates to the issuer. The issuer can decide whether the TPM is allowed to join, and if so, it creates a credential for the platform. The credential is BBS+ signature on a commitment to the TPM chosen secret key \( gsk \), and on attribute values as determined by the issuer. Note that the issuer can choose the attribute values, as we expect the issuer to issue only credentials containing attributes where it knows the ‘correct’ attribute values, such as the model or vendor of the TPM (which it knows as the TPM authenticated), or an expiration date of the credential. After receiving a credential, the platform can sign a message m by creating a signature proof-of-knowledge proving that it has a credential. A basename \(\texttt {bsn}\) controls linkability. Choosing a fresh \(\texttt {bsn}\) yields a signature that cannot be linked to any signature that the platform previously generated, meaning the platform can be fully anonymous. Only when it chooses to reuse a basename, the signatures based on the same basename can be linked, i.e., a verifier can notice that they stem from the same platform. The platform also chooses which attributes it will disclose to a verifier.
. On a high level, it is similar to previous work on qSDH-based DAA. A platform, consisting of a TPM and a host, must once run the join protocol before it can create signatures. In the join protocol, the TPM authenticates to the issuer. The issuer can decide whether the TPM is allowed to join, and if so, it creates a credential for the platform. The credential is BBS+ signature on a commitment to the TPM chosen secret key \( gsk \), and on attribute values as determined by the issuer. Note that the issuer can choose the attribute values, as we expect the issuer to issue only credentials containing attributes where it knows the ‘correct’ attribute values, such as the model or vendor of the TPM (which it knows as the TPM authenticated), or an expiration date of the credential. After receiving a credential, the platform can sign a message m by creating a signature proof-of-knowledge proving that it has a credential. A basename \(\texttt {bsn}\) controls linkability. Choosing a fresh \(\texttt {bsn}\) yields a signature that cannot be linked to any signature that the platform previously generated, meaning the platform can be fully anonymous. Only when it chooses to reuse a basename, the signatures based on the same basename can be linked, i.e., a verifier can notice that they stem from the same platform. The platform also chooses which attributes it will disclose to a verifier.
Our protocol is parametrized by L, the amount of attributes a credential contains, attribute sets \(\mathbb {A}_1, \ldots , \mathbb {A}_L\), and l, the leakage of the secure channels used. For simplicity of the presentation, we describe our construction supporting only selective disclosure as attribute predicates, although it is simple to see how the construction can be extended to allow for more advanced predicates using standard proof techniques. We describe the predicates using a set \(D \subseteq \{1, \ldots , L\}\) indicating which attributes are disclosed, and a tuple \(I = (a_1, \ldots , a_L)\) setting the desired attribute values. For example, the predicate \(D \leftarrow \{2\}\), \(I = (\bot , 123, \bot )\) is only true for platforms with credentials in which the second attribute value equals 123. Let \(\bar{D} = \{1, \ldots , L\} \setminus D\) be the set of undisclosed attributes.
We assume that a common reference string functionality  and a certificate authority functionality
and a certificate authority functionality  are available to all parties.
are available to all parties.  will be used to provide the protocol participants with the system parameters consisting of a security parameter \(\tau \), a bilinear group \(\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T\) of prime order p with generators \(g_1, h_0, \ldots , h_L\) of \(\mathbb {G}_1\) and \(g_2\) of \(\mathbb {G}_2\) and bilinear map e, generated via \(\mathcal {G}(1^\tau )\).
will be used to provide the protocol participants with the system parameters consisting of a security parameter \(\tau \), a bilinear group \(\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T\) of prime order p with generators \(g_1, h_0, \ldots , h_L\) of \(\mathbb {G}_1\) and \(g_2\) of \(\mathbb {G}_2\) and bilinear map e, generated via \(\mathcal {G}(1^\tau )\).  allows the issuer to register his public key. We further use random oracles \(H_1 : \{0,1\}^* \rightarrow \mathbb {G}_1\) that is used for the computation of pseudonyms and \(H: \{0,1\}^* \rightarrow \{0,1\}^\tau \) which is used for the Fiat-Shamir heuristic in the zero-knowledge proofs.
allows the issuer to register his public key. We further use random oracles \(H_1 : \{0,1\}^* \rightarrow \mathbb {G}_1\) that is used for the computation of pseudonyms and \(H: \{0,1\}^* \rightarrow \{0,1\}^\tau \) which is used for the Fiat-Shamir heuristic in the zero-knowledge proofs.
The TPM and issuer must have an authenticated communication channel in the join protocol. This can be achieved in multiple ways, we abstract away from this by using an ideal functionality for this authenticated channel. As the host forwards messages, it can block the communication, so the standard  does not capture the desired security. Instead we use
does not capture the desired security. Instead we use  which was introduced by Camenisch et al. [15] specifically for this type of authenticated channel. The communication between a TPM and host is modeled using secure message transmission functionality
which was introduced by Camenisch et al. [15] specifically for this type of authenticated channel. The communication between a TPM and host is modeled using secure message transmission functionality  . For definitions of the standard functionalities
. For definitions of the standard functionalities  and
and  we refer to [20, 21].
we refer to [20, 21].
For the sake of readability, we will not explicitly call  for communication between a TPM and host, nor write down that parties query
for communication between a TPM and host, nor write down that parties query  and
and  to retrieve the system parameters and the issuer public key. When a party receives an input or message it does not expect, e.g., protocol messages received out of order, or any of the protocol checks fails, the protocol outputs with failure message \(\bot \). For efficiency, a host should precompute values \(e(g_1, g_2)\) and \(e(h_0, w)\) after joining and a verifier should in addition precompute \(e(h_i, g_2)\) for \(i = 0, \ldots , L\) to minimize the number of pairing computations, but for readability we write the full pairing function.
to retrieve the system parameters and the issuer public key. When a party receives an input or message it does not expect, e.g., protocol messages received out of order, or any of the protocol checks fails, the protocol outputs with failure message \(\bot \). For efficiency, a host should precompute values \(e(g_1, g_2)\) and \(e(h_0, w)\) after joining and a verifier should in addition precompute \(e(h_i, g_2)\) for \(i = 0, \ldots , L\) to minimize the number of pairing computations, but for readability we write the full pairing function.
5.1 Our DAA Protocol with Extensions 
Issuer Setup. In the setup phase, the issuer \(\mathcal {I} \) creates a key pair of the BBS+- signature scheme and registers the public key with  .
.
-
1.
\(\mathcal {I}\) upon input
 generates his key pair:
generates his key pair:-
Check that \( sid = (\mathcal {I}, sid ')\) for some \( sid '\).
-
Choose
 and set \(w \leftarrow g_2^x\). Prove knowledge of the private key by creating
and set \(w \leftarrow g_2^x\). Prove knowledge of the private key by creating  . Initiate
. Initiate  .
. -
Register the public key \(w, \pi \) at
 , and store the secret key x.
, and store the secret key x. -
Output
 .
.
-
Join Request. The join protocol runs between the issuer \(\mathcal {I} \) and a platform, consisting of a TPM \(\mathcal {M} _i\) and a host \(\mathcal {H} _j\). The platform authenticates to the issuer and, if the issuer allows the platform to join with certain attributes, obtains a credential that subsequently enables the platform to create signatures. A unique sub-session identifier \( jsid \) distinguishes several join sessions that might run in parallel.
-
1.
\(\mathcal {H} _j\) upon input
 parses \( sid = (\mathcal {I}, sid ')\) and sends the message
parses \( sid = (\mathcal {I}, sid ')\) and sends the message  over \(\mathcal {I} \).
over \(\mathcal {I} \). -
2.
\(\mathcal {I} \) upon receiving
 from a party \(\mathcal {H} _j\) chooses a fresh nonce
from a party \(\mathcal {H} _j\) chooses a fresh nonce  and sends (sid, jsid, n) back to \(\mathcal {H} _j\).
and sends (sid, jsid, n) back to \(\mathcal {H} _j\). -
3.
\(\mathcal {H} _j\) upon receiving \(( sid , jsid , n)\) from \(\mathcal {I} \), sends \(( sid , jsid , n)\) to \(\mathcal {M} _i\).
-
4.
\(\mathcal {M} _i\) upon receiving \(( sid , jsid , n)\) from \(\mathcal {H} _j\), generates its secret key:
-
Check that no key record exists.
-
Choose
 and store the key as \(( sid , \mathcal {H} _j, gsk , \bot )\).
and store the key as \(( sid , \mathcal {H} _j, gsk , \bot )\). -
Set \(Q \leftarrow h_1^{ gsk }\) and compute
 .
. -
Store key record \(( sid , \mathcal {H} _j, gsk )\).
-
Send \((Q, \pi _1)\) via the host to \(\mathcal {I} \) using
 .
.
-
-
5.
\(\mathcal {H} _j\) notices \(\mathcal {M} _i\) sending \((Q, \pi _1)\) over
 to the issuer, it appends its own identity in the unauthenticated part of the message and forwards the full message to the issuer. It also keeps state as \(( jsid , Q)\).
to the issuer, it appends its own identity in the unauthenticated part of the message and forwards the full message to the issuer. It also keeps state as \(( jsid , Q)\). -
6.
\(\mathcal {I} \) upon receiving \((Q, \pi _1)\) authenticated by \(\mathcal {M} _i\) and identity \(\mathcal {H} _j\) unauthenticated over
 , it verifies \(\pi _1\) and checks that
, it verifies \(\pi _1\) and checks that  . It stores \(( jsid , Q, \mathcal {M} _i, \mathcal {H} _j)\) and outputs
. It stores \(( jsid , Q, \mathcal {M} _i, \mathcal {H} _j)\) and outputs  .
.
Join Proceed. The join session is completed when the issuer receives an explicit input telling him to proceed with join session \( jsid \) and issue attributes \( attrs = (a_1, \ldots , a_L)\).
-
1.
\(\mathcal {I} \) upon input
 generates the BBS+ credential:
generates the BBS+ credential:-
Retrieve the record \(( jsid , Q, \mathcal {M} _i, \mathcal {H} _j)\) and add
 .
. -
Choose random \(e, f \in \mathbb {Z} _p\).
-
\(A \leftarrow (g_1 \cdot h_0^f \cdot Q \cdot \prod _{i = 1}^L h_{i+1}^{a_i})^{1/(e+x)}\)
-
Send the credential to the host by sending \(( sid , jsid , A, e, f, attrs )\) to \(\mathcal {H} _j\) over
 .
.
-
-
2.
\(\mathcal {H} _j\) upon receiving \(( sid , jsid , A, e, f, attrs )\) from \(\mathcal {I}\) verifies and stores the credential.
-
Check that \(e(A, w g_2^e) = e(g_1 \cdot h_0^f \cdot Q \cdot \prod _{i = 1}^L h_{i+1}^{a_i}, g_2)\).
-
Store \(( sid , \mathcal {M} _i, (A, e, f), attrs )\) and output
 .
.
-
Sign Request. The sign protocol runs between a TPM \(\mathcal {M} _i\) and a host \(\mathcal {H} _j\). After joining, together they can sign a message m with respect to a basename \(\texttt {bsn}\), attribute predicate (D, I), and signature-based revocation list \(\texttt {SRL} \). Again, we use a unique sub-session identifier \( ssid \) to allow for multiple sign sessions.
-
1.
\(\mathcal {H} _j\) upon input
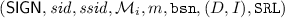 checks whether his attributes fulfill the predicate and randomizes the BBS+ credential:
checks whether his attributes fulfill the predicate and randomizes the BBS+ credential:-
Retrieve the join record \(( sid ,\mathcal {M} _i, (A, e, f), attrs )\).
-
Check that the attributes fulfill the predicate: Parse I as \((a_1', \ldots , a_L')\) and \( attrs \) as \((a_1, \ldots , a_L)\) and check that \(a_i = a_i'\) for every \(i \in D\).
-
Choose
 and set \(A' \leftarrow A \cdot h_0^a\).
and set \(A' \leftarrow A \cdot h_0^a\). -
Send \(( sid , ssid , m, \texttt {bsn}, (D, I), \texttt {SRL})\) to \(\mathcal {M} _i\) and store \(( sid , ssid , a)\)
-
-
2.
\(\mathcal {M} _i\) upon receiving \(( sid , ssid , m, \texttt {bsn}, (D, I), \texttt {SRL})\) from \(\mathcal {H} _j\) asks for permission to proceed.
-
Check that a join record \(( sid , \mathcal {H} _j, gsk )\) exists.
-
Store \(( sid , ssid , m, \texttt {bsn}, (D, I), \texttt {SRL})\) and output
 .
.
-
Sign Proceed. The signature is completed when \(\mathcal {M} _i\) gets permission to proceed for \( ssid \).
-
1.
\(\mathcal {M} _i\) upon input
 computes the pseudonym \(\texttt {nym}\) and starts the computation of the following zero knowledge proof.
computes the pseudonym \(\texttt {nym}\) and starts the computation of the following zero knowledge proof. 
-
Retrieve join record \(( sid , \mathcal {H} _j, gsk )\) and sign record \(( sid , ssid , m, \texttt {bsn}, (D, I), \texttt {SRL})\).
-
Set \(\texttt {nym}\leftarrow H_1(\texttt {bsn})^{ gsk }\).
-
Take
 and compute \(E \leftarrow h_1^{r_ gsk }\) and \(L \leftarrow H_1(\texttt {bsn})^{r_ gsk }\).
and compute \(E \leftarrow h_1^{r_ gsk }\) and \(L \leftarrow H_1(\texttt {bsn})^{r_ gsk }\). -
Send \(( sid , ssid , E, L, \texttt {nym})\) to \(\mathcal {H} _j\).
-
-
2.
\(\mathcal {H} _j\) upon receiving \(( sid , ssid , E, L, \texttt {nym})\) from \(\mathcal {M} _i\), completes the commitment phase of the zero-knowledge proof.
-
Take
 , and
, and  .
. -
Compute t-value
$$\begin{aligned} t&\leftarrow e(A', g_2)^{r_e} e(h_0, g_2)^{r_b} e(E, g_2) e(h_0, w)^{r_a} \prod _{i \in \bar{D}} e(h_{i+1}, g_2)^{r_{a_i}} \\&= e(A'^{r_e} \cdot h_0^{r_b} \cdot E \cdot \prod _{i \in \bar{D}}h_{i+1}^{\ r_{a_i}}, g_2) e(h_0, w)^{r_a} \end{aligned}$$ -
Compute \(c' \leftarrow H(A', \texttt {nym}, t, L, g_1, h_0, \ldots , h_L, w)\).
-
Send \(( sid , ssid , c')\) to \(\mathcal {M} _i\).
-
-
3.
\(\mathcal {M} _i\) upon receiving \(( sid , ssid , c')\) from \(\mathcal {H} _j\).
-
Take a nonce
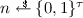 .
. -
Compute \(c \leftarrow H(n, c', m, \texttt {bsn}, (D, I), \texttt {SRL})\).
-
Set \(s_ gsk \leftarrow r_ gsk + c \cdot gsk \).
-
Send \(( sid , ssid , s_ gsk )\) to \(\mathcal {H} _j\).
-
-
4.
\(\mathcal {H} _j\) upon receiving \(( sid , ssid , s_ gsk )\) from \(\mathcal {M} _i\), completes the zero-knowledge proof.
-
Set \(b \leftarrow f + a \cdot e\), \(s_{a_i} \leftarrow r_{a_i} + c a_i\) for \(i \in \bar{D}\), \(s_e \leftarrow r_e - c e\), \(s_a \leftarrow r_a + c a\), \(s_b \leftarrow r_b + c a e\).
-
Set \(\pi \leftarrow (c, s_ gsk , \{s_{a_i}\}_{i \in \bar{D}}, s_e, s_a, s_b, n)\).
-
-
5.
As signature-based revocation is used, a revocation list \(\texttt {SRL} \) containing tuples \((\texttt {bsn}_i, \texttt {nym}_i)\) is given, and the platform must prove that \(H_1(\texttt {bsn}_i)^{ gsk } \ne \texttt {nym}_i\). It does so using the Camenisch-Shoup proof of inequality of discrete logarithms [18]: take a random \(\gamma \), compute \(C \leftarrow (H_1(\texttt {bsn}_i)^{ gsk }/\texttt {nym}_i)^\gamma \), and prove \(SPK\{(\alpha , \beta ): C = H_1(\texttt {bsn}_i)^\alpha (\frac{1}{\texttt {nym}_i})^\beta \wedge 1 = H_1(\texttt {bsn})^\alpha (\frac{1}{\texttt {nym}})^\beta \}\). For every \((\texttt {bsn}_i, \texttt {nym}_i) \in \texttt {SRL} \), the platform takes the following steps.
-
(a)
Host \(\mathcal {H} _j\) sends \(( sid , ssid , \texttt {bsn}_i)\) to \(\mathcal {M} _i\).
-
(b)
Upon receiving \(( sid , ssid , \texttt {bsn}_i)\), the TPM \(\mathcal {M} _i\) starts the commitment phase of this proof of non-revocation.
-
Take
 and compute \(t'_{i, 1} \leftarrow H_1(\texttt {bsn}_i)^{r_{i, \alpha }}\), \(t'_{i, 2} \leftarrow H_1(\texttt {bsn})^{r_{i, \alpha }}\), \(K \leftarrow H_1(\texttt {bsn}_i)^ gsk \).
and compute \(t'_{i, 1} \leftarrow H_1(\texttt {bsn}_i)^{r_{i, \alpha }}\), \(t'_{i, 2} \leftarrow H_1(\texttt {bsn})^{r_{i, \alpha }}\), \(K \leftarrow H_1(\texttt {bsn}_i)^ gsk \). -
Send \(( sid , ssid , t'_{i, 1}), t'_{i, 2}, K)\) to \(\mathcal {H} _j\).
-
-
(c)
Upon receiving \(( sid , ssid , t_{i, 1}'), t_{i, 2}', K)\), \(\mathcal {H} _j\) completes the commitment phase of the non-revocation proof.
-
Take
 and set \(C_i \leftarrow (K/\texttt {nym}_i)^{\gamma _i}\).
and set \(C_i \leftarrow (K/\texttt {nym}_i)^{\gamma _i}\). -
Check \(C_i \ne 1_{\mathbb {G}_1}\).
-
Take
 and set \(t_{i, 1} \leftarrow t_{i, 1}'^{i, \beta } \cdot (\frac{1}{\texttt {nym}_i})^{r_{i, \beta }}\) and \(t_{i, 2} \leftarrow t_{i, 2}'^{\gamma _i} \cdot (\frac{1}{\texttt {nym}})^{r_{i, \beta }}\).
and set \(t_{i, 1} \leftarrow t_{i, 1}'^{i, \beta } \cdot (\frac{1}{\texttt {nym}_i})^{r_{i, \beta }}\) and \(t_{i, 2} \leftarrow t_{i, 2}'^{\gamma _i} \cdot (\frac{1}{\texttt {nym}})^{r_{i, \beta }}\). -
Compute \(c' \leftarrow H(C, \texttt {bsn}_i, \texttt {bsn}, \texttt {nym}_i, \texttt {nym}, n, t_{i, 1}, t_{i, 2})\)
-
Send \(( sid , ssid , c')\) to \(\mathcal {M} _i\).
-
-
(d)
\(\mathcal {M} _i\) upon receiving \(( sid , ssid , c')\) from \(\mathcal {H} _j\)
-
Take nonce
 and compute \(c \leftarrow H(n_i, c)\).
and compute \(c \leftarrow H(n_i, c)\). -
Set \(s_{i, \alpha }' \leftarrow r_{i, \alpha } + c \cdot gsk \) and send \(( sid , ssid , s_{i, \alpha }', n_i)\) to \(\mathcal {H} _j\).
-
-
(e)
Upon receiving \(( sid , ssid , s_{i, \alpha }', n_i)\) from \(\mathcal {M} _i\), host \(\mathcal {H} _j\) finishes the non-revocation proof.
-
Compute \(c \leftarrow H(n_i, c')\).
-
Set \(s_{i, \alpha } \leftarrow \gamma \cdot s_{i, gsk }'\) and \(s_{i, \beta } \leftarrow r_{i, \beta } + c \cdot \gamma \).
-
Set \(\pi _i \leftarrow (c, n_i, C_i, s_{i, \alpha }, s_{i, \beta })\).
-
-
(a)
-
6.
The host outputs
 .
.
Verify. The verify algorithm allows one to check whether a signature \(\sigma \) on message m with respect to basename \(\texttt {bsn}\), attribute disclosure (D, I), private key revocation list \(\texttt {RL} \), and signature revocation list \(\texttt {SRL} \) is valid.
-
1.
\(\mathcal {V}\) upon input
 verifies the signature:
verifies the signature:-
Parse \(\sigma \) as \((A', \texttt {nym}, \pi , \{\pi _i\})\).
-
Verify \(\pi \) with respect to \(A'\) and \(\texttt {nym}\):
-
Parse \(\pi \) as \((c, s_ gsk , \{s_{a_i}\}_{i \in \bar{D}}, s_e, s_a, s_b, n)\).
-
Set \(\hat{L} \leftarrow h_1^{s_ gsk } \cdot \texttt {nym}^{-c}\) and
$$\begin{aligned} \hat{t} \leftarrow e(A', g_2^{s_e} \cdot w^{-c}) e(h_0, g_2)^{s_b} e(h_1, g_2)^{s_ gsk }&e(h_0, w)^{s_a} \prod _{i \in \bar{D}} e(h_{i+1}, g_2)^{s_{a_i}} \\&\cdot {e(g_1,g_2)^c \prod _{i \in D}e(h_{i+1}, g_2)^{a_i \cdot c}} \end{aligned}$$ -
Check \(c = H(n, H(A', \texttt {nym}, t, L, g_1, h_0, \ldots , h_L, w), m, \texttt {bsn}, (D, I), \texttt {SRL})\).
-
-
For every \((\texttt {bsn}_i, \pi _i) \in \texttt {SRL} \):
-
Parse \(\pi _i\) as \((c, n_i, C_i, s_{i, \alpha }, s_{i, \beta })\).
-
Check \(C \ne 1_{\mathbb {G}_1}\).
-
Set \(\hat{t}_{i, 1} \leftarrow H(\texttt {bsn}_i)^{s_{i, \alpha }}\frac{1}{\texttt {nym}_i}^{s_{i, \beta }}\) and \(\hat{t}_{i, 2} \leftarrow H(\texttt {bsn})^{s_{i, \alpha }}\frac{1}{\texttt {nym}}^{s_{i, \beta }}\).
-
Check \(c = H(n_i, H(C, \texttt {bsn}_i, \texttt {bsn}, \texttt {nym}_i, \texttt {nym}, n, \hat{t}_{i, 1}, \hat{t}_{i, 2}))\).
-
-
If all tests pass, set \(f \leftarrow 1\), otherwise \(f \leftarrow 0\).
-
Output
 .
.
-
Link. The verify algorithm allows one to check whether two signatures \(\sigma , \sigma '\), on messages \(m, m'\) respectively, that were generated for the same basename \(\texttt {bsn}\) were created by the same TPM.
-
1.
\(\mathcal {V}\) upon input
 verifies the signatures and compares the pseudonyms contained in \(\sigma , \sigma '\):
verifies the signatures and compares the pseudonyms contained in \(\sigma , \sigma '\):-
Check that both signatures \(\sigma , \sigma '\) are valid with respect to \(m, \texttt {bsn}, p , \texttt {SRL} \) and \(m', \texttt {bsn}, p ', \texttt {SRL} '\) respectively. Output \(\bot \) if they are not both valid.
-
Parse the signatures as \((A', \texttt {nym}, \pi , \{\pi _i\}) \leftarrow \sigma \), \((A'', \texttt {nym}', \pi ', \{\pi _i'\})\leftarrow \sigma '\).
-
If \(\texttt {nym}= \texttt {nym}'\), set \(f \leftarrow 1\), otherwise \(f \leftarrow 0\).
-
Output
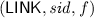 .
.
-
5.2 Comparison with Previous DAA Schemes
Our protocol is very similar to the most recent qSDH-based DAA schemes [13, 22, 25]. However, a few key changes were needed to achieve provable security and address the problems mentioned in Sect. 2. First, we use a BBS+ signature for the membership credential, instead of the simplified credential where the s-value is ommited as used in the recent schemes [13, 22, 25]. The BBS+ is proven to be unforgeable, and with this extra element, the proof of knowledge which is part of DAA signatures allows one to extract valid credentials, whereas in the most recent schemes one could not.
Compared to the most recent EPID scheme by Brickell and Li [14], we introduce a way to split the workload between a TPM and host, and add basenames steering linkability. The usage of basenames is required to prevent the TPM from serving as a static Diffie-Hellman oracle towards the host. For non-revocation proofs, the platform must prove that its pseudonym \(\texttt {nym}= B^{ gsk }\) is based on a different key than a pseudonym in a revoked signature \(\texttt {nym}' = B'^{ gsk '}\). A host proving the inequality of the keys with the help of a TPM using the method by Camenisch and Shoup will learn \(B'^{ gsk }\), for any \(B'\) of its choosing. By requiring basenames, i.e., \(B = H_1(\texttt {bsn})\), learning \(B'^{ gsk } = H_1(\texttt {bsn})^ gsk \) does not give a corrupt host any information, as in the random oracle model this can be simulated without knowing \( gsk \).
For the reason mentioned above, the fully anonymous option \(\texttt {bsn}= \bot \) from previous DAA schemes is not supported by our scheme, but we argue that this does not affect privacy: A platform can choose a fresh basename it only uses once to be fully anonymous. Any verifier that accepts fully anonymous signatures can simply accept signatures with respect to any basename.
Compared to the existing DAA-A scheme [25], we store all attributes except the secret key on the host for efficiency. This still guarantees unforgeability with an honest TPM and corrupt host. Anonymity is not affected either, as in either case, the host must be trusted for anonymity.
In Table 1 we compare the computational efficiency of our scheme with the other qSDH-based DAA schemes. In particular, we show the computational cost for the TPM in the sign algorithm, for the host in the sign algorithm, and for the verifier in the verify algorithm, as these are the algorithms that will be used frequently. We denote k exponentiations in group \(\mathbb {G}_i\) by \(k \mathbb {G}_i\), \(k \mathbb {G}_i^j\) denotes k j-multi-exponentiations, and kP denotes k pairing operations. Table 2 we compare the size of credentials and signatures with other DAA schemes. Here, \(k \mathbb {G}\) denotes the bits required to represent k elements of \(\mathbb {G}\), and H denotes the bit length of the hash output. CU15-1 denotes the LRSW-based DAA-A scheme by Chen and Urian [25], and CU15-2 the qSDH-based instantiation. We analyzed both schemes for signatures with only the secret key on the TPM, which is used to create a pseudonym, and all other attributes held by the host. We let L denote the amount of attributes, with D the amount of disclosed attributes and U the amount of undisclosed attributes. Revocation lists and revocation checks are omitted for these efficiency numbers. To compare this scheme with previous DAA schemes, we consider the efficiency without attributes, i.e., \(L = D = U = 0\). In computation, our scheme is as efficient as the scheme by Brickell and Li [13], which is currently the most efficient DAA scheme. Our credentials contain one extra element of \(\mathbb {Z} _p\) to achieve provable security. Signatures in our scheme are one element of \(\mathbb {G}_1\) smaller than signatures in the Brickell and Li scheme, which follows from the fact that we always use a basename, so we do not need to transmit the base for the computation of the pseudonym.
We stress that many of the listed schemes are not provably secure, whereas we rigorously prove our scheme secure.
6 Security Analysis
Theorem 2
The protocol  presented in Sect. 5 securely realizes
presented in Sect. 5 securely realizes  in the
in the  -hybrid model using random oracles and static corruptions, if the DL, DDH and JOC version of the qSDH assumptions hold, and the proofs-of-knowledge are online extractable.
-hybrid model using random oracles and static corruptions, if the DL, DDH and JOC version of the qSDH assumptions hold, and the proofs-of-knowledge are online extractable.
Due to space constraints, the proof is given in the full version of the paper [16].
7 Conclusion
DAA is one of the most complex cryptographic protocols deployed in practice. It is implemented in multiple platforms for trusted computing, including the Trusted Computing Group’s TPM and Intel’s SGX. A number of functional extensions to DAA have been proposed, including signature-based revocation and embedding of attributes. However, as we have shown in this paper, the security models and security proofs of the proposed DAA schemes based on the qSDH assumptions are not satisfactory. This includes the extended DAA schemes and the standardized DAA schemes. Bleichenbacher’s attack [5] on PKCS#1 demonstrates the importance of rigorous security proofs, in particular for cryptographic standards. It remains as future work, to revisit the concerned standards to eliminate the schemes’ flaws and ensure that they are provably secure.
As a first step towards this, we have in this paper proposed a new DAA scheme with support for attributes and signature-based revocation. Our scheme is as efficient as the most efficient existing DAA scheme. While the existing schemes do not have valid security proofs, our scheme is proven secure in the model by Camenisch et al. [15], extended to support attributes and signature-based revocation. As a side result, we have proven the BBS+ signature scheme to be secure in type-3 pairing settings, meaning our scheme can be used with the most efficient pairing-friendly elliptic curve groups.
References
Au, M.H., Susilo, W., Mu, Y.: Constant-size dynamic k-TAA. In: Prisco, R., Yung, M. (eds.) SCN 2006. LNCS, vol. 4116, pp. 111–125. Springer, Heidelberg (2006)
Barreto, P.S.L.M., Naehrig, M.: Pairing-friendly elliptic curves of prime order. In: Preneel, B., Tavares, S. (eds.) SAC 2005. LNCS, vol. 3897, pp. 319–331. Springer, Heidelberg (2006)
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: CCS 1993 (1993)
Bernhard, D., Fuchsbauer, G., Ghadafi, E., Smart, N.P., Warinschi, B.: Anonymous attestation with user-controlled linkability. Int. J. Inf. Secur. 12(3), 219–249 (2013)
Bleichenbacher, D.: Chosen ciphertext attacks against protocols based on the RSA encryption standard PKCS #1. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 1–12. Springer, Heidelberg (1998)
Boneh, D., Boyen, X.: Short signatures without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 56–73. Springer, Heidelberg (2004)
Boneh, D., Boyen, X.: Short signatures without random oracles and the SDH assumption in bilinear groups. J. Cryptology 21(2), 149–177 (2007)
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004)
Brickell, E., Camenisch, J., Chen, L.: Direct anonymous attestation. In: CCS 2004 (2004)
Brickell, E., Chen, L., Li, J.: A new direct anonymous attestation scheme from bilinear maps. In: Lipp, P., Sadeghi, A.-R., Koch, K.-M. (eds.) Trust 2008. LNCS, vol. 4968, pp. 166–178. Springer, Heidelberg (2008)
Brickell, E., Chen, L., Li, J.: Simplified security notions of direct anonymous attestation and a concrete scheme from pairings. Int. J. Inf. Secur. 8(5), 315–330 (2009)
Brickell, E., Li, J.: Enhanced privacy ID: a direct anonymous attestation scheme with enhanced revocation capabilities. In: WPES 2007 (2007)
Brickell, E., Li, J.: A pairing-based DAA scheme further reducing TPM resources. Cryptology ePrint Archive, Report 2010/067 (2010)
Brickell, E., Li, J.: Enhanced privacy ID from bilinear pairing for hardware authentication and attestation. Int. J. Inf. Priv. Secur. Integrity 1(1), 3–33 (2011)
Camenisch, J., Drijvers, M., Lehmann, A.: Universally composable direct anonymous attestation. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9615, pp. 234–264. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49387-8_10
Camenisch, J., Drijvers, M., Lehmann, A.: Anonymous Attestation Using the Strong Diffie Hellman Assumption Revisited. Cryptology ePrint Archive, Report 2016/663 (2016)
Camenisch, J., Kiayias, A., Yung, M.: On the portability of generalized schnorr proofs. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 425–442. Springer, Heidelberg (2009)
Camenisch, J.L., Shoup, V.: Practical verifiable encryption and decryption of discrete logarithms. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 126–144. Springer, Heidelberg (2003)
Camenisch, J.L., Stadler, M.A.: Efficient group signature schemes for large groups. In: Kaliski Jr., B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 410–424. Springer, Heidelberg (1997)
Canetti, R.: Universally composable signature, certification, and authentication. In: Computer Security Foundations Workshop (2004)
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. Cryptology ePrint Archive, Report 2000/067 (2000)
Chen, L.: A DAA scheme requiring less TPM resources. In: Bao, F., Yung, M., Lin, D., Jing, J. (eds.) Inscrypt 2009. LNCS, vol. 6151, pp. 350–365. Springer, Heidelberg (2010)
Chen, L., Morrissey, P., Smart, N.P.: Pairings in trusted computing. In: Galbraith, S.D., Paterson, K.G. (eds.) Pairing 2008. LNCS, vol. 5209, pp. 1–17. Springer, Heidelberg (2008)
Chen, L., Page, D., Smart, N.P.: On the design and implementation of an efficient DAA scheme. In: Gollmann, D., Lanet, J.-L., Iguchi-Cartigny, J. (eds.) CARDIS 2010. LNCS, vol. 6035, pp. 223–237. Springer, Heidelberg (2010)
Chen, L., Urian, R.: DAA-A: direct anonymous attestation with attributes. In: Conti, M., Schunter, M., Askoxylakis, I. (eds.) TRUST 2015. LNCS, vol. 9229, pp. 228–245. Springer, Heidelberg (2015)
Chen, X., Feng, D.: Direct anonymous attestation for next generation TPM. J. Comput. 3(12), 43–50 (2008)
Costan, V., Devadas, S.: Intel SGX explained. Cryptology ePrint Archive, Report 2016/086 (2016)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987)
Galbraith, S.D., Paterson, K.G., Smart, N.P.: Pairings for cryptographers. Discrete Appl. Math. 156(16), 3113–3121 (2008)
International Organization for Standardization. ISO/IEC 20008: Information technology - Security techniques - Anonymous digital signatures (2013)
International Organization for Standardization. ISO/IEC 11889: Information technology - Trusted platform module library (2015)
Lysyanskaya, A., Rivest, R.L., Sahai, A., Wolf, S.: Pseudonym systems (Extended Abstract). In: Heys, H.M., Adams, C.M. (eds.) SAC 1999. LNCS, vol. 1758, pp. 184–199. Springer, Heidelberg (2000)
Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 223–238. Springer, Heidelberg (1999)
Trusted Computing Group: TPM main specification version 1.2 (2004)
Trusted Computing Group. TPM library specification, family “2.0” (2014)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Camenisch, J., Drijvers, M., Lehmann, A. (2016). Anonymous Attestation Using the Strong Diffie Hellman Assumption Revisited. In: Franz, M., Papadimitratos, P. (eds) Trust and Trustworthy Computing. Trust 2016. Lecture Notes in Computer Science(), vol 9824. Springer, Cham. https://doi.org/10.1007/978-3-319-45572-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-45572-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-45571-6
Online ISBN: 978-3-319-45572-3
eBook Packages: Computer ScienceComputer Science (R0)






 . (The roman numbers are labels for the different checks made within the functionality and will be used as references in the analysis of the functionality and the proof.)
. (The roman numbers are labels for the different checks made within the functionality and will be used as references in the analysis of the functionality and the proof.)



 ,
,  ,
,  and compute
and compute 
 generates his key pair:
generates his key pair: and set
and set  . Initiate
. Initiate  .
. , and store the secret key x.
, and store the secret key x. .
. parses
parses  over
over  from a party
from a party  and sends (sid, jsid, n) back to
and sends (sid, jsid, n) back to  and store the key as
and store the key as  .
. .
. to the issuer, it appends its own identity in the unauthenticated part of the message and forwards the full message to the issuer. It also keeps state as
to the issuer, it appends its own identity in the unauthenticated part of the message and forwards the full message to the issuer. It also keeps state as  , it verifies
, it verifies  . It stores
. It stores  .
. generates the BBS+ credential:
generates the BBS+ credential: .
. .
. .
.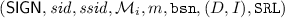 checks whether his attributes fulfill the predicate and randomizes the BBS+ credential:
checks whether his attributes fulfill the predicate and randomizes the BBS+ credential: and set
and set  .
. computes the pseudonym
computes the pseudonym 
 and compute
and compute  , and
, and  .
.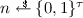 .
. and compute
and compute  and set
and set  and set
and set  and compute
and compute  .
. verifies the signature:
verifies the signature: .
. verifies the signatures and compares the pseudonyms contained in
verifies the signatures and compares the pseudonyms contained in 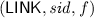 .
.