Abstract
We present an identity-Based encryption (IBE) scheme that is group homomorphic for addition modulo a “large” (i.e. superpolynomial) integer, the first such group homomorphic IBE. Our first result is the construction of an IBE scheme supporting homomorphic addition modulo a poly-sized prime e. Our construction builds upon the IBE scheme of Boneh, LaVigne and Sabin (BLS). BLS relies on a hash function that maps identities to \(e^{\text {th}}\) residues. However there is no known way to securely instantiate such a function. Our construction extends BLS so that it can use a hash function that can be securely instantiated. We prove our scheme  secure under the (slightly modified) \(e^{\text {th}}\) residuosity assumption in the random oracle model and show that it supports a (modular) additive homomorphism. By using multiple instances of the scheme with distinct primes and leveraging the Chinese Remainder Theorem, we can support homomorphic addition modulo a “large” (i.e. superpolynomial) integer. We also show that our scheme for \(e > 2\) is anonymous by additionally assuming the hardness of deciding solvability of a special system of multivariate polynomial equations. We provide a justification for this assumption by considering known attacks.
secure under the (slightly modified) \(e^{\text {th}}\) residuosity assumption in the random oracle model and show that it supports a (modular) additive homomorphism. By using multiple instances of the scheme with distinct primes and leveraging the Chinese Remainder Theorem, we can support homomorphic addition modulo a “large” (i.e. superpolynomial) integer. We also show that our scheme for \(e > 2\) is anonymous by additionally assuming the hardness of deciding solvability of a special system of multivariate polynomial equations. We provide a justification for this assumption by considering known attacks.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Identity-Based Encryption (IBE), first proposed by Shamir [1], and first constructed by Boneh and Franklin [2] (based on bilinear pairings) and Cocks [3] (based on quadratic residuosity), is centered around the notion that a user’s public key can be efficiently derived from an identity string and system-wide public parameters. The public parameters are chosen by a Trusted Authority (TA) along with a master secret key, which is used to extract secret keys for user identities. In this work, we present an IBE that is group homomorphic for addition modulo a smooth square-free integer. An encryption scheme is said to be group homomorphic if its decryption algorithm is a group homomorphism (known as Group Homomorphic Encryption (GHE) [4]). Although GHE only permits evaluation of a single algebraic operation, it is a very powerful primitive for the following reasons:
-
1.
It is used as a building block in protocols for Private Information Retrieval [5], Electronic Voting [6,7,8,9,10], Oblivious Polynomial Evaluation [11], Private Outsourced Computation [12] and the Millionaire’s Problem [13].
-
2.
Fully Homomorphic Encryption (FHE) is currently impractical for many applications, and even if it were to become more practical, it may add unnecessary overhead, especially in applications that only require a single algebraic operation.
GHE is the “classical” flavor of homomorphic encryption. It allows unbounded applications of the group operation. Goldwasser and Micali [14] constructed the first GHE scheme. The Goldwasser-Micali (GM) cryptosystem supports addition modulo 2 i.e. the XOR operation. Other additively-homomorphic GHE schemes from the literature include Benaloh [6], Naccache-Stern [15], Okamoto-Uchiyama [16], Paillier [17] and Damgård-Jurik [10]. Other instances of GHE include [18,19,20].
Existing identity-based GHE (IBGHE) schemes such as those based on pairings are typically multiplicatively homomorphic. It is a well-known that a scheme with a multiplicative homomorphism can be transformed into one with an additive homomorphism, where the addition takes place in the exponent, and a discrete logarithm problem must be solved to recover the result. In this case, we usually get a bounded (aka “quasi”) additively homomorphic scheme, but it is not group homomorphic in the sense of the definition considered in this paper since one cannot perform an unbounded number of homomorphic operations. However, to the best of our knowledge, the only existing “pure” (i.e. supporting modular addition) additively-homomorphic instance of IBGHE in the literature is the variant of the Cocks scheme due to Clear, Hughes and Tewari [21] that is XOR-homomorphic i.e. it supports addition modulo 2. Applications of IBGHE are explored in [21] but can be extended to private information retrieval (PIR) [22] (instantiating the protocol from [5] with an IBGHE scheme instead of a public-key GHE scheme), data aggregation in wireless sensor networks (IBE has been applied to wireless sensor networks already in [23,24,25,26]) and participatory sensing (Günther et al. [27] use additively homomorphic IBE for data aggregation in a participatory sensing system).
1.1 Our Results
Our main contribution is the construction of an IBGHE for addition modulo a poly-sized prime e. Our construction builds on the IBE scheme of Boneh, LaVigne and Sabin (BLS) [28], which uses a hash function that maps identities to \(e^{\text {th}}\) residues; there is no known way to securely instantiate such a function. We extend BLS so that it uses a hash function that can be securely instantiated. We prove our scheme  secure under a (slightly modified) \(e^{\text {th}}\) residuosity assumption in the random oracle model. Indeed this is the same assumption that BLS is proved secure under. We then show that our scheme supports homomorphic addition modulo a poly-sized prime e and prove that it satisfies the properties of an IBGHE.
secure under a (slightly modified) \(e^{\text {th}}\) residuosity assumption in the random oracle model. Indeed this is the same assumption that BLS is proved secure under. We then show that our scheme supports homomorphic addition modulo a poly-sized prime e and prove that it satisfies the properties of an IBGHE.
Our second contribution is to use multiple instances of the scheme with distinct primes and to leverage the Chinese Remainder Theorem to support homomorphic addition modulo a “large” (i.e. superpolynomial) integer, the first such IBE scheme supporting an unbounded number of operationsFootnote 1, solving an open problem mentioned in [21]. Below we consider the advantages of a scheme that supports homomorphic addition with such a “large” range.
Our third contribution is to show that our scheme for \(e > 2\) is anonymous by additionally assuming the hardness of deciding solvability of a special system of multivariate polynomial equations. We investigate this problem from a cryptanalytic perspective and provide justification in light of known attacks for assuming its hardness.
1.2 Practicality and Applications
While the space complexity of ciphertexts in our scheme is high, requiring \(e^2\) group elements, there are contexts where it may be of import, which we now discuss.
Pairings-based IBE schemes that support an additive homomorphism in the exponent rely on Pollard’s lambda algorithm to extract the result. Let B be a bound on the result. Pollard’s lambda algorithm has time complexity of \(O(\sqrt{B})\). Suppose we require B to be exponentially large. The runtime for extracting the result with Pollard’s lambda algorithm is exponential for such B. In contrast, our CRT scheme gives polynomial running time for this case. We also compare with LWE-based IBE schemes. The GPV scheme [29] is perhaps the simplest LWE-based IBE scheme and its security is also proved in the random oracle model. We consider a comparison for 80 bits of security and \(B = 2^{80}\). We used the estimator of Albrecht, Player and Scott [30] to derive suitable parameters for LWE for an instantiation of GPV. For 80 bits of security and \(B = 2^{80}\), the size of a ciphertext in GPV (modified to support an additive homomorphism with bound B) is approximately the same as ours (of the order of 3 MB). Our scheme however has significantly smaller public parameters - by a factor of several thousand but has considerably worse running time for encryption, decryption and evaluation.
An example real-world application is that of data aggregation, a common practice in Machine Learning and related fields. Günther et al. [27] use additively homomorphic IBE for data aggregation in participatory sensing. A bound of \(2^{80}\) might be required if the data were real numbers with high precision requirements, which can be represented as integers in fixed point form.
2 Preliminaries
2.1 Notation
A quantity is said to be negligible with respect to some parameter \(\lambda \), written \(\mathsf {negl}(\lambda )\), if it is asymptotically bounded from above by the reciprocal of all polynomials in \(\lambda \).
For a probability distribution D, we denote by \(x \xleftarrow {\$}D\) that x is sampled according to D. If S is a set, \(y \xleftarrow {\$}S\) denotes that y is sampled from x according to the uniform distribution on S.
The support of a predicate \(f : A \rightarrow \{0, 1\}\) for some domain A is denoted by \(\mathsf {supp}(f)\), and is defined by the set \(\{a \in A : f(a) = 1\}\).
The set of contiguous integers \(\{1, \ldots , k\}\) for some \(k > 1\) is denoted by [k].
2.2 Identity Based Encryption
Definition 1
An Identity Based Encryption (IBE) scheme is a tuple of PPT algorithms (G, K, E, D) defined with respect to a message space \(\mathcal {M}\), an identity space \(\mathcal {I}\) and a ciphertext space \(\hat{\mathcal {C}}\) as follows:
-
 :
:On input (in unary) a security parameter \(\lambda \), generate public parameters \(\mathsf {PP}\) and a master secret key \(\mathsf {MSK}\). Output \((\mathsf {PP}, \mathsf {MSK})\).
-
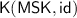 :
:On input master secret key \(\mathsf {MSK}\) and an identity \(\mathsf {id} \in \mathcal {I}\): derive and output a secret key \(\mathsf {sk}_{\mathsf {id}}\) for identity \(\mathsf {id}\).
-
 :
:On input public parameters \(\mathsf {PP}\), an identity \(\mathsf {id} \in \mathcal {I}\), and a message \(m \in \mathcal {M}\), output a ciphertext \(c \in \mathcal {C}\subseteq \hat{\mathcal {C}}\) that encrypts m under identity \(\mathsf {id}\).
-
 :
:On input a secret key \(\mathsf {sk}_{\mathsf {id}}\) for identity \(\mathsf {id} \in \mathcal {I}\) and a ciphertext \(c \in \hat{\mathcal {C}}\), output \(m^\prime \) if c is a valid encryption under identity \(\mathsf {id}\); output a failure symbol \(\bot \) otherwise.
2.3 Public-Key GHE
An important subclass of partial homomorphic encryption is the class of public-key encryption schemes that admit a group homomorphism between their ciphertext space and plaintext space. This class corresponds to what is considered “classical” HE [4], where a single group operation is supported, most usually addition. Gjøsteen [18] examined the abstract structure of these cryptosystems in terms of groups, and characterized their security as relying on the hardness of a subgroup membership problem. Armknecht, Katzenbeisser and Peter [4] rigorously formalized the notion, and called it group homomorphic encryption (GHE). We recap with the formal definition of GHE by Armknecht, Katzenbeisser and Peter [4].
Definition 2
(GHE, Definition 1 in [4]). A public-key encryption scheme \(\mathcal {E} = (G, E, D)\) is called group homomorphic, if for every \((\mathsf {pk}, \mathsf {sk}) \leftarrow G(1^\lambda )\), the plaintext space \(\mathcal {M}\) and the ciphertext space \(\hat{\mathcal {C}}\) (written in multiplicative notation) are non-trivial groups such that
-
the set of all encryptions \(\mathcal {C}:= \{c \in \hat{\mathcal {C}} \mid c \leftarrow E_\mathsf {pk}(m), m \in \mathcal {M}\}\) is a non-trivial subgroup of \(\hat{\mathcal {C}}\)
-
the restricted decryption \(D_{\mathsf {sk}}^*:= D_{\mathsf {sk} | \mathcal {C}}\) is a group epimorphism (surjective homomorphism) i.e.
$$\begin{aligned} D_{\mathsf {sk}}^*\text { is surjective and } \forall c, c^\prime \in \mathcal {C}\; : \; D_{\mathsf {sk}}(c \cdot c^\prime ) = D_{\mathsf {sk}}(c) \cdot D_{\mathsf {sk}}(c^\prime ) \end{aligned}$$ -
\(\mathsf {sk}\) contains an efficient decision function \(\delta : \hat{\mathcal {C}} \rightarrow \{0, 1\}\) such that
$$\begin{aligned} \delta (c) = 1 \iff c \in \mathcal {C}\end{aligned}$$ -
the decryption on \(\hat{\mathcal {C}} \setminus \mathcal {C}\) returns the symbol \(\bot \).
2.4 Identity-Based Group Homomorphic Encryption (IBGHE)
Definition 3
(Identity Based Group Homomorphic Encryption (IBGHE), Based on [21]). Let \(\mathcal {E} = (G, K, E, D)\) be an IBE scheme with message space \(\mathcal {M}\), identity space \(\mathcal {I}\) and ciphertext space \(\widehat{\mathcal {C}}\). The scheme \(\mathcal {E}\) is group homomorphic if for every \((\mathsf {PP}, \mathsf {MSK}) \leftarrow G(1^\lambda )\), every \(\mathsf {id} \in \mathcal {I}\), and every \(\mathsf {sk}_{\mathsf {id}} \leftarrow K(\mathsf {MSK}, \mathsf {id})\), the message space \((\mathcal {M}, \cdot )\) is a non-trivial group, and there is a binary operation \(*: \widehat{\mathcal {C}}^2 \rightarrow \widehat{\mathcal {C}}\) such that the following properties are satisfied for the restricted ciphertext space \(\widehat{\mathcal {C}_{\mathsf {id}}} = \{c \in \widehat{\mathcal {C}} : D_{\mathsf {sk}_{\mathsf {id}}}(c) \ne \bot \}\):
-
GH.1: The set of all encryptions \(\mathcal {C}_{\mathsf {id}} = \{c \mid c \leftarrow E(\mathsf {PP}, \mathsf {id}, m), m \in \mathcal {M}\} \subseteq \widehat{\mathcal {C}_{\mathsf {id}}}\) is a non-trivial group with respect to the operation \(*\).
-
GH.2: The restricted decryption \(D_{\mathsf {sk}_{\mathsf {id}}}^*:= D_{\mathsf {sk}_{\mathsf {id}} | \mathcal {C}_{\mathsf {id}}}\) is surjective and \(\forall c, c^\prime \in \mathcal {C}_{\mathsf {id}} \quad D_{\mathsf {sk}_{\mathsf {id}}}(c *c^\prime ) = D_{\mathsf {sk}_{\mathsf {id}}}(c) \cdot D_{\mathsf {sk}_{\mathsf {id}}}(c^\prime )\).
We are interested in schemes whose plaintext space forms a group and which allow that operation to be homomorphically applied an unbounded number of times. There exist schemes however that do not satisfy all the requirements of GHE, namely their ciphertext space does not form a group but instead forms a quasigroup (a group without associativity). We can define what we call Quasigroup Homomorphic Encryption (QHE) analogously to Definition 2 by replacing the term ‘group’ with ‘quasigroup’ in the definition. An example of such a scheme is the Cocks’ IBE [3], which was shown to be inherently XOR-homomorphic by Joye [31].
2.5 \(e^{\text {th}}\) Residuosity
An integer x is said to be a quadratic residue modulo an integer m if x is congruent to a square modulo m. We denote the set of quadratic residues modulo p as \(\mathbb {QR}(m)\). The Legendre symbol of an integer x modulo a prime p is defined as
The Jacobi symbol generalizes the Legendre symbol to composite moduli. For a composite modulus \(m = p_1^{a_1} \cdots p_n^{a_n}\), it is defined as
We now generalize quadratic residues to \(e^{\text {th}}\) power residues. We define the \(e^{\text {th}}\) power residue symbol as follows:
Definition 4
(Based on Definition 4.1 in [32]). Let \(e \ge 2\) be an integer, and let \(\zeta _e \in \bar{\mathbb {Q}}\) be a primitive \(e^{\text {th}}\) root of unity (note that \(\bar{\mathbb {Q}}\) is the algebraic closure of \(\mathbb {Q}\)). Let K be the number field \(\mathbb {Q}(\zeta _e)\), and let \(\mathcal {O}_K = \mathbb {Z}[\zeta _e]\) be the ring of integers in K. Let \(\mathfrak {p}\) be a prime ideal of \(\mathcal {O}_K\) that does not contain e. For \(x \in \mathcal {O}_K\), the \(e^{\text {th}}\) power residue symbol of \(x \text { mod }{\mathfrak {p}}\), denoted \(\genfrac(){}0{x}{\mathfrak {p}}_e\) is defined as
where i is the unique integer modulo e such that \(\zeta _e^i \equiv x^{(\mathcal {N}(\mathfrak {p}) - 1)/e} \pmod {\mathfrak {p}}\) and \(\mathcal {N}(\mathfrak {p})\) is the norm of \(\mathfrak {p}\).
If \(\mathfrak {a}\) is an ideal that factors as \(\mathfrak {a} = \mathfrak {p_1}^{k_1} \cdots \mathfrak {p_n}^{k_n}\) where \(\mathfrak {p_1}, \ldots , \mathfrak {p_n}\) are prime ideals, then \(\genfrac(){}0{x}{\mathfrak {a}}_e\) is defined as
Let \(e \ge 2\) be an integer. Let N be a positive integer. An integer \(x \in \mathbb {Z}_N^*\) is said to be an \(e^{\text {th}}\) residue modulo N if there is an integer \(y \in \mathbb {Z}_N^*\) such that \(y^e \equiv x \text { mod }{N}\). We denote the set of \(e^{\text {th}}\) residues in \(\mathbb {Z}_N^*\) by \(\mathbb {ER}(N)\). A superset of \(\mathbb {ER}(N)\) is the set of integers in \(\mathbb {Z}_N^*\) with a power residue symbol of 1, which we denote as \(\mathbb {PR}(N)\).
Definition 5
(\(e^{\text {th}}\) Residuosity (ER) Assumption). For a PPT algorithm  that generates two equally sized primes p and q, the \(e^{\text {th}}\) residuosity assumption is that the following two distributions are computationally indistinguishableFootnote 2
that generates two equally sized primes p and q, the \(e^{\text {th}}\) residuosity assumption is that the following two distributions are computationally indistinguishableFootnote 2


Let \(N = pq\) be a product of two primes p and q with \(p \equiv q \equiv 1 \text { mod }{e}\). An \(e^{\text {th}}\) root of unity in \(\mathbb {Z}_N\) is an integer \(\mu \) such that \(\mu ^e \equiv 1 \text { mod }{N}\). The trivial root of unity is 1. A root of unity \(\mu \) is said to be degenerate if either \(\mu \equiv 1 \text { mod }{p}\) or \(\mu \equiv 1 \text { mod }{q}\) since given such a \(\mu \) one can trivially learn the factorization of N. For one of the schemes in this work, it is necessary to publish a nontrivial, non-degenerate root of unity as part of the public parameters. This is in order to compute the \(e^{\text {th}}\) power residue symbol which is needed for the scheme. It is believed that revealing such a root of unity does not make factorization of N easier, but nevertheless it serves as additional information for the adversary, and therefore must be made explicit in the assumption we use for security. Hence, we follow [28] and modify the ER assumption to incorporate this information.
Definition 6
(Modified \(e^{\text {th}}\) Residuosity (MER) Assumption, [28]). Let \(\mathcal {Z}\) be the set of nontrivial, non-degenerate roots of unity in \(\mathbb {Z}_N\). For a PPT algorithm  that generates two equally sized primes p and q, the modified \(e^{\text {th}}\) residuosity assumption is that the following two distributions are computationally indistinguishable
that generates two equally sized primes p and q, the modified \(e^{\text {th}}\) residuosity assumption is that the following two distributions are computationally indistinguishable


3 Our Additively Homomorphic IBE
Boneh, LaVigne and Sabin [28] presented an IBE scheme whose security relies on the MER assumption. However, their scheme uses a hash function that maps identity strings to \(e^{\text {th}}\) residues in \(\mathbb {Z}_N\). It is not known how such a function can be instantiated without compromising security. We extend their construction so that it uses a hash function that can be instantiated. We then prove our construction secure under the MER assumption in the random oracle model. We show that the construction is group homomorphic for the additive group \((\mathbb {Z}_e, +)\) for prime e i.e. we show it meets the criteria for IBGHE. This is the only additively group-homomorphic IBE we are aware of with a message space larger than 2 elements. First, we need to introduce some functions that are used by the scheme along with an overview on how \(e^{\text {th}}\) power residue symbols are computed for integers in \(\mathbb {Z}_N\).
3.1 \(e^{\text {th}}\) Power Residue Symbols in \(\mathbb {Z}_N\)
Let \(e \ge 2\) be an integer. Let \(N = pq\) be a product of two primes p and q with \(p \equiv q \equiv 1 \text { mod }{e}\). The symbol \(\genfrac(){}0{x}{N}_e\) for integers x is always 1 for odd e and \(\pm 1\) for even e, so for \(e > 2\), we need to find a way to extract more information about x so we can map it to one of e symbols. We follow the approach taken in [32].
Let \(\zeta _e\) and K be as defined in Definition 4. Note that we can take K to be \(\mathbb {Q}[x]/\varPhi _e(x)\) where \(\varPhi _e(x)\) is the \(e^{\text {th}}\) cyclotomic polynomial; accordingly, we have \(\zeta _e = x\). Given p and q, we can compute an element \(\mu \in \mathbb {Z}_N^*\) that is a primitive root of unity modulo p and modulo q. In schemes described later, we require that \(\mu \) be published as part of the public parameters. For a fixed \(\mu \), we define the ideal \(\mathfrak {N} = N\mathcal {O}_K + (\zeta _e - \mu )\mathcal {O}_K\). Let \(\mu _p = \mu \text { mod }{p}\) and \(\mu _q = \mu \text { mod }{q}\). We also define the ideals \(\mathfrak {p} = p\mathcal {O}_K + (\zeta _e - \mu _p)\mathcal {O}_K\) and \(\mathfrak {q} = q\mathcal {O}_K + (\zeta _e - \mu _q)\mathcal {O}_K\). It holds that \(\mathfrak {N} = \mathfrak {p}\mathfrak {q}\). Squirrel [33] gives a polynomial time algorithm for computing the \(e^{\text {th}}\) residue symbol \(\genfrac(){}0{x}{\mathfrak {a}}_e\) for any \(x \in \mathcal {O}_K\) and any ideal in \(\mathcal {O}_K\) (such as \(\mathfrak {N}\) for example). It is an interesting problem for future work to find a more efficient algorithm tailored to the ideal \(\mathfrak {N}\).
Furthermore, we define a function \(J_N : \mathbb {Z}_N \rightarrow \{0, \ldots , e - 1\}\) as follows
Additionally, we define \(J_p\) analogous to \(J_N\) except with ideal \(\mathfrak {p}\) and modulus p, and similarly, we define \(J_q\) using ideal \(\mathfrak {q}\) and modulus q. When an integer x is an \(e^{\text {th}}\) power residue modulo N, we have \(J_N(x) = 0\). We establish some important properties:
-
$$\begin{aligned} J_N(x) \equiv J_p(x) + J_q(x) \quad \text { mod }{e} \quad \forall x \in \mathbb {Z}_N \end{aligned}$$(3.1)
-
Homomorphic property
$$\begin{aligned} J_N(xy) \equiv J_N(x) + J_N(y) \quad \text { mod }{e} \quad \forall x, y \in \mathbb {Z}_N^*\end{aligned}$$(3.2)
The homomorphic property is also satisfied by \(J_p\) and \(J_q\).
3.2 Boneh, LaVigne and Sabin (BLS) Scheme
We now describe the BLS scheme. While the scheme is described as an IBE in [28], as aforementioned, there is no efficient means to securely realize the hash function it depends onFootnote 3. We present it here as a public-key scheme, and in fact the security proof in [28] treats it as such.
The scheme is parameterized by a prime e. Note the scheme employs the function \(J_N\) which implicitly uses the root of unity \(\mu \) published in the public key.
-
 : Generate two RSA primes p and q with \(e|p - 1\) and \(e|q-1\) and let \(N = pq\). Uniformly choose a nontrivial, nondegenerate root of unity \(\mu \in \mathbb {Z}_N\). Uniformly sample an integer \(r \xleftarrow {\$}\mathbb {Z}_N^*\) and set \(v \leftarrow r^e \text { mod }{N}\). Output \((\mathsf {pk} := (N, \mu , v), \mathsf {sk} := r)\).
: Generate two RSA primes p and q with \(e|p - 1\) and \(e|q-1\) and let \(N = pq\). Uniformly choose a nontrivial, nondegenerate root of unity \(\mu \in \mathbb {Z}_N\). Uniformly sample an integer \(r \xleftarrow {\$}\mathbb {Z}_N^*\) and set \(v \leftarrow r^e \text { mod }{N}\). Output \((\mathsf {pk} := (N, \mu , v), \mathsf {sk} := r)\). -
 : Given public key \(\mathsf {pk} := (N, \mu , v)\) and message \(m \in \{0, \ldots , e - 1\}\), perform the following steps. Generate a uniformly random polynomial \(f(x) \xleftarrow {\$}\mathbb {Z}_N^*[x]\) of degree \(e - 1\) and compute \(g(x) \leftarrow f(x)^e \text { mod }{x^e - v}\). Choose a uniformly random \(t \xleftarrow {\$}\mathbb {Z}_N^*\) and compute the polynomial \(c(x) \leftarrow \frac{g(x)}{t}\). Output \(\mathsf {CT} := (c(x), d := m + J_N(t) \text { mod }{e})\).
: Given public key \(\mathsf {pk} := (N, \mu , v)\) and message \(m \in \{0, \ldots , e - 1\}\), perform the following steps. Generate a uniformly random polynomial \(f(x) \xleftarrow {\$}\mathbb {Z}_N^*[x]\) of degree \(e - 1\) and compute \(g(x) \leftarrow f(x)^e \text { mod }{x^e - v}\). Choose a uniformly random \(t \xleftarrow {\$}\mathbb {Z}_N^*\) and compute the polynomial \(c(x) \leftarrow \frac{g(x)}{t}\). Output \(\mathsf {CT} := (c(x), d := m + J_N(t) \text { mod }{e})\). -
 : Given secret key \(\mathsf {sk} := r\) and ciphertext \(\mathsf {CT} := (c(x), d)\), output \(d + J_N(c(r)) \text { mod }{e}\).
: Given secret key \(\mathsf {sk} := r\) and ciphertext \(\mathsf {CT} := (c(x), d)\), output \(d + J_N(c(r)) \text { mod }{e}\).
BLS is proven semantically secure under the MER assumption in the standard model.
3.3 Our Construction
Our approach to circumventing the uninstantiability of the hash function employed in the IBE-version of BLS is akin to the original Cocks scheme. As part of the public parameters, we publish \(e - 1\) \(e^{\text {th}}\) non-residues (with \(J_N(x) = 0\) for all non-residues x). Then for any integer a satisfying \(J(a) = 0\), either a is an \(e^{\text {th}}\) residue or its product with one of the \(e - 1\) non-residues is an \(e^{\text {th}}\) residue. We also make some simplifications to BLS such as removing an element of \(\mathbb {Z}_e\) from the ciphertext. We assume a hash function \(H : \{0, 1\}^*\rightarrow \{x \in \mathbb {Z}_N : J_N(x) = 0\}\) that maps identity strings to elements of \(x \in \mathbb {Z}_N\) with \(J_N(x) = 0\) (i.e. the power residue symbol of the element is 1).
The scheme is parameterized with a prime e. We make use of the functions \(J_N\) and \(J_p\) defined earlier which implicitly use a root of unity \(\mu \) published in the public parameters.
Remark 1
We sometimes omit “mod N” for ease of presentation. This is particularly the case for products involving the elements \(\alpha _i\) (as described below) to avoid clutter.
-
 : Generate two RSA primes p and q with \(e|p - 1\) and \(e|q-1\) and let \(N = pq\). Sample uniformly an element \(\gamma \xleftarrow {\$}\mathbb {Z}_N^*\) with \(J_N(\gamma ) = 0\) and \(J_p(\gamma ) \ne 0\). For every \(i \in [e]\), set \(\alpha _i \leftarrow \gamma ^{i - 1} \text { mod }{N}\). Uniformly choose a nontrivial, nondegenerate root of unity \(\mu \in \mathbb {Z}_N\). Output \(\mathsf {PP} := (N, \mu , \alpha _1, \ldots , \alpha _e)\) and \(\mathsf {MSK} := (p, q, \alpha _1, \ldots \alpha _e)\).
: Generate two RSA primes p and q with \(e|p - 1\) and \(e|q-1\) and let \(N = pq\). Sample uniformly an element \(\gamma \xleftarrow {\$}\mathbb {Z}_N^*\) with \(J_N(\gamma ) = 0\) and \(J_p(\gamma ) \ne 0\). For every \(i \in [e]\), set \(\alpha _i \leftarrow \gamma ^{i - 1} \text { mod }{N}\). Uniformly choose a nontrivial, nondegenerate root of unity \(\mu \in \mathbb {Z}_N\). Output \(\mathsf {PP} := (N, \mu , \alpha _1, \ldots , \alpha _e)\) and \(\mathsf {MSK} := (p, q, \alpha _1, \ldots \alpha _e)\). -
 : Given master secret key \(\mathsf {MSK} := (p, q, \alpha _1, \ldots , \alpha _e)\) and an identity string \(\mathsf {id} \in \{0, 1\}^*\), compute \(a \leftarrow H(\mathsf {id})\). Check which of \(\alpha _1 \cdot a, \ldots , \alpha _e \cdot a\) is an \(e^{\text {th}}\) residue and let the index in the list be i. Then compute the \(e^{\text {th}}\) root of \(\alpha _i \cdot a\) using p and q; denote this root by r. Output \(\mathsf {sk}_{\mathsf {id}} = (i, r)\).
: Given master secret key \(\mathsf {MSK} := (p, q, \alpha _1, \ldots , \alpha _e)\) and an identity string \(\mathsf {id} \in \{0, 1\}^*\), compute \(a \leftarrow H(\mathsf {id})\). Check which of \(\alpha _1 \cdot a, \ldots , \alpha _e \cdot a\) is an \(e^{\text {th}}\) residue and let the index in the list be i. Then compute the \(e^{\text {th}}\) root of \(\alpha _i \cdot a\) using p and q; denote this root by r. Output \(\mathsf {sk}_{\mathsf {id}} = (i, r)\). -
 : Given public parameters \(\mathsf {PP} := (N, \mu , \alpha _1, \ldots , \alpha _e)\), an identity string \(\mathsf {id} \in \{0, 1\}^*\) and a message \(m \in \{0, \ldots , e - 1\}\), first compute \(a \leftarrow H(\mathsf {id})\). We define the subalgorithm \(\mathcal {E}\) that takes an integer v and message \(m^\prime \) as input and outputs a polynomial in \(\mathbb {Z}_N[x]\). \(\mathcal {E}(v, m^\prime ):\)
: Given public parameters \(\mathsf {PP} := (N, \mu , \alpha _1, \ldots , \alpha _e)\), an identity string \(\mathsf {id} \in \{0, 1\}^*\) and a message \(m \in \{0, \ldots , e - 1\}\), first compute \(a \leftarrow H(\mathsf {id})\). We define the subalgorithm \(\mathcal {E}\) that takes an integer v and message \(m^\prime \) as input and outputs a polynomial in \(\mathbb {Z}_N[x]\). \(\mathcal {E}(v, m^\prime ):\)-
Generate a uniformly random polynomial \(f(x) \xleftarrow {\$}\mathbb {Z}_N^*[x]\) of degree \(e - 1\).
-
Compute \(g(x) \leftarrow f(x)^e \text { mod }{x^e - v}\).
-
Choose a uniformly random \(t \xleftarrow {\$}\mathbb {Z}_N^*\) such that \(J(t) = m^\prime \).
-
Output the polynomial \(c(x) = t \cdot g(x)\).
The encryption algorithm outputs \(\mathsf {CT} = (a, \mathcal {E}(\alpha _1 \cdot a, m), \ldots , \mathcal {E}(\alpha _{e} \cdot a, m))\).
-
-
 On input a secret key \(\mathsf {sk}_{\mathsf {id}} := (i, r)\) and a ciphertext \(\mathsf {CT} := (a, c_1(x), \ldots , c_e(x))\), output \(m \leftarrow J_N(c_i(r))\).
On input a secret key \(\mathsf {sk}_{\mathsf {id}} := (i, r)\) and a ciphertext \(\mathsf {CT} := (a, c_1(x), \ldots , c_e(x))\), output \(m \leftarrow J_N(c_i(r))\).
Correctness The correctness of decryption follows in the same way as BLS; since, \(f(x)^3 = g(x)^3 + (x^3 - \alpha _i \cdot a)\), we have \(f(r)^3 = g(r)^3\) when \(r^3 \equiv \alpha _i \cdot a\) and \(J_N(tg(r)^3) = J_N(t)\). It is necessary that the product of one of the \(\alpha _i\)’s with a gives an \(e^{\text {th}}\) residue. An element of \(v \in \mathbb {Z}_N^*\) is an \(e^{\text {th}}\) residue iff \(J_N(v) = J_p(v) = 0\). Let \(k = J_p(a)\). Then multiplying a with an element \(\alpha \) satisfying \(J_N(\alpha ) = 0\) and \(J_p(\alpha ) = e - k\) guarantees that the resulting element is an \(e^{\text {th}}\) residue (recall that \(J_p(xy) = Jp(x) + Jp(y) \text { mod }{e}\)). So we need to show that for each \(z \in \mathbb {Z}_e\), there is an \(\alpha _i\) with \(J_p(\alpha _i) = z\). In the setup, we sample a \(\gamma \) with \(J_N(\gamma ) = 0\) and \(J_p(\gamma ) \ne 0\). Let \(g = J_p(\gamma )\). Then \(J_p(\gamma ^j) = jg \text { mod }e\) for \(j \in \{0, \ldots , e - 1\}\) and since e is prime, this generates all elements in the additive group \(\mathbb {Z}_e\).
Security Now we will reduce the security of our construction to that of BLS. When we refer to BLS hereafter, we will assume that its encryption algorithm is the same as \(\mathcal {E}\) above i.e. it outputs a polynomial \(\mathsf {CT} := c(x) = t\cdot g(x)\). This does not affect its security. However, there is an obstacle that we must contend with in the security reduction. Given a BLS public key, we cannot generate a \(\gamma \in \mathbb {PR}(N) \setminus \mathbb {ER}(N)\) (note that this is precisely the set \(\{x : J_N(x) = 0 \wedge J_p(x) \ne 0\}\)) with probability 1 which is needed to correctly simulate the public parameters of our scheme. To address this, we consider a modified BLS scheme, denoted \(\text {BLS}^\prime \), that generates such a \(\gamma \) and outputs it as part of the public key. We first show that \(\text {BLS}^\prime \) is semantically secure under the MER assumption. Then we will base our security reduction on \(\text {BLS}^\prime \).
Lemma 1
\(\text {BLS}^\prime \) is IND-CPA secure under the MER assumption.
Proof
We will prove the lemma via a hybrid argument.
Game 0: This is the real IND-CPA game.
Game 1: We make one change from Game 0, namely we set \(\gamma \leftarrow u^e \text { mod }{N}\) for a uniformly chosen \(u \xleftarrow {\$}\mathbb {Z}_N^*\).
Game 0 and Game 1 are computationally indistinguishable due to MER. In Game 0, \(\gamma \) is sampled uniformly from \(\mathbb {PR}(N) \setminus \mathbb {ER}(N)\) and in Game 1, \(\gamma \) is sampled uniformly from \(\mathbb {ER}(N)\).
Game 2: The change we make in this game is to encrypt a fixed element \(w \in \mathbb {Z}_e\) instead of \(m_b\), where \(m_0 \in \mathbb {Z}_e\) and \(m_1 \in \mathbb {Z}_e\) are the challenge messages and b is a random bit. The adversary has a zero advantage in this game.
Game 1 and Game 2 are computationally indistinguishable by the semantic security of BLS. Given a BLS public key \((N, \mu , v)\), we use these values in the public key and generate \(\gamma \) as in Game 2. When the adversary provides the challenge plaintexts \((m_0, m_1)\), we choose a random b and forward the challenge plaintexts \((m_b, w)\) to the BLS challenger, and return the challenge ciphertext \(\mathsf {CT}^*\) provided by the BLS challenger. If \(\mathsf {CT}^*\) encrypts \(m_b\) then Game 1 is perfectly simulated whereas if it encrypts w, Game 2 is perfectly simulated. Therefore, a non-negligible advantage distinguishing the hybrids implies a non-negligible advantage breaking the semantic security of BLS. \(\square \)
Theorem 1
Our scheme is IND-ID-CPA secure under the MER assumption in the random oracle model.
Proof
Let \(\mathcal {A}\) be the adversary in the IND-ID-CPA game against our scheme. We show that a non-negligible advantage by \(\mathcal {A}\) implies a non-negligible advantage against the IND-CPA security of \(\text {BLS}^\prime \). We construct a simulator \(\mathcal {S}\) that interacts in the IND-CPA game and simulates the view of \(\mathcal {A}\). The hash function H in our IBE scheme is modeled as a random oracle. We now describe how \(\mathcal {S}\) works.
Given a public key \((N, \mu , v, \gamma )\) of \(\text {BLS}^\prime \) by the IND-CPA challenger, \(\mathcal {S}\) uses this information to construct public parameters \((N, \mu , \alpha _1, \ldots , \alpha _e)\), which it gives to \(\mathcal {A}\). Let Q be the number of non-adaptive calls to the random oracle H. We assume that \(\mathcal {A}\) makes a call to H for identity \(\mathsf {id}\) prior to making a secret key query for \(\mathsf {id}\). The simulator picks a random \(k \in [Q]\). The simulator answers calls to H as follows. On the j-th call to H with identity string \(\mathsf {id}_j\), perform the following steps:
-
If \(j = k\):
-
Choose a random \(i \xleftarrow {\$}[e]\).
-
Add tuple \((\mathsf {id}_k, \bot , i)\) to table T.
-
Output \(v \cdot \alpha _i^{-1} \text { mod }{N}\).
-
-
Else:
-
Choose a random \(i \xleftarrow {\$}[e]\).
-
Choose a random \(r \xleftarrow {\$}\mathbb {Z}_N^*\).
-
Add tuple \((\mathsf {id}_j, r, i)\) to T.
-
Output \(r^e \cdot \alpha _i^{-1}\).
-
The simulator handles secret key queries as follows. On querying the secret key for identity \(\mathsf {id}\), perform the following steps.
-
If \(\mathsf {id} = \mathsf {id}_k\), output a random bit and abort the simulation.
-
Fetch tuple \((\mathsf {id}_j, r, i)\) from T with \(\mathsf {id}_j = \mathsf {id}\).
-
Output r.
When \(\mathcal {A}\) sends its target identity \(\mathsf {id}^*\) and pair of challenge plaintexts \((m_0, m_1)\), the simulator checks if \(\mathsf {id}^*= \mathsf {id}_k\). If this is not the case, \(\mathcal {S}\) outputs a random bit and aborts. Otherwise, it forwards \((m_0, m_1)\) to the IND-CPA challenger. Subsequently, the IND-CPA challenger gives \(\mathcal {S}\) its challenge ciphertext \(\mathsf {CT}^*:= c^*(x)\). The simulator performs the following steps:
-
Fetch \((\mathsf {id}_k, \bot , i)\) from T.
-
Set \(c_i(x) \leftarrow c^*(x)\).
-
Set \(a \leftarrow v \cdot \alpha _i^{-1} \text { mod }{N}\)
-
Compute \(c_j(x) \leftarrow \mathcal {E}(\alpha _j \cdot a, u_j)\) with \(u_j \xleftarrow {\$}\mathbb {Z}_e\) for all \(j \in [e]\setminus \{i\}\).
-
Set \(\mathsf {CT} \leftarrow (a, c_1(x), \ldots , c_e(x))\).
The simulator then gives \(\mathsf {CT}\) to \(\mathcal {A}\) as its challenge ciphertext. We claim that \(\mathsf {CT}\) is identically distributed to a ciphertext in the real game. Firstly, since \(a \cdot \alpha _i \equiv v \text { mod }{N}\), we have that \(c_i(x)\) is perfectly simulated. For all other \(j \in [e]\) with \(j \ne i\), the element \(a \cdot \alpha _j\) is an \(e^{\text {th}}\) non-residue. It is shown in [28] that ciphertext polynomials computed with an \(e^{\text {th}}\) non-residue give no information about the plaintext. Therefore, in the view of \(\mathcal {A}\), the challenge ciphertext \(\mathsf {CT}\) is perfectly simulated. Finally, \(\mathcal {S}\) outputs \(\mathcal {A}\)’s guess bit. The probability that the simulation does not abort is \(1{\slash }Q\). It follows that if \(\mathcal {A}\) has advantage \(\epsilon \) attacking the IND-ID-CPA security of our scheme then \(\mathcal {S}\) has advantage \(\epsilon /Q\) attacking the IND-CPA security of \(\text {BLS}^\prime \). Since a non-negligible \(\epsilon \) would contradict Lemma 1 assuming MER holds, the result follows. \(\square \)
3.4 Homomorphism
We now show that our construction is additively homomorphic for the group \((\mathbb {Z}_e, +)\). Given two ciphertexts \(\mathsf {CT}_1 := (a, c_1(x), \ldots , c_e(x))\) and \(\mathsf {CT}_2 := (a, d_1(x), \ldots , d_e(x))\) encrypted with the same identity \(\mathsf {id}\) with \(a = H(\mathsf {id})\), we compute the i-th component of the resulting ciphertext as \(e_i(x) = c_i(x) \cdot d_i(x) \pmod {x^e - \alpha _i \cdot a}\) for \(i \in [e]\). Consider the i-th component of the ciphertexts such that \(\alpha _i \cdot a \in \mathbb {Z}_N\) is an \(e^{\text {th}}\) residue. Suppose we have that \(c_i(x) = t_1 \cdot f_1(x)^e \pmod {x^e - \alpha _i \cdot a}\) and \(d_i(x) = t_2 \cdot f_2(x)^e \pmod {x^e - \alpha _i \cdot a}\). Let r be the \(e^{\text {th}}\) root of \(\alpha _i \cdot a\). To see that multiplication modulo \((x^e - \alpha _i \cdot a)\) is homomorphic, observe that
Recall the homomorphic property of \(J_N\) i.e. \(J_N(xy) = J_N(x) + J_N(y) \text { mod }{e}\).
Keeping with the notation we have established so far, let us first fix some identity \(\mathsf {id} \in \{0, 1\}^*\). Let (i, r) be a secret key for \(\mathsf {id}\). The ciphertext space \(\hat{\mathcal {C}}_\mathsf {id}\) is defined as follows:

The binary operation \(*\) can be defined on \(\hat{\mathcal {C}}\) as follows: given two ciphertexts \(\mathsf {CT}_1 := (a_1, c_1(x), \ldots , c_e(x))\) and \(\mathsf {CT}_2 := (a_2, d_1(x), \ldots , d_e(x))\), their product under \(*\) is defined as \(\mathsf {CT}^\prime := (a_1, c_1(x) \cdot d_1(x) \pmod {x^e - \alpha _1 \cdot a_1}, \ldots , c_e(x) \cdot d_e(x) \pmod {x^e - \alpha _e \cdot a_1}\) if \(a_1 = a_2\), and \(\mathsf {CT}^\prime := Z\) otherwise, where \(Z \in \hat{\mathcal {C}}\) is the null ciphertext.
Lemma 2
\((\hat{\mathcal {C}}_\mathsf {id}, *)\) is a group.
Proof
It is sufficient to consider a single component of the ciphertext because the same analysis applies for each component. Let \(v = \alpha _i \cdot a\) for some j. We can view the j-th component as an element in the ring \(R_a = \mathbb {Z}_N[x]/(x^e - v)\). Let c(x) be the j-th polynomial component of a ciphertext in \(\hat{\mathcal {C}}_\mathsf {id}\). By definition, c(x) is invertible. Consider the case where \(j = i\). By definition, we have \(\genfrac(){}0{c(r)}{\mathfrak {N}}_e \ne 0\). Applying \(*\) to c(x) and any other element of \(\hat{\mathcal {C}}_\mathsf {id}\) preserves this condition. Therefore \(\hat{\mathcal {C}_\mathsf {id}}\) is closed under \(*\). It follows \((\hat{\mathcal {C}}_f, *)\) is a group. \(\square \)
We denote the set of legal encryptions under identity \(\mathsf {id}\) by \(\mathcal {C}_\mathsf {id}\). We have the following straightforward lemma:
Lemma 3
\((\mathcal {C}_\mathsf {id}, *)\) is a subgroup of \(\hat{\mathcal {C}}_\mathsf {id}\).
Proof
We focus on a single component, say the j-th, of a ciphertext. Let c(x) be such a component. Then c(x) is of the form \(t \cdot f(x)^e\) for some f(x) that is a unitFootnote 4 in \(\mathbb {Z}_N[x]/(x^e - \alpha _j \cdot a)\) and \(t \in \mathbb {Z}_N^*\). Naturally we have that \(c(x) \in \hat{\mathcal {C}}_\mathsf {id}\). Multiplying c(x) by another element d(x) with the same form yields an element of the same form. \(\square \)
Theorem 2
Our scheme is an IBGHE scheme i.e. it satisfies Definition 3.
Proof
By Lemma 3 the scheme satisfies GH.1. By the derivation given in Eqs. 3.3–3.7 the scheme satisfies GH.2. Therefore the scheme is an IBGHE. \(\square \)
3.5 Homomorphic Addition Modulo a “Large” Modulus
Our scheme supports homomorphic addition modulo a “small” (i.e. poly-sized) prime. However if we use multiple instances of the scheme with distinct primes, we can leverage the Chinese Remainder Theorem to support addition modulo a square-free integer M provided M factors into a polynomial number of poly-sized primes. Hence we can support modular addition with an exponentially-large modulus. This is the first IBE scheme admitting a modular additive homomorphism with a superpolynomial modulus, solving an open problem mentioned in [21].
Concretely, suppose our desired square-free modulus is \(M = p_1 \cdots p_n\). We employ n instances of our scheme \(\{\mathcal {E}_i\}_{i \in [n]}\) with the e parameter for \(\mathcal {E}_i\) set to \(p_i\) for all \(i \in [n]\).
-
 : Output \((\mathsf {PP} := (\mathsf {PP_1}, \ldots , \mathsf {PP}_n), \mathsf {MSK} := (\mathsf {MSK}_1, \ldots , \mathsf {MSK}_n)\) where
: Output \((\mathsf {PP} := (\mathsf {PP_1}, \ldots , \mathsf {PP}_n), \mathsf {MSK} := (\mathsf {MSK}_1, \ldots , \mathsf {MSK}_n)\) where  for \(i \in [n]\).
for \(i \in [n]\). -
 : Output \(\mathsf {sk} := (\mathsf {sk}_1, \ldots , \mathsf {sk}_n)\) where
: Output \(\mathsf {sk} := (\mathsf {sk}_1, \ldots , \mathsf {sk}_n)\) where  for \(i \in [n]\).
for \(i \in [n]\). -
 : Output \(c := (c_1, \ldots , c_n)\) where
: Output \(c := (c_1, \ldots , c_n)\) where  for \(i \in [n]\).
for \(i \in [n]\). -
 Output \(\mathsf {CRT}((m_1, \ldots , m_n), (p_1, \ldots , p_n))\) where
Output \(\mathsf {CRT}((m_1, \ldots , m_n), (p_1, \ldots , p_n))\) where 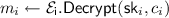 for \(i \in [n]\).
for \(i \in [n]\). -
Additive Homomorphism: Let \(*^i\) denote the binary operation on the ciphertext space of \(\mathcal {E}_i\). We define \(*\), the binary operation on the ciphertext space of this construction, as follows:
-
\(c *c^\prime = (c_1, \ldots , c_n) *(c'_1, \ldots , c'_n) \triangleq (c_1 *^1 c'_1, \ldots , c_n *^n c'_n)\)
-
The ciphertext space complexity of this scheme is \(\sum p_i^2\).
3.6 Anonymity
The XOR-homomorphic scheme CHT mentioned earlier is not anonymous as a result of a test due to GalbraithFootnote 5. Consider an identity \(\mathsf {id}\) and let \(a = H(\mathsf {id})\). Ciphertexts in CHT are a pair of polynomials \((c(x), d(x)) \in (\mathbb {Z}_N[x])^2\). We will consider only a single ciphertext component here, say the first (c(x)), which is encrypted with respect to a. The observations also hold with respect to the second component by replacing a with \(-a\). We define Galbraith’s Test for ciphertext polynomials as the function \(\mathsf {GT} : \mathbb {Z}_N \times \mathbb {Z}_N[x] \rightarrow \{-1, 0, +1\}\) given by
For encryptions c(x) (recall we are just considering one component) encrypted under identity \(\mathsf {id}\), we have \(\mathsf {GT}(a, c(x)) = 1\). For encryptions \(c'(x)\) under a different identity, it is the case that \(\mathsf {GT}(a, c'(x)) = 1\) with probability negligibly close to 1/2.
For convenience, let us denote our scheme that extends BLS, as described above, for the case of \(e = 2\) (i.e. admitting an XOR homomorphism) by \(\mathcal {E}_2\). Although \(\mathcal {E}_2\) is algorithmically different to CHT, it shares many of the same properties. In particular it is easy to see that Galbraith’s test is applicable in the same way. An anonymous variant of CHT was proposed in [35] and the techniques are also applicable to \(\mathcal {E}_2\). However the approach to achieve anonymity in [35] loses the homomorphic property i.e. one cannot homomorphically operate on anonymized ciphertexts.
We now turn our attention to investigating whether our scheme for the case of \(e > 2\) is anonymous. We will denote our scheme for this case by \(\mathcal {E}_e\). As usual, for identity \(\mathsf {id}\), we let \(a = H(\mathsf {id})\). We define the ciphertext space \(\hat{C}\) for a single component as \(\hat{C} := \{c(x) \in \mathbb {Z}^*_N[x] : \mathsf {deg}(c(x)) = e - 1\}\) (the analysis holds analogously for the other components). Now consider the subset \(C_a \subset \hat{C}\), which are the set of polynomials (for a single component) in the image of the encryption algorithm with respect to a; that is, we have \(C_a := \{t \cdot f(x)^e \text { mod }{x^e - a} : t \in \mathbb {Z}_N^*, f(x) \in \mathbb {Z}_N^*[x], \mathsf {deg}(f(x)) = e - 1\}\). Also we need to define a subset \(C_a^{(0)} \subset C_a\) of \(C_a\) that corresponds to encryptions of the identity element 0 with respect to a.
Definition 7
(Algebraic Equation Set). The algebraic equation set for a ciphertext \(c(x) \in \hat{C}\) with respect to a is derived as follows. The unknowns are the coefficients \(z_0, ..., z^{e - 1}\) of the polynomial f(x) generated during encryption. Raising f(x) to the power of e and reducing according to the equivalence relation \(x^e \equiv a\) induced by the quotient of the ring \(\mathbb {Z}_N^*[x]/(x^e - a)\) yields a set of e multivariate polynomials in \(z_0, ..., z^{e - 1}\) of degree e, one for each coefficient of the result. The algebraic equation set is formed by letting the polynomial for the i-th coefficient of the result equal to \(c_i\) for \(i \in {0, \ldots , e - 1}\). For example, the algebraic equation set for \(e = 3\) is
We now define a subset \(C_a^{{(0)}}{'} \subset C_a^{(0)}\) of the honest encryptions of 0 as \(C_a^{{(0)}}{'} := \{t \cdot f(x)^e \text { mod }{x^e - a} : t \in \mathbb {ER}(N), f(x) \in \mathbb {Z}_N^*[x], \mathsf {deg}(f(x)) = e - 1\}\) i.e. the \(t \in \mathbb {Z}^*_N\) used during encryption is an \(e^{\text {th}}\) residue. We have the following lemma.
Lemma 4
The algebraic equation set for \(c(x) \in \hat{C}\) with respect to a has a solution if and only if \(c(x) \in C_a^{{(0)}}{'}\).
Proof
Let \(R = \mathbb {Z}_N^*[x]/(x^e - a)\). A solution to the algebraic equation set for c(x) is a polynomial f(x) such that \(f(x)^e = c(x)\) (in R). Therefore \(t = 1\), an \(e^{\text {th}}\) residue and thus we have \(c(x) \in C_a^{{(0)}}{'}\). Conversely, let c(x) be an element of \(C_a^{{(0)}}{'}\). We can write \(c(x) = t \cdot f(x)^e \in R\). Since \(t = r^e\) is an \(e^{\text {th}}\) residue for some \(r \in \mathbb {Z}_N^*\), we have that \(r \cdot f(x) \in R\) is a solution to the algebraic equation set, which secures the lemma. \(\square \)
We have an additional lemma.
Lemma 5
The sets \(C_a^{(0)}\) and \(C_a^{{(0)}}{'}\) are computationally indistinguishable assuming the hardness of MER.
Proof
An algorithm that distinguishes between \(C_a^{(0)} \setminus C_a^{{(0)}}{'}\) and \(C_a^{{(0)}}{'}\) can be used to construct an algorithm that solves MER. Given a MER challenge \(t \in \{x \in \mathbb {Z}_N : J_N(t) = 0\}\), an element c(x) is generated by computing \(t \cdot f(x)^e \text { mod }{x^e - a}\) for \(f(x) \xleftarrow {\$}\mathbb {Z}^*_N[x], \mathsf {deg}(f(x)) = e - 1\). If t is a non-residue then c(x) is uniformly distributed in the first distribution. Otherwise, it is uniformly distributed in the second distribution. An algorithm that distinguishes the distributions can thus solve MER. By extension, the statement of the lemma follows. \(\square \)
Let \(A = \{x \in \mathbb {Z}_N^*: J_N(x) = 0\}\). We are now ready to define the assumption under which we prove anonymity of \(\mathcal {E}_e\).
Definition 8
(Special Polynomial Equations Solvability (SPES(e) Assumption). Given \((a, c(x)) \in A \times \hat{C}\) where \(a \xleftarrow {\$}A\), consider an algorithm \(\mathcal {A}\) that decides the solvability of the algebraic equation set for c(x) with respect to a. Let S be the set of instances in \(A \times \hat{C}_a\) that are solvable and let \(\bar{S}\) be the unsolvable instances. The advantage of \(\mathcal {A}\) deciding correctly \(\mathsf {Adv}_\mathcal {A}\) is defined as
The SPES(e) assumption for prime \(e > 2\) is that for every PPT algorithm \(\mathcal {A}\) it holds that \(\mathsf {Adv}_\mathcal {A} < \mathsf {negl}(\lambda )\).
Remark 2
Deciding solvability of a system of multivariate polynomial equations in general is NP-complete. However for the special system of equations of interest here, with certain structure, we must make an explicit assumption about the hardness of deciding its solvability.
Lemma 6
The sets \(C_a\) and \(\hat{C} \setminus C_a\) are computationally indistinguishable for \(a \xleftarrow {\$}A\) assuming the hardness of SPES and MER.
Proof
By semantic security of \(\mathcal {E}_e\), via the MER assumption, shown in Theorem 1, it holds that \(C_a\) is computationally instinguishable from \(C_a^{(0)}\). Then by invoking Lemma 5, we have that \(C_a^{(0)}\) is computationally indistinguishable from \(C_a^{{(0)}}{'}\). Now Lemma 4 tells us that the solvable instances for SPES are the set \(C_a^{{(0)}}{'}\). The unsolvable instances are \(\hat{C} \setminus C_a^{{(0)}}{'}\). By the hardness of SPES, these sets are therefore computationally indistinguishable. The result follows. \(\square \)
Theorem 3
\(\mathcal {E}_e\) for \(e > 2\) is anonymous under the SPES and MER assumptions.
Proof
In the anonymity security game, the adversary chooses two target identities \(\mathsf {id}\) and \(\mathsf {id}'\).
Game 0: This is the real game.
Game 1: In this game, we change how the challenge ciphertext is generated if the challenger’s bit \(\beta = 0\) (i.e. using identity \(\mathsf {id})\). If \(\beta = 0\), we sample the challenge ciphertext uniformly from \(\hat{C}\) instead of \(C_a\) where a is what is returned by \(H(\mathsf {id})\).
To invoke Lemma 6 to argue indistinguishability of \(\hat{C}\) and \(C_a\), we need to program the output of the random oracle H on identity \(\mathsf {id}\) to be a, which is distributed correctly. In a similar manner to the proof of Theorem 1, we must guess one of the identities the adversary chooses from its queries to H and abort with a random bit if we guessed incorrectly. This step loses a factor of roughly \(1{\slash }Q\) where Q is the number of queries to H prior choosing the target identities.
Game 2: In this game, we change how the challenge ciphertext is generated if the challengers bit \(\beta = 1\) (i.e. using identity \(\mathsf {id}'\)). If \(\beta = 1\), we sample the challenge ciphertext uniformly from \(\hat{C}\) instead of \(C_b\) where b is what is returned by \(H(\mathsf {id}')\).
Indistinguishability follows in the same manner as the transition between Game 0 to Game 1.
The adversary has zero advantage in this game as it learns no information about \(\beta \). The result follows. \(\square \)
3.7 Cryptanalytic Investigation of SPES
The main practical approach for solving a system of multivariate polynomial equations is via computing a reduced Gröbner basis. For a sufficient number of equations, solvability can be decided by checking if the reduced Gröbner basis is {1} [36], which means the system is inconsistent (no solution exists). Buchberger [36, 37] introduced an algorithm for computing a Gröbner basis. The time complexity of this algorithm is difficult to analyze but is estimated to be doubly exponential in the number of variables. Therefore for \(e = \varOmega (\log {\lambda })\) with security parameter \(\lambda \) this approach is intractable. For such values of e, a standard technique is to use resultants to eliminate variables. However to eliminate variables such that only a constant number remain, leads to polynomials with superpolynomial degree in \(\lambda \). In view of this state of affairs, since Gröbner basis computation is the best known practical approach for solving multivariate equations, we conjecture that SPES(e) is hard for \(e = \varOmega (\log \lambda )\). We now focus on small (constant) values of e. For example we are interested in knowing whether SPES(3) is hard.
We used a variant of Buchberger’s algorithm in Sage to compute Gröbner bases and conduct experimental analysis. Our experimental results show that with overwhelming probability the reduced Gröbner basis in the lexicographic monomial ordering for the SPES(e) system consists of e polynomials where the last polynomial (when ordered lexicographically) in the basis is a univarate polynomial in \(z_{e - 1}\) of the form \(\sum _{i = 0}^{e^{e - 1}} a_i z_{e - 1}^{i \cdot e}\) for coefficients \(a_i \in Z_N\). This is the case whether the system is solvable or not. Buchberger’s criterion for unsolvability, i.e. checking if the reduced Gröbner basis is {1}, does not pertain because we have an insufficient number of equations. We now have a univariate polynomial over \(Z_N\). However to the best of our knowledge, there are no known feasible attacks on deciding solvability of such polynomials when N is an RSA modulus. Inspecting the form of the univariate polynomial above, it is not difficult to see that deciding solvability of polynomials of this form for general coefficients \(a_i\) is at least as hard as the \(e^{\text {th}}\) residuosity problem. This gives evidence that the problem we are faced with (for a certain distribution of coefficients) has the potential to be hard but we cannot provide a reduction or firmer conclusion on its exact hardness for the distribution of coefficients encountered. Nevertheless, in light of the evidence, we conjecture that SPES(e) is hard for constant prime \(e > 2\). We invite the community to conduct further cryptanalysis.
Notes
- 1.
LWE-based additively homomorphic IBE can be constructed with an a superpolynomial range but supporting only a theoretically bounded number of operations, albeit the bound is more than sufficient for practical purposes.
- 2.
Any PPT distinguisher has only a negligible advantage (in \(\lambda \)) of distinguishing the distributions.
- 3.
This is with absolute correctness. There is an alternative approach to the one we present here that achieves probabilistic correctness, but the parameters can be set so that it is correct with all but negligible probability. It is however less space efficient. The idea is that the hash function gives multiple (say \(k = \mathsf {poly}(\lambda )\)) elements whose \(e^{\text {th}}\) residue symbol is 1 and at least one of them will be an \(e^{\text {th}}\) residue with all but negligible probability. The ciphertext contains k encryptions, as opposed to \(e < k\) in our approach, thus making this approach less space-efficient than ours.
- 4.
We omitted an explicit check for this in the encryption algorithm since a non-unit occurs with negligible probability.
- 5.
Reported as emerging from personal communication in [34].
References
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Boneh, D., Franklin, M.: Identity-based encryption from the Weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_13
Cocks, C.: An identity based encryption scheme based on quadratic residues. In: Honary, B. (ed.) Cryptography and Coding 2001. LNCS, vol. 2260, pp. 360–363. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45325-3_32
Armknecht, F., Katzenbeisser, S., Peter, A.: Group homomorphic encryption: characterizations, impossibility results, and applications. Des. Codes Cryptogr. 67, 1–24 (2012)
Kushilevitz, E., Ostrovsky, R.: Replication is not needed: single database, computationally-private information retrieval. In: Proceedings of the 38th Annual Symposium on Foundations of Computer Science, FOCS 1997, pp. 364–373. IEEE Computer Society, Washington, DC (1997)
Benaloh, J.D.C.: Verifiable secret-ballot elections. Ph.D. thesis, Yale University, New Haven, CT, USA (1987). AAI8809191
Cohen, J.D., Fischer, M.J.: A robust and verifiable cryptographically secure election scheme. In: Proceedings of the 26th Annual Symposium on Foundations of Computer Science, pp. 372–382. IEEE Computer Society, Washington, DC (1985)
Cramer, R., Franklin, M., Schoenmakers, B., Yung, M.: Multi-authority secret-ballot elections with linear work. In: Maurer, U. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 72–83. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68339-9_7
Cramer, R., Gennaro, R., Schoenmakers, B.: A secure and optimally efficient multi-authority election scheme. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 103–118. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_9
Damgård, I., Jurik, M.: A generalisation, a simplification and some applications of Paillier’s probabilistic public-key system. In: Kim, K. (ed.) PKC 2001. LNCS, vol. 1992, pp. 119–136. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44586-2_9
Naor, M., Pinkas, B.: Oblivious polynomial evaluation. SIAM J. Comput. 35, 1254–1281 (2006)
Sander, T., Young, A.L., Yung, M.: Non-interactive cryptocomputing for nc\(^{\text{1}}\). In: FOCS, pp. 554–567. IEEE Computer Society (1999)
Fischlin, M.: A cost-effective pay-per-multiplication comparison method for millionaires. In: Naccache, D. (ed.) CT-RSA 2001. LNCS, vol. 2020, pp. 457–471. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45353-9_33
Goldwasser, S., Micali, S.: Probabilistic encryption. J. Comput. Syst. Sci. 28, 270–299 (1984). See also preliminary version in 14th STOC, 1982
Naccache, D., Stern, J.: A new public key cryptosystem based on higher residues. In: Gong, L., Reiter, M.K., (eds.) ACM Conference on Computer and Communications Security, pp. 59–66. ACM (1998)
Okamoto, T., Uchiyama, S.: A new public-key cryptosystem as secure as factoring. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 308–318. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054135
Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 223–238. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_16
Gjøsteen, K.: Homomorphic cryptosystems based on subgroup membership problems. In: Dawson, E., Vaudenay, S. (eds.) Mycrypt 2005. LNCS, vol. 3715, pp. 314–327. Springer, Heidelberg (2005). https://doi.org/10.1007/11554868_22
Gjøsteen, K.: Symmetric subgroup membership problems. In: Vaudenay, S. (ed.) PKC 2005. LNCS, vol. 3386, pp. 104–119. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30580-4_8
Damgård, I.: Towards practical public key systems secure against chosen ciphertext attacks. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 445–456. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_36
Clear, M., Hughes, A., Tewari, H.: Homomorphic encryption with access policies: characterization and new constructions. In: Youssef, A., Nitaj, A., Hassanien, A.E. (eds.) AFRICACRYPT 2013. LNCS, vol. 7918, pp. 61–87. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38553-7_4
Chor, B., Kushilevitz, E., Goldreich, O., Sudan, M.: Private information retrieval. J. Assoc. Comput. Mach. 45, 965–981 (1998)
Oliveira, L., Scott, M., Lopez, J., Dahab, R.: TinyPBC: pairings for authenticated identity-based non-interactive key distribution in sensor networks. In: 5th International Conference on Networked Sensing Systems, INSS 2008, pp. 173–180 (2008)
Liu, A., Ning, P.: TinyECC: a configurable library for elliptic curve cryptography in wireless sensor networks. In: IPSN 2008: Proceedings of the 7th International Conference on Information Processing in Sensor Networks, pp. 245–256. IEEE Computer Society, Washington, DC (2008)
Oliveira, L.B., Aranha, D.F., Morais, E., Daguano, F., López, J., Dahab, R.: TinyTate: computing the tate pairing in resource-constrained sensor nodes. In: IEEE International Symposium on Network Computing and Applications, pp. 318–323 (2007)
Szczechowiak, P., Kargl, A., Scott, M., Collier, M.: On the application of pairing based cryptography to wireless sensor networks. In: WiSec 2009: Proceedings of the Second ACM Conference on Wireless Network Security, pp. 1–12. ACM, New York (2009)
Günther, F., Manulis, M., Peter, A.: Privacy-enhanced participatory sensing with collusion resistance and data aggregation. In: Gritzalis, D., Kiayias, A., Askoxylakis, I. (eds.) CANS 2014. LNCS, vol. 8813, pp. 321–336. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-12280-9_21
Boneh, D., LaVigne, R., Sabin, M.: Identity-based encryption with \(e\)th residuosity and its incompressibility. (TRUST Conference, poster presentation). http://www.truststc.org/education/reu/13/Papers/SabinM_Paper.pdf
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: STOC 2008: Proceedings of the 40th Annual ACM Symposium on Theory of Computing, pp. 197–206. ACM, New York (2008)
Albrecht, M.R., Player, R., Scott, S.: On the concrete hardness of learning with errors. J. Math. Cryptol. 9, 169–203 (2015)
Joye, M.: On Identity-Based Cryptosystems from Quadratic Residuosity. http://joye.site88.net/papers/gcocks.pdf
Freeman, D.M., Goldreich, O., Kiltz, E., Rosen, A., Segev, G.: More constructions of lossy and correlation-secure trapdoor functions. J. Cryptol. 26, 39–74 (2013)
Squirrel, D.: Computing reciprocity symbols in number fields. Thesis (B.A.) Reed College (1997)
Boneh, D., Gentry, C., Hamburg, M.: Space-efficient identity based encryption without pairings. In: FOCS, pp. 647–657. IEEE Computer Society (2007)
Clear, M., Tewari, H., McGoldrick, C.: Anonymous IBE from quadratic residuosity with improved performance. In: Pointcheval, D., Vergnaud, D. (eds.) AFRICACRYPT 2014. LNCS, vol. 8469, pp. 377–397. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-06734-6_23
Buchberger, B.: An algorithmic criterion for the solvability of a system of algebraic equations. In: Buchberger, B., Winkler, F. (eds.) Gröbner Bases and Applications. London Mathematical Society Lecture Notes Series, vol. 251, pp. 535–545. Cambridge University Press (1998)
Buchberger, B.: Introduction to Gröbner bases. In: Buchberger, B., Winkler, F. (eds.) Gröbner Bases and Applications. London Mathematical Society Lecture Notes Series, vol. 251, pp. 3–31. Cambridge University Press (1998)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Clear, M., McGoldrick, C. (2019). Additively Homomorphic IBE from Higher Residuosity. In: Lin, D., Sako, K. (eds) Public-Key Cryptography – PKC 2019. PKC 2019. Lecture Notes in Computer Science(), vol 11442. Springer, Cham. https://doi.org/10.1007/978-3-030-17253-4_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-17253-4_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17252-7
Online ISBN: 978-3-030-17253-4
eBook Packages: Computer ScienceComputer Science (R0)





 :
: :
: :
: :
: : Generate two RSA primes p and q with
: Generate two RSA primes p and q with  : Given public key
: Given public key  : Given secret key
: Given secret key  : Generate two RSA primes p and q with
: Generate two RSA primes p and q with  : Given master secret key
: Given master secret key  : Given public parameters
: Given public parameters  On input a secret key
On input a secret key  : Output
: Output  for
for  : Output
: Output  for
for  : Output
: Output  for
for  Output
Output 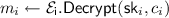 for
for 