Vortex Shedding and Flow-Induced Vibration of Two Cylinders in Tandem

Abstract

This paper presents a study of the interaction between a fluid flow and two cylinders in a tandem arrangement. The cylinders are identical in size and either rigidly mounted, or elastically mounted but restricted to one degree of freedom in the cross-flow direction. The Reynolds number is $Re=UD/\nu =200$ where U is the freestream velocity, D is the cylinder diameter and $\nu$ is the kinematic viscosity. The sharp interface immersed boundary method is used to conduct two-dimensional simulations of the interaction between fluid and the two structures as a function of elasticity level quantified by the reduced velocity ($U^*=U/f_{N} \cdot D$) where $f_N$ is the natural structural frequency of each cylinder in vacuo, and pitch p which is the streamwise distance between the centres of the two cylinders. In the first stage, aerodynamic forces, frequency spectrum and amplitude of oscillation have been measured as a function of p for rigid cylinder system. The results showed that in the rigid two-cylinder system, there are four distinct regimes. In the second stage, a similar study with varying pitch but also with varying reduced velocity, $U^*$, has been conducted for elastically mounted cylinders. It is found that for systems with very small p, the behaviour is highly nonlinear and the oscillation of both bodies exceeds that of a single isolated cylinder. Over a critical value of p the oscillation of the front cylinder is very similar to a single cylinder system and is therefore essentially independent of pitch. However, the rear cylinder behaviour is strongly dependent on the pitch. The rear cylinder can oscillate with an amplitude which is higher or lower than the amplitude of oscillation for a single cylinder depending on the $U^*$ value.

4.1 Introduction

The vortex shedding in the wake of bluff bodies can cause motion of structures in situations ranging from off-shore structures, to electricity wires, to wind turbines. This phenomenon can be destructive or useful based on the application. Interaction of fluid and a single cylinder system has been studied for many years, including rigidly mounted immovable cylinders [1], cylinders where motion is imposed externally [2] and elastically mounted cylinders free to respond to the flow [3]. If the cylinder is elastically mounted and the frequency of the Kármán vortex shedding is close to the natural frequency of the structure, a high-amplitude resonance-type of oscillation occurs. This vortex-induced vibration occurs for a range of natural frequencies of the structure [4].

Although studying the interaction of fluid and a single isolated structure is of fundamental importance, investigating this concept for multi-structure systems is highly important in a practical sense as groups of closely spaced structures are ubiquitous in both engineering and nature. The flow interference which is the effect of the presence of other bodies in the flow has a significant importance in aerodynamics and hydrodynamics. This interference can lead to phenomena such as wake-induced galloping and wake-induced vibration [5, 6].

The simplest system in which flow interference can be studied is a system of two cylinders that are rigidly mounted. The arrangement of structures is classified to three different groups including tandem, side-by-side and staggered arrangements. In tandem arrangement, the line connecting the centre of all the bodies is parallel to the free stream direction, while in the side-by-side arrangement, this line is in the cross-flow direction. The staggered arrangement can be considered as combination of these two previous arrangements as the connecting line makes an angle to the free stream direction which is not zero or 90$^\circ$. Systems in these arrangements have been studied investigating the impact of cylinder spacing [7,8,9,10], showing a range of flow regimes that appear to be essentially independent of Re. Extending further are a series of studies of two elastically mounted cylinders in a tandem arrangements [11] and in a staggered arrangement [12].

Here, the flow behaviour of two cylinders in a tandem arrangement is studied primarily as a function of the distance between the cylinders, or pitch p. First, the cylinders are rigidly mounted. The results confirm the major flow regimes found in previous studies, showing four distinct regimes as a function of the pitch. Second, the cylinders are elastically mounted and the pitch p and the elasticity (quantified by the reduced velocity $U^*$) is varied. The most important finding is that over a critical value of p, the front cylinder behaviour is essentially the same as that of an isolated cylinder, and further increases in pitch have little impact. However, the behaviour of the rear cylinder is found to be strongly dependent on the pitch p and this is quantified in terms of the cylinder oscillations amplitude.

4.2 Methodology

The sharp interface immersed boundary method has been implemented to simulate the fluid and cylindrical structures in two dimensions. The implementation used is described in detail and shown to be accurate in simulating fluid-structure interaction problems in [13] and the basic method closely follows that presented in [14], therefore only a brief overview is provided here. In this method the stationary and vibrating cylinders are modeled by a Lagrangian set of finite immersed elements in an underlying Cartesian grid.

The incompressible Navier–Stokes equations govern the motion of the fluid

$$\begin{aligned} \begin{array}{c} \frac{\partial \mathbf {u}}{\partial \tau } = - (\mathbf {u}\cdot \nabla )\mathbf {u}- \nabla P + \frac{1}{Re}\nabla ^2 \mathbf {u}+ \mathbf {A}_b,\\ \nabla \cdot \mathbf {u}=0, \end{array} \end{aligned}$$

(4.1)

where $\tau = tU/D$ is the time non-dimensionalised by the advective time scale, $\mathbf {u}$ is the velocity field non-dimensionalised by the free-stream velocity U, P is the pressure field non-dimensionalised by $\rho U^2$, and $\mathbf {A}_b$ is a generic acceleration term that models the presence of an immersed boundary. A second-order central finite-difference scheme is used to spatially discretise these equations. Time integration is implemented using a second-order accurate two-way time-splitting scheme which first takes a “velocity sub-step” by integrating the advection, diffusion and immersed boundary acceleration terms to an intermediate time. The pressure is then integrated in a “pressure sub-step” from this intermediate time to the end of the timestep, using a pressure field found by solving a Poisson equation that is formed by enforcing continuity at the end of the pressure sub-step.

When the bodies are elastically mounted, the equation of motion of each of the structures (Eq. 4.2) which will be coupled to Navier–Stokes equations via the immersed boundary acceleration term (Eq. 4.1) is given by

$$\begin{aligned} m\ddot{y}+ky=F(t) \end{aligned}$$

(4.2)

where m, k and F(t) are mass, stiffness and the time dependent force caused by fluid stresses. y, $\dot{y}$ and $\ddot{y}$ are respectively the displacement, velocity and acceleration of the cylinder. The stiffness is expressed in this study via the reduced velocity $U^* = U/(f_N \cdot D)$, where $f_N = \sqrt{k/m}/(2\pi )$ is the natural structural frequency of the cylinder structure. The acceleration term in the Navier–Stokes equations (Eq. 4.1) is affected by the body motion, and the fluid forces in Eq. (4.2) come from the fluid stresses, proving a two-way coupling between the fluid and structural equations.

At the immersed boundary, a no-slip boundary condition is applied such that

$$\begin{aligned} \mathbf {u}_i={\dot{\mathbf{X_i}}} \end{aligned}$$

(4.3)

where the $\mathbf {u}_i$ represents the velocity component of fluid and ${\dot{\mathbf{X_i}}}$ is the velocity of the boundary. A Neumann condition ($\partial P/\partial \mathbf {n} = 0$) where $\mathbf {n}$ is the normal vector enforces a zero pressure gradient at the surface. The presence of the boundary is enforced by identifying ghost points—points in the Cartesian mesh which are inside the boundary but have neighbours in the fluid. A stencil is formed for these points that involves the boundary condition at the closest point on the boundary to the ghost node. This modified stencil is what provides the immersed boundary acceleration term in Eq. (4.1), and the ghost point values then make it possible to simply interpolate fluid field values such as pressure and traction to the immersed surface to calculate forces. Body motion is therefore relatively simply implemented as the only requirement is to identify the ghost points at each timestep and construct the interpolation stencil.

The outer domain boundary conditions are standard for an open flow. For the velocity, a freestream condition is applied upstream and laterally, and a Neumann condition ($\partial \mathbf {u}/\partial \mathbf {n} = 0$) is applied at the outflow. For the pressure, a Neumann condition ($\partial P/\partial \mathbf {n} = 0$) is applied at the upstream and lateral boundaries, and a Dirichlet condition $P=0$ applied at the outflow.

The justification and validation of this set of boundary conditions for tandem two-cylinder system was provided in [12, 13, 15].

The initial condition for all the simulations is assumed to start from rest. Since all the simulations started from rest, the presence of any hysteresis was not assessed.

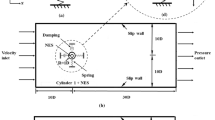
The two cylinders are symmetrically spaced on sides of the origin point. A box with a regular grid spacing and dimensions of $(p+4)D \times 4D$ is placed with origin in its centre. The inlet and outlet distance from the closest sides of the box is 13D and 35D in x-direction. In y-direction 13D is the lateral distance and is considered from the top and bottom edges of the box. Total number of nodes is 2048 and 1024 in x-direction and y-direction, respectively. The smallest mesh size is $\varDelta x = D/128$ in the box around the bodies. A schematic description of this defined mesh domain is shown in Fig. 4.1.

A mesh convergence study was investigated for the same code and similar set-up in [12]. The convergence data was reproduced and shown in Table 1 of [12].

This code has previously being compared to the published results for similar fluid-structure interaction problems from multiple different codes and has been shown faithfully to reproduce the results [12, 13].

Fig. 4.1

Schematic description of the defined domain which controls the mesh resolution for the present study. The small box around the cylinders has the dimensions of $(p+4)D \times 4D$

Fig. 4.2

Schematic description of the present study for a rigid-cylinder system and b elastically mounted system, where D is diameter, p is pitch, U is free stream velocity, Re is Reynolds number of free stream, k is spring stiffness and m is mass of the cylinder

4.3 Results

The base investigation starts with two rigidly mounted cylinders in a tandem arrangement as a limiting case for examining the elastically-mounted cylinders. The schematic description of the system is provided in Fig. 4.2.

4.3.1 Rigidly-Mounted Cylinders

The data for maximum lift coefficient, mean drag coefficient and frequency spectrum for the rigid two-cylinder system as a function of p are presented in Fig. 4.3.

Fig. 4.3

The plots of maximum lift coefficient, mean drag coefficient and frequency spectrum for a first cylinder, b second cylinder. The horizontal red lines are representative of the corresponding parameter value for a single cylinder system. The vertical dashed lines are used to separate the regimes

There are four distinct regimes as a function of p. Example images of each regime showing contours of vorticity are provided in Fig. 4.4.

In the first regime which is for closely placed cylinders ($p \le 1.8$), they behave as a single streamlined structure. The separated flow from the front cylinder reattaches to the rear cylinder and stable recirculation appears in the gap between the two rigid cylinders.

By increasing p in the range of $1.8 < p \le 3.6$, in regime 2, the flow in the gap experiences some fluctuations. However, the separated flow from the front cylinder still reattaches to the rear cylinder, and there is no distinct vortex formation and shedding in the gap.

Further increase in p results in the commencement of regime 3. This regime is marked by the onset of full vortex formation and shedding in the gap ($3.6 < p \le 4.6$) from the front cylinder. Effectively a single vortex occupies the entire gap between the cylinders.

With increasing p, with the formation of a second vortex in the gap, the flow conditions switch to regime 4. The frequency of vortex shedding for both of the cylinders is almost identical and converges to the single cylinder vortex shedding frequency for large values of p.

For a very high p, the parameters for the front cylinder converges to those of a single cylinder system. Interestingly, when the cylinders are far enough apart, even for very large values of p, the rear cylinder parameters, including $C_{L_{max}}$ and $\overline{C_{D}}$ converges to a different value due to the flow interference effect of the front cylinder.

Fig. 4.4

Flow visualizations of two-rigid cylinder system with a $p=1.5$ (regime 1), b $p=3.0$ (regime 2), c $p=4.0$ (regime 3), d $p=7.0$ (regime 4). All the flow visualizations are in the same phase (maximum lift coefficient of rear cylinder). Vorticity fields are shown by red and blue colors for positive and negative signs, respectively

Fig. 4.5

Amplitude of oscillation for a front cylinder and b rear cylinder as a function of $U^*$ for systems with different pitch. The lines are used to provide a better visual guide

4.3.2 Elastically-Mounted Cylinders

In the next stage, elastically-mounted cylinders with one degree of freedom oscillation in cross-flow direction have been studied.

One representative pitch from each regime of rigid cylinder system has been selected—$p = 1.5, 3, 4, 7$—and the study extended to elastically-mounted systems as a function of $U^*$ for these pitches. The maximum cross-flow displacement for each representative pitch with different values of $U^*$ for front and rear cylinders in comparison to the single cylinder oscillation are presented in Fig. 4.5.

As can be seen, the effect of adding an additional cylinder on the front cylinder is subtle, while the rear cylinder presents completely different behaviour. When $p=1.5$, the behaviour of two cylinders are different from the systems with larger value of p and both of the cylinders oscillate with higher amplitude of oscillation when $U^*$ is high enough. Once the distance between two cylinders increases, there is a loss of feedback from the rear to the front cylinder, and the amplitude of oscillation for the elastically mounted front cylinder converges to that of the single cylinder system. This critical pitch which is in the range of $1.5< P_{cr}<3.0$ is considerably shorter than critical value of p in the rigidly mounted two-cylinder system for the onset of vortex shedding form the front cylinder.

Figure 4.6 presents the response of the single cylinder and the front cylinder in two-cylinder system in terms of the maximum lift coefficient $C_{L_{max}}$, maximum amplitude of oscillation $A_{max}$, frequency of oscillation f and phase lag between the lift force and oscillation as a function of reduced velocity $U^*$.

Fig. 4.6

From top to bottom, the $C_{L_{max}}$, $A_{max}$, frequency of oscillation and phase lag between displacement and lift force data is shown for the single cylinder and the front cylinder of two-cylinder system as a function of $U^*$. The corresponding data for single cylinder is shown with $\large {\bullet }$, and the front cylinder data is shown with $\large {\circ }$, $\times$, $\blacktriangle$ and $\blacksquare$ when p $=$ 1.5, 3.0, 4.0 and 7.0

As can be seen in this figure, by increasing pitch to $p>1.5$ the oscillation and lift force properties get closer to the single cylinder properties.

The oscillation of the rear cylinder is different from the single cylinder. For low values of $U^*$, the front cylinder has higher amplitude of oscillation while higher $U^*$ values, rear cylinder oscillates with higher amplitude for all the values of p that were tested.

By comparing the data for all values of pitch, the highest amplitude of oscillation of the system can be seen for the rear cylinder when $U^*=7.0$ for all values of p.

The frequency of oscillation for the rear cylinder is shown in Fig. 4.7. The highest amplitude, when $U^*=7.0$, is concurrent with a frequency of oscillation close to the natural frequency. This indicates the synchronization in the system. Since this is a non-linear phenomenon and resonance is a linear phenomenon, it would be an over simplification to consider this non-linear high amplitude oscillation as resonance.

Fig. 4.7

The primary frequency of oscillation for the rear cylinder in two-cylinder system with different p. The natural frequency of oscillation is shown by the solid line

The flow visualization of the elastically-mounted system for $U^* = 7.0$ for all values of p is presented in Fig. 4.8. In all the images, the rear cylinder is at its maximum displacement.

Fig. 4.8

Flow visualizations for elastically-mounted systems when the rear cylinder is in the maximum cross-flow displacement from the starting point and $U^*=7.0$ with a $p=1.5$, b $p=3.0$, c $p=4.0$ and d $p=7.0$. Vorticity fields are shown by red and blue colors for positive and negative signs, respectively. The initial position of each cylinder is shown by +

When $p=1.5$, although the separated flow reattaches the rear cylinder in rigid cylinder, there are strong fluctuations in the gap of the elastically-mounted system, driving an oscillation of both cylinders that is much larger than that for a single isolated cylinder. A previous study [12] has shown this mode is driven by a complicated interaction where vortices are forced between the gap between the bodies, such that the negative vortex from the top of the front cylinder interacts with the positive vortex formed at the bottom of the rear cylinder. For this to occur the two cylinders need to oscillate essentially out of phase, as is evident in Fig. 4.8a.

For the larger pitches $p \geqslant 3$, the images in Figs. 4.8b–d show that the vortex formation process from the front cylinder is basically unaffected by the presence of the rear cylinder. It is also clear that there is some similarity of the vortex formation process from the rear cylinder and its interaction with the vortices impinging on the rear cylinder from the front cylinder. The wake behind the two bodies for $p = 3, 4, 7$ all display a variant of a 2P wake [2], with two pairs of oppositely signed vortices formed per cycle of oscillation. However, it appears that the phase of the oscillation between the front and rear cylinders adjusts so that the positive vortex (shown in red) formed from the front cylinder passes under the rear cylinder when the rear cylinder is at the peak of its motion.

4.4 Conclusion

The rigid cylinder system simulation results with different pitch confirm the experimental and high Re results by Zdravkovich [7]. There are four distinct regimes for aerodynamic forces and frequency spectrum of two rigid cylinders as a function of p. By increasing the p to high values, the studied parameters converge to specific values. Although these converged values are very close to single-cylinder values for the front cylinder, there is a considerable difference for the rear cylinder. This conclusion indicates the importance of studying systems with multiple structures.

In elastically-mounted cylinder systems, the cylinders are free to oscillate in the transverse direction to the free stream. It is found that the elasticity (the reduced velocity) has a significant impact on the behaviour of the flow. For two cylinders with short pitch of $p = 1.5$ (which is much less than the critical value of p for the onset of vortex shedding in the gap between cylinders in the equivalent rigid system) large amplitude oscillations and associated vortex shedding can be observed for both cylinders once $U^{*}$ is large enough. For cylinders with longer pitch, the vortex shedding from, and the motion of, the front cylinder is basically independent of pitch, and the rear cylinder motion adjusts to maintain a consistent motion with respect to the arrival of a vortex shed from the front cylinder.