Keywords

1 Introduction

Computing the eigenvalue decomposition of symmetric matrices is one of the most investigated problems in numerical linear algebra [6, 11]. For a matrix of moderate size, having reduced the symmetric matrix into a symmetric tridiagonal one by means of a similarity orthogonal transformation, the problem reduces to the computation of the eigendecomposition of a tridiagonal matrix.

There are different methods to compute the eigenvalues of symmetric tridiagonal matrices, such as the bisection method [14], the QR method [14] and divide & conquer methods [2, 7]. For computing the eigenvectors one can use inverse iteration [14], the QR method [14] and the multiple relatively robust representations algorithm [5, 13, 15]. The latter algorithm is based on the twisted factorization of the involved tridiagonal matrix to determine the position where the sought eigenvector has a large entry [5, 15, 16].

Once an eigenvalue is computed, a deflation algorithm was proposed in [4] in order to remove it from the tridiagonal matrix and reduce the dimension of the problem by one. Such an algorithm can also be used to compute the eigenvector associated to the computed eigenvalue and it is based on the twisted factorization used in [5, 15].

In this manuscript we consider a modified version of the aforementioned algorithm to compute an eigenvector of a symmetric tridiagonal matrix, supposing the corresponding eigenvalue is known.

Without loss of generality, we consider only the real case. The complex Hermitian one can be handled in the same way.

We illustrate the behavior of the proposed method with some numerical examples. The manuscript is organized as follows. In Sect. 2 the notation used in the manuscript is given. In Sect. 3 the main features of the QR method are described. The proposed algorithm is described in Sect. 4, followed by the section of numerical examples and by the conclusions.

2 Notations and Definitions

Matrices are denoted with upper case letters and their entries with lower case letters, i.e., the element (i, j) of the matrix T is denoted by t i,j.

The submatrix of the matrix B made by the rows i, i + 1, i + 2, …, i + k, with 1 ≤ i ≤ n − k, 0 ≤ k ≤ n − i, and columns j, j + 1, j + 2, …, j + l, with 1 ≤ j ≤ n − l, 0 ≤ l ≤ n − j, is denoted by B i:i+k,j:j+l. If the matrix T is symmetric, the submatrix made by the rows and columns i, i + 1, i + 2, …, i + k, with 1 ≤ i ≤ n − k, 0 ≤ k ≤ n − i, is simply denoted by T i:i+k.

The identity matrix of order n is denoted by I n or by I if there is no ambiguity.

The matrix T − κI, with \( \kappa \in {\mathbb {R}}, \) is denoted by T(κ).

The principal diagonal of a matrix \( B \in {\mathbb {R}}^{m \times n}\) is denoted by diag(B).

The machine precision is denoted by ε.

The ith vector of the canonical basis of \( {\mathbb {R}}^n\) is denoted by \({\mathbf {e}}_i^{(n)},\) or simply by e i, if there is no ambiguity.

Definition 1

Given \( B \in {\mathbb {R}}^{m \times n}, m \ge n,\) let B = UΣV T be its singular value decomposition, with \( U \in {\mathbb {R}}^{m \times m}, V \in {\mathbb {R}}^{n \times n} \) orthogonal and \( \varSigma \in {\mathbb {R}}^{m \times n} \) diagonal, with \({\mathrm {diag}}(\varSigma ) = \left [\begin {array}{cccc} \sigma _1, & \sigma _2, & \cdots & \sigma _n \end {array} \right ]^T, \) and σ i ≥ σ i+1, i = 1, …, n − 1.

The columns of B are said ε-linear dependent if σ n ≤ ε∥B∥2.

The columns of B are said strongly linear independent if σ n ≫ ε∥B∥2 > 0.

3 Implicit QR Method

Let \( T \in {\mathbb {R}}^{ n \times n} \) be the symmetric tridiagonal matrix

$$\displaystyle \begin{aligned} T= \left[ \begin{array}{ccccc} t_{1,1} & t_{1,2} & & \\ t_{2,1} & t_{2,2} & \ddots & \\ & \ddots & \ddots & t_{n-1,n} \\ & & t_{n,n-1} & t_{n,n} \end{array} \right], \end{aligned}$$

with t i,i+1 = t i+1,i, i = 1, …, n − 1.

Let us suppose that T is irreducible, i.e., t i,i+1≠0, i = 1, …, n − 1 and let T = XΛX T be its eigenvalue decomposition, with \( X \in {\mathbb {R}}^{ n \times n} \) orthogonal, and \(\varLambda \in {\mathbb {R}}^{ n \times n} \) diagonal, with diag(Λ) = [λ 1, …, λ n]T. Since T is irreducible, then λ i≠λ j, with i≠j, i, j = 1, …, n.

The Implicit QR (IQR) method is the standard method for computing the eigenvalue decomposition of matrices of moderate size [6]. In particular, MATLAB uses the LAPACK routine DSYEV, based on the QR method, to compute eigenvalues and eigenvectors of a real symmetric matrix [1].

Given a symmetric irreducible tridiagonal matrix \( T \in {\mathbb {R}}^{n \times n}\), and \( \kappa \in {\mathbb {R}},\) one sweep of IQR with shift κ consists of computing the similarity transformation

$$\displaystyle \begin{aligned} \hat{T}^{(n)} = \hat{G}_{n-1} \hat{G}_{n-2} \cdots \hat{G}_{1} \hat{T}^{(1)} \hat{G}^T_{1} \cdots \hat{G}^T_{n-2} \hat{G}^T_{n-1}, \end{aligned}$$

where \( \hat {T}^{(1)} =T \) and \( \hat {G}_i,\; i=1,\ldots , n-1, \) are Givens rotations

$$\displaystyle \begin{aligned} \hat{G}_i= \left[ \begin{array}{cccc} I_{i-1} & & & \\ & \hat{c}_i & \hat{s}_i & \\ & -\hat{s}_i & \hat{c}_i & \\ & & & I_{n-i-1} \end{array} \right],\quad i=1,\ldots, n-1. \end{aligned}$$

with \( \hat {c}_i^2 + \hat {s}_i^2=1. \) Without loss of generality, we assume that \( \hat {c}_i \ge 0. \) Hence the matrix \( \hat {Q} \) in (1) is uniquely defined.

In particular, \( \hat {G}_1 \) is the Givens rotation acting on the first two rows of \( \hat {T}^{(1)}, \) whose coefficients \( \hat {c}_1 \) and \( \hat {s}_1 \) are such that

$$\displaystyle \begin{aligned} \left[ \begin{array}{rc} \hat{c}_1 & \hat{s}_1 \\ -\hat{s}_1 & \hat{c}_1 \end{array} \right] \left[ \begin{array}{c} \hat{t}_{1,1}^{(1)} - \kappa \\ \hat{t}_{2,1}^{(1)} \end{array} \right] = \left[ \begin{array}{c} \hat{\alpha}_1 \\ 0 \end{array} \right], \end{aligned}$$

with \( \hat {\alpha }_1 = \| \left [ \begin {array}{cc} \hat {t}_{1,1}^{(1)} - \kappa , & \hat {t}_{2,1}^{(1)} \end {array}\right ] \|{ }_2. \) The structure of the matrix \( \hat {T}^{(2)}= \hat {G}_{1} \hat {T}^{(1)} \hat {G}^T_{1} \) differs from the one of a tridiagonal matrix for an entry different from 0 in position (3, 1) (and, symmetrically, in position (1, 3)), called “bulge”.

Each of the other Givens rotations \( \hat {G}_i\) are applied to move the bulge one position downward along the second subdiagonal/superdiagonal and eventually remove it [11], i.e, the matrix

$$\displaystyle \begin{aligned}\hat{T}^{(i)} = \hat{G}_{i-1} \hat{G}_{i-2} \cdots \hat{G}_{1} \hat{T}^{(1)} \hat{G}^T_{1} \cdots \hat{G}^T_{i-2} \hat{G}^T_{i-1}, \end{aligned}$$

has the bulge in position (i − 1, i + 1) (and, symmetrically, in position (i + 1, i − 1)), \( \hat {T}^{(i+1)} = \hat {G}_{i} \hat {T}^{(i)} \hat {G}^T_{i} \) has the bulge in position (i, i + 2) (and, symmetrically, in position (i + 2, i)), and so on. The matrix

$$\displaystyle \begin{aligned} \hat{Q} = \hat{G}_{n-1} \hat{G}_{n-2} \cdots \hat{G}_{1} \end{aligned} $$
(1)

is orthogonal Hessenberg.

In the sequel, we call the sweep of the IQR method described above a “forward” IQR (FIQR) sweep because it starts from the top-left corner of \(\hat {T}_1 \) and ends in the bottom-right one.

The IQR method can also be implemented in a “backward” fashion, i.e., starting from the bottom-right corner of T and ending in the top-left corner [9]. We will refer to one sweep of this procedure as a backward IQR (BIQR) sweep.

Let \(\tilde {T}^{(1)}=T. \) In a BIQR sweep with shift κ, a sequence of Givens rotations

$$\displaystyle \begin{aligned} \tilde{G}_i= \left[ \begin{array}{cccc} I_{n-i-1} & & & \\ & \tilde{c}_i & \tilde{s}_i & \\ & -\tilde{s}_i & \tilde{c}_i & \\ & & & I_{i-1} \end{array} \right],\quad i=1,\ldots, n-1, \end{aligned}$$

with \( \tilde {c}_i^2 + \tilde {s}_i^2=1, \) is determined in the following way.

The coefficients \( \tilde {c}_1 \) and \( \tilde {s}_1 \) of \( \tilde {G}_1\) are computed such that

$$\displaystyle \begin{aligned} \left[ \begin{array}{cc} \tilde{t}^{(1)}_{n,n-1},& \tilde{t}^{(1)}_{n,n}-{ \kappa} \end{array}\right] \left[ \begin{array}{rc} \tilde{c}_1 & \tilde{s}_1 \\ -\tilde{s}_1 & \tilde{c}_1 \end{array} \right] = \left[ \begin{array}{cc} 0,& \tilde{\alpha}_{n} \end{array}\right], \end{aligned}$$

with \( \tilde {\alpha }_{n}= \| \left [ \begin {array}{cc} \tilde {t}^{(1)}_{n,n-1},& \tilde {t}^{(1)}_{n,n}- { \kappa } \end {array}\right ] \|{ }_2. \) The matrix \( \tilde {T}^{(2)}=\tilde {G}^T_1 \tilde {T}^{(1)} \tilde {G}_1\) has a bulge in position (n, n − 2) (and, symmetrically, in position (n − 2, n)).

The Givens rotations \( \tilde {G}_i, \; i=2,\ldots ,n-1,\) are sequentially applied to \( \tilde {T}^{(2)}\) to move the bulge upward along the second subdiagonal and eventually remove it in the matrix \( \tilde {T}^{(n)} = \tilde {G}^T_{n-1}\tilde {G}^T_{n-2} \cdots \tilde {G}^T_1 \tilde {T}^{(1)} \tilde {G}_1 \cdots \tilde {G}_{n-2} \tilde {G}_{n-1}.\)

Let \( \tilde {Q}= \tilde {G}_1 \cdots \tilde {G}_{n-2} \tilde {G}_{n-1}.\) Without loss of generality, we assume \(\tilde {c}_i \ge 0, \) which makes the matrix \( \tilde {Q}\) uniquely defined.

Let λ be an eigenvalue of T with corresponding eigenvector x. In infinite precision arithmetic, if λ is chosen as shift κ in the FIQR sweep, λ shows up in position (n, n) of \(\hat {T}^{(n)}. \) Moreover, \(\hat {t}_{n-1,n}^{(n)}=\hat {t}_{n,n-1}^{(n)}=0\), and \( {{\mathbf {x}}}= \hat {Q}(:,n). \) In particular, since

$$\displaystyle \begin{aligned} \begin{array}{@{}l@{}} \hat{Q}= \\ \; \left[ \begin{array}{r@{\hspace{.4cm}}r@{\hspace{.4cm}}r@{\hspace{.4cm}}r@{\hspace{.4cm}}r@{\hspace{.4cm}}r} \hat{c}_1 & -\hat{s}_1 \hat{c}_2 & \hat{s}_1 \hat{s}_2 \hat{c}_3 & \ddots &-1^n \hat{c}_{n-1} \prod_{i=1}^{n-2} \hat{s}_i & -1^{n+1} \prod_{i=1}^{n-1} \hat{s}_i \\ \hat{s}_1 & \hat{c}_1 \hat{c}_2 &-\hat{c}_1 \hat{s}_2 \hat{c}_3 & \ddots &-1^{n-1} \hat{c}_1 \hat{c}_{n-1} \prod_{i=2}^{n-2} \hat{s}_i & -1^{n} \hat{c}_1 \prod_{i=2}^{n-1} \hat{s}_i \\ & \hat{s}_1 & \hat{c}_1 \hat{c}_2 & \ddots & \vdots \hspace{1.2cm} & \vdots \hspace{1.2cm} \\ & & \ddots & \ddots & -\hat{c}_{n-3}\hat{s}_{n-2} \hat{c}_{n-1} & \hat{c}_{n-3}\hat{s}_{n-2} \hat{s}_{n-1} \\ & & & \hat{s}_{n-2}& \hat{c}_{n-2} \hat{c}_{n-1} & -\hat{c}_{n-2}\hat{s}_{n-1} \\ & & & & \hat{s}_{n-1} & \hat{c}_{n-1} \end{array} \right], \end{array} \end{aligned}$$

then

$$\displaystyle \begin{aligned} {{\mathbf{x}}}=\hat{Q}(:,n)= \left[ \begin{array}{c} -1^{n+1} \prod_{i=1}^{n-1} \hat{s}_i \\ -1^{n} \hat{c}_1 \prod_{i=2}^{n-1} \hat{s}_i \\ -1^{n-1} \hat{c}_2 \prod_{i=3}^{n-1} \hat{s}_i \\ \vdots \\ \hat{c}_{n-3}\hat{s}_{n-2} \hat{s}_{n-1} \\ -\hat{c}_{n-2}\hat{s}_{n-1} \\ \hat{c}_{n-1} \end{array} \right]. \end{aligned} $$
(2)

Analogously, in infinite precision arithmetic, if λ is chosen as shift κ in the BIQR sweep, λ shows up in position (1, 1) of \(\tilde {T}^{(n)}. \) Moreover, \(\tilde {t}_{1,2}^{(n)}=\tilde {t}_{2,1}^{(n)}=0\), and \( {{\mathbf {x}}}= \tilde {Q}(1,:)^T, \)

$$\displaystyle \begin{aligned} {{\mathbf{x}}}= \left[ \begin{array}{c} \tilde{c}_{n-1} \\ -\tilde{c}_{n-2}\tilde{s}_{n-1} \\ \tilde{c}_{n-3}\tilde{s}_{n-2} \tilde{s}_{n-1} \\ \vdots \\ -1^{n-1} \tilde{c}_2 \prod_{i=3}^{n-1} \tilde{s}_i \\ -1^{n} \tilde{c}_1 \prod_{i=2}^{n-1} \tilde{s}_i \\ -1^{n+1} \prod_{i=1}^{n-1} \tilde{s}_i \\ \end{array} \right]. \end{aligned} $$
(3)

Therefore, for a given eigenvalue λ, it is suggested in [11] to apply one sweep of either forward or backward IQR with shift λ to compute the corresponding eigenvector with O(n) floating point operations [11].

Unfortunately, forward instability can occur in floating point arithmetic in one forward/backward IQR sweep with shift λ and the last column of \( \hat {Q}\) (the first row of \(\tilde {Q}\)) may be far from the sought eigenvector [12].

In particular, forward instability occurs at step j of one sweep of FIQR if and only if the shift κ is very close to one of the eigenvalues of \(\hat {T}^{(j)}_{1:j,1:j}\) and the last entry of the corresponding eigenvector is tiny [12]. As a consequence, the entries \(t^{(j)}_{j,j-1}\) and \(t^{(j)}_{j,j+1}\) are “sufficiently” smallFootnote 1 [12]. By (2), the last component of the eigenvector is given by \( \hat {c}_j. \) Hence, forward instability happens if κ is very close to one of the eigenvalues of \(\hat {T}_{1:j,1:j}\) and \( \hat {c}_j \sim O(\varepsilon ). \) This means that the first j columns of \(\hat {T}_{1:j,1:j}\) are ε-linear dependent.

The same phenomenon can occur in a BIQR sweep.

To examine in which step of a IQR sweep forward instability can occur, let us consider the following Corollary [8, p.149].

Corollary 1

Let \( A \in {\mathbb {R}}^{n \times n} \) be a symmetric matrix and let B be a submatrix obtained by deleting r rows from A. Then

$$\displaystyle \begin{aligned} \sigma_k(A) \ge \sigma_k(B) \ge \sigma_{k+r}(A),\;\; k=1,\ldots,n, \end{aligned}$$

where σ ℓ(A) ≡ 0, if ℓ > n.

Let us suppose that σ n−1(T(λ)) ≫ ε > σ n(T(λ)) = 0 and σ j−1(T 1:j,:(λ)) ≫ σ j(T 1:j,:(λ)) ∼ O(ε), for a j ∈{2, …, n}. By Corollary 1, all the submatrices T 1:j+ℓ,:(λ) are ε-singular, ℓ = 1, …, n − j, and

$$\displaystyle \begin{aligned} \sigma_{j+\ell}(T_{1:j+\ell,:}(\lambda))\ge \sigma_{j+\ell}(T_{1:j+\ell,1:j+\ell}(\lambda)), \quad \ell =1,\ldots, n-j, \end{aligned}$$

i.e., the submatrices T 1:j+ℓ,1:j+ℓ(λ) are ε-singular as well.

On the other hand,

$$\displaystyle \begin{aligned} \begin{array}{c} \sigma_{j-1}(T_{n-j+1:n,:}(\lambda))\ge \sigma_{n-1}(T(\lambda)) \gg \varepsilon, \\ \sigma_{j-1}(T_{n-j+1:n,:}(\lambda)) \ge \sigma_{j}(T_{n-j+1:n,n-j+1:n}(\lambda)) \ge \sigma_{j}(T_{n-j+1:n,:}(\lambda)). \end{array} \end{aligned}$$

This means that forward instability is not encountered in the first n − j − 1 steps of FIQR and in the first j steps of BIQR.

In the following example it is shown how the sequences \(\{ \hat {c}_j\}_{j=1}^{n-1} \) and \(\{ \tilde {c}_j\}_{j=1}^{n-1}, \) computed in floating point arithmetic, differ from those computed in infinite precision arithmetic.

Example 1

Let \( T \in {\mathbb {R}}^{n \times n}, \; n= 100, \) be a symmetric irreducible tridiagonal matrix with its entries generated by the MATLAB function randn.Footnote 2

Let \(T= X^{(M)} \varLambda ^{(M)} X^{(M)^T} \) be the eigenvalue decomposition of T computed by using the MATLAB function eig, with \( \varLambda ^{(M)} ={\mathrm {diag}}(\lambda ^{(M)}_1\lambda ^{(M)}_2,\ldots ,\lambda ^{(M)}_n),\) with \(\lambda ^{(M)}_i\ge \lambda ^{(M)}_{i+1}\; i=1,\ldots , n-1.\)

We report the behaviour of one sweep of F/B IQR with shift \(\lambda ^{(M)}_{19},\) although a similar behavior can be observed if we choose almost any \(\lambda ^{(M)}_{i}, \; i=1,\ldots , n,\) as a shift.

Let \( ( \bar {\lambda }, \bar {{\mathbf {x}}} )\) be the eigenpair computed by a few steps of inverse iteration with initial guess \((\lambda ^{(M)}_{19}, X^{(M)}(:,19)). \) In this way, \( \bar {{\mathbf {x}}} \) is computed with higher accuracy with respect to X (M)(:, 19)).

Let \(\{ \check {c}_i\}_{i=1}^{n-1} \) and \(\{ \bar {c}_i\}_{i=1}^{n-1} \) be the sequence of the cosines of the Givens matrices \(\{ \check {G}_i\}_{i=1}^{n-1} \) and \(\{ \bar {G}_i\}_{i=1}^{n-1}, \) determined in order to transform \( \bar {{\mathbf {x}}} \) to e n and e 1, respectively, i.e.,

$$\displaystyle \begin{aligned} \check{G}_i= \left[ \begin{array}{cccc} I_{n-i-1} & & & \\ & \check{c}_i & \check{s}_i & \\ & -\check{s}_i & \check{c}_i & \\ & & & I_{i-1} \end{array} \right], \;\; \mbox{such that} \;\; \check{G}_{n-1}\check{G}_{n-2} \cdots \check{G}_1 \bar{{\mathbf{x}}} = {\mathbf{e}}_n, \end{aligned}$$
$$\displaystyle \begin{aligned} \bar{G}_i= \left[ \begin{array}{cccc} I_{i-1}& & & \\ & \bar{c}_i & \bar{s}_i & \\ & -\bar{s}_i & \bar{c}_i & \\ & & & I_{n-i-1} \end{array} \right], \;\;\mbox{such that} \;\; \bar{G}_1\cdots \bar{G}_{n-2}\bar{G}_{n-1} \bar{{\mathbf{x}}} = {\mathbf{e}}_1.\end{aligned} $$

Without loss of generality, we assume \(\check {c}_i \ge 0 \) and \(\bar {c}_i \ge 0, \) i = 1, …, n − 1.

Since \( \bar {{\mathbf {x}}} \) is computed with high accuracy, the sequences \(\{ \check {c}_i\}_{i=1}^{n-1} \) and \(\{ \bar {c}_i\}_{i=1}^{n-1}, \) are computed with high accuracy, too [10].

In infinite precision arithmetic, the sequences \(\{ \check {c}_i\}_{i=1}^{n-1} \) and \(\{ \hat {c}_i\}_{i=1}^{n-1} \) should be the same, while in floating point arithmetic the sequence \(\{ \hat {c}_i\}_{i=1}^{n-1} \) can depart from the sequence \(\{ \check {c}_i\}_{i=1}^{n-1} \) due to the forward instability [10]. The same holds for the sequences \(\{ \bar {c}_i\}_{i=1}^{n-1} \) and \(\{ \tilde {c}_i\}_{i=1}^{n-1}. \)

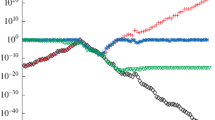
The sequences \(\{ \hat {c}_i\}_{i=1}^{n-1}, \ \{ \check {c}_i \}_{i=1}^{n-1} \), \(\{ |\hat {t}_{i-1,i}^{(i)}|+|\hat {t}_{i,i+1}^{(i)}|\}_{i=1}^{n-1} \), \( \{ \check {\sigma }_i \}_{i=1}^{n-1}, \) and \(\{ \hat {\sigma }_i\}_{i=1}^{n-1}, \) with \( \check {\sigma }_i =\min ({\mathrm {svd}}(T_{:,i:n}(\lambda ^{(M)}_{19}) ))\) and \( \hat {\sigma }_i =\min ({\mathrm {svd}}(T_{i:n,i:n}(\lambda ^{(M)}_{19}))), \) denoted respectively by “∗”, “+ ”, “∘”, “◇” and “∇”, are displayed in Fig. 1 on a logarithmic scale.

Fig. 1
figure 1

Sequences \(\{ \hat {c}_i\}_{i=1}^{n-1}, \ \{ \check {c}_i \}_{i=1}^{n-1} \), \(\{ |\hat {t}_{i-1,i}^{(i)}|+|\hat {t}_{i,i+1}^{(i)}|\}_{i=1}^{n-1} \), \( \{ \check {\sigma }_i \}_{i=1}^{n-1}, \) and \(\{ \hat {\sigma }_i\}_{i=1}^{n-1}, \) denoted respectively by “asterisk”, “plus”, “circle”, “diamond” and “triangledown”, related to \( T(\lambda ^{(M)}_{19})\), with T the matrix of Example 1 and \(\lambda ^{(M)}_{19}\) the 19th ordered eigenvalue computed by eig of MATLAB

Full size image

We can observe that the first and the third sequence have a similar behaviour. The same can be said for the second and the fifth sequence. Moreover, the two sequences of cosines \(\{ \hat {c}_i\}_{i=1}^{n-1}\) and \(\{ \check {c}_i \}_{i=1}^{n-1} \) are similar until forward instability occurs, i.e., until \( \hat {c}_i \) and \( |\hat {t}_{i-1,i}^{(i)}|+|\hat {t}_{i,i+1}^{(i)}| \) are both greater than \(O(\sqrt {\varepsilon }). \)

The sequences \(\{ \tilde {c}_i\}_{i=1}^{n-1}, \ \{ \bar {c}_i \}_{i=1}^{n-1} \), \(\{ |\tilde {t}_{n-i-1,n-i-2}^{(i)}|+|\tilde {t}_{n-i,n-i-1}^{(i)}|\}_{i=1}^{n-1} \), \( \{ \check {\sigma }_i \}_{i=1}^{n-1}, \) and \(\{ \hat {\sigma }_i\}_{i=1}^{n-1}, \) with \( \check {\sigma }_i =\min ({\mathrm {svd}}(T_{:,1:i}(\lambda ^{(M)}_{19}) ))\), \( \hat {\sigma }_i =\min ({\mathrm {svd}}(T_{1:i,1:i}(\lambda ^{(M)}_{19}))), \) denoted respectively by “∗”, “+ ”, “∘”, “◇” and “∇”, are displayed in Fig. 2 in logarithmic scale.

Fig. 2
figure 2

Sequences \(\{ \tilde {c}_i\}_{i=1}^{n-1}, \ \{ \bar {c}_i \}_{i=1}^{n-1} \), \(\{ |\tilde {t}_{n-i-1,n-i-2}^{(i)}|+|\tilde {t}_{n-i,n-i-1}^{(i)}|\}_{i=1}^{n-1} \), \( \{ \bar {\sigma }_i \}_{i=1}^{n-1}, \) and \(\{ \tilde {\sigma }_i\}_{i=1}^{n-1}, \) denoted respectively by “asterisk”, “plus”, “circle”, “diamond” and “triangledown”, related to \( T(\lambda ^{(M)}_{19})\), with T the matrix of Example 1 and \(\lambda ^{(M)}_{19}\) the 19th ordered eigenvalue computed by eig of MATLAB

Full size image

Also in this case, the first and the third sequence have a similar behaviour and the same can be said for the second and the fifth sequence. Moreover, the two sequences of cosines \(\{ \tilde {c}_i\}_{i=1}^{n-1}\) and \(\{ \bar {c}_i \}_{i=1}^{n-1} \) are similar until forward instability occurs, i.e., until \( \tilde {c}_i \) and \(|\tilde {t}_{n-i-1,n-i-2}^{(i)}|+|\tilde {t}_{n-i,n-i-1}^{(i)}| \) are both greater than \(O(\sqrt {\varepsilon }). \)

Summarizing, forward instability occurs if the smallest singular value \(\sigma _j^{(j)}\) of T 1:j,1:j(λ) is close to the machine precision ε, for a certain j ∈{1, …, n}. As a consequence, the elements of the last column of \( \hat {Q} \) of index greater than j begin to depart from the elements of the eigenvector \(\bar {{\mathbf {x}}}.\) Moreover, \( \hat {t}^{(j)}_{j,j-1} \approx \hat {t}^{(j)}_{j+1,j} \approx O(\sqrt {\varepsilon }),\) where \( \hat {t}^{(j)}_{i,k}\) is the (i, k) entry of the matrix obtained after having applied j Givens rotations in the forward IQR sweep with shift \(\bar {\lambda }\) to \(T_{1:n}(\bar {\lambda }) \) [12]. The same holds to one sweep of BIQR, i.e., the first row of the upper Hessenberg matrix \( \tilde {Q} \) is accurately computed as far as the smallest singular value of T j:n(λ) is large enough, for a certain j ∈{1, …, n}.

Hence, the main issue is to determine the index j.

In the next section we consider the problem of determining the index j such that the computed eigenvector will be obtained by \( \hat {Q}(1:j,n) \) and \( \tilde {Q}(1,j+1:n)^T, \) i.e., gluing together the first j entries of \( \hat {Q} \) and the last n − j entries of the first row of \(\tilde {Q}. \)

4 Computation of the Eigenvector

In this section we describe a technique to determine the index j used for constructing the sought eigenvector by fetching the first j entries of the last column of \( \hat {Q} \) and the last n − j entries of the first row of \( \tilde {Q}. \)

If σ n−1(T(λ)) ≫ σ n(T(λ)) and forward instability occurs at step j of one sweep of FIQR with shift λ, the sequence \( \{\hat {c}_i\}_{i=1}^{n}\) begins to depart from the sequence \( \{\check {c}_i\}_{i=1}^{n}\) around the index j. Analogously, the sequence \( \{\tilde {c}_i\}_{i=1}^{n}\) begins to depart from the sequence \( \{\bar {c}_i\}_{i=1}^{n}\) around the index n − j. Therefore, the sought index j can be computed in the following way.

The sequence \( \{\hat {c}_i\}_{i=1}^{n-1} \) generated by one FIQR sweep, is computed until \(\hat {c}_{\hat {\jmath }} < tol_1\) and \(|\hat {t}_{\hat {\jmath }-1,\hat {\jmath }}^{(\hat {\jmath })}|+|\hat {t}_{\hat {\jmath },\hat {\jmath }+1}^{(\hat {\jmath })}|< tol_2,\) with tol 1 and tol 2 fixed tolerances and \( 1 \le \hat {\jmath }\le n-1.\)

The sequence \( \{\tilde {c}_i\}_{i=1}^{n-1}, \) generated by one BIQR sweep, is thus computed until \(\tilde {c}_{\tilde {\jmath }} < tol_1\) and \(|\tilde {t}_{\tilde {\jmath }-1,\tilde {\jmath }}^{(\tilde {\jmath })}|+|\tilde {t}_{\tilde {\jmath },\tilde {\jmath }+1}^{(\tilde {\jmath })}|< tol_2.\)

Hence, the sought index j is computed as the index \( {\bar {\jmath }} \) such that

$$\displaystyle \begin{aligned} \hat{c}_{\bar{\jmath}}+\tilde{c}_{\bar{\jmath}} \ge \hat{c}_i+\tilde{c}_i, \quad i,{\bar{\jmath}} \in [ \tilde{\jmath}, \hat{\jmath}], i \ne {\bar{\jmath}}, \end{aligned}$$

i.e., the index \( {\bar {\jmath }} \) is chosen so that the columns of \( T_{:, 1:{\bar {\jmath }}} \) and \( T_{:, {\bar {\jmath }}:n} \) are strongly linear independent.

The last column of \( \hat {Q} \) in (2) depends on all the Givens coefficients \( \hat {c}_i \) and \( \hat {s}_i, \ i=1,\ldots , n-1, \) while the first row of \( \tilde {Q}\) in (3) depends on all the Givens coefficients \( \tilde {c}_i \) and \( \tilde {s}_i, \ i=1,\ldots , n-1. \)

Therefore, at the first sight one can say that both the last column of \( \hat {Q} \) and the first row of \( \tilde {Q}\) must be computed in order to construct the sought eigenvector even though the “splitting” index j is already determined.

In the sequel we show that the sought approximation of the eigenvector can be computed relying only on the knowledge of \( \hat {c}_i \) and \( \hat {s}_i, \ i=1,\ldots , j-1, \) and \( \tilde {c}_i \) and \( \tilde {s}_i, \ i=1,\ldots ,n-j+1. \) In fact, once the index j is determined, we observe that the “good” part of the vector (2) can be written as

$$\displaystyle \begin{aligned} \hat{{\mathbf{x}}}_{1:j}= \left[ \begin{array}{@{}c@{}} -1^{n+1} \prod_{i=1}^{n-1} \hat{s}_i \\ -1^{n} \hat{c}_1 \prod_{i=2}^{n-1} \hat{s}_i \\ -1^{n-1} \hat{c}_2 \prod_{i=3}^{n-1} \hat{s}_i \\ \vdots \\ -1^{j+1} \hat{c}_{j-2} \prod_{i=j-1}^{n-1} \hat{s}_i \\ -1^{j} \hat{c}_{j-1} \prod_{i=j}^{n-1} \hat{s}_i \\ -1^{j-1} \hat{c}_{j} \prod_{i=j+1}^{n-1} \hat{s}_i \end{array} \right]= \gamma^{(u)}\hat{{\mathbf{x}}}^{(u)}, \end{aligned}$$

while the “good” part of the vector (2) can be written as

$$\displaystyle \begin{aligned} \tilde{{\mathbf{x}}}_{n-j:n}= \left[ \begin{array}{@{}c@{}} -1^{n-j-1}\tilde{c}_{n-j} \prod_{i=n-j+1}^{n-1} \tilde{s}_i \\ -1^{n-j}\tilde{c}_{n-j-1}\prod_{i=n-j}^{n-1} \tilde{s}_i \\ -1^{n-j+1}\tilde{c}_{n-j-2}\prod_{i=n-j-1}^{n-1} \tilde{s}_i \\ \vdots \\ -1^{n-1} \tilde{c}_2 \prod_{i=3}^{n-1} \tilde{s}_i \\ -1^{n} \tilde{c}_1 \prod_{i=2}^{n-1} \tilde{s}_i \\ -1^{n+1} \prod_{i=1}^{n-1} \tilde{s}_i \\ \end{array} \right]= \gamma^{(b)}\tilde{{\mathbf{x}}}^{(b)}, \end{aligned}$$

where \( \gamma ^{(u)}=\prod _{i=j+1}^{n-1} \hat {s}_i, \; \gamma ^{(b)}=\prod _{i=n-j+1}^{n-1} \tilde {s}_i,\)

$$\displaystyle \begin{aligned} \hat{{\mathbf{x}}}^{(u)}=\left[ \begin{array}{@{}c@{}} -1^{n+1} \prod_{i=1}^{j} \hat{s}_i \\ -1^{n} \hat{c}_1 \prod_{i=2}^{j} \hat{s}_i \\ -1^{n-1} \hat{c}_2 \prod_{i=3}^{j} \hat{s}_i \\ \vdots \\ -1^{j+1} \hat{c}_{j-2} \prod_{i=j-1}^{j} \hat{s}_i \\ -1^{j} \hat{c}_{j-1} \hat{s}_j \\ -1^{j-1} \hat{c}_{j} \end{array} \right], \; \tilde{{\mathbf{x}}}^{(b)}= \left[ \begin{array}{@{}c@{}} -1^{n-j-1}\tilde{c}_{n-j} \\ -1^{n-j}\tilde{c}_{n-j-1} \tilde{s}_{n-j} \\ -1^{n-j+1}\tilde{c}_{n-j-2}\prod_{i=n-j-1}^{n-j} \tilde{s}_i \\ \vdots \\ -1^{n-1} \tilde{c}_2 \prod_{i=3}^{n-j} \tilde{s}_i \\ -1^{n} \tilde{c}_1 \prod_{i=2}^{n-j} \tilde{s}_i \\ -1^{n+1} \prod_{i=1}^{n-j} \tilde{s}_i \\ \end{array} \right]. \end{aligned}$$

Hence, we first normalize both vectors in this way,

$$\displaystyle \begin{aligned} \check{{\mathbf{x}}}_{1:j} =\frac{\hat{{\mathbf{x}}}^{(u)}_{1:j}}{\hat{{\mathbf{x}}}^{(u)}_{j}}, \quad \check{{\mathbf{x}}}_{j+1:n} =\frac{\tilde{{\mathbf{x}}}_{2:n-j+1}^{(b)} }{\tilde{{\mathbf{x}}}_{1}^{(b)}}, \end{aligned}$$

i.e., we divide the first vector by its last component and the second one by its first one in order to have 1 as the j-th entry of the first vector and as the first entry of the second one, and finally we normalize \(\check {{\mathbf {x}}}\) such that \(\| \check {{\mathbf {x}}} \|{ }_2=1.\)

The corresponding MATLAB code to compute the eigenvector associated to a given eigenvalue of a symmetric tridiagonal matrix is freely available and can be downloaded at http://users.ba.cnr.it/iac/irmanm21/TRID_SYM.

5 Deflation

Once the eigenvector \(\check {{\mathbf {x}}}\) has been computed, we can apply to it a sequence of n − 1 Givens rotations G i in order to transform it either to \( \pm {\mathbf {e}}_1^{(n)} \) or to \( \pm {\mathbf {e}}_n^{(n)}, \) where \( \pm {\mathbf {e}}_i^{(n)}, \;i=1,\ldots ,n,\) is the ith vector of the canonical basis of \( {\mathbb {R}}^n. \)

The same Givens rotations G i are applied to the matrix T obtaining

$$\displaystyle \begin{aligned} \check{T}= G_{n-1}G_{n-2}\cdots G_{1} T G_{1}^T \cdots G_{n-2}^T G_{n-1}^T. \end{aligned} $$
(4)

If the eigenvector \( \check {{\mathbf {x}}}\) is computed in an accurate way and satisfies particular properties, it has been shown in [9, 10] that \(\check {T}\) in (4) is still tridiagonal with the entry (2, 1) equal to zero if the Givens rotations are applied in a backward fashion or the entry (n, n − 1) is equal to zero if the Givens rotations are applied in a forward manner. In the first case the last row and column can be dropped and the other eigenvalues to be computed are the eigenvalues of \( \check {T}_{1:n-1}. \) In the other case, the first row and column are removed and the other eigenvalues are the eigenvalues of \( \check {T}_{2:n}. \)

6 Numerical Examples

All the numerical experiments of this section are performed in MATLAB Ver. 2014b, with machine precision ε ∼ 2.22 × 10−16. We have compared the results obtained computing the eigenvector matrix with the following techniques: eig of MATLAB, MR 3 and the proposed method, denoted by MTV.Footnote 3 For the second and the third method, the eigenvalues are computed by the bisection method [14].

For all the experiments, the tolerances tol 1 and tol 2 were chosen equal to \( n \sqrt {\varepsilon }, \) with n the order of the matrix.

Example 2

In this example we consider symmetric tridiagonal matrices \( T_n \in {\mathbb {R}}^{n \times n}, \; n=128, 256, 512, 1024 \) whose elements are generated by the MATLAB function randn.

The latter matrices can be downloaded at http://users.ba.cnr.it/iac/irmanm21/TRID$_$SYM. In Table 1 the orthogonality of the computed eigenvectors with the considered three methods are displayed. In column 5, the average lengths of the computed intervals in which to search the index j are reported.

Table 1 Accuracy of the orthogonality of the computed eigenvectors computed by eig of MATLAB (second column), by MR 3 (third column) and by the proposed method (fourth column)
Full size table

In Table 2 the accuracy of the residuals of the computed eigenvectors with the considered three methods are displayed.

Table 2 Accuracy of the residuals of the eigenvectors computed by eig of MATLAB (second column), by MR 3 (third column) and by the proposed method (fourth column)
Full size table

We can conclude that the eigenvectors obtained with the proposed procedure are computed in an accurate way.

Example 3

In this example \( T_n \in {\mathbb {R}}^{n \times n}, \; n=128, 256, 512, 1024 \) are the Jacobi matrices associated to the Chebyshev polynomials of first kind [3], whose eigenvalues are

$$\displaystyle \begin{aligned} \cos\left(\frac{i \pi}{n+1}\right),\quad i=1\ldots,n. \end{aligned}$$

In Table 3 the orthogonality of the computed eigenvectors with the considered three methods are displayed. We do not report the average lengths of the computed intervals in which to search the index j in this case, since there is no premature deflation for such matrices.

Table 3 Accuracy of the orthogonality of the computed eigenvectors computed by eig of MATLAB (second column), by MR 3 (third column) and by the proposed method (fourth column)
Full size table

In Table 4 the accuracy of the residuals of the computed eigenvectors with the considered three methods are displayed.

Table 4 Accuracy of the residuals of the eigenvectors computed by eig of MATLAB (second column), by MR 3 (third column) and by the proposed method (fourth column)
Full size table

We can conclude that the eigenvectors obtained with the proposed procedure are computed in an accurate way.

7 Conclusions

Recently, Malyshev and Dhillon have proposed an algorithm for deflating the tridiagonal matrix, once an eigenvalue has been computed. Starting from the above mentioned algorithm, a method for computing the eigenvectors of a symmetric tridiagonal matrix T has been proposed. It requires the computation of an index j which determines the premature deflation in the implicit QR method. The index j is computed considering the two sequences of cosines generated by a sweep of forward and backward QR method with shift the computed eigenvalue. The sought eigenvector is obtained form the first j Givens coefficients generated by the forward implicit QR method and from the last n − j Givens coefficients generated by the backward implicit QR method.

The overall complexity for computing an eigenvector depends linearly on the size of the matrix.

The numerical tests show the reliability of the proposed technique.