Abstract
The constructive martingale representation theorem of functional Itô calculus is extended, from the space of square integrable martingales, to the space of local martingales. The setting is that of an augmented filtration generated by a Wiener process.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Consider a complete
probability space  on which lives an n-dimensional Wiener process W. Let \(\underline{\mathcal {F}} = (\mathcal {F}_t)_{0\le t \le T}\) denote the augmentation under
on which lives an n-dimensional Wiener process W. Let \(\underline{\mathcal {F}} = (\mathcal {F}_t)_{0\le t \le T}\) denote the augmentation under  of the filtration generated by W until the constant terminal time \(T<\infty \). One of the main results of Itô calculus is the martingale representation theorem which in the present setting is as follows: Let M be a RCLL local martingale relative to
of the filtration generated by W until the constant terminal time \(T<\infty \). One of the main results of Itô calculus is the martingale representation theorem which in the present setting is as follows: Let M be a RCLL local martingale relative to  , then there exists a progressively measurable n-dimensional process \(\varphi \) such that
, then there exists a progressively measurable n-dimensional process \(\varphi \) such that
In particular, M has continuous sample paths a.s.
Considerable effort has in the literature been made in order to find explicit formulas for the integrand \(\varphi \), i.e. in order to find constructive representations of martingales, mainly using Malliavin calculus, see e.g. [8, 15, 16, 20] and the references therein. The recently developed functional Itô calculus includes a new type of constructive representation of square integrable martingales due to Cont and Fournié see e.g. [1, 3,4,5]. The main result of the present paper is an extension of this result to local martingales.
The organization of the paper is as follows. Section 9.2 is based on [1] and contains a brief and heuristic account of the relevant parts of functional Itô calculus including the constructive martingale representation theorem for square integrable martingales. Section 9.3 contains the local martingale extension of this theorem and a simple example.
2 Constructive Representation of Square Integrable Martingales
Denote an n-dimensional sample path by \(\omega \). Denote a sample path stopped at t by \(\omega _t\), i.e. let \(\omega _t(s) = \omega (t \wedge s), 0\le s \le T\). Consider a real-valued functional of sample paths \(F(t,\omega )\) which is non-anticipative (essentially meaning that \(F(t,\omega ) =F(t,\omega _t)\)). The horizontal derivative at \((t,\omega )\) is defined by
The vertical derivative at \((t,\omega )\) is defined by
where
Higher order vertical derivatives are obtained by vertically differentiating vertical derivatives.
One of the main results of functional Itô calculus is the functional Itô formula, which is just the standard Itô formula with the usual time and space derivatives replaced by the horizontal and vertical derivatives. If the functional F is sufficiently regular (regarding e.g. continuity and boundedness of its derivatives), which we write as  , then the functional Itô formula holds, see [1, ch. 5,6]. We remark that [12] contains another version of this result.
, then the functional Itô formula holds, see [1, ch. 5,6]. We remark that [12] contains another version of this result.
Using the functional Itô formula it easy to see that if Z is a martingale satisfying

then, for every \(t\in [0,T]\),
We may therefore define the vertical derivative with respect to the process W of a martingale Z satisfying (9.1) as the  -a.e. unique process \(\nabla _WZ\) given by
-a.e. unique process \(\nabla _WZ\) given by
Let \(\mathcal {C}_b^{1,2}(W)\) be the space of processes Z which allow the representation in (9.1). Let \(\mathcal {L}^2(W)\) be the space of progressively measurable processes \(\varphi \) satisfying the condition \(E[\int _0^T\varphi (s)'\varphi (s)ds]<\infty \). Let \(\mathcal {M}^2(W)\) be the space of square integrable martingales with initial value 0. Let \(D(W) = \mathcal {C}_b^{1,2}(W) \cap \mathcal {M}^2(W)\).
It can be shown that \(\{\nabla _WZ: Z \in D(W)\}\) is dense in \(\mathcal {L}^2(W)\) and that D(W) is dense in \(\mathcal {M}^2(W)\) [1, ch. 7]. Using this it is possible to show that the vertical derivative operator \(\nabla _W(\cdot )\) admits a unique extension to \(\mathcal {M}^2(W)\), in the following sense: For \(Y \in \mathcal {M}^2(W)\) the (weak) vertical derivative \(\nabla _W Y\) is the unique element in \(\mathcal {L}^2(W)\) satisfying
for every \(Z\in D(W)\), where \(\nabla _WZ\) is defined in (9.2). The constructive martingale representation theorem ([1, ch. 7]) follows:
Theorem 9.1
(Cont and Fournié) For any square integrable martingale Y relative to  and every \(t\in [0,T]\),
and every \(t\in [0,T]\),
3 Constructive Representation of Local Martingales
This section contains an extension of the vertical derivative \(\nabla _W(\cdot )\) and the constructive martingale representation in Theorem 9.1 to local martingales. Let \(\mathcal {M}^{{\tiny {\text {loc}}}}(W)\) denote the space of local martingales relative to  with initial value zero and RCLL sample paths. In Theorem 9.2 we extend the vertical derivative to \(\mathcal {M}^{{\tiny {\text {loc}}}}(W)\). Using this extension we can formulate the constructive martingale representation theorem also for local martingales, see Theorem 9.3.
with initial value zero and RCLL sample paths. In Theorem 9.2 we extend the vertical derivative to \(\mathcal {M}^{{\tiny {\text {loc}}}}(W)\). Using this extension we can formulate the constructive martingale representation theorem also for local martingales, see Theorem 9.3.
Before extending the definition of the vertical derivative to \(\mathcal {M}^{{\tiny {\text {loc}}}}(W)\) we recall the definition of a local martingale.
Definition 9.1
M is said to be a local martingale if there exists a sequence of non-decreasing stopping times \(\{\theta _n\}\) with \(\lim _{n \rightarrow \infty } \theta _n= \infty \) a.s. such that the stopped local martingale \(M(\cdot \wedge \theta _n)\) is a martingale for each \(n\ge 1\).
Theorem 9.2
(Definition of \(\nabla _W(\cdot )\) on \(\mathcal {M}^{{\tiny {\text {loc}}}}(W)\) )
-
There exists a progressively measurable
 -a.e. unique extension of the vertical derivative \(\nabla _W(\cdot )\) from \(\mathcal {M}^2(W)\) to \(\mathcal {M}^{{\tiny {\text {loc}}}}(W)\), such that, for \(M \in \mathcal {M}^{{\tiny {\text {loc}}}}(W)\), $$\begin{aligned} \begin{array}{rcl} M(t) &{} =&{} \int _0^t\nabla _WM(s)'dW(s), 0 \le t \le T, \text{ and } \\ &{}&{} \int _0^T|\nabla _WM(t)|^2dt <\infty \text{ a.s. } \end{array} \end{aligned}$$(9.4)
-a.e. unique extension of the vertical derivative \(\nabla _W(\cdot )\) from \(\mathcal {M}^2(W)\) to \(\mathcal {M}^{{\tiny {\text {loc}}}}(W)\), such that, for \(M \in \mathcal {M}^{{\tiny {\text {loc}}}}(W)\), $$\begin{aligned} \begin{array}{rcl} M(t) &{} =&{} \int _0^t\nabla _WM(s)'dW(s), 0 \le t \le T, \text{ and } \\ &{}&{} \int _0^T|\nabla _WM(t)|^2dt <\infty \text{ a.s. } \end{array} \end{aligned}$$(9.4) -
Specifically, for \(M \in \mathcal {M}^{{\tiny {\text {loc}}}}(W)\) the vertical derivative \(\nabla _WM\) is defined as the progressively measurable
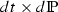 -a.e. unique process satisfying
-a.e. unique process satisfying  (9.5)
(9.5)where \(\nabla _WM_n\) is the vertical derivative of \(M_n:= M(\cdot \wedge \tau _n) \in \mathcal {M}^2(W)\) and \(\tau _n\) is given by
$$\begin{aligned} \tau _n = \theta _n \wedge \inf \{s\in [0,T]:|M(s)| \ge n\}\wedge T \end{aligned}$$(9.6)where \(\{\theta _n\}\) is an arbitrary sequence of stopping times of the kind described in Definition 9.1.
Remark 9.1
Note that if M in Theorem 9.2 satisfies
for some process \(\gamma \), then \(\gamma = \nabla _WM\)  -a.e. It follows that the extended vertical derivative \(\nabla _WM\) defined in Theorem 9.2 does not depend (modulo possibly on a null set
-a.e. It follows that the extended vertical derivative \(\nabla _WM\) defined in Theorem 9.2 does not depend (modulo possibly on a null set  ) on the particulars of the chosen stopping times \(\{\theta _n\}\).
) on the particulars of the chosen stopping times \(\{\theta _n\}\).
Proof
The martingale representation theorem implies that, for \(M \in \mathcal {M}^{{\tiny {\text {loc}}}}(W)\), there exists a progressively measurable process \(\varphi \) satisfying
Therefore, if we can prove that

then it follows that there exists a progressively measurable process, denote it by \(\nabla _WM\), which is  -a.e. uniquely defined by (9.5) and satisfies
-a.e. uniquely defined by (9.5) and satisfies

which in turn implies that the integrals of \(\nabla _WM\) and \(\varphi \) coincide in the way that (9.7) implies (9.4). All we have to do is therefore to prove that (9.8) holds.
Let us recall some results about stopping times and martingales. The stopped local martingale \(M(\cdot \wedge \theta _n)\) is a martingale for each n, by Definition 9.1. Stopped RCLL martingales are martingales. The minimum of two stopping times is a stopping time and the hitting time
is, for each n, in the present setting, a stopping time. Using these results we obtain that \(M(\cdot \wedge \theta _n \wedge \inf \{s\in [0,T]:|M(s)| \ge n\}\wedge T) = M(\cdot \wedge \tau _n)\) is a martingale, for each n. Moreover, M is by the standard martingale representation result a.s. continuous. Hence, we may define a sequence of, a.s. continuous, martingales \(\{M_n\}\) by
where the last equality follows from (9.7). Now, use the definition of \(\tau _n\) in (9.6) to see that
for any t and n, and that in particular \(M_n\) is, for each n, a square integrable martingale. Moreover, (9.9) implies that \(M_n\) satisfies
Since each \(M_n\) is a square integrable martingale we may use Theorem 9.1 on \(M_n\), which together with (9.10) implies that
where \(\nabla _WM_n\) is the vertical derivative of \(M_n\) with respect to W (defined in (9.3)) and where we also used the continuity of the Itô integrals. The equality of the two Itô integrals in (9.11) implies that

The local martingale property of M implies that \(\lim _{n \rightarrow \infty } \theta _n= \infty \;a.s.\) Using this and the definition of \(\tau _n\) in (9.6) we conclude that for almost every \(\omega \in \varOmega \) and each \(t \in [0,T]\) there exists an \(N(\omega ,t)\) such that
It follows from (9.12) and (9.13) that there exists an \(N(\omega ,t)\) such that

which means that (9.8) holds. \(\square \)
If M is a RCLL local martingale then \(M-M(0) \in \mathcal {M}^{{\tiny {\text {loc}}}}(W)\), which implies that \(\nabla _W(M-M(0))\) is defined in Theorem 9.2. This observation allows us to extend the definition of the vertical derivative to RCLL local martingales not necessarily starting at zero in the following obvious way.
Definition 9.2
The vertical derivative of a local martingale M relative to  with RCLL sample paths is defined as the progressively measurable
with RCLL sample paths is defined as the progressively measurable  unique process \(\nabla _WM\) satisfying
unique process \(\nabla _WM\) satisfying
where \(\nabla _W(M-M(0))(t)\) is defined in Theorem 9.2.
The following result is an immediate consequence of Theorem 9.2 and Definition 9.2.
Theorem 9.3
If M is a local martingale relative to  with RCLL sample paths, then
with RCLL sample paths, then
where \(\nabla _WM(s)\) is defined in Definition 9.2.
Let us try to clarify the theory by studying a simple example. It is straightforward to extend the results above to the case when the Wiener process W is replaced by an adapted process X given by
where \(\sigma \) is a matrix-valued adapted process satisfying suitable assumptions, mainly invertibility, see also [1, 4]. Thus, a local martingale M can be represented as
and the relationship between the vertical derivatives with respect to W and X is \(\nabla _W M(t)' = (\nabla _X M(t)')\sigma (t)\), cf. (9.15). As example consider the one-dimensional case and let X with \(X(0)=0\) be given by (9.15) under the assumption that \(\sigma (s)\) is a deterministic function of time and let M be given by \(M(t)= F(t,X_t)\) where F is the non-anticipative functional \(F(t,\omega ) = \omega ^3(t)- 3\int _0^t\omega (s)\sigma ^2(s)ds\), i.e. let M be the local martingale defined by
In this case the vertical derivative simplifies to the standard derivative, that is, \(\nabla F_\omega (t,\omega ) = 3\omega ^2(t)\), see also [1, 4] (we remark that the horizontal derivative is \(\mathcal {D} F(t,\omega ) = -3\omega (t)\sigma ^2(t)\)). In this case, \(\nabla _X M(t) = 3X^2(t)\) and
which we remark is easily found using the standard Itô formula. Note that this also means that \(\nabla _W M(t) = 3X^2(t)\sigma (t) = \nabla _X M(t)\sigma (t)\).
Concluding Remarks
Many of the applications that rely on martingale representation are within mathematical finance. A particular application that may benefit from the local martingale extension of the present paper is optimal investment theory, in which the discounted (using the state price density) optimal wealth process is a (not necessarily square integrable) martingale, see e.g. [9, ch. 3], see also [13]. In particular, using functional Itô calculus it is possible to derive an explicit formula for the optimal portfolio in terms of the vertical derivative of the discounted optimal wealth process, see also [14]. Similar explicit formulas for optimal portfolios based on the Malliavin calculus approach to constructive martingale representation have, under restrictive assumptions, been studied extensively, see e.g. [2, 6, 7, 10, 11, 17,18,19]. The general connection between Malliavin calculus and functional Itô calculus is studied in e.g. [1, 4].
References
Bally, V., Caramellino, L., Cont, R., Utzet, F., Vives, J.: Stochastic Integration by Parts and Functional Itô Calculus. Springer, Berlin (2016)
Benth, F.E., Di Nunno, G., Løkka, A., Øksendal, B., Proske, F.: Explicit representation of the minimal variance portfolio in markets driven by Lévy processes. Math. Financ. 13(1), 55–72 (2003)
Cont, R., Fournié, D.-A.: Change of variable formulas for non-anticipative functionals on path space. J. Funct. Anal. 259(4), 1043–1072 (2010)
Cont, R., Fournié, D.-A.: Functional Itô calculus and stochastic integral representation of martingales. Ann. Prob. 41(1), 109–133 (2013)
Cont, R., Lu, Y.: Weak approximation of martingale representations. Stoch. Process. Appl. 126(3), 857–882 (2016)
Detemple, J., Rindisbacher, M.: Closed-form solutions for optimal portfolio selection with stochastic interest rate and investment constraints. Math. Financ. 15(4), 539–568 (2005)
Nunno, Di G., Øksendal, B.: Optimal portfolio, partial information and Malliavin calculus. Stoch.: Int. J. Probab. Stoch. Process. 81(3–4), 303–322 (2009)
Karatzas, I., Ocone, D.L., Li, J.: An extension of Clark’s formula. Stoch.: Int. J. Probab. Stoch. Process. 37(3), 127–131 (1991)
Karatzas, I., Shreve, S.E.: Methods of Mathematical Finance (Stochastic Modelling and Applied Probability). Springer, Berlin (1998)
Lakner, P.: Optimal trading strategy for an investor: the case of partial information. Stoch. Process. Appl. 76(1), 77–97 (1998)
Lakner, P., Nygren, L.M.: Portfolio optimization with downside constraints. Math. Financ. 16(2), 283–299 (2006)
Levental, S., Schroder, M., Sinha, S.: A simple proof of functional Itô’s lemma for semimartingales with an application. Stat. Probab. Lett. 83(9), 2019–2026 (2013)
Lindensjö, K.: Optimal investment and consumption under partial information. Math. Meth. Oper. Res. 83(1), 87–107 (2016)
Lindensjö, K.: An Explicit Formula for Optimal Portfolios in Complete Wiener Driven Markets: a Functional Itô Calculus Approach (2017). arXiv:1610.05018
Malliavin, P.: Stochastic Analysis, Grundlehren der Mathematischen Wissenschaften, vol. 313, pp XII, 347. Springer, Berlin (2015)
Nualart, D.: The Malliavin Calculus and Related Topics (Probability and Its Applications, 2nd edn. Springer, Berlin (2006)
Ocone, D.L., Karatzas, I.: A generalized Clark representation formula, with application to optimal portfolios. Stoch.: Int. J. Probab. Stoch. Process. 34(3–4), 187–220 (1991)
Okur, Y.Y.: White noise generalization of the Clark-Ocone formula under change of measure. Stoch. Anal. Appl. 28(6), 1106–1121 (2010)
Pham, H., Quenez, M.-C.: Optimal portfolio in partially observed stochastic volatility models. Ann. Appl. Probab. 11(1), 210–238 (2001)
Rogers, L.C.G., Williams, D.: Diffusions, Markov Processes and Martingales, vol. 2, Itô calculus. Cambridge University Press, Cambridge (2000)
Acknowledgements
The author is grateful to Mathias Lindholm for helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Lindensjö, K. (2018). Constructive Martingale Representation in Functional Itô Calculus: A Local Martingale Extension. In: Silvestrov, S., Malyarenko, A., Rančić, M. (eds) Stochastic Processes and Applications. SPAS 2017. Springer Proceedings in Mathematics & Statistics, vol 271. Springer, Cham. https://doi.org/10.1007/978-3-030-02825-1_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-02825-1_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-02824-4
Online ISBN: 978-3-030-02825-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




 -a.e. unique extension of the vertical derivative
-a.e. unique extension of the vertical derivative 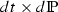 -a.e. unique process satisfying
-a.e. unique process satisfying 