Heat Transfer Analysis in a Micropolar Fluid with Non-Linear Thermal Radiation and Second-Order Velocity Slip

Abstract

This study addresses the thermal energy transport in a slippery sheet-driven flow of a micropolar fluid analysing the effect of radiative heat flux. The solution of PDEs of the governing the flow is derived numerically by the application of self-similarity transformations and Runge-Kutta Fehlberg algorithm along with shooting method. The computational results are discussed graphically for several selected flow parameters. Results of this analysis are compared with the published results and are seen to tally very closely.

1 Introduction

Micropolar fluids are used to model liquids containing arbitrarily oriented rigid spherical particles dispersed in a viscous medium, neglecting the fluids particles deformation. The mechanics of micropolar fluids, emerged from the theory developed by Eringen [1], has been an interesting area of research owing to the wide range of applications in industry. For example, polymeric liquids, real fluids with suspensions, liquid crystals, animal blood and exotic lubricants are modelled by micropolar fluids. Yacob and Ishak [2] obtained dual solutions to the problem of a micropolar fluid due to a sheet of shrinking. Energy transfer in fluids flowing over surfaces of stretching on account of thermal radiation has effective industrial applications in solar power technology, furnace design, solar ponds, heat exchangers, satellites and space vehicles. Sarojamma et al. [3] explored dual stratification effect on the oblique stagnation point flow of a non-classical Casson fluid. Recently, researchers are investigating the non-linear thermal radiative heat transfer and consequently the equation governing the temperature becomes strongly non-linear. Mahantesh et al. [4] reported the effects of non-linear thermal radiation coupled with dual diffusion on the 3-D flow of a nanofluid. Wall slip flows with different aspects have been analysed [5, 6]. All these studies pertain to slip flows of first order. However, slip flows with second order occur in many fields of industry. In spite of the need to analyse the slip effect of second order on fluid flows, not much attention has been paid on it. Fang and Aziz [7] analysed the flow of a viscous liquid with second-order slip considering the stretch and shrink effects, respectively. Ibrahim [8] examined the MHD micropolar fluid flow considering the first and second-order slips. Analysis of heat transfer with non-linear thermal radiation and second-order slip flow of a micropolar fluid has not yet been addressed. This investigation addresses the effect of non-linear thermal radiation and velocity slip of order two in a micropolar fluid flow.

2 Mathematical Formulation

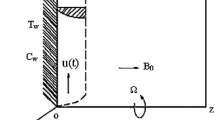
We propose a thin elastic sheet which issues from a narrow slit at the origin of a Cartesian co-ordinate system. The sheet at y = 0 is taken to be parallel to the x-axis and moves in its own plane with a velocity u _w = ax. The surface temperature T _w is assumed as constant. The flow is subjected to a constant transverse magnetic field of strength B ₀ which is assumed to be applied in the positive y-direction, normal to the surface. The flow equations after boundary layer approximations are given by

$$\displaystyle \begin{gathered} {} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 \end{gathered} $$

(1)

$$\displaystyle \begin{gathered} {} u\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y}=\frac{(\mu+k)}{\rho}\left(\frac{\partial^{2} u}{\partial y^{2}}\right)+\frac{k}{\rho}\frac{\partial N}{\partial y}-\frac{\sigma {B_0^2}}{\rho} u +g_{1} \beta_{T} \left(T-T_\infty\right) \end{gathered} $$

(2)

$$\displaystyle \begin{gathered} {} u\frac{\partial N}{\partial x}+v\frac{\partial N}{\partial y}=\frac{\varOmega}{\rho j}\frac{\partial^{2} N}{\partial y^{2}}-\frac{k}{\rho j}\left(2N+\frac{\partial u}{\partial y}\right) \end{gathered} $$

(3)

$$\displaystyle \begin{gathered} {} u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{K}{\rho c_p}\frac{\partial^{2} T}{\partial y^{2}}+\frac{16\sigma^*}{3k^{*}\rho c_p}\frac{\partial}{\partial y}\left(T^3\frac{\partial T}{\partial y}\right) \end{gathered} $$

(4)

The boundary conditions are

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} u=u_w+U_{slip}, v=0, N=-n\frac{\partial u}{\partial y}, T=T_w \quad at \quad y=0 \\ u \rightarrow 0, N \rightarrow 0, T \rightarrow T_{\infty}, \mbox \quad {as} \quad y \rightarrow \infty \end{array} \end{aligned} $$

(5)

where, u and v are velocity components along x and y directions, respectively. The nomenclature of u _w, a, μ, k, σ, ρ, j, K, c _p, A, B, K _n, $l=\min \left [\frac {1}{K_{n}},1\right ]$, α (0 ≤ α ≤ 1), λ,ν, Ω, n (0 ≤ n ≤ 1) can be found in [8] and σ ^∗, k ^∗ can be found in [3]; g ₁ is acceleration due to gravity, β _T is coefficient of thermal expansion, T is the temperature inside the boundary layer, and T _∞ is ambient temperature. Slip velocity at the surface, following Wu [9], is given by

$$\displaystyle \begin{aligned}\begin{array}{c} U_{slip}=\frac{2}{3}\left(\frac{(3-\alpha l^{3})}{\alpha}-\frac{3}{2}\frac{(1-l^{2})}{K_{n}}\right)\lambda \frac{\partial u}{\partial y}-\frac{1}{4}\left(l^{4}+\frac{2}{K_{n}^{2}}(1-l^{2})\right)\lambda^{2} \frac{\partial^{2} u}{\partial y^{2}} \end{array}\end{aligned}$$

$$\displaystyle \begin{aligned} U_{slip}=A \frac{\partial u}{\partial y}+B \frac{\partial^{2} u}{\partial y^{2}} \end{aligned} $$

(6)

N is the microrotation or angular velocity, whose direction of rotation is normal to the x − y plane, Ω is given by Ω = (μ + k∕2)j = μ(1 + β∕2)j, where β = k∕μ is the material parameter which describes the coupling of the linear and angular motion which arises due to the microrotation of the fluid molecules. Therefore β symbolises the coupling between Newtonian and rotational viscosities. If β → 0 we see that k → 0 which corresponds to the case of Newtonian fluid; hence β → 0 corresponds to a viscous fluid.

3 Method of Solution

We define

$$\displaystyle \begin{aligned} u=\frac{\partial \psi}{\partial y}=axf^{\prime}, v=-\frac{\partial \psi}{\partial x}=-\sqrt{a\nu}f \end{aligned} $$

(7)

where ψ(x, y) is the stream function. We define the following similarity transformations for dimensionless variables

$$\displaystyle \begin{aligned} \eta=\sqrt{\frac{a}{\nu}}y, \psi=\sqrt{a\nu}xf(\eta), N=ax\sqrt{\frac{a}{\nu}}g(\eta), \theta(\eta)=\frac{T-T_{\infty}}{T_{w}-T_{\infty}} \end{aligned} $$

(8)

where f, θ, g are dimensionless variables. Using the above similarity transformation and dimensionless variables, the governing equations (1)–(4) are reduced into the ordinary differential equations as follows:

$$\displaystyle \begin{aligned} (1+\beta)f^{\prime \prime \prime }+ff^{\prime \prime }-(f^{\prime})^{2}+\beta g^{\prime}-M f^{\prime}+Gr\theta=0 \end{aligned} $$

(9)

$$\displaystyle \begin{aligned} \left(1+\frac{\beta}{2}\right)g^{\prime \prime}-\beta(2g+f^{\prime \prime})+fg^{\prime}-f^{\prime}g=0 \end{aligned} $$

(10)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \theta^{\prime \prime}+Nr[(1+(\theta_{w}-1)\theta)^{3}]\theta^{\prime \prime}+3Nr[(\theta_{w}-1)(1+(\theta_{w}-1)\theta)^{2}] (\theta^{\prime})^{2} \\ +Pr f\theta^{\prime}=0 \end{array} \end{aligned} $$

(11)

With boundary conditions

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} f(0)=0, f^{\prime}(0)=1+h_{1}f^{\prime \prime}(0)+h_{2}f^{\prime \prime \prime}(0), g(0)=-nf^{\prime \prime}(0), \\ \theta(0)=1 \quad at \quad \eta=0 \end{array} \end{aligned} $$

(12)

$$\displaystyle \begin{aligned} f^{\prime}(\infty) \rightarrow0, g(\infty) \rightarrow 0, \theta(\infty) \rightarrow 0 \quad as \quad \eta \rightarrow \infty \end{aligned} $$

(13)

where $M=\frac {\sigma B_{0}^{2}}{\rho a}$ is the magnetic parameter, Gr = g ₁ β _T(T _w − T _∞)∕au _w is the thermal Grashof number, Pr = (ρc _p ν)∕K is the Prandtl number, $Nr= (16\sigma ^* T_\infty ^3)/(3Kk^* )$ is the thermal radiation parameter, θ _w = T _w∕T _∞ is the temperature ratio parameter and

$h_1=A\sqrt {{a}/{\nu }}$, h ₂ = Ba∕ν Nu _x are the first- and second-order velocity slip parameters, respectively.

The skin friction coefficient C _fand local Nusselt number Nu _x are defined by

$$\displaystyle \begin{aligned} C_{f}=\frac{\tau_{w}}{\rho u_{w}^{2}}, Nu_{x}=\frac{x q_{w}}{K(T_{w}-T_{\infty})} \end{aligned} $$

(14)

where the wall shear stress τ _w and the surface heat flux q _w are given by

$$\displaystyle \begin{aligned} \tau_{w}=\left((\mu+k)\frac{\partial u}{\partial y}+kN\right)_{y=0}, q_{w}=-K\left(1+\frac{16\sigma^{*}T^{3}}{3Kk^{*}}\right)\left(\frac{\partial T}{\partial y}\right)_{y=0} \end{aligned} $$

(15)

Using Eq. (15) in Eq. (14), we obtain

$$\displaystyle \begin{aligned}C_{f} \sqrt{Re_{x}} = -\left(1+ \beta (1-n) \right) f^{\prime \prime} (0), \frac{Nu_{x}}{\sqrt{Re_{x}}} = -\left(1+Nr \left[ 1+(\theta_{w}-1) \theta (0) \right]^{3}\right) \theta^{\prime}(0) \end{aligned}$$

where Re _x = U _w x∕ν is a local Reynolds number.

The set of differential equations (9)–(11) along with the conditions (12) and (13) are solved numerically standard RKF-45 method.

In order to confirm the accuracy of our numerical procedure, we compared our results, viz. − f ^′′(0) for various slip factors h ₁ with those of Sahoo and Do [6] and Ibrahim [8] when β = M = h ₂ = n = Gr = Pr = Nr = 0. Values of − θ ^′(0) are compared with those of Ishak [10] and Ibrahim [8] for various values of Pr in the absence of β, M, h ₁, h ₂, n, Gr, Nr and are presented in Table 1. It is seen that there is an excellent agreement with them. Table 2 shows that − f ^′′(0) and − θ ^′(0) are compared with Ibrahim [8] in the absence of thermal buoyancy force and thermal radiation for various M, β, h ₂. From this we observe that our results are very close to those evaluated by Ibrahim [8].

Table 1 Comparison values of − f ^′′(0) and − θ ^′(0) with slip factor h ₂ and Pr when β = M = Gr = Nr = θ _w = h ₂ = n = 0

Table 2 Comparison values of − f ^′′(0) and − θ ^′(0) with M, β, h ₂ when h ₁ = 1, Pr = 1, n = 0.5, Gr = 0, Nr = 0

4 Results and Discussion

Influence of the various physical parameters that emerged in this study on the flow variables has been presented through graphs and discussed.

Figure 1 shows the variation of the material parameter (β) on the velocity, and its influence is seen to increase the velocity. From Fig. 2 for any value of β , microrotation is observed to diminish near the boundary till η = 0.75, and afterwards it increases and eventually satisfies the free stream condition. Further microrotation is seen to enhance with β.

Fig. 1

Effect of β on f ^′

Fig. 2

Effect of β on g

Figure 3 indicates that presence of magnetic field suppresses the velocity due to the Lorentz force developed as a result of the applied magnetic field which has a tendency to resist the fluid flow. Also, increase in the strength of magnetic field causes further reduction in the velocity due to stronger Lorentz forces. Magnetic field is seen to have a decreasing influence on the microrotation.

Fig. 3

Effect of M on f ^′, g

Figure 4 displays the variation of both velocity and microrotation in the boundary layer for different values of Gr. It is seen that velocity increases with increase in the buoyancy parameter Gr as thermal buoyancy assists the fluid flow in the boundary layer. The microrotation is observed to diminish near the boundary till η = 1.4, and later it increases up to η = 7 and eventually attains the free stream velocity. It can be noticed that temperature has an exactly opposite trend to that of the two velocities for the same variation of Gr.

Fig. 4

Effect of Gr on f ^′, g, θ

Influence of first-order slip parameter on both velocity and microrotation components is to reduce in their magnitude as illustrated in Fig. 5. Second-order slip variations on velocities are plotted in Fig. 6. The impact of second-order slip parameter on velocities is qualitatively similar to that of first-order slip parameter.

Fig. 5

Effect of h ₁ on f ^′, g

Fig. 6

Effect of h ₂ on f ^′, g

Figure 7 indicates the variation of thermal radiation parameter on temperature. When θ _w > 1, i.e., when heat flow takes place from boundary to the fluid, the temperature is increased as Nr increases. For the same set of values of Nr, a reversal trend is seen in temperature when θ _w < 1 since heat flow is towards the boundary.

Fig. 7

Effect of Nr on θ

The effect of (n) on microrotation g is shown in Fig. 8. The microrotation g is found to increase rapidly near the boundary with increasing values of n due to larger velocity gradients and away from the boundary velocity shows an opposite trend.

Fig. 8

Effect of n on g

5 Conclusion

Some of the highlights of the analysis are:

• Microrotation across the flow shows a decreasing trend near the boundary, while it increases in the region for an increment in (Gr).

• Microrotation is seen to have an increasing trend for with increase in n.

• Thinner momentum boundary layers are formed for higher values of the slip parameters.