Keywords

1 Introduction

Both network security and computer security systems collectively make up cybersecurity systems. Each of the security systems basically has an antivirus software, a firewall, and an IDS. The IDSs is involved in the discovery, determination, and identification of unauthorized access, usage, alteration, destruction, or duplication of an information system [1]. The security of these systems can be violated through external (from an outsider) and internal attacks (from an insider). Until now, much efforts are devoted to studies on the improvement of network and information security systems, and several studies exist on IDS and its taxonomy [1,2,3,4]. Machine learning has recently gained much interest from different fields such as control, communication, robotics, and several engineering fields. In this study, a machine learning approach was deployed to address the issues of intrusion detection in computer systems. It is a challenging task to automate ID processes, as has earlier been ascertained by Sommer and Paxson who applied ML techniques to ID systems and outlined the challenges of automating network attack detection processes [5]. The specific approaches of using ML techniques for network intrusion detection and their and challenges have been previously outlined [6]. Some of the major problems of the current network ID systems such as high rates of false-positive alarms, false negative or missed detections, as well as data overload (a situation where the network operator is overloaded with information, making it difficult to monitor data) have been discussed [6].

Several ML algorithms have been used to detect anomalies in the behavior of ID systems. This is achieved by training the ML algorithms with the normal network traffic patterns, making them capable of determining traffic patterns that differ from the normal pattern [5]. Although some ML techniques can effectively detect certain forms of attack, no single method has been developed that can be universally applied to detect multiple types of attack. Intrusion detection systems can be generally divided into two system (anomaly and misuse) based on their mode of detection [6]. The anomaly-based detection system flags any abnormal network behavior as an intrusion, but the misuse-based detection system relies on the signature of established previous attacks to detect new intrusions. Several anomaly-based detection systems have been developed based on different ML techniques [6, 9, 11]. For instance, several studies have used single learning techniques like neural networks, support vector machines, and genetic algorithms to design ID systems [5]. Other systems such as the hybrid or ensemble systems are designed by combining different ML techniques [10, 11]. These techniques are particularly developed as classifiers for the classification or recognition of the status of an incoming Internet access (normal access or an intrusion). One of the significant algorithms of machine learning is the ELM first proposed by Huang. The ELM has been widely investigated and applied severally [12]. Several ID systems have been proposed based on the use of ELM as the core algorithm [6, 13, 14]. Furthermore, there is a heavy influx of network traffic data through the ID system which needs to be processed [7]. This study, therefore, focuses on the development of a scalable method that can improve the effectiveness of network ID systems in the detection of different classes of network attack.

2 Overview of Fast Learning Network

In the past few decades, the demand for even the high performing single hidden layer Feedforward Neural Network (FNN) has waned due to some application challenges [4]. To solve these issues, Guang Bin Huang proposed the Extreme Learning Machine (ELM) [3] whose major function is the transformation of a single hidden layer FNN into a linear least square solving a problem; it then, calculates the output weights through the Moore–Penrose (MP) generalized inverse. There are several advantages of ELM, first, it avoids repeated calculation of iteration, has a fast learning speed; cannot be trapped at the local minimum, ensure output weights uniqueness, has a simplified network framework, presents a better generalization ability and regression accuracy. Several scholars have successfully implemented the ELM learning algorithm and theory [5, 6] in pattern classification, function approximation [7,8,9], system identification and so on [10, 12]. The other issue is the handling of information incorporation in the ELM when multiple varying data sources are available [15]. Therefore, the kernel-based ELM (KELM) has been proposed by comparing the modeling process between SVM and ELM [16]. The results show that KELM performs better and is more robust compared to the basic ELM [15] in solving non-separable linearly samples. The KELM also performed better than ELM, KELM in solving regression prediction tasks. It achieved a comparative or better performance with a faster learning speed and easier implementation in several applications, including 2-D profiles reconstruction, hyperspectral remote sensing image classification [17, 18], activity recognition, and diagnosis of diseases [19, 20]. KELM has also been used for online prediction of hydraulic pumps features, location of damage spot in aerospace, and behavior identification [21, 22]. However, [15] the training of KELM is an unstable process; the learning parameters must be manually adjusted; and it utilizes randomly generated hidden node parameters. The adjustment of the learning parameters requires human input, and could influence the classification performance. Its kernel function parameters also need a careful selection process to achieve an optimal solution. There are many works that provide optimization methods based on KELM parameters. The metaheuristics have been suggested for tackling the problems of parameter setting in KELM. Some of the suggested metaheuristics are genetic algorithm (GA)  [18], and AdaBoost framework [23]. [24] used adaptive artificial bee colony (AABC) algorithm for parameter optimization and selection of KELM features. The features were evaluated based on Parkinson’s disease dataset. In [25], the authors proposed the chaotic moth-flame optimization (CMFO) strategy to optimize KELM parameters. Also, an active operators particle swam optimization algorithm (APSO) was proposed in [15] for obtaining an optimal initial set of KELM parameters. The evaluated model (APSO-KELM) based on standard genetic datasets show the APSO-KELM to have a higher classification performance compared to the current ELM and KELM. However, the results of this work show KELM to have a better accuracy compared to ELM, showing the need to introduce the kernel function. In other words, the optimize kernel parameter results showed no fluctuation and an increasing coverage with iteration. Meanwhile, there are some issues with ELM such as the need for additional hidden neurons in some regression applications compared to the conventional neural network (NN) learning algorithms. This may cause the trained ELM to require more reaction time when presented with new test samples. Furthermore, any increase in the number of hidden layer neurons also results to an exponential increase in the number of thresholds and weights of random initialization. These values may not be the optimized parameters [26, 27]. In 2013, Li et al. suggested a novel ELM-based artificial neural network for fast learning network (FLN) [13]. FLN is a double parallel FNN made up of a single layer FNN and a single hidden layer FNN. The received information at the input layer is transmitted to the hidden and output layers (first, the message gets to the neurons of the hidden layer before being transmitted to the output layer). Therefore, the FLN can perform nonlinear approximation like other general NN. Contrarily, the information is directly transferred from the input layer to the output layer, giving the FLN the ability to establish the linear relationship between the input and the output. Hence, the FLN can handle linear problems with a high accuracy, and can also infinitely approximate nonlinear systems. FLN can also solve the issue associated with the conventional NN which does not demand iterative calculation. This work start with Sect. 2 provides the introduction. Section 3 explain the data set KDD details. Section 4 provides overview of the methodology. Section 5 provides the experiments and analysis of the results.

3 Overview of the Methodology

3.1 Fast Learning Network

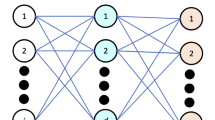
The FLN was presented by [37] as a novel variant of the ELM [38]. It is structured as a combination of two NNs, the first one as an SLFNN and the second an MLFNN. The FLN depends on three layers, namely, input, hidden, and output layers. The FLN structure is shown in Fig. 1,

Fig. 1.
figure 1

Structure of FLN

Full size image

The equations of deriving the output of the FLN based on the provided matrices and vectors and they are presented in the following equations.

$$ y_{j} = f(w^{oi} x_{j} + {\text{c}} + \sum\nolimits_{k = 1}^{m} {w_{k}^{oh} {\text{g}}\, (w_{k}^{in} x_{j} + b_{k} )} ) $$
(1)

Where

  • \( {\mathbf{w}}^{{{\mathbf{oi}}}} = \left[ {{\mathbf{w}}_{1}^{{{\mathbf{oi}}}} , {\mathbf{w}}_{2}^{{{\mathbf{oi}}}} , \ldots ..,{\mathbf{w}}_{{\mathbf{i}}}^{{{\mathbf{oi}}}} } \right] \) is the weight vector connecting the output nodes and input nodes.

  • \( {\mathbf{w}}_{{\mathbf{k}}}^{{{\mathbf{in}}}} = \left[ {{\mathbf{w}}_{{{\mathbf{k}}1}}^{{{\mathbf{in}}}} , {\mathbf{w}}_{{{\mathbf{k}}2}}^{{{\mathbf{in}}}} , \ldots \ldots ,{\mathbf{w}}_{{{\mathbf{km}}}}^{{{\mathbf{in}}}} } \right] \) is weight vector connecting the input nodes and hidden node

  • \( {\mathbf{w}}_{{\mathbf{k}}}^{{{\mathbf{oh}}}} = \left[ {{\mathbf{w}}_{{1{\mathbf{k}}}}^{{{\mathbf{oh}}}} ,{\mathbf{w}}_{{2{\mathbf{k}}}}^{{{\mathbf{oh}}}} \ldots \ldots ..,{\mathbf{w}}_{{{\mathbf{ik}}}}^{{{\mathbf{oh}}}} } \right] \) is weight vector connecting the output nodes and hidden node, a more compact representation is given as follows

The matrix \( \varvec{W} = \left[ {\begin{array}{*{20}c} {W^{oi} } & {W^{oh} } & c \\ \end{array} } \right] \) can be called output weights, and G is the hidden layer output matrix of FLN, the ith row of G is the ith hidden neuron’s output vector with respect to inputs \( x_{1} .x_{2} \ldots .x_{N} \). To solve the model, the minimum norm least-squares solution of the linear system can be written as follows: A more compact representation is given as follows:

$$ {\text{Y}} = f(w^{oi} {\text{x}} + w^{oh} {\text{G}} + {\text{c)}} = f\left( {\left[ {w^{oi} w^{oh} c} \right]\left[ {\begin{array}{*{20}c} X \\ G \\ I \\ \end{array} } \right]} \right) $$
(2)
$$ = f\left( {W\left[ {\begin{array}{*{20}c} X \\ G \\ I \\ \end{array} } \right]} \right) $$
(3)

Where

$$ H = \left[ {X\,G\,I} \right]^{T} $$
(4)
$$ {\text{G}}(W_{1}^{in} , \cdots ,W_{m}^{in} ,b_{1} , \cdots ,b_{m} , \cdots ,X_{N} ) $$
(5)
$$ = \left[ {\begin{array}{*{20}c} {g\left( {W_{1}^{in} X_{1} + b_{1} } \right)} & \cdots & {g\left( {W_{1}^{in} X_{N} + b_{1} } \right)} \\ \vdots & \ddots & \vdots \\ {g\left( {W_{m}^{in} X_{1} + b_{m} } \right)} & \cdots & {g(W_{m}^{in} X_{N} + b_{m} } \\ \end{array} } \right]_{m \times N} $$
$$ {\text{W}} = \left[ {W^{oi} W^{oh} C} \right]_{{1 \times \left( {n + m = 1} \right)}} $$
(6)
$$ {\text{I}} = \left[ {11 \cdots 1} \right]_{1 \times N} $$
(7)

In order to resolve the model, a Moore Penrose based equation is given as follows.

$$ {\hat{\mathbf{w}}} = {\mathbf{f}}^{ - 1} \left( {\mathbf{Y}} \right)\left( {\left[ {\varvec{X}^{\varvec{T}} \varvec{G}^{\varvec{T}} \varvec{I}^{\varvec{T}} } \right] \left[ {\begin{array}{*{20}c} X \\ G \\ I \\ \end{array} } \right]} \right)^{ - 1} {\mathbf{H}}^{{\mathbf{T}}} $$
(8)
$$ {\hat{\mathbf{w}}} = {\mathbf{f}}^{ - 1} \left( {\mathbf{Y}} \right)\left( {{\mathbf{X}}^{{\mathbf{T}}} {\mathbf{X}} + {\mathbf{G}}^{{\mathbf{T}}} {\mathbf{G}} + {\mathbf{I}}^{{\mathbf{T}}} {\mathbf{I}}} \right)^{ - 1} {\mathbf{H}}^{{\mathbf{T}}} $$
(9)

An algorithm that explains the learning of the FLN is presented in the flowchart depicted in Fig. 2. The algorithm starts by random initialization of the weights between the input and hidden layers and the biases of the hidden layer. Then, the G matrix is determined depending on the input-hidden matrix. This matrix represents the output matrix of the hidden layer. Next, the input-output matrix \( w^{oi} \) and \( w^{oh} \) are determined based on the Moore–Penrose equations. As a result, a complete FLN model is formulated

Fig. 2.
figure 2

Flowchart of the FLN learning model

Full size image

3.2 Kernel Fast Learning Network

A kernel function in machine learning is a measurement of the closeness between input sample data defined over a feature denoted as \( {\text{K(x,x}}^{{\prime }} ) \) [39]. In a recent study, [16] suggested that the hidden layer of an SLFN does not need to be formulated as a nodes of single layer; instead, a mechanisms of feature mapping can be a wide range used to replace the hidden layer.

This approach has been exemplified in this work as previously reported by [16] to convert an FLN model to a kernel-based model. By recalling the output of Eq. (3), replacing the output weight W with the output weight based on the Moore–Penrose generalized inverse ŵ as Eq. (8), and replacing H with Eq. (4), we can obtain Eq. (13) as follows:

$$ W^{ \wedge } = Y^{ \wedge } H^{T} (H\,H^{T} )^{ - L} $$
$$ \begin{aligned} Y & = f\left( {Y^{ \wedge } H^{T} \left( {H\,H^{T} } \right)^{ - 1} H^{T} } \right) \\ & = f\left( {Y^{ \wedge } \left( {H\,H^{T} } \right)^{ - 1} H^{T} H} \right) \\ \end{aligned} $$
$$ \begin{aligned} {\text{Y}} & = {\text{f}}\left( {{\text{f}}\left( {\text{Y}} \right)^{ - 1} \left( {\left[ {{\text{X}}^{\text{T}} \,{\text{G}}^{\text{T}} \,{\text{I}}^{\text{T}} } \right]\left[ {\begin{array}{*{20}c} X \\ G \\ I \\ \end{array} } \right]} \right)^{ - 1} \left[ {{\text{X}}^{\text{T}} \,{\text{G}}^{\text{T}} \,{\text{I}}^{\text{T}} } \right]\left[ {\begin{array}{*{20}c} X \\ G \\ I \\ \end{array} } \right]} \right) \\ {\text{Y}} & = {\text{f}}\left( {{\text{f}}\left( {\text{Y}} \right)^{ - 1} \left( {{\text{X}}^{\text{T}} {\text{X}} + {\text{G}}^{\text{T}} {\text{G}} + {\text{I}}^{\text{T}} {\text{I}}} \right)^{ - 1} \left( {{\text{X}}^{\text{T}} {\text{X}} + {\text{G}}^{\text{T}} {\text{G}} + {\text{I}}^{\text{T}} {\text{I}}} \right)} \right) \\ \end{aligned} $$
$$ {\text{Y}} = {\text{f}}\left( {{\text{f}}\left( {\text{Y}} \right)^{ - 1} \left( {\left[ {{\text{X}}^{\text{T}} \,{\text{G}}^{\text{T}} \,{\text{I}}^{\text{T}} } \right]\left[ {\begin{array}{*{20}c} X \\ G \\ I \\ \end{array} } \right]} \right)^{ - 1} \left[ {{\text{X}}^{\text{T}} \,{\text{G}}^{\text{T}} \,{\text{I}}^{\text{T}} } \right]\left[ {\begin{array}{*{20}c} X \\ G \\ I \\ \end{array} } \right]} \right) $$
(10)
$$ {\text{Y}} = {\text{f}}\left( {{\text{f}}\left( {\text{Y}} \right)^{ - 1} \left( {{\text{X}}^{\text{T}} {\text{X}} + {\text{G}}^{\text{T}} {\text{G}} + {\text{I}}^{\text{T}} {\text{I}}} \right)^{ - 1} \left( {{\text{X}}^{\text{T}} {\text{X}} + {\text{G}}^{\text{T}} {\text{G}} + {\text{I}}^{\text{T}} {\text{I}}} \right)} \right) $$
(11)

Moreover, through the addition of a small positive quantity (i.e., the stability factor) \( 1/\uplambda \) to the diagonal of \( {\mathbf{H}}^{{\mathbf{T}}} {\mathbf{H}} \), thus yielding a more “stable” solution, we can represent Y as [16] follows:

$$ {\text{Y}} = {\text{f}}\left( {{\text{f}}\left( {\text{Y}} \right)^{ - 1} \left( {{\text{k}}_{1} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right) + {\text{k}}_{2} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right) + {\text{k}}_{3} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right) + 1/\uplambda } \right)^{ - 1} \left( {{\text{k}}_{1} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right) + {\text{k}}_{2} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right) + {\text{k}}_{3} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right)} \right)} \right) $$
(12)

Generally, the selection of the output neurons’ active function \( {\text{f}}\left( \cdot \right) \) is often linear, such that \( {\text{f}}\left( {\text{x}} \right) = {\text{x}} \). Then, Eq. (12) can be written as follows:

$$ {\text{Y}} = {\text{Y }}\left( {{\text{k}}_{1} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right) + {\text{k}}_{2} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right) + {\text{k}}_{3} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right) + 1/\uplambda} \right)^{ - 1} \left( {{\text{k}}_{1} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right) + {\text{k}}_{2} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right) + {\text{k}}_{3} \left( {{\text{x}}.{\text{x}}^{{\prime }} } \right)} \right) $$
(13)

Substituting in the location of \( k_{1} \),\( k_{2} \),\( k_{3} \) three kernels, and in the location of \( \lambda \) a regularization factor, we obtain a MKFLN model. The power of this model is with using 3 kernels for performing the separation which is expected to outperform the classical one kernel ELM variant. However, there are two problems to be addressed. The first one is the computational concern when using kernels calculation, especially if the size of the dataset is huge. The second one is the criticality of selection suitable kernels for classification due to the sensitivity of the performance to the kernel type. Therefore, a framework for to make the developed MKFLN feasible for practical applications is designed.

However, the kernel-based learning methods usually uilize a large memory system for learning dilemmas with large data sets and are therefore modified to reduced kernel extreme learning machine (RKELM) (Deng et al. 2013). A modification to RKFLN called reduced kernel FLN has also been proposed. The kernel-based and basic ELMs have shown superior generalization and better scalability for multiclass problems with superior generalization, and considerable scalability for multiclass classification problems with much lower training times than those of SVMs [16]. These issues create the ELM an appealing learning paradigm for applied in large-scale problems, such as the IDSs.

Nevertheless, kernels are utilized in learning approaches, particularly those with potentially large amounts of memory for ML problems, with huge datasets such as IDS, which requires the collection of wide data in traffic network. To treat this issue, RKELM takes Huang’s kernel-based ELM and, instead of computing k(x,x) over the entire input data, computes \( {\text{k}}(\tilde{x},x) \), where \( \tilde{x} \) is a randomly chosen subset of the input data. [40] adapted the method of reduced kernel by selecting a small random subset \( \tilde{X} = \left\{ {x_{i} \}_{i = 1}^{{\tilde{n}}} } \right. \) from the original data points \( {\text{X = }}\left\{ {x_{i} \}_{i = 1}^{n} } \right. \) with \( \tilde{n} \ll n \) and using \( {\text{k(x,}}\tilde{x}) \) in place of k(,X,X) to cut the problem size and computing time. As mentioned previously, FLN is better than ELM; to address this issue, RKELM is swapped out for RKFLN. Hence, RKFLN is expected to be better than RKELM. An assumption supposes that multiplying each kernel in RKFLN by a weight provides better results.

3.3 Particle Swarm Optimization

The PSO was first introduced by Li et al. [23] as a parallel evolutionary computation technique which was insired by the social behavior of swarm. The performance of PSO can be significantly affected by the selected tuning parameters (commonly called exploration– exploitation tradeoff). Exploration is the ability of an algorithm to explore all the segments of the search space in an effort to establish a good optimum, better known as the global best. Exploitation on the other hand is the ability of an algorithm to concentrate on its immediate environment and within the surrounding of a better performing solution to effectively establish the optimum. Irrespective of the research efforts in recent times, the selection of algorithmic parameters is still a great problem [41]. In the PSO algorithm, the objective function is used for the evaluation of its solutions, and to operate on the corresponding fitness values. The position of each particle is kept (including its solution), and its velocity and fitness are also evaluated [42]. The PSO algorithm has many practical applications [43,44,45,46]. The position and velocity of each particle is modified to establish an best solution for each iteration using the following relationship:

$$ v_{i} (k + 1) = wv_{i} k + c1r1(xbest,local - x_{i} ) + c2r2(xbest,global) - x_{i} ) $$
(14)
$$ x_{i} \left( {k + 1} \right) = xk + v\left( {k + 1} \right) $$
(15)

Each particle’s velocity and position are denoted as the vectors \( v_{k } = \left( {v_{k1} , \ldots ,v_{kd} } \right) \) and \( x_{i } = \left( {x_{i1} , \ldots ,x_{id} } \right) \), respectively. In (14), \( x \) vectors is the best local and best global positions; \( c1 \) and \( c2 \) represents the acceleration factors referred to as cognitive and social parameters; \( r1 \) and \( r2 \) represents randomly selected number in the range of 0 and 1; \( k \) stands for the iteration index; and \( w \) is the inertia weight parameter [47]. \( x_{i} \) of a particle is updated using (15).

4 Experiments and Analysis

4.1 Implementing of Multi Kernel Based on Fast Learning Network

As it has been mentioned in the previous section, RKFLN has two problems to be solved before we can apply it, the first one is the computational complexity of applying three kernels at the same time, and the second one is the selection of the kernels and its parameters. The initial one is solved through using reduced kernel approach, and the other one is solved through preparing a set of kernels and selecting out of them. In order to make the model more optimized, three weighting factors of using the kernels are imported in the model \( \alpha_{1} \),\( \alpha_{2} \),\( \alpha_{3} \) and \( \lambda \). The parameters \( \alpha_{1} \),\( \alpha_{2} \), and \( \alpha_{3} \) are weighting factors for the kernels \( k_{1} \),\( k_{2} \), and \( k_{3} \), the parameter \( \lambda \) is the regularization parameter. The new model after optimizing is written as

$$ Y = f (Y^{ \wedge } \left( {\alpha_{1}^{*} K_{1} + \alpha_{2}^{*} K_{2} + \alpha_{3}^{*} K_{3} + \frac{1}{{\lambda^{*} }}} \right)^{ - 1} \left( {\alpha_{1}^{*} K_{1} + \alpha_{2}^{*} K_{2} + \alpha_{3}^{*} K_{3} } \right) $$

where the vector \( (\alpha_{1}^{*} ,\alpha_{2}^{*} ,\alpha_{3}^{*} , \lambda^{*} ) \) denotes the optimal parameters of the model, they have the constraint

$$ \alpha_{1}^{*} + \alpha_{2}^{*} + \alpha_{3}^{*} = 1,\alpha_{1} ,\alpha_{2} ,\alpha_{3} \in .\left[ {1\,0} \right]\lambda^{*} \in \left[ {0\,1} \right] $$

In order to determine convenient values for these weights that multiplying each kernel in RKFLN. PSO will be used. Herein, \( k_{1} \),\( k_{2} \), and \( k_{3} \), are multiplied by the weights \( \alpha_{1} \),\( \alpha_{2} \), and \( \alpha_{3} \) respectively, the optimization goal is to find the best weights values that give the highest testing accuracy over validation samples. Beside the searching for the weights values, the optimization process will also look for the best value for the regularization coefficient.

4.2 Experiments of Optimization Multi Kernel Fast Learning Network

This ssection describe our experimental also provide classification performanc results. In order to evaluate the PSO-RKFLN developed model, this work cover teasting results with the KDD Cup99 dataset. Optimize the RKFLN parameters to enhance the accuracy of IDS, we proposed several models such as RKFLN, RKELM, and PSO-RKELM as bunchmarks. Figure 3 shown classification evaluation measures, and Table 1 shown the comparestion results between the models.

Fig. 3.
figure 3

Evaluation measures of classification

Full size image
Table 1. Results of evaluatiom measures of different models
Full size table

For PSO parameters formulae such as c1 = c2 = 1.42, w = 0.75 and number of particles = 5. The KDD 99 training set with duplicates removed for the first set of sets with a dataset consisting of 145,585 split into a training set of 72,792 training examples and 72,792 testing samples. For this study we used all 41 attributes of the data.

5 Summary

In this work, using Machine learning based on the intrusion-detection system, it’s attractive for many researchers. This work provides model based on optimize of a multi kernel of fast learning network. The derived model was rigorously compared to four models, including basic ELM, basic FLN, Reduce Kernel ELM (RK-ELM), and RK-FLN. The approach was tested on the KDD Cup99 intrusion detection dataset. The accuracy of our model (PSO-RKFLN) is slightly higher than other models. For a future work, we recommend checking this model with a different number of neurons to measures and evaluate the complexity of the model.