1 Introduction

The artificial neural networks (ANNs) have been frequently used in a variety of applications with great success due to their ability to approximate complex nonlinear mappings directly from input patterns [1, 2]. Namely, ANNs do not require a user-specified problem solving algorithm, but they could learn from existing examples, much like human beings. In addition, ANNs have inherent generalization ability. This means that ANNs could identify and synchronously respond to the patterns that are similar with but not identical to the ones that are employed to train ANNs. However, the free parameters of ANNs would be defined by learning from the given training samples according to gradient descent algorithms, which makes the learning process relatively slow and brings some issues related to its local minima. Owing to these shortages, it could take much more time to train ANNs and have a suboptimal solution [3].

For these problems, a new artificial neural network, extreme learning machine (ELM), is proposed by Huang et al. [4]. Recently, ELM is a novel single hidden layer feedforward neural network (SLFN) where the input weights and the bias of hidden nodes are generated randomly without tuning and the output weights are determined analytically. ELM owns an extremely fast learning algorithm and good generalization capability. Up to now, the ELM has been successfully applied in various areas [5–7]. The ELM overcomes most issues encountered in traditional learning methods, such as the stopping criterion, number of epochs, learning rate and local minima. However, there are still some insufficiencies in ELM. ELM tends more hidden neurons than conventional tuning-based learning algorithms in many applications, which would make a trained ELM need longer time for responding to unknown testing samples [8, 9].

This paper proposes a novel fast learning network (FLN) based on the thought of ELM. The FLN is a double parallel forward neural network (DPFNN) [10, 11], which is a parallel connection of a multilayer feedforward neural network and a single layer feedforward neural network, and the DPFNN’s output nodes not only receive the recodification of the external information through the hidden nodes, but also receive the external information itself directly through the input nodes. In FLN, the input weights and hidden layer biases are randomly generated, and the weight values of the connection between the output layer and the input layer and the weight values connecting the output node and the input nodes are analytically determined based on least squares methods. Compared with other methods, FLN with a smaller number of hidden units can achieve good generalization performance and stability at a very fast speed on most applications.

The paper is organized as follows: the proposed fast learning network is given in Sect. 2. Section 3 shows the performance evaluation of the FLN. Finally, Sect. 4 summarizes the conclusions of this paper.

2 Fast learning network

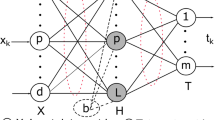
In this section, a novel artificial neural network called fast learning network, which is a double parallel forward neural network, is proposed based on the least squares methods. The fast learning network, as shown in Fig. 1, is described as follows in detail.

Fig. 1
figure 1

Structure of the fast learning network

Full size image

2.1 Approximation problem

The fast learning network called FLN is a parallel connection of a single layer feedforward neural network and a three layer feedforward neural network: input layer, hidden layer and output layer. Suppose, there are N arbitrary distinct samples \( \left\{ {{\mathbf{x}}_{i} ,{\mathbf{y}}_{i} } \right\} \), in which \( {\mathbf{x}}_{i} = \left[ {x_{i1} ,x_{i2} , \ldots ,x_{in} } \right]^{T} \in R^{n} \) is the n-dimensional feather vector of the ith sample, and \( {\mathbf{y}}_{i} = \left[ {y_{i1} ,y_{i2} , \ldots y_{il} } \right]^{T} \in R^{l} \) is the corresponding l-dimensional output vector. The FLN has m hidden layer nodes. W in is the m × n input weight matrix, \( {\mathbf{b}} = \left[ {b_{1} ,b_{2} , \ldots ,b_{m} } \right] \) is the biases of hidden layer nodes, and W oh is a l × m matrix which consists of the weight values of the connection between the output layer and the hidden layer. W oi is a l × n weight matrix which contains weight values of the connection between the output layer and the input layer. \( {\mathbf{c}} = \left[ {c_{1} ,c_{2} , \cdots ,c_{l} } \right]^{T} \) is the biases of output layer nodes. \( g\left( \cdot \right) \) and \( f\left( \cdot \right) \) are the active functions of hidden nodes and output nodes.

Then, the FLN is mathematically modeled as:

$$ \left\{ \begin{aligned} y_{j1} & = f\left( {\sum\limits_{r = 1}^{n} {W_{1r}^{oi} x_{jr} + c_{1} } + \sum\limits_{k = 1}^{m} {W_{1k}^{oh} } g\left( {b_{k} + \sum\limits_{t = 1}^{n} {W_{kt}^{in} x_{jt} } } \right)} \right) \\ y_{j2} & = f\left( {\sum\limits_{r = 1}^{n} {W_{2r}^{oi} x_{jr} } + c_{2} + \sum\limits_{k = 1}^{m} {W_{2k}^{oh} } g\left( {b_{k} + \sum\limits_{t = 1}^{n} {W_{kt}^{in} x_{jt} } } \right)} \right)\quad j = 1,2, \cdots ,N \\ \vdots \\ y_{jl} & = f\left( {\sum\limits_{r = 1}^{n} {W_{lr}^{oi} x_{jr} } + c_{l} + \sum\limits_{k = 1}^{m} {W_{lk}^{oh} } g\left( {b_{k} + \sum\limits_{t = 1}^{n} {W_{kt}^{in} x_{jt} } } \right)} \right) \\ \end{aligned} \right. $$
(1)

Equation (1) could be transformed into the following form:

$$ {\mathbf{y}}_{j} = f\left( {{\mathbf{W}}^{oi} {\mathbf{x}}_{j} + {\mathbf{c}} + \sum\limits_{k = 1}^{m} {{\mathbf{W}}_{k}^{oh} } g\left( {{\mathbf{W}}_{k}^{in} {\mathbf{x}}_{j} + b_{k} } \right)} \right)\quad j = 1,2, \cdots ,N $$
(2)

where \( {\mathbf{W}}^{oi} = \left[ {{\mathbf{W}}_{1}^{oi} ,{\mathbf{W}}_{2}^{oi} , \ldots ,{\mathbf{W}}_{l}^{oi} } \right] \) is the weight vector connecting the jth output node and the input nodes, \( {\mathbf{W}}_{k}^{oh} = \left[ {W_{1k}^{oh} ,W_{2k}^{oh} , \ldots ,W_{lk}^{oh} } \right]^{T} \) is the weight vector connecting the kth hidden node and the output nodes, and \( {\mathbf{W}}_{k}^{in} = \left[ {W_{k1}^{in} ,W_{k2}^{in} , \ldots ,W_{km}^{in} } \right]^{T} \)is the weight vector connecting the kth hidden node and the input nodes.

Then, Eq. (2) can be rewritten compactly as Eq. (3)

$$ {\mathbf{Y}} = f\left( {{\mathbf{W}}^{oi} {\mathbf{X}} + {\mathbf{W}}^{oh} {\mathbf{G}} + {\mathbf{c}}} \right) = f\left( {\left[ {{\mathbf{W}}^{oi} {\mathbf{W}}^{oh} {\mathbf{c}}} \right]\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]} \right) = f\left( {{\mathbf{W}}\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]} \right) $$
(3)
$$ \begin{aligned} {\mathbf{G}}\left( {{\mathbf{W}}_{1}^{in} , \cdots ,{\mathbf{W}}_{m}^{in} ,b_{1} , \cdots ,b_{m} ,{\mathbf{x}}_{1} , \cdots ,{\mathbf{x}}_{N} } \right) = \left[ {\begin{array}{*{20}c} {g\left( {{\mathbf{W}}_{1}^{in} {\mathbf{x}}_{1} + b_{1} } \right)} & \cdots & {g\left( {{\mathbf{W}}_{1}^{in} {\mathbf{x}}_{N} + b_{1} } \right)} \\ \vdots & \ddots & \vdots \\ {g\left( {{\mathbf{W}}_{m}^{in} {\mathbf{x}}_{1} + b_{m} } \right)} & \cdots & {g\left( {{\mathbf{W}}_{m}^{in} {\mathbf{x}}_{N} + b_{m} } \right)} \\ \end{array} } \right]_{m \times N} \hfill \\ \end{aligned} $$
(4)
$$ {\mathbf{W}} = \left[ {{\mathbf{W}}^{oi} {\mathbf{W}}^{oh} {\mathbf{c}}} \right]_{{l \times \left( {n + m + 1} \right)}} $$
(5)
$$ {\mathbf{I}} = \left[ {11 \cdots 1} \right]_{1 \times N} $$
(6)

The matrix \( {\mathbf{W}} = \left[ {{\mathbf{W}}^{oi} {\mathbf{W}}^{oh} {\mathbf{c}}} \right] \) could be called as output weights. G is called the hidden layer output matrix of FLN; the ith row of G is the ith hidden neuron’s output vector with respect to inputs \( {\mathbf{x}}_{1} ,{\mathbf{x}}_{2} , \ldots ,{\mathbf{x}}_{N} \).

2.2 Minimum norm least squares solution

For the input weights and biases of the hidden layer, many research results show that the input weights and hidden biases need not be adjusted at all and can be arbitrarily given [12–16]. Based on these researches, this proposed FLN could randomly generate the input weights W in and biases \( {\mathbf{b}} = \left[ {b_{1} ,b_{2} , \ldots ,b_{m} } \right] \) of the hidden layer. After that, the FLN could be thought of a linear system, and the output weights W could be analytically determined through the following form:

$$ \left\| {f\left( {{\hat{\mathbf{W}}}\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]} \right) - {\mathbf{Y}}} \right\| = \mathop {\hbox{min} }\limits_{{\mathbf{W}}} \left\| {f\left( {{\mathbf{W}}\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]} \right) - {\mathbf{Y}}} \right\| $$
(7)

For an invertible activation function \( f\left( \cdot \right) \), the output weights are also analytically determined by Eq. (8)

$$ \left\| {{\hat{\mathbf{W}}}\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right] - f^{ - 1} \left( {\mathbf{Y}} \right)} \right\| = \mathop {\hbox{min} }\limits_{{\mathbf{W}}} \left\| {{\mathbf{W}}\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right] - f^{ - 1} \left( {\mathbf{Y}} \right)} \right\| $$
(8)

where \( f^{ - 1} \left( \cdot \right) \) is the invertible function of \( f\left( \cdot \right) \).

According to the Moore–Penrose generalized inverse [17, 18], the minimum norm least-squares solution of the linear system could be written as:

$$ {\hat{\mathbf{W}}} = f^{ - 1} \left( {\mathbf{Y}} \right)\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]^{ + } = f^{ - 1} \left( {\mathbf{Y}} \right){\mathbf{H}}^{ + } $$
(9)

where \( {\mathbf{H}} = \left[ {{\mathbf{X}}\;\,{\mathbf{G}}\;\;{\mathbf{I}}} \right]^{T} = \left[ {{\mathbf{X}}^{T} \;\,{\mathbf{G}}^{T} \;\;{\mathbf{I}}^{T} } \right] \).

Then

$$ \left\{ \begin{aligned} {\mathbf{W}}^{oi} & = {\hat{\mathbf{W}}}\left( {1:l,\;1:n} \right) \\ {\mathbf{W}}^{oh} & = {\hat{\mathbf{W}}}\left( {1:l,\;n + 1:\left( {n + m} \right)} \right) \\ {\mathbf{c}} & = {\hat{\mathbf{W}}}\left( {1:l,\;n + m + 1} \right) \\ \end{aligned} \right. $$
(10)

If the \( {\text{rank}}\left( {\mathbf{H}} \right) = N \), Eq. (9) could be rewritten as

$$ \begin{aligned} {\hat{\mathbf{W}}} & = f^{ - 1} \left( {\mathbf{Y}} \right)\left( {\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]^{T} \left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]} \right)^{ - 1} \left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]^{T} \\ & = f^{ - 1} \left( {\mathbf{Y}} \right)\left( {\left[ {{\mathbf{X}}^{T} {\mathbf{G}}^{T} {\mathbf{I}}^{T} } \right]\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]} \right)^{ - 1} \left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]^{T} \\ & = f^{ - 1} \left( {\mathbf{Y}} \right)\left( {{\mathbf{X}}^{T} {\mathbf{X}} + {\mathbf{G}}^{T} {\mathbf{G}} + {\mathbf{I}}^{T} {\mathbf{I}}} \right)^{ - 1} {\mathbf{H}}^{T} \\ \end{aligned} $$
(11)

If the \( {\text{rank}}\left( {\mathbf{H}} \right) = m + n + 1 \), Eq. (9) could be rewritten as

$$ \begin{aligned} {\hat{\mathbf{W}}} & = f^{ - 1} \left( {\mathbf{Y}} \right)\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]^{T} \left( {\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ {\mathbf{I}} \hfill \\ \end{gathered} \right]^{T} } \right)^{ - 1} \\ & = f^{ - 1} \left( {\mathbf{Y}} \right){\mathbf{H}}^{T} \left( {{\mathbf{HH}}^{T} } \right)^{ - 1} \\ \end{aligned} $$
(12)

2.3 Simplifying model

In general, the output neurons’ active function \( f\left( \cdot \right) \) is often chosen linear, namely \( f\left( x \right) = x \), and the output biases \( {\mathbf{c}} = \left[ {c_{1} ,c_{2} , \cdots ,c_{l} } \right]^{T} \) are often set as zeros. Then, the FLN’s mathematical model (Eq. (1)) could be rewritten as

$$ \left\{ \begin{aligned} y_{j1} & = \sum\limits_{r = 1}^{n} {W_{1r}^{oi} x_{jr} } + \sum\limits_{k = 1}^{m} {W_{1k}^{oh} } g\left( {b_{k} + \sum\limits_{t = 1}^{n} {W_{kt}^{in} x_{jt} } } \right) \\ y_{j2} & = \sum\limits_{r = 1}^{n} {W_{2r}^{oi} x_{jr} } + \sum\limits_{k = 1}^{m} {W_{2k}^{oh} } g\left( {b_{k} + \sum\limits_{t = 1}^{n} {W_{kt}^{in} x_{jt} } } \right) \\ \vdots \\ y_{jl} & = \sum\limits_{r = 1}^{n} {W_{lr}^{oi} x_{jr} } + \sum\limits_{k = 1}^{m} {W_{lk}^{oh} } g\left( {b_{k} + \sum\limits_{t = 1}^{n} {W_{kt}^{in} x_{jt} } } \right) \\ \end{aligned} \right.,\quad j = 1,2, \cdots ,N $$
(13)

And simultaneously, Eqs. (3) and (5) could be, respectively, transformed into Eqs. (14) and (15)

$$ {\mathbf{Y}} = {\mathbf{W}}^{oi} {\mathbf{X}} + {\mathbf{W}}^{oh} {\mathbf{G}} = \left[ {{\mathbf{W}}^{oi} {\mathbf{W}}^{oh} } \right]\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right] = {\mathbf{W}}\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right] $$
(14)
$$ {\mathbf{W}} = \left[ {{\mathbf{W}}^{oi} {\mathbf{W}}^{oh} } \right]_{{l \times \left( {n + m} \right)}} $$
(15)

The hidden layer’s output matrix G is still calculated by Eq. (4). And Eq. (7) and Eq. (8) could be rewritten as Eq. (15).

$$ \left\| {{\hat{\mathbf{W}}}\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right] - {\mathbf{Y}}} \right\| = \mathop {\hbox{min} }\limits_{{\mathbf{W}}} \left\| {{\mathbf{W}}\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right] - {\mathbf{Y}}} \right\| $$
(15)

The output weights \( {\mathbf{W}} = \left[ {{\mathbf{W}}^{oi} {\mathbf{W}}^{oh} } \right] \) could be analytically determined by the Moore–Penrose generalized inverse.

$$ {\hat{\mathbf{W}}} = {\mathbf{Y}}\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right]^{ + } = {\mathbf{YH}}^{ + } $$
(16)
$$ \left\{ \begin{aligned} {\mathbf{W}}^{oi} & = {\hat{\mathbf{W}}}\left( {1:l,1:n} \right) \\ {\mathbf{W}}^{oh} & = {\hat{\mathbf{W}}}\left( {1:l,n + 1:\left( {n + m} \right)} \right) \\ \end{aligned} \right. $$
(17)

where \( {\mathbf{H}} = \left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right] \).

And if the \( {\text{rank}}\left( {\mathbf{H}} \right) = N \), Eq. (16) could be rewritten as

$$ \begin{aligned} {\hat{\mathbf{W}}} & = {\mathbf{Y}}\left( {\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right]^{T} \left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right]} \right)^{ - 1} \left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right]^{T} \\ & = {\mathbf{Y}}\left( {\left[ {{\mathbf{X}}^{T} {\mathbf{G}}^{T} } \right]\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right]} \right)^{ - 1} \left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right]^{T} \\ & = {\mathbf{Y}}\left( {{\mathbf{X}}^{T} {\mathbf{X}} + {\mathbf{G}}^{T} {\mathbf{G}}} \right)^{ - 1} {\mathbf{H}}^{T} \\ \end{aligned} $$
(18)

And if the \( {\text{rank}}\left( {\mathbf{H}} \right) = m + n \), Eq. (16) could be rewritten as

$$ \begin{aligned} {\hat{\mathbf{W}}} & = {\mathbf{Y}}\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right]^{T} \left( {\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} {\mathbf{X}} \hfill \\ {\mathbf{G}} \hfill \\ \end{gathered} \right]^{T} } \right)^{ - 1} \\ & = {\mathbf{YH}}^{T} \left( {{\mathbf{HH}}^{T} } \right)^{ - 1} \\ \end{aligned} $$
(19)

As seen from the above learning process, as the FLN is a parallel connection of a single layer feedforward neural network and a multilayer feedforward network, the output layer nodes not only get the recodification of the external information through the hidden layer nodes, but also get the external information itself directly through the input layer nodes. In addition, many literatures has shown that a single layer feedforward neural network in solving the linear problem with higher efficiency, a multilayer feedforward network can very well realize the complex non-linear mapping from the inputs to the outputs. Then, the FLN has the advantages of the two neural networks, but the ELM does not. So, the FLN with a same or a smaller number of hidden units can achieve much better generalization performance and stability than ELM. In addition, in FLN, the input weights and hidden layer biases are randomly assigned, and the other weights could be analytically determined by least squares methods. So, the FLN could overcome most issues encountered in traditional learning methods and simultaneously own very fast learning speed.

2.4 Learning algorithm for FLN

Suppose, given a training set \( S = \left\{ {\left( {{\mathbf{x}}_{i} ,{\mathbf{y}}_{i} } \right)|{\mathbf{x}}_{i} \in R^{n} ,{\mathbf{y}}_{i} \in R^{l} } \right\} \), hidden node number m and activation function \( g\left( \cdot \right) \), then the FLN could be summarized as follows:

  1. 1.

    Randomly generate the input weight matrix \( {\mathbf{W}}^{in} \) and the bias matrix b.

  2. 2.

    Calculate the hidden output matrix G using Eq. (3).

  3. 3.

    Calculate the combination matrix W using Eq. (9) or Eq. (16).

  4. 4.

    Determine FLN’s model parameters Eq. (10) or Eq. (17).

3 Experimental study and discussion

In order to evaluate the proposed FLN algorithm, the FLN is applied to the benchmark problems listed in Table 1, which include 9 regression applications (Auto MPG, Servo, California housing, Bank domains, Machine CPU, Abalone, Delta ailerons, Delta elevators, Boston housing), which are selected from the website: http://www.liaad.up.pt/~ltorgo/Regression/DataSets.html and often adopted to test various learning algorithms [18, 19]. In addition, another three regression methods are employed for performance comparisons.

Table 1 Specification of real-world regression data sets
Full size table

All evaluations for back propagation (Bp), support vector machine (SVM), ELM and FLN are carried out in Windows XP and Matlab 7.1 environment running on a desktop with AMD Phenom (tm) 9,650 processor 2.31 GHz and 2G RAM. For all data sets listed in Table 1, their observations are randomly split into two parts (training set and testing set) according to the number of samples listed in Table 1.

In order to state the superiority of the FLN, another three methods, SVM, Bp and ELM, are employed to compare the regression accuracy and generalization performance. Firstly, the number of hidden neurons is set as 30 for Bp, ELM and FLN, and the sigmoid function Eq. (20) is chosen as the activation function for the ELM and FLN algorithms.

$$ g\left( x \right) = \frac{1}{{1 + \exp \left( { - x} \right)}} $$
(20)

In addition, for each problem, we estimate the regression accuracy using different combination of cost parameters C and the kernel parameters γ, \( C = \left[ {2^{ - 2} ,2^{ - 1} , \ldots ,2^{11} ,2^{12} } \right] \) and \( \gamma = \left[ {2^{ - 10} ,2^{ - 9} , \ldots ,2^{3} ,2^{4} } \right] \), so the SVM would be tried \( 15 \times 15 = 225 \) parameter combinations \( \left( {C,\gamma } \right) \) in order to find one to make SVM show best performance. Here, the search parameter combination process is thought of a part of the training process.

Every experiment is repeated 30 times. The mean and its standard deviations (SD) of root-mean-square error (RMSE) for the four methods are given in Table 2 for training samples and Table 3 for testing samples.

$$ {\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {y_{i} - \hat{y}_{i} } \right)^{2} } } $$
(21)
$$ {\text{SD}} = \sqrt {\frac{{\sum\nolimits_{{i = 1}}^{n} {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} _{i} - \overline{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }} } \right)^{2} } }}{{n - 1}}} $$
(22)
Table 2 Comparison of the mean and its standard deviation of RMSE and the running time for SVM, BP, ELM and FLN using training samples
Full size table
Table 3 Comparison of the mean and standard deviation of RMSE and the running time for SVM, BP, ELM and FLN using testing samples
Full size table

As seen from Table 2, for the training samples for data sets, compare with Bp and ELM, the FLN shows better regression accuracy on the all regression applications listed in Table 1. In addition, for the standard deviations, the FLN shows better performance on five applications (Auto MPG, Servo, Bank domains, Machine CPU and Delta ailerons), ELM on three applications (Abalone, Delta elevators and Boston housing) and Bp on one (California housing). Compared with SVM, for the regression accuracy, the FLN shows better superiority on five applications (Auto MPG, Servo, Bank domains, Machine CPU and Delta ailerons) and SVM on the other four applications. For the learning time, the ELM needs the least one; the next is FLN, then Bp, and the last SVM. In short, although the SVM shows better regression performance on some applications than FLN, it spends much more time to search better parameter combination. Although the ELM needs less learning time than ELM, the regression performance is not better than the FLN.

As seen from Table 3, for testing samples for data sets, compared with SVM, Bp and ELM, the FLN shows the best generalization ability on seven applications (Auto MPG, Servo, California housing, Bank domains, Abalone, Delta ailerons and Delta elevators), and for the other two data sets (Machine CPU and Boston housing), the SVM shows best. For the stability, the SVM has best performance on one application (Servo), ELM on two applications (Abalone and Boston housing) and FLN on the other six ones. In short, the FLN has the better generalization ability and stability on most applications.

In addition, in order to further state the FLN validity, the hidden neurons of ELM and FLN are reset as 20, and the sigmoid function is still adopted as the activation function. The related results are reported in Table 4.

Table 4 Comparison of the mean and standard deviation of RMSE and the running time for ELM and FLN using training and testing samples
Full size table

As seen from Table 4, we could know that, although ELM needs a little less learning and responding time than the FLN on most data sets, the FLN shows much better regression accuracy on the all data sets and also has the better generalization ability on 8 data sets. The ELM shows better generalization ability on one application (Machine CPU).

As seen from Tables 2, 3 and 4, with the hidden neurons reducing, the regression accuracy of ELM and FLN would reduce on all data sets, and the learning and responding time is also reducing on most applications. However, the generalization ability is increasing on 2 applications (Auto MPG and Machine CPU) for ELM and on 4 applications (Auto MPG, Servo, Machine CPU and Abalone) for FLN. In addition, whatever the number of hidden neurons is 30 or 20, if only the number of hidden neurons is set as the same number, the FLN could show better regression accuracy and generalization ability on most applications than ELM.

Compared with ELM with 30 hidden neurons, for the training samples of all data sets, although the ELM shows better regression accuracy than the FLN with 20 hidden neurons on six regression applications (Auto MPG, Servo, California housing, Machine CPU, Abalone and Delta ailerons), the FLN with 20 hidden neurons could show better superiority on only three applications (Bank domains, Delta elevators and Boston housing). For testing set for all applications, the FLN with 20 hidden neurons could show better generalization ability than ELM with 30 hidden neurons on seven applications (Auto MPG, Servo, Bank domains, Machine CPU, Abalone, Delta ailerons and Boston housing). However, the ELM shows better performance than the FLN on only two applications (California housing and Delta elevators). In addition, the FLN could have better stability than ELM on most regression applications according to the standard deviations, and a faster speed for both learning and testing than ELM under the assigned number of hidden neurons. Especially, the more the data set contains samples, the less time FLN spends in learning and testing than ELM. Therefore, the proposed FLN with less hidden neurons could achieve good generalization performance and stability with much more compact networks and fast speed.

In addition, in order to state the validity of the sigmoid function, another two activation functions: ‘Hardlim’ and ‘Sine,’ are employed to compare the performance of the FLN. Here, the number of hidden neurons is still set as 20. The related results are recorded in Table 5.

$$ {\text{`Hardlim'}}:g\left( x \right) = \left\{ \begin{gathered} 1\quad x \ge 0 \hfill \\ 0\quad x < 0 \hfill \\ \end{gathered} \right. $$
(23)
$$ {\text{`Sine'}}:g\left( x \right) = \sin (x) $$
(24)
Table 5 The mean and standard deviation of RMSE for FLN with 20 hidden nodes and different activation functions
Full size table

As seen from Table 5, for the training sample of all data sets, the FLN with ‘Sigmoid’ has a better regression accuracy on six applications (Auto MPG, Servo, Bank domains Machine CPU, Delta ailerons and Delta elevators) and the FLN with ‘Sine’ on three applications (California housing, Abalone and Boston housing). For the testing samples of data sets, the FLN with ‘Sigmoid’ has the better generalization ability than the FLN with the other two activation functions on seven applications, the FLN with ‘Hardlim’ on one application (Machine CPU) and the FLN with ‘Sine’ on one application (Boston housing). According to the standard deviation of RMSE, the FLN with ‘Sigmoid’ has better stability for the training and testing sample on most applications. So, the ‘Sigmoid’ as the activation function of FLN makes the regression accuracy, generalization ability and stability of FLN better.

As observed from Fig. 2, it shows the relationship between the generalization performance of FLN and its network size for the Bank domains. The testing RMSE decreases with the increase in the number of hidden layer neurons, so the generalization performance of FLN is more and more stable with the increase in the number of hidden layer neurons.

Fig. 2
figure 2

The relationship between the generalization performance and number of hidden neurons

Full size image

In summation, the FLN with much more compact networks and fast speed could achieve good generalization performance and stability on most functions. So, the FLN could be thought of an effective machine learning tool.

4 Real-world design problem

For studying the influence of adjustable boiler operation parameters for the thermal efficiency and NO x emissions of a 330 WM double-furnace coal-fired boiler, 20 cases were carried out under various operating conditions. The boiler equips a coal pulverizing system with intermediate silo, 4 coal pulverizers, 4 mill exhausters and 32 pulverized fuel feeders. In order to set up a function between the thermal efficiency/NO x emissions and operating conditions, the proposed FLN is employed.

Firstly, as seen from the Table 1 of the Ref. [20], Cases 1–3, Case 4, Cases 5–6, Cases 7–14 and Cases 15–20, respectively, work in different properties of coal-fired. According to the coal characteristics, the 20 cases are divided into two parts: training samples (17 cases: Cases 1–2, Cases 4–11, Cases 13–16 and Cases 18–20) and testing samples (3 cases: Case 3, Case 12 and Case 17), in order to set up the function relation between the thermal efficiency/NO x emissions and operating conditions, and test its validity. The thermal efficiency/NO x emissions mainly depend on 26 operational conditions given as follows.

  • The boiler load (MW).

  • The coal feeder rotation speed (CFRS, r min−1), including A, B, C, D levels.

  • The primary air velocity, including A, B, C, D levels.

  • The secondary air velocity (m s−1), including AA, AB, BC, CD, DE levels.

  • The oxygen content in the flue gas (OC,  %).

  • The exhaust gas temperature (EGT,  °C).

  • The over fire air port (OFA,  %)

  • The separated over fire air port (SOFA,  %).

  • The coal characteristics including content of carbon (Car,  %), hydrogen (Har,  %), oxygen (Oar,  %), nitrogen (Nar,  %), water (War,  %), volatile (Var,  %), heat value (Qdw.ar, kJ/kg).

The proposed FLN is adopted to set up mathematical models of the thermal efficiency/NO x emissions, which could state the mapping relation between the thermal efficiency/NO x emissions and operational conditions. The complex mapping function relation could be simplified as a model which is shown in Fig. 3.

Fig. 3
figure 3

Simplified boiler model

Full size image

In order to test the model repeatability and validity, every experiment is repeated 30 times. The minimum, maximum, median and mean of the root-mean-square error (RMSE) have been recorded for the training samples. And simultaneously, the minimum, maximum, median and mean of the prediction values are also recorded for testing samples. For the thermal efficiency, the training time and related values of RMSE are given in Table 6, the prediction values of training samples are shown in Fig. 4, its error comparisons are shown in Fig. 5, and the prediction values of testing samples are given in Table 7. For NO x emissions, the training time and related values of RMSE are given in Table 8, the prediction values of training samples are shown in Fig. 6, its error comparisons are shown in Fig. 7, and the prediction values of testing samples are given in Table 9.

Table 6 Training time and related values of RMSE for the thermal efficiency
Full size table
Fig. 4
figure 4

The prediction values of the thermal efficiency for training samples

Full size image
Fig. 5
figure 5

The prediction errors of the thermal efficiency for training samples

Full size image
Table 7 Prediction values of testing samples for the thermal efficiency
Full size table
Table 8 Training time and related values of RMSE for NO x emissions
Full size table
Fig. 6
figure 6

The prediction values of the thermal efficiency for training samples

Full size image
Fig. 7
figure 7

The prediction errors of NO x emissions for training samples

Full size image
Table 9 Prediction values of testing samples for NO x emissions
Full size table

As to the comparison of the thermal efficiency’s model, just as we can see from Tables 6, 7 and Figs. 4, 5, the minimum, maximum, median and mean of the RMSE and the prediction values of testing samples remain unchanged for Bp, SVM and LSSVM in 30 training models. Although these values have some variations for FLN, these variations are too small. But for ELM, the minimum, maximum, median and mean of RMSE are different, and the difference is very large. So, ELM’s prediction errors of training samples are not shown in Fig. 5. For the prediction precision of training samples, the FLN’s RMSE is the least among all the 5 methods, whose values achieve 10−13. The runtime of training process is also the least, except for ELM. As seen from the prediction values of testing samples, the LSSVM’s prediction errors are the least one, secondly FLN. The Bp’s prediction values are same for different cases, and ELM’s some prediction values of testing samples overstep the limitation of the thermal efficiency. Therefore, we could think the ELM and BP are out of work for the prediction of the thermal efficiency. In a word, although LSSVM has better generalization ability than FLN, FLN’s generalization ability is also very well and better than those of Bp, SVM and ELM; in addition, FLN’s learning time and RMSE of training samples are much better than any one of Bp, SVM and LSSVM.

As to the comparison of NO x emissions’ model, just as we can see from Tables 8, 9 and Figs. 6, 7, the minimum, maximum, median and mean of the RMSE and the prediction values of testing samples keep unchanged as the thermal efficiency’s model for Bp, SVM and LSSVM. Although there are tiny variations in these values of FLN, they are negligible. But for ELM, there are very large variations in these values, so ELM’s prediction errors of training samples are not shown in Fig. 6. According to the RMSE, the training precision of FLN is the best among the five methods, and simultaneously, the FLN needs the least training time. For the predicted NO x emission of testing samples, the prediction values of Bp and SVM are same for different cases, and some ELM’s prediction values overstep the limitation of NO x emissions; therefore, we may think the ELM, BP and SVM are out of work for the prediction of NO x emissions. Although the predicted NO x emissions of FLN are not better than those of LSSVM for Case 12, majority of predicted NO x emissions of FLN outperform those of LSSVM for Case 3 and Case 17 in 30 prediction models. So, the FLN has very good prediction precision and generalization ability with little runtime for training process.

In summary, the FLN has very good prediction precision and generalization ability and simultaneously needs little learning time in the training process. So, the FLN may set up very good models of the thermal efficiency and NO x emissions and proves to be a good effective learning method.

5 Conclusions

This paper proposes a novel artificial neural network, fast learning network (FLN), which is a double parallel forward neural network. In FLN, the input weights and hidden layer biases are randomly generated like ELM, and the other weights and biases are would be analytically determined based on least squares methods. In order to test FLN’s validity, it is applied to 9 regression problems. Experimental results show that compared with SVM, Bp and ELM, the FLN with the same hidden neurons can achieve better regression accuracy, generalization performance and stability at a very fast speed. Although the hidden neuron’s number of FLN is less than that of ELM, the FLN still has better generalization performance and stability than ELM on most applications. In addition, the FLN is applied to a 330 WM coal-fired boiler. Compared with other learning methods (such as Bp, ELM, SVR and LSSVR), the FLN can achieve better regression accuracy, generalization performance and stability at a high speed. So, the FLN could be a useful machine learning tool and be applied to various applications like other intelligent learning machines.