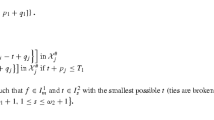Improved Fully Polynomial Approximation Schemes for the Maximum Lateness Minimization on a Single Machine with a Fixed Operator or Machine Non-Availability Interval

Abstract

In this paper we consider the single machine scheduling problem with one non-availability interval to minimize the maximum lateness where jobs have positive tails. Two cases are considered. In the first one, the non-availability interval is due to the machine maintenance. In the second case, the non-availibility interval is related to the operator who is organizing the execution of jobs on the machine. The contribution of this paper consists in an improved FPTAS for the maintenance non-availability interval case and its extension to the operator non-availability interval case. The two FPTASs are strongly polynomial and outperform the recent ones by Kacem, Kellerer and Seifaddini presented in [12].

Supported by the LCOMS EA 7306, a research unit of the Université de Lorraine, and by the University of Graz.

1 Introduction

In this paper we investigate some improvements to the previous work by Kacem, Kellerer and Seifaddini [12]. We consider the single machine scheduling problem with one non-availability interval to minimize the maximum lateness where jobs have positive tails. Two cases are considered. In the first one, the non-availability interval is due to the machine maintenance. In the second case, the non-availibility interval is related to the operator who is organizing the execution of jobs on the machine. An operator non-availability period is a time interval in which no job can start, and neither can complete. The main difference between machine non-availability (MNA) and operator non-availability (ONA) consists in the fact that a job can be processed but cannot start neither finish during the ONA period. However, the machine non-availability interval is a completely forbidden period. Rapine et al. [18] have described the applications of this problem in the planning of a chemical experiments as follows: Each experiment is performed by an automatic system (a robot), during a specified amount of time, but a chemist is required to control its start and completion. At the beginning, the chemist launches the process (preparation step). The completion step corresponds to the experimental analysis, which is to be done in a no-wait mode to stop chemical reactions. Here, the automatic system is available all the time, where the chemists may be unavailable due to planned vacations or activities. This induces operator (chemist) non-availability intervals when experiments (jobs) can be performed by the automatic system (machine), but cannot neither start nor complete.

The study of this family of scheduling problems has been motivated by different applications in logistics. First, the production scheduling by integrating the different sources of non-availability (machine and/or operator sources) is an important application (see for example, Brauner et al. [1], Rapine et al. [18]). Moreover, the maximum lateness minimization in scheduling theory is known as equivalent to the maximum delivery date minimization, where the delivery times can be seen as transportation durations (see for example, Carlier [2], Kacem and Kellerer [9], Dessouky and Margenthaler [4]). Other online applications can be found in Kacem and Kellerer [11].

2 Related Works

The MNA case of this type of problems has been studied in the literature under various criteria (a sample of these works includes Lee [15], Kacem [8], Kacem et al. [13], Kubzin and Strusevich [14], Qi et al. [16, 17], Schmidt [19], He et al. [6]). However, few papers studied the problem we consider in this paper. Lee [15] explored the Jackson’s sequence and proved that it is a 2-approximation. Recently, Yuan et al. developed an interesting PTAS (Polynomial Approximation Scheme) for the studied problem [21]. Kacem [8] presented a first Fully Polynomial Time Approximation Scheme (FPTAS) for the maximum lateness minimization. It is well-known that an FPTAS is the best possible approximation scheme for an NP-hard problem, unless P = NP (see for example, Kacem and Kellerer [10], Gens and Levner [5], Ibarra and Kim [7], Sahni [20]). That is why this paper is a good attempt to design more efficient approximation heuristics and approximation schemes to solve the studied problem.

For the ONA case, few works have been published. Brauner et al. [1] considered the problem of single machine scheduling with ONA periods. They analyzed this problem on a single machine with the makespan as a minimization criterion and they showed that the problem is NP-hard with one ONA period. They also considered the problem with K ONA periods such that the length of each ONA period is no more than $\frac{1}{\lambda }$ times the total processing time of all jobs. They introduced a worst-case ratio smaller than $1+\frac{2K}{\lambda }$ for the so-called algorithm LS (list scheduling). They presented an approximation algorithm with a worst-case ratio close to $2+\frac{K-1}{\lambda }$. The natural case of periods where the duration of the periods is smaller than any processing time of any job, has been considered by Rapine et al. [18]. They proved that the problem can be solved in polynomial time if there is only one ONA period. It was shown that the problem is NP-hard if one has $K\ge 2$ small non-availability periods and the worst-case ratio of LS is no more than $\frac{K+1}{2}$ and the problem does not admit an FPTAS for $K\ge 3$ unless P = NP.

Recently, Chen et al. [3] considered the single machine scheduling with one ONA period to minimize the total completion time. The problem is NP-hard even if the length of the ONA period is smaller than the processing time of any job. They have also presented an algorithm with a tight worst-case ratio of $\frac{20}{17}$. They showed that the worst-case ratio of SPT is at least $\frac{5}{3}$.

For more details, the previous paper by Kacem, Kellerer and Seifaddini [12] contains an overview on these problems.

3 Contributions

The contribution of this paper consists in an improved FPTAS for the maintenance non-availability interval case and its extension for the ONA interval case. The two FPTASs are strongly polynomial and they have reduced time complexities compared to [12]. These contributions are summarized in Table 1 for both cases.

This note is organized as follows. Section 4 recalls the exact formulation of the maintenance non-availability interval case and the improved FPTAS. Section 5 is devoted to the extension to the operator non-availability interval case and to the presentation of the associated FPTAS. Finally, Sect. 6 concludes the paper.

Table 1. Summary of results

4 Case Under MNA Interval

The considered problem ($\mathcal {P}$) can be formulated as follows. We have to schedule a set J of n jobs on a single machine, where every job j has a processing time $p_{j}$ and a tail $q_{j}$ (or delivery time). The machine can process at most one job at a time and it is unavailable between $T_{1}$ and $T_{2}$ (i.e., $(T_{1},T_{2})$ is a forbidden interval). Preemption of jobs is not allowed (jobs have to be performed under the non-resumable scenario). All jobs are ready to be performed at time 0. With no loss of generality, we consider that all data are integers and that jobs are indexed according to Jackson’s rule [15] (i.e., jobs are indexed in nonincreasing order of tails). Therefore, we assume that $q_{1}\ge q_{2}\ge \ldots \ge q_{n}$. Let $C_{j}\left( S\right)$ denote the completion time of job j in a feasible schedule S for the problem and let $\mathcal {\varphi }_{S}(\mathcal {P})$ be the maximum lateness (or the delivery date) yielded by schedule S for instance $\mathcal {I}$ of ($\mathcal {P}$):

$$\begin{aligned} \mathcal {\varphi }_{S}(\mathcal {I})=\max _{1\le j\le n}\left( C_{j}\left( S\right) +q_{j}\right) \end{aligned}$$

(1)

The aim is to find a feasible schedule S by minimizing the maximum lateness. We also denote by $\mathcal {\varphi }^{*}(\mathcal {I})$ the minimal maximum lateness for instance $\mathcal {I}$. Due to the dominance of Jackson’s order, an optimal schedule is composed of two sequences of jobs scheduled in nondecreasing order of their indexes [15]. If all the jobs can be inserted before $T_{1}$, the instance studied ($\mathcal {I}$) has obviously a trivial optimal solution obtained by Jackson’s rule. We therefore consider only the problems in which all the jobs cannot be scheduled before $T_{1}$. Moreover, we consider that every job can be inserted before $T_{1}$ (i.e., $p_{j}\le T_{1}$ for every $j\in J$). It is useful to recall that Lee [15] explored the Jackson’s sequence JS and proved that its deviation to the optimal maximum lateness cannot exceed the largest processing time, which is equivalent to state that JS is a 2-approximation.

4.1 The Improved Procedure

The proposed FPTAS is based on the modification of the one proposed in [12] by Kacem, Kellerer and Seifaddini.

First, as described in [12], we use the simplification technique based on merging small jobs proposed in [9]. We simplify the input instance $\mathcal {I}$ as follows. Given an arbitrary $\varepsilon >0$, with the assumption that $1/\varepsilon$ is integer, we split the interval $[0,\max _{j\in J}\{q_{j}\}]$ in $1/\varepsilon$ equal length intervals and we round up every tail $q_{j}$ to the next multiple of $\varepsilon q_{\max }$ ($q_{\max }=\max _{j\in J}\{q_{j}\}$). The new instance is denoted as $\mathcal {I}^{\prime }$. Then, J is divided into at most $1/\varepsilon$ subsets J(k) ($1\le k\le 1/\varepsilon$) where jobs in J(k) have identical tails of $k\varepsilon q_{\max }$. The second modification consists in reducing the number of small jobs in every subset J(k). Small jobs are those having processing times less than $\varepsilon P/2$ where $P=\sum _{j=1}^{n}p_{j}$. The reduction is done by merging the small jobs in each J(k) so that we obtain new greater jobs having processing times between $\varepsilon P/2$ and $\varepsilon P$. The small jobs are taken in the order of their index in this merging procedure. At most, for every subset J(k), a single small job remains. We re-index jobs according to nondecreasing order of their tails. The new instance we obtain is denoted as $\mathcal {I} ^{\prime \prime }$. Clearly, the number of jobs remaining in the simplified instance $\mathcal {I}^{\prime \prime }$ is less than $3/\varepsilon$. These reductions are recalled for self-consistency and their details are available in Kacem et al. [12]. It is worthy to note that such reductions cannot increase the optimal solution value of $\mathcal {I}$ too much and they can be done in linear time.

We apply a modified dynamic programming algorithm $DP_{\varepsilon }$ to instance $\mathcal {I}^{\prime \prime }$ using the Jackson’s sequence JS to obtain an upper bound for the maximum lateness. The main idea of $DP_{\varepsilon }$ is to remove a special part of the states generated by a dynamic programming algorithm. Therefore, the modified algorithm becomes faster and yields an approximate solution instead of the optimal schedule. First, we define the following parameters:

$$ \overline{n}=\min \{n,3/\varepsilon \}, $$

$$ \omega _{1}=\left\lceil \frac{4\overline{n}}{\varepsilon }\right\rceil , $$

$$ \omega _{2}=\left\lceil \frac{2}{\varepsilon }\right\rceil , $$

$$ \delta _{1}=\frac{\mathcal {\varphi }_{JS}\left( \mathcal {I}^{\prime \prime }\right) }{\omega _{1}} $$

and

$$ \delta _{2}=\frac{T_{1}}{\omega _{2}}. $$

We split $\left[ 0,\mathcal {\varphi }_{JS}\left( \mathcal {I}^{\prime \prime }\right) \right)$ into $\omega _{1}$ equal subintervals $I_{m}^{1}=\left[ (m-1)\delta _{1},m\delta _{1}\right) _{1\le m\le \omega _{1}}$. We also split $\left[ 0,T_{1}\right)$ into $\omega _{2}$ equal subintervals $I_{s} ^{2}=\left[ (s-1)\delta _{2},s\delta _{2}\right) _{1\le s\le \omega _{2}}$ of length $\delta _{2}$. Moreover, we define the two singletons $I_{\omega _{1} +1}^{1}=\left\{ \mathcal {\varphi }_{JS}\left( \mathcal {I}^{\prime \prime }\right) \right\}$ and $I_{\omega _{2}+1}^{2}=\left\{ T_{1}\right\}$. Our algorithm $DP_{\varepsilon }$ generates reduced sets $\mathcal {X}_{j}^{\#}$ of states $\left[ t,f\right]$ where t is the total processing time of jobs assigned before $T_{1}$ in the associated partial schedule and f is the maximum lateness of the same partial schedule. It is described in Algorithm 1.

4.2 Algorithm $DP_{\varepsilon }$ is an Improved FPTAS

Compared to the previous FPTAS presented in [12], our new algorithm keeps two approximate states in every box $I_{m}^{1}\times I_{s}^{2}$ ($1\le m\le \omega _{1}+1,1\le s\le \omega _{2}+1$) instead of a single approximate state. As a consequence, the loss in terms of variable t will be reduced as it can be shown in the proof of the following theorem. Thus, the interval length $\delta _{2}$ is taken larger compared to [12]. Moreover, in the following proof we will use a tighter recursive relation on the closeness of the approximate states and those originally generated by the standard dynamic algorithm. As a result, we will show that the new algorithm $DP_{\varepsilon }$ outperforms the one provided in [12] by a linear factor in n or $1/\varepsilon$.

Theorem 1

Given an arbitrary $\varepsilon >0$, the modified algorithm $DP_{\varepsilon }$ yields an output $\mathcal {\varphi }_{DP_{\varepsilon }}\left( \mathcal {I}^{\prime \prime }\right)$ such that:

$$\begin{aligned} \mathcal {\varphi }_{DP_{\varepsilon }}\left( \mathcal {I}^{\prime \prime }\right) -\mathcal {\varphi }^{*}\left( \mathcal {I}^{\prime \prime }\right) \le \varepsilon \mathcal {\varphi }^{*}\left( \mathcal {I}^{\prime \prime }\right) . \end{aligned}$$

(2)

Proof

First, we recall the idea of the dynamic programming algorithm [8] which is necessary to explain the proof. Indeed, the problem can be optimally solved by applying the following dynamic programming algorithm DP. This algorithm generates iteratively some sets of states. At every iteration j, a set $\mathcal {X}_{j}$ composed of states is generated ($1\le j\le \overline{n}$). Each state $\left[ t,f\right]$ in $\mathcal {X}_{j}$ can be associated to a feasible schedule for the first j jobs. Variable t denotes the completion time of the last job scheduled before $T_{1}$ and f is the maximum lateness of the corresponding schedule. This dynamic programming is given in Algorithm 2.

Let $UB=\mathcal {\varphi }_{JS}\left( \mathcal {T}^{\prime \prime }\right)$ be an upper bound on the optimal maximum lateness for problem $\left( \mathcal {T}^{\prime \prime }\right)$ obtained by Jackson’s sequence. We add the restriction that for every state $\left[ t,f\right]$ the relation $f\le UB$ must hold.

The main idea of the FPTAS is to remove a special part of the states generated by the dynamic programming algorithm. Therefore, the modified algorithm $DP_{\varepsilon }$ becomes faster and yields an approximate solution instead of the optimal schedule. The worst-case analysis of our FPTAS is based on the comparison of the execution of algorithms DP and $DP_{\varepsilon }$, which can be summarized by the following relations. For every state $\left[ t,f\right]$ in $\mathcal {X} _{j}$ there exists a state $\left[ t^{\#},f^{\#}\right]$ in $\mathcal {X} _{j}^{\#}$ such that:

$$\begin{aligned} t-\delta _{2}\le t^{\#}\le t \end{aligned}$$

(3)

and

$$\begin{aligned} f^{\#}\le f+\delta _{2}+j\delta _{1} \end{aligned}$$

(4)

The two relations can be proved by induction on j.

First, for $j=1$ we have $\mathcal {X}_{1}^{\#}=\mathcal {X}_{1}$. Therefore, the statement is trivial. Now, assume that the statement holds true up to level $j-1$. Consider an arbitrary state $\left[ t,f\right]$ $\in$ $\mathcal {X}_{j}$. Algorithm DP introduces this state into $\mathcal {X}_{j}$ when job j is added to some feasible state for the first $j-1$ jobs. Let $\left[ t^{\prime },f^{\prime }\right]$ be the above feasible state. Two cases can be distinguished: either $\left[ t,f\right] =\left[ t^{\prime }+p_{j} ,\max \left\{ f^{\prime },t^{\prime }+p_{j}+q_{j}\right\} \right]$ or $\left[ t,f\right] =\left[ t^{\prime },\max \left\{ f^{\prime },T_{2} +\sum _{i=1}^{j}p_{i}-t^{\prime }+q_{j}\right\} \right]$ must hold. For proving the statement for level j we will distinguish two cases.

Case 1: $\left[ t,f\right] =\left[ t^{\prime }+p_{j},\max \left\{ f^{\prime },t^{\prime }+p_{j}+q_{j}\right\} \right]$

Since $\left[ t^{\prime },f^{\prime }\right] \in \mathcal {X}_{j-1}$, there exists $\left[ t^{\prime \#},f^{\prime \#}\right] \in \mathcal {X}_{j-1}^{\#}$ such that $t^{\prime }-\delta _{2}\le t^{\prime \#}\le t^{\prime }$ and $f^{\prime \#}\le f^{\prime }+\delta _{2}+\left( j-1\right) \delta _{1}$.

Consequently, the state $\left[ t^{\prime \#}+p_{j},\max \left\{ f^{\prime \#},t^{\prime \#}+p_{j}+q_{j}\right\} \right]$ is feasible (since $t^{\prime \#}+p_{j}\le t^{\prime }+p_{j}=t\le T_{1}$) and it is generated by Algorithm $DP_{\varepsilon }$ at iteration j. However it may be removed when reducing the state subset. Let $\left[ \lambda ,\mu \right]$ and $\left[ \alpha ,\beta \right]$ be the two possible states in set $\mathcal {X}_{j}^{\#}$ that remain in the same box as the state $\left[ t^{\prime \#}+p_{j},\max \left\{ f^{\prime \#},t^{\prime \#}+p_{j}+q_{j}\right\} \right]$ (with $\lambda \le t^{\prime \#}+p_{j}\le \alpha$). Hence, we have two situations to consider: $t^{\prime }+p_{j}\ge \alpha$ or $t^{\prime }+p_{j}<\alpha$.

Subcase 1.a: $t^{\prime }+p_{j}\ge \alpha .$ In this subcase, we can verify that the state $\left[ \alpha ,\beta \right]$ fulfills (3). Indeed, $\alpha \le t^{\prime }+p_{j}=t$ and by definition $\alpha \ge t^{\prime \#}+p_{j}\ge t^{\prime }-\delta _{2}+p_{j}=t-\delta _{2}$. Thus, we have

$$ t-\delta _{2}\le \alpha \le t. $$

Subcase 1.b: $t^{\prime }+p_{j}<\alpha .$ In this subcase, we can verify that the state $\left[ \lambda ,\mu \right]$ fulfills (3). Indeed, $\lambda \le t^{\prime \#}+p_{j}\le t^{\prime }+p_{j}=t$ and by definition $\lambda \ge \alpha -\delta _{2}>t^{\prime }+p_{j}-\delta _{2} =t-\delta _{2}$. Thus, we have

$$ t-\delta _{2}\le \lambda \le t. $$

On the other hand, the two values $\mu$ and $\beta$ are in the same subinterval as the value $\max \left\{ f^{\prime \#},t^{\prime \#}+p_{j} +q_{j}\right\}$. Therefore, the kept state will have a maximum lateness value less or equal to $\max \{\mu ,\beta \}$. Then, we conclude that

$$\begin{aligned} \max \{\mu ,\beta \}&\le \max \left\{ f^{\prime \#},t^{\prime \#}+p_{j} +q_{j}\right\} +\delta _{1}\\&\le \max \left\{ f^{\prime }+\delta _{2}+\left( j-1\right) \delta _{1},t^{\prime }+p_{j}+q_{j}\right\} +\delta _{1}\\&\le \max \left\{ f^{\prime },t^{\prime }+p_{j}+q_{j}\right\} +\delta _{2}+j\delta _{1}\\&=f+\delta _{2}+j\delta _{1}. \end{aligned}$$

Consequently, the statement holds for level j in this case.

Case 2: $\left[ t,f\right] =\left[ t^{\prime },\max \left\{ f^{\prime },T_{2}+\sum _{i=1}^{j}p_{i}-t^{\prime }+q_{j}\right\} \right]$

Since $\left[ t^{\prime },f^{\prime }\right] \in \mathcal {X}_{j-1}$, there exists $\left[ t^{\prime \#},f^{\prime \#}\right] \in \mathcal {X} _{j-1}^{\#}$ such that $t^{\prime }-\delta _{2}\le t^{\prime \#}\le t^{\prime }$ and $f^{\prime \#}\le f^{\prime }+\delta _{2}+\left( j-1\right) \delta _{1}$.

Consequently, the state $\left[ t^{\prime \#},\max \left\{ f^{\prime \#},T_{2}+\sum _{i=1}^{j}p_{i}-t^{\prime \#}+q_{j}\right\} \right]$ is generated by Algorithm $DP_{\varepsilon }$ in iteration j. However, it may be removed when reducing the state subset. Let $\left[ \lambda ^{\prime } ,\mu ^{\prime }\right]$ and $\left[ \alpha ^{\prime },\beta ^{\prime }\right]$ be the states in $\mathcal {X}_{j}^{\#}$ that are kept in the same box as $[t^{\prime \#},\max \{f^{\prime \#},T_{2}+\ \sum _{i=1}^{j}p_{i}$ $-t^{\prime \#}+q_{j}\}]$ and having $\lambda ^{\prime }\le t^{\prime \#}\le \alpha ^{\prime }$. Again, we have two situations to be considered: $t^{\prime }\ge \alpha ^{\prime }$ or $t^{\prime }<\alpha ^{\prime }$.

Subcase 2.a: $t^{\prime } \ge \alpha ^{\prime }.$ In this subcase, we can verify that the state $\left[ \alpha ^{\prime },\beta ^{\prime }\right]$ fulfills (3). Indeed, $\alpha ^{\prime }\le t^{\prime }=t$ and by definition $\alpha ^{\prime }\ge t^{\prime \#}\ge t^{\prime }-\delta _{2}=t-\delta _{2}$. Thus, we have

$$ t-\delta _{2}\le \alpha ^{\prime }\le t. $$

Subcase 2.b: $t^{\prime }<\alpha ^{\prime }$. In this subcase, we can verify that the state $\left[ \lambda ^{\prime },\mu ^{\prime }\right]$ fulfills (3). Indeed, $\lambda ^{\prime }\le t^{\prime \#}\le t^{\prime }=t$ and by definition $\lambda ^{\prime }\ge \alpha ^{\prime }-\delta _{2}>t^{\prime }-\delta _{2}=t-\delta _{2}$. Thus, we have

$$ t-\delta _{2}\le \lambda ^{\prime }\le t. $$

On the other hand, the values $\mu ^{\prime }$ and $\beta ^{\prime }$ are in the same subinterval as $\max \{f^{\prime \#},T_{2}+\ \sum _{i=1}^{j}p_{i}$ $-t^{\prime \#}+q_{j}\}$. Therefore, the kept state will have a maximum lateness value less or equal to $\max \{f^{\prime \#},T_{2}+\ \sum _{i=1} ^{j}p_{i}$ $-t^{\prime \#}+q_{j}\}+\delta _{1}$. Moreover,

$$ \max \left\{ f^{\prime \#},T_{2}+\sum _{i=1}^{j}p_{i}-t^{\prime \#} +q_{j}\right\} +\delta _{1}\le \max \left\{ X,Y\right\} +\delta _{1} $$

where $X=f^{\prime }+\delta _{2}+\left( j-1\right) \delta _{1}$ and $Y=T_{2}+\sum _{i=1}^{j}p_{i}-t^{\prime }+\delta _{2}+q_{j}$. Thus,

$$\begin{aligned} \max \{\mu ^{\prime },\beta ^{\prime }\}&\le \max \left\{ f^{\prime },T_{2} +\sum _{i=1}^{j}p_{i}-t^{\prime }+q_{j}\right\} +\max \{\delta _{2}+j\delta _{1},\delta _{2}+\delta _{1}\}\\&\le f+\delta _{2}+j\delta _{1}. \end{aligned}$$

In conclusion, the statement holds also for level j in the second case, and this completes our inductive proof. Now, we give the proof of Eq. (2). By definition, the optimal solution can be associated to a state $\left[ t^{*},f^{*}\right]$ in $\mathcal {X}_{\overline{n}}$. From Eq. (4), there exists a state $\left[ t^{\#},f^{\#}\right]$ in $\mathcal {X}_{\overline{n}}^{\#}$ such that:

$$\begin{aligned} f^{\#}&\le f^{*}+\delta _{2}+\overline{n}\delta _{1}\\&=f^{*}+\frac{T_{1}}{\omega _{2}}+\overline{n}\frac{\mathcal {\varphi }_{JS}\left( \mathcal {I}^{\prime \prime }\right) }{\omega _{1}}\\&=f^{*}+\frac{T_{1}}{\left\lceil \frac{2}{\varepsilon }\right\rceil }+\overline{n}\frac{\mathcal {\varphi }_{JS}\left( \mathcal {I}^{\prime \prime }\right) }{\left\lceil \frac{4\overline{n}}{\varepsilon }\right\rceil }\\&\le f^{*}+\varepsilon \frac{T_{1}}{2}+\varepsilon \frac{\mathcal {\varphi }_{JS}\left( \mathcal {I}^{\prime \prime }\right) }{4}\\&\le \left( 1+\varepsilon \right) \mathcal {\varphi }^{*}\left( \mathcal {I}^{\prime \prime }\right) . \end{aligned}$$

Since $\mathcal {\varphi }_{DP_{\varepsilon }}\left( \mathcal {I}^{\prime \prime }\right) \le f^{\#}$, we conclude that Eq. (2) holds.

It can be easily seen that the proposed modified algorithm $DP_{\varepsilon }$ can be implemented in $O\left( \overline{n}\log \overline{n}+\overline{n}^{2}/\varepsilon ^{2}\right)$ time. The schedule obtained by $DP_{\varepsilon }$ for instance $\mathcal {I}^{\prime \prime }$ can be easily converted into a feasible one for instance $\mathcal {I}$. This can be done in $O\left( n\right)$ time.

To summarize, we conclude that Algorithm $DP_{\varepsilon }$ is an FPTAS and it can be implemented in $O\left( n\log n+\min \{n,1/\varepsilon \}^{2} /\varepsilon ^{2}\right)$ time.

5 Consequences: An Improved FPTAS for the ONA Case

Here, the studied problem ($\varPi$) can be formulated as follows. An operator has to schedule a set J of n jobs on a single machine, where every job j has a processing time $p_{j}$ and a tail $q_{j}$. The machine can process at most one job at a time if the operator is available at the starting time and the completion time of such a job. The operator is unavailable during $(T_{1},T_{2})$. Preemption of jobs is not allowed (jobs have to be performed under the non-resumable scenario). All jobs are ready to be performed at time 0. Without loss of generality, we consider that all data are integers and that jobs are indexed according to Jackson’s rule. The aim is to find a feasible schedule S by minimizing the maximum lateness. Again, if all the jobs can be inserted before $T_{1}$, the instance studied ($\mathcal {I}$) has obviously a trivial optimal solution obtained by Jackson’s rule. We therefore consider only the problems in which all the jobs cannot be scheduled before $T_{1}$. Moreover, we consider that every job can be inserted before $T_{1}$ (i.e., $p_{j}\le T_{1}$ for every $j\in J$).

As it has been done in Kacem et al. [12], an FPTAS can be established for $\varPi$. The procedure is based on guessing the so-called straddling job and its starting time from a finite set of approximate values, which leads to $O(\frac{n}{\varepsilon })$ auxiliary MNA problems ($\mathcal {P}$). Thus, the application of $DP_{\varepsilon }$ to all these auxiliary problems can lead to an improved FPTAS as the following theorem claims:

Theorem 2

Problem $\varPi$ admits an FPTAS and this scheme can be implemented in $O(n\left( \ln n\right) /\varepsilon +n\min \{n,3/\varepsilon \}^{2} /\varepsilon ^{3})$ time.

Proof

The proof is a straightforward from [12] and Theorem 1.

6 Conclusion

In this paper we consider the single machine scheduling problem with one non-availability interval to minimize the maximum lateness where jobs have positive tails. Two cases are considered. In the first one, the non-availability interval is due to the machine maintenance. In the second case, the non-availibility interval is related to the operator who is organizing the execution of jobs on the machine. The contribution of this paper consists in an improved FPTAS for the maintenance non-availability interval case and its extension to the operator non-availability interval case. The two FPTASs are strongly polynomial and outperform our previous ones published in the literature.

As a research perspective, we are extending the ideas of this paper in order to improve some existing FPTASs for other scheduling problems.