Dynamic Opportunistic Spectrum Access with Channel Bonding in Mesh Networks: A Game-Theoretic Approach

Abstract

The opportunistic spectrum access with dynamic users and channel bonding technology in mesh networks is studied in this paper. Different from the traditional static and fixed transmitting model, nodes would change their states between active and silent, due to their traffic demand. Also, the channel bonding technology, which mitigates interference and improves throughput significantly, is employed in this paper. The interference mitigation problem with channel bonding is modeled as a distributed and non-cooperative game. We proved it to be an exact potential game. Based on the good property of the potential game, it guarantees the existence of at least one pure Nash equilibrium (NE). Due to the potential function is formulated as the aggregate interference of the network, the final optimal NE point also achieves the minimization of the system’s total interference. A multiple-agent learning algorithm is designed to approach the NE points. Compared with other algorithms, simulation results show that the modified algorithm achieves a lower interference performance, and the channel bonding contributes to the throughput performance.

1 Introduction

With the wireless technologies fast developed, the wireless traffic data has shown an explosive improvement. The opportunistic spectrum access (OSA) has been regarded as a promising technology, to solve the spectrum shortage and improve the spectrum efficiency. Many excellent studies have been done about the OSA in many fields.

In the related researches, the users are always static and keep transmitting data all the time. However, users have different traffic demands and can change state between active and silent based on demand requirement. The static user assumption does not describe the dynamic property in the practical wireless communication well. Furthermore, there are some new technologies can be used in spectrum assignment, such as partially overlapping channels and channel bonding. But the new technologies have not been considered and investigated with the OSA well.

The dynamics property makes user dynamic participating the channel access competition. In this way, it also make a influence to other users. To model the dynamic characteristics, we investigated the node’s interference with channel bonding situation. The throughput performance is also formulated based on the interference. However, the throughput is too much complicated, and hard to analyze the formulation or design a proper game model to couple with. Hence, based on the correlative relationship between the interference and throughput, we model interference mitigation game to achieve a higher throughput. To summarize, the contributions of this paper are as follows:

• We considered an opportunistic spectrum access problem in canonical networks. The dynamic issue about node participation and channel bonding technology were jointly considered.

• The dynamic spectrum access problem with channel bonding was modeled as an interference mitigation game, and was proved to be an exact potential game, which has at least one pure Nash equilibrium. Based on the potential function design, the system total interference was also minimized with the NE points.

• The modified multiple-agent learning algorithm was modified to approach the Nash equilibrium. Nodes could update their channel selection strategies same time. The algorithm converged to a Nash equilibrium (NE) which optimize the total system’s interference.

2 Related Works

Authors in [4] presented a comprehensive survey about the opportunistic access from methods and models, especially for the interaction among multiple users. The dynamics for opportunistic spectrum access has been studied in many studies. In a previous work [7], a dynamic player participation problem in channel allocation was studied. A binary interference model was employed instead of the physical interference. Authors in [9] extended the binary interference model to hyper-graph model and also considered the dynamic issues. A joint dynamic user and asymmetric interference model was investigated in [6]. The channel access problem was modeled into an ordinary potential game with ALOHA mechanism.

The channel bonding technology improves the channel capacity significantly. Authors in [3] investigated the average channel throughput at the medium access control layer. A comprehensive introduction about channel bonding for kinds of networks and discussed the channel bonding for cognitive radio networks, especially for sensing situations in [1]. A recently research [2] studied about a distributed and coordinated channel bonding selection method with only limited feedback under SINR and collision-protocol models.

In this paper, we studied the dynamic spectrum access problem with channel bonding technology. An interference mitigation game is modeled, and proved to be an exact potential game. A modified multiple-agent learning algorithm was designed to approach the Nash equilibrium.

3 System Model and Problem Formulation

3.1 System Model

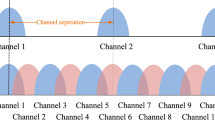
In this paper, we consider a distributed mesh network, as shown in Fig. 1. The mesh network is a kind of canonical networks, where nodes are collections of entities. A classical example of canonical network is the 802.11-based WLAN, where nodes are collections of some users located in a relatively small region. In mesh networks, one communication node also represents a collections of nearby users. Nodes make the spectrum resource allocation strategies for their belonging users to achieve a high throughput performance.

We consider a mesh network with N nodes and M channels in this paper. Different from the traditional mesh networks, we assume that nodes might be dynamic due to their traffic demands. In other words, nodes may change states between silent and active based on their traffic. This dynamic transmitting behavior is more common and practical in wireless communication systems, but might bring about some differences in modeling and formulating the spectrum assignment problem. For example, the network interference topology is changing with varying node states.

Besides the dynamic node state, the channel bonding technology is also employed in this paper. As the bandwidth increases through bonding channels together, the throughput performance is also improved, with the total fixed power consumption. The channel bonding also influences the interference and throughput formulation.

Fig. 1.

The system model of mesh networks with dynamic nodes.

3.2 Problem Formulation

Denote the node set as $\mathcal {N}=\{1,2,\ldots ,N\}$ and channel set as $\mathcal {M}=\{1,2,\ldots ,M\}$. Denote the active probability of node n as $0<\theta _n \le 1$, which means node n is active with the probability $\theta _n$. Denote the distance between node n and node i is $d_{ni}$. Considering the node in canonical networks is a collection of communication entities, we regard the node as a combination of transmitter and receiver. Denote the communication range of one node is as $D_{range}$.

For the node n, denote its strategy as $a_n=\{c_{n1},c_{n2}\}, c_{n1,n2}\in \mathcal {M}, c_{n2}=c_{n1}+1$. In this paper, we only consider the 2-channel bonding situations. For the more than 2-channel situations, the problem formulation and the corresponding theoretic analysis are also similar. Therefore, we only consider the 2-channel situations in this paper. Assume the power consumption of node n on each channel is equal and denote as $P_n$. For node n with channel strategy $a_n$, denote the neighbor set $\mathcal {J}_n$ as follows:

$$\begin{aligned} \mathcal {J}_n=\{i: \left| {c_{i1}-c_{n1}} \right| \le 1 \}. \end{aligned}$$

(1)

The neighbor set $\mathcal {J}_n$ means that the two nodes have at least one same channel selection. To distinguish neighbor set with the different channels, denote the $\mathcal {J}_{n1}$ and $\mathcal {J}_{n2}$ are the corresponding nodes set for channel $c_{n1}$ and $c_{n2}$.

Therefore, the expectation of node n’ interference on channel $c_{n1}$ is as follows:

$$\begin{aligned} I_n^{c_{n1}}(a_n,a_{-n})=\sum _{i\in \mathcal {J}_{n1}} \theta _n\theta _i P_i d_{in}^{\alpha } \end{aligned}$$

(2)

where $\alpha$ is the fade loss factor.

Considering the dynamic state of nodes, the active state of node n is as $\lambda _n=0,1,1$ represents to be active. The total state of all nodes are $\varLambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _N\}$. Therefore, the state of node n on channel $c_{n1}$ is $\varLambda (J_{n1})$. Hence, the probability is as follows:

$$\begin{aligned} Pr[\varLambda (J_{n1})]=\prod _{i\in \mathcal {J}_{n1}} \theta _i\lambda _i + (1-\theta _i)(1-\lambda _i). \end{aligned}$$

(3)

The throughput of node n on channel $c_{n1}$ is as follows:

$$\begin{aligned} r_n^{c_{n1}}(a_n,a_{-n})=\sum _{\varLambda (J_{n1})} \theta _nPr[\varLambda (J_{n1})]\log (1+\frac{P_nD_{range}}{N_0+I_n^{c_n1}(\varLambda (J_{n1}))}). \end{aligned}$$

(4)

Therefore, the throughput of node n is as follows:

$$\begin{aligned} r_n(a_n,a_{-n})=r_n^{c_{n1}}+r_n^{c_{n2}}, \end{aligned}$$

(5)

Thus, the objectives in this paper is to achieve high throughput for each node. Formally,

$$\begin{aligned} P: \arg \max \limits _{a_n} r_n(a_n,a_{-n}) \end{aligned}$$

(6)

4 Potential Game with Interference Mitigation

4.1 Game Model

We formulate the interference mitigation problem with channel bonding as a distributed and non-cooperative game. The game is denoted as $\mathcal {G}=\{\mathcal {N}, \mathcal {A}, \mathcal {E}, u_n\}$, where $\mathcal {N}$ is the node set, $\mathcal {A}$ is the nodes strategy space, and $\mathcal {E}$ is the network topology. The utility function is denoted as $u_n(\mathbf a _n, \mathbf a _{-n})$. We define the utility function as follows:

$$\begin{aligned} u_n(a_n,a_{-n})=I_n^{c_{n1}}+I_n^{c_{n2}}, \end{aligned}$$

(7)

where the utility function is just the expectation of the total interference of node n. For low interference, the corresponding throughput is commonly high. Based on the relationship between interference and throughput, we focus on the interference mitigation problem instead of the complex throughput formulation. The proposed dynamic spectrum access with channel bonding is as follows:

$$\begin{aligned} \mathcal {G}: \min u_n(a_n, a_{-n}), \forall n \in \mathcal {N}. \end{aligned}$$

(8)

4.2 Analysis of the Nash Equilibrium

Definition 1

(NE): The channel bonding and selection strategies of all users are $(\mathbf a _1^*, \mathbf a _1^*, \ldots , \mathbf a _1^*)$ is a pure strategy NE if and only if no user can improve its utility by deviating unilaterally, i.e.,

$$\begin{aligned} u(a_n^*, a_{-n}^*) \le u(a_n', a_{-n}^*), \forall n \in \mathcal {N}, \forall a_n \in \mathcal {A}, a_n' \ne a_n^* \end{aligned}$$

(9)

Definition 2

(Exact Potential Game) [5, 11]: A game $\mathcal {G}$ is an exact potential game if there exists a function $\varPhi$ such that

$$\begin{aligned} \varPhi (a_n^*, a_{-n}^*)-\varPhi (a_n', a_{-n}^*)= u_n(a_n^*, a_{-n}^*)-u_n(a_n', a_{-n}^*), \forall a_n^* \in \mathcal {A}_n, a_n' \ne a_n^* \end{aligned}$$

(10)

The function $\varPhi$ is the potential function for the game $\mathcal {G}$.

Theorem 1:

The proposed opportunistic spectrum access game $\mathcal {G}$ is an exact potential game, which has at least one pure NE.

Proof

We design the potential function of the game is as:

$$\begin{aligned} \varPhi (a_n, a_{-n})=\frac{1}{2}\sum _{i\in \mathcal {N}} u_i(a_i,a_{-i}). \end{aligned}$$

(11)

which is just the total interference of all nodes in the network.

when node n changes its channel selection from $a_n$ to $a'n$, the changes in potential function is as follows.

$$\begin{aligned} \begin{aligned}&\varPhi (a_n,a_{-n})-\varPhi (a'_n,a_{-n}) \\&=\frac{1}{2}\sum _{i\in \mathcal {N}} u_i(a_i,a_{-i})- \frac{1}{2}\sum _{i\in \mathcal {N}} u_i(a'_n,a_{-i}) \\&=\frac{1}{2} \sum _{c\cup d\cup n} u_i(a_i,a_{-i}) -\frac{1}{2} \sum _{c\cup d\cup n} u_i(a'_i,a_{-i}) \\&= \frac{1}{2}*2*[I_n(a_n,a_{-n})-I_n(a'_n,a_{-n})] \\&= u_n(a_n,a_{-n})-u_n(a'_n,a_{-n}) \end{aligned} \end{aligned}$$

(12)

The total node set except node n can be divided into four parts due to the influence by the strategy change: (a) both in the neighbor set of $a_n$ and $a'_n$, (b) none in the two set, (c) with $a_n$ but not with $a'_n$ and (d) with $a'_n$ but not with $a_n$. For the part (a) and (b), the strategy change does not make any change for them. For the parts (c) and (d), due to the symmetric property of interference, the change is just the as the change in utility function. Therefore, the change in potential function is same as the change in utility function. Hence, the proposed interference mitigation game is an exact potential game. Based on the lemma, there exists at least one Nash equilibrium. Due to the potential function is formulated as the aggregate interference of the network, the final optimal NE point also achieves the minimization of the system’s total interference.

Remark:

Based on the proof in [8], for the two correlative metrics when one follows the potential game, they other one also keeps the trends. Then for interference and throughput, in most situations, a lower interference would bring about a higher throughput. Only some special situations this relation cannot be guaranteed. Therefore, it is reasonable that we can improve the throughput through mitigating the interference in this paper.

4.3 Dynamic Spectrum Access with Channel Bonding Algorithm

In this paper, we modify the multiple-agent learning algorithm [10, 13] into the dynamic spectrum access game, to approach the NE points.

Theorem 2

The modified multiple-agent learning algorithm converges to the NE points.

Proof

Due to the proposed game have been proved to be an exact potential game, the finite improvement property (FIP) exists. With following the FIP, players can improve the utility step by step. Compared with the traditional better reply algorithm, the modified multiple-agent learning algorithm makes all users update their strategies same time. The convergence of the modified is guaranteed by the FIP in [12]. The proof is similar and we omit the process in this paper.

5 Simulation Results and Discussions

In this section, we compared three algorithms: (i) the modified multi-agent learning algorithm, (ii) a random channel access algorithm, where users select channel randomly, and (iii) the modified multi-agent learning algorithm without channel bonding. The basic simulation parameters are set as follows: the number of channels $M=4$, the number of users $N=10$, the power on each channel 0.1 W¹, the noise power $N_0=-110$ dBm, the path fade loss $\alpha =-3$ and the communication range $D_{range}=30$ m. We assume users are located in a 200 m $\times$ 200 m area. The active probability is in the range $[0.3-0.9]$.

The total interference performance is compared in Fig. 2. From this figure, it is obviously that the random access algorithm achieves worst and largest interference. The multi-agent learning algorithm achieves better performance than the random access algorithm.

Fig. 2.

The total interference of system with different algorithms.

The total throughput performance is compared in Fig. 3. From the figure, we can find that the multi-agent learning algorithm achieves best throughput performance than the other two algorithms, especially for the non-channel bonding situations. It is indicated that the channel bonding technology improves the channel capacity significantly. The total throughput performance with different active probabilities is compared in Fig. 4. It is obviously that the throughput is decreasing with an increasing active probability.

Fig. 3.

The total throughput of system with different algorithms.

Fig. 4.

The total throughput of system with different active probabilities.

6 Conclusion

The opportunistic spectrum access with dynamics users and channel bonding technology in mesh networks was studied in this paper. We investigated the interference of the dynamic users with channel bonding mechanism and formulated the throughput of users. The interference mitigation problem with channel bonding is modeled as a distributed and non-cooperative game. We proved it to be an exact potential game. Based on the good property of the potential game, it guarantees the existence of at least one pure Nash equilibrium (NE). Due to the potential function is formulated as the aggregate interference of the network, the final optimal NE point also achieves the minimization of the system’s total interference. A multiple-agent learning algorithm is designed to approach the NE points. According to the correlative relationship between interference and throughput, a high throughput was guaranteed by a low interference. A multiple-agent learning algorithm is designed to approach the NE points. Simulation results show that the modified multiple-agent learning algorithm achieves better performance compared with other algorithms, and the channel bonding contributes to the throughput performance.