Game-Theoretic MAC-Layer Interference Coordination with Orthogonal Channels

Abstract

In this chapter, we consider the problem of opportunistic spectrum access in a kind of networks, where the users are spatially located and direct interaction/interference only emerges between neighboring users Y. Xu, J. Wang, Q. Wu et al. IEEE J. Sel. Signal Process (6(2):180–194, 2012), Y. Xu, Q. Wu, J. Wang, et al. IEICE Trans. Commun. (E95-B(3):991–994, 2012), H. Li, Z. Han, Competitive spectrum access in cognitive radio networks: Graphical game and learning, (2010), M. Azarafrooz, R. Chandramouli, Distributed learning in secondary spectrum sharing graphical game, (2011), M. Liu, et al. Congestion games with resource reuse and applications in spectrum sharing, (2009), C. Peng, H. Zheng, B. Zhao, Mob. Netw. App. (11(4):555–576, 2006), [1–6]. We investigate this problem from a perspective of interference minimization. Note that the commonly used interference model in the literature is the PHY-layer interference models, in which the focus is to minimize the amount of experienced interference C. Lacatus, D. Popescu, IEEE J. Sel. Topics Signal Process (1(1):189–202, 2007), [7]. In methodology, the PHY-layer interference model is more suitable for wireless communication systems with interference channel models, e.g., the code-division multiple access (CDMA) and orthogonal frequency-division multiple access (OFDMA) systems.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

3.1 Introduction

In this chapter, we consider the problem of opportunistic spectrum access in a kind of networks, where the users are spatially located and direct interaction/interference only emerges between neighboring users [1–6]. We investigate this problem from a perspective of interference minimization. Note that the commonly used interference model in the literature is the PHY-layer interference models, in which the focus is to minimize the amount of experienced interference [7]. In methodology, the PHY-layer interference model is more suitable for wireless communication systems with interference channel models, e.g., the code-division multiple access (CDMA) and orthogonal frequency-division multiple access (OFDMA) systems. However, it may not suitable for wireless communication systems with collision channel model, e.g., carrier sensing multiple access (CSMA). In particular, it was recently reported in [8] that the traditional PHY-layer interference model is not applicable for collision channels, e.g., in the 802.11b-based networks.

To capture the mutual interference behavior in multiple access control mechanisms, this chapter considers a new interference metric, called the MAC-layer interference, which is defined as the number of neighboring users choosing the same channel. Compared with the traditional PHY-layer interference model, the MAC-layer interference essentially determines whether two users interfere with each other or not. Based on this definition, we formulate a MAC-layer interference minimization game, and then propose an uncoupled learning algorithm, called the binary log-linear learning algorithm. It is proved that the learning algorithm asymptotically achieves the optimal NE solution and minimizes the aggregate MAC-layer interference. Note that the main analysis and results in this chapter were presented in [9].

3.2 Motivation, Definition, and Discussion of MAC-Layer Interference

3.2.1 Motivation and Definition

Due to the open attribute of wireless transmissions, mutual interference is unavoidable in multiuser wireless systems. In the literature, the commonly used model is the PHY-layer interference model [7], in which the focus is to minimize the amount of experienced interference. However, it is noted that the PHY-layer interference model is more suitable for communication systems with interference channel models, e.g., CDMA and OFDMA systems, and not applicable for communication systems with collision channel model, e.g., CSMA and Aloha.

Recently, the experimental results reported in [8] show that for wireless communication systems with CSMA, some interesting features can be observed. In particular, let us consider two nodes (links), which are equipped with 802.11a/b/g cards. It is emphasized here that the considered node (link) actually consists of a transmitter and a receiver located closely [8]. The lognormal fading model is considered, as it addresses the medium-scale path loss well. Specifically, the signal strength (RSS) received at a link from the other link is

$$\begin{aligned} S = P_t d^{-\beta } e^X, \end{aligned}$$

(3.1)

where $P_t$ is the transmitting power, d is the physical distance between the two nodes, $\beta$ is the path loss exponent, and X is a Gaussian variable with zero-mean and variance $\sigma ^2$. Note that the lognormal fading is usually measured in the dB-spread form which is characterized by $\sigma =0.1\log (10)\sigma _\mathrm{{dB}}$. As indicated by the empirical measurements [10], the dB-spread of the lognormal fading typically ranges from 4 to 12 dB.

According to the principle of CSMA, a link can hear the transmission of the other link if the received RSS is greater than a threshold $S_{th}$. In the experiment, we set $P_t=1$ W, $\beta =2$, $\sigma _\mathrm{{dB}}=6$ dB, and $S_{th}=8.1633\times 10^{-6}$ W. Denote $s_1$ and $s_2$ as the achievable throughput of node1 and node2, respectively, when the other node is inactive, and $s'_1$ and $s'_2$ as their achievable throughput when both nodes are active simultaneously. Then, the relationship between the normalized ratio $\gamma =\frac{s'_1+s'_2}{s_1+s_2}$ and the distance d is used to investigate the effect of interference on the throughput [8]. By simulating $10^6$ independent trials and then taking the expected value, we illustratively present the simulation result in Fig. 3.1. Similar to the important observations shown in [8], there are two interesting results:

• The throughput ratio sharply increases from 0.5 (severe interference) to 1 (almost no interference) with a slight increase in the physical distance. As a result, it can be divided into three regions, i.e., interference region, transitional region, and non-interference region, as shown in the figure.

• The throughput ratio in both interference and non-interference regions does not change with the distance, while increasing linearly with the distance in the transitional region.

Some explanations from the perspective of interference are given below: (i) when the two nodes are located in the interference region, only one node can transmit successfully at a time, as they can hear the transmission of each other. In other words, they interfere with each other; (ii) when located in the non-interference region, they can transmit successfully and simultaneously as they do not hear transmission of each other. In other words, there is no interference; and (iii) when located in the transitional region, they can probabilistically hear each other due to the randomness of channel fading. In other words, there exists probabilistic interference, which will be discussed in the subsequent.

Fig. 3.1

The effect of mutual interference on the normalized throughput ratio

As the span of the transitional region $d_2-d_1$ is relatively small, a simplified interference model can be used to analyze interference among the users. Specifically, if the throughput ratio is less than a threshold, e.g., 0.95, mutual interference between the two nodes exists, and no interference otherwise. Denote the distance corresponding to the interference threshold as $d_0$, $d_1<d_0<d_2$. It motivates us to define the following MAC-layer interference:

$$\begin{aligned} \alpha =\left\{ \begin{array}{l} 1,\;\;\;\;x\le d_0 \\ 0,\;\;\;\;x > d_0, \\ \end{array} \right. \end{aligned}$$

(3.2)

where x is the distance between the two nodes. As a result, the normalized throughput is approximately given by $R=\frac{1}{1+\alpha }$, which provides a good approximation for the measured results [8]. Therefore, although sacrificing a little accuracy, efficient opportunistic spectrum access approaches can be developed using the MAC-layer interference model.

An illustrative comparison of the PHY-layer and MAC-layer interference is presented in Fig. 3.2. In traditional models, the PHY-layer interference is a decreasing function of the physical distance. It is noted from Fig. 3.2b that the PHY-layer interference model does not coincide with the measured results in the context of CSMA. For instance, decreasing the distance of two nodes located in the interference region definitely increases the PHY-layer interference for both; however, it does not lead to decrease in the throughput. Again, the PHY-layer interference models are essentially more suitable for interference channels, while the MAC-layer interference models are more suitable for collision channels.

For multiuser systems, the normalized throughput of user n is given by $\frac{1}{1+\sum _{m} \alpha _{mn}}$, where $\alpha _{mn}$ is the interference indicator between n and m. Then, the MAC-layer interference experienced by user n in a multiuser system is defined as

$$\begin{aligned} I_n=\sum _{m} \alpha _{mn}. \end{aligned}$$

(3.3)

Fig. 3.2

The illustrative comparison of the PHY-layer and MAC-layer interference models. a The measured normalized throughput versus the distance between two links. b The comparison of the proposed MAC-layer interference and traditional PHY-layer interference

3.2.2 Discussion on the Impact of Channel Fading

In this part, we discuss some issues related to channel fading, which is an important attribute of wireless channel. Generally, the received signal strength (RSS) at a node from the node is given by $P_{t}x^{-\beta }\varepsilon$, where $P_t$ is the transmitting power, x is the physical distance, $\beta$ is the path loss exponent, and $\varepsilon$ is the instantaneous random component of the path loss [10], e.g., lognormal fading and Rayleigh fading. Generally, a link can hear the transmission of the other link if the RSS is greater than a threshold. In the following, we discuss the impact of channel fading on the MAC-layer interference model in the three regions, respectively:

• In the interference region, the large-scale path loss component, i.e., $P_{t}x^{-\beta }$, is strong enough. Thus, one node can deterministically hear the transmission of the other node no matter what are the instantaneous realizations of channel fading. In other words, the impact of channel fading is concealed by the strong large-scale path loss component.

• In the transitional region, the large-scale path loss component is medium. Thus, the received RSS is randomly fluctuating around the interference threshold. As a result, one node can probabilistically hear the transmission of the other node.

• In the non-interference region, the large-scale path loss component is weak. Thus, one node cannot hear transmission of the other node. In other words, the impact of channel fading is eliminated by the far physical distance.

Remark 3.1

In order to address the interference model in the transitional region more concisely, we can extend the binary interference model to a real-valued one. In particular, an improved MAC-layer interference can be defined as follows:

$$\begin{aligned} \alpha '=\left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x\le d_1 \\ \frac{x-d_1}{d_2-d1},\;\;\;\;\;\;\;\;d_1<x<d_2 \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x \ge d_2 \\ \end{array} \right. \end{aligned}$$

(3.4)

Note that $\alpha '$ is (3.4) a continuous value ranging in [0, 1]. In particular, $\alpha ' =1$ and $\alpha '=0$ correspond to the same meanings as those in (4.3), while $0<\alpha '<1$ corresponds to the probabilistic interference in the transitional region. Similarly, the normalized throughput of a node is then given by $R=\frac{1}{1+\alpha '}$, which fits the measured results well. The real-valued interference model is more precise than the binary interference model characterized by (4.3), as it captures the randomness of channel fading in the transitional region. For presentation of analysis, we only consider the binary interference model in this chapter. Following similar methodology presented in this chapter, the analysis of real-valued MAC-layer interference model can be found in [12].

3.3 System Model and Problem Formulation

3.3.1 Bilateral Interference Networks

Consider a wireless canonical network consisting of N secondary users, in which each user represents a closely located pair of transmitter and receiver [1]. There are M licensed channels owned by the primary users and can be opportunistically used by the secondary users when not occupied. Due to the limited transmitting power of the users, mutual interference only occurs among nearby users [3, 4]. As a result, we can characterize the limited range of interference by an un-directional graph ${G}=(\mathbb {N},\mathbb {E})$, where $\mathbb {N}=\{1,\ldots ,N\}$ is the vertex set and $\mathbb {E} \subset \mathbb {N} \times \mathbb {N}$ is the edge set. Each vertex represents a user, and the edges correspond to the potential mutual interference relationship among the users when transmitting on the same channel. Although the mutual interference is inherently determined by the received RSS, we can use a distance-relevant interference model as analyzed above. Specifically, if the distance between two users m and n, denoted as $D_{mn}$, is less than a threshold $D_0$, they can interfere with each other when simultaneously transmitting on the same channel; thus, m and n are connected by an edge, i.e., there is an edge $e_{mn}=(m,n)\in \mathbb {E}$. For simplicity of analysis, it is assumed that the interference is bilateral between any two users, i.e., user m is also interfered by user n if it interferes with n. We call this kind of networks bilateral interference cognitive radio networks (BI-CRNs).

The spectrum available opportunity is characterized by a channel availability vector ${C}_n$, $n \in \mathbb {N}$. In particular, ${C}_n=\{{C}_{n1}, {C}_{n2},\ldots ,{C}_{nM}\}$, where ${C}_{nm}=1$ implies that channel m is available for user n, while ${C}_{nm}=0$ means that it is occupied and not available. Note that due to their different localizations, the spectrum opportunities vary from user to user. For simplicity of analysis, it is assumed that spectrum sensing is perfect. Furthermore, the spectrum opportunities are quasi-static in time. Note that such an assumption holds in some realistic networks where the spectrum opportunities are slow-varying, e.g., IEEE 802.22 [11]. An illustrative example of a BI-CRN with six users, two primary users, and four licensed channels is shown in Fig. 3.3.

Fig. 3.3

An example of the BI-CRN with four licensed channels. Note that users 1 and 3 interfere with each other when transmitting on the same channel, whereas user 1 will never interfere with user 2 directly. a Deployment of the considered BI-CRN b The un-directional graph

3.3.2 MAC-Layer Interference Minimization

Due to hardware limitation, it is assumed that all the users can sense all channels simultaneously but transmit on only one channel at a time [13]. Denote $\mathbb {J}_n$ as the neighboring user set of user n, i.e.,

$$\begin{aligned} \mathbb {J}_n=\{i\in \mathbb {N}: (i,n)\in \mathbb {E}\}, \end{aligned}$$

(3.5)

Suppose that user n chooses a channel $a_n$, $a_n \in \{1,\ldots ,M\}$, for transmission. Some efficient distributed approaches such as CSMA and distributed TDMA can be applied to coordinate the transmissions among neighboring and interfering users. Thus, the individual achievable throughput of user n under channel selection profile $a=\{a_1,\ldots ,a_N\}$ can be expressed by

$$\begin{aligned} r_n(a_1,\ldots ,a_N) = \frac{f(c_n+1)R_{a_n}}{c_n+1}, \end{aligned}$$

(3.6)

where f(k), $0<f(k)\le 1$, is the throughput loss function when there are k users competing for a single channel [14], which is decreasing over k. $R_{a_n}$ is the transmission rate of channel $a_n$, and $c_n$ is the number of neighboring users also choosing the same channel with user n, i.e.,

$$\begin{aligned} c_n=\sum _{j\in \mathbb {J}_n} \delta (a_n,a_j), \end{aligned}$$

(3.7)

where $\delta (x,y)$ is the following indicator function:

$$\begin{aligned} \delta (x,y) = \left\{ \begin{array}{l} 1,\;\;x=y \\ 0,\;\;x \ne y. \\ \end{array} \right. \end{aligned}$$

(3.8)

Therefore, the network throughput can be expressed as

$$\begin{aligned} R(a_1,\ldots ,a_N)= \sum _{n \in \mathbb {N}} r_n. \end{aligned}$$

(3.9)

As the decision variables (channel selection) are discrete, the problem of maximizing network throughput is a combinatorial problem on a graph and hence is NP-hard. Motivated by the previous work on minimizing the aggregate PHY-layer interference [7], we consider minimizing the MAC-layer interference in this chapter. Note that the MAC-layer interference experienced by user n is then given by $c_n$. From the user side, it is desirable to minimize the value of $c_n$, as minimizing $c_n$ implies maximizing its individual achievable throughput. Thus, from the network side, it is also desirable to minimize the lower aggregate MAC-layer interference. Based on this consideration, we can quantitatively characterize the aggregate MAC-layer interference experienced by all the users as follows:

$$\begin{aligned} I_g(a_1,\ldots ,a_N)=\sum \limits _{n \in \mathbb {N}} c_n \end{aligned}$$

(3.10)

Consequently, the optimization objective is to find an optimal channel selection $a^{opt}$ such that the aggregate MAC-layer interference is minimized, i.e.,

$$\begin{aligned} P1:\;\;\;\;a^{opt}\in \mathop {\arg } \min \; I_g. \end{aligned}$$

(3.11)

Again, due to the higher-order of computational complexity, P1 is hard to resolve even in a centralized manner, not to mention in a distributed manner. Furthermore, the incomplete information constraint, i.e., lack of information about other users, brings about more challenges and difficulties.

3.4 MAC-Layer Interference Minimization Game

Due to the nature of distributed decision-making, we formulate the problem of interference mitigation in BI-CRNs as a non-cooperative game. Different from the game models in the last chapter, the formulated game in this chapter belongs to local interaction games (also known as graphical game) [1], in which the utility of a player only depends on the actions its neighboring users.

3.4.1 Graphical Game Model

Formally, the formulated MAC-layer interference minimization game is denoted as ${G}=[\mathbb {N},{\{{{A}_n}\}_{n\in \mathbb {N}}},{\{{\mathbb {J}_n}\}_{n\in \mathbb {N}}},{\{{u_n}\}_{n\in \mathbb {N}}}]$, where $\mathbb {N} = \{1,\ldots ,N\}$ is the set of players, ${A}_n=\{m\in \mathbb {M}: C_{nm}=1\}$ is the set of player n’s available actions (channels), $\mathbb {J}_n$ is the neighboring set of player n, and $u_n$ is its utility function. Generally, in global interactive games, the utility function of each player n is determined by $u(a_n,a_{-n})$, where ${a_n} \in {{A}_n}$ is the chosen action of player n and $a_{-n} \in {A}_1 \otimes \cdots {A}_{n-1} \otimes {A}_{n+1} \ldots {A}_N$ denotes the action profile all the players except n. However, due to the limited interference in the considered BI-CRNs, the achievable throughput of a player is only determined by its own action as well as the action profile of its neighboring users. Therefore, the utility function can be expressed as $u_n(a_n,a_{\mathbb {J}_n})$, where $a_{{\mathbb {J}_n}}$ is the action profile of n’s neighboring set. In the MAC-layer interference mitigation game, the utility function is defined as follows:

$$\begin{aligned} \begin{array}{l} {u_n}({a_n},a_{\mathbb {J}_n}) = L_n- c_n(a_n,a_{\mathbb {J}_n}), \end{array} \end{aligned}$$

(3.12)

where $c_n(a_n,a_{\mathbb {J}_n})\equiv c_n(a_1,\ldots ,a_N)$ is the MAC-layer interference experienced by n and $L_{n}$ is a positive constant satisfying $L_{n} > |\mathbb {J}_n|$, where |X| denotes the cardinality of set X. Therefore, the purpose of adding $L_n$ in the utility function is to keep the utility function positive, which makes the received payoffs compatible with the proposed learning algorithms. Moreover, $L_n$ can be determined by the users independently and autonomously. As each player in a non-cooperative game maximizes its individual utility function, the proposed game can be expressed as

$$\begin{aligned} {G}: \;\;\;\;\;\;\;\; \mathop {\max }\limits _{a_n \in A_n} u_n(a_n,a_{\mathbb {J}_n}),\forall n \in \mathbb {N} \end{aligned}$$

(3.13)

3.4.2 Analysis of Nash Equilibrium

In this part, we analyze the properties of Nash equilibrium (NE) of G in terms of existence of NE and performance bounds.

Theorem 3.1

The formulated MAC-layer interference mitigation game G is an exact potential game which has at least one pure strategy NE point.

Proof

According to the definition of exact potential game presented in Chap. 1 (See Definition 1.2 therein), we need to prove that there is a potential function such that the change in the utility function caused by the unilateral action deviation of an arbitrary player is the same as that in the potential function. For the formulated MAC-layer interference mitigation game, the following potential function is constructed:

$$\begin{aligned} \varPhi ({a_n},{a_{ - n}}) = -\frac{1}{2} \sum \limits _{n \in \mathbb {N}} c_n(a_1,\ldots ,a_N). \end{aligned}$$

(3.14)

Now, suppose that there is an arbitrary player n unilaterally changing its channel selection from $a_n$ to $\bar{a}_n$. Following the similar lines given in our previous work [1, 2], it can be verified that the following equation always holds:

$$\begin{aligned} \varPhi (\bar{a}_n,{a_{ - n}}) - \varPhi ({a_n},{a_{ - n}}) = {u_n}(\bar{a}_n, a_{\mathbb {J}_n}) - {u_n}({a_n},a_{\mathbb {J}_n}), \end{aligned}$$

(3.15)

which shows that the MAC-layer interference mitigation game G is an exact potential game. Thus, Theorem 5.1 follows.    $\square$

As the users in the non-cooperative games are selfish, the NE solutions maybe inefficient, which is known as tragedy of commons [15]. In the following, we investigate the performance bounds of NE solutions of the MAC-layer interference game. To begin with, the aggregate MAC-layer interference of a pure strategy NE $a_{\text {NE}}=\{a^*_1,\ldots ,a^*_N\}$ is given by

$$\begin{aligned} U(a_{\text {NE}})=\sum \limits _{n \in \mathbb {N}} {c_n}({a_n^*},a^*_{\mathbb {J}_n}) \end{aligned}$$

(3.16)

Generally, the MAC-layer interference mitigation game G may have multiple pure strategy NE points but the number is hard to calculate [16]. The following theorems characterize the performance bounds of the game.

Theorem 3.2

The aggregate MAC-layer interference of any pure strategy NE solution is bounded by $U(a_{\text {NE}}) \le \sum _{n=1}^N\frac{|\mathbb {J}_n|}{|{A}_n|}$, for any network topology and spectrum opportunities.

Proof

Refer to [9].    $\square$

From Theorem 4.2, it is known that the larger number of available channels ($|{A}_n|$) and smaller number of neighboring users ($|\mathbb {J}_n|$) are preferable, as can be expected in any multiuser multichannel networks. In particular, the performance bound can be refined for some special kinds of systems.

Proposition 3.1

If all the channels are available to each user, then the aggregate MAC-layer interference at any NE solution is bounded by $U(a_{\text {NE}}) \le \frac{2N}{M}$.

Proof

Since all the channels are available to each user, we have $|{A}_n|=M, \forall n \in \mathbb {N}$. Thus, the following equation follows:

$$\begin{aligned} U_(a_{\text {NE}}) \le \sum _{n=1}^N \frac{|\mathbb {J}_n|}{M}, \end{aligned}$$

(3.17)

which can be straightforwardly obtained by Theorem 4.2 directly. Moreover, it can be verified that the following always holds for any network topology:

$$\begin{aligned} \sum _{n=1}^N |\mathbb {J}_n|=2N \end{aligned}$$

(3.18)

Now, combining (3.18) and (3.17) proves this proposition.    $\square$

Theorem 3.3

The best pure strategy NE point of G is a global minimum of the MAC-layer interference mitigation problem P1.

Proof

According to (3.14), the potential function of the formulated game and the aggregate MAC-layer interference are related by $\varPhi ({a_n},{a_{ - n}})=-\frac{1}{2} I_g ({a_n},{a_{ - n}})$. Thus, we have

$$\begin{aligned} a^{opt}\in \mathop {\arg } \max \; \varPhi ({a_n},{a_{ - n}}). \end{aligned}$$

(3.19)

which is obtained from (3.11). That is, any channel selection profile minimizing the aggregate MAC-layer interference maximizes the potential function. Recalling the important property of potential game, i.e., any global or local maximizer of the potential function constitutes a pure strategy NE point [17], it is known that the best pure strategy NE point is a global minimum of P1, which proves Theorem 3.3.    $\square$

The result shown in Theorem 3.3 is interesting and promising, since the global optimality emerges as the result of distributed and selfish decisions via game design and optimization.

3.5 The Binary Log-Linear Learning Algorithms for Achieving Best NE

3.5.1 Algorithm Description

As the MAC-layer interference mitigation problem is now formulated as an exact potential game, there are large number of learning algorithms to achieve pure strategy NE, e.g., best response dynamic [17], spatial adaptive play [1], and fictitious play [18]. However, these algorithms belong to coupled algorithms and hence need to know information about other players. Although the stochastic automata learning algorithm, which was applied in the last chapter, is uncoupled, it may converge to a suboptimal solution. Thus, in this chapter, an uncoupled and optimal distributed learning algorithm, called the binary log-linear learning algorithm, is applied to achieve the best NE.

The binary log-linear learning algorithm is described in Algorithm 2. The key idea is that only a player is randomly chosen to explores the channels. Based on the explanation results, the player updates its selection using the log-linear rule. Some practical concerns of Algorithm 1 are discussed as follows: (i) in the step of player selection, the selection of an autonomous and random player can be achieved using a 802.11 DCF-like contention mechanisms over a common control channel (CCC) [1, 19], and (ii) the following stop criterions can be used: (i) the maximum iteration number is reached, and (ii) the variation of the achieved utility during a certain period is trivial.

Note that the utility function, i.e., the experienced MAC-layer interference, cannot be measured directly by the users; we use the following simple method to estimate the MAC-layer interference experienced by a user. Of course, other more practical but also completed methods for estimating the number of competing users can also be used, e.g., [23, 24]. The reason we use such a simple method is our focus in designing game-theoretic distributed MAC-layer interference mitigation approach but not the estimation algorithms. Specifically, suppose that there are total H slots in each estimation period and $T_{n}$ is the number of slots in which user n successfully access the channel. As a result, the maximum-likelihood estimation (MLE) of the MAC-layer interference experienced by user n can be calculated by

$$\begin{aligned} \hat{s}_n= \frac{H}{T_n}-1, \end{aligned}$$

(3.21)

which further implies that the MLE of the received payoff in an estimation period is expressed as

$$\begin{aligned} {\hat{u}}_n=L_n+1-\frac{H}{T_n} \end{aligned}$$

(3.22)

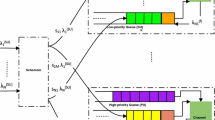
Based on the above estimation approach, an illustrative diagram of the binary log-linear learning algorithm for the formulated MAC-layer interference mitigation game is shown in Fig. 3.4.

Fig. 3.4

The illustrative diagram of the binary log-linear learning algorithm for the formulated MAC-layer interference mitigation game

3.5.2 Convergence Analysis

Let $\mathbb {A}$ be the set of available channel profiles of all the players, i.e., $\mathbb {A}={A}_1 \otimes \cdots \otimes {A}_N$, then the properties of the binary log-linear learning algorithm are characterized by the following theorems.

Theorem 3.4

For the binary log-linear learning algorithm, the unique stationary distribution $\mu (a) \in \varDelta (\mathbb {A})$ of any channel selection profile ${s} \in \mathbb {A}$, $\forall \beta >0$, is given as

$$\begin{aligned} \mu (a)= \frac{\exp \{ \beta \varPhi (a)\}}{\sum \nolimits _{s \in \mathbb {A}} \exp \{ \beta \varPhi (s)\}}, \end{aligned}$$

(3.23)

where $\varPhi (\cdot )$ is the potential function given in (3.14).

Proof

The proof follows the methodology presented in [1, 20–22]. Detailed lines are not presented here and can be found in [9].    $\square$

Theorem 3.5

With a sufficiently large $\beta$, the binary log-linear learning algorithm asymptotically minimizes the aggregate MAC-layer interference $I_g$.

Proof

Based on Theorem 3.4 and the similar lines for proof presented in our previous work [1] (see Theorem 4 therein), it can be proved that when $\beta$ goes sufficiently large, the binary log-linear algorithm asymptotically converges to a channel selection profile that maximizes the potential function. Now, applying again the relationship between the potential function and the original optimization objective, i.e., $\varPhi (a)=-\frac{1}{2}I_g(a)$, Theorem 3.5 can be obtained.    $\square$

3.6 Simulation Results and Discussion

In this section, simulation results are presented to validate the proposed game-theoretic distributed channel selection solution for MAC-layer interference mitigation. Although the game formation and learning algorithm are only theoretically analyzed for scenarios with no fading, it is shown by simulation results that the proposed game-theoretic solution is also suitable for scenarios with fading. Also, it is suitable for scenarios with both bilateral and unilateral interferences.

Fig. 3.5

The simulated small network. (Each circle represents a CR user, and the dashed lines represent the bilateral interferences between the users)

3.6.1 Scenario Setup

In the simulation study, the users are randomly located in a region. For simplicity, it is assumed that the idle probabilities of all the channels are the same, which is denoted as $\theta$, $0 < \theta <1$, and the spectrum opportunities are randomly generated according to the idle probabilities independently. However, it should be pointed out that the spectrum opportunities are quasi-static, i.e., they vary slowly in time, or are static during the convergence of the learning algorithm. Furthermore, we assume that different channels support the same transmission rate $R=1\mathrm {Mbps}$ for the users. The users use a perfect CSMA/CA mechanism to share the idle channels. As a result, the achievable throughput of a user is approximately determined by $\frac{R}{c_n+1}$, which is obtained by setting the throughput loss function to be one, i.e., $f(c_n+1)\approx 1$ in (4.7).

3.6.2 Scenario with No Fading

In this subsection, we consider scenarios with no fading, where only the large-scale path loss is considered. The learning parameter in the payoff-based log-linear learning algorithm is set to $\beta =10+k/50$, where k is the iteration number. In all simulations, the estimation period is set to $H=100$.

3.6.2.1 Convergence Behavior

In this part, the convergence behavior of the proposed learning algorithm is studied. Specifically, we study a small network as shown in Fig. 3.5, which involves nine CR users and three channels. A scenario with all channels being available for the users is considered. In such a scenario, it provides with the same spectrum opportunities and hence the expected convergence behavior of the learning algorithms can be studied by taking independent trials and then taking the expected results. For the presented network, the expected convergence behaviors of the proposed learning algorithm are shown in Fig. 3.6, which are obtained by simulating 1000 independent trials and then taking the average results. It is noted that the proposed learning algorithm converges to the global optimum in about 400 iterations. The results validate the asymptotical optimality of the proposed learning algorithm.

Fig. 3.6

The expected convergence behaviors of the proposed learning algorithms

In the following, the effect of the estimate interval H on the convergence of the proposed learning algorithm is shown in Fig. 3.7. The results show that there is a tradeoff between speed and performance with regard to the estimate interval H. It is noted from the figure that larger H leads to higher estimation accuracy while leading to relatively slower convergence speed, as can be expected. Thus, the choice of the estimate period H is application-dependent in practice.

Fig. 3.7

The effect of the estimate interval H on the convergence of proposed learning algorithm ($\beta =10+k/50$)

3.6.2.2 Throughput Performance

In this part, we compare the achievable throughput of five methods: throughput maximization using exhaustive search (TMax-ES), random selection, interference minimization using the proposed learning algorithm (Imin-Proposed), interference minimization using spatial adaptive play (Imin-SAP) [1], and interference minimization using best response (Imin-BR) [17]. In the TMax-ES approach, the aggregate network throughput as characterized by (3.9) is directly maximized using an exhaustive search method. In the random selection scheme, each user randomly chooses a channel from its available channel set. In comparison, SAP and BR are two commonly coupled learning algorithms for potential games, which need the information of other users. In addition, the SAP algorithm asymptotically converges to the global maxima of the potential function, while the BR algorithm achieves its global or local maxima randomly.

Fig. 3.8

Companion results of five channel selection methods for the simulated small network with no fading (The learning parameter of the learning algorithms is set to $\beta =10+k/50$)

(i) Small networks For the small network (see Fig. 3.5), the comparison results of the expected network throughput are shown in Fig. 3.8. It is noted from the figure that the proposed learning algorithm achieves higher network throughput than the BR algorithm and the random selection approach. Furthermore, the throughput gap increases as the channel idle probability $\theta$ increases. The reason is that in NE solutions of the game, the users are spread over different channels and hence there is less interference (collision) among the users. Again, this result is due to the fact that all pure strategy NE points of the game minimize the aggregate MAC-layer interference globally or locally, as characterized by Theorems 5.1, 4.2, and 3.3.

It is noted that the proposed learning algorithm achieves the same performance with that of Imin-SAP. The SAP algorithm is an efficient learning algorithm for potential game, as it asymptotically maximizes the potential function [1], i.e., minimizing the aggregate MAC-layer interference in the formulated MAC-layer interference mitigation game. In comparison, the proposed learning algorithm does not need any information about other players while the SAP needs information about other players. In addition, although the proposed learning asymptotically minimizes the aggregate MAC-layer interference, there is a throughput gap between Imin-Proposed and TMax-ES. The reason is as follows: although a lower aggregate MAC-layer interference would lead to higher network throughput as can be expected, a quantitative characterization between minimizing the MAC-layer interference and maximizing the network throughput directly is hard to obtain. Even so, the proposed learning algorithm is desirable for practical applications, as it achieves higher network throughput.

(ii) Large networks We consider a relatively large network as shown in Fig. 3.9, which consists of 20 users and three channels. Figure 3.10 shows the comparison results of the expected network throughput of different solutions. Due to intolerable complexity, the TMax-ES method cannot be applied in this scenario. It is noted that the throughput performance of the proposed learning algorithm is very close to the Imin-SAP approach. These results validate that the proposed learning algorithm is also for large networks.

Fig. 3.9

The simulated large CRN

Fig. 3.10

Companion results of four methods for the simulated large network with no fading

3.6.3 Scenario with Fading

As fading is common in wireless networks, we study the performance of the proposed learning algorithm in scenarios with lognormal fading. The parameters are set as follows: the transmitting power of all users is $P_t=1$ W, the path loss exponent is $\beta =2$, and the dB-spread is 6 dB. Moreover, it is assumed that the detection threshold of CSMA is $8.1633\times 10^{-6}$ W. Simulation results show that the proposed learning algorithm also converge for channels with lognormal fading. However, since their convergence trend is similar to that presented in Fig. 3.6, it is not presented here in order to avoid unnecessary repetition.

For the considered small and large networks, the comparison results for the achievable network throughput are shown in Figs. 3.11 and 3.12, respectively. It is noted that the proposed algorithm also achieves the same performance with that of Imin-SAP, and outperforms both the BR approach and random selection approach. These results validate the effectiveness of the proposed learning algorithm for scenarios with fading.

Fig. 3.11

Throughput companion for the simulated small network with lognormal fading ($P_t=1$ W, $\beta =2$ and $\sigma _\mathrm{{dB}}=6$ dB)

Fig. 3.12

Throughput companion for the simulated large network with lognormal fading ($P_t=1$ W, $\beta =2$ and $\sigma _\mathrm{{dB}}=6$ dB)

3.7 Extension to Unilateral Interference CRNs

The above presented analysis is for bilateral interference networks. However, we would like to point out that there are some scenarios involving unilateral interference relationships among the users, e.g., cognitive ad hoc networks. For those networks, the mutual interference relationships can be characterized by a directional graph rather than an undirected graph. We call this kind of networks, unilateral interference cognitive radio networks (UI-CRNs).

3.7.1 System Model

To make it more practical, we then extend BI-CRNs to UI-CRNs in this section. For the unilateral interference networks, a CR receiver suffers from interference from other CR transmitters if the distance between them is less than a predefined threshold, $D_I$. For simplicity of analysis, we assume that the available spectrum opportunities are identical for any CR transmitter and its dedicated receiver. Then, the heterogeneous spectrum opportunities are also characterized by the channel availability vectors $C_n$, as discussed before.

The interference relationship is now characterized by a directional graph $\mathbf {G}_d=(\mathbb {N},\mathbb {E})$. The graph $\mathbf {G}_d$ consists of a set of nodes which is exactly the CR user set $\mathscr {N}$, and a set of edges $\mathscr {E} \subset \mathbb {N}^2$. Denote each edge as an ordered pair (i, j); then, if there is an edge from user i to j, i.e., $(i,j)\in \mathscr {E}$, it means that the transmission of node i interferes with node j when simultaneously transmitting on the same channel. An example of the deployment for the considered unilateral interference cognitive radio network is shown in Fig. 3.13a and the corresponding directional interference graph is shown in Fig. 3.13b.

Following the same methodology used for BI-CRNs, similar definitions for UI-CRNs can also be given. Then, a similar network collision minimization game can be established accordingly. For reducing unnecessary repetition, they are not presented here. For UI-CRNs, the network-centric goal is also to minimize the aggregate MAC-layer interference. However, due to the unilateral interference relationship, it is no longer a potential game. This makes the analysis of the convergence of the proposed uncoupled learning algorithms a formidable task and an open problem.

Fig. 3.13

An example of the considered UI-CRN with four CR links. (In such a network, the interference is unilateral, e.g., CR link 1 does not interfere with link 2 but it is interfered by link 2.) a Deployment of the considered UI-CRN b The interference graph

3.7.2 Simulation Results

Although there is a lack of theoretic analysis, as discussed above, we evaluate the performance of the proposed uncoupled algorithms by simulation study. Specifically, the deployment of the considered UI-CRN is shown in Fig. 3.14. For the considered UI-CRN, the expected convergence behaviors of the proposed learning algorithm are shown in Fig. 3.15. The results are obtained by simulating 1000 independent trials and then taking the average. It is noted that it asymptotically converges to global optimum in about 450 iterations.

Fig. 3.14

An unilateral interference CRN with nine CR users (links) and three licensed channels (Each circle represents a CR link, double arrows represent bilateral interferences, and single arrows represent unilateral interferences)

Fig. 3.15

The convergence behaviors of the two algorithms for the simulated UI-CRN ($H=200$)

Fig. 3.16

Companion results of four channel selection methods (For the learning algorithms, we set $H=200$)

The comparison results of expected network throughput obtained using five methods (exhaustive search, random selection, the proposed algorithm, SAP, and BR) are shown in Fig. 3.16. As for the UI-CRNs, it is also noted from the figure that the proposed learning algorithm achieves higher network throughput than the BR algorithm and the random selection approach. Also, it achieves almost the same throughput with the SAP algorithm. Therefore, we claim that the proposed learning algorithms are not only suitable for BI-CRNs, but also suitable for UI-CRNs, although it lacks rigorous theoretical analysis.

3.8 Concluding Remarks

Compared with traditional PHY-layer interference model, e.g., the one considered in Chap. 2, the MAC-layer interference model in this chapter coincides with the experiment results for collision channel models. Moreover, it admits mathematical tractability as it only cares about whether two users interfere with each other or not. Also, the binary log-linear learning algorithm can achieve the best NE of exact potential games. Thus, the results presented in this chapter provide efficient distributed solutions for resource allocation problems over graph/network.