Hierarchical Growth Is Necessary and (Sometimes) Sufficient to Self-assemble Discrete Self-similar Fractals

Abstract

In this paper, we prove that in the abstract Tile Assembly Model (aTAM), an accretion-based model which only allows for a single tile to attach to a growing assembly at each step, there are no tile assembly systems capable of self-assembling the discrete self-similar fractals known as the “H” and “U” fractals. We then show that in a related model which allows for hierarchical self-assembly, the 2-Handed Assembly Model (2HAM), there does exist a tile assembly systems which self-assembles the “U” fractal and conjecture that the same holds for the “H” fractal. This is the first example of discrete self similar fractals which self-assemble in the 2HAM but not in the aTAM, providing a direct comparison of the models and greater understanding of the power of hierarchical assembly.

M. J. Patitz—This author’s research was supported in part by National Science Foundation Grants CCF-1422152 and CAREER-1553166.

1 Introduction

Systems composed of large, disorganized collections of simple components which autonomously self-assemble into complex structures have been observed in nature, and have also been artificially designed as well as theoretically modeled. These studies have shown the remarkable power of self-assembling systems to be algorithmically directed across a wide diversity of models with varying dynamics which determine the ways in which the constituent components can combine. At two ends of an important dimension in this spectrum of dynamics are models in which the atomic components can only combine to growing structures one at a time, e.g. the tile-based abstract Tile Assembly Model (aTAM) [20], and those in which arbitrarily large assemblies of previously combined components can combine with each other, e.g. the 2-Handed Assembly Model (2HAM) [2, 4, 5, 15]. Even though models such as the aTAM which are strictly bound to one-tile-at-a-time growth have been shown to be computationally universal and very powerful in terms of the structures which can self-assemble within them, it has been shown that the hierarchical growth allowed by models such as the 2HAM can afford even greater powers [2].

In pursuit of understanding the boundaries of what is possible in these models, the self-assembly of aperiodic structures has been studied. For example, in [17], a 2HAM system with temperature parameter equal to 1 is given which self-assembles aperiodic patterns. Aperiodic structures are theoretically fundamental to the concept of Turing universal computation as well as embodied in many mathematical and natural systems as fractals. In fact, the complex aperiodic structure of fractals, as well as their pervasiveness in nature, have inspired much previous work on the self-assembly of fractal structures [6, 19], especially discrete self-similar fractals (DSSF’s) [1, 7, 12, 13, 16, 18, 19]. In a tribute to their complex structure, previous work has shown the impossibility of self-assembly of several DSSF’s in the aTAM and 2HAM [1, 12,13,14, 16, 18, 19] yet there have also been results showing some models and systems in which their self-assembly is possible [3, 7, 10, 11]. Quite notably, a recent result [8] is the first to achieve non-scaled self-assembly of a DSSF in the 2HAM. That work showed that DSSF’s with generators (i.e. initial stages which define the shapes of the infinite series of stages) that have square, or 4-sided, boundaries can self-assemble in the 2HAM. However, they also gave an example of a DSSF with a 3-sided generator that does not. While previous work has shown sparsely-connected fractals which don’t self-assemble in the aTAM or 2HAM [2, 14], the recent results hinted that perhaps only extremely well-connected fractals, such as those that have 4-sided generators, may be able to self-assemble in the 2HAM, while perhaps none may be able to in the aTAM. In this paper, we continue this line of research into the self-assembly of DSSFs in the aTAM and 2HAM.

In this paper, we specifically consider aTAM and 2HAM systems which finitely self-assemble DSSFs. Finite self-assembly was defined to better understand how 2HAM systems self-assemble infinite shapes (e.g. DSSF’s). Intuitively, a shape S, finitely self-assembles in a tile assembly system if any finite producible assembly of the system can continue to self-assemble into the shape S. Finite self-assembly is a less constrained version of strict self-assembly. Intuitively, a shape S strictly self-assembles in a tile assembly system if it places tiles on – and only on – points in S. Note that strict self-assembly implies finite self-assembly but the converse is not true in general. For example, a tile system could produce an infinite non-terminal producible assembly that has the property that it cannot self-assemble into the target shape S, but any finite producible assembly of the system could self-assemble into S. To further advance the possibility that no DSSF’s may self-assemble in the aTAM, we provide impossibility results about fractals with more inter-stage connectivity than any previous fractal whose strict self-assembly in the aTAM was shown to be impossible. In particular, our impossibility results give two fractals which cannot be finitely self-assembled by any aTAM system, which implies that those fractals cannot be strictly self-assembled by any aTAM system either. However, our results also show that the landscape in the 2HAM is more convoluted. Namely, although [8] exhibited a fractal with a 3-sided generator that does not finitely self-assemble in the 2HAM, here we show one which does. This proves that the boundary between what can and cannot self-assemble in the 2HAM is less understood. Notably, our impossibility results and constructions are the first to give a head-to-head contrast of the powers of the aTAM and 2HAM to self-assemble DSSF’s. In [2], shapes are defined which finitely self-assemble in the 2HAM but not in the aTAM, as well as shapes which strictly self-assemble in the aTAM but not in the 2HAM. In this paper, we prove that the hierarchical process of growth attainable in the 2HAM is necessary and sufficient for the self-assembly of certain DSSF’s. Moreover, the construction techniques to build them in the 2HAM do not follow traditional growth patterns of “stage-by-stage” growth, but rely fundamentally on combinations of components across a spectrum of hierarchical levels. Due to space constraints, we only sketch our proofs in this version of the paper. For full details, please see the online version [9].

2 Preliminaries

Throughout this paper, we use standard definitions of, and terminology related to, the aTAM, 2HAM and discrete self-similar fractals. For more details of each, please refer to the full version of the paper [9]. In this section, we include only the few definitions unique to this paper.

2.1 Definitions for the aTAM and 2HAM

Let $\varvec{\alpha }$ be an assembly sequence of an aTAM system. In the following, $\varvec{\alpha }[i]$ denotes the tile that $\varvec{\alpha }$ places at assembly step i. We say that $\varvec{\alpha }[i]$ is the parent of $\varvec{\alpha }[j]$ if $i < j$ and $\varvec{\alpha }[j]$ binds to $\varvec{\alpha }[i]$. Furthermore, we say that tile $\varvec{\alpha }[i]$ is the ancestor of a tile $\varvec{\alpha }[k]$ if either $\varvec{\alpha }[i]$ is the parent of $\varvec{\alpha }[k]$, or there exists an index j, such that, $i< j < k$, $\varvec{\alpha }[j]$ is the parent of $\varvec{\alpha }[k]$ and $\varvec{\alpha }[i]$ is the ancestor of $\varvec{\alpha }[j]$. Note that $\varvec{\alpha }[j]$ implicitly refers to both the tile type and location, and the parent and ancestor relationships, in general, depend on the given assembly sequence $\varvec{\alpha }$.

For an infinite shape $X\subseteq \mathbb {Z}^2$ and an aTAM or 2HAM system $\mathcal {T}$, we say that $\mathcal {T}$ finitely self-assembles X if every finite producible assembly of $\mathcal {T}$ has a possible way of growing into an assembly that places tiles exactly on those points in X. In this paper we consider finite self-assembly of DSSF’s (in the strict sense).

2.2 The U-Fractal and H-Fractal

For the definition of discrete self-similar fractal (DSSF)¹ See [9].

Definition 1

The $\mathbf{U}$ fractal is the DSSF whose generator consists of exactly the points $\{(0,0),(0,1),(0,2),(1,0),(2,0),(2,1),(2,2)\}$.

Definition 2

The $\mathbf{H}$ fractal is the DSSF whose generator consists of exactly the points $\{(0,0),(0,1),(0,2),(1,1),(2,0),(2,1),(2,2)\}$.

3 Brief Proof of the Impossibility of Finite Self-assembly of the H fractal in the aTAM

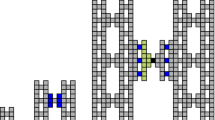
The $\mathbf H$ fractal is defined as shown in Fig. 1. Let $h_i$ be the i-th stage of $\mathbf H$. We call the center tile of $h_i$, denoted as $center(h_i)$, the tile in the center of the stage that connects the left and right halves of $h_i$.

Let $B^\mathbf{H }_0 = \{(0,0),(0,1),(0,2),(2,0),(2,1),(2,2)\}$. For stages $i > 1$, we call the following set of 6 points the bottleneck points of $h_i$, or $B^\mathbf{H }_i$:

$B^\mathbf{H }_i = \left\{ \left. \left( 3^{i-1}+\frac{3^{i-2}-1}{2},3^{i-1}+\frac{3^{i-2}-1}{2}\right) + 3^{i-2}b \; \right| \; b \in B^\mathbf{H }_0 \right\}$. An example of the bottleneck points for a few stages of $\mathbf H$ can be seen in Fig. 1. In what follows, we will use the term “bottleneck tile” to refer to the tile placed (by some assembly sequence) at that bottleneck point.

Fig. 1.

First three stages of the $\mathbf H$ fractal, with the left-most being the generator. The bottleneck points of stages 2 and 3 (blue). (Color figure online)

The top, middle and bottom bottleneck points of $h_i$ are denoted as top(i), middle(i) and bottom(i). We will refer to the points in $h_i$ in between its center tile and left bottleneck points as its left-center. Assuming $\mathbf H$ finitely self-assembles in some TAS $\mathcal {T}$, then every tile placed in the left-center of $h_i$, for all $i \ge j$ for some $j \in \mathbb {N}$, has as an ancestor, relative to some $\mathcal {T}$ assembly sequence $\varvec{\alpha }$, at least one bottleneck point. We call a tile in the left-center of $h_i$ top-left-placed if top(i) is its ancestor and middle(i) and bottom(i) are not its ancestors. We define middle-left-placed and bottom-left-placed tiles (in the left-center of $h_i$) similarly. Note that, if the parent of the center tile of $h_i$ is adjacent to the left, then every tile in the left-center of $h_i$ must have some bottleneck point (either top, middle or bottom) in the left half of $h_i$ as an ancestor.

Theorem 1

$\mathbf H$ does not finitely self-assemble in the aTAM.

Proof

For the sake of obtaining a contradiction, assume there exists an aTAM TAS $\mathcal {T}= (T,\sigma ,\tau )$ in which $\mathbf H$ finitely self-assembles. We will show that $\mathbf H$ does not finitely self-assemble in $\mathcal {T}$. Without loss of generality, we will assume that $|\sigma | = 1$, i.e. that $\mathcal {T}$ is singly-seeded but our proof technique will hold for any TAS $\mathcal {T}$ with finite seed assembly. Since the location of $\sigma$ must be within $\mathbf H$, let s be the stage number of the smallest stage of $\mathbf H$ which contains $\sigma$.

Let $c = 6|T|^6$. If $\mathbf H$ finitely self-assembles in $\mathcal {T}$, then every producible assembly in $\mathcal {T}$ has domain contained in $\mathbf H$. Let $\varvec{\alpha }$ be the shortest assembly sequence in $\mathcal {T}$ whose result has domain $h_{c+s+2}$, subject to the additional constraint that, when multiple locations could receive a tile in a given step, $\varvec{\alpha }$ always places a tile in a location of the smallest possible stage.

By our choice of c, we know that there are at least 6 stages of $\mathbf H$ whose respective bottleneck points are identically tiled by $\varvec{\alpha }$. Since, in any assembly sequence, the center tile of each stage of $\mathbf H$ either has a parent adjacent to the left or right, it follows, without loss of generality, that there are at least 3 stages, namely $h_i$, $h_j$ and $h_k$, for $i< j < k$, whose respective bottleneck points are identically tiled by $\varvec{\alpha }$ and whose respective center tiles have parents adjacent to the left.

Relative to $\varvec{\alpha }$, there are three cases to consider: (1) and (2) some top-left-placed (bottom-left-placed) tile of the left-center of $h_j$ is placed at a point that is not contained in an $h_{j-3}$, appropriately-translated, so that $center(j-3)$, appropriately-translated, is top(j) (bottom(j)), or (3) some middle-left-placed tile of the left-center of $h_j$ is placed at a point that is not contained in an $h_{j-2}$, appropriately-translated, so that $center(j-2)$, appropriately-translated, is top(j). (Intuitively, these are conditions specifying how far growth from each bottleneck tile extends toward its neighbors before utilizing cooperation with growth from them.) Note that, if none of these cases apply, then the left-center of $h_j$ wouldn’t assemble completely and $\mathbf H$ wouldn’t finitely self-assemble in $\mathcal {T}$.

Case 1: Use $\varvec{\alpha }$ to create a new valid assembly sequence in $\mathcal {T}$ as follows. Starting from the seed, run $\varvec{\alpha }$ until the step at which it places the first bottleneck tile on the left side of $h_j$. Then, begin recording a sub-sequence of $\varvec{\alpha }$ and denote this sub-sequence as $\varvec{\alpha }'$. As we run $\varvec{\alpha }$ forward from this point, until it places the last tile of $h_j$, whenever a top-left-placed tile in $h_j$ is placed by $\varvec{\alpha }$, we add that tile placement (type and location) to $\varvec{\alpha }'$. In this way, $\varvec{\alpha }'$ becomes a sub-sequence of $\varvec{\alpha }$ that records the growth of the top-placed sub-assembly – and only the top-placed sub-assembly – of the left-center of $h_j$.

Now, reset $\varvec{\alpha }$ to the seed and begin its forward growth until the placement of the first bottleneck tile on the left side of $h_i$ (recall $i < j$). At this point, merge $\varvec{\alpha }$ and $\varvec{\alpha }'$ as follows. For each tile position $\varvec{p}$ in $\varvec{\alpha }'$, we translate it so that the new position, $\varvec{p}'$, is the point with the same relative offset from the top-left bottleneck position of $h_i$ as $\varvec{p}$ was from the top-left bottleneck position of $h_j$. Continue to run $\varvec{\alpha }$ forward by performing all tile placements up to, and including, the placement of top(i), with the exception of the middle(i), bottom(i), or any descendants thereof. As soon as $\varvec{\alpha }$ places top(i), we follow the tile placements of the modified $\varvec{\alpha }'$. The result is a valid assembly sequence up to the point of the placement of at least one tile outside of $\mathbf H$ (since the portion of the left-center of $h_j$ grown by $\varvec{\alpha }'$ doesn’t fit within the locations of $\mathbf H$ available in $h_i$). Thus, $\mathbf H$ does not finitely self-assemble in $\mathcal {T}$. A similar scenario, but for a different fractal, in which such out-of-bounds growth may occur, is depicted in Fig. 2b.

Case 2: This case is symmetric to the previous case.

Case 3: First, create an assembly sub-sequence $\varvec{\alpha }''$ that records the tile placements of only the middle-placed tiles of $h_j$, similar to the construction of $\varvec{\alpha }'$ in Case 1. Then, run $\varvec{\alpha }$ forward, starting from the seed, performing all tile placements up to, and including, the placement of the middle(k), with the exception of top(k) or bottom(k), or descendants thereof. As soon as $\varvec{\alpha }$ places middle(k), we follow the tile placements of the modified $\varvec{\alpha }''$, appropriately-translated, from $h_j$ to $h_k$. Here, we are essentially replaying the assembly of a smaller stage within a larger stage. The result is a valid assembly sequence up to the point of the placement of at least one tile outside of $\mathbf H$ (due to the specifically different scales of portions of $\mathbf H$ in $h_j$ and $h_k$). Thus, $\mathbf H$ does not finitely self-assemble in $\mathcal {T}$.    $\square$

Corollary 1

$\mathbf H$ does not strictly self-assemble in the aTAM.

Since strict self-assembly of a shape S by a system $\mathcal {T}$ implies finite self-assembly of S by $\mathcal {T}$, Corollary 1 follows from Theorem 1.

4 Impossibility of Finite Self-assembly of the U Fractal in the aTAM

The $\mathbf U$ fractal is defined as shown in Fig. 2a.

Theorem 2

$\mathbf U$ does not finitely self-assemble in the aTAM.

Due to space constraints, we only give brief description of the proof of Theorem 2. Essentially, the proof is very similar to that of Theorem 1. $\mathbf U$ has bottlenecks (which can be seen in Fig. 2a) similar to $\mathbf H$, and in a similar way, it is impossible for the portion of stages inside of the bottlenecks to self-assemble since the tiles at bottleneck locations of multiple stages must be identical, and growth which would have to be possible within one stage would be able to grow out of bounds of $\mathbf U$ in a different stage. An example can be seen in Fig. 2b, and more details of the proof can be found in the full version of the paper [9].

Fig. 2.

(a) First three stages of the $\mathbf U$ fractal, with the leftmost being the generator. The bottleneck points of stages 2 and 3 are colored blue. (b) Depiction of how top-placed growth from stage 5 would go out of bounds of $\mathbf U$ in stage 3 and stage 4. (left) A portion of stage 5 showing the 3 bottleneck tiles in black, and possible horizontal and vertical growth from the top bottleneck tile. (middle and right) Stages 3 and 4. The black tile is the top left bottleneck tile, the green locations are those which correctly match the smaller stage, and the red are those which go out of bounds of $\mathbf U$. Clearly, all tiles in green positions will be able to grow, and then erroneous growth is forced to occur immediately east of the green tiles, where no other tiles could prevent this growth. (Note that only a single tile needs to be placed in a red location to break the shape of $\mathbf U$.) (Color figure online)

Corollary 2

$\mathbf U$ does not strictly self-assemble in the aTAM.

5 U-Fractal Finitely Self-assembles in the 2HAM

In this section we show how to finitely self-assemble the U-fractal, $\mathbf {U}$, DSSF in the 2HAM (with scale factor of 1) at temperature 2. We will present our construction under the assumption that a particular assembly sequence is followed. We then show that the construction also holds for an arbitrary choice of assembly sequence. Due to space constraints, we present the main idea of the construction and give more detail in the full version of the paper [9]. First, we state our main positive result.

Theorem 3

Let $\mathbf {U}$ be the U-fractal DSSF. There exists a 2HAM TAS $\mathcal {T}_\mathbf{{U}} = (T_\mathbf{{U}}, 2)$ that finitely self-assembles $\mathbf {U}$. Moreover, $\mathcal {T}_\mathbf{{U}}$ has the property that for every stage $s\ge 1$ and every terminal assembly $\alpha \in \mathcal {A}_{\Box }[\mathcal {T_\mathbf{{U}}}]$, $U_{s} \subset \mathrm{dom} \;(\alpha )$ (modulo translation).

We now introduce notation useful for describing the sets of points (including singleton sets) in a fractal. We start with a notation for the address of a point in a stage $U_n$ of $\mathbf {U}$. Figure 3 describes this notation for $U_3$. Similar notation for $U_n$ is defined recursively.

Fig. 3.

(left) Address labels of each point in the generator of $\mathbf U$, (right) The black location is contained within stage three, and its address is dab (i.e. it is location d in a stage one copy (outlined in red), within location a of a stage two copy (outlined in green), within location b of stage three.) (Color figure online)

Fig. 4.

The set of dark gray points of $U_3$ are referred to as a stage-2 ladder

The address of a point in $U_n$ is a string of n symbols of $\{a, b, c, d, e, f, g\}$. Therefore, to define a subset, S say, of points in $U_n$, it is convenient to use regular expressions to describe the strings corresponding to addresses of points in S. Figure 4 depicts a set of points in $U_3$ which we refer to as a stage-2 ladder. This set is defined by the regular expression [defg][abc][ab]| [abcdefg]d[ab]| [abcd][efg][ab] | [defg][ab]c| [ef]cc| [abef]dc| [abcd][ef]c| [ab]gc.

We also introduce terminology for some of the more important shapes that the 2HAM system which self-assembles $\mathbf {U}$ self-assembles. These shapes are stage-n ladders, left rungs, and right rungs. Figure 5 depicts a stage-2 ladder. The two rightmost supertiles in Fig. 9 depict left and right rungs where the rightmost supertile is a right rung. Let $S_n$ by the set of points in $U_{n+1}$ with addresses given by the expression ${.}\{n\}[abc]$ (i.e. strings of length $n+1$ ending in a, b, or c. In other words, $S_n$ is $\{(x, y + m*3^n) | (x,y)\in U_n, m\in \{0, 1, 2\} \}$. Also let B be the set of westernmost, easternmost, and sothernmost points of $S_n$. Then, a stage-n ladder is the shape defined to be the points in $S_n \setminus B$. Figure 5 (right) depicts a supertile with the shape of a stage-3 ladder. We are now ready to present the construction which shows Theorem 3.

Fig. 5.

A depiction of a stage-2 ladder (left) and a stage-3 ladder (right). Dark gray squares denote tile locations where tiles may contain an edge that has a special glue called an “indicating glue”. The goal of the construction is to define a 2HAM system that 1) self-assembles 10 types of stage-2 ladder supertiles (the type of a stage-2 ladder supertile depends on whether or not tiles at dark gray locations contain indicating glues), and 2) for $n\ge 3$ self-assembles 10 types of stage-n ladder supertiles from stage-$(n-1)$ ladder supertiles such that the stage-n ladder supertile contains tiles that have indicating glues (at locations shown in dark gray locations in the figure on the right for stage-3 ladder supertiles)

5.1 U-Fractal Construction Overview

In this section, we describe a 2HAM system that finitely self-assembles U. We do this by describing the supertiles producible in the 2HAM system and note that tiles can be defined so that these supertiles self-assemble. We first describe base supertiles that initially self-assemble and then describe how these base supertiles can bind to self-assemble supertiles that contain larger and larger stages of $\mathbf {U}$. In all, the supertiles which self-assemble in $\mathcal {T}_\mathbf{{U}}$ are as follows.

• 1. 12 different types of base supertiles that are hard-coded to self-assemble, 10 of which have the shape of a stage-2 ladder, and 2 of which have the shape of either a left or right rung. We call these supertiles stage-2 ladder supertiles and left or right rung supertiles respectively. Figures 8 and 9 (left two supertiles) depict the 10 different stage-2 ladder supertiles. The two righmost supertiles shown in Fig. 9 are left and right rung supertiles.

• 2. For each n, 12 different types of supertiles self-assemble which have the shape of a stage-n ladder. We call these supertiles stage-n ladder supertiles. Figure 5 (right) shows a stage-3 ladder supertile.

• 3. Supertiles which we refer to as grout supertiles are hard-coded to bind to stage-n ladders for any $n\in \mathbb {N}$. For all $n \ge 2$, grout supertiles bind to stage-n ladders (and also bind to left and right rungs as a special case) to yield supertiles that expose glues which bind in some assembly sequence to yield a stage-$(n+1)$ ladder. Figure 6 depicts 6 stage-2 ladders and 6 stage-2 rungs with grout supertiles attached. We refer to a stage-n ladder supertile (resp. rung supertile) with grout supertiles attached such that no more grout supertiles can attach as a grouted stage-n ladder supertiles (resp. rung supertile). Finally, grout supertiles that bind to stage-n ladders are referred to as “grout for stage-$(n+1)$”. As we will see there are 10 different types of grout corresponding to the 10 different types of stage-2 ladder supertiles.

Fig. 6.

A schematic depiction of grouted stage-2 ladder supertiles and grouted rung supertiles. There are 6 types of ladder supertiles shown here. Tiles shown as yellow squares contain strength-1 glues which we call “binding glues” that allow the depicted grouted ladder supertiles to bind. Tiles shown as green or blue squares may contain edges with indicating glues and whether or not an indicating glues is on an edge of a tile at a green or blue location depends on which of the 10 typegs of grout that binds (i.e. which type of stage-3 verson of a stage-2 ladder supertile is self-assembling.) Note that tiles in locations shown as blue squares are contained in a stage-2 ladder supertile (Color figure online).

Throughout this section we describe the self-assembly of the above supertiles by describing a particular assembly sequence. We note that there are many other assembly sequences for $\mathcal {T}_\mathbf{{U}}$ and many possible producible supertiles. This is due to the fact that proper subassemblies of the supertiles described above are themselves producible. Nevertheless, we show that this nondeterminism does not prevent $\mathbf {U}$ from being finitely self-assembled. For now, we consider assembly sequences such that for $n\ge 3$, 1) stage-$(n-1)$ ladder supertiles completely self-assemble before grout supertiles for stage-n bind, 2) grout for stage-n binds to stage-$(n-1)$ ladder supertiles until a grouted stage-n ladder supertile self-assembles (i.e. grout supertiles bind to stage-$(n-1)$ ladder supertiles until no other grout supertiles can bind), and 3) stage-n ladder supertiles self-assemble from grouted ladder supertiles of previous stages. Figure 7 depicts such an assembly sequence for $n=3$. Note that grout supertiles bind to completed stage-2 ladder and rung supertiles before the stage-3 ladder self-assembles.

Referring to Fig. 5, the main idea behind the construction is to defined a tile set which self-assembles base supertiles and grout supertiles. Grout supertiles bind to base supertiles to yield supertiles which in turn bind to yield stage-3 ladder and rung supertiles. In particular, the stage-3 ladder and rung supertiles which self-assemble are analogous to (i.e. are higher stage versions of) stage-2 base and rung supertiles. See Fig. 5 (left and right) for more detail. We now describe base and grout supertiles, the tiles that self-assemble them, as well as the assembly sequences for these supertiles and higher stages of $\mathbf {U}$ in more detail.

Fig. 7.

An assembly sequence where grouted stage-2 ladder and rung supertiles bind to yield a stage-3 ladder supertile. Note that the result of this assembly sequence is a stage-3 ladder supertile.

Fig. 8.

(Right) A depiction of 8 types of the stage-2 ladder supertiles. Each of the 8 figures is labeled with a regular expression defining the set of points in $U_4$ where $r = (r1|r2)$ such that $r1 = [defg][abc]|[abcdefg]d|[abcd][efg]$ and $r2 = [defg][ab]|[ef][cd]|[ab][dg]|[abcd][ab]$. The label also describes where these stage-2 supertiles will be located within a stage-3 ladder supertile (the tile locations of which are a subset of $U_4$). We will use these labels to refer to a stage-2 ladder supertile type. We also note that there are two versions of stage-2 ladder supertiles with type r[ab]c and two versions with type with type r[ef]c.

The 12 Base-Supertiles. The tile set which initially self-assembles stage-2 ladder supertiles and rung supertiles are defined so that these supertiles contain tiles that expose special glues in specific locations; possible locations for special glues are shown in dark gray in the Figs. 8 and 9. We call these special glues indicating glues. The purpose of indicating glues will be described in Sect. 5.1. In this section we describe the 12 different types of base supertiles, starting with the 10 stage-2 ladder supertiles.

Fig. 9.

A depiction of 2 stage-2 ladder supertiles labeled using the same scheme as described in Fig. 8 (right) and a depiction of stage-2 left and right rungs (right). The rightmost supertile is the right rung.

Stage-2 ladder supertiles are hard-coded to self-assemble via particular assembly sequences described in Fig. 10. As we will see, enforcing such assembly sequences will help ensure proper self-assembly of consecutive ladder stages. For now, we assume that the stage-2 ladder supertiles completely self-assemble prior to binding to supertiles to yield larger assemblies. Tile types are defined so that 10 different types of stage-2 ladder supertiles that self-assemble. Referring to the stage-2 ladder supertiles in Figs. 8 and 9, tiles can be hard-coded so that edges of tiles shown as dark gray squares expose indicating glues. The type of a stage-2 ladder supertile is uniquely determined by the locations and types of indicating glues on edges of the tiles that it contains. Moreover, for each base supertile, all of the indicating glues are distinct. We note that a stage-2 ladder supertile’s type also determines its location as a subassembly of a stage-3 ladder supertile.

Fig. 10.

To self-assemble each stage-2 ladder supertile, glues for each of the tiles in the supertile are hard-coded. In particular, the abutting edges of tiles at locations corresponding to each square of the left and middle supertiles shown here contain matching strength-2 glues and each such glue is unique for each base supertile. Tiles shown as blue squares of a stage-2 ladder supertile have strength-2 glues on their west edges and strength-1 glues on their east edge. This ensures that the “left half” (left) and “right half” (middle) (or portions of each) sufficiently self-assemble before each half binds (Color figure online).

Except for tiles containing indicating glues, the non-abutting north (respectively south, east, and west) edges of northernmost (respectively southernmost, easternmost and westernmost) tiles of complete stage-2 ladders contain strength-1 glues, all with the same glue type which we label n (s, e, and w respectively). We call such glues generic glues. Generic glues are not shown in figures. The purpose of these glues is to facilitate the binding of grout supertiles as such supertiles bind to yield grouted stage-2 ladder supertiles. For each of the 10 types of stage-2 ladder supertiles, tiles at locations depicted by gray squares in Fig. 8 contain indicating glues (the purpose of which we describe in more detail next). Finally, in addition to stage-2 ladder supertiles, tiles are hard-coded so that left and right rungs self-assemble. These supertiles also contain indicating glues at tiles with locations shown as gray squares in Fig. 9 (two leftmost figures). We next describe grout supertiles.

Grout Supertiles. There are 10 different types of grout supertiles corresponding to the 10 different types of stage-2 ladder supertiles. Intuitively, grout binds to ladder supertiles to yield grouted ladder supertiles. For $n\ge 3$, appropriate grouted ladder supertiles with stage less than n bind to yield a stage-n ladder supertile. The resulting stage-n ladder supertile will contain tiles with edges that contain glues identical to the indicating glues of one of the 10 types of stage-2 ladder supertiles. Therefore, the indicating glues of edges of tiles of a stage-n ladder supertile determine the type for the stage-n ladder supertile. The type of stage-n ladder supertile that results is determined by the type of grout that binds to the ladder supertiles with stage less than n that bind to yield the stage-n ladder supertile. Figure 6 shows 6 different types of stage-2 ladder supertiles bound to grout supertiles (shown in red, green, and yellow). The 4 types of stage-2 ladder supertiles not shown in Fig. 6 only bind during the self-assembly of a stage-n ladder supertile for $n \ge 4$. Figure 6 also shows stage-2 left and right rungs that are bound to grout as well as grout supertiles which consist only of red tiles. Tiles belonging to supertiles depicted in Fig. 6 as yellow tiles expose binding glues which allow for the binding of these supertiles. The locations of these yellow tiles are determined by the indicating glues of the stage-2 ladder supertiles. We next describe the grout supertiles that bind and how they bind to 3 types of stage-2 ladder supertiles. The grout supertiles that bind and how they bind to the other types of stage-2 ladder supertiles is similar.

Fig. 11.

A schematic depiction of 5 supertiles. From left to right, the first supertile is a grouted stage-2 ladder supertile with type r[ef]a, the next supertile is a grouted stage-2 ladder supertile with type r[ef]b, the next supertile is a grouted stage-2 ladder supertile with type r[ef]c, the next supertile is a grouted stage-2 with type r[ef]d, and the last supertile is a a grouted right rung supertile. Glue labels shown here are for reference purposes only and do not correspond to the label in the definition of the tile set for $\mathcal {T}_\mathbf{{U}}$. Note that many of the glues of these supertiles are not depicted and the bound strength-1 glues shown here are intended to indicate how the grout supertiles cooperatively bind

Like stage-2 ladder and rung supertiles, grout supertiles are hard-coded to self-assemble and there are 10 different types of grout supertiles which self-assemble. We describe the grout supertiles which bind to the stage-2 ladder supertiles with types r[ef]a, r[ef]b, r[ef]c, and r[ef]d. Let L be a stage-2 ladder supertile with type r[ef]b. We denote as $L'$ the supertile that is the result of grout binding to L until no more grout supertiles can bind. We refer to the labels for the glues shown in the second figure from the left in Fig. 11. First, we note that the grout supertiles shown with green tiles initially binds. The abutting edges of this supertile with no glues shown in the figure have strength-2 glues that hard-code the self-assembly of this supertile. This is also the case with the other grout supertiles shown in Fig. 11. Note that grout supertiles are defined to cooperatively bind to L to partially surround this supertile. We now describe the glues labeled a through h. The glue labeled a is a strength-1 glue that encodes the type of grout that binds to L. The glue labeled h is a non-generic “helper” glue. Together a and h cooperate to permit the binding of $L'$ to a grouted stage-2 supertile with type r[ef]a, B say, iff the grout types of $L'$ and B are the same. The glues b and c belong to a grout supertile that only ever binds stage-2 ladder supertiles; this can be enforced by the definition of the tile types which self-assemble grout supertiles. b and c do not encode the grout type as this is not necessary for the construction, but they do allow for a grouted right rung supertile (such as the one depicted in the rightmost figure of Fig. 11) to bind. As shown in Fig. 7, this is important for allowing stage-3 ladder supertile to self-assemble from $L'$.

Fig. 12.

A schematic depiction of a grouted stage-2 ladder supertiles bound to a grouted right rung supertiles.

Then, just as glues a and h allow for a grouted stage-2 supertile to bind to glues of north edges of tiles of $L'$, e and f permit a grouted stage-2 supertile to bind to glues of south edges of tiles of $L'$. The glue labeled g will either be an indicating glue or a generic glue (an e glue in particular) depending on the type of grout that binds to L. If the grout type corresponds to type r[ef]c or r[ef]d, then g will be an indicating glue corresponding to the indicating glue of a tile of a stage-2 ladder supertile of type r[ef]c or r[ef]d respectively. The d glue allows for grout supertiles to continue to bind after a grouted right rung supertiles binds. This scenario is depicted in Fig. 12. Finally, the glue labeled i in Fig. 12 encodes the grout type.

Now let M be a stage-2 ladder supertile with type r[ef]a. We refer to the glue labels for the glues shown in the leftmost figure in Fig. 11. Most of these glues serve similar purposes to the glues of L and there are two main differences. First, a will either be a generic glue, n, or a glue which serves the same purpose as the glue h in L. In the latter case, we call a a “helper glue”. If the type of grout that binds to M is type r[ef]b or r[ef]c, then a will be a helper glue. This helper glue will facilitate the self-assembly of a stage-4 ladder supertile. If the type of grout that binds to M is any other type of grout, then, a is a generic glue. Finally, if the type of grout that binds to M is r[ab]a, r[ab]b, r[ab]c, or r[ab]d, then the glue labeled g is an indicating glue that is identical to the corresponding indicating glue of an edge of a tile in a stage-2 ladder supertile with type r[ab]a, r[ab]b, r[ab]c, or r[ab]d. Otherwise, g will be a generic e glue.

Next let N be a stage-2 ladder supertile with type r[ef]c. We refer to the glue labels for the glues shown in the third figure from the left in Fig. 11. Once again, most of these glues serve similar purposes to the glues of L or M. The main difference is that the d glue is a generic s glue and thus grout does not bind to the south edges of the southernmost tiles of N. This is crucial for allowing grout to bind along these south edges in the assembly of higher ladder stages. At this point, we also note that there are two versions of stage-2 ladder supertile with type r[ef]c. The first version has two indicating glues, one on the east edge of each of the blue tiles in Fig. 11, and the second version has generic e glues instead of these indicating glues. Moreover, there are two versions of grout supertiles with type r[ef]c. Grout with type r[ab]a, r[ab]b, r[ab]c (both versions), or r[ab]d can only bind to a stage-2 ladder with type r[ef]c iff the type is of the first version. The purpose of the indicating glues on edges of these blue tiles will are utilized in the self-assembly of ladder supertiles of stage $\ge 4$.

Finally let P be a stage-2 ladder supertile with type r[ef]d. We refer to the glue labels for the glues shown in the fourth figure from the left in Fig. 11. Once again, most of these glues serve similar purposes to the glues of N. However, in this this case, there is one major difference. Namely, grout supertiles not only bind to the west edges of tiles of P, but they also bind to east edges as well. The green supertile with tiles containing edges with glues g and h initiate such growth. The glue labeled h (resp. e) is a generic n (resp. s) glue. The glues labeled g and f are binding glues. Glues g and h do not encode a grout type and are identical to the binding glues of a right rung supertile. This allows a grouted P to serve the purpose of a grouted right rung supertile in the self-assembly of a stage-4 ladder.

Fig. 13.

A schematic depiction of a grouted stage-3 supertile. Note the similarity between the pattern of glues labeled here and the glues of the second figure from the left in Fig. 11. Many of the glues not depicted here are strength-2 glues which are hard-coded to allow either grout supertiles to self-assemble, stage-2 ladder supertiles to self-assemble, or rung supertiles to self-assemble. Glues depicted as strength-1 glues are intended to indicate how grout supertiles cooperatively bind. Glue labels shown here are for reference purposes only and are not the labels in the definition of the tile set for $\mathcal {T}_\mathbf{{U}}$.

Note that tile types which self-assemble grout supertiles that bind to stage-2 ladder and rung supertiles can be defined so that (1) tiles at locations corresponding to yellow squares in Fig. 6 contain edges with binding glues that permit the self-assembly a stage-3 ladder supertile, and (2) binding glues depend (though not necessarily all of the glues will) on the type of grout which binds. Binding glues enable appropriate grouted stage-2 ladder and/or rung supertiles to bind to yield a stage-3 ladder supertile. We also note that tile types which self-assemble grout supertiles can be defined so that (1) the grouted stage-2 ladder and/or rung supertiles which bind to yield a stage-3 ladder supertile all contain the same type of grout supertiles, (2) tiles at locations corresponding to green squares in Fig. 6 contain edges with indicating glues, and (3) the indicating glues of an edge of a tile in a stage-3 ladder supertile are identical to the indicating glues of exactly one type of stage-2 ladder supertile; which type depends on the type of grout supertiles contained in the stage-3 ladder supertile.

Finite Self-assembly of Stage-n Ladder Supertiles for n $\mathbf{{\ge }}$ 2. In Sect. 5.1 we saw that tile types can be defined to self-assemble base supertiles and grout supertiles such that there is an assembly sequences where these supertiles bind to yield stage-3 ladder supertiles. Moreover, the stage-3 ladder supertiles which self-assemble contain tiles with edges that contain indicating glues that are identical to the indicating glues to one of the stage-2 ladder supertile types, giving 10 types of stage-3 ladder supertiles.

For $n\ge 3$, we note that copies of the same grout supertiles which bind to stage-2 ladder and rung supertiles can bind to stage-$(n-1)$ ladder supertiles, yielding grouted stage-$(n-1)$ supertiles such that appropriate grouted stage-$(n-1)$ supertiles can bind to yield a stage-n ladder supertile. Moreover, the stage-n ladder supertiles which self-assemble contain tiles with edges that contain indicating glues that are identical to the indicating glues to one of the stage-$(n-1)$ ladder supertile types, and thus identical to indicating glues of one of the stage-2 ladder supertiles. See Fig. 13 for a depictions of how grout supertiles bind to a stage-3 ladder supertile with type r[ef]b.

5.2 Final Remarks

Theorems 1 and 2 show that the H-fractal and the U-fractal cannot be finitely self-assembled by any aTAM system. Therefore, Theorem 3 shows the power that hierarchical self-assembly has over single tile attachment by showing that there is 2HAM system which finitely self-assembles the U-fractal. We conjecture that one can also give a 2HAM system that finitely self-assembles the H-fractal.

Conjecture 1

Let $\mathbf {H}$ be the H-fractal DSSF. There exists a 2HAM TAS $\mathcal {T}_\mathbf{{H}} = (T_\mathbf{{H}}, 2)$ that finitely self-assembles $\mathbf {H}$.

We’ve described the self-assembly of stage-n ladder supertiles via particular assembly sequences of $\mathcal {T}_\mathbf{{U}}$, ignoring many others and many producible supertiles. [9] describes how our construction ensures finite self-assembly of $\mathbf {U}$ despite these many possible assembly sequence and producible supertiles. Finally, our system self-assembles higher and higher stages of the ladder supertiles. Note that $\mathbf {U}$, by definition, only contains points in the first quadrant of the plane. Moreover, the westernmost points (resp. southernmost points) are a vertical (resp. horizontal) line of points. We call these points the “boundary” of $\mathbf {U}$. Only self-assembling higher and higher stages of ladder supertiles would give a system that finitely self-assembles $\mathbf {U}$ without points on the boundary. In [9] we give a simple tweak that ensures there is an assembly sequence from any producible assembly sequence to a terminal assembly with domain equal to $\mathbf {U}$ (including boundary points).